物理学简明教程马文蔚第1至8章课后习题答案详解 115页

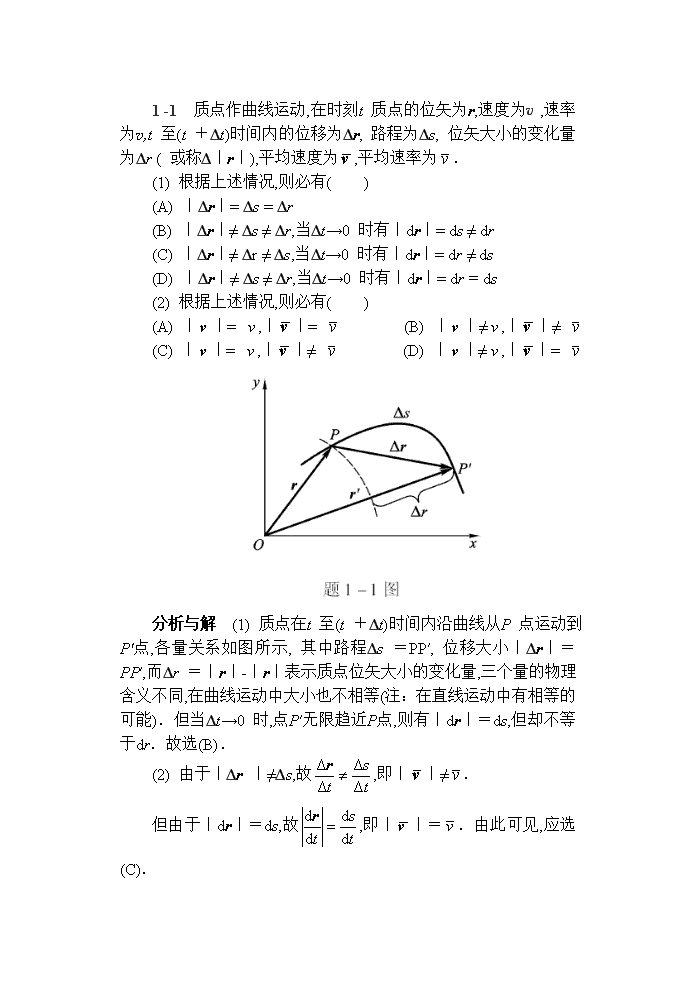
'1-1　质点作曲线运动,在时刻t质点的位矢为r,速度为v,速率为v,t至(t＋Δt)时间内的位移为Δr,路程为Δs,位矢大小的变化量为Δr(或称Δ｜r｜),平均速度为,平均速率为．(1)根据上述情况,则必有(　　)(A)｜Δr｜=Δs=Δr(B)｜Δr｜≠Δs≠Δr,当Δt→0时有｜dr｜=ds≠dr(C)｜Δr｜≠Δr≠Δs,当Δt→0时有｜dr｜=dr≠ds(D)｜Δr｜≠Δs≠Δr,当Δt→0时有｜dr｜=dr=ds(2)根据上述情况,则必有(　　)(A)｜｜=,｜｜=　　　(B)｜｜≠,｜｜≠(C)｜｜=,｜｜≠(D)｜｜≠,｜｜=分析与解　(1)质点在t至(t＋Δt)时间内沿曲线从P点运动到P′点,各量关系如图所示,其中路程Δs＝PP′,位移大小｜Δr｜＝PP′,而Δr＝｜r｜-｜r｜表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注：在直线运动中有相等的可能)．但当Δt→0时,点P′无限趋近P点,则有｜dr｜＝ds,但却不等于dr．故选(B)．(2)由于｜Δr｜≠Δs,故,即｜｜≠．但由于｜dr｜＝ds,故,即｜｜＝．由此可见,应选(C)． 1-2　一运动质点在某瞬时位于位矢r(x,y)的端点处,对其速度的大小有四种意见,即(1)；　(2)；　(3)；　(4)．下述判断正确的是(　　)(A)只有(1)(2)正确　　　　(B)只有(2)正确(C)只有(2)(3)正确(D)只有(3)(4)正确分析与解　表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率．通常用符号vr表示,这是速度矢量在位矢方向上的一个分量；表示速度矢量；在自然坐标系中速度大小可用公式计算,在直角坐标系中则可由公式求解．故选(D)．1-3　一个质点在做圆周运动时,则有(　　)(A)切向加速度一定改变,法向加速度也改变(B)切向加速度可能不变,法向加速度一定改变(C)切向加速度可能不变,法向加速度不变(D)切向加速度一定改变,法向加速度不变分析与解　加速度的切向分量aｔ起改变速度大小的作用,而法向分量an起改变速度方向的作用．质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的．至于aｔ是否改变,则要视质点的速率情况而定．质点作匀速率圆周运动时,aｔ恒为零；质点作匀变速率圆周运动时,aｔ为一不为零的恒量,当aｔ改变时,质点则作一般的变速率圆周运动．由此可见,应选(B)．1-4　质点的运动方程为和，式中x,y的单位为m,t的单位为ｓ。试求：(1)初速度的大小和方向；(2)加速度的大小和方向． 分析　由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成算出速度和加速度的大小和方向．解　(1)速度的分量式为当t＝0时,vox＝-10m·ｓ-1,voy＝15m·ｓ-1,则初速度大小为设vo与x轴的夹角为α,则α＝123°41′(2)加速度的分量式为,则加速度的大小为设a与x轴的夹角为β,则β＝-33°41′(或326°19′)1-5　质点沿直线运动,加速度a＝4-t2,式中a的单位为m·ｓ-2,t的单位为ｓ．如果当t＝3ｓ时,x＝9m,v＝2m·ｓ-1,求质点的运动方程．分析　本题属于运动学第二类问题,即已知加速度求速度和运动方程,必须在给定条件下用积分方法解决．由和可得和．如a＝a(t)或v＝v(t ),则可两边直接积分．如果a或v不是时间t的显函数,则应经过诸如分离变量或变量代换等数学操作后再做积分．解　由分析知,应有得(1)由得(2)将t＝3ｓ时,x＝9m,v＝2m·ｓ-1代入(1)(2)得v0＝-1m·ｓ-1,x0＝0.75m．于是可得质点运动方程为1-6　飞机以100m·ｓ-1的速度沿水平直线飞行,在离地面高为100m时,驾驶员要把物品空投到前方某一地面目标处,问：(1)此时目标在飞机正下方位置的前面多远？分析　物品空投后作平抛运动．忽略空气阻力的条件下,由运动独立性原理知,物品在空中沿水平方向作匀速直线运动,在竖直方向作自由落体运动．到达地面目标时,两方向上运动时间是相同的．因此,分别列出其运动方程,运用时间相等的条件,即可求解． 此外,平抛物体在运动过程中只存在竖直向下的重力加速度．为求特定时刻t时物体的切向加速度和法向加速度,只需求出该时刻它们与重力加速度之间的夹角α或β．由图可知,在特定时刻t,物体的切向加速度和水平线之间的夹角α,可由此时刻的两速度分量vx、vy求出,这样,也就可将重力加速度g的切向和法向分量求得．解　(1)取如图所示的坐标,物品下落时在水平和竖直方向的运动方程分别为x＝vt,　y＝1/2gt2飞机水平飞行速度v＝100m·s-1,飞机离地面的高度y＝100m,由上述两式可得目标在飞机正下方前的距离1-7　一质点沿半径为R的圆周按规律运动,v0、b都是常量．(1)求t时刻质点的总加速度。分析　在自然坐标中,s表示圆周上从某一点开始的曲线坐标．由给定的运动方程s＝s(t),对时间t求一阶、二阶导数,即是沿曲线运动的速度v和加速度的切向分量aｔ,而加速度的法向分量为an＝v2/R．这样,总加速度为a＝aｔeｔ＋anen．至于质点在t时间内通过的路程,即为曲线坐标的改变量Δs＝st-s0．因圆周长为2πR,质点所转过的圈数自然可求得．解　(1)质点作圆周运动的速率为其加速度的切向分量和法向分量分别为,故加速度的大小为其方向与切线之间的夹角为 1-8　一升降机以加速度1.22m·ｓ-2上升,当上升速度为2.44m·ｓ-1时,有一螺丝自升降机的天花板上松脱,天花板与升降机的底面相距2.74m．计算：(1)螺丝从天花板落到底面所需要的时间；(2)螺丝相对升降机外固定柱子的下降距离．分析　在升降机与螺丝之间有相对运动的情况下,一种处理方法是取地面为参考系,分别讨论升降机竖直向上的匀加速度运动和初速不为零的螺丝的自由落体运动,列出这两种运动在同一坐标系中的运动方程y1＝y1(t)和y2＝y2(t),并考虑它们相遇,即位矢相同这一条件,问题即可解；另一种方法是取升降机(或螺丝)为参考系,这时,螺丝(或升降机)相对它作匀加速运动,但是,此加速度应该是相对加速度．升降机厢的高度就是螺丝(或升降机)运动的路程．解1　(1)以地面为参考系,取如图所示的坐标系,升降机与螺丝的运动方程分别为当螺丝落至底面时,有y1＝y2,即(2)螺丝相对升降机外固定柱子下降的距离为解2　(1)以升降机为参考系,此时,螺丝相对它的加速度大小a′＝g＋a,螺丝落至底面时,有(2)由于升降机在t时间内上升的高度为 则1-9　一无风的下雨天,一列火车以v1＝20.0m·ｓ-1的速度匀速前进,在车内的旅客看见玻璃窗外的雨滴和垂线成75°角下降．求雨滴下落的速度v2．(设下降的雨滴作匀速运动)分析　这是一个相对运动的问题．设雨滴为研究对象,地面为静止参考系Ｓ,火车为动参考系Ｓ′．v1为Ｓ′相对Ｓ的速度,v2为雨滴相对Ｓ的速度,利用相对运动速度的关系即可解．解　以地面为参考系,火车相对地面运动的速度为v1,雨滴相对地面竖直下落的速度为v2,旅客看到雨滴下落的速度v2′为相对速度,它们之间的关系为(如图所示),于是可得1-10　如图(a)所示,一汽车在雨中沿直线行驶,其速率为v1,下落雨滴的速度方向偏于竖直方向之前θ角,速率为v2′,若车后有一长方形物体,问车速v1 为多大时,此物体正好不会被雨水淋湿？分析　这也是一个相对运动的问题．可视雨点为研究对象,地面为静参考系Ｓ,汽车为动参考系Ｓ′．如图(a)所示,要使物体不被淋湿,在车上观察雨点下落的方向(即雨点相对于汽车的运动速度v2′的方向)应满足．再由相对速度的矢量关系,即可求出所需车速v1．解　由［图(b)］,有而要使,则1-11　用水平力FN把一个物体压着靠在粗糙的竖直墙面上保持静止．当FN逐渐增大时,物体所受的静摩擦力Ff的大小(　　) (A)不为零,但保持不变(B)随FN成正比地增大(C)开始随FN增大,达到某一最大值后,就保持不变(D)无法确定分析与解　与滑动摩擦力不同的是,静摩擦力可在零与最大值μFN范围内取值．当FN增加时,静摩擦力可取的最大值成正比增加,但具体大小则取决于被作用物体的运动状态．由题意知,物体一直保持静止状态,故静摩擦力与重力大小相等,方向相反,并保持不变,故选(A)．1-12　一段路面水平的公路,转弯处轨道半径为R,汽车轮胎与路面间的摩擦因数为μ,要使汽车不至于发生侧向打滑,汽车在该处的行驶速率(　　)(A)不得小于　　　　(B)必须等于(C)不得大于(D)还应由汽车的质量m决定分析与解　由题意知,汽车应在水平面内作匀速率圆周运动,为保证汽车转弯时不侧向打滑,所需向心力只能由路面与轮胎间的静摩擦力提供,能够提供的最大向心力应为μFN．由此可算得汽车转弯的最大速率应为v＝μRg．因此只要汽车转弯时的实际速率不大于此值,均能保证不侧向打滑．应选(C)．1-13　一物体沿固定圆弧形光滑轨道由静止下滑,在下滑过程中,则(　　)(A)它的加速度方向永远指向圆心,其速率保持不变(B)它受到的轨道的作用力的大小不断增加(C)它受到的合外力大小变化,方向永远指向圆心(D)它受到的合外力大小不变,其速率不断增加 分析与解　由图可知,物体在下滑过程中受到大小和方向不变的重力以及时刻指向圆轨道中心的轨道支持力FN作用,其合外力方向并非指向圆心,其大小和方向均与物体所在位置有关．重力的切向分量(mgcosθ)使物体的速率将会不断增加(由机械能守恒亦可判断),则物体作圆周运动的向心力(又称法向力)将不断增大,由轨道法向方向上的动力学方程可判断,随θ角的不断增大过程,轨道支持力FN也将不断增大,由此可见应选(B)．1-14　图(a)示系统置于以a＝1/4g的加速度上升的升降机内,A、B两物体质量相同均为m,A所在的桌面是水平的,绳子和定滑轮质量均不计,若忽略滑轮轴上和桌面上的摩擦,并不计空气阻力,则绳中张力为(　　)(A)5/8mg　　(B)1/2mg　　(C)mg　　(D)2mg分析与解　本题可考虑对A、B两物体加上惯性力后,以电梯这个非惯性参考系进行求解．此时A、B两物体受力情况如图(b)所示,图中a′为A、B两物体相对电梯的加速度,ma′为惯性力．对A、B两物体应用牛顿第二定律,可解得FＴ＝5/8mg．故选(A)．讨论　对于习题1-14这种类型的物理问题,往往从非惯性参考系(本题为电梯)观察到的运动图像较为明确,但由于牛顿定律只适用于惯性参考系,故从非惯性参考系求解力学问题时,必须对物体加上一个虚拟的惯性力．如以地面为惯性参考系求解,则两物体的加速度aA和aB均应对地而言,本题中aA和aB的大小与方向均不相同．其中aA应斜向上．对aA、aB、a和a ′之间还要用到相对运动规律,求解过程较繁．有兴趣的读者不妨自己尝试一下．1-16　一质量为m的小球最初位于如图(a)所示的A点,然后沿半径为r的光滑圆轨道ADCB下滑．试求小球到达点C时的角速度和对圆轨道的作用力．分析　该题可由牛顿第二定律求解．在取自然坐标的情况下,沿圆弧方向的加速度就是切向加速度aｔ,与其相对应的外力Fｔ是重力的切向分量mgsinα,而与法向加速度an相对应的外力是支持力FN和重力的法向分量mgcosα．由此,可分别列出切向和法向的动力学方程Fｔ＝mdv/dt和Fn＝man．由于小球在滑动过程中加速度不是恒定的,因此,需应用积分求解,为使运算简便,可转换积分变量．倡该题也能应用以小球、圆弧与地球为系统的机械能守恒定律求解小球的速度和角速度,方法比较简便．但它不能直接给出小球与圆弧表面之间的作用力．解　小球在运动过程中受到重力P和圆轨道对它的支持力FN．取图(b)所示的自然坐标系,由牛顿定律得(1) (2)由,得,代入式(1),并根据小球从点A运动到点C的始末条件,进行积分,有得则小球在点C的角速度为由式(2)得　　由此可得小球对圆轨道的作用力为负号表示F′N与en反向．1-17　光滑的水平桌面上放置一半径为R的固定圆环,物体紧贴环的内侧作圆周运动,其摩擦因数为μ,开始时物体的速率为v0,求：(1)t时刻物体的速率；(2)当物体速率从v0减少到1/2v0时,物体所经历的时间及经过的路程．分析　运动学与动力学之间的联系是以加速度为桥梁的,因而,可先分析动力学问题．物体在作圆周运动的过程中,促使其运动状态发生变化的是圆环内侧对物体的支持力FN和环与物体之间的摩擦力Fｆ,而摩擦力大小与正压力FN′成正比,且FN与FN′ 又是作用力与反作用力,这样,就可通过它们把切向和法向两个加速度联系起来了,从而可用运动学的积分关系式求解速率和路程．　　　　　　　　解　(1)设物体质量为m,取图中所示的自然坐标,按牛顿定律,有由分析中可知,摩擦力的大小Fｆ＝μFN,由上述各式可得取初始条件t＝0时v＝v0,并对上式进行积分,有(2)当物体的速率从v0减少到1/2v0时,由上式可得所需的时间为物体在这段时间内所经过的路程2-1　对质点组有以下几种说法：(1)质点组总动量的改变与内力无关；(2)质点组总动能的改变与内力无关；(3)质点组机械能的改变与保守内力无关．下列对上述说法判断正确的是(　　)(A)只有(1)是正确的　　　　(B)(1)、(2)是正确的 (C)(1)、(3)是正确的(D)(2)、(3)是正确的分析与解　在质点组中内力总是成对出现的,它们是作用力与反作用力．由于一对内力的冲量恒为零,故内力不会改变质点组的总动量．但由于相互有作用力的两个质点的位移大小以及位移与力的夹角一般不同,故一对内力所作功之和不一定为零,应作具体分析,如一对弹性内力的功的代数和一般为零,一对摩擦内力的功代数和一般不为零,对于保守内力来说,所作功能使质点组动能与势能相互转换,因此保守内力即使有可能改变质点组的动能,但也不可能改变质点组的机械能．综上所述(1)(3)说法是正确的．故选(C)．2-2　有两个倾角不同、高度相同、质量一样的斜面放在光滑的水平面上,斜面是光滑的,有两个一样的物块分别从这两个斜面的顶点由静止开始滑下,则(　　)(A)物块到达斜面底端时的动量相等(B)物块到达斜面底端时动能相等(C)物块和斜面(以及地球)组成的系统,机械能不守恒(D)物块和斜面组成的系统水平方向上动量守恒分析与解　对题述系统来说,由题意知并无外力和非保守内力作功,故系统机械能守恒．物体在下滑过程中,一方面通过重力作功将势能转化为动能,另一方面通过物体与斜面之间的弹性内力作功将一部分能量转化为斜面的动能,其大小取决其中一个内力所作功．由于斜面倾角不同,故物体沿不同倾角斜面滑至底端时动能大小不等．动量自然也就不等(动量方向也不同)．故(A)(B)(C)三种说法均不正确．至于说法(D)正确,是因为该系统动量虽不守恒(下滑前系统动量为零,下滑后物体与斜面动量的矢量和不可能为零．由此可知,此时向上的地面支持力并不等于物体与斜面向下的重力),但在水平方向上并无外力,故系统在水平方向上分动量守恒．2-3　如图所示,质量分别为m1和m2的物体A和B,置于光滑桌面上,A和B之间连有一轻弹簧．另有质量为m1和m2的物体C和D分别置于物体A与B之上,且物体A和C、B和D之间的摩擦因数均不为零．首先用外力沿水平方向相向推压A和B,使弹簧被压缩,然后撤掉外力,则在A和B弹开的过程中,对A、B、C、D以及弹簧组成的系统,有(　　)(A)动量守恒,机械能守恒　　　　(B)动量不守恒,机械能守恒(C)动量不守恒,机械能不守恒(D)动量守恒,机械能不一定守恒 分析与解　由题意知,作用在题述系统上的合外力为零,故系统动量守恒,但机械能未必守恒,这取决于在A、B弹开过程中C与A或D与B之间有无相对滑动,如有则必然会因摩擦内力作功,而使一部分机械能转化为热能,故选(D)．2-4　如图所示,子弹射入放在水平光滑地面上静止的木块后而穿出．以地面为参考系,下列说法中正确的说法是(　　)(A)子弹减少的动能转变为木块的动能(B)子弹-木块系统的机械能守恒(C)子弹动能的减少等于子弹克服木块阻力所作的功(D)子弹克服木块阻力所作的功等于这一过程中产生的热分析与解　子弹-木块系统在子弹射入过程中,作用于系统的合外力为零,故系统动量守恒,但机械能并不守恒．这是因为子弹与木块作用的一对内力所作功的代数和不为零(这是因为子弹对地位移大于木块对地位移所致),子弹动能的减少等于子弹克服阻力所作功,子弹减少的动能中,一部分通过其反作用力对木块作正功而转移为木块的动能,另一部分则转化为热能(大小就等于这一对内力所作功的代数和)．综上所述,只有说法(C)的表述是完全正确的．2-5　质量为m的物体,由水平面上点O以初速为v0抛出,v0与水平面成仰角α．若不计空气阻力,求：(1)物体从发射点O到最高点的过程中,重力的冲量；(2)物体从发射点到落回至同一水平面的过程中,重力的冲量． 分析　重力是恒力,因此,求其在一段时间内的冲量时,只需求出时间间隔即可．由抛体运动规律可知,物体到达最高点的时间,物体从出发到落回至同一水平面所需的时间是到达最高点时间的两倍．这样,按冲量的定义即可求得结果．另一种解的方法是根据过程的始、末动量,由动量定理求出．解1　物体从出发到达最高点所需的时间为则物体落回地面的时间为于是,在相应的过程中重力的冲量分别为解2　根据动量定理,物体由发射点O运动到点A、B的过程中,重力的冲量分别为2-6　高空作业时系安全带是非常必要的．假如一质量为51.0kg 的人,在操作时不慎从高空竖直跌落下来,由于安全带的保护,最终使他被悬挂起来．已知此时人离原处的距离为2.0m,安全带弹性缓冲作用时间为0.50s．求安全带对人的平均冲力．分析　从人受力的情况来看,可分两个阶段：在开始下落的过程中,只受重力作用,人体可看成是作自由落体运动；在安全带保护的缓冲过程中,则人体同时受重力和安全带冲力的作用,其合力是一变力,且作用时间很短．为求安全带的冲力,可以从缓冲时间内,人体运动状态(动量)的改变来分析,即运用动量定理来讨论．事实上,动量定理也可应用于整个过程．但是,这时必须分清重力和安全带冲力作用的时间是不同的；而在过程的初态和末态,人体的速度均为零．这样,运用动量定理仍可得到相同的结果．解1　以人为研究对象,按分析中的两个阶段进行讨论．在自由落体运动过程中,人跌落至2m处时的速度为(1)在缓冲过程中,人受重力和安全带冲力的作用,根据动量定理,有(2)由式(1)、(2)可得安全带对人的平均冲力大小为解2　从整个过程来讨论．根据动量定理有2-7　如图所示,在水平地面上,有一横截面S＝0.20m2的直角弯管,管中有流速为v＝3.0m·ｓ-1的水通过,求弯管所受力的大小和方向． 分析　对于弯曲部分AB段内的水而言,由于流速一定,在时间Δt内,从其一端流入的水量等于从另一端流出的水量．因此,对这部分水来说,在时间Δt内动量的增量也就是流入与流出水的动量的增量Δp＝Δm(vB-vA)；此动量的变化是管壁在Δt时间内对其作用冲量I的结果．依据动量定理可求得该段水受到管壁的冲力F；由牛顿第三定律,自然就得到水流对管壁的作用力F′＝-F．解　在Δt时间内,从管一端流入(或流出)水的质量为Δm＝ρυSΔt,弯曲部分AB的水的动量的增量则为Δp＝Δm(vB-vA)＝ρυSΔt(vB-vA)依据动量定理I＝Δp,得到管壁对这部分水的平均冲力从而可得水流对管壁作用力的大小为作用力的方向则沿直角平分线指向弯管外侧．2-8　质量为m′的人手里拿着一个质量为m的物体,此人用与水平面成α角的速率v0向前跳去．当他达到最高点时,他将物体以相对于人为u的水平速率向后抛出．问：由于人抛出物体,他跳跃的距离增加了多少？(假设人可视为质点)分析　人跳跃距离的增加是由于他在最高点处向后抛出物体所致．在抛物的过程中,人与物之间相互作用力的冲量,使他们各自的动量发生了变化．如果把人与物视为一系统,因水平方向不受外力作用,故外力的冲量为零,系统在该方向上动量守恒．但在应用动量守恒定律时,必须注意系统是相对地面(惯性系)而言的,因此,在处理人与物的速度时,要根据相对运动的关系来确定．至于,人因跳跃而增加的距离,可根据人在水平方向速率的增量Δv 来计算．解　取如图所示坐标．把人与物视为一系统,当人跳跃到最高点处,在向左抛物的过程中,满足动量守恒,故有式中v为人抛物后相对地面的水平速率,v-u为抛出物对地面的水平速率．得人的水平速率的增量为而人从最高点到地面的运动时间为所以,人跳跃后增加的距离2-9　一质量为0.20kg的球,系在长为2.00m的细绳上,细绳的另一端系在天花板上．把小球移至使细绳与竖直方向成30°角的位置,然后从静止放开．求：(1)在绳索从30°角到0°角的过程中,重力和张力所作的功；(2)物体在最低位置时的动能和速率；(3)在最低位置时的张力．分析　(1) 在计算功时,首先应明确是什么力作功．小球摆动过程中同时受到重力和张力作用．重力是保守力,根据小球下落的距离,它的功很易求得；至于张力虽是一变力,但是,它的方向始终与小球运动方向垂直,根据功的矢量式,即能得出结果来．(2)在计算功的基础上,由动能定理直接能求出动能和速率．(3)在求最低点的张力时,可根据小球作圆周运动时的向心加速度由重力和张力提供来确定．解　(1)如图所示,重力对小球所作的功只与始末位置有关,即在小球摆动过程中,张力FＴ的方向总是与运动方向垂直,所以,张力的功(2)根据动能定理,小球摆动过程中,其动能的增量是由于重力对它作功的结果．初始时动能为零,因而,在最低位置时的动能为小球在最低位置的速率为(3)当小球在最低位置时,由牛顿定律可得2-10　一质量为m的质点,系在细绳的一端,绳的另一端固定在平面上．此质点在粗糙水平面上作半径为r的圆周运动．设质点的最初速率是v0．当它运动一周时,其速率为v0/2．求：(1)摩擦力作的功；(2)动摩擦因数；(3)在静止以前质点运动了多少圈？分析　质点在运动过程中速度的减缓,意味着其动能减少；而减少的这部分动能则消耗在运动中克服摩擦力作功上．由此,可依据动能定理列式解之．解　(1)摩擦力作功为 (1)(2)由于摩擦力是一恒力,且Fｆ＝μmg,故有(2)由式(1)、(2)可得动摩擦因数为(3)由于一周中损失的动能为,则在静止前可运行的圈数为圈2-11　如图(a)所示,A和B两块板用一轻弹簧连接起来,它们的质量分别为m1和m2．问在A板上需加多大的压力,方可在力停止作用后,恰能使A在跳起来时B稍被提起．(设弹簧的劲度系数为k)分析　运用守恒定律求解是解决力学问题最简捷的途径之一．因为它与过程的细节无关,也常常与特定力的细节无关．“守恒”则意味着在条件满足的前提下,过程中任何时刻守恒量不变．在具体应用时,必须恰当地选取研究对象(系统),注意守恒定律成立的条件．该题可用机械能守恒定律来解决．选取两块板、弹簧和地球为系统,该系统在外界所施压力撤除后(取作状态1),直到B板刚被提起(取作状态2),在这一过程中,系统不受外力作用,而内力中又只有保守力(重力和弹力)作功,支持力不作功,因此,满足机械能守恒的条件．只需取状态1和状态2,运用机械能守恒定律列出方程,并结合这两状态下受力的平衡,便可将所需压力求出． 解　选取如图(b)所示坐标,取原点O处为重力势能和弹性势能零点．作各状态下物体的受力图．对A板而言,当施以外力F时,根据受力平衡有F1＝P1＋F(1)当外力撤除后,按分析中所选的系统,由机械能守恒定律可得式中y1、y2为M、N两点对原点O的位移．因为F1＝ky1,F2＝ky2及P1＝m1g,上式可写为F1-F2＝2P1(2)由式(1)、(2)可得F＝P1＋F2(3)当A板跳到N点时,B板刚被提起,此时弹性力F′2＝P2,且F2＝F′2．由式(3)可得F＝P1＋P2＝(m1＋m2)g应注意,势能的零点位置是可以任意选取的．为计算方便起见,通常取弹簧原长时的弹性势能为零点,也同时为重力势能的零点．2-12　如图所示，一质量为m的木块静止在光滑水平面上，一质量为m/2的子弹沿水平方向以速率射入木块一段距离L(此时木块滑行距离恰为s)后留在木块内，求：（1）木块与子弹的共同速度v,此过程中木块和子弹的动能各变化了多少？（2）子弹与木块间的摩擦阻力对木块和子弹各作了多少功？（3）证明这一对摩擦阻力的所作功的代数和就等于其中一个摩擦阻力沿相对位移L所作的功.(4)证明这一对摩擦阻力所作功的代数和就等于子弹-木块系统总机械能的减少量(亦即转化为热的那部分能量).题3-20图分析 对子弹-木块系统来说，满足动量守恒，但系统动能并不守恒，这是因为一对摩擦内力所做功的代数和并不为零，其中摩擦阻力对木块作正功，其反作用力对子弹作负功，后者功的数值大于前者，通过这一对作用力与反作用力所做功，子弹将一部分动能转移给木块，而另一部分却转化为物体内能.本题（3）、（4）两问给出了具有普遍意义的结论，可帮助读者以后分析此类问题.解（1）子弹-木块系统满足动量守恒，有解得共同速度对木块对子弹（2）对木块和子弹分别运用质点动能定理，则对木块对子弹（3）设摩擦阻力大小为,在两者取得共同速度时，木块对地位移为s，则子弹对地位移为L+s,有对木块对子弹得式中L即为子弹对木块的相对位移，“-”号表示这一对摩擦阻力（非保守力）所作功必定会使系统机械能减少.(4)对木块 对子弹两式相加，得即两式相加后实为子弹-木块系统作为质点系的动能定理表达式，左边为一对内力所作功，右边为系统动能的变化量.2-13　一质量为m的地球卫星,沿半径为3RE的圆轨道运动,RE为地球的半径．已知地球的质量为mE．求：(1)卫星的动能；(2)卫星的引力势能；(3)卫星的机械能．分析　根据势能和动能的定义,只需知道卫星的所在位置和绕地球运动的速率,其势能和动能即可算出．由于卫星在地球引力作用下作圆周运动,由此可算得卫星绕地球运动的速率和动能．由于卫星的引力势能是属于系统(卫星和地球)的,要确定特定位置的势能时,必须规定势能的零点,通常取卫星与地球相距无限远时的势能为零．这样,卫星在特定位置的势能也就能确定了．至于卫星的机械能则是动能和势能的总和．解　(1)卫星与地球之间的万有引力提供卫星作圆周运动的向心力,由牛顿定律可得则(2)取卫星与地球相距无限远(r→∞)时的势能为零,则处在轨道上的卫星所具有的势能为(3)卫星的机械能为 2-14　如图(a)所示,天文观测台有一半径为R的半球形屋面,有一冰块从光滑屋面的最高点由静止沿屋面滑下,若摩擦力略去不计．求此冰块离开屋面的位置以及在该位置的速度．　　分析　取冰块、屋面和地球为系统,由于屋面对冰块的支持力FN始终与冰块运动的方向垂直,故支持力不作功；而重力P又是保守内力,所以,系统的机械能守恒．但是,仅有一个机械能守恒方程不能解出速度和位置两个物理量；因此,还需设法根据冰块在脱离屋面时支持力为零这一条件,由牛顿定律列出冰块沿径向的动力学方程．求解上述两方程即可得出结果．解　由系统的机械能守恒,有 (1)根据牛顿定律,冰块沿径向的动力学方程为(2)冰块脱离球面时,支持力FN＝0,由式(1)、(2)可得冰块的角位置冰块此时的速率为v的方向与重力P方向的夹角为α＝90°-θ＝41.8°2-15　如图所示,把质量m＝0.20kg的小球放在位置A时,弹簧被压缩Δl＝7.5×10-2m．然后在弹簧弹性力的作用下,小球从位置A由静止被释放,小球沿轨道ABCD运动．小球与轨道间的摩擦不计．已知是半径r＝0.15m的半圆弧,AB相距为2r．求弹簧劲度系数的最小值．分析 　若取小球、弹簧和地球为系统,小球在被释放后的运动过程中,只有重力和弹力这两个保守内力作功,轨道对球的支持力不作功,因此,在运动的过程中,系统的机械能守恒．运用守恒定律解题时,关键在于选好系统的初态和终态．为获取本题所求的结果,初态选在压缩弹簧刚被释放时刻,这样,可使弹簧的劲度系数与初态相联系；而终态则取在小球刚好能通过半圆弧时的最高点C处,因为这时小球的速率正处于一种临界状态,若大于、等于此速率时,小球定能沿轨道继续向前运动；小于此速率时,小球将脱离轨道抛出．该速率则可根据重力提供圆弧运动中所需的向心力,由牛顿定律求出．这样,再由系统的机械能守恒定律即可解出该弹簧劲度系数的最小值．解　小球要刚好通过最高点C时,轨道对小球支持力FN＝0,因此,有(1)取小球开始时所在位置A为重力势能的零点,由系统的机械能守恒定律,有(2)由式(1)、(2)可得2-16　如图所示,质量为m、速度为v的钢球,射向质量为m′的靶,靶中心有一小孔,内有劲度系数为k的弹簧,此靶最初处于静止状态,但可在水平面上作无摩擦滑动．求子弹射入靶内弹簧后,弹簧的最大压缩距离．分析　这也是一种碰撞问题．碰撞的全过程是指小球刚与弹簧接触直至弹簧被压缩到最大,小球与靶刚好到达共同速度为止,在这过程中,小球和靶组成的系统在水平方向不受外力作用,外力的冲量为零,因此,在此方向动量守恒．但是,仅靠动量守恒定律还不能求出结果来．又考虑到无外力对系统作功,系统无非保守内力作功,故系统的机械能也守恒．应用上述两个守恒定律,并考虑到球与靶具有相同速度时,弹簧被压缩量最大这一条件,即可求解．应用守恒定律求解,可免除碰撞中的许多细节问题．解　设弹簧的最大压缩量为x0．小球与靶共同运动的速度为v1 ．由动量守恒定律,有(1)又由机械能守恒定律,有(2)由式(1)、(2)可得2-17　质量为m的弹丸A,穿过如图所示的摆锤B后,速率由v减少到v/2．已知摆锤的质量为m′,摆线长度为l,如果摆锤能在垂直平面内完成一个完全的圆周运动,弹丸速度v的最小值应为多少？分析　该题可分两个过程分析．首先是弹丸穿越摆锤的过程．就弹丸与摆锤所组成的系统而言,由于穿越过程的时间很短,重力和的张力在水平方向的冲量远小于冲击力的冲量,因此,可认为系统在水平方向不受外力的冲量作用,系统在该方向上满足动量守恒．摆锤在碰撞中获得了一定的速度,因而具有一定的动能,为使摆锤能在垂直平面内作圆周运动,必须使摆锤在最高点处有确定的速率,该速率可由其本身的重力提供圆周运动所需的向心力来确定；与此同时,摆锤在作圆周运动过程中,摆锤与地球组成的系统满足机械能守恒定律,根据两守恒定律即可解出结果．解　由水平方向的动量守恒定律,有(1)为使摆锤恰好能在垂直平面内作圆周运动,在最高点时,摆线中的张力FＴ ＝0,则(2)式中v′h为摆锤在圆周最高点的运动速率．又摆锤在垂直平面内作圆周运动的过程中,满足机械能守恒定律,故有(3)解上述三个方程,可得弹丸所需速率的最小值为2-18　如图所示,一质量为m′的物块放置在斜面的最底端A处,斜面的倾角为α,高度为h,物块与斜面的动摩擦因数为μ,今有一质量为m的子弹以速度v0沿水平方向射入物块并留在其中,且使物块沿斜面向上滑动．求物块滑出顶端时的速度大小．分析　该题可分两个阶段来讨论,首先是子弹和物块的撞击过程,然后是物块(包含子弹)沿斜面向上的滑动过程．在撞击过程中,对物块和子弹组成的系统而言,由于撞击前后的总动量明显是不同的,因此,撞击过程中动量不守恒．应该注意,不是任何碰撞过程中动量都是守恒的．但是,若取沿斜面的方向,因撞击力(属于内力)远大于子弹的重力P1和物块的重力P2在斜面的方向上的分力以及物块所受的摩擦力Fｆ,在该方向上动量守恒,由此可得到物块被撞击后的速度．在物块沿斜面上滑的过程中,为解题方便,可重新选择系统(即取子弹、物块和地球为系统),此系统不受外力作用,而非保守内力中仅摩擦力作功,根据系统的功能原理,可解得最终的结果．解　在子弹与物块的撞击过程中,在沿斜面的方向上,根据动量守恒有 (1)在物块上滑的过程中,若令物块刚滑出斜面顶端时的速度为v2,并取A点的重力势能为零．由系统的功能原理可得(2)由式(1)、(2)可得2-19　如图所示,一个质量为m的小球,从内壁为半球形的容器边缘点A滑下．设容器质量为m′,半径为R,内壁光滑,并放置在摩擦可以忽略的水平桌面上．开始时小球和容器都处于静止状态．当小球沿内壁滑到容器底部的点B时,受到向上的支持力为多大？分析 　由于桌面无摩擦,容器可以在水平桌面上滑动,当小球沿容器内壁下滑时,容器在桌面上也要发生移动．将小球与容器视为系统,该系统在运动过程中沿水平桌面方向不受外力作用,系统在该方向上的动量守恒；若将小球、容器与地球视为系统,因系统无外力作用,而内力中重力是保守力,而支持力不作功,系统的机械能守恒．由两个守恒定律可解得小球和容器在惯性系中的速度．由于相对运动的存在,小球相对容器运动的轨迹是圆,而相对桌面运动的轨迹就不再是圆了,因此,在运用曲线运动中的法向动力学方程求解小球受力时,必须注意参考系的选择．若取容器为参考系(非惯性系),小球在此参考系中的轨迹仍是容器圆弧,其法向加速度可由此刻的速度(相对于容器速度)求得．在分析小球受力时,除重力和支持力外,还必须计及它所受的惯性力．小球位于容器的底部这一特殊位置时,容器的加速度为零,惯性力也为零．这样,由法向动力学方程求解小球所受的支持力就很容易了．若仍取地面为参考系(惯性系),虽然无需考虑惯性力,但是因小球的轨迹方程比较复杂,其曲率半径及法向加速度难以确定,使求解较为困难．解　根据水平方向动量守恒定律以及小球在下滑过程中机械能守恒定律可分别得(1)(2)式中vm、vm′分别表示小球、容器相对桌面的速度．由式(1)、(2)可得小球到达容器底部时小球、容器的速度大小分别为由于小球相对地面运动的轨迹比较复杂,为此,可改为以容器为参考系(非惯性系)．在容器底部时,小球相对容器的运动速度为(3)在容器底部,小球所受惯性力为零,其法向运动方程为(4)由式(3)、(4)可得小球此时所受到的支持力为3－1　有两个力作用在一个有固定转轴的刚体上：(1)这两个力都平行于轴作用时，它们对轴的合力矩一定是零；(2)这两个力都垂直于轴作用时，它们对轴的合力矩可能是零；(3)当这两个力的合力为零时，它们对轴的合力矩也一定是零； (4)当这两个力对轴的合力矩为零时，它们的合力也一定是零．对上述说法下述判断正确的是(　　)(A)只有(1)是正确的　　　　　　　(B)(1)、(2)正确，(3)、(4)错误(C)(1)、(2)、(3)都正确，(4)错误(D)(1)、(2)、(3)、(4)都正确分析与解　力对轴之力矩通常有三种情况：其中两种情况下力矩为零：一是力的作用线通过转轴，二是力平行于转轴(例如门的重力并不能使门转)．不满足上述情况下的作用力(含题述作用力垂直于转轴的情况)对轴之矩不为零，但同时有两个力作用时，只要满足两力矩大小相等，方向相反，两力矩对同一轴的合外力矩也可以为零，由以上规则可知(1)(2)说法是正确．对于(3)(4)两种说法，如作用于刚体上的两个力为共点力，当合力为零时，它们对同一轴的合外力矩也一定为零，反之亦然．但如这两个力为非共点力，则以上结论不成立，故(3)(4)说法不完全正确．综上所述，应选(B)．3－2　关于力矩有以下几种说法：(1)对某个定轴转动刚体而言，内力矩不会改变刚体的角加速度；(2)一对作用力和反作用力对同一轴的力矩之和必为零；(3)质量相等，形状和大小不同的两个刚体，在相同力矩的作用下，它们的运动状态一定相同．对上述说法下述判断正确的是(　　)(A)只有(2)是正确的(B)(1)、(2)是正确的(C)(2)、(3)是正确的(D)(1)、(2)、(3)都是正确的分析与解　刚体中相邻质元之间的一对内力属于作用力与反作用力，且作用点相同，故对同一轴的力矩之和必为零，因此可推知刚体中所有内力矩之和为零，因而不会影响刚体的角加速度或角动量等，故(1)(2)说法正确．对说法(3)来说，题述情况中两个刚体对同一轴的转动惯量因形状、大小不同有可能不同，因而在相同力矩作用下，产生的角加速度不一定相同，因而运动状态未必相同，由此可见应选(B)．3－3　均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动，如图所示，今使棒从水平位置由静止开始自由下落，在棒摆到竖直位置的过程中，下述说法正确的是(　　)(A)角速度从小到大，角加速度不变(B)角速度从小到大，角加速度从小到大(C)角速度从小到大，角加速度从大到小 (D)角速度不变，角加速度为零分析与解　如图所示，在棒下落过程中，重力对轴之矩是变化的，其大小与棒和水平面的夹角有关．当棒处于水平位置，重力矩最大，当棒处于竖直位置时，重力矩为零．因此在棒在下落过程中重力矩由大到小，由转动定律知，棒的角加速亦由大到小，而棒的角速度却由小到大(由机械能守恒亦可判断角速度变化情况)，应选(C)．3－4　一汽车发动机曲轴的转速在12s内由1.2×103r·min-1均匀的增加到2.7×103r·min-1．(1)求曲轴转动的角加速度；(2)在此时间内，曲轴转了多少转？分析　这是刚体的运动学问题．刚体定轴转动的运动学规律与质点的运动学规律有类似的关系，本题为匀变速转动．解　(1)由于角速度ω＝2πn(n为单位时间内的转数)，根据角加速度的定义，在匀变速转动中角加速度为(2)发动机曲轴转过的角度为在12s内曲轴转过的圈数为圈3－5　一飞轮由一直径为30㎝，厚度为2.0㎝的圆盘和两个直径为10㎝，长为8.0㎝的共轴圆柱体组成，设飞轮的密度为7.8×103kg·m-3， 求飞轮对轴的转动惯量．分析　根据转动惯量的可叠加性，飞轮对轴的转动惯量可视为圆盘与两圆柱体对同轴的转动惯量之和；而匀质圆盘、圆柱体对轴的转动惯量的计算可查书中公式，或根据转动惯量的定义，用简单的积分计算得到．解　根据转动惯量的叠加性，由匀质圆盘、圆柱体对轴的转动惯量公式可得3－6　一燃气轮机在试车时，燃气作用在涡轮上的力矩为2.03×03N·m，涡轮的转动惯量为25.0kg·m2．当轮的转速由2.80×103r·min-1增大到1.12×104r·min-1时，所经历的时间t为多少？分析　由于作用在飞轮上的力矩是恒力矩，因此，根据转动定律可知，飞轮的角加速度是一恒量；又由匀变速转动中角加速度与时间的关系，可解出飞轮所经历的时间．该题还可应用角动量定理直接求解．解1　在匀变速转动中，角加速度，由转动定律，可得飞轮所经历的时间解2　飞轮在恒外力矩作用下，根据角动量定理，有则 3－7　电风扇接通电源后一般经5s后到达额定转速,而关闭电源后经16s后风扇停止转动，已知电风扇的转动惯量为，设启动时电磁力矩和转动时的阻力矩均为常数，求启动时的电磁力矩.分析由题意知和均为常数，故启动时电风扇在和共同作用下，作匀加速转动，直至到达额定转速，关闭电源后，电风扇仅在的作用下作匀减速转动.运用匀变速转动的运动学规律和转动定律既可求解.解设启动时和关闭电源后，电风扇转动时的角加速度分别为和，则启动过程关闭电源后联解以上各式并将以及、、、值代入，得3－8　一质量为m′、半径为R的均匀圆盘，通过其中心且与盘面垂直的水平轴以角速度ω转动，若在某时刻，一质量为m的小碎块从盘边缘裂开，且恰好沿垂直方向上抛，问它可能达到的高度是多少？破裂后圆盘的角动量为多大？分析　盘边缘裂开时，小碎块以原有的切向速度作上抛运动，由质点运动学规律可求得上抛的最大高度.此外，在碎块与盘分离的过程中，满足角动量守恒条件，由角动量守恒定律可计算破裂后盘的角动量. 解　(1)碎块抛出时的初速度为由于碎块竖直上抛运动，它所能到达的高度为(2)圆盘在裂开的过程中，其角动量守恒，故有式中为圆盘未碎时的角动量；为碎块被视为质点时，碎块对轴的角动量；L为破裂后盘的角动量.则3－9　一位溜冰者伸开双臂来以1.0绕身体中心轴转动，此时的转动惯量为1.33,她收起双臂来增加转速，如收起双臂后的转动惯量变为0.48.求（1）她收起双臂后的转速；（2）她收起双臂前后绕身体中心轴的转动动能各为多少？分析 各种物体（含刚体和变形体）在运动过程中，只要对空间某定点或定轴的外力矩之和为零，则物体对同一点或轴的角动量就守恒，在本题中当溜冰者绕身体中心轴转动时，人体重力和地面支持力均与该轴重合，故无外力矩作用，满足角动量守恒.此时改变身体形状（即改变对轴的转动惯量）就可改变转速，这是在体育运动中经常要利用的物理规律.解（1）由分析知，有则（2）收起双臂前收起双臂后此时由于人体内力做功，有3－10　一质量为1.12kg，长为1.0m的均匀细棒，支点在棒的上端点，开始时棒自由悬挂.以100N的力打击它的下端点，打击时间为0.02s.(1)若打击前棒是静止的，求打击时其角动量的变化；(2)棒的最大偏转角. 分析　该题属于常见的刚体转动问题，可分为两个过程来讨论：(1)瞬间的打击过程.在瞬间外力的打击下，棒受到外力矩的角冲量，根据角动量定理，棒的角动量将发生变化，则获得一定的角速度.(2)棒的转动过程.由于棒和地球所组成的系统，除重力(保守内力)外无其他外力做功，因此系统的机械能守恒，根据机械能守恒定律，可求得棒的偏转角度.解　(1)由刚体的角动量定理得(2)取棒和地球为一系统，并选O处为重力势能零点.在转动过程中，系统的机械能守恒，即由式(1)、(2)可得棒的偏转角度为3－11　质量为0.50kg，长为0.40m的均匀细棒，可绕垂直于棒的一端的水平轴转动.如将此棒放在水平位置，然后任其落下，求：(1)当棒转过60° 时的角加速度和角速度；(2)下落到竖直位置时的动能；(3)下落到竖直位置时的角速度.　　　分析　转动定律M＝Jα是一瞬时关系式，为求棒在不同位置的角加速度，只需确定棒所在位置的力矩就可求得.由于重力矩是变力矩，角加速度也是变化的，因此，在求角速度时，就必须根据角加速度用积分的方法来计算(也可根据转动中的动能定理，通过计算变力矩的功来求).至于棒下落到竖直位置时的动能和角速度，可采用系统的机械能守恒定律来解，这是因为棒与地球所组成的系统中，只有重力作功(转轴处的支持力不作功)，因此，系统的机械能守恒.解　(1)棒绕端点的转动惯量由转动定律M＝Jα可得棒在θ位置时的角加速度为当θ＝60°时，棒转动的角加速度由于，根据初始条件对式(1)积分，有则角速度为 (2)根据机械能守恒，棒下落至竖直位置时的动能为(3)由于该动能也就是转动动能，即，所以，棒落至竖直位置时的角速度为第四章　机械振动4-1　一个质点作简谐运动，振幅为A，在起始时刻质点的位移为，且向x轴正方向运动，代表此简谐运动的旋转矢量为（　　）题4-１图分析与解（B）图中旋转矢量的矢端在x轴上投影点的位移为－A/2，且投影点的运动方向指向Ox轴正向，即其速度的x分量大于零，故满足题意．因而正确答案为（B）．4-2　一简谐运动曲线如图（a）所示，则运动周期是（　　）(A)2.62s(B)2.40s(C)2.20s（D）2.00s题4-2图 分析与解　由振动曲线可知，初始时刻质点的位移为A/2，且向x轴正方向运动．图（ｂ）是其相应的旋转矢量图，由旋转矢量法可知初相位为-．振动曲线上给出质点从A/2处运动到x=0处所需时间为1s，由对应旋转矢量图可知相应的相位差，则角频率，周期.故选（B）．4-3　两个同周期简谐运动曲线如图（a）所示，x1的相位比x2的相位（　　）（A）落后（B）超前（C）落后（D）超前分析与解　由振动曲线图作出相应的旋转矢量图（b）即可得到答案为（B）．题4-３图4-4　两个同振动方向、同频率、振幅均为A的简谐运动合成后，振幅仍为A，则这两个简谐运动的相位差为（　　）（A）60（B）90（C）120（D）180分析与解　由旋转矢量图可知两个简谐运动1和2的相位差为120时，合成后的简谐运动3的振幅仍为A.正确答案为（C）．题4-4图 4-5　若简谐运动方程为，式中x的单位为m，t的单位为s.求：（1）振幅、频率、角频率、周期和初相；（2）时的位移、速度和加速度．分析　可采用比较法求解．将已知的简谐运动方程与简谐运动方程的一般形式作比较，即可求得各特征量．运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入值后，即可求得结果．解　（1）将与比较后可得：振幅A＝0.10m，角频率，初相＝0.25，则周期，频率．（２）时的位移、速度、加速度分别为4-6　一放置在水平桌面上的弹簧振子，振幅A＝2.0×10-2m，周期T＝0.50ｓ．当t＝0时，（1）物体在正方向端点；（2）物体在平衡位置、向负方向运动；（3）物体在x＝-1.0×10-2m处，向负方向运动；（4）物体在x＝-1.0×10-2m处，向正方向运动．求以上各种情况的运动方程．分析　在振幅A和周期T已知的条件下，确定初相φ是求解简谐运动方程的关键．初相的确定通常有两种方法．（1）解析法：由振动方程出发，根据初始条件，即t＝0时，x＝x0和v＝v0来确定φ值．（2）旋转矢量法：如图（a）所示，将质点P在Ox轴上振动的初始位置x0和速度v0的方向与旋转矢量图相对应来确定φ．旋转矢量法比较直观、方便，在分析中常采用． 题4-6图解　由题给条件知A＝2.0×10-2m，，而初相φ可采用分析中的两种不同方法来求．解析法：根据简谐运动方程，当时有，．当（1）时，，则；（2）时，，，因，取；（3）时，，，由，取；（4）时，，，由，取．旋转矢量法：分别画出四个不同初始状态的旋转矢量图，如图（b）所示，它们所对应的初相分别为，，，． 振幅A、角频率ω、初相φ均确定后，则各相应状态下的运动方程为（1）（2）（3）（4）4-7　有一弹簧，当其下端挂一质量为m的物体时，伸长量为9.8×10-2m．若使物体上、下振动，且规定向下为正方向．（1）当t＝0时，物体在平衡位置上方8.0×10-2ｍ处，由静止开始向下运动，求运动方程．（2）当t＝０时，物体在平衡位置并以0.6ｍ·s-1的速度向上运动，求运动方程．分析　求运动方程，也就是要确定振动的三个特征物理量A、ω和φ．其中振动的角频率是由弹簧振子系统的固有性质（振子质量m及弹簧劲度系数k）决定的，即，k可根据物体受力平衡时弹簧的伸长来计算；振幅A和初相φ需要根据初始条件确定．题4-7图解　物体受力平衡时，弹性力F与重力P的大小相等，即F＝mg．而此时弹簧的伸长量Δl＝9.8×10-2m．则弹簧的劲度系数k＝F／Δl＝mg／Δl．系统作简谐运动的角频率为　　（1）设系统平衡时，物体所在处为坐标原点，向下为x 轴正向．由初始条件t＝0时，x10＝8.0×10-2m、v10＝0可得振幅；应用旋转矢量法可确定初相［图（a）］．则运动方程为　　（2）t＝０时，x20＝0、v20＝0.6ｍ·s-1，同理可得；［图（b）］．则运动方程为4-8　某振动质点的x-t曲线如图（a）所示，试求：（1）运动方程；（2）点P对应的相位；（3）到达点P相应位置所需的时间．分析　由已知运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题．本题就是要通过x－t图线确定振动的三个特征量A、ω和，从而写出运动方程．曲线最大幅值即为振幅A；而ω、通常可通过旋转矢量法或解析法解出，一般采用旋转矢量法比较方便．解　（1）质点振动振幅A＝0.10ｍ．而由振动曲线可画出t0＝0和t1＝4ｓ时旋转矢量，如图（b）所示．由图可见初相（或），而由得，则运动方程为 题4-8图（2）图（a）中点P的位置是质点从A／2处运动到正向的端点处．对应的旋转矢量图如图（c）所示．当初相取时，点P的相位为（如果初相取成，则点P相应的相位应表示为．（3）由旋转矢量图可得，则．4-9　质量为10g的物体沿x的轴作简谐运动，振幅A=10cm，周期T=4.0s，t=0时物体的位移为且物体朝x轴负方向运动，求（1）t=1.0s时物体的位移；（2）t=1.0s时物体受的力；（3）t=0之后何时物体第一次到达x=5.0cm处；（4）第二次和第一次经过x=5.0cm处的时间间隔.分析根据题给条件可以先写出物体简谐运动方程.其中振幅A，角频率均已知，而初相可由题给初始条件利用旋转矢量法方便求出.有了运动方程，t时刻位移x和t时刻物体受力也就可以求出.对于（3）、（4）两问均可通过作旋转矢量图并根据公式很方便求解.解由题给条件画出t=0时该简谐运动的旋转矢量图如图（a）所示，可知初相.而A=0.10m，.则简谐运动方程为(1)t=1.0s时物体的位移 （2）t=1.0s时物体受力（3）设t=0时刻后，物体第一次到达x=5.0cm处的时刻为t，画出t=0和t=t时刻的旋转矢量图，如图（b）所示，由图可知，A与A的相位差为，由得（4）设t=0时刻后，物体第二次到达x=5.0cm处的时刻为t,画出t=t和t=t时刻的旋转矢量图，如图（c）所示，由图可知，A与A的相位差为，故有题4-9图4-10　图（a）为一简谐运动质点的速度与时间的关系曲线，且振幅为2cm ，求（1）振动周期；（2）加速度的最大值；（3）运动方程．分析　根据v-t图可知速度的最大值vmax，由vmax＝Aω可求出角频率ω，进而可求出周期T和加速度的最大值amax＝Aω2．在要求的简谐运动方程x＝Acos（ωt＋φ）中，因为A和ω已得出，故只要求初相位φ即可．由v－t曲线图可以知道，当t＝0时，质点运动速度v0＝vmax/2＝Aω/2，之后速度越来越大，因此可以判断出质点沿x轴正向向着平衡点运动．利用v0＝－Aωsinφ就可求出φ．解　（1）由得，则（2）（3）从分析中已知，即因为质点沿x轴正向向平衡位置运动，则取，其旋转矢量图如图（b）所示．则运动方程为　题4-10图4-11　有一单摆，长为1.0m，最大摆角为5°，如图所示．（1）求摆的角频率和周期；（2）设开始时摆角最大，试写出此单摆的运动方程；（3）摆角为3°时的角速度和摆球的线速度各为多少？ 题4-11图分析　单摆在摆角较小时（θ＜5°）的摆动，其角量θ与时间的关系可表示为简谐运动方程，其中角频率ω仍由该系统的性质（重力加速度g和绳长）决定，即．初相φ与摆角θ，质点的角速度与旋转矢量的角速度（角频率）均是不同的物理概念，必须注意区分．解　（1）单摆角频率及周期分别为（2）由时可得振动初相，则以角量表示的简谐运动方程为　　（３）摆角为3°时，有，则这时质点的角速度为线速度的大小为　　讨论 　质点的线速度和角速度也可通过机械能守恒定律求解，但结果会有极微小的差别．这是因为在导出简谐运动方程时曾取，所以，单摆的简谐运动方程仅在θ较小时成立．4-12　如图（a）所示，质量为1.0×10-2kg的子弹，以500m·s-1的速度射入木块，并嵌在木块中，同时使弹簧压缩从而作简谐运动，设木块的质量为4.99kg，弹簧的劲度系数为8.0×103N·m-1，若以弹簧原长时物体所在处为坐标原点，向左为x轴正向，求简谐运动方程．题4-12图分析　可分为两个过程讨论．首先是子弹射入木块的过程，在此过程中，子弹和木块组成的系统满足动量守恒，因而可以确定它们共同运动的初速度v0，即振动的初速度．随后的过程是以子弹和木块为弹簧振子作简谐运动．它的角频率由振子质量m1＋m2和弹簧的劲度系数k确定，振幅和初相可根据初始条件（初速度v0和初位移x0）求得．初相位仍可用旋转矢量法求．解　振动系统的角频率为由动量守恒定律得振动的初始速度即子弹和木块的共同运动初速度v0为又因初始位移x0＝0，则振动系统的振幅为图（b）给出了弹簧振子的旋转矢量图，从图中可知初相位 ，则简谐运动方程为4-13　如图（a）所示，一劲度系数为k的轻弹簧，其下挂有一质量为m1的空盘．现有一质量为m2的物体从盘上方高为h处自由落入盘中，并和盘粘在一起振动．问：（1）此时的振动周期与空盘作振动的周期有何不同？（2）此时的振幅为多大？题4-13图分析　原有空盘振动系统由于下落物体的加入，振子质量由m1变为m1+m2，因此新系统的角频率（或周期）要改变．由于，因此，确定初始速度v0和初始位移x0是求解振幅A的关键．物体落到盘中，与盘作完全非弹性碰撞，由动量守恒定律可确定盘与物体的共同初速度v0，这也是该振动系统的初始速度．在确定初始时刻的位移x0时，应注意新振动系统的平衡位置应是盘和物体悬挂在弹簧上的平衡位置．因此，本题中初始位移x0，也就是空盘时的平衡位置相对新系统的平衡位置的位移．解　（1）空盘时和物体落入盘中后的振动周期分别为可见T′＞T，即振动周期变大了．（2）如图（b）所示，取新系统的平衡位置为坐标原点O ．则根据分析中所述，初始位移为空盘时的平衡位置相对粘上物体后新系统平衡位置的位移，即式中为空盘静止时弹簧的伸长量，l2＝为物体粘在盘上后，静止时弹簧的伸长量．由动量守恒定律可得振动系统的初始速度，即盘与物体相碰后的速度式中是物体由h高下落至盘时的速度．故系统振动的振幅为本题也可用机械能守恒定律求振幅A．4-14　质量为0.10kg的物体，以振幅1.0×10-2m作简谐运动，其最大加速度为4.0ｍ·s-1求：（1）振动的周期；（2）物体通过平衡位置时的总能量与动能；（3）物体在何处其动能和势能相等？（4）当物体的位移大小为振幅的一半时，动能、势能各占总能量的多少？分析　在简谐运动过程中，物体的最大加速度，由此可确定振动的周期T．另外，在简谐运动过程中机械能是守恒的，其中动能和势能互相交替转化，其总能量E＝kA2/2．当动能与势能相等时，Ek＝EP＝kA2/4．因而可求解本题．解　（1）由分析可得振动周期　　（2）当物体处于平衡位置时，系统的势能为零，由机械能守恒可得系统的动能等于总能量，即 　　（3）设振子在位移x0处动能与势能相等，则有得　　（４）物体位移的大小为振幅的一半（即）时的势能为则动能为4-15　已知两同方向、同频率的简谐运动的运动方程分别为；．求：（1）合振动的振幅及初相；（2）若有另一同方向、同频率的简谐运动，则为多少时，x1＋x3的振幅最大？又为多少时，x2＋x3的振幅最小？题4-15图分析　可采用解析法或旋转矢量法求解.由旋转矢量合成可知，两个同方向、同频率简谐运动的合成仍为一简谐运动，其角频率不变；合振动的振幅，其大小与两个分振动的初相差相关．而合振动的初相位 解　（1）作两个简谐运动合成的旋转矢量图（如图）．因为，故合振动振幅为合振动初相位（2）要使x1＋x3振幅最大，即两振动同相，则由得要使x1＋x3的振幅最小，即两振动反相，则由得4-16　两个同频率的简谐运动1和2的振动曲线如图（a）所示，求（1）两简谐运动的运动方程x1和x2；（2）在同一图中画出两简谐运动的旋转矢量，并比较两振动的相位关系；（3）若两简谐运动叠加，求合振动的运动方程．分析　振动图已给出了两个简谐运动的振幅和周期，因此只要利用图中所给初始条件，由旋转矢量法或解析法求出初相位，便可得两个简谐运动的方程．解　（1）由振动曲线可知，A＝0.1ｍ，T＝2ｓ，则ω＝2π／T＝πｓ-1．曲线1表示质点初始时刻在x＝0处且向x轴正向运动，因此φ1＝－π／2；曲线2表示质点初始时刻在x＝A/2处且向x轴负向运动，因此φ2＝π／3．它们的旋转矢量图如图（b）所示．则两振动的运动方程分别为　和（2）由图（b）可知振动2超前振动1的相位为5π／6．（3） 其中则合振动的运动方程为　　　题4-16图4-17　图（a）表示t＝0时的简谐波的波形图，波沿x轴正方向传播，图（b）为一质点的振动曲线．则图（a）中所表示的x＝0处振动的初相位与图（b）所表示的振动的初相位分别为（　　）题4-17图（Ａ）均为零　　　　　（Ｂ）均为　　　　　（Ｃ）均为（Ｄ）与（Ｅ）与分析与解　本题给了两个很相似的曲线图，但本质却完全不同．求解本题要弄清振动图和波形图不同的物理意义．图（a）描述的是连续介质中沿波线上许许多多质点振动在t 时刻的位移状态．其中原点处质点位移为零，其运动方向由图中波形状态和波的传播方向可以知道是沿y轴负向，利用旋转矢量法可以方便的求出该质点振动的初相位为π/2．而图（b）是一个质点的振动曲线图，该质点在t＝0时位移为0，t＞0时，由曲线形状可知，质点向y轴正向运动，故由旋转矢量法可判知初相位为－π/2，答案为（D）．4-18一横波以速度u沿x轴负方向传播，t时刻波形曲线如图（a）所示，则该时刻（）（A）A点相位为（B）B点静止不动（C）C点相位为（D）D点向上运动分析与解由波形曲线可知，波沿x轴负向传播，B、D处质点均向y轴负方向运动，且B处质点在运动速度最快的位置.因此答案（B）和（D）不对.A处质点位于正最大位移处，C处质点位于平衡位置且向y轴正方向运动，它们的旋转矢量图如图（b）所示.A、C点的相位分别为0和.故答案为（C）题4-18图4-19　如图所示，两列波长为λ的相干波在点P相遇．波在点S1振动的初相是φ1，点S1到点P的距离是r1．波在点S2的初相是φ2，点S2到点P的距离是r2，以k代表零或正、负整数，则点P是干涉极大的条件为（　　）分析与解　P是干涉极大的条件为两分振动的相位差，而两列波传到P点时的两分振动相位差为 ，故选项（D）正确．题4-19图4-20　一横波在沿绳子传播时的波动方程为，式中y的单位为m，t的单位为s．（1）求波的振幅、波速、频率及波长；（2）求绳上质点振动时的最大速度；（3）分别画出t＝1s和t＝2s时的波形，并指出波峰和波谷．画出x＝1.0ｍ处质点的振动曲线并讨论其与波形图的不同．分析　（1）已知波动方程（又称波函数）求波动的特征量（波速u、频率u、振幅A及波长λ等），通常采用比较法．将已知的波动方程按波动方程的一般形式书写，然后通过比较确定各特征量（式中前“-”、“+”的选取分别对应波沿x轴正向和负向传播）．比较法思路清晰、求解简便，是一种常用的解题方法．（2）讨论波动问题，要理解振动物理量与波动物理量之间的内在联系与区别．例如区分质点的振动速度与波速的不同，振动速度是质点的运动速度，即v＝dy/dt；而波速是波线上质点运动状态的传播速度（也称相位的传播速度、波形的传播速度或能量的传播速度），其大小由介质的性质决定．介质不变，波速保持恒定．（3）将不同时刻的t值代入已知波动方程，便可以得到不同时刻的波形方程y＝y（x），从而作出波形图．而将确定的x值代入波动方程，便可以得到该位置处质点的运动方程y＝y（t），从而作出振动图．解　（1）将已知波动方程表示为 与一般表达式比较，可得则（2）绳上质点的振动速度则（3）t＝1ｓ和t＝2ｓ时的波形方程分别为波形图如图（a）所示．x＝1.0m处质点的运动方程为振动图线如图（b）所示．波形图与振动图虽在图形上相似，但却有着本质的区别．前者表示某确定时刻波线上所有质点的位移情况，而后者则表示某确定位置的一个质点，其位移随时间变化的情况．题4-20图4-21　波源作简谐运动，其运动方程为，它所形成的波形以30ｍ·ｓ-1的速度沿一直线传播．（1 ）求波的周期及波长；（2）写出波动方程．分析　已知波源运动方程求波动物理量及波动方程，可先将运动方程与其一般形式进行比较，求出振幅A、角频率ω及初相φ0，而这三个物理量与波动方程的一般形式中相应的三个物理量是相同的．再利用题中已知的波速u及公式ω＝2πν＝2π／T和λ＝uT即可求解．解　（1）由已知的运动方程可知，质点振动的角频率．根据分析中所述，波的周期就是振动的周期，故有波长为λ＝uT＝0.25ｍ（２）将已知的波源运动方程与简谐运动方程的一般形式比较后可得A＝4.0×10-3m，，φ0＝0故以波源为原点，沿x轴正向传播的波的波动方程为4-22　图示为平面简谐波在t＝0时的波形图，设此简谐波的频率为250Hz，且此时图中质点P的运动方向向上．求：（1）该波的波动方程；（2）在距原点O为7.5m处质点的运动方程与t＝0时该点的振动速度．分析　（1）从波形曲线图获取波的特征量，从而写出波动方程是建立波动方程的又一途径．具体步骤为：1.从波形图得出波长λ、振幅A和波速u＝λu；2.根据点P的运动趋势来判断波的传播方向，从而可确定原点处质点的运动趋向，并利用旋转矢量法确定其初相φ0．（2）在波动方程确定后，即可得到波线上距原点O为x处的运动方程y＝y（t），及该质点的振动速度u＝dy/dt．解　（1）从图中得知，波的振幅A＝0.10m，波长λ＝20.0m，则波速u＝λu＝5.0×103ｍ·ｓ-1．根据t＝0时点P向上运动，可知波沿Ox轴负向传播，并判定此时位于原点处的质点将沿Oy 轴负方向运动．利用旋转矢量法可得其初相φ0＝π/3．故波动方程为（2）距原点O为x＝7.5ｍ处质点的运动方程为t＝0时该点的振动速度为题4-22图4-23　平面简谐波的波动方程为,式中y和x的单位为m，t的单位为s,求：（1）t＝2.1s时波源及距波源0.10m两处的相位；（2）离波源0.80m及0.30m两处的相位差．解　（1）将t＝2.1s和x＝0代入题给波动方程，可得波源处的相位将t＝2.1s和x′＝0.10m代入题给波动方程，得0.10m处的相位为（2）从波动方程可知波长λ＝1.0m．这样，x1＝0.80m与x2＝0.30m两点间的相位差 4-24　两相干波波源位于同一介质中的A、B两点，如图（a）所示．其振幅相等、频率皆为100Hz，B比A的相位超前π．若A、B相距30.0m，波速为u＝400m·s-1，试求AB连线上因干涉而静止的各点的位置．题4-24图分析　两列相干波相遇时的相位差．因此，两列振幅相同的相干波因干涉而静止的点的位置，可根据相消条件获得．解　以A、B两点的中点O为原点，取坐标如图（b）所示．两波的波长均为λ＝u/u＝4.0m．在A、B连线上可分三个部分进行讨论．1.位于点A左侧部分因该范围内两列波相位差恒为2π的整数倍，故干涉后质点振动处处加强，没有静止的点．2.位于点B右侧部分显然该范围内质点振动也都是加强，无干涉静止的点．3.在A、B两点的连线间，设任意一点P距原点为x．因，，则两列波在点P的相位差为 根据分析中所述，干涉静止的点应满足方程得因x≤15m，故k7．即在A、B之间的连线上共有15个静止点．4-25图（a）是干涉型消声器结构的原理图，利用这一结构可以消除噪声．当发动机排气噪声声波经管道到达点A时，分成两路而在点B相遇，声波因干涉而相消．如果要消除频率为300Hz的发动机排气噪声，则图中弯管与直管的长度差Δr＝r2－r1至少应为多少？（设声波速度为340m·s-1）题4-25图分析　一列声波被分成两束后再相遇，将形成波的干涉现象．由干涉相消条件，可确定所需的波程差，即两管的长度差Δr．解　由分析可知，声波从点A分开到点B相遇，两列波的波程差Δr＝r2-r1，故它们的相位差为由相消静止条件Δφ＝（2k＋1）π，（k＝0，±1，±2，…）得Δr＝（2k＋1）λ／2根据题中要求令k＝0得Δr至少应为 讨论　在实际应用中，由于噪声是由多种频率的声波混合而成，因而常将具有不同Δr的消声单元串接起来以增加消除噪声的能力．图（b）为安装在摩托车排气系统中的干涉消声器的结构原理图．4-26　一警车以25m·s-1的速度在静止的空气中行驶，假设车上警笛的频率为v=800Hz．求：（1）静止站在路边的人听到警车驶近和离去时的警笛声波频率；（2）如果警车追赶一辆速度为15m·s-1的客车，则客车上人听到的警笛声波的频率是多少？（设空气中的声速u＝330m·s-1）分析　由于声源与观察者之间的相对运动而产生声多普勒效应，由多普勒频率公式可解得结果．在处理这类问题时，不仅要分清观察者相对介质（空气）是静止还是运动，同时也要分清声源的运动状态．解　（1）根据多普勒频率公式，当声源（警车）以速度s＝25m·s-1运动时，静止于路边的观察者所接收到的频率为警车驶近观察者时，式中s前取“－”号，故有警车驶离观察者时，式中s前取“＋”号，故有（2）客车的速度为=15m·s-1,声源（警车）与客车上的观察者作同向运动时，观察者收到的频率为4-27蝙蝠在洞穴中飞来飞去，能非常有效地用超声波脉冲导航.假如蝙蝠发出的超声波频率为39kHz，当它以声速的的速度朝着表面平直的岩壁飞去时，试求它听到的从岩壁反射回来的超声波频率为多少？分析由题意可知，蝙蝠既是波的发出者，又是波的接收者. 设超声波的传播速度为u.首先，蝙蝠是声源，发出信号频率为v，运动速度为，岩壁是接收者，利用多普勒频率公式，即可求得岩壁接收到的信号频率.经岩壁反射后频率不变，即岩壁发射信号频率为，这时蝙蝠是波的接收者，其运动速度为，再次利用多普勒频率公式，可求得蝙蝠接收到的信号频率.解将蝙蝠看成波源，则由分析可知，岩壁接收到的信号频率为，在蝙蝠接收岩壁反射信号时，又将它看成接收者.则蝙蝠接收到的信号频率为第五章气体动理论5－1　图示两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线.如果和分别表示氧气和氢气的最概然速率，则(　　)(A)图中表示氧气分子的速率分布曲线且(B)图中表示氧气分子的速率分布曲线且(C)图中表示氧气分子的速率分布曲线且(D)图中表示氧气分子的速率分布曲线且 分析与解　由可知，在相同温度下，由于不同气体的摩尔质量不同，它们的最概然速率也就不同.因，故氧气比氢气的要小，由此可判定图中曲线应是对应于氧气分子的速率分布曲线.又因，所以.故选(B)．题5-1图5－2　在一个体积不变的容器中，储有一定量的某种理想气体，温度为时，气体分子的平均速率为，分子平均碰撞次数为，平均自由程为，当气体温度升高为时，气体分子的平均速率、平均碰撞频率和平均自由程分别为(　　)(A)　(B)(C)(D)分析与解　理想气体分子的平均速率，温度由升至，则平均速率变为；又平均碰撞频率，由于容器体积不变，即分子数密度n不变，则平均碰撞频率变为；而平均自由程，n不变，则也不变．因此正确答案为(B)． 5－3　处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同，分子的平均平动动能也相同，则它们(　　)(A)温度，压强均不相同　　(B)温度相同，但氦气压强大于氮气的压强(C)温度，压强都相同(D)温度相同，但氦气压强小于氮气的压强分析与解　理想气体分子的平均平动动能，仅与温度有关．因此当氦气和氮气的平均平动动能相同时，温度也相同．又由物态方程，当两者分子数密度n相同时，它们压强也相同．故选(C)．5－5　两个相同的刚性容器，一个盛有氢气，一个盛氦气(均视为刚性分子理想气体).开始时它们的压强和温度都相同，现将3J热量传给氦气，使之升高到一定的温度.若使氢气也升高同样的温度，则应向氢气传递热量为(　　)(A)6J　　　(B)3J　　　(C)5J　　(D)10J分析与解　当容器体积不变，即为等体过程时系统不作功，根据热力学第一定律Q＝ΔE＋W，有Q＝ΔE.而由理想气体内能公式，可知欲使氢气和氦气升高相同温度，须传递的热量.再由理想气体物态方程pV＝RT，初始时，氢气和氦气是具有相同的温度、压强和体积，因而物质的量相同，则.因此正确答案为(C).5－6　一定量理想气体分别经过等压，等温和绝热过程从体积膨胀到体积，如图所示，则下述正确的是(　　)（A）吸热最多，内能增加（B）内能增加，作功最少 （C）吸热最多，内能不变（D）对外作功，内能不变分析与解由绝热过程方程常量，以及等温过程方程pV=常量可知在同一p-V图中当绝热线与等温线相交时，绝热线比等温线要陡，因此图中为等压过程，为等温过程，为绝热过程.又由理想气体的物态方程可知，p-V图上的pV积越大，则该点温度越高.因此图中.对一定量理想气体内能，，由此知，，而由理想气体作功表达式知道功的数值就等于p-V图中过程曲线下所对应的面积，则由图可知.又由热力学第一定律Q＝W＋ΔE可知.因此答案A、B、C均不对.只有（D）正确.题5-6图5－7　一台工作于温度分别为327℃和27℃的高温热源与低温源之间的卡诺热机，每经历一个循环吸热2000J，则对外作功(　　)(A)2000J　(B)1000J　　(C)4000J　　(D)500J分析与解　热机循环效率η＝W/Q吸，对卡诺机，其循环效率又可表为：η＝ 1－，则由W/Q吸＝1－可求答案.正确答案为(B).7－5　有一个体积为的空气泡由水面下深的湖底处(温度为)升到湖面上来．若湖面的温度为，求气泡到达湖面的体积．(取大气压强为)分析　将气泡看成是一定量的理想气体，它位于湖底和上升至湖面代表两个不同的平衡状态．利用理想气体物态方程即可求解本题．位于湖底时，气泡内的压强可用公式求出，其中ρ为水的密度(常取)．解　设气泡在湖底和湖面的状态参量分别为(p1，V1，T1)和(p2,V2，T2)．由分析知湖底处压强为，利用理想气体的物态方程可得空气泡到达湖面的体积为5－8　有N个质量均为m的同种气体分子，它们的速率分布如图所示.(1)说明曲线与横坐标所包围的面积的含义；(2)由N和求a值；(3)求在速率/2到3/2间隔内的分子数；(4)求分子的平均平动动能. 题5-8图分析　处理与气体分子速率分布曲线有关的问题时，关键要理解分布函数的物理意义.，题中纵坐标，即处于速率v附近单位速率区间内的分子数.同时要掌握的归一化条件，即.在此基础上，根据分布函数并运用数学方法(如函数求平均值或极值等)，即可求解本题.解　(1)由于分子所允许的速率在0到2的范围内，由归一化条件可知图中曲线下的面积即曲线下面积表示系统分子总数N.(2)从图中可知，在0到区间内，；而在0到2区间，.则利用归一化条件有(3)速率在/2到3/2间隔内的分子数为 (4)分子速率平方的平均值按定义为故分子的平均平动动能为5－9在标准状况下，1cm中有多少个氮分子？氮分子的平均速率为多大？平均碰撞次数为多少?平均自由程为多大？（已知氮分子的有效直径）分析标准状况即为压强，温度.则由理想气体物态方程可求得气体分子数密度n，即单位体积中氮分子的个数.而氮气分子的平均速率、平均碰撞次数和平均自由程可分别由公式，和直接求出.解由分析可知，氮分子的分子数密度为即中约有个.氮气的摩尔质量为M=28×10－3kg·mol－1，其平均速率为=454则平均碰撞次数为 平均自由程为讨论本题主要是对有关数量级有一个具体概念.在通常情况下，气体分子平均以每秒几百米的速率运动着，那么气体中进行的一切实际过程如扩散过程、热传导过程等好像都应在瞬间完成，而实际过程都进行得比较慢，这是因为分子间每秒钟上亿次的碰撞导致分子的自由程只有几十纳米，因此宏观上任何实际过程的完成都需要一段时间.5－10　一容器内储有氧气，其压强为，温度为27℃，求：(1)气体分子的数密度；(2)氧气的密度；(3)分子的平均平动动能；分析　在题中压强和温度的条件下，氧气可视为理想气体．因此，可由理想气体的物态方程、密度的定义以及分子的平均平动动能与温度的关系等求解．又因可将分子看成是均匀等距排列的，故每个分子占有的体积为，由数密度的含意可知，即可求出．解　(1)单位体积分子数(2)氧气的密度(3)氧气分子的平均平动动能 5－11当温度为0时，可将气体分子视为刚性分子，求在此温度下：（1）氧分子的平均动能和平均转动动能；（2）氧气的内能；（3）氦气的内能.分析（1）由题意，氧分子为刚性双原子分子，则其共有5个自由度，其中包括3个平动自由度和2个转动自由度.根据能量均分定理，平均平动动能，平均转动动能.（2）对一定量理想气体，其内能为，它是温度的单值函数.其中i为分子自由度，这里氧气i=5、氦气i=3.而为气体质量，M为气体摩尔质量，其中氧气；氦气.代入数据即可求解它们的内能.解根据分析当气体温度为T=273K时，可得（1）氧分子的平均平动动能为氧分子的平均转动动能为（2）氧气的内能为（3）氦气的内能为 5－12　在容积为2.0×10-3m3的容器中，有内能为6.75×102J的刚性双原子分子某理想气体.(1)求气体的压强；(2)设分子总数为5.4×1022个，求分子的平均平动动能及气体的温度.分析　(1)一定量理想气体的内能，对刚性双原子分子而言，i＝5.由上述内能公式和理想气体物态方程pV＝RT可解出气体的压强.(2)求得压强后，再依据题给数据可求得分子数密度，则由公式p＝nkT可求气体温度.气体分子的平均平动动能可由求出.解　(1)由和pV＝RT可得气体压强(2)分子数密度n＝N/V，则该气体的温度气体分子的平均平动动能为5－13　容积为1m3的容器储有1mol氧气，以v＝10的速度运动，设容器突然停止，其中氧气的80％的机械运动动能转化为气体分子热运动动能.试求气体的温度及压强各升高了多少.分析　容器作匀速直线运动时，容器内分子除了相对容器作杂乱无章的热运动外，还和容器一起作定向运动.其定向运动动能(即机械能)为. 按照题意，当容器突然停止后，80％定向运动动能转为系统的内能.对一定量理想气体内能是温度的单值函数，则有关系式：成立，从而可求ΔT.再利用理想气体物态方程，可求压强的增量.解　由分析知，其中为容器内氧气质量.又氧气的摩尔质量为，解得ΔT＝6.16×10-2K当容器体积不变时，由pV＝RT得5－14　位于委内瑞拉的安赫尔瀑布是世界上落差最大的瀑布，它高979m.如果在水下落的过程中，重力对它所作的功中有50％转换为热量使水温升高，求水由瀑布顶部落到底部而产生的温差.(水的比热容c为4.18×103J·kg－1·K－1)分析　取质量为m的水作为研究对象，水从瀑布顶部下落到底部过程中重力作功W＝mgh，按题意，被水吸收的热量Q＝0.5W，则水吸收热量后升高的温度可由Q＝mcΔT求得.解　由上述分析得mcΔT＝0.5mgh水下落后升高的温度ΔT＝0.5gh/c＝1.15K 5－15　如图所示，1mol氦气，由状态沿直线变到状态，求这过程中内能的变化、对外作的功、吸收的热量.分析由题8-4分析可知功的数值就等于p-V图中过程曲线下所对应的面积，又对一定量的理想气体其内能，而氦气为单原子分子，自由度i=3，则1mol氦气内能的变化，其中温度的增量可由理想气体物态方程求出.求出了过程内能变化和做功值，则吸收的热量可根据热力学第一定律求出.解由分析可知，过程中对外作的功为内能的变化为吸收的热量题5-15图 5－16　如图所示，在绝热壁的汽缸内盛有1mol的氮气，活塞外为大气，氮气的压强为1.51×105Pa，活塞面积为0.02m2.从汽缸底部加热，使活塞缓慢上升了0.5m.问(1)气体经历了什么过程？(2)汽缸中的气体吸收了多少热量？(根据实验测定，已知氮气的摩尔定压热容Cp，m＝29.12J·mol－1·K－1，摩尔定容热容CV,m＝20.80J·mol-1·K-1)题5-16图分析　因活塞可以自由移动，活塞对气体的作用力始终为大气压力和活塞重力之和.容器内气体压强将保持不变.对等压过程，吸热.ΔT可由理想气体物态方程求出.解　(1)由分析可知气体经历了等压膨胀过程.(2)吸热.其中ν＝1mol，Cp,m＝29.12Ｊ·mol－1·Ｋ－1.由理想气体物态方程pV＝νRT，得ΔT＝(p2V2－p1V1)/R＝p(V2－V1)/R＝p·S·Δl/R则5－17　一压强为1.0×105Pa,体积为1.0×10－3m3的氧气自0℃加热到100℃.问：(1)当压强不变时，需要多少热量?当体积不变时，需要多少热量?(2)在等压或等体过程中各作了多少功?分析　(1)由量热学知热量的计算公式为.按热力学第一定律，在等体过程中，；在等压过程中， (2)求过程的作功通常有两个途径.①利用公式；②利用热力学第一定律去求解.在本题中，热量Q已求出，而内能变化可由得到.从而可求得功W.解　根据题给初态条件得氧气的物质的量为氧气的摩尔定压热容，摩尔定容热容.(1)求Qp、QV等压过程氧气(系统)吸热等体过程氧气(系统)吸热(2)按分析中的两种方法求作功值①利用公式求解.在等压过程中，，则得而在等体过程中，因气体的体积不变，故作功为②利用热力学第一定律Q＝ΔE＋W求解.氧气的内能变化为 　由于在(1)中已求出Qp与QV，则由热力学第一定律可得在等压过程、等体过程中所作的功分别为5－18　如图所示，系统从状态A沿ABC变化到状态C的过程中，外界有326J的热量传递给系统，同时系统对外作功126J.当系统从状态C沿另一曲线CA返回到状态A时，外界对系统作功为52J，则此过程中系统是吸热还是放热？传递热量是多少？题5-18图分析　已知系统从状态C到状态A，外界对系统作功为WCA，如果再能知道此过程中内能的变化ΔECA，则由热力学第一定律即可求得该过程中系统传递的热量QCA.由于理想气体的内能是状态(温度)的函数，利用题中给出的ABC过程吸热、作功的情况，由热力学第一定律即可求得由A至C过程中系统内能的变化ΔEAC，而ΔEAC＝－ΔECA，故可求得QCA.解　系统经ABC过程所吸收的热量及对外所作的功分别为QABC＝326J，　WABC＝126J则由热力学第一定律可得由A到C过程中系统内能的增量ΔEAC＝QABC－WABC＝200J由此可得从C到A，系统内能的增量为 ΔECA＝－200J从C到A，系统所吸收的热量为QCA＝ΔECA＋WCA＝－252J式中负号表示系统向外界放热252J.这里要说明的是由于CA是一未知过程，上述求出的放热是过程的总效果，而对其中每一微小过程来讲并不一定都是放热.8－8　一定量的空气，吸收了1.71×103J的热量，并保持在1.0×105Pa下膨胀，体积从1.0×10－2m3增加到1.5×10－2m3，问空气对外作了多少功？它的内能改变了多少？分析　由于气体作等压膨胀，气体作功可直接由W＝p(V2－V1)求得.取该空气为系统，根据热力学第一定律Q＝ΔE＋W可确定它的内能变化.在计算过程中要注意热量、功、内能的正负取值.解　该空气等压膨胀，对外作功为W＝p(V2－V1)＝5.0×102J其内能的改变为ΔE＝Q－W＝1.21×103J8－12　如图所示，使1mol氧气(1)由A等温地变到B；(2)由A等体地变到C，再由C等压地变到B.试分别计算氧气所作的功和吸收的热量.题8-12图 分析　从p－V图(也称示功图)上可以看出，氧气在AB与ACB两个过程中所作的功是不同的，其大小可通过求出.考虑到内能是状态的函数，其变化值与过程无关，所以这两个不同过程的内能变化是相同的，而且因初、末状态温度相同TA＝TB，故ΔE＝0，利用热力学第一定律Q＝W＋ΔE，可求出每一过程所吸收的热量.解　(1)沿AB作等温膨胀的过程中，系统作功由分析可知在等温过程中，氧气吸收的热量为QAB＝WAB＝2.77×103Ｊ　　(2)沿A到C再到B的过程中系统作功和吸热分别为WACB＝WAC＋WCB＝WCB＝(VB－VC)＝2.0×103ＪQACB＝WACB＝2.0×103Ｊ8－15　图(ａ)是某单原子理想气体循环过程的V－T图，图中VC＝2VA.试问：(1)图中所示循环是代表制冷机还是热机？(2)如是正循环(热机循环)，求出其循环效率.题8-15图 分析　以正、逆循环来区分热机和制冷机是针对p－V图中循环曲线行进方向而言的.因此，对图(ａ)中的循环进行分析时，一般要先将其转换为p－V图.转换方法主要是通过找每一过程的特殊点，并利用理想气体物态方程来完成.由图(ａ)可以看出，BC为等体降温过程，CA为等温压缩过程；而对AB过程的分析，可以依据图中直线过原点来判别.其直线方程为V＝KT，C为常数.将其与理想气体物态方程pV＝RT比较可知该过程为等压膨胀过程(注意：如果直线不过原点，就不是等压过程).这样，就可得出p－V图中的过程曲线，并可判别是正循环(热机循环)还是逆循环(制冷机循环)，再参考题8－14的方法求出循环效率.解　(1)根据分析，将V－T图转换为相应的p－V图，如图(ｂ)所示.图中曲线行进方向是正循环，即为热机循环.(2)根据得到的p－V图可知，AB为等压膨胀过程，为吸热过程.BC为等体降压过程，CA为等温压缩过程，均为放热过程.故系统在循环过程中吸收和放出的热量分别为CA为等温线，有TA＝TC；AB为等压线，且因VC＝2VA，则有TA＝TB/2.对单原子理想气体，其摩尔定压热容Cp，m＝5R/2，摩尔定容热容CV，m＝3R/2.故循环效率为5－21　有一以理想气体为工作物质的热机，其循环如图所示，试证明热 分析　该热机由三个过程组成，图中AB是绝热过程，BC是等压压缩过程，CA是等体升压过程.其中CA过程系统吸热，BC过程系统放热.本题可从效率定义出发,利用热力学第一定律和等体、等压方程以及γ＝Cp,m/CV,m的关系来证明.题5-21图证　该热机循环的效率为其中QBC＝Cp,m(TC－TB)，QCA＝CV,m(TA－TC)，则上式可写为在等压过程BC和等体过程CA中分别有TB/V1＝TC/V2,TA/p1＝TC/p2,代入上式得5-22　一卡诺热机的低温热源温度为7℃，效率为40％，若要将其效率提高到50％，问高温热源的温度需提高多少？ 解　设高温热源的温度分别为、,则有，　其中T2为低温热源温度.由上述两式可得高温热源需提高的温度为5－23　一小型热电厂内，一台利用地热发电的热机工作于温度为227℃的地下热源和温度为27℃的地表之间.假定该热机每小时能从地下热源获取1.8×1011Ｊ的热量.试从理论上计算其最大功率为多少？分析　热机必须工作在最高的循环效率时，才能获取最大的功率.由卡诺定理可知，在高温热源T1和低温热源T2之间工作的可逆卡诺热机的效率最高，其效率为η＝1－T2/T1.由于已知热机在确定的时间内吸取的热量，故由效率与功率的关系式，可得此条件下的最大功率.解　根据分析，热机获得的最大功率为5－24　在夏季，假定室外温度恒定为37℃，启动空调使室内温度始终保持在17℃.如果每天有2.51×108J的热量通过热传导等方式自室外流入室内，则空调一天耗电多少？(设该空调制冷机的制冷系数为同条件下的卡诺制冷机制冷系数的60％) 题8-21图分析　耗电量的单位为kW·h，1kW·h＝3.6×106J.图示是空调的工作过程示意图.因为卡诺制冷机的制冷系数为，其中T1为高温热源温度(室外环境温度)，T2为低温热源温度(室内温度).所以，空调的制冷系数为e＝ek·60％＝0.6T2/(T1－T2)另一方面，由制冷系数的定义，有e＝Q2/(Q1－Q2)其中Q1为空调传递给高温热源的热量，即空调向室外排放的总热量；Q2是空调从房间内吸取的总热量.若Q′为室外传进室内的热量，则在热平衡时Q2＝Q′.由此，就可以求出空调的耗电作功总值W＝Q1－Q2.解　根据上述分析，空调的制冷系数为　　在室内温度恒定时，有Q2＝Q′.由e＝Q2/(Q1－Q2)可得空调运行一天所耗电功 W＝Q1－Q2＝Q2/e＝Q′/e＝2.89×107J=8.0kW·h6－1　电荷面密度均为＋σ的两块“无限大”均匀带电的平行平板如图(A)放置，其周围空间各点电场强度E(设电场强度方向向右为正、向左为负)随位置坐标x变化的关系曲线为图(B)中的(　　)分析与解　“无限大”均匀带电平板激发的电场强度为，方向沿带电平板法向向外，依照电场叠加原理可以求得各区域电场强度的大小和方向.因而正确答案为(B).6－2　下列说法正确的是(　　)(A)闭合曲面上各点电场强度都为零时，曲面内一定没有电荷(B)闭合曲面上各点电场强度都为零时，曲面内电荷的代数和必定为零(C)闭合曲面的电通量为零时，曲面上各点的电场强度必定为零(D)闭合曲面的电通量不为零时，曲面上任意一点的电场强度都不可能为零分析与解　依照静电场中的高斯定理，闭合曲面上各点电场强度都为零时，曲面内电荷的代数和必定为零，但不能肯定曲面内一定没有电荷；闭合曲面的电通量为零时，表示穿入闭合曲面的电场线数等于穿出闭合曲面的电场线数或没有电场线穿过闭合曲面，不能确定曲面上各点的电场强度必定为零；同理闭合曲面的电通量不为零，也不能推断曲面上任意一点的电场强度都不可能为零，因而正确答案为(B).6－3　下列说法正确的是(　　) (A)电场强度为零的点，电势也一定为零(B)电场强度不为零的点，电势也一定不为零(C)电势为零的点，电场强度也一定为零(D)电势在某一区域内为常量，则电场强度在该区域内必定为零分析与解　电场强度与电势是描述电场的两个不同物理量，电场强度为零表示试验电荷在该点受到的电场力为零，电势为零表示将试验电荷从该点移到参考零电势点时，电场力作功为零.电场中一点的电势等于单位正电荷从该点沿任意路径到参考零电势点电场力所作的功；电场强度等于负电势梯度.因而正确答案为(D).6－5　一半径为R的半球壳，均匀地带有电荷，电荷面密度为σ，求球心处电场强度的大小.分析　这仍是一个连续带电体问题，求解的关键在于如何取电荷元.现将半球壳分割为一组平行的细圆环，如图所示，从教材第5－3节的例1可以看出，所有平行圆环在轴线上P处的电场强度方向都相同，将所有带电圆环的电场强度积分，即可求得球心O处的电场强度.解　将半球壳分割为一组平行细圆环，任一个圆环所带电荷元，在点O激发的电场强度为由于平行细圆环在点O激发的电场强度方向相同，利用几何关系，统一积分变量，有 积分得6－6　地球周围的大气犹如一部大电机，由于雷雨云和大气气流的作用，在晴天区域，大气电离层总是带有大量的正电荷，云层下地球表面必然带有负电荷.晴天大气电场平均电场强度约为，方向指向地面.试求地球表面单位面积所带的电荷(以每平方厘米的电子数表示).分析　考虑到地球表面的电场强度指向地球球心，在大气层中取与地球同心的球面为高斯面，利用高斯定理可求得高斯面内的净电荷.解　在大气层临近地球表面处取与地球表面同心的球面为高斯面，其半径(为地球平均半径).由高斯定理地球表面电荷面密度单位面积额外电子数6－7　两个带有等量异号电荷的无限长同轴圆柱面，半径分别为R1和R2＞R1)，单位长度上的电荷为λ.求离轴线为r处的电场强度：(1)r＜R1，(2)R1＜r＜R2，(3)r＞R2. 分析　电荷分布在无限长同轴圆柱面上，电场强度也必定沿轴对称分布，取同轴圆柱面为高斯面，只有侧面的电场强度通量不为零，且，求出不同半径高斯面内的电荷.即可解得各区域电场的分布.解　作同轴圆柱面为高斯面，根据高斯定理r＜R1，　　在带电面附近，电场强度大小不连续，电场强度有一跃变R1＜r＜R2，r＞R2，在带电面附近，电场强度大小不连续，电场强度有一跃变 这与5－20题分析讨论的结果一致.6－8　两个同心球面的半径分别为R1和R2，各自带有电荷Q1和Q2.求：(1)各区域电势分布，并画出分布曲线；(2)两球面间的电势差为多少？分析　通常可采用两种方法(1)由于电荷均匀分布在球面上，电场分布也具有球对称性，因此，可根据电势与电场强度的积分关系求电势.取同心球面为高斯面，借助高斯定理可求得各区域的电场强度分布，再由可求得电势分布.(2)利用电势叠加原理求电势.一个均匀带电的球面，在球面外产生的电势为在球面内电场强度为零，电势处处相等，等于球面的电势其中R是球面的半径.根据上述分析，利用电势叠加原理，将两个球面在各区域产生的电势叠加，可求得电势的分布.解1　(1)由高斯定理可求得电场分布 由电势可求得各区域的电势分布.当r≤R1时，有当R1≤r≤R2时，有当r≥R2时，有(2)两个球面间的电势差解2　(1)由各球面电势的叠加计算电势分布.若该点位于两个球面内，即r≤R1，则 若该点位于两个球面之间，即R1≤r≤R2，则若该点位于两个球面之外，即r≥R2，则(2)两个球面间的电势差6－9　一圆盘半径R＝3.00×10－2m.圆盘均匀带电，电荷面密度σ＝2.00×10－5C·m－2.(1)求轴线上的电势分布；(2)根据电场强度与电势梯度的关系求电场分布；(3)计算离盘心30.0cm处的电势和电场强度.分析　将圆盘分割为一组不同半径的同心带电细圆环，利用带电细环轴线上一点的电势公式，将不同半径的带电圆环在轴线上一点的电势积分相加，即可求得带电圆盘在轴线上的电势分布，再根据电场强度与电势之间的微分关系式可求得电场强度的分布.解　(1)带电圆环激发的电势由电势叠加，轴线上任一点P的电势的 (1)　　(2)轴线上任一点的电场强度为(2)电场强度方向沿x轴方向.(3)将场点至盘心的距离x＝30.0cm分别代入式(1)和式(2)，得当x＞＞R时，圆盘也可以视为点电荷，其电荷为.依照点电荷电场中电势和电场强度的计算公式，有由此可见，当x＞＞R时，可以忽略圆盘的几何形状，而将带电的圆盘当作点电荷来处理.在本题中作这样的近似处理，E和V的误差分别不超过0.3％和0.8％，这已足以满足一般的测量精度.6－10　在一次典型的闪电中，两个放电点间的电势差约为109Ｖ，被迁移的电荷约为30C.(1)如果释放出来的能量都用来使0℃的冰融化成0℃的水，则可溶解多少冰？(冰的融化热L＝3.34×105J·kg)(2)假设每一个家庭一年消耗的能量为300kW·h，则可为多少个家庭提供一年的能量消耗？解　(1)若闪电中释放出来的全部能量为冰所吸收，故可融化冰的质量即可融化约90吨冰.(2)一个家庭一年消耗的能量为 一次闪电在极短的时间内释放出来的能量约可维持3个家庭一年消耗的电能.6－11　一真空二极管，其主要构件是一个半径R１＝5.0×10－4m的圆柱形阴极和一个套在阴极外，半径R２＝4.5×10－3m的同轴圆筒形阳极．阳极电势比阴极电势高300V，阴极与阳极的长度均为L＝2.5×10－２m．假设电子从阴极射出时的速度为零．求：（１）该电子到达阳极时所具有的动能和速率；（２）电子刚从阳极射出时所受的力．分析　（1）由于半径R１＜＜L，因此可将电极视作无限长圆柱面，阴极和阳极之间的电场具有轴对称性．从阴极射出的电子在电场力作用下从静止开始加速，电子所获得的动能等于电场力所作的功，也即等于电子势能的减少．由此，可求得电子到达阳极时的动能和速率．（2）计算阳极表面附近的电场强度，由F＝qE求出电子在阴极表面所受的电场力．解　（1）电子到达阳极时，势能的减少量为由于电子的初始速度为零，故 因此电子到达阳极的速率为（2）两极间的电场强度为两极间的电势差负号表示阳极电势高于阴极电势．阴极表面电场强度电子在阴极表面受力这个力尽管很小，但作用在质量为９.1１×10－3１kg的电子上，电子获得的加速度可达重力加速度的5×10１5倍．6－12　一导体球半径为R１，外罩一半径为R2的同心薄导体球壳，外球壳所带总电荷为Q，而内球的电势为V０．求此系统的电势和电场的分布．分析　若，内球电势等于外球壳的电势，则外球壳内必定为等势体，电场强度处处为零，内球不带电．若，内球电势不等于外球壳电势， 则外球壳内电场强度不为零，内球带电．一般情况下，假设内导体球带电q，导体达到静电平衡时电荷的分布如图所示．依照电荷的这一分布，利用高斯定理可求得电场分布．并由或电势叠加求出电势的分布．最后将电场强度和电势用已知量V0、Q、R１、R2表示．解　根据静电平衡时电荷的分布，可知电场分布呈球对称．取同心球面为高斯面，由高斯定理，根据不同半径的高斯面内的电荷分布，解得各区域内的电场分布为r＜R１时，　R１＜r＜R2时，r＞R2时，由电场强度与电势的积分关系，可得各相应区域内的电势分布．r＜R１时，R１＜r＜R2时，　 r＞R2时，　也可以从球面电势的叠加求电势的分布．在导体球内（r＜R１）在导体球和球壳之间（R１＜r＜R2）在球壳外（r＞R2）由题意　得代入电场、电势的分布得r＜R１时，；R１＜r＜R2时，　 ；r＞R2时，；6－13　两线输电线，其导线半径为3.26mm，两线中心相距0.50m，导线位于地面上空很高处，因而大地影响可以忽略．求输电线单位长度的电容．解　由教材第六章6－4节例3可知两输电线的电势差因此，输电线单位长度的电容代入数据6－14　在A点和B点之间有5个电容器，其连接如图所示．（1）求A、B两点之间的等效电容；（2）若A、B之间的电势差为12V，求UAC、UCD和UDB．解　（1）由电容器的串、并联，有 求得等效电容CAB＝4μF．（2）由于，得6－15　半径为0.10cm的长直导线，外面套有内半径为1.0cm的共轴导体圆筒，导线与圆筒间为空气．略去边缘效应，求：（1）导线表面最大电荷面密度；（2）沿轴线单位长度的最大电场能量．分析　如果设长直导线上单位长度所带电荷为λ，导线表面附近的电场强度查表可以得知空气的击穿电场强度Eb＝3.0×106（V／m），只有当空气中的电场强度E≤Eb空气才不会被击穿，由于在导线表面附近电场强度最大，因而可以求出σ的极限值．再求得电场能量密度，并通过同轴圆柱形体元内电场能量的积分求得单位长度的最大电场强度．解　（1）导线表面最大电荷面密度 显然导线表面最大电荷面密度与导线半径无关．（2）由上述分析得，此时导线与圆筒之间各点的电场强度为(其他)沿轴线单位长度的最大电场能量7－1　两根长度相同的细导线分别多层密绕在半径为R和r的两个长直圆筒上形成两个螺线管，两个螺线管的长度相同，R＝2r，螺线管通过的电流相同为I，螺线管中的磁感强度大小BR、Br满足（　　）（A）　（B）　（C）　（D）分析与解　在两根通过电流相同的螺线管中，磁感强度大小与螺线管线圈单位长度的匝数成正比．根据题意，用两根长度相同的细导线绕成的线圈单位长度的匝数之比因而正确答案为（C）。7－2　一个半径为r的半球面如图放在均匀磁场中，通过半球面的磁通量为（　　） （A）　　　　　　（B）（C）（D）分析与解　作半径为r的圆S′与半球面构成一闭合曲面，根据磁场的高斯定理，磁感线是闭合曲线，闭合曲面的磁通量为零，即穿进半球面S的磁通量等于穿出圆面S′的磁通量；．因而正确答案为（D）．7－3　下列说法正确的是（　　）（A）闭合回路上各点磁感强度都为零时，回路内一定没有电流穿过（B）闭合回路上各点磁感强度都为零时，回路内穿过电流的代数和必定为零（C）磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度必定为零（D）磁感强度沿闭合回路的积分不为零时，回路上任意一点的磁感强度都不可能为零分析与解　由磁场中的安培环路定律，磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度不一定为零；闭合回路上各点磁感强度为零时，穿过回路的电流代数和必定为零。因而正确答案为（B）．7－7　如图所示，已知地球北极地磁场磁感强度B的大小为6.0×10－5T．如设想此地磁场是由地球赤道上一圆电流所激发的，此电流有多大？ 流向如何？解　设赤道电流为I，则由教材第7－4节例2知，圆电流轴线上北极点的磁感强度因此赤道上的等效圆电流为由于在地球地磁场的Ｎ极在地理南极，根据右手螺旋法则可判断赤道圆电流应该是由东向西流，与地球自转方向相反．7－8　如图所示，有两根导线沿半径方向接触铁环的a、b两点，并与很远处的电源相接。求环心O的磁感强度． 分析　根据叠加原理，点O的磁感强度可视作由ef、be、fa三段直线以及acb、adb两段圆弧电流共同激发．由于电源距环较远，．而be、fa两段直线的延长线通过点O，由于，由毕－萨定律知．流过圆弧的电流I1、I2的方向如图所示，两圆弧在点O激发的磁场分别为,其中I1、I2分别是圆弧acb、adb的弧长，由于导线电阻R与弧长l成正比，而圆弧acb、adb又构成并联电路，故有将B1、B2叠加可得点O的磁感强度B．解　由上述分析可知，点O的合磁感强度7－9　如图所示，几种载流导线在平面内分布，电流均为I，它们在点O的磁感强度各为多少？ 分析　应用磁场叠加原理求解．将不同形状的载流导线分解成长直部分和圆弧部分，它们各自在点O处所激发的磁感强度较容易求得，则总的磁感强度解　（ａ）长直电流对点O而言，有，因此它在点O产生的磁场为零，则点O处总的磁感强度为1/4圆弧电流所激发，故有B0的方向垂直纸面向外．（ｂ）将载流导线看作圆电流和长直电流，由叠加原理可得B0的方向垂直纸面向里．（c）将载流导线看作1/2圆电流和两段半无限长直电流，由叠加原理可得B0的方向垂直纸面向外．7－10　已知10mm2裸铜线允许通过50A电流而不会使导线过热．电流在导线横截面上均匀分布．求：（1）导线内、外磁感强度的分布；（2）导线表面的磁感强度． 分析　可将导线视作长直圆柱体，电流沿轴向均匀流过导体，故其磁场必然呈轴对称分布，即在与导线同轴的圆柱面上的各点，B大小相等．方向与电流成右手螺旋关系．为此，可利用安培环路定理，求出导线表面的磁感强度．解　（1）围绕轴线取同心圆为环路L，取其绕向与电流成右手螺旋关系，根据安培环路定理，有在导线内r＜R，，因而在导线外r＞R，，因而磁感强度分布曲线如图所示．（2）在导线表面磁感强度连续，由I＝50A，，得 7－11　有一同轴电缆，其尺寸如图（ａ）所示．两导体中的电流均为I，但电流的流向相反，导体的磁性可不考虑．试计算以下各处的磁感强度：（1）r＜R1；（2）R1＜r＜R2；（3）R2＜r＜R3；（4）r＞R3．画出B－r图线．分析　同轴电缆导体内的电流均匀分布，其磁场呈轴对称，取半径为r的同心圆为积分路径，，利用安培环路定理，可解得各区域的磁感强度．解　由上述分析得r＜R1R1＜r＜R2 R2＜r＜R3r＞R3磁感强度B（r）的分布曲线如图（ｂ）．7－4　一根无限长平行直导线载有电流I，一矩形线圈位于导线平面内沿垂直于载流导线方向以恒定速率运动（如图所示），则（　　）（A）线圈中无感应电流（B）线圈中感应电流为顺时针方向（C）线圈中感应电流为逆时针方向（D）线圈中感应电流方向无法确定分析与解　由右手定则可以判断，在矩形线圈附近磁场垂直纸面朝里，磁场是非均匀场，距离长直载流导线越远，磁场越弱．因而当矩形线圈朝下运动时，在线圈中产生感应电流， 感应电流方向由法拉第电磁感应定律可以判定．因而正确答案为（B）．7－5　将形状完全相同的铜环和木环静止放置在交变磁场中，并假设通过两环面的磁通量随时间的变化率相等，不计自感时则（　　）（A）铜环中有感应电流，木环中无感应电流（B）铜环中有感应电流，木环中有感应电流（C）铜环中感应电动势大，木环中感应电动势小（D）铜环中感应电动势小，木环中感应电动势大分析与解　根据法拉第电磁感应定律，铜环、木环中的感应电场大小相等，但在木环中不会形成电流．因而正确答案为（A）．7－6　对位移电流，下述四种说法中哪一种说法是正确的是（　　）（A）位移电流的实质是变化的电场（B）位移电流和传导电流一样是定向运动的电荷（C）位移电流服从传导电流遵循的所有定律（D）位移电流的磁效应不服从安培环路定理分析与解　位移电流的实质是变化的电场．变化的电场激发磁场，在这一点位移电流等效于传导电流，但是位移电流不是走向运动的电荷，也就不服从焦耳热效应、安培力等定律．因而正确答案为（A）．7－12　一铁心上绕有线圈100匝，已知铁心中磁通量与时间的关系为，求在时，线圈中的感应电动势．分析　由于线圈有N匝相同回路，线圈中的感应电动势等于各匝回路的感应电动势的代数和，在此情况下，法拉第电磁感应定律通常写成，其中称为磁链．解　线圈中总的感应电动势 当时，．7－13　有两根相距为d的无限长平行直导线，它们通以大小相等流向相反的电流，且电流均以的变化率增长．若有一边长为d的正方形线圈与两导线处于同一平面内，如图所示．求线圈中的感应电动势．分析　本题仍可用法拉第电磁感应定律来求解．由于回路处在非均匀磁场中，磁通量就需用来计算（其中B为两无限长直电流单独存在时产生的磁感强度B1与B2之和）．为了积分的需要，建立如图所示的坐标系．由于B仅与x有关，即，故取一个平行于长直导线的宽为ｄx、长为d的面元ｄS，如图中阴影部分所示，则，所以，总磁通量可通过线积分求得（若取面元，则上述积分实际上为二重积分）．本题在工程技术中又称为互感现象，也可用公式求解．解1　穿过面元ｄS的磁通量为 因此穿过线圈的磁通量为再由法拉第电磁感应定律，有解2　当两长直导线有电流I通过时，穿过线圈的磁通量为线圈与两长直导线间的互感为当电流以变化时，线圈中的互感电动势为试想：如线圈又以速率v沿水平向右运动，如何用法拉第电磁感应定律求图示位置的电动势呢？此时线圈中既有动生电动势，又有感生电动势．设时刻t，线圈左端距右侧直导线的距离为ξ，则穿过回路的磁通量，它表现为变量I和ξ的二元函数，将Φ代入即可求解，求解时应按复合函数求导，注意，其中，再令ξ＝d即可求得图示位置处回路中的总电动势．最终结果为两项，其中一项为动生电动势，另一项为感生电动势．7－14　如图（ａ）所示，把一半径为R的半圆形导线OP置于磁感强度为B的均匀磁场中，当导线以速率v水平向右平动时，求导线中感应电动势E的大小，哪一端电势较高？ 分析　本题及后面几题中的电动势均为动生电动势，除仍可由求解外（必须设法构造一个闭合回路），还可直接用公式求解．在用后一种方法求解时，应注意导体上任一导线元ｄl上的动生电动势.在一般情况下，上述各量可能是ｄl所在位置的函数．矢量（v×B）的方向就是导线中电势升高的方向．解1　如图（ｂ）所示，假想半圆形导线OP在宽为2R的静止形导轨上滑动，两者之间形成一个闭合回路．设顺时针方向为回路正向，任一时刻端点O或端点P距形导轨左侧距离为x，则即由于静止的形导轨上的电动势为零，则E＝－2RvB．式中负号表示电动势的方向为逆时针，对OP段来说端点P的电势较高．解2　建立如图（c）所示的坐标系，在导体上任意处取导体元ｄl，则 由矢量（v×B）的指向可知，端点P的电势较高．解3　连接OP使导线构成一个闭合回路．由于磁场是均匀的，在任意时刻，穿过回路的磁通量常数.由法拉第电磁感应定律可知，E＝0又因E＝EOP＋EPO即EOP＝－EPO＝2RvB由上述结果可知，在均匀磁场中，任意闭合导体回路平动所产生的动生电动势为零；而任意曲线形导体上的动生电动势就等于其两端所连直线形导体上的动生电动势．上述求解方法是叠加思想的逆运用，即补偿的方法．7－15　长为L的铜棒，以距端点r处为支点，以角速率ω绕通过支点且垂直于铜棒的轴转动.设磁感强度为B的均匀磁场与轴平行，求棒两端的电势差．分析　应该注意棒两端的电势差与棒上的动生电动势是两个不同的概念，如同电源的端电压与电源电动势的不同．在开路时，两者大小相等，方向相反（电动势的方向是电势升高的方向， 而电势差的正方向是电势降落的方向）．本题可直接用积分法求解棒上的电动势，亦可以将整个棒的电动势看作是OA棒与OB棒上电动势的代数和，如图（ｂ）所示．而EOA和EOB则可以直接利用第８－2节例1给出的结果．解1　如图（ａ）所示，在棒上距点O为l处取导体元ｄl，则因此棒两端的电势差为当L＞2r时，端点A处的电势较高解2　将AB棒上的电动势看作是OA棒和OB棒上电动势的代数和，如图（ｂ）所示．其中,则7－16　如图（ａ）所示，在“无限长”直载流导线的近旁，放置一个矩形导体线框，该线框在垂直于导线方向上以匀速率v向右移动，求在图示位置处，线框中感应电动势的大小和方向． 分析　本题亦可用两种方法求解．其中应注意下列两点：1．当闭合导体线框在磁场中运动时，线框中的总电动势就等于框上各段导体中的动生电动势的代数和．如图（ａ）所示，导体eh段和fg段上的电动势为零［此两段导体上处处满足］，因而线框中的总电动势为其等效电路如图（ｂ）所示．2．用公式求解，式中Φ是线框运动至任意位置处时，穿过线框的磁通量．为此设时刻t时，线框左边距导线的距离为ξ，如图（c）所示，显然ξ是时间t的函数，且有．在求得线框在任意位置处的电动势E（ξ）后，再令ξ＝d，即可得线框在题目所给位置处的电动势．解1　根据分析，线框中的电动势为由Eef＞Ehg可知，线框中的电动势方向为efgh．解2　设顺时针方向为线框回路的正向．根据分析，在任意位置处，穿过线框的磁通量为相应电动势为 令ξ＝d，得线框在图示位置处的电动势为由E＞0可知，线框中电动势方向为顺时针方向．7－17　在半径为R的圆柱形空间中存在着均匀磁场，B的方向与柱的轴线平行．如图（ａ）所示，有一长为l的金属棒放在磁场中，设B随时间的变化率为常量．试证：棒上感应电动势的大小为分析　变化磁场在其周围激发感生电场，把导体置于感生电场中，导体中的自由电子就会在电场力的作用下移动，在棒内两端形成正负电荷的积累，从而产生感生电动势．由于本题的感生电场分布与上题所述情况完全相同，故可利用上题结果，由计算棒上感生电动势．此外，还可连接OP、OQ，设想PQOP构成一个闭合导体回路，用法拉第电磁感应定律求解， 由于OP、OQ沿半径方向，与通过该处的感生电场强度Ek处处垂直，故，OP、OQ两段均无电动势，这样，由法拉第电磁感应定律求出的闭合回路的总电动势，就是导体棒PQ上的电动势．证1　由法拉第电磁感应定律，有证2　由题８－17可知，在r＜R区域，感生电场强度的大小设PQ上线元ｄx处，Ek的方向如图（b）所示，则金属杆PQ上的电动势为讨论　假如金属棒PQ有一段在圆外，则圆外一段导体上有无电动势？该如何求解？'