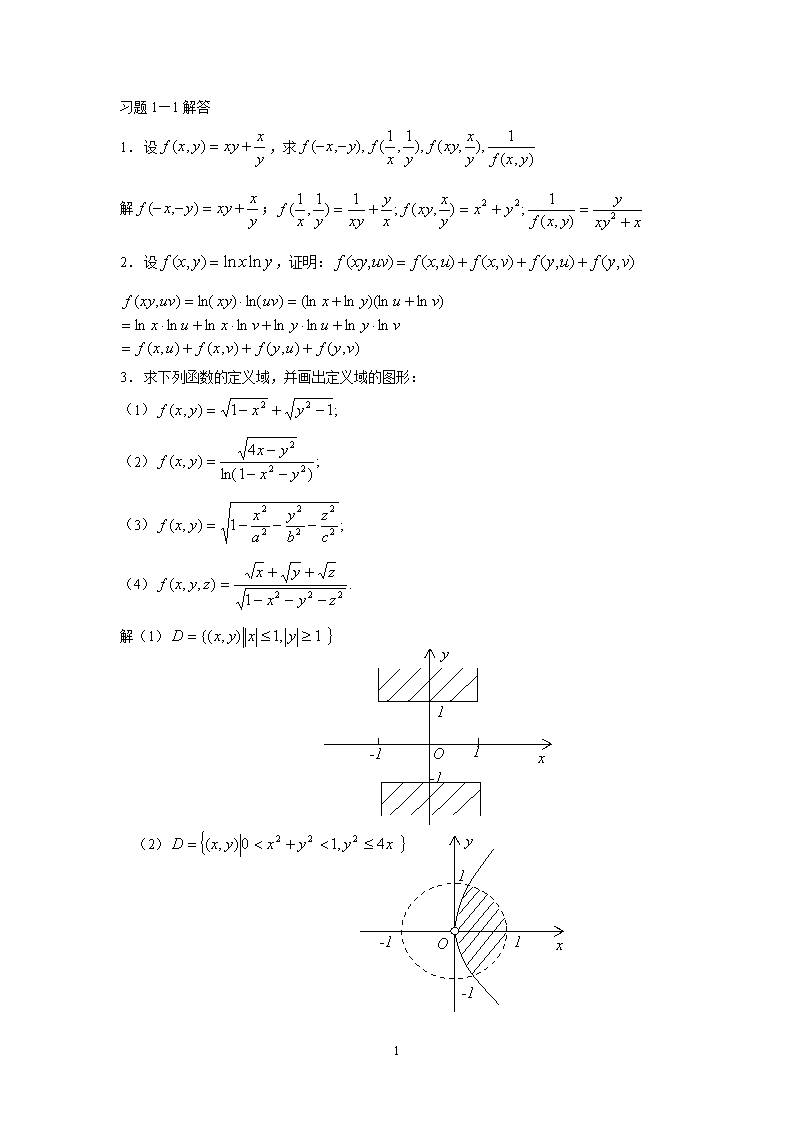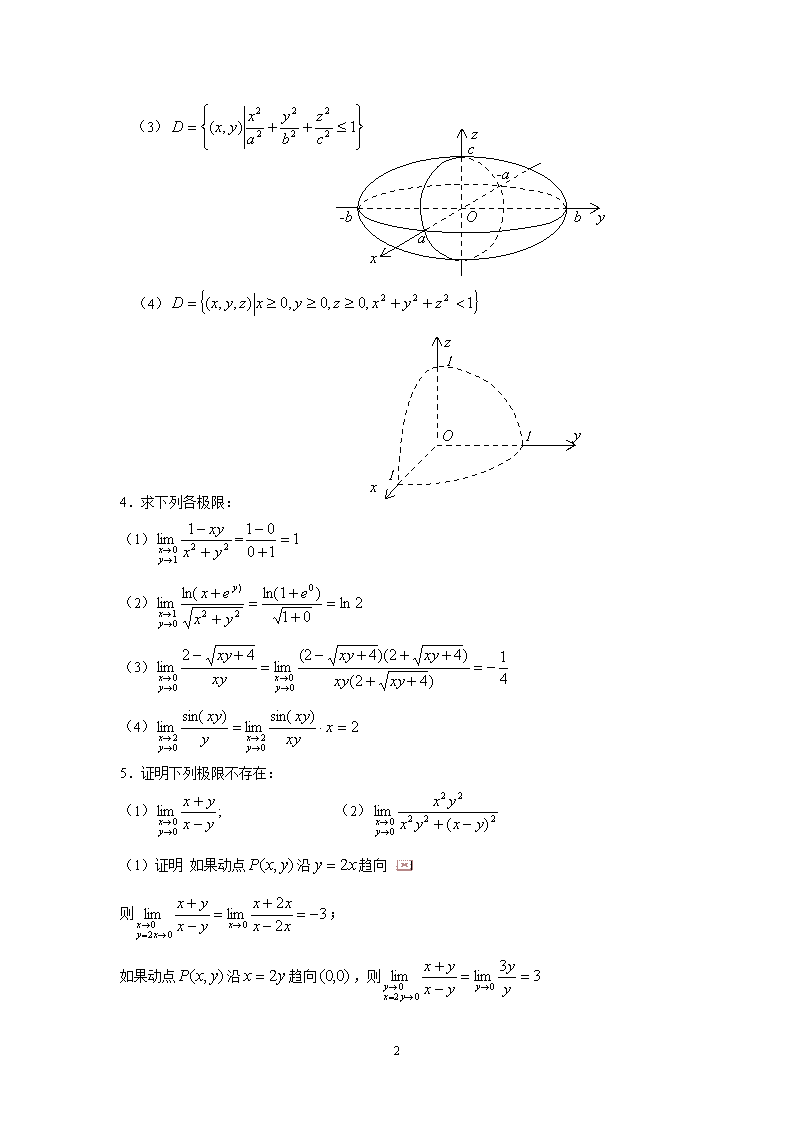微积分 第一章习题解答(下).doc 18页

'习题1—1解答1．设，求解；2．设，证明：3．求下列函数的定义域，并画出定义域的图形：（1）（2）（3）（4）yx11-1-1O解（1）yx11-1-1O（2）18 yx-a-bcOzab（3）（4）yx１Oz１１4．求下列各极限：（1）=（2）（3）（4）5．证明下列极限不存在：（1）（2）（1）证明如果动点沿趋向则；如果动点沿趋向，则18 所以极限不存在。（2）证明：如果动点沿趋向则；如果动点沿趋向，则所以极限不存在。6．指出下列函数的间断点：（1）；（2）。解（1）为使函数表达式有意义，需，所以在处，函数间断。（2）为使函数表达式有意义，需，所以在处，函数间断。习题1—21．（1）；.(2)(3),lnz=yln(1+xy)，两边同时对y求偏导得;(4),18 (5);(6),,;2.(1);(2).3,.4.5.(1),,;(2),,,;(3),,;18 (4),,.6.设对角线为z,则,,当时,=-0.05(m).7.设两腰分别为x、y,斜边为z,则，,,设x、y、z的绝对误差分别为、、,当时,=0.124,z的绝对误差z的相对误差.8.设内半径为r，内高为h，容积为V，则,,,,当时,.习题1—31.==.18 2.====.3.(1)=,=.(2)=,=,=.(3)=,=,=.(4)==,=.4.(1),,,,(2),,.18 5,,,.6(1)设,,,,,=,=,18 =,,(3)设,,=,=.(4)设,,,,7.设,,,,,1.8.设,,.9.(1)方程两边同时对x求导得解之得18 (2)方程两边同时对z求导得解之得(3)方程两边同时对x求偏导得解之得同理方程两边同时对y求偏导得解之得习题1－41．求下列函数的方向导数（1）解：（2）解：18 （3）与轴夹角为解：由题意知则（4）1．求下列函数的梯度（1）18 解：,)(2)解：，）。1．一个登山者在山坡上点处，山坡的高度z由公式近似，其中x和y是水平直角坐标，他决定按最陡的道路上登，问应当沿什么方向上登。解：按最陡的道路上登，应当沿（3，4）方向上登。2．解：沿方向3．解：设路径为，在点处在点的切向量为平行于切向量因为过18 习题1-51、求曲线在对应于点处的切线及法平面方程。解：当时，，故所求切线方程为：，即:法平面方程为：即:2、求下列空间曲线在指定点处的切线和法平面方程（1）在点解：将方程两端对x求导，得在处故所求的切线方程为：法平面方程：（2）在点解法1：将方程两端对x求导，得Þ当时，有，18 故所求的切线方程为：法平面方程：即：解法2：将方程组两端求微分：得∴曲线在点处的切向量为3.（题略）解：（1）令F（x，y，z）=arctg-z,=-1，曲面在点P的切平面方程为：-，即：x-y-2z-=0；法线方程为：，即：；（2）令则，，曲面在点(1,1,1)点处的切平面的法向量为：故所求的切平面方程为：即：法线方程为：（3）令F（x，y，z）=2+2-8，=-16ln2，曲面在点P的切平面方程为：4ln2（x-2）-4ln2（y-2）-16ln2（z-1）=0，即：x-y-4z=0，法线方程为：，即：18 4、解：，又∵抛物线在(1,2)点处的切线斜率为：∴抛物线在(1,2)点处偏向x轴正向的切线方向为∴故所求的方向导数为：习题1-61（题略）.解：由,有x=2,y=-2,即P(2,-2)为f(x,y)的驻点,又D（P）=4>0,=-2故P(2,-2)为f(x,y)的极大值点,其极大值为f(2,-2)=8.2（题略）.解：由有驻点：(5,6)和，而∴在点(5,6)取得极小值又∵∴在点不取得极值18 3、求在闭区域上的最大值和最小值解：由，得唯一驻点(0,0)又∵在边界即椭圆上,由，得驻点：∴所有可能的极值点为：(0,0)(2,0)(-2,0)（0,-1）(0,1)相应的函数值为：044-1-14、求抛物线和直线之间的最短距离。解：设P(x,y)为抛物线上任意一点，它到直线的距离为，d最小当且仅当最小此问题即是求在条件下的最小值。解法1（用拉格朗日乘数法）设由，即得唯一驻点故由实际问题知抛物线和直线之间的最短距离在在，为：解法2（转化为无条件极值）设抛物线上点，它到直线的距离为18 ∵d最小当且仅当最小设∴Þ唯一驻点∴当时，有极小值，从而该极小值就是所求的最小值（∵唯一驻点）∵=故抛物线和直线之间的最短距离为5、求抛物线被平面截成一椭圆，求原点到此椭圆的最长与最短距离。解：设椭圆上任意一点为(x,y,z)，它到原点的距离为此问题即是求在条件下的最大值和最小值。令由由①-②得若代入①，得，18 再代入④，<0,不合题意，有代入④，⑤由，解得，∴驻点为：和∴，由实际问题知，所求最大值和最小值存在，分别为和6（题略）.解:设圆柱高为H,圆锥高为h,圆柱圆锥底半径为r,则浮标体积V=,故:3V-=0(1)浮标表面积S(r,h,H)=令L(r,h,H)=+由=0（2）=0(3)(4)有,代入（3）有,故,r=h,再由（2），有H=h,h=,(r,,)为S(r,h,H)唯一驻点，由于实际问题存在最值，故当H=h,时,材料最省。18 7（题略）解设BC=a,则横截面积S=(BC+AD)h=,湿周由(1)(2)由(2)有1-2cos,,由(1),h=,即()为唯一驻点，故当,h=时，湿周最小.18'