数学理科选修4-4《极坐标》完整版 经典习题及详细答案.doc 29页

'数学理科选修4-4第一讲《极坐标》习题一．选择题1．已知，下列所给出的不能表示点的坐标的是（）A．B．C．D．2．点，则它的极坐标是（）A．B．C．D．3．极坐标方程表示的曲线是（）A．双曲线B．椭圆C．抛物线D．圆4．圆的圆心坐标是（）A．B．C．D．5．在极坐标系中，与圆相切的一条直线方程为（）A．B．C．D．6、已知点则为（）A、正三角形　B、直角三角形　C、锐角等腰三角形　D、直角等腰三角形　　7、表示的图形是（）A．一条射线B．一条直线C．一条线段D．圆8、直线与的位置关系是（）第29页共21页 　A、平行　　B、垂直　C、相交不垂直　　D、与有关，不确定9.两圆,的公共部分面积是（）A.B.C.D.10.已知点的球坐标是,的柱坐标是,求.A．B．C．D．二．填空题11．极坐标方程化为直角坐标方程是12．圆心为，半径为3的圆的极坐标方程为13．已知直线的极坐标方程为，则极点到直线的距离是14、在极坐标系中，点P到直线的距离等于____________。15、与曲线关于对称的曲线的极坐标方程是_______________。三．解答题16．说说由曲线得到曲线的变化过程，并求出坐标伸缩变换。17．已知，O为极点，求使是正三角形的点坐标。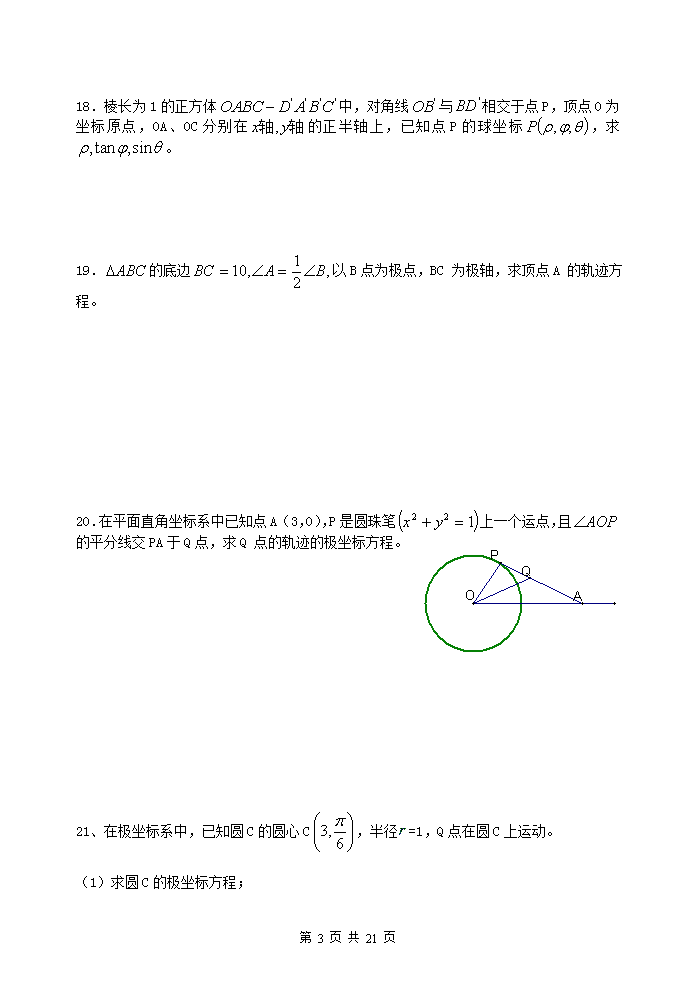第29页共21页 18．棱长为1的正方体中，对角线与相交于点P，顶点O为坐标原点，OA、OC分别在的正半轴上，已知点P的球坐标，求。19．的底边以B点为极点，BC为极轴，求顶点A的轨迹方程。20．在平面直角坐标系中已知点A（3，0），P是圆珠笔上一个运点，且的平分线交PA于Q点，求Q点的轨迹的极坐标方程。21、在极坐标系中，已知圆C的圆心C，半径=1，Q点在圆C上运动。（1）求圆C的极坐标方程；第29页共21页 （2）若P在直线OQ上运动，且OQ∶QP=2∶3，求动点P的轨迹方程。22、建立极坐标系证明：已知半圆直径∣AB∣=2（>0），半圆外一条直线与AB所在直线垂直相交于点T，并且∣AT∣=2。若半圆上相异两点M、N到的距离∣MP∣，∣NQ∣满足∣MP∣∶∣MA∣=∣NQ∣∶∣NA∣=1，则∣MA∣+∣NA∣=∣AB∣。　23．如图，，D是垂足，H是AD上任意一点，直线BH与AC交于E点，直线CH与AB交于F点，求证：第29页共21页 选修4-4第一讲《极坐标》答案一．选择题题号12345678910答案ACDABD　ABCA二．填空题11．；12．；13．；14．；15．三．解答题16．解：的图象上的点的纵坐标不变，横坐标缩短为原来的，得到，再将其纵坐标伸长为原来的3倍，横坐标不变，得到曲线。设，变换公式为将其代入得，17.或18.19.解:设是曲线上任意一点,在中由正弦定理得:得A的轨迹是:20.解:以O为极点,轴正半轴为极轴建立极坐标系,设,第29页共21页 21．（1）（2）22．证法一：以A为极点，射线AB为极轴建立直角坐标系，则半圆的的极坐标方程为，设，则，，又，，是方程的两个根，由韦达定理：，证法二：以A为极点，射线AB为极轴建立直角坐标系，则半圆的的极坐标方程为，设又由题意知，在抛物线上，，，是方程的两个根，由韦达定理：，23．证明：以BC所在的直线为轴，AD所在的直线为轴建立直角坐标系，设，，，，则，即，即，即，即第29页共21页 ，高二数学理科选修4-4第二讲参数方程测试题班别姓名学号一．选择题（每题5分共60分）1．设椭圆的参数方程为，，是椭圆上两点，M，N对应的参数为且，则()A．B．C．D．2.直线：3x-4y-9=0与圆：，(θ为参数)的位置关系是()A.相切B.相离C.直线过圆心D.相交但直线不过圆心3.经过点M(1，5)且倾斜角为的直线，以定点M到动点P的位移t为参数的参数方程是()A.B.C.D.4.参数方程(t为参数)所表示的曲线是()A.一条射线B.两条射线C.一条直线D.两条直线第29页共21页 5．若动点(x,y)在曲线(b>0)上变化，则x2+2y的最大值为()(A)；(B)；(C)(D)2b。6．实数x、y满足3x2＋2y2=6x，则x2＋y2的最大值为（）A、　　B、4C、　D、57．曲线的参数方程为(t是参数)，则曲线是()A、线段　　B、双曲线的一支　　C、圆　　D、射线8．已知动园：，则圆心的轨迹是()A、直线　　　B、圆　　　　C、抛物线的一部分　　　　D、椭圆9．在参数方程（t为参数）所表示的曲线上有B、C两点，它们对应的参数值分别为t1、t2，则线段BC的中点M对应的参数值是()10．设,那么直线与圆的位置关系是()A、相交　　B、相切　　C、相离　　D、视的大小而定11．下列参数方程（t为参数）中与普通方程x2-y=0表示同一曲线的是()第29页共21页 12．已知过曲线上一点P，原点为O，直线PO的倾斜角为，则P点坐标是()A、（3，4）　　B、　　C、(-3，-4)　　　D、二．填空题（每题5分共25分）13．过抛物线y2=4x的焦点作倾斜角为的弦，若弦长不超过8，则的取值范围是____________。14．直线上与点距离等于的点的坐标是15．圆锥曲线的准线方程是16．直线过点，倾斜角是，且与直线交于，则的长为17．曲线（α为参数）与曲线（β为参数）的离心率分别为e1和e2，则e1＋e2的最小值为_______________.三．解答题（共65分）18．19．已知方程。（1）试证：不论如何变化，方程都表示顶点在同一椭圆上的抛物线；第29页共21页 （2）为何值时，该抛物线在直线x=14上截得的弦最长？并求出此弦长。20．已知椭圆上两个相邻顶点为A、C，又B、D为椭圆上的两个动点，且B、D分别在直线AC的两旁，求四边形ABCD面积的最大值。21.已知过点P(1，-2)，倾斜角为的直线l和抛物线x2=y+m(1)m取何值时，直线l和抛物线交于两点?(2)m取何值时，直线l被抛物线截下的线段长为.第29页共21页 第二讲参数方程测试题答案题号123456789101112答案BDABABDDBBDD13．;14．;15．;16．;17．18．解：把直线参数方程化为标准参数方程19（1）把原方程化为，知抛物线的顶点为它是在椭圆上；（2）当时，弦长最大为12。20、21．(1)m＞,(2)m=3第29页共21页 高二数学理科选修4-4参数方程单元练习 (一)选择题：[   ]A．(2，-7)          B．(1，0)A．20°  B．70°C．110°    D．160°[   ]A．相切 B．相离C．直线过圆心   D．相交但直线不过圆心A．椭圆     B．双曲线C．抛物线     D．圆[   ]C．5         D．6(二)填空题：第29页共21页 8．设y=tx(t为参数)，则圆x2+y2-4y=0的参数方程是______．10．当m取一切实数时，双曲线x2-y2-6mx-4my+5m2-1=0的中心的轨迹方程为______．(三)解答题：时矩形对角线的倾斜角α．13．直线l经过两点P(-1，2)和Q(2，-2)，与双曲线(y-2)2-x2=1相交于两点A、B，(1)根据下问所需写出l的参数方程；(2)求AB中点M与点P的距离．第29页共21页 14．设椭圆4x2+y2=1的平行弦的斜率为2，求这组平行弦中点的轨迹．15．若不计空气阻力，炮弹运行轨道是抛物线．现测得我炮位A与炮击目标B在同一水平线上，水平距离为6000米，炮弹运行的最大高度为1200米．试求炮弹的发射角α和发射初速度v0(重力加速度g=9.8米/秒2)．第29页共21页 参数方程单元练习答案提示(一)1．C 2．C 3．D 4．B 5．A(二)6．(1，0)，(-5，0)7.4x2-y2=16(x≥2)9．(-1，5)，(-1，-1)10．2x+3y=0(三)11．圆x2+y2-x-y=0．14．取平行弦中的一条弦AB在y轴上的截距m为参数，并设A(x1，第29页共21页 设弦AB的中点为M(x，y)，则15．在以A为原点，直线AB的x轴的直角坐标系中，弹道方程是它经过最高点(3000，1200)和点B(6000，0)的时间分别设为t0和2t0，代入参数方程，得第29页共21页 高二数学理科选修4-4极坐标与参数方程单元考试一、选择题（每小题5分，共25分）1、已知点M的极坐标为，下列所给出的四个坐标中能表示点M的坐标是（）。A.B.C.D.2、直线：3x-4y-9=0与圆：，(θ为参数)的位置关系是()A.相切B.相离C.直线过圆心D.相交但直线不过圆心3、在参数方程（t为参数）所表示的曲线上有B、C两点，它们对应的参数值分别为t1、t2，则线段BC的中点M对应的参数值是（）4、曲线的参数方程为(t是参数)，则曲线是（）A、线段　　B、双曲线的一支　　C、圆　　D、射线5、实数x、y满足3x2＋2y2=6x，则x2＋y2的最大值为（）A、　　B、4C、　D、5第29页共21页 二、填空题（每小题5分，共30分）1、点的极坐标为。2、若A，B，则|AB|=___________，___________。（其中O是极点）3、极点到直线的距离是_____________。4、极坐标方程表示的曲线是____________。5、圆锥曲线的准线方程是。6、直线过点，倾斜角是，且与直线交于，则的长为。三、解答题（第1题14分，第2题16分，第3题15分；共45分）1、求圆心为C，半径为3的圆的极坐标方程。2、已知直线l经过点P(1,1),倾斜角，（1）写出直线l的参数方程。（2）设l与圆相交与两点A、B，求点P到A、B两点的距离之积。3、求椭圆。第29页共21页 第29页共21页 高二选修4-4极坐标与参数方程单元考试【试题答案】一、选择题：1、D2、D3、B4、D5、B二、填空题：1、或写成。2、5，6。3、。4、5、。6、。三、解答题1、1、如下图，设圆上任一点为P（），则而点OA符合2、解：（1）直线的参数方程是（2）因为点A,B都在直线l上，所以可设它们对应的参数为t1和t2,则点A,B的坐标分别为以直线L的参数方程代入圆的方程整理得到①因为t1和t2是方程①的解，从而t1t2＝－2。所以|PA|·|PB|=|t1t2|＝|－2|＝2。3、（先设出点P的坐标，建立有关距离的函数关系）第29页共21页 高二数学理科坐标系与参数方程测验题1.已知点P的极坐标是（1，），则过点P且垂直极轴的直线极坐标方程是.2.在极坐标系中，曲线一条对称轴的极坐标方程.3.在极坐标中，若过点(3，0)且与极轴垂直的直线交曲线于A、B两点.则|AB|=.4.已知三点A(5，)，B(-8，)，C(3，)，则ΔABC形状为.5.已知某圆的极坐标方程为：ρ2–4ρcon(θ-π/4)+6=0则：①圆的普通方程；②参数方程；③圆上所有点（x,y）中xy的最大值和最小值分别为、.6.设椭圆的参数方程为，，是椭圆上两点，M、N对应的参数为且，则大小关系是.7.直线：3x-4y-9=0与圆：，(θ为参数)的位置关系是.8.经过点M0(1，5)且倾斜角为的直线，以定点M0到动点P的位移t为参数的参数方程是.且与直线交于,则的长为.9.参数方程(t为参数)所表示的图形是.10.方程(t是参数)的普通方程是.与x轴交点的直角坐标是11.画出参数方程（为参数）所表示的曲线.12.已知动园：，则圆心的轨迹是.第29页共21页 13.已知过曲线上一点P，原点为O，直线PO的倾斜角为，则P点坐标是.14.直线(t为参数)上对应t=0,t=1两点间的距离是.15.直线(t为参数)的倾斜角是.16.设,那么直线与圆的位置关系是.17.直线上与点距离等于的点的坐标是.18.过抛物线y2=4x的焦点作倾斜角为的弦，若弦长不超过8，则的取值范围是________________________________.19.若动点(x,y)在曲线(b>0)上变化，则x2+2y的最大值为.20.曲线(α为参数)与曲线(β为参数)的离心率分别为e1和e2,则e1＋e2的最小值为_______________.第29页共21页 坐标系与参数方程测验题答案1.ρcosθ=-1；2.；3.；4.等边三角形；5.(x-2)2+(y-2)2=2;;9、1；6.θ1>θ2；7.相交；8.10+6；9.两条射线；10.x-3y=5(x≥2);(5,0)；12.椭圆；13.；14.;15.700；16.相切；17.（-1，2）或（-3，4）；18.；19.；20.第29页共21页 高二数学理科选修4-4学情调查第I卷一、选择题：本大题共10题，每小题3分，共30分。在每一题给出的四个选项中，只有一项是符合题目要求的，请把正确答案代号填在第II卷的选择题答案表中。1.曲线的极坐标方程化为直角坐标为（）。A.B.C.D.2.已知点P的极坐标是（1，），则过点P且垂直极轴的直线方程是（）。A.B.C.D.3.直线的参数方程是（）。A.（t为参数）B.（t为参数）C.（t为参数）D.（t为参数）4.方程（t为参数）表示的曲线是（）。A.一条直线B.两条射线C.一条线段D.抛物线的一部分5.参数方程（为参数）化为普通方程是（）。A.B.C.D.6.设点P对应的复数为-3+3i，以原点为极点，实轴正半轴为极轴建立极坐标系，则点P的极坐标为（）A.(，)B.(，)C.(3，)D.(-3，)7.在符合互化条件的直角坐标系和极坐标系中，直线l：与曲线C：相交，则k的取值范围是（）。A.B.C.D.但8.已知过曲线上一点P原点O的直线PO的倾斜角为，则P点坐标是A、（3，4）　　B、　　C、(-3，-4)　　　D、第29页共21页 9.若圆的方程为（为参数），直线的方程为（t为参数），则直线与圆的位置关系是（）。A.相交过圆心B.相交而不过圆心C.相切D.相离0xy0xy0xy0xy10.参数方程（为参数）所表示的曲线是（）。ABCD二、填空题：本大题共有4小题，每小题4分，共16分。把答案填在第II卷指定横线上。11.在同一平面直角坐标系中，直线变成直线的伸缩变换是。12.在极坐标中，若过点（3，0）且与极轴垂直的直线交曲线于A、B两点，则|AB|=。13.设直线参数方程为（为参数），则它的斜截式方程为。14.三、解答题：本大题有6题,，共54分，解答应写出文字说明，证明过程或演算步骤。把答案填在第II卷指定的横线上。(8分+8分+8分+10分+10分+10分)15.把下列参数方程化为普通方程，并说明它们各表示什么曲线：（8分）⑴（为参数）；⑵（为参数）16.求以椭圆内一点A(1，－1)为中点的弦所在直线的方程。（8分）第29页共21页 17.已知x、y满足，求的最值。（8分）18.如图，点A在直线x=5上移动，等腰△OPA的顶角∠OPA为120°（O，P，A按顺时针方向排列），求点P的轨迹方程。19.如图，过抛物线（＞0）的顶点作两条互相垂直的弦OA、OB。⑴设OA的斜率为k，试用k表示点A、B的坐标；第29页共21页 0xyAMB⑵求弦AB中点M的轨迹方程。（10分）20.在气象台A正西方向300千米处有一台风中心，它以每小时40千米的速度向东北方向移动，距台风中心250千米以内的地方都要受其影响。问：从现在起，大约多长时间后，气象台A所在地将遭受台风影响？持续多长时间？（10分）（注：，）选修4-4考试卷数学科答案一．选择题（每小题3分，共30分）第29页共21页 题号12345678910答案BCCBDAADBD二．填空题（每小题4分，共16分）11．；12．；13．；14．。三．解答题（8分+8分+8分+10分+10分+10分,共54分）15．（8分）解：⑴．∵∴两边平方相加，得即∴曲线是长轴在x轴上且为10，短轴为8，中心在原点的椭圆。⑵．∵∴由代入，得∴∴它表示过（0，）和(1,0)的一条直线。16．（8分）解：设以A(1，－1)为中点的弦所在的直线方程为，把它代入得即∵弦以A(1，－1)为中点，∴交点所对应的参数和有：＋＝0∴∴＝0，∴∴所求的直线方程为即x－4y－5＝017．（8分）解：由可知曲线表示以（1，-2）为圆心，半径等于2的圆。令，则（其中）∵-11∴当时，S有最大值，为当时，S有最小值，为∴S最大值为；S最小值为。第29页共21页 18．（10分）解：取O为极点，x正半轴为极轴，建立极坐标系，则直线x=5的极坐标方程为rcosq=5设A（r0，q0），P（r，q）把<2>代入<1>，得点P的轨迹的极坐标方程为：0xyAMB19．（10分）解：⑴．∵依题意可知直线OA的斜率存在且不为0∴设直线OA的方程为（）∴联立方程解得以代上式中的，解方程组解得∴A（，），B（，）。⑵．设AB中点M（x，y），则由中点坐标公式，得消去参数k，得；即为M点轨迹的普通方程。B1yx0AB220．（10分）解：如图，以气象台为坐标原点，正东方向为x轴正方向，建立直角坐标系，则现在台风中心B1的坐标为（-300，0）。根据题意，可知，t小时后，B的坐标为（，），即（，），因为以台风中心为圆心，以250千米为半径的圆上或圆内的点将遭受台风影响，所以B在圆上或圆内时，气象台将受台风影响。所以令，即整理得解得，故大约2小时后，气象台A所在地将遭受台风影响，大约持续6个半小时。第29页共21页'