理论力学第三版(周衍柏)习题答案.doc 160页

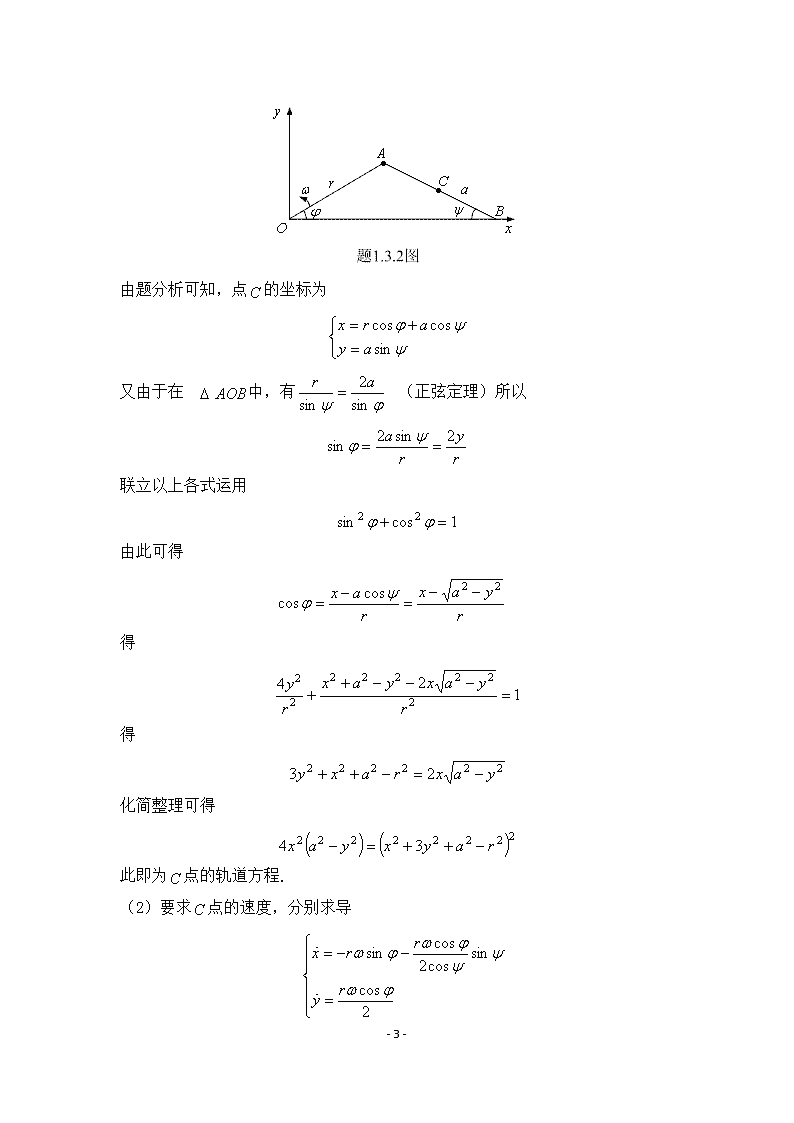
'第一章质点力学第一章习题解答1.1由题可知示意图如题1.1.1图:设开始计时的时刻速度为,由题可知枪弹作匀减速运动设减速度大小为.则有:由以上两式得再由此式得证明完毕.1.2解由题可知,以灯塔为坐标原点建立直角坐标如题1.2.1图.设船经过小时向东经过灯塔,则向北行驶的船经过小时经过灯塔任意时刻船的坐标-160- ，船坐标，则船间距离的平方即对时间求导船相距最近，即，所以即午后45分钟时两船相距最近最近距离km1.3解如题1.3.2图-160- 由题分析可知，点的坐标为又由于在中，有（正弦定理）所以联立以上各式运用由此可得得得化简整理可得此即为点的轨道方程.（2）要求点的速度，分别求导-160- 其中又因为对两边分别求导故有所以1.4解如题1.4.1图所示，绕点以匀角速度转动，在上滑动，因此点有一个垂直杆的速度分量点速度又因为所以点加速度-160- 1.5解由题可知，变加速度表示为由加速度的微分形式我们可知代入得对等式两边同时积分可得：（为常数）代入初始条件：时，，故即又因为所以对等式两边同时积分，可得：1.6解由题可知质点的位矢速度-160- ①沿垂直于位矢速度又因为，即即（取位矢方向，垂直位矢方向）所以故即沿位矢方向加速度垂直位矢方向加速度对③求导对④求导把③④⑦⑧代入⑤⑥式中可得1.7解由题可知-160- ①②对①求导③对③求导④对②求导⑤对⑤求导⑥对于加速度，我们有如下关系见题1.7.1图即⑦--⑧对⑦⑧俩式分别作如下处理：⑦，⑧即得⑨--⑩⑨+⑩得⑾把④⑥代入⑾得同理可得1.8解以焦点为坐标原点，运动如题1.8.1图所示]-160- 则点坐标对两式分别求导故如图所示的椭圆的极坐标表示法为对求导可得（利用）又因为即所以故有-160- 即（其中为椭圆的半短轴）1.9证质点作平面运动，设速度表达式为令为位矢与轴正向的夹角，所以所以又因为速率保持为常数，即为常数对等式两边求导所以即速度矢量与加速度矢量正交.1.10解由题可知运动轨迹如题1.10.1图所示，-160- 则质点切向加速度法向加速度，而且有关系式①又因为②所以③④联立①②③④⑤又把两边对时间求导得-160- 又因为所以⑥把⑥代入⑤既可化为对等式两边积分所以1.11解由题可知速度和加速度有关系如图1.11.1所示两式相比得-160- 即对等式两边分别积分即此即质点的速度随时间而变化的规律.1.12证由题1.11可知质点运动有关系式①②所以，联立①②，有又因为所以，对等式两边分别积分，利用初始条件时，1.13证（）当，即空气相对地面上静止的，有.式中质点相对静止参考系的绝对速度，指向点运动参考系的速度，指运动参考系相对静止参考系的速度.可知飞机相对地面参考系速度：=，即飞机在舰作匀速直线运动.所以飞机来回飞行的总时间-160- .（）假定空气速度向东，则当飞机向东飞行时速度飞行时间当飞机向西飞行时速度飞行时间故来回飞行时间即同理可证，当空气速度向西时，来回飞行时间（c）假定空气速度向北.由速度矢量关系如题1.13.1图-160- 所以来回飞行的总时间同理可证空气速度向南时，来回飞行总时间仍为1.14解正方形如题1.14.1图。由题可知设风速,,当飞机，故飞机沿此边长6正方形飞行一周所需总时间-160- 1.15解船停止时，干湿分界线在蓬前3，由题画出速度示意图如题.15.1图故又因为，所以由图可知所以=81.16解以一岸边为轴，垂直岸的方向为轴.建立如题1.16.1图所示坐标系.-160- 所以水流速度又因为河流中心处水流速度为所以。当时，即①--②得，两边积分③联立②③，得④同理，当时，即⑤由④知，当时，代入⑤得有-160- ，所以船的轨迹船在对岸的了；靠拢地点，即时有1.17解以为极点，岸为极轴建立极坐标如题.17.1图.船沿垂直于的方向的速度为，船沿径向方向的速度为和沿径向的分量的合成，即①--②②/①得，对两积分：设为常数，即代入初始条件时，.设有得-160- 1.18解如题1.18.1图质点沿下滑，由受力分析我们可知质点下滑的加速度为.设竖直线，斜槽，易知，由正弦定理即①又因为质点沿光滑面下滑，即质点做匀速直线运动.所以②有①②欲使质点到达点时间最短，由可知，只需求出的极大值即可，令把对求导-160- 极大值时，故有由于是斜面的夹角，即所以1.19解质点从抛出到落回抛出点分为上升和下降阶段.取向上为正各力示意图如题1.19.1图，上升时下降时题1.19.1图则两个过程的运动方程为：上升①下降：②对上升阶段:即-160- 对两边积分所以③即质点到达的高度.对下降阶段：即④由③=④可得1.20解作子弹运动示意图如题1.20.1图所示.题1.20.1图水平方向不受外力，作匀速直线运动有①-160- 竖直方向作上抛运动，有②由①得③代入化简可得因为子弹的运动轨迹与发射时仰角有关，即是的函数，所以要求的最大值.把对求导，求出极值点.即所以，代入的表达式中可得：此即为子弹击中斜面的地方和发射点的距离的最大值1.21解阻力一直与速度方向相反，即阻力与速度方向时刻在变化，但都在轨道上没点切线所在的直线方向上，故用自然坐标比用直角坐标好.-160- 轨道的切线方向上有：①轨道的法线方向上有：②由于角是在减小的，故③由于初末状态由速度与水平方向夹角来确定，故我们要想法使①②变成关于的等式由①即④把代入可得⑤用④⑤可得-160- 即，两边积分得⑥代入初始条件时，即可得代入⑥式，得⑦又因为所以⑧把⑦代入⑧积分后可得1.22各量方向如题1.22.1图.-160- 电子受力则电子的运动微分方程为②-③-④由②，即⑤代入③整理可得⑥对于齐次方程的通解非齐次方程的特解-160- 所以非齐次方程的通解代入初始条件：时，得时，得,故⑦同理，把⑦代入⑤可以解出把⑦代入⑤代入初条件时，，得.所以）1.23证（a）在1.22题中，时，则电子运动受力电子的运动微分方程①-②-③对②积分-160- ④对④再积分又故（为一常数）此即为抛物线方程.当时则电子受力则电子的运动微分方程为①-②-③同1.22题的解法，联立①-②解之，得于是-160- 及电子轨道为半径的圆.1.24解以竖直向下为正方向，建立如题1.24.2图所示坐标，题1.24.1图题1.24.2图以①开始所在位置为原点.设①-②-③处物体所处坐标分别为，则3个物体运动微分方程为：①-②-③由②于③与、之间是，即不可伸长轻绳连接，所以有，即④之间用倔强系数弹性绳联结.故有⑤由①⑤得⑥由②③④得-160- ⑦代入①，有⑧代入⑥，有⑨此即为简谐振动的运动方程.角频率所以周期解⑨得以初始时③为原点，时，.所以⑩代入①得联立-③④⑧⑩得1.25解，选向下为正方向，滑轮刚停时物体所在平衡位置为坐标原点.建立如题.25.1图所示坐标系.-160- 题2.15.1图原点的重力势能设为0.设弹簧最大伸长.整个过程中，只有重力做功，机械能守恒：①-②联立①②得弹簧的最大张力即为弹簧伸长最长时的弹力，为最大张力，即1.26解以绳顶端为坐标原点.建立如题1.26.1图所示坐标系.-160- 题1.26.1图设绳的弹性系数为,则有①当脱离下坠前，与系统平衡.当脱离下坠前，在拉力作用下上升，之后作简运.运动微分方程为②联立①②得③齐次方程通解非齐次方程③的特解所以③的通解代入初始条件：时，得；故有即为在任一时刻离上端的距离.1.27解对于圆柱凸面上运动的质点受力分析如图1-24.-160- 运动的轨迹的切线方向上有:①法线方向上有：②对于①有（为运动路程，亦即半圆柱周围弧长）即又因为即③设质点刚离开圆柱面时速度，离开点与竖直方向夹角，对③式两边积分④刚离开圆柱面时即⑤联立④⑤得-160- 即为刚离开圆柱面时与竖直方向夹角.1.28解建立如题1.28.1图所示直角坐标.椭圆方程①从滑到最低点，只有重力做功.机械能守恒.即②设小球在最低点受到椭圆轨道对它的支持力为则有：③为点的曲率半径.的轨迹：得；又因为-160- 所以故根据作用力与反作用力的关系小球到达椭圆最低点对椭圆压力为方向垂直轨道向下.1.29解质点作平面直线运动，运动轨迹方程为①-②由曲线运动质点的受力分析，我们可以得到：③-④因为曲线上每点的曲率⑤所以⑥⑦把⑥⑦代入曲率公式⑤中所以-160- ⑧由④即，又有数学关系可知，即所以⑨把⑧⑨代入①1.30证当题1.29所述运动轨迹的曲线不光滑时，质点的运动方程为：①②③④⑤由1.29题可知②由数学知识知③把①③④代入②⑤这是一个非齐次二阶微分方程.解为当时，得-160- 即当，时，即故有1.31证：单摆运动受力分析如图1.31.1图所示。因为①即所以又单摆摆角很小，有=上式即化为：②此即为一个标准的有阻尼振动方程。设为固有频率，又由于，即阻力很小的情况。方程②的解为-160- 所以单摆振动周期结论得证。1.32解：设楔子的倾角为，楔子向右作加速度的匀加速运动，如图1.32.1图。我们以楔子为参考系，在非惯性系中来分析此题，则质点受到一个大小为的非惯性力，方向与相反。质点在楔子这个非惯性系中沿斜面下滑，沿斜面的受力分析：①垂直斜面受力平衡：②联立①②得此即楔子相对斜面的加速度。对斜面的压力与斜面对的支持力等大反方向。同理可得当楔子向左作加速度为的匀加速运动时，质点的和楔子对斜面的压力为综上所述可得-160- 1.33解设钢丝圆圈以加速度向上作匀加速运动如题1.33.1图，我们以钢丝圆圈作参考系，在圆圈这个非惯性系里来分析此题。圆圈上的小环会受到一个大小为方向与相反的惯性力的作用，则圆环运动到圆圈上某点，切线方向受力分析：①法线方向受力分析有：②对①两边同乘以即两边同时积分③把③代入②可解得同理可解出，当钢丝圆圈以加速度竖直向下运动时小环的相对速度-160- 综上所述，小环的相对速度圈对小环的反作用力1.34证：（1）当火车所受阻力为常数时，因为功率与牵引力有如下关系：所以即对两边积分（2）当阻力和速度成正比时，设=，为常数。同理由（1）可知即对两边积分1.35解锤的压力是均匀增加的，设，为常数，由题意可知-160- ，得，所以，即故两边同时积分得，①又因为当增至极大值后，又均匀减小到0，故此时有为常数，所以即②-160- 由①得③整个过程压力所做功又因为即对上式两边分段积分得1．36解（a）保守力满足条件对题中所给的力的表达式，代入上式即所以此力是保守力，其势为-160- (b)同（a），由所以此力是保守力，则其势能为1.37解（a）因为质子与中子之间引力势能表达式为故质子与中子之间的引力（b）质量为的粒子作半径为的圆运动。动量矩-160- 由（a）知提供粒子作圆周运动的向心力，方向是沿着径向，故当半径为的圆周运动两式两边同乘以即又因为有做圆周运动的粒子的能量等于粒子的动能和势能之和。所以1.38解要满足势能的存在，即力场必须是无旋场，亦即力为保守力，所以即得-160- 为常数满足上式关系，才有势能存在。势能为：1.39证质点受一与距离成反比的力的作用。设此力为①又因为即②当质点从无穷远处到达时，对②式两边分别积分：当质点从静止出发到达时，对②式两边分别积分：得-160- 所以质点自无穷远到达时的速率和自静止出发到达时的速率相同。1.40解由题可知（因为是引力，方向与径向相反所以要有负号）由运动微分方程即①对上式两边积分故又因为与的方向相反，故取负号。即1.41证画出有心力场中图示如题1.41.图，我们采用的是极坐标。所以-160- 又由于常数即由图所示关系，又有，故即由动能定理沿方向得1.42证（）依据上题结论，我们仍然去极坐标如题1.42.1图。质点运动轨迹为一圆周，则其极坐标方程为①由①②得②即③故即力与距离5次方成正比，负号表示力的方向与径向相反。（）-160- 质点走一对数螺旋线，极点为力心，我们仍采用极坐标。对数螺旋线为常数。有根据题1.41，常数，有故得证。1.43证由毕耐公式质点所受有心力做双纽线运动故故-160- 1.44证由毕耐公式将力带入此式因为所以即令上式化为这是一个二阶常系数废气次方程。解之得微积分常数，取，故有令-160- 所以1.45证由题意可知，质点是以太阳为力心的圆锥曲线，太阳在焦点上。轨迹方程为在近日点处在远日点处由角动量守恒有所以1.46解因为质点速率所以又由于即又因为所以-160- 两边积分即1.47证（）设地球轨道半径为。则彗星的近日点距离为。圆锥曲线的极坐标方程为彗星轨道为抛物线，即。近日点时。故近日点有即①又因为所以②（彗星在单位时间内矢径扫过的面积）扫过扇形面积的速度③又因为故两边积分④从数学上我们可以得到两轨道交点为地球轨道半径处。-160- 即即⑤又因为所以⑥把⑤⑥代入④（⑥式代入时取“+”即可）故彗星在地球轨道内停留的时间为⑦设地球绕太阳运动一周的时间为。因为假定地球运动轨道为圆形，所以又由于，有地球绕太阳运动单位时间内矢径扫过的面积。扫过扇形速度-160- ⑧（）由证明（）知彗星在地球轨道内停留时间对此式求极大值，即对求导，使即即得验证故为极大值，代入⑧式可知1.48解由§1.9给出的条件：人造地球卫星近、远点距离分别为-160- 地球半径有椭圆运动中的能量方程可知：①②为卫星运行的椭圆轨道的长轴把代入①②有近地点速率远地点速率运动周期（参见1.47）其中为运动轨道的半长轴所以1.49证由行星绕太阳作椭圆运动的能量方程为为椭圆的半长轴。令-160- 又因为，上式化为：因为即所以①又因为行星椭圆轨道运动周期即常数，故又因为为正焦弦的一半所以-160- ②由题意可知即③把②③代入①可得化简可得即两边积分，由题设即1.50解质点在有心力场中运动，能量和角动量均守恒。无穷远处势能为零。-160- 所以①②任意一处由②代入①所以第二章质点组力学第二章习题解答2.1解均匀扇形薄片，取对称轴为轴，由对称性可知质心一定在轴上。-160- 有质心公式设均匀扇形薄片密度为，任意取一小面元，又因为所以对于半圆片的质心，即代入，有2.2解建立如图2.2.1图所示的球坐标系-160- 把球帽看成垂直于轴的所切层面的叠加（图中阴影部分所示）。设均匀球体的密度为。则由对称性可知，此球帽的质心一定在轴上。代入质心计算公式，即2.3解建立如题2.3.1图所示的直角坐标，原来与共同作一个斜抛运动。当达到最高点人把物体水皮抛出后，人的速度改变，设为，此人即以的速度作平抛运动。由此可知，两次运动过程中，在达到最高点时两次运动的水平距离是一致的（因为两次运动水平方向上均以作匀速直线运动，运动的时间也相同）。所以我们只要比较人把物抛出后水平距离的变化即可。第一次运动：从最高点运动到落地，水平距离-160- ①②③第二次运动:在最高点人抛出物体，水平方向上不受外力，水平方向上动量守恒，有可知道水平距离跳的距离增加了=2.4解建立如图2.4.1图所示的水平坐标。以，为系统研究，水平方向上系统不受外力，动量守恒，有①对分析；因为②在劈上下滑，以为参照物，则受到一个惯性力（方向与加速度方向相反）。如图2.4.2图所示。所以相对下滑。由牛顿第二定律有②-160- 所以水平方向的绝对加速度由②可知③④联立①④，得⑤把⑤代入①，得⑥负号表示方向与轴正方向相反。求劈对质点反作用力。用隔离法。单独考察质点的受力情况。因为质点垂直斜劈运动的加速度为0，所以⑦把⑥代入⑦得，⑧水平面对劈的反作用力。仍用隔离法。因为劈在垂直水皮方向上无加速度，所以⑨于是⑩2.4解因为质点组队某一固定点的动量矩-160- 所以对于连续物体对某一定点或定轴，我们就应该把上式中的取和变为积分。如图2.5.1图所示薄圆盘，任取一微质量元，所以圆盘绕此轴的动量矩=2.6解炮弹达到最高点时爆炸，由题目已知条件爆炸后，两者仍沿原方向飞行知，分成的两个部分，，速度分别变为沿水平方向的，，并一此速度分别作平抛运动。由前面的知识可知，同一高处平抛运动的物体落地时的水平距离之差主要由初速度之差决定。进而转化为求，。炮弹在最高点炮炸时水平方向上无外力，所以水平方向上的动量守恒：①以质点组作为研究对象，爆炸过程中能量守恒：②联立①②解之，得所以落地时水平距离之差-160- =2.7解建立如题2.7.1图所示的直角坐标系。当沿半圆球下滑时，将以向所示正方向的反向运动。以、组成系统为研究对象，系统水平方向不受外力，动量守恒，即相对于地固连的坐标系的绝对速度为相对的运动速度②故水平方向③竖直方向④在下滑过程中，只有保守力（重力）做功，系统机械能守恒：（以地面为重力零势能面）⑤=⑥把③④代入⑥=⑦-160- 把①③代入⑤2.8证以连线为轴建立如题2.8.1图所示的坐标。设初始速度为与轴正向夹角碰撞后，设、运动如题2.8.2图所示。、速度分别为、，与轴正向夹角分别为、。以、为研究对象，系统不受外力，动量守恒。方向：①垂直轴方向有：②可知③整个碰撞过程只有系统内力做功，系统机械能守恒：④由③④得即两球碰撞后速度相互垂直，结论得证。2.9解-160- 类似的碰撞问题，我们一般要抓住动量守恒定理和机械能守恒定理得运用，依次来分析条件求出未知量。设相同小球为，初始时小球速度，碰撞后球的速度为，球的速度以碰撞后球速度所在的方向为轴正向建立如题2.9.1图所示的坐标(这样做的好处是可以减少未知量的分解，简化表达式)。以、为系统研究，碰撞过程中无外力做功，系统动量守恒。方向上有：①方向上有：②又因为恢复系数即=③用①-③④用④代入②得求在各种值下角的最大值，即为求极致的问题。我们有-160- 得即=0所以即由因为=故=所以2.10以为研究对象。当发生正碰撞后，速度分别变为，，随即在不可伸长的绳约束下作圆周运动。以的连线为轴建立如题2.10.1图所示。-160- 碰撞过程中无外力做功，动量守恒：①随即在的约束下方向变为沿轴的正向，速度变为故方向上有②故恢复系数定义有：=即③联立①②③得2.11解如图所示，-160- 有两质点，中间有一绳竖直相连，坐标分别为：，质量为，开始时静止。现在有一冲量作用与，则作用后，得到速度，仍静止不动：。它们的质心位于原点，质心速度我为现在把坐标系建在质心上，因为系统不再受外力作用，所以质心将以速率沿轴正向匀速正向、反向运动。由于质心系是惯性系，且无外力，所以，分别以速率绕质心作匀速圆周运动，因而他们作的事圆滚线运动。经过时间后，如图所示：于是在系中的速度的速度：因此2.12解-160- 对于质心系的问题，我们一般要求求出相对固定参考点的物理量，在找出质心的位置和质心运动情况，由此去计算物体相对或绝对物理量及其间的关系。由题可知，碰前速度为，速度。碰后速度，分别设为。碰撞过程中无外力做功，动量守恒。①有恢复系数②联立①②得再由质点组质心的定义：为质心对固定点位矢，，分别为，对同一固定点的位矢所以（质点组不受外力，所以质心速度不变。）设两球碰撞后相对质心的速度，。（负号表示与相反）同理，碰撞前两球相对质心的速度（负号表示方向与相反）所以开始时两球相对质心的动能：-160- ==2.13用机械能守恒方法；在链条下滑过程中，只有保守力重力做功，所以链条的机械能守恒。以桌面所平面为重力零势能面。有2.14此类题为变质量问题，我们一般研究运动过程中质量的变化与力的关系以竖直向上我轴正向建立如题2.14.1图所示坐标。绳索离地面还剩长时受重力则所以-160- 求地板的压力，有牛顿第三定律知，只需求出地板对绳索的支持力即可，它们是一对作用力与反作用力。这是我们以快要落地的一小微元作为研究对象。它的速度由变为0。用动量守恒，有==又因为=2.15解这是一道变质量的问题，对于此类问题，我们由书上p.137的（2.7.2）式①来分析。以机枪后退方向作为轴争先，建立如题2.15.1图的坐标。竖直方向上支持力与重力是一对平衡力。水平方向上所受合外力F即为摩擦力②单位时间质量的变化③由①②式-160- 所以2.16解这是一个质量增加的问题。雨滴是本题。导致雨滴变化的微元的速度。所以我们用书上p.138的（2.7.4）式分析①雨滴的质量变化是一类比较特殊的变质量问题。我们知道处理这类问题常常理想化模型的几何形状。对于雨滴我们常看成球形，设其半径为，则雨滴质量是与半径的三次方成正比（密度看成一致不变的）。②有题目可知质量增加率与表面积成正比。即③为常数。我们对②式两边求导④由于③=④，所以⑤对⑤式两边积分⑥⑦-160- 以雨滴下降方向为正方向，对①式分析⑧（为常数）当时，，所以2.17证这是变质量问题中的减质量问题，我们仍用书上p.137(2.7.2)式①来分析。设空火箭质量，燃料质量。以向上为正方向，则火箭任一时刻的质量②喷气速度2074是指相对火箭的速度，即。有①式化简对两边积分-160- ㏑③此既火箭速度与时间的关系。当火箭燃料全部燃尽所用时间，由题意知④代入③可得火箭最终的速度，（即速度的最大值）.考虑到其中，易知当时，恒成立，即为的增函数。又当时，=11.25而要用此火箭发射人造太阳行星需要的速度至少应为第二宇宙速度。故所携带燃料重量至少是空火箭重量的300倍。2.18证要使火箭上升，必须有发动机推力火箭的重量，即即火箭才能上升，结论得证。由于喷射速度是常数，单位时间放出的质量-160- 质量变化是线性规律①火箭飞行速度②又因为燃料燃烧时间③代入②得火箭最大速度=又因为②式又可以写成积分可得④从开始到燃烧尽这一段时间内火箭上升高度。把③代入④得之后火箭作初速度为的竖直上抛运动。可达高度故火箭能达到的最大高度=2.19证假设该行星做椭圆运动，质量为，周期为。某一时刻位置为-160- ，速度为，则=-又因为于是=第三章刚体力学第三章习题解答3.1解如题3.1.1图。均质棒受到碗的弹力分别为，棒自身重力为。棒与水平方向的夹角为。设棒的长度为。由于棒处于平衡状态，所以棒沿轴和轴的和外力为零。沿过点且与轴平行的合力矩为0。即：①②-160- ③由①②③式得：④又由于即⑤将⑤代入④得：3.2解如题3.2.1图所示，均质棒分别受到光滑墙的弹力，光滑棱角的弹力，及重力。由于棒处于平衡状态，所以沿方向的合力矩为零。即①由①②式得：-160- 所以3.3解如题3.3.1图所示。棒受到重力。棒受到的重力。设均质棒的线密度为。由题意可知，整个均质棒沿轴方向的合力矩为零。3.4解如题3.4.1图。-160- 轴竖直向下，相同的球、、互切，、切于点。设球的重力大小为，半径为，则对、、三个球构成的系统来说，在轴方向的合力应为零。即：①对于球，它相对于过点与轴平行的轴的合力矩等于零。即：②由式得：3.5解如题3.5.1图。-160- 梯子受到地面和墙的弹力分别为，，受地面和墙的摩擦力分别为，。梯子和人的重力分别为，且。设梯长为，与地面夹角为。由于梯子处于平衡，所以①②且梯子沿过点平行于轴的合力矩为零。即：③又因梯子是一个刚体。当一端滑动时，另一端也滑动，所以当梯与地面的倾角达到最小时，④⑤由①②③④⑤得：所以3.6解（a）取二原子的连线为轴，而轴与轴通过质心。为质心，则，，轴即为中心惯量主轴。设、的坐标为，因为为质心（如题3.6.2图）-160- 故①且②由①②得所以中心惯量主轴：（b）如题3.6.3图所示，该原子由、、三个原子构成。-160- 为三个原子分子的质心。由对称性可知，图中、、轴即为中心惯量主轴。设、、三原子的坐标分别为，因为为分子的质心。所以=①又由于②③由①②③得：故该分子的中心主转动惯量3.7解如题3.7.1图所示。沿轴平行于平切椭球得切面为一椭圆，则该椭圆方程为：-160- 可求该切面的面积故积分同理可求故中心主转动惯量：又由于椭球体积故将代入得：3.8解设表示距球心为的一薄球壳的质量，则-160- 所以该球对球心的转动惯量①在对称球中，绕直径转动时的转动惯量②又球的质量③又绕直径的回转半径④由①②③④得3.9解如题3.9.1图所示坐标系。为正方体中心。、、分别与正方体的边平行。由对称性可知，、、轴就是正方体的中心惯量主轴。设正方体的边长为-160- 。设为平行于轴的一小方条的体积，则正方体绕轴的转动惯量根据对称性得易求正方体的对角线与、、轴的夹角都为。且故正方体绕对角线的转动惯量①又由于②绕对角线的回转半径③由①②③得3.10解如题3.10.1图。轴过点垂直纸面向外。均质圆盘的密度为。设盘沿顺时针转动，则沿-160- 的方向有即①为转盘绕轴的转动惯量：（为盘的质量），②（为盘转动的角频率，负号因为规定顺时针转动）=③由①②③得又因为故所以得3.11解如题3.11.1图所示，-160- 设轴通过点垂直纸面指向外。则对轴有：设通风机转动的角速度大小为，由于通风机顺时针转动。所以，将代入上式得：。又由于，解得：故当时，㏑。又由于（为通风机转动的角度）设，故当㏑时，，时间内通风机转动的转数3.12解如题3.12.1图，-160- 第3.12.1图坐标与薄片固连，则沿轴方向有：且①现取如图阴影部分的小区域，该区域受到的阻力对轴的力矩所以②又薄片对轴的转动惯量③由①②③得：当时，3.13解如题3.13.1图所示，-160- 坐标系的原点位于圆弧最顶点。设圆弧平衡时，质心的坐标为。如图所示圆弧偏离平衡位置一小角度，则满足微分方程为圆弧相对于轴的转动惯量。当很小时，，代入上式得：①圆弧上对应转角为的一小段圆弧的坐标为质心的纵坐标上式中为圆弧的线密度②又③其中，将②③代入①得④解④式得通解-160- 微振动周期3.14解如题3.14.1图所示坐标系。由动量定理及动量矩定理得：①②③其中又根据机械能守恒定律得：④由①②③④解得：-160- 3.15解如题3.15.1图所示坐标系。由于球作无滑滚动，球与地面的接触的速度与地面一致，等于零，所以点为转动瞬心。以为基点。设球的角速度，则设轮缘上任意一点，与轴交角为，则故当时，得最高点的速度当和时分别得到最高点和最低点的加速度3.16解如题3.16.1图所示，-160- 由题意知该时刻瞬心一定处在的垂线中。设瞬心为。则易知的方向如图，在中即为与边的夹角大小。3.17解如题3.17.1图所示，-160- 点为极轴的原点，极轴过点，所以在杆上任意一点。设。设的坐标为再来求瞬心的轨迹。由于点速度沿弧面，点的速度沿杆。现分别作与的垂线交于点，则即为瞬心（见题3.17.1图）。当点的极角为时，易知点的极角，故点的极径易证明为等腰三角形。有又因为﹤，所以﹤0。所以点轨迹位于轴上方，半径为的半圆，如图虚线所示。3.18解如题3.18.1图所示。由于圆盘作无滑滚动，所以为圆盘的瞬心，故-160- ，设圆盘匀速转动的角速度为，则①因为点的速度沿地面水平向右，分别作和的垂线交于点，则点即为杆的瞬心。且得由几何知识可知与竖直方向夹角为，又知又，所以②又。即：得③④由①②③④解得：3.19解如题3.19.1图，-160- 固定坐标系。杆从水平位置摆到竖直位置过程中只有重力做功，故机械能守恒。设此时的角速度为，则右边第一项为质心运动动能，第二项为杆绕质心转动的动能。解上式得：在杆脱离悬点后，根据动量定理和动量矩定理：①②③③式中为杆绕质心的转动惯量，为沿过质心平行于轴的合力矩，易知，又，代入③式得即杆将作匀速转动。解①②得④-160- 所以质心的轨迹为一抛物线。故当时，杆的质心下降，代入④式得故时间内杆的转数3.20解如题3.20.1图，设圆柱体的转动角速度为，设它受到地面的摩擦力为，由动量定理和动量矩定理知：①②对于滑块。由动量定理知：③④以为基点：假设绳不可拉伸。则。故⑤由①②③④⑤解得：-160- 3.21解（1）如题3.21.1图。设轴过点垂直纸面向外。绳子上的弹力为。对于飞轮，根据动量矩定理，在轴方向：①②为物块下落的加速度。因为物块的加速度应与点加速度一样大小，故③由①②③解得：（2）假若飞轮受到的阻尼力矩为的话，由（1）问知，飞轮的角加速度。现在来求绳子脱落以后飞轮的角加速度。同样根据动量矩，在轴方向：可以证明：类似于位移、加速度、初速度和末速度之间的关系式。角位移、角加速度、角初速度、角末速度之间也有类似的关系：-160- ④对于绳子脱落到停止转动的过程有：⑤④⑤式中指绳子脱落时飞轮的角加速度，由④⑤解得：3.22解如题3.22.1图。轴与速度方向一致，轴垂直纸面向外。设球的半径为，则球绕任一直径的转动惯量。由动量定理和动量矩定理可知：①②③④由①②③④得：设球与板的接触点为，则时刻点的速度为：-160- ⑤⑥球由滑动变为滚动的条件是：⑦由⑤⑥⑦解得：3.23解如题3.23.1图所示。设圆柱的半径为，与木板之间的摩擦力为，弹力为，木板受地面的摩擦力为，弹力为，对木板由动量定理得：①②对圆柱，由角动量定理和动量定理得：③④-160- ⑤其中为圆柱绕中心轴的转动惯量，所以⑥⑦无滑滚动的条件：⑧由①～⑧式解得3.24解如题3.24.1图，坐标不与圆柱固连，是固定坐标系。由于﹥，所以圆柱与斜面接触的边缘有相对与斜面向上的运动趋势，所以斜面对圆柱的摩擦力沿斜面向下。对圆柱：①②③④-160- 由①②③④式得设从到的过程中，圆柱的速度从变到，角速度从变到，所以3.25解如题3.25.1图。设大球和小球的半径分别为，。分别为大球和小球的球心，为方向竖直向下的定线，为小球上的一动线。当小球位于大球顶端时，与重合。设，与竖直方向的夹角为，根据无滑条件：①②③④⑤从最高点运动到图示位置过程中，机械能守恒，即⑥-160- ⑦由①～⑦解得3.26如题3.26.1图所示坐标系。设杆的长度为，质量为。受到墙和地面的作用力分别为，当杆与地面的倾斜角为时，质心的坐标为：对上两式求时间导数，的质心的速度和加速度：①②③④由②③④得-160- ⑤对⑤式求时间导数得⑥又由动量定理⑦当杆脱离墙时，有⑧由①⑤⑥⑦⑧得⑨所以3.27解如题3.27.1图，设为杆与地面的倾角，为杆脱离墙时的值。设杆脱离墙时，杆的角速度为横纵速度分别为当杆落地时，质心的横纵速度分别为杆的角速度为。当由变为0的过程中，机械能守恒：①-160- 又因为此过程中杆已离开墙，所以杆在水平方向受力为零，故质心水平方向匀速，即②又点只有水平方向的速度，根据,知当杆落地时，与有如下关系：③且由3.26题式①得：④将②③④代入①得：⑤由3.26题式⑤⑨得⑥⑦将⑥⑦代入⑤得3.28解如题3.28.1图。对圆柱有如下基本运动微分方程：①-160- ②③④⑤由①②③④得⑥将⑤代入⑥得3.29解如题3.29.1图。设斜面的倾角为，实心球或球壳的质量为，半径为，转动惯量为，则可列出下列方程：①②又有无滑动条件③由①②③式得④-160- ⑤⑥将⑤⑥代入④得⑦对初速为0的匀加速运动，时间，加速度，位移有如下关系：⑧当时，将⑦代入⑧得：故实心球滚得快些。3.30解如题3.30.1土图以为轴。为轴。建立与碾轮一起转动的动坐标系，设碾轮绕轴转动的角速度，水平轴的转动角速度为。所以点的合角速度为又因为点和点的速度为0，所以即为瞬时轴。设与地面成夹角，由于沿瞬时轴方向，所以：-160- 故第四章转动参考系第四章习题解答4.1解如题4.1.1图所示.坐标系的原点位于转动的固定点，轴沿轴与角速度的方向一致，即设点沿运动的相对速度为则有题意得：故在点时的绝对速度-160- 设与轴的夹角为，则故与边的夹角为，且指向左上方。点时绝对速度设的夹角为，则,故与边的夹角为，且指向左下方。4.2解如题4.2.1图所示，以转动的方向为极角方向建立坐标系。轴垂直纸面向外，设点相对速度①设绝对速度的量值为常数，则：-160- ②对②式两边同时球时间导数得：依题意故解得通解当时，，将其带入①式游客的知：时，即最后有4.3解如题4.3.1图所示，直角坐标的原点位于圆锥顶点轴过圆锥的对称轴.点在轴上对应的一点，且有，所以点的绝对加速度：最后有-160- 4.4解如题4.4.1图所示，题4.4.1图坐标系是以轴转动的坐标系.图中画出的是曲线的一段，在任意一点处，假设某质点在此处静止，则该质点除了受重力、钢丝的约束力之外，还会受惯性离心力的作用，，方向沿轴正向，在作用下，致信处于平衡状态，则有①②有①得③又因为过原点.对上式积分得抛物线有③得将代入②的反作用力-160- 4.5以直管为参照系，方向沿管，沿竖直轴建立坐标系，则小球受力为：故沿方向运动的微分方程为：①有初始条件：可得①式解为故当邱刚离开管口时，即时.则得所以此时：故当球刚要离开管口时的相对速度为，绝对速度为，小球从开始运动到离开管口所需时间为4.6解以光滑细管为参考系，沿管，沿水平轴建立坐标系，如题4.6.1图所示，-160- 则小球受力为：故沿方向运动的微分方程为：①方程的通解而方程①的特解为：故方程①的通解为：初始条件为当时，故可得所以质点相对于管的运动规律为：-160- 4.7解以水平细管为参考系，沿管，沿竖直转动轴向上建立坐标系，如题图4.7.1图所示则易得质点反方向的运动微分方程为：①②将方程①②作简单变换可得：化简得其通解为：初始条件为：故可得：故4.8解以抛物线形金属丝为参照物沿抛物线在顶点的切线方向，沿竖直轴建立坐标系，-160- 则小环的运动微分方程为：①②故代入①②得化简即得4.9解一当小环相对平衡时，由上题可知即要求为常数，故故解二以地面为参照系，则小球受力，如图4-8所示.其中-160- 为固定地面的坐标系，故平衡时有：4.10解以地面为参考系，则小环的运动微分方程为：其中为与圆心的连线和通过点的直径间所夹的角化简得4.11解以地面为非惯性参考系，建立坐标系，指正南，竖直向上，发射点为原点，炮弹的运动微分方程为：①②③初始条件为-160- 故将①②③积分一次代入初始条件后得：④⑤⑥有⑥可得落地时间：⑦其中所以将展开可得由式及初始条件可得所以炮弹落地时的横向偏离为4.12解以地面为非惯性，建立坐标系指向正南，-160- 竖直向上，上抛点为原点，质点的运动微分方程为：①初始条件为：如上题同理可得②③④代入①式得有④式求出落地时间为：有③式得：将代入得复落至地面时：第五章分析力学-160- 第五章习题解答5.1解如题5.1.1图杆受理想约束，在满足题意的约束条件下杆的位置可由杆与水平方向夹角所唯一确定。杆的自由度为1，由平衡条件：即mgy=0①变换方程y=2rcossin-=rsin2②故③代回①式即因在约束下是任意的，要使上式成立必须有：rcos2-=0④又由于cos=-160- 故cos2=代回④式得5.2解如题5.2.1图三球受理想约束，球的位置可以由确定，自由度数为1，故。得由虚功原理-160- 故①因在约束条件下是任意的，要使上式成立，必须故②又由得：③由②③可得5.3解如题5.3.1图，在相距2a的两钉处约束反力垂直于虚位移，为理想约束。去掉绳代之以力T，且视为主动力后采用虚功原理，一确定便可确定ABCD的位置。因此自由度数为1。选为广义坐。由虚功原理：-160- w①又取变分得代入①式得：化简得②设因在约束条件下任意，欲使上式成立，须有：由此得5.4解自由度，质点位置为。由①-160- 由已知得故②约束方程③联立②③可求得或又由于故或5.5解如题5.5.1图-160- 按题意仅重力作用，为保守系。因为已知，故可认为自由度为1.选广义坐标，在球面坐标系中，质点的动能：由于所以又由于故取Ox为零势，体系势能为：故力学体系的拉氏函数为：-160- 5.6解如题5.6.1图.平面运动，一个自由度.选广义坐标为，广义速度因未定体系受力类型，由一般形式的拉格朗日方程①在广义力代入①得：②在极坐标系下：③故-160- 将以上各式代入②式得5.7解如题5.7.1图又由于所以①取坐标原点为零势面②拉氏函数③-160- 代入保守系拉格朗日方程得代入保守系拉格朗日方程得5.8解：如图5.8.1图.(1)由于细管以匀角速转动，因此=可以认为质点的自由度为1.(2)取广义坐标.(3)根据极坐标系中的动能-160- 取初始水平面为零势能面，势能:拉氏函数①(4)，代入拉氏方程得：(5)先求齐次方程的解.②特解为故①式的通解为③在时：④⑤联立④⑤得-160- 将代回式③可得方程的解为：5.9解如题5.9.1图.（1）按题意为保守力系，质点被约束在圆锥面内运动，故自有度数为2.（2）选广义坐标，.（3）在柱坐标系中：以面为零势能面，则：拉氏函数-160- -①（4）因为不显含，所以为循环坐标，即常数②对另一广义坐标代入保守系拉氏方程③有得④所以此质点的运动微分方程为（为常数）所以5.10解如题5.10.1图.-160- （1）体系自由度数为2.（2）选广义坐标（3）质点的速度劈的速度故体系动能以面为零势面，体系势能：其中为劈势能.拉氏函数①（4）代入拉格郎日方程得：②-160- 代入拉格郎日方程得③联立②，③得5.11解如题5.11.1图（1）本系统内虽有摩擦力，但不做功，故仍是保守系中有约束的平面平行运动，自由度（2）选取广义坐标（3）根据刚体力学其中绕质心转动惯量选为零势面，体系势能：其中C为常数.-160- 拉氏函数(4)代入保守系拉氏方程得：对于物体，有5.12解如题5.12.1图.（1）棒作平面运动，一个约束，故自由度.（2）选广义坐标（3）力学体系的动能-160- 根据运动合成又故设为绕质心的回转半径，代入①得动能②（4）由③（其中）则④因为、在约束条件下任意且独立，要使上式成立，必须：⑤（5）代入一般形式的拉氏方程得：⑥又-160- 代入一般形式的拉氏方程得：⑦⑥、⑦两式为运动微分方程（6）若摆动角很小，则，代入式得：，代入⑥⑦式得：⑧又故代入⑧式得：（因为角很小，故可略去项）5.13解如题5.13.1图(1)由于曲柄长度固定，自由度.-160- (2)选广义坐标，受一力矩，重力忽略，故可利用基本形式拉格朗日方程：①(3)系统动能②（4）由定义式③（5）代入①得：得5.14.解如题5.14.1图.-160- （1）因体系作平面平行运动，一个约束方程：(2)体系自由度，选广义坐标.虽有摩擦，但不做功，为保守体系（3）体系动能：轮平动动能轮质心转动动能轮质心动能轮绕质心转动动能.①以地面为零势面，体系势能则保守系的拉氏函数②(1)因为不显含，得知为循环坐标.故=常数③-160- 开始时：则代入得又时，所以5.15解如题5.15.1图（1）本系统作平面平行运动，干限制在球壳内运动，自由度；选广义坐标，体系摩擦力不做功，为保守力系，故可用保守系拉氏方程证明①（2）体系动能=球壳质心动能+球壳转动动能+杆质心动能+杆绕中心转动动能-160- ②其中代入②得以地面为零势面，则势能：（其中为常数）(3)因为是循环坐标，故常熟③而代入①式得④联立③、④可得（先由③式两边求导，再与④式联立）⑤⑤试乘并积分得：-160- 又由于当5.16解如题图5.16.1.（1）由已知条件可得系统自由度.（2）取广义坐标.（3）根据刚体力学，体系动能：①又将以上各式代入①式得：设原点为零势能点，所以体系势能体系的拉氏函数-160- ②(1)因为体系只有重力势能做工，因而为保守系，故可采用③代入③式得即（5）解方程得5.17解如题5.17.1图（1）由题设知-160- 系统动能①取轴为势能零点，系统势能拉氏函数②（2）体系只有重力做功，为保守系，故可采用保守系拉氏方程.代入拉氏方程得：又代入上式得-160- 即③同理又代入上式得④令代入③④式得：欲使有非零解，则须有解得周期-160- 5.18解如题5.18.1图（1）系统自由度（2）取广义坐标广义速度（3）因为是微震动，体系动能：以为势能零点，体系势能拉氏函数（4）即-160- ①同理②同理③设代入①②③式得欲使有非零解，必须解之-160- 又故可得周期5.19解如题5.19.1图（1）体系自由度（2）取广义坐标广义速度（3）体系动能体系势能体系的拉氏函数（4）体系中只有弹力做功，体系为保守系，可用①-160- 将以上各式代入①式得：②先求齐次方程③设代入③式得要使有非零，必须即又故通解为：其中-160- 又存在特解有②③式可得式中及为积分常数。5.20解：以速度我广义速度，根据定义①根据公式（5.5.10）又有①得-160- 5.21解取在转动坐标系的速度为广义速度，则在固定坐标系中的速度：，自由质点的动能，设质点势能为，则质点的拉氏函数根据定义：在转动坐标系中：上式中为质点的位矢，为质点相对于固定坐标系的速度。5.22解：取在广义坐标根据教材（3.9.21）和（3.9.19）式得动能：势能：根据定义式-160- 故因为所以为第一积分.又故得为第二个第一积分.同理即得为第三个第一积分.5.23解如题5.23.1图,-160- 由5.6题解得小球的动能①根据定义②得③根据哈密顿函数的定义代入③式后可求得:④由正则方程得:⑤⑥代入⑤得整理得-160- 5.24如题5.24.1图,⑴小球的位置可由确定,故自由度⑵选广义坐标,广义速度.⑶小球动能又由①式得设小球势能为V,取固定圆球中心O为零势点,则小球拉氏函数=①根据定义-160- 有根据正则方程④⑤对式两边求时间导得：故小球球心切向加速度5.25解根据第二章§2.3的公式有：①根据泊松括号的定义：②所以-160- 同理可知：,由②得：同理可得：,5.26解由题5.25可知的表达式因为故同理可求得：-160- 即5.27证取广义坐标因为又因为所以-160- 5.28解如题5.28.1图(1)小环的位置可以由角唯一确定，因此体系的自由度，取广义坐标，广义速度。小球的动能：以为势能零点，则小环势能所以拉氏函数（2）由哈密顿原理故所以又由于-160- 所以因为是任意的，所以有被积式为0，即化简得5.29解参考5.23题，设，体系的拉氏函数①根据哈密顿原理故②因为所以又因为-160- ③因为是任意的，所以有5.30解如题5.30.1图，复摆位置可由角度唯一确定，自由度，取广义坐标，设为复摆重心与悬点之间的距离。复摆的动能：取为势能零点，则势能：复摆的拉氏量：①由哈密顿原：故又因为-160- ②因为的任意性所以有：根据已知很小，③可求得：其中为初相位。周期5.31解如题5.31.1图，参考题5.9，体系拉氏函数①根据哈密顿原理：-160- 故②因为代入②式得：所以③又因为，且和的任意性所以所以运动微分方程为：常数5.32证因为母函数不是的显函数，为正则变换。-160- 5.33证由为母函数，故为正则变换。又且当，变为时5.34证：由①又故②由于-160- 代入②式得得所以存在母函书使：因此，这种变换是正则变换.5.35解:由于故①②由②得又有又-160- ③④又故⑤当时,由③式得:即当时,-160-'