运筹学习题解答.doc 83页

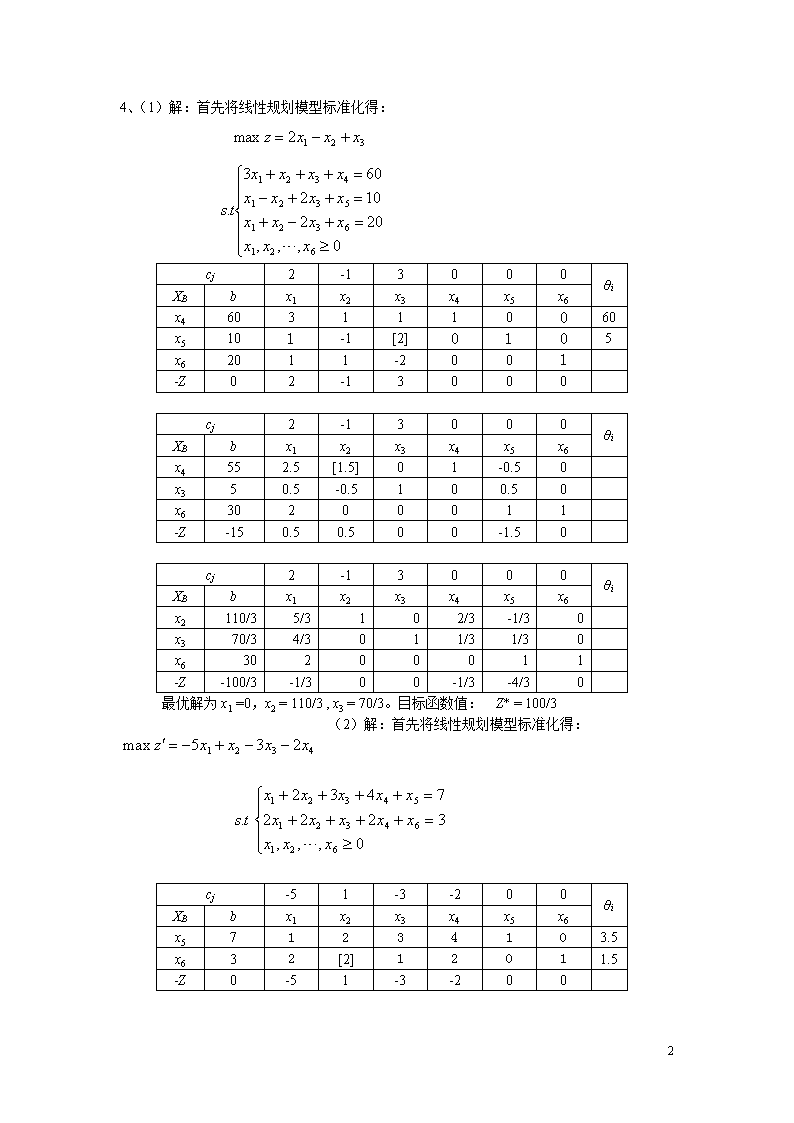
'《管理运筹学教程》习题参考答案第一章线性规划1、解：设每天应生产A、B、C三种型号的产品分别为件。则线性规划模型为：2、解：设5种债劵的投资额分别为件。则线性规划模型为：3、（1）解：对原问题标准化，令＝－，（2）解：对原问题标准化，令＝－，（3）解：对原问题标准化，令83 4、（1）解：首先将线性规划模型标准化得：cj2-13000θiXBbx1x2x3x4x5x6x46031110060x5101-1[2]0105x62011-2001-Z02-13000cj2-13000θiXBbx1x2x3x4x5x6x4552.5[1.5]01-0.50x350.5-0.5100.50x630200011-Z-150.50.500-1.50cj2-13000θiXBbx1x2x3x4x5x6x2110/35/3102/3-1/30x370/34/3011/31/30x630200011-Z-100/3-1/300-1/3-4/30最优解为x1=0，x2=110/3,x3=70/3。目标函数值：Z*=100/3（2）解：首先将线性规划模型标准化得：cj-51-3-200θiXBbx1x2x3x4x5x6x571234103.5x632[2]12011.5-Z0-51-3-20083 cj-51-3-200θiXBbx1x2x3x4x5x6x54-10221-1x21.5110.5100.5-Z-1.5-60-3.5-30-0.5最优解为x1=0，x2=1.5,x3=0,x4=0。目标函数值：Z*=1.55、(1)利用大M法。解:在上述问题中加入松弛变量和人工变量得：这里M是一个充分大的正数,取基变量为x4,x6，可得如下表cj23-5-M0-MθiXBbx1x2x3x4x5x6x47111100x6102-510-11-Z023-5-M0-M由于x4,x6为基变量，因此它们对应的检验数行的检验数应为0，经变换得初始单纯形表。cj23-5-M0-MθiXBbx1x2x3x4x5x6x471111007x610[2]-510-115-Z17M2+3M3-4M-5+2M0-M0cj23-5-M0-MθiXBbx1x2x3x4x5x6x420[3.5]0.510.5-0.5x151-2.50.50-0.50.5-Z-10+2M08+3.5M-6+0.5M01+0.5M-1-1.5Mcj23-5-M0-MθiXBbx1x2x3x4x5x6x24/7010.1428570.2857140.142857-0.14286x145/7100.8571430.714286-0.142860.142857-Z102/700-7.14286-2.28571-M-0.142860.142857-M最优解为x1=45/7，x2=4/7,x3=0。目标函数值：Z*=102/7利用两阶段法。先在以上问题的约束条件中加入松弛变量、人工变量，给出第一阶段的线性规划问题：83 这里取基变量为x4,x6，可得如下表cj000-10-1θiXBbx1x2x3x4x5x6x47111100x6102-510-11-Z0000-10-1由于x4,x6为基变量，因此它们对应的检验数行的检验数应为0，经变换得初始单纯形表。cj000-10-1θiXBbx1x2x3x4x5x6x471111007x610[2]-510-115-Z173-420-10cj000-10-1θiXBbx1x2x3x4x5x6x420[3.5]0.510.5-0.5x151-2.50.50-0.50.5-Z203.50.500.5-1.5cj000-10-1θiXBbx1x2x3x4x5x6x24/7011/72/71/7-1/7x145/7100.8571430.714286-0.142860.142857-Z0000-10-1这里x4、x6是人工变量。第一阶段我们已求得W=0,因人工变量x6=x4=0，所以(45/7,4/7,0,0)T是原问题的基本可行解。于是可以开始第二阶段的计算。将第一阶段的最终计算表中的人工变量列取消，并将目标函数系数换成原问题的目标函数系数，重新计算检验数行，可得如下第二阶段的初始单纯形表cj23-50θiXBbx1x2x3x5x24/7011/71/7x145/7100.857143-0.14286-Z102/700-7.14286-0.14286所有检验数sj£0，所以x1=45/7，x2=4/7,x3=0是原线性规划问题的最优解。目标函数值：Z*=102/7。83 (2)利用大M法。解:在线性规划中加入人工变量得：这里M是一个充分大的正数,取基变量为x5,x6,x7，可得如下表cj-4-100-M-M-MθiXBbx1x2x3x4x5x6x7x533100100x6643-10010x741201001-Z0-4-100-M-M-M由于x5,x6,x7为基变量，因此它们对应的检验数行的检验数应为0，经变换得初始单纯形表。（红色为答案错误的）cj-4-100-M-M-MθiXBbx1x2x3x4x5x6x7x53[3]1001001x6643-100103/2x7412010014-Z13M-4+8M-1+6M-MM000cj-4-100-M-M-MθiXBbx1x2x3x4x5x6x7x1111/3001/3003x620[5/3]-10-4/3106/5x7305/301-1/3019/5-Z4+5M01/3+10/3M-MM4/3-8/3M00cj-4-100-M-M-MθiXBbx1x2x3x4x5x6x7x10.6100.201/15-0.203x21.201-0.60-0.80.60－x7100[1]11-111-Z3.6+M000.2+MM1.6-0.2-2M0cj-4-100-M-M-MθiXBbx1x2x3x4x5x6x7x10.4100-0.20.40-0.2383 x21.80100.6-0.200.6－x3100111-111-Z3.4000-0.21.4-M-M-0.2-M最优解为x1=0.4，x2=1.8,x3=1。目标函数值：Z*=3.4利用两阶段法。先在约束条件中加入人工变量，给出第一阶段的线性规划问题：取基变量为x5,x6,x7，可得如下表cj0000-1-1-1θiXBbx1x2x3x4x5x6x7x533100100x6643-10010x741201001-w00000-1-1-1由于x5,x6,x7为基变量，因此它们对应的检验数行的检验数应为0，经变换得初始单纯形表。cj0000-1-1-1θiXBbx1x2x3x4x5x6x7x53[3]1001001x6643-100103/2x7412010014-w1386-11000cj0000-1-1-1θiXBbx1x2x3x4x5x6x7x1111/3001/3003x620[4/3]-10-4/3103/2x7304/3011/3019/4-w5010/3-118/300cj0000-1-1-1θiXBbx1x2x3x4x5x6x7x10.6100.200.6-0.203x21.201-0.60-0.80.60－x7100[1]11-111-w100110-2083 cj0000-1-1-1θiXBbx1x2x3x4x5x6x7x10.4100-0.20.40-0.23x21.80100.6-0.200.6－x3100111-111-w00000-1-1-1这里x5,x6,x7是人工变量。第一阶段我们已求得W=0,因人工变量x5＝x6＝x7=0，所以(0.4,1.8,1,0)T是原问题的基本可行解。于是可以开始第二阶段的计算。将第一阶段的最终计算表中的人工变量列取消，并将目标函数系数换成原问题的目标函数系数，重新计算检验数行，可得如下第二阶段的初始单纯形表cj-4-100θiXBbx1x2x3x4x10.4100-0.2x21.80100.6x310011-Z3.4000-2最优解为x1=0.4，x2=1.8,x3=1。目标函数值：Z*=3.46、（1）解：将线性规划问题化为对偶问题（2）解：将线性规划问题化为对偶问题7、用对偶单纯形法求解线性规划问题。（1）解：将模型转化为cj-4-12-1800xBbx1x2x3x4x5x4-3-2-2-110x5-5[-2]-3-101-Z0-4-12-180083 θi2418cj-4-12-1800xBbx1x2x3x4x5x420101-1x12.511.50.50-0.5-Z100-6-160-2可得原问题最优解X*=（2.5，0，0），Z*=10（2）解：将模型转化为进一步可以变为cj-40-6-2500xBby1y2y3y4y5y4-60-12[-1]10y5-50-2-1-101-Z0-40-6-2500θ40－25cj-40-6-2500xBby1y2y3y4y5y4601-21-10y510-1-30-11-Z1500-15-560-250可得原问题最优解X*=（25，0），Z*=15008、已知线性规划问题（1）求原问题和对偶问题的最优解；(2)在不改变最优基的条件下，确定的目标函数系数的变化范围；（3）在不改变最优基的条件下，确定右边常数项系数的变化范围。解：原问题的单纯形表83 cj41200θiXBbx1x2x3x4x5x42[8]31101/4x58611014/3-Z041200cj41200θiXBbx1x2x3x4x5x11/413/8[1/8]1/802x56.50-5/41/4-3/4126-Z-10-0.51.5-0.50cj41200θiXBbx1x2x3x4x5x3283110x56-2-20-11-Z-4-12-50-20（1）可得原问题最优解X*=（0，0，2），最优值Z*=4对偶问题最优解（2，0），最优值Z*=4（2）如果系数的改变，使即时，原最优方案不发生改变。如果系数的改变，使即解得，这时原最优方案不发生改变。（3）如果改变，则解得83 即右边常数项系数在的范围内变化时并不影响最优方案。9、解：原问题的单纯形表cj-551300θiXBbx1x2x3x4x5x420-11[3]1020/3x59012410019-Z0-551300cj-551300θiXBbx1x2x3x4x5x320/3-1/3[1/3]11/3020x570/346/32/30-10/3135-Z-260/3-2/32/30-13/30cj-551300θiXBbx1x2x3x4x5x220-11310x510160-2-41-Z-10000-2-50可得原问题最优解X*=（0，20，0），最优值Z*=100(1)如果改变，则cj-551300θiXBbx1x2x3x4x5x230-11310x5-30160[-2]-41-Z-15000-2-50cj-551300θiXBbx1x2x3x4x5x2-152310[-5]1.5x315-8012-0.5-Z-120-1600-1-1cj-551300θiXBbx1x2x3x4x5x43-4.6-0.201-0.3x391.20.4100.183 -Z-117-20.6-0.200-1.3即第一个约束条件的右端的常数项由20变为30时，则最优方案调整为X=(0,0,9)T,目标值为117。（2）如果改变，则cj-551300θiXBbx1x2x3x4x5x220-11310x5-10160[-2]-41-Z-10000-2-50cj-551300θiXBbx1x2x3x4x5x252310-51.5x35-8012-0.5-Z-90-1600-1-1即第二个约束条件的右端的常数项由90变为70时，则最优方案调整为X=(0,5,5)T,目标值为90。(3)目标函数中的系数由13变为8，由于是非基变量，因此改变为8时，使这时原最优方案不发生改变。(4)由于是非基变量，它对应的系数矩阵变化时，不会改变，它只影响单纯形表列，只是对检验数有影响，因此。这时原最优方案不发生改变。(5)以x6为基变量，将上式反映到最终单纯形表中得到cj-5513000XBbx1x2x3x4x5x6x220-113100x510160-2-410x650235001-10000-2-500在上表中，x2、x5、x6为基变量，因此所对应的检验数应为0，因此经计算得下表。cj-551300083 XBbx1x2x3x4x5x6x220-113100x510160-2-410x6-1050[-4]-301-10000-2-500利用对偶单纯形法计算得cj-5513000XBbx1x2x3x4x5x6x212.52.7510-1.2500.75x51513.500-2.51-0.5x32.5-1.25010.750-0.25-95-2.500-3.50-0.5增加约束后，最优方案调整为X=(0,12.5,2.5)T,目标值为95。10、解：初始方案为：ABC日产量（供应量）甲矿100100200乙矿150100250日销量（需要量）100150200经过调整的最优方案为ABC日产量（供应量）甲矿50150200乙矿50200250日销量（需要量）100150200则运输量最少为50×90＋50×80＋150×70＋200×80=3500011、解：初始方案为：ABCD日产量（供应量）甲矿10060160乙矿8020100丙矿14080220日销量（需要量）80140120140经过调整的最优方案为ABCD日产量（供应量）甲矿12040160乙矿8020100丙矿14080220日销量（需要量）80140120140则运输量最少为20×80＋140×50＋120×110＋40×110＋20×90＋80×60=3280012、解：由于已知各面食加工厂制作单位面粉食品的利润及各面粉厂到各面食加工厂之间的单位运价，可得各面粉厂的面粉在不同面食加工厂制作单位面粉食品的利润，见下表面食厂面粉厂ABC甲99983 乙853丙457由于要求的是利润最大化，再一点，该问题是产销不平衡问题，增加一个虚拟的面食厂D，他的需求量为10，各面粉厂到面食厂的运价为0。在伏格尔方法中从行差额和列差额中选出最大者，选择它所在的行或列中的最大元素进行分配运量。得初始方案为：ABCD面食厂需求量甲02020乙151530丙101020面食厂需求量15252010由于所求的是最大化，因此要求检验数全部小于等于零时为最优方案。经过计算知，上述方案为最优方案：ABCD面食厂需求量甲02020乙151530丙101020面食厂需求量15252010则最大利润为15×8＋0×6＋15×5＋10×5＋20×9＋10×0=42513、解：设为买第一种包装的袋数，为买第二种包装的袋数，则数学模型为14、解：设为第i辆平板车装类箱子的数量，。则箱数的约束为重量的约束为厚度的约束为83 特殊约束自然约束目标函数是使浪费的空间最小，也就是装的越多，空间浪费的越少。15、（1）解：求相应的线性规划（LP）得（LP）的最优解首先注意其中一个非整数变量的解，如，在松弛问题中的解，于是原问题增加两个约束条件，将两个约束分别并入原问题的松弛问题（LP）中，形成两个分支，即后继问题（LP1）和(LP2)，这并不影响原问题的可行域。解（LP1），得最优解为再解（LP2），得最优解为继续对（LP1）进行分解。对（LP1）增加两个约束条件，将两个约束分别并入（LP1）中，形成两个分支，即后继问题（LP11）和(LP12)，这并不影响（LP1）的可行域。解（LP11），得最优解为再解（LP12），无最优解。因此得原问题的最优解为。(2)解：求相应的线性规划（LP）83 得（LP）的最优解首先注意其中一个非整数变量的解，如，在松弛问题中的解，于是原问题增加两个约束条件，将两个约束分别并入原问题的松弛问题（LP）中，形成两个分支，即后继问题（LP1）和(LP2)，这并不影响原问题的可行域。解（LP1），得最优解为再解（LP2），无最优解。继续对（LP1）进行分解。对（LP1）增加两个约束条件，将两个约束分别并入（LP1）中，形成两个分支，即后继问题（LP11）和(LP12)，这并不影响（LP1）的可行域。解（LP11），得最优解为再解（LP12），得最优解为。继续对（LP12）进行分解。对（LP12）增加两个约束条件，将两个约束分别并入（LP12）中，形成两个分支，即后继问题（LP121）和（LP122），这并不影响（LP12）的可行域。解（LP121），得最优解为再解（LP122），无最优解。继续对（LP121）进行分解。对（LP121）增加两个约束条件，将两个约束分别并入（LP121）中，形成两个分支，即后继问题（LP1211）和（LP1212）。解（LP1211），得最优解为。83 再解（LP1212），无最优解为。因此得原问题的最优解为。16、解：通过观察的方法找一个可行解，易得(x1,x2,x3,x4)=(0,0,0，1)符合约束条件，计算出其目标函数值Z=4。对于极小化问题，当然希望z≤4，于是增加一个约束条件，后加的约束条件称为过滤条件。过滤条件为：◎目标函数可以改写成：因为5，、4、3，2是递减的，变量(x2,x4,x3,x1)也按下述顺序取值（0，0，0，0），（0，0，0，1），（0，0，1，0），（0，0，1，1）等.◎点(x2,x4,x3,x1)约束条件是否满足条件Z值◎①②③（0，0，0，0）0√不满足（0，0，0，1）2不满足（0，0，1，0）3√不满足（0，0，1，1）5不满足（0，1，0，0）4√√√满足（1，0，0，0）5不满足（0，1，0，1）6不满足（0，1，1，0）7不满足（1，0，0，1）7不满足（1，0，1，0）8不满足（1，1，0，0）9不满足（0，1，1，19不满足（1，0，1，110不满足（1，1，0，111不满足（1，1，1，012不满足（1，1，1，114不满足得最优解(x2,x4,x3,x1)＝（0，1，0，0），最优值z＝4。（2）83 解：通过观察的方法找一个可行解，易得(x1,x2,x3)=(1,0,0)符合约束条件，计算出其目标函数值Z=2。对于极大化问题，当然希望z≥2，于是增加一个约束条件，后加的约束条件称为过滤条件。过滤条件为：◎目标函数可以改写成：因为-1，1，2是递增的，变量(x3，x2,x1)也按下述顺序取值（0，0，0），（0，0，1），（0，1，0），（0，1，1）等。◎点(x3，x2,x1)约束条件是否满足条件Z值◎①②③④（0，0，0）0不满足（0，0，1）2√√√√满足2（0，1，0）1不满足（0，1，1）3√√√√满足3改进过滤条件，用◎代替过滤条件，再继续进行。点(x3，x2,x1)约束条件是否满足条件Z值◎①②③④（1，0，0）-1不满足（1，0，1）1不满足（1，1，0）0不满足（1，1，1）2不满足至此，z值已不能再改进，即得到最优解。最优解为(x3，x2,x1)＝（0，1，1）；最优值为z=3。83 17、有4个工人，要指派他们分别完成4项工作，每人做各项工作所消耗的时间如表2，问如何分配工作可使总的消耗时间为最少？表2工作工人ABCD甲15182124乙19232218丙26171618丁19212317解：首先进行行、列变换，使每一行和每一列都出现0元素。在第一列减去15，第二列减去17，第三列减去16，第四列减去17，然后再从第二行中减去1。得首先进行行、列变换，使每一行和每一列都出现0元素。如上表中第一行减去7，第二行减去5，第三行减去4，第四行减去2，然后再从第四列中减去1。得01573550110014570进行试指派，寻找最优解。由有0元素最少的行开始，圈出一个0元素，用◎表示，然后划去同行同列的其他0元素，这样依次进行，得◎157355◎11ø◎1457ø由于独立的0元素个数少于矩阵的阶数，因此作最少的直线覆盖所有的0元素。在没有◎的行打√；对打√的行上的所有0元素的列打√号；再对打√的列上有◎的行上打√号。重复以上步骤，直到得不出新的打√号的行列为止。最后对没有打√号的行画横线，将打有√号的列画竖线。◎157355◎√11ø◎1457ø√√由于覆盖直线个数3少于矩阵阶数4，故进行变换，以增加0元素。在没有被直线覆盖的部分中找出最小元素3；然后对没有覆盖的行中各元素中减去这个最小元素3；被直线覆盖的列中各元素都加上这个最小元素3。这样在没有覆盖的元素中又增加了0元素。015100220110041240再进行试指派，寻找最优解。◎151083 ø22ø11ø◎4124◎由于独立的0元素个数仍然少于矩阵的阶数，因此作最少的直线覆盖所有的0元素。◎1510√ø22ø√11ø◎1124◎√√√004100110120051130再进行试指派，寻找最优解。ø◎410◎11ø12ø◎5113◎0100100000100001得到最优解的指派方案为：甲－B，乙－A，丙－C，丁－D；最少消耗时间为70。第二章目标规划一、思考题1，答：因为在经营管理实际中，决策者不仅要考虑资源的最佳配置和有效利用，还要考虑到市场、竞争对手、替代品的政策法律环境等多方面的影响因素和指标要求，此时线性规划模型不能完全解决问题。2，答：一般目标规划是将多个目标函数写成一个由偏差变量构成的函数求最小值，并按多个目标的重要性，给定优先等级和权重，顺序求最小值。按决策者的意愿，对于事先给定的目标值，分为三种情况：（1）当约束要求目标不超过目标值，目标函数求正偏差变量最小。（2）当约束要求目标不低于目标值，目标函数求负偏差变量最小。（3）当约束要求目标等于目标值，目标函数求正负偏差变量之和最小。3，答：（一）初始基变量的选择83 首先选择所有的负偏差变量为初始基变量；如果负偏差变量数小于约束方程数，则增加选择不同约束条件的松弛变量；如果负偏差变量和松弛变量的总数还小于约束方程数时，则需要加入人工变量，此时引入的M将被视作最高优先级，即0级优先级：。（二）满意解的判断当所有非基变量的检验数大于等于零时，目标规划问题获得最优解。非基变量的检验数为：，由于，，所以当非基变量检验数中的首项系数时，获得满意解。（三）入基变量和出基变量的选择入基变量的选择：选择检验数首项系数为负的非基变量入基，若有多个首项系数为负，则取其中检验数首项优先级最高系数最小的非基变量入基。如果首项优先级相同且系数相等，再比较第二个优先级的系数···。若有两个及两个以上的非基变量检验数（的所有各项系数）都相等，这些非基变量中有决策变量时，则首先选择决策变量入基；若它们同时是决策变量或偏差变量，则可以选择其中下标最小的变量入基。出基变量的选择：与单纯形法相同。4，答：序列解法不需要使用优先级系数，而是将单纯形法应用于不同目标层次的线性规划问题。单纯形法适用于能给目标确定优先级的场合，序列解法适用于目标层次不需确定优先级的场合。5，答：第一个问题：看最优解是否唯一或是否为最后一个层次。如果是，则不再继续求解，已获得满意解；如果不是，则需要继续下一层次目标的求解。第二个问题：如果z*＝0，则在加入第二层次目标约束后从约束条件中删去第一层次目标函数含有的偏差变量；如果z*>0，则加入第二层次目标约束后，将第一层次的目标函数（令其等于z*）作为附加约束加入到第二层次约束条件中。6，判断以下各种说法的正确性1）正偏差变量大于等于零，负偏差变量小于等于零。答：错，都大于等于零。2）目标约束一定是等式约束。答：对。3）一对正负偏差变量至少一个大于零。答：错。4）一对正负偏差变量至少一个等于零。答：对。5）要求至少达到目标值的目标函数是。答：对。6）要求不超过目标值的目标函数是。答：错。要求正偏差变量最小。二、选择题7，答：正确的是C、E。83 8.答：应该选择D。9．答：应该选择A。三、计算题10，x1x2120图1图解法第1题（1）解：对于，桔黄色内的部分满足要求，对于，蓝色内的部分满足要求，所以满意解是＝2，＝0，＝1，其它偏差变量都等于零。x22Cx101图2图解法第2题83 （1）解：对于，桔黄色内的部分满足要求，对于，蓝色内的部分满足要求，由图2知无法满足，所以满意解在点c取到，满意解是＝0，＝3，＝5，＝4，＝1，其它偏差变量都等于零。11，（1）解：初始基变量为三个负偏差变量，得到初始单纯形表如表1。表1题2(1)的初始单纯形表00002001603040811422100-1000100-1000100-1203040-8-4010000-1-2000201非基变量的检验数分别为和，因此应当入基，用最小比值法确定应当出基。换基后，通过计算求得新的基本可行解，见表2。表2题2(1)的第一次迭代单纯形表000020002010201001/23/23/21/8-1/8-1/8-1/81/81/80100-1000100-14020/340/3001000000-3/21/8-1/80201可得，入基，出基。换基后，通过计算求得新的基本可行解，见表3。表3题2(1)的第二次迭代单纯形表0000200050/320/3101000101/6-1/120-1/61/120-1/32/3-11/3-2/3100100-1001000000000110183 此时所有变量的检验数的首项系数都已经大于等于零，因此获得了满意解如下：＝50/3，＝20/3，=10，其它偏差变量都等于零。（1）解：初始基变量为四个负偏差变量，得到初始单纯形表如表4。表4题2(2)的初始单纯形表000000040605020111011011000-100001000-100001000-100001000-1406050--1-101010000-10000001000-100000001由上表得，入基，出基。换基后，通过计算求得新的基本可行解，见表5。表5题2(2)的第一次迭代单纯形表0000000040201020100010-111-1-10-111001000-100001000-100001000-1-2010-0010010000011-10001000-100000001由上表得，入基，出基。换基后，通过计算求得新的基本可行解，见表6。表6题2(2)的第二次迭代单纯形表00000000050101020100001-1100-10001001000-1001-110-11-100001000-1-10-20001001000083 00000010000-100000001由上表得，入基，出基。换基后，通过计算求得新的基本可行解，见表7。表7题2(2)的第三次迭代单纯形表000000000501020101000010000-100010011-10-1-111-101-110-10001000-10010010000000000100000001-1-1101此时所有变量的检验数的首项系数都已经大于等于零，因此获得了满意解如下：＝50，＝10，=20，=10，其它偏差变量都等于零。12，1）用单纯形法求解；解：初始单纯形表如表8。表8题3的初始单纯形表0005003506942111022-211000-100001000-100001000-100001000-139/2-2-1-201000000-1-200010000-510000005030001000000由上表得，入基，出基。换基后，通过计算求得新的基本可行解，见表9。表9题3的第一次迭代单纯形表83 0005003502582111000011000-100001000-100001000-10-2-22122-2-115/2---100100002-2-100001002-2-50000005-10130001000000由上表得，入基，出基。换基后，通过计算求得新的基本可行解，见表10。表10题3的第二次迭代单纯形表0005003350131031/2021/200011/2-111/2-1/21-1-1/201000-100001000-10-10001000-3--0010000000001-1010000-23/20-13/213/20005300001000000由表10得，入基，出基。换基后，通过计算求得新的基本可行解，见表11。表11题3的第三次迭代单纯形表00050033505/231321/202000010-10001001/2110-1/2-1-10001000-10-1001100-15-13/2-00100000000000100000-23/2000-13/213/205300010-11000083 由表11得，入基，出基。换基后，通过计算求得新的基本可行解，见表12。表12题3的第四次迭代单纯形表00050030505332100000010-100010011-10-1-110001000-10-204120-4-1--3/420010000000000010000000005-505-20230010-110000由表12得，入基，出基。换基后，通过计算求得新的基本可行解，见表13。表13题3的第五次迭代单纯形表000500300013/233/45/4100000010-10001001/21-1/41/4-1/2-11/4-1/41/201/4-1/4-1/20-1/41/4001000-10--3/420010000000000010000000000050030010-110000此时所有变量的检验数的首项系数都已经大于等于零，因此获得了满意解如下：＝13/2，＝5/4，=3，=3/4，其它偏差变量都等于零。由于非基变量的检验数为0，所以此题有多个解。由图解法容易得到在（＝13/2，＝5/4）和（＝9，＝0）两点间的连线都是满意解。2）目标函数分别变为如下两种情况，请分析解的变化a)b)（假设和的按比例变动）。83 解：对于上面两种情况，在第一、第二目标相继满足的情况下（即＝＝0），关于的目标实际上已经无法有效满足，这时和优先级的顺序不影响满意解的结果，所以a）和b）的解均不变。13.解：设，分别表示每周生产A,S型号的微型计算机的台数。第一个目标要求每周总利润不低于10000元，即第二个目标要求A型机至少每周生产10台，S型机每周至少生产15台，即这里在第二目标中对两种产品使用了不同的权重，主要是考虑到A,S型号的微型计算机的利润不同：300/450＝2/3，所以A和S型号的微型计算机权重为2和3。第三个目标要求工序一每周生产时间最好等于150小时，工序二生产时间可适当超过其能力75小时，即综合以上各指标要求，得到该问题的目标规划模型如下：14.解：设是从第产地运往销地的商品数，则对a）83 对b）对c）对d）对e）对f）其中4580是由线性规划得到的运费最小值。其它有关供应量和需求量的约束照样成立，得到该问题的目标规划模型如下：产量约束：83 15,解：设表示i商标（红、黄、蓝）中j等级的数量（i，j＝1，2，3），表示m商标每天的产量（m＝1，2，3），则对于1）对于2）其中2500是由线性规划得到的利润最大值。对于3）其它约束：综合以上各指标要求，得到该问题的目标规划模型如下：83 第三章动态规划1.计算图中所示的从A到E的最短路线及其长度。83 11114443233532352353883515467最短路线长度为8。2.解：A.按动态规划要求确定以下参数：（1）将卸货问题按零售店分为四个阶段，顺序1、2、3、4。（2）各阶段的状态参数表示为分配给第k至第4个零售店的总货物箱数。（3）是分配给第k个店的货物箱数。（4）状态转移方程。（5）最优指标函数B.分阶段计算当00000114412255233663446645566566666当83 000000010108404818201208554051251123012308576540613971134012340857866540614101181145012345085788666540614111212811460123450857886666546141113131211483 6808当0000000101028082082012024128012104012301230246131280131412611440123402468141312801415161482165012345024689141413128014161718169318601202414141414161883 34566891013128019201710420当60123456046777720181614128020222221191571222C.从第一个阶段开始寻找最优决策序列，步骤如下：（1）由或2可知，在零售店1卸下1箱或2箱。（2）由或可知，①当在店1卸下1箱时，则在店2卸下3箱；②当在店1卸下2箱时，则在店2卸下2箱。（3）由可知，在店3卸下1箱。（4）由可知，在店4卸下1箱。由以上分析可知，有两个最优方案，利润都是22。方案Ⅰ：零售店1234箱数1311方案Ⅱ：零售店1234箱数22113.解：A.确定参数（1）将三个地区按1、2、3顺序分成三个阶段。（2）各阶段状态参数是在第k个地区之后（包含第k个地区）有零售店总数，是在第k个地区的零售店数目。（3）最优指标函数是从第k个地区开始到最后为止的最大利润83 B.00000111010122141423316163441717400000001010121001012112201201217141001422171223012301217211614100162627212274012340121721221716141001728313122233183 4012340162530323127221203143474232247所以，方案为：地区123零售店2114.解：A.（1）每月的生产存储计划作为一个阶段，共分六阶段。（2）——每月月初的库存量；——各阶段的生产量；——第k阶段（月）的需求量。（3）指标函数取为总成本本期成本：从k阶段开始到最后为止最低总成本递推公式是：B.分段计算：期末存货以后各时期成本总成本0114001410100183 总成本023*24+034+001141383535112*14+124+10114129262620*10+214+20114116171630*0+31144总成本03*434+044+001352669706912*3424+134+144+10123526166061616021234*14+224+234+244+201233526164515252505030*1230+314+324+334+3012335261643843434138总成本83 1444+106911411423*434+244+201696010510610532*3424+334+344+301269605096979796总成本03*434+044+01211410514814914812*3424+134+144+11231141059613914014113921*2314+224+234+21231141059613013113213030*120+314+324+312311410596117122123117总成本01234*14+024+034+044+0012314813913011716216316416116183 C.总结以上可得每个月的最优生产与库存计划月份k月初存货月末存货最优生产量该月成本总成本103444161231001173104451144003346950133435610001即第一、第三个月各生产四百个，第四、五个月各生产三百个，总成本为161千元。5.解：A.按月份分为四个阶段：各月初的存货，：每个月的生产量，：每个月的销售量。（单位均为百件）。指标函数取为总成本，各阶段成本从k阶段开始到最后为止最低总成本递推公式是：B.分段计算：。027+0007116+1007200+2002总成本83 0345*8+09+010+0012772151612121234*7+18+19+1012772151612122123*6+27+28+20127721516121230*120+36+37+30127721016121040*10+46+41272111211500+52277总成本05*678910*10+011+012+013+014+015+0012345121212101172223242325222214*569+110+111+10121212122223242283 789*12+113+114+13451011723252223*45678*8+29+210+211+212+213+2012345121212101172223242325222232*34567*7+38+39+310+311+312+2012345121212101162223242325222241*23456+47+48+49+410+411+4012345121212101172223242325222250*123450+56+57+58+59+510+5012345121212101171723242325221760*10+66+612121218241883 2347+68+69+63451011723252270*1230+76+77+78+723451210117192325221980*120+86+87+8345101171825221890*10+96+9451172022201000+10571717总成本13*45678*9101112138+19+110+111+112+113+114+115+116+117+118+101234567891022222222221718191820173132333435313335353836由上可得该厂在四个月内的最优生产计划（三种方案）：Ⅰ.1月份生产300件，2月份生产500件，3月份生产500件；Ⅱ.1月份生产300件，2月份生产1000件；Ⅲ.1月份生产800件，3月份生产500件。83 三种方案总成本均为3100元。第四章网络分析1、（提示）：将三个容器中各有多少酒量定为一个状态，如初始状态，每一个状态作为图的一个节点。然后对每一状态，找出在此状态下可能倒酒的方法及其可能产生的状态。并将有状态转移关系的两个节点用直线连接起来。这样不断地派生下去就会形成一个由节点(状态)和线（状态的转移关系）构成的图。找到初始状态和目标状态的路线，即找到了平分8升酒的倒酒方法。2、（提示）：课文中图4-5是过河问题的模型图，可以用相邻矩阵表示。将该矩阵连乘，当矩阵中元素第一次出现不为0的数值时其值就代表的道路或过河的方案数目，其连乘的数目即表示完成过河所必须的最少来回摆渡次数。（注：利用该相邻矩阵的结构特点，可以简化矩阵运算的阶数）3，解：最小生成树为：最小生成树的权值为：43.5。4，解：最短线路为：［主行,］，，，,总长度为：4203.（1）解：令，其余83 SACDBET45617685（2,2）2145第一次迭代：∵最小，∴令第二次迭代：∵和最小，∴令第三次迭代：∵最小，∴令第四次迭代：∵最小，∴令第五次迭代：∵最小，∴令83 ∴最短路径长16，路线有两条：或（2）解：同法克求出最短路为：，路长17。2347522634652234354852ASBEITCFDGH6，.求网络的最大流。（1）SBCTDA(3,4)(2,5)(3,3)(3,5)(2,2)(0,1)(2,2)(0,1)(0,2)解：第一次迭代，得出增广链：第二次迭代，得出增广链：因为都有饱和弧，不再存在增广链，所以标号停止，当前流就是最大流。最大流如图所示。（2）解：最大流如图，最大流为2583 SABTEDCGHF(3,3)(0,4)(3,7)(5,5)(8,15)(0,12)(1,18)(1,7)(8,13)(11,11)(9,9)(12,15)(3,6)(10,10)(5,8)(9,9)(2,10)7，解：令第１年初为，第１年底为，第２年底为，第３年底为，则画图如下：45118615用标号法求得最短线路径为：，路长14（千元）所以最佳方案为第１年初买进设备到第２年底卖出，同时购进新设备到第３年底卖出。总费用为1.4万元。8，解：令。其余各点赋Ｔ标号第一次迭代：，∴令第二次迭代：∴令第三次迭代：∴第四次迭代：∵∴83 　　∴∴令第五次迭代：∴令∵∴仍为－１∴第六次迭代：∴令∴∴最短路线为9，解：最小费用流为：（弧旁数字为）(4,4,1)(1,5,3)(2,2,4)(1,1,1)(0,1,2)(3,3,3)(5,5,2)(2,3,1)(0,2,4)最小费用为37，最大流量为5。10，解：最小费用最大流为：（弧旁数字为）83 (16,16,1)(6,15,4)(14,14,1)(8,17,3)(8,11,2)(0,13,6)(8,8,2)最小费用为110，最大流量为22。11，（1）1→2→3→5→1→15→12→11→10→5→6→3→4→7→6→9→7→8→13→9→12→13→14→10→1151110121314213456987（2）10→4→1→3→7→9→13→10→11→5→6→12→11→14→12→8→6→2→5→4→3→9→101234567891011121314（2）2→1→5→2→6→5→9→10→6→7→11→10→14→9→13→14→15→16→12→15→11→12→8→4→3→7→8→3→283 1234567891011121314151612，（A）最佳邮路就是使走的重复街道的总长度最短的投递路线。图中有8个奇点：A、C、E、G、H、J、K、L。则求最佳邮路问题就等价于求最优的奇点对组合方案。即为：LE、AC、GH、KJ（图中已标明），路长为3+2+2+3=10。11233332344FGHIJD1CAB(A)KLE（B）同上，其最优奇点对组合方案如图所示。路长为1+1+1+1+3+1+1=9。1111111122222444(B)22313，83 ①3②③④⑤⑥⑦⑧333542567ACFJIEBHGD路线周期（1）a：①→②→④→⑥→⑦→⑧3+5+3+2=13b：①→②→④→⑦→⑧3+5+5+2=15c：①→②→④→⑤→⑧3+5+7+4=19d：①→③→④→⑥→⑦→⑧3+6+3+2=14e：①→③→④→⑦→⑧3+6+5+2=16f：①→③→④→⑤→⑧3+6+7+4=20g：①→③→⑤→⑧3+3+4=10（2）关键路线为：①→③→④→⑤→⑧总完工期为20天。14，网络图：①②③④⑤⑥⑦ABCDGHEF15，网络图：①③④⑤⑥⑦ABCDGEF②16，（1）网络图：①②③④⑤⑥⑦22111114141414661200ACGIDFHEB123306544（2）各节点时间参数如图所示。（3）作业C：②→⑤83 17，解：（1）正常情况下，总工期为20天，关键路线①→③→④→⑤。（2）解：从关键路线上考虑可缩短2天的作业有3个，费用率为作业1—33—44—520.51所以以作业3—4为缩短时间对象，且不影响关键路线：①→③→④→⑤。∴，追加费用为。（3）选作业3—4为缩短时间对象，受本身极限时间限制，最多能缩短3天。则天。追加费用为。再选择作业4—5为缩短时间对象，当缩短一天时，此时。追加费用为。此时关键路线变为2条：①→③→④→⑤和①→③→⑤。此时缩短总周期的方案有两个：方案ⅠⅡ缩短作业费用率1—323—5，4—50.5+1∴选择方案Ⅱ，，追加费用累计为。第五章决策论83 1决策指人（们）在求生存与发展过程中，以对事物发展规律及主客观条件的认识为依据，寻求并实现某种最佳（满意）的准则和行动方案。决策的要素主要包括有]：决策单元、准则体系、决策结构和环境、决策规则等。2根据不同的标准，我们可以把决策分为不同的类型。（1）按决策的作用范围分类，决策问题可以分为：战略决策、管理决策和业务决策。战略决策就是认识、分析和解决有关系统指导思想和全局发展的重大问题，通常包括系统长期目的、目标和发展方针的确定，行动过程的选择，以及为实现目标所需要的重要资源的分配等。管理决策又叫战术决策或策略决策，它是指对企业的人力、资金、物资等资源进行合理配置，以及经营组织机构加以改变的一种决策，具有局部性、中期性与战术性的特点。业务决策又叫执行性决策，是日常工作中为提高生产效率和工作效率而做出的决策。（2）按决策问题的不同性质或决策的重复程度分类，可以分为：1程序化决策和非程序化决策。程序化决策又称为常规决策，是指可按照既定的程序、模式和标准进行的决策。在实际生活中，无论是个人还是组织活动，有相当一部分属于程序化决策。非程序化决策是指不能按既定的模式和程序所做出的决策。它一般用于解决所遇到的重大的、不经常出现的问题。非程序化决策事实上要体现决策者的创造性，而且风险也比较高。所以，非程序化的决策权一般为组织的高层管理人员所掌握。83 （3）按决策问题所处的条件分类，可以分为：确定型决策、风险型决策和完全不确定型决策。确定型决策指决策的主要约束条件已十分明确和肯定，每个备选方案的预测期结果比较确定，只要对不同的方案进行比较，从中选优就可以做出选择的决策。风险型决策是一种不确定性决策，指决策面临的自然状态是已知的，且可以对未来每种状态出现的可能性有一个主观概率值，但哪种状态将出现是不确定的。此时决策的结果受概率估计值的影响，因而对方案的选择带有一定的风险性，故称这种决策为风险型决策。完全不确定型决策是指决策者对未来事件虽然有一定程度的了解，知道可能出现的各种自然状态，但又无法确定各种自然状态可能发生的概率的情况下所做的决策。（4）按决策主体分类可以分为个人决策和群体决策。如果决策的分析活动、设计活动、选择活动由一个人来完成，这种决策称为个人决策。如果决策的分析活动、设计活动、选择活动由包括两个人以上的群体完成，这种决策称为多人（群）决策。3多准则决策就是用多个准则（目标/属性）对事物进行比较、排列和排序。经典的多准则决策可以划分成两个重要的领域，即多目标决策（MODM）和多属性决策（MADM）。这两种决策的主要差别在于：前者的决策空间是连续的，即其备选方案数有无限多个，而后者的决策空间(决策变量)是离散的，其中的备选方案数量为有限个，因此，有些文献也称之为有限方案多目标决策问题；本质上前者研究的是未知方案的规划设计问题，求解这类问题的关键是向量优化，即数学规划问题，而后者研究的是已知有限方案的评价选择问题，这类问题求解的核心是对各备选方案进行评价后排定优劣次序，再从中择优。4层次分析法大体可以分为以下4个步骤：83 （1）分析系统中各因素之间的关系，建立系统的递阶层次结构。层次大体可以分为三类：最高层——顶层只有一个元素，一般它是所需解决问题的总目标要求，故也称总目标（准则）层；中间层——包括为了实现总目标所涉及的中间环节，它可以由若干层次组成，包括所需要考虑的约束，多级子准则等；最底层——表示为了实现准则可供选择的各种措施、备选方案，故称方案层。同一层次的各元素关于上一层中的某一准则的重要性进行两两比较，构造两两比较判断矩阵。（3）由判断矩阵计算被比较元素对于该准则的相对权重。（4）计算各层元素对系统总目标的合成权重，并进行排序。层次分析法与已有的其他决策方法比较，有以下一些特点：（1）层次分析法适用于解决有许多评价标准，但又没有共同的尺度来衡量的决策问题。（2）回答成对比较系数时，采用同等、稍微、相当、非常、极端灯模糊分类，可以减轻决策者的负担。（3）遇到不满足一致性的数据，与修正数据相比，理解不一致性是容易的。（4）对复杂的或是构造不明确问题，可在一定的限制条件下进行部分比较考察，然后，再作综合的评价。（5）层次分析法是一种定性定量相结合，系统化、层次化的分析方法，在决策中充分考虑到了经验与直觉。（6）83 层次分析法可以解决那些没有数据或者很难得到数据但是又必须作出决策的问题。5，效用函数根据决策者对风险态度的不同而不同。由于决策者不同的风险态度，效用函数也有不同类型。如图所示：A直线型效用函数决策者对决策风险保持中立态度。B保守型效用函数决策者对决策风险持厌恶态度。曲线中间部分上凸越厉害，表示讨厌风险的程度越高。C冒险型效用函数决策者对决策风险持冒险态度。曲线中间的下凹越厉害，代表决策者的冒险型越大。D渴望型效用函数当损益值比较小的时候决策者具有一定的冒险精神，当损益值增加到某个值后，决策者就转为保守态度。6解：（1）采用最大最小准则进行求解，如表：自然状态方案最小收益值A32402929B21284521C3842272783 最大最小决策准则29从表中看出，采用最大最小准则时的最优方案为方案A。（2）采用最大最大准则进行求解，如表：自然状态方案最小收益值A32402940B21284545C38422742最大最大决策准则45从表中看出，采用最大最小准则时的最优方案为方案B。（3）采用的乐观系数的赫威斯准则进行决策，如表自然状态方案最大收益值最小收益值折衷收益值A324029402935.6B212845452135.4C384227422736赫威斯决策准则36从表中看出，采用的乐观系数的赫威斯准则进行决策，最有方案为方案C。7解：本题可用期望收益决策法进行决策。开工方案：元不开工方案：元根据计算，开工方案能够获利8000元，不开工方案则损失5000元，所以，开工方案为决策最优方案。83 8解：（1）画出决策树，如下（2）计算各点的期望损益值点2：（万元）点3：（万元）比较两个方案的期望损益值，可知应该选择方案：建设大工厂。9解:设：钻井，：不钻井。：有油，：无油。则可以画出问题决策树如下。设决策人风险中立。钻第一口井：的期望效益为的期望效用为0，所以应该选。同理可得，在钻第二口井时，的期望效益为0，的期望效用为－10，应该选。钻第n口井时，83 的期望效益为20－10n，的期望效用为－10n+10。而20-10n>-10n+10,所以仍应选。从上面分析，似乎不论钻多少口井，只要没有油就应该选择继续钻下去。这样做得前提是对的绝对信任。实际中连续钻几口井都无油时，就要怀疑的正确性，而不应该再继续钻下去了。10解：在各项指标种，投资成本、环境污染程度为成本型属性，其他为效益型属性。将决策矩阵进行规范化，得到规范化的决策矩阵,如表所示。决策矩阵0.74550.93430.681110.76470.677710.72460.7926110.618910.71950.86670.87490.99040.98710.90240.4643采用一般加权和法对方案的属性值进行集结，求得各个方案的综合属性值分别为：83 按照综合属性值的大小对企业进行排序故最佳企业为。11解：记：生产产品A，生产产品B。为甲的效用函数，为乙的效用函数。作效用曲线如下图。，。因此，甲应该选择生产产品B。，。因此，乙也应该选择生产产品B。83 12解：记：选择第一种玩法，：选择第二种玩法；：翻开第一张为红，：翻开第一张为黑。则可以画出决策树如下：选第一种情况下：第一章为红：，，故应选。第一章为黑：，，故应选。第一种玩法的期望效用为：。第二种玩法的期望效用为：。根据计算，此人应该选择第一种玩法。第六章对策论1.解释名词：对策论完全信息不完全信息子对策后续对策解：对策论亦称博弈论，是矛盾和合作的规范研究，是研究决策者的行为发生直接相互作用情况下的决策以及这种决策均衡的理论，也就是说，研究当一个决策者的行为选择受到其他决策者行为的影响，并且他的决策也影响其他决策者的决策时的合理选择问题。当每个参与人的特征、支付函数（参与人选择的行动组合借助于它决定参与人的支付）以及策略空间在所有的参与人中是共同知识时，我们说这个对策具有完全信息。当它们，特别是支付函数，不是共同知识时，就说这个对策具有不完全信息。子对策的定义见定义6-5。从每一个信息集开始的对策的剩余部分称为一个“后续对策”83 ，这不同于子对策，因为子对策必须开始于单结信息集，并且不能切割信息集，而后续对策可以始于任何完全信息集（不论是否为单结）。2.，解：两种情况下的支付矩阵如下：不实行“最惠客待遇”III高价低价高价20,20低价12,12实行“最惠客待遇”III高价低价高价20,20低价12,12采用画线法，我们发现，在不实行“最惠客待遇”的情况下，两商店都选择低价，都获得支付12。在实行“最惠客待遇”的情况下，有两个纯策略纳什均衡：(高价,高价)和（低价,低价）。(高价,高价)是一个支付占优均衡，两商店可以获得较高的支付，这一均衡更有可能被选择。在实行“最惠客待遇”的情况下，动态地来说，采取高价策略以后，商场不再有降价的激励。这样，商场可以获得比较高的利润，顾客实际上没有享受任何“优惠”。3.解：广告对策支付矩阵为甲乙花费10花费6花费102,29,-1花费6-1,96,6如果将广告花费为10的看作非合作行为，而花费为6的看作合作行为，那么，（2,2）（对应于高广告费）是一个纳什均衡点。虽然两个宾馆在（6,6）点比在(2,2)点要好，但是，（6,6）是不稳定的，因为没有一个宾馆单方面改变策略而获得更高的支付。这样，为了保护市场份额，每个宾馆必须花费大量的广告费用。4.解：根据题意，两公司的支付矩阵如下表克拉克宝洁研发不研发83 研发40,20不研发60,40采用划线法可知，该对策的纳什均衡是（研发,研发），劣于两公司都不研发。也就是说，两公司陷入了囚徒困境。那么，为什么没有产生“不研发”这个合作行为？由于几方面的理由，包含研发的囚徒困境是特别难以解决的。第一，一家公司很难用监视价格的办法监视竞争对手的研发活动；第二，完成一个能导致重大产品改进的研发项目要花费好几年功夫，因而两公司合作直到两者间“欺诈”为止的投桃报李策略，不大可能起作用，因为一公司可能直到竞争对手宣布一种新的、改进的产品之前都很难发觉竞争对手一直在秘密进行研发，而此时该公司再投入研发项目可能已经太晚了。宝洁和金伯利—克拉克的研发支出也起到了阻止进入的作用。除了品牌名称的认同外，这两家公司已经积累了如此多的技术诀窍和生产的熟练性，以至于对任何刚进入该市场的企业都有可观的成本优势。为了夺取甚至只是很小的市场份额，进入者除了建造新工厂以外，必须花费大量的资金用于研发。在进入者开始生产以后，还必须不断花费大量资金于研发以不断降低成本。而且仅当宝洁和金伯利—克拉克停止进行研发，进入才是有利可图的，此时进入者能够赶上并最终获得一定的成本优势。但正如我们已经看到的，宝洁和金伯利—克拉克都进行研发。5.,解：它应该不对公司T的股份出价。注意公司T只有在出价大于其当前管理下的每股价值时才会接受出价。设你出价50美元，那么，公司T只有在开发项目的结果在当前管理下的每股价值为50美元或更少时才会接受该出价。在0美元到100美元之间的任何价值出现的机会都相等，因而公司T的股票的期望值，给定它接受出价，即开发项目结果的价值低于50美元的前提时，为25美元，从而在公司A的管理下价值将是美元，这是低于50美元的。实际上，对任何价格，如果出价被接受，公司A能期望得到的价值只有。6,解：（1）根据支付矩阵可以发现，两企业究竟采用哪种策略更好完全取决于对方选择何种策略，因此，该对策没有占优均衡。（2）运用划线法很容易找出该对策有两个纯策略纳什均衡：（高档，低档）和（低档，高档）。此外，该对策还有一个混合策略纳什均衡：设企业甲生产高档彩电的概率为，企业乙生产高档彩电的概率为。于是，甲的预期支付为其一阶条件为解之得83 由于支付矩阵的对称性，可得这样，混合策略组合是一个混合策略纳什均衡。7,解：记参与人I的混合策略为，参与人II的混合策略为。这样，参与人I的预期支付为其一阶条件为，，解之得，，由于对称性，类似地有，，这样，混合策略组合是混合策略纳什均衡。值得注意，这与对策的鞍点是一样的。8,解：（1）完全信息静态对策。该对策的支付矩阵如下：III克扣不克扣偷懒50,40100,不偷懒10,11060,60采用画线法，可得该对策的纳什均衡为（偷懒,克扣），工人和老板陷入了囚徒困境。（50,40）(100,-10)(10,110)(60,60)克扣不克扣克扣不克扣偷懒不偷懒III（2）完全信息动态对策，其对策树如下83 采用逆向归纳法，对最优策略加粗，发现子对策纳什均衡为（偷懒,克扣）。9,解：采用画线法可知，阶段对策惟一的纳什均衡是（低质量，不购买），双方获得的支付为（0，0）。效率高的（高质量，买）不是纳什均衡，因此一次性对策的结果是不理想的。在无限次重复对策中，我们构造下列触发策略组合。商店的策略：第一阶段销售高质量商品；如果以前阶段一直销售高质量商品且顾客总是购买，则继续销售高质量商品，否则销售低质量商品。顾客的策略：第一个顾客选择购买，第二个及以后的顾客的选择是，如果商店以前未卖过低质量商品时选择买，否则选择不买。首先分析商店的策略。给定消费者的策略，如果商店销售低质量商品，可以得到3单位短期利润，由于以后每阶段顾客不再购买利润为0；如果商店总是卖高质量商品，则每一阶段都得到1单位利润。设厂商长期利益的贴现率为，那么当也就是时，商店会始终销售高质量商品，否则就会一开始就销售低质量商品。如果以前曾经销售过低质量商品，那么，因为顾客不会再购买，因此，永远销售低质量商品是不合理的。现在分析顾客的策略。因为当时商店不会坚持上述触发策略，因此，直接假定成立。由于每个顾客进行的不是重复对策，他们关心的仍然是当前支付，预期本阶段商品为高质量会购买，否则不购买。先讨论第一阶段顾客的选择。根据商店的策略，商店第一阶段会销售高质量商品，因此，该阶段顾客选择买。再考虑以后各阶段顾客的选择。给定商店的策略，如果其以前未销售过低质量商品，它就会继续销售高质量商品，顾客应该买；如果其曾销售过低质量商品，肯定会继续销售低质量商品，顾客应选择不买。因此，在这个商店和顾客群体之间的无限次重复对策中，只要商店的贴现率，那么，上述触发策略组合就是一个子对策完美纳什均衡，商店会坚持卖高质量商品。10，解：参与人1的策略空间为，参与人2的策略空间为，参与人1的类型空间为，参与人2只有一个类型。参与人1的利润函数为类企业1对企业2产量的反应函数为，由于参与人2不知道参与人1的类型，所以参与人2最大化它的预期利润函数这样，参与人2的最优反应函数为83 联合三个反应函数，可解得贝叶斯纳什均衡产量为，，11.解：根据纳什均衡的定义，可以发现该对策有两个纯策略纳什均衡：和。根据完美贝叶斯均衡的定义，纳什均衡，加上参与人II的相应判断：参与人I没有采用L的情况下，判断参与人I采用M，即，构成该对策的一个完美贝叶斯均衡，即12.解：的条件是，，，，后三个不等式可以化为和。因此，该对策的核心是13.解：（1）这个对策的特征函数是（2）假设是对策的核心中的一分配方案，那么，必须满足，，，，，将与相加，产生。注意到83 。这样，两不等式必须是紧的。同时解它们作为等式，产生和。类似地，也可以证明，于是。这样，对策的核心是分配方案。核心强调参与人1的重要性。（3）为了计算，列出所有不包含参与人1的联盟，我们计算和如表a。表a参与人1的Shapley值的计算2/601/620000002/620000001/62000000因为参与人1平均增加价值于是，Shapley值建议分配给参与人1的支付为4000000/3。为了计算参与人2的Shapley值，我们列出表b。表b参与人2的Shapley值的计算2/601/620000001/602/60这样，参与人2的Shapley值为更进一步，参与人3的Shapley值为这样，按照Shapley值分配，似乎比按照核心分配更公平。83 第七章存储论经济订购批量存贮模型(M1)1,解：利用上述公式，可求得最优存贮量=1140.2(箱)订货间隔时间=2.668(天)年存贮费＝年订货费＝＝6841(元)例题结论的实际操作：(1)、进货间隔时间2.67天（无法操作）延长为3天，于是每次订货量变为Q=R/365=3000•52•3/365＝1282箱；(2)、为保证供应决定多存贮200箱，于是第1次进货为1282＋200＝1482箱，以后每次1282箱；(3)、若需提前1（或2）天订货，则应在剩下货物量为R/365=3000•52/365=427箱（或854箱）时就订货，这称为再订货点。2，解：R=6000台/月，c3=1200元，K=20元，c1=0.10元/月。应用（7.3）～（7.5）式答：每两月生产一次，每次生产12000只3，解：如以R表示某种物资的年需用量，该物资的单价k=100元/件，一次订货费C3为250元/次，r表示存贮费率，即存贮每元物资一年所需的存贮费用为12.5%，年需要量R=6240件/年。按公式（7.3）～(7.5)，经济订货周期与每次订货量为：=83 平均存贮费为：允许缺货的经济生产批量模型(M2)4，解：利用（7.9）～(7.16)可求得：最优存贮周期=12.8(天)经济生产批量最大存贮量(件)根据有关费用的计算式，得到：年存贮费年生产准备年缺货费总费用C*=42897(元/年)5，解这是属于允许缺货，一订货就进货，缺货要补的模型。已知P=80000/12，R=20000/12，c1=0.10，c2=0.20，c3=350，由（7.9）式最佳订货周期　　　≈2.9(个月)，合0.242年最佳经济批量是（7.10）式，(个)最大存贮量（7.14）式，（个）其他参数值如下：经济生产批量存贮模型(M3)7.6一种专用书架，市场的年需求量为R=4900个／年，存储费C1=1000元／个•年，生产厂的年生产能力p=9800个／年，其生产准备费用为C3=500元／次,不允许缺货。求最低成本的生产组织。解：满足利用（7.17）、（7.18）、（7.21）上述公式，可求得83 最优生产量(个)周期7.4(天)，或=0.202（年）年存贮费＝年生产准备＝4900/99*500=24747.5(元/年)总费用=49497.5(元/年)7，解：已知，该零件每年的存贮费为/年.件；C3=200元/次，P=50件/天，R=26件/天。由（7.18）式得到可近似地安排每两个月组织一次生产，需求26*60=1560(件)，每次生产天数为1560/50=31(天)。如此安排，按(7.21)式，平均最小存贮费为：最大库存量为：7.8解本例特点是补充除需要入库时间(相当于生产时间)外，还需考虑拖后时间。因此，订购时间应在存贮降为零之前的第5天。除此之外，本例和模型三的假设条件完全一致。本例的存贮状态图见图7.7。从图7.7可见，拖后时间为[O，t0]，存贮量L应恰好满足这段时间的需求，故L=Rt0。根据题意，有P=2件／天，R=1件／天，C1=300×2％×1/30=0.2元／天·件，C3=20元／次，to=5天，L=1×5=5件。代入式(7.17)～(7.21)可算得：最优存贮周期(天)经济生产批量=20(件)83 结束生产时间=20/2=10(天)最大存贮量=10(件)平均存贮费用=2×20/20=2(元/天)允许缺货的经济订购批量模型(M4)7.9解：1）不允许缺货时，按订货方式，用模型1公式：(件)/年2）允许缺货时，利用模型4公式（7.22）～（7.27）经济订购批量(件)最优存贮周期(天)订货次数最大存贮量(件)平均存贮费用(元/年)可以看出：允许缺货的最小总费用比不允许缺货的要少。7.10解不允许水泥有缺货时，R=100，C1=0.08，C3=100,由(7.3)、(7.4)和（7.5）式,分别为：（天），(吨)(元/天)。故每隔5天订货一次，订货量500吨，费用40元/天(不含货款)。此处允许水泥有缺货时，c2=2。由公式(7.23)，得（吨）；（天），所以，当允许水泥有缺货时，建筑公司的订货周期延长了，且每次的订购量相对地增加了，尽管这里增加的不是很大。7.11解：R=6000台/月，c3=1200元/次，K=20元/只，c1=0.10元/月·只，C2=1元/月·只。83 应用（7.22）、（7.23）、（7.26）、（7.27）式订货周期订货量最大缺货量1144（只）最小总费用（不含成本费用120000元/月）经济订货批量折扣模型(M5)7.12解：对不同折扣情况按经济订货批量模型计算订货1～49个：K＝500元／个，C1＝100元／个•年计算,Q*＝35(个)，存贮费1750元，订货费（8.57次）1714元，购货费150000元，C*=153464元；订货50～99个：K＝480元／个，C1＝96元／个年计算，Q*＝35(个)，实际取Q*＝50(个)，存贮费2400元，订货费（6次）1200元，购货费144000元，C*=147600元；订货100个以上：K＝475元／个，C1＝95元／个年计算，Q*＝36(个)，实际取Q*＝100(个)，存贮费4760元，订货费（3次）600元，购货费142500元，C*=147860元。综合上述结果，最优订货为Q*＝50(个)7.13　解　根据模型一，在单价不变的情况下求出最佳订购批量为　　　　　　　　　（个）本模型中，由于订购批量不同，订货周期长短不一样，所以才利用平均单位货物所需费用比较优劣。当然也可以利用单位时间内的平均总费用，按（7.29）式。因10000＜Q0＜30000,故应计算作为比较的标准。本例中83 由于min｛C(Q0),C(Q2),C(Q3)｝=C(Q2),所以，最佳经济批量是　Q*=30000　(个)。需求为离散随机变量单周期模型(M6)7.14解：由公式（7.33），k/(k+h)=（v-u）/（v–u+h）=0.8814；（r=1001～1350）时，累积概率Sp（r）=0.92（r=1001～1300）时，累积概率Sp（r）=0.82故最优订购量为：1350双。应分为3批订货，共需资金=3×500+1350×80=109500(元)7.15解此题属于单时期需求是离散随机变量的存贮模型。已知u=5,v=10,w=2.由（7.33）式，得k=v–u=5表示每售出一件物品的获利；h=u–w=3表示每处理一件物品的损失，即。因为P(17)=0.12，P(18)=0.18，P(19)=0.23，P(20)=0.13，所以P(17)+P(18)+P(19)=0.53＜0.625;P(17)+P(18)+P(19)+P(20)=0.66＞0.625,故最佳订货批量Q*=20（件）。7.16上例中，若因缺货造成的损失为每件25元的话，问最佳经济批量又该是多少？解凡售出一件商品的获利数，应看成是有形的获利数与潜在的获利数之和，在公式（7.33）中，若将损失25元视为潜在的获利，对于本题，显然有k=(10-5)+25=30,h=5-2=3由（7.33），得通过计算累计概率，可得Q*=24（件）需求为连续随机变量的单周期的存贮模型(M7)7.17解：均匀分布U[a,b]情况下，分布函数为线性函数：得到，=856(本)，且挂历有剩余的概率为5／9，挂历脱销的概率为4／9。7.18解：k=(20-15)-(20-19)=4元／kg（存储不足时的损失）h=15-5=10元／kg（生产过剩时的损失）正态分布N(m,s2)情况下，分布函数满足：83 查表得；所以，=944(kg)，且产品有剩余的概率为0.286，缺货的概率为0.714。需求为连续随机变量的订货批量，再订货点模型(M8)7.19解：平均年需求R＝850´52＝44200（箱）年存贮费C1＝48´20％＝9.6（元／箱•年）于是，=1517（箱），年平均订货次数R/Q*＝29次P(一周需求量≤r)=F[(r-850)/120]=1－a=0.95查表得(r-850)/120=1.645，再订货点r=1047箱安全存贮量：1047－850＝197箱出现缺货：29´5％＝1.45次；不出现缺货：29´95％＝27.55次7.20解：(1)不允许缺货时，R=4000件/月,k=150元/件,C1=150*10%=15元/件·年,C3=500元/次。(2)允许缺货时，缺货费为100元／(件·年)，C2=100元/件·年7.21解：(1)R=150件/月,C1=0.96元/件·月,C3=400元/次。求经济订购批量(EOQ)。(2)总费用可以超过原最低费用的10％，因此83 ，求出，得到订货量为7.22解：R=300万件/年,C1=0.1元/件·月,C3=100元/次。库存占用资金每年利息、保险等费用为年平均库存金额的20％。可以考虑计入存贮费中，因此按C1=0.12元/件·月计算。先求(EOQ)提高订货量为Q=30000件每月订货8.333次，因此订货费为833.3元/月，存贮费为货款为总费用C3=833.3+1800+240000=242633（元/月）提高订货量为Q=50000件每月订货5次，因此订货费为500元/月，存贮费为货款为总费用C3=500+3000+235000=238500（元/月）=238500。结论：每月订货5次，每次订货50000件，费用最省。7.23解：C2=600元/吨,C1=50元/吨,C3=500元/次,k=400元/吨。先计算累积概率。按模型9考虑。（参考例7.11）需求量r(吨)2030405060概率P(r)O.1O.20.3O.3O.1累积概率F0.10.30.60.91.0转折概率为F(r≤20)=0.1；F(r≤30)=0.3；F(r≤40)=0.6。得出83 将s=20、30吨代入（7.49）判断该式是否成立？s=20时，上式不成立；s=30时，上式成立；因此，最优(s,S)的存贮策略为（30，40）7.24解：按模型8考虑。已知C2=6元/件,C1=1元/件,C3=50元/次,k=3元/件。s=5,s=6,s=7依次代入下式，判断公式(7.44)是否成立，并选择最小的s：即s=5时,满足公式（7.44），据此，最优存贮策略为（5，8）。第八章排队论1.解：83 ∴（1）修理店空闲时间的概率：（2）店内有三个顾客的概率：（3）店内至少有一个顾客的概率：（4）系统中顾客的平均数：（5）顾客在系统内的平均消耗时间：（6）等待服务的顾客平均数：（7）顾客等待的平均时间：（8）顾客在店内消耗15分钟以上的概率：2.解：∴（1）排队等待顾客的平均人数：83 （2）等待的顾客多于2人的概率：（3）要使等待顾客的平均数为2人，接待速度应为多少。∴∴3.解：模型为（1）加油站空闲的概率和损失的概率：空闲的概率：损失的概率相当于系统满员的概率：（2）加油站内汽车的平均数：（3）汽车在加油站内的平均时间：4、解：根据题意，83 人人分分忙时的概率==78%闲时概率=22%5、解：，，人分；分人闲时的概率===78%6、解：为单服务员、定时服务系统：人分分人闲时概率==34%7，解：该系统模型为[1]，（1）保管员空闲的概率为83 (2)5个工人都在工具间的概率：（3）系统内的平均人数：（4）平均排队人数：（5）工人的平均排队时间：[2]，用表格法N=5，，，查A-2表，得，8，解：系统为类型。（1）理发馆空闲的概率：（2）顾客理发平均要花的时间：83 ∵∴（3）若理发馆内只能允许3人等待，损失的概率是：9，解：该系统模型为（1）状态转移图①③④⑤⑥②0（2）10，某产品的最后一道工序是抛光，已知产品到达的速率为10件/时，抛光工序的加工时间相同，平均服务时间为12件/时，解：，（1）空闲时间比由83 （2）计算因该模型中∴∴（3）由这时11，解：该系统属于类型：（1）系统中无人之概率：（2）在系统中逗留的顾客平均数，排队等待的顾客平均数：∵83 ∴（3）在系统中顾客等待的平均时间12，解：该系统模型为建立状态转移图①③④⑤②0求：（1）两个修理工空闲的概率：（2）一个修理工空闲的概率：83 （3）未被服务的空闲机器的期望台数：13，解：服务时间服从正态分布，则店内顾客数的平均值：14、同8题，用表格法计算各参数，并与第8题的答案比较。解：C=m=2,查附录A-1表，m=2,,得到r-1.2,Lq=0.6748:r=1.4,Lq=1.3449.用插值法得到r=1.25,Lq=0.6748+0.1675=0.8423，83'