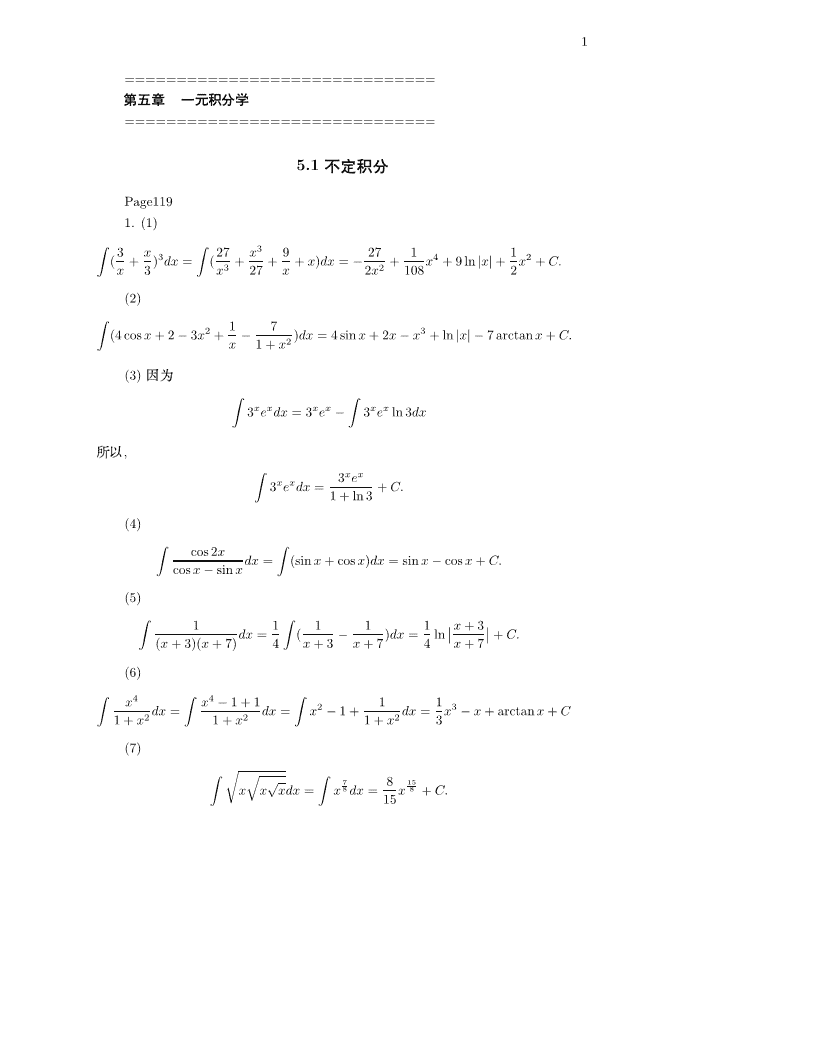《一元分析学》第五章(积分学)习题解答.pdf 49页

'1==============================UZXYW==============================5.1RPage1191.(1)ZZ3x27x392711(+)3dx=(+++x)dx=−+x4+9ln|x|+x2+C.x3x327x2x21082(2)Z2173(4cosx+2−3x+−)dx=4sinx+2x−x+ln|x|−7arctanx+C.x1+x2(3)sZZ3xexdx=3xex−3xexln3dx_,Z3xexxx3edx=+C.1+ln3(4)ZZcos2xdx=(sinx+cosx)dx=sinx−cosx+C.cosx−sinx(5)ZZ11111x+3dx=(−)dx=ln+C.(x+3)(x+7)4x+3x+74x+7(6)ZZZx4x4−1+111dx=dx=x2−1+dx=x3−x+arctanx+C1+x21+x21+x23(7)ZrqZ√7815xxxdx=x8dx=x8+C.15 2(8)ZrrZ1+x1−x2(+)dx=√dx=2arcsinx+C.1−x1+x1−x2(9)j(4)(10)ZZe−x12xexex(2x−√)dx=(ex2x−√)dx=−arcsinx+C.1−x21−x21+ln2(11)ZZtan2xdx=(sec2x−1)dx=tanx−x+C.(12)ZZ111cosxcos2xdx=(cosx+cos3x)dx=sinx+sin3x+C.226′(x)=(sinx−cosx)2=1−sinx,2sF22_F(x)=x+cosx+C,πππsF(2)=2+C=0,_C=−2,"πF(x)=x+cosx−.2′(x)=2x−2,23f5,f_f(x)=x−2x+C,s"Aia;(1,0),_f(1)=0,5C=1,"f(x)=x2−2x+1.′3kx4+C,4f5,f(x)=kx(76ksZ),_f(x)=4s"Aia;(1,6),(2,−9),_kf(1)=+C=6,4f(2)=4k+C=−95,k=−4,C=7,"4f(x)=−x+7.P1241(1)ZZ2lnxlnxdx=lnxd(lnx)=+C.x2 3(2)ZZ(1+x)2011(1+x)2010dx=(1+x)2010d(1+x)=+C.2011(3)ZZZ111x11√(√+√)dx=qd(√)+√qd(3x)3−x21−3x2√233√21−(x/3)1−(3x)x1√=arcsin√+√arcsin3x+C.33(4)ZZ1121dx=sec5xd(5x)=tan5x+C.cos25x55(5)ZZ11−cosxdx=dx1+cosx(1+cosx)(1−cosx)Z1−cosx=dx2sinxZZ1dsinx=dx−22sinxsinx1=−cotx++C.sinx(6)ZZ111dx=d(lnx)=−+C.332xlnxxlnx2lnx(7)ZZZtanx1tan2x2dx=tanxdtanx=tanx−tanxdx=+Ccos2xcos2x2(8)ZZsin2x111dx=−d(1+cos2x)=+C.(1+cos2x)22(1+cos2x)22(1+cos2x)(9)ZZarcsinx12√dx=arcsinxdarcsinx=(arcsinx)+C.1−x22(10)ZZZ1ex1dx=dx=d(ex)=arctanex+C.ex+e−x1+e2x1+(ex)2 4xππ2tdt,(11)#x=atant,&dx=asec;t=arctana∈(−2,2)-,cost>0,√22℄a+x=asect,_"RZZ√asec2t1x+a2+x2=dt=dt=ln|sect+tant|+C=ln+C.asectcosta(12)ZZx11212√dx=pdx=arcsinx+C.1−x421−(x2)22(13)Z√Zsinx√√√√dx=2sinxdx=−2cosx+C.x(14)ZZsinx+cosx132√dx=√d(sinx−cosx)=(sinx−cosx)3+C.332sinx−cosxsinx−cosx(15)Z√x√dx=1−3x(16)ZZ11pdx=pdlnx=arcsinlnx+C.22x1−lnx1−lnx(17)Z√Z1+lnx√23=1+lnxd(1+lnx)=(1+lnx)2+C.x3(18)ZZsinxcosx11212dx=d(sinx)=arctan(sinx)+C.1+sin4x21+(sin2x)22(19)ZZ111√dx=d(arctanx)=−+C.(arcsinx)21−x2(arcsinx)2arcsinx√1+x=t,2(20)#&x=t−1,dx=2tdt,Z√Z1+x−12t(t−1)√dx=dt1+x+1t+1Z2=2(t−2+)dtt+1=t2−4t+4ln|t+1|+C√√=1+x−41+x+4ln(1+x+1)+C. 5(21)ZZxppp√tan1+x2dx=tan1+x2d(1+x2)1+x2Z1pp=−√d(cos1+x2)=−ln|cos1+x2|+C.cos1+x2(22)α<β,pZ6*%!sα0,B!-6q,<,&%[0,1]q21εpR(x)=>6;x=q1X,a*sr1,r2,...,rk.
B[0,1]Eq2εVT={∆1,∆2···∆n},|kTk<.}T6zs76△i′s2k′′′b{ri}6;6z(7XZ62k),△isb{ri}6;6z&%△i1′′6f(x)6)ωi"Bωi2,)DX1X1εωi′△xi′6△xi′6·2k||T||<.222i′i′ε′′′′6%△if(x)6)ωi2,)DXεXεωi′′△xi′′6△xi′′<.22i′′i′′_XXXωi△xi=ωi′△xi′+ωi′′△xi′′<ε.ii′i′′R1℄f(x)%[0,1](p;f(x)dx=0.03.(1)f(x)6=-06f(x)<1,;f(x)6;sx=0fx=1(n=1,2···).n",B∀ε>0,%z[ε,1]f(x)1X;,)XnDf(x)%[ε,1]p."*%lT,ωi∆xi<ε.
%lT6"xi=1;O,[0,1]6Xl,;%z[0,ε]ω0∆x0<ε,)DXnXnωi∆xi=ωi∆xi+ω0∆x0<ε+ε=2ε.i=0i=i 19",m%5.5.1-f(x)%[0,1]p.(2)f(x)6=-−16f(x)61,;f(x)6;sx=0fx=1(n=1,2···).n",B∀ε>0,%z[ε,1],f(x)1X;,)XnDf(x)%[ε,1]p."*%lT,ωi∆xi<ε.
%lT6"xi=1;O,[0,1]6Xl,;%z[0,ε]ω0∆x0<ε,)DXnXnωi∆xi=ωi∆xi+ω0∆x0<ε+ε=2ε.i=0i=i"f(x)%[0,1]p.4.TT[0,1]6Fl,Z"+-,%Fz[xi−1,xi],Xnωi=2.)Dωi∆xi=2,℄f(x)p.|f(x)|≡1Cp.i=15.H,G.yB[0,1]6F?z[α,β],?*%η∈[α,β],5f(η)60.B[0,1]6FV:0=x00.Xn6.sf(x)%[a,b]p,_B∀ε>0,*%7l,ωi∆xi<ε,i=1176ωi=Mi−miTf(x)%9iXz6).T,f(x)%Sz6)s11M−m1iiηi=−=6ωi,miMimiMiΛ2"XnXn1εηi∆xi6Λ2ωi∆xi<Λ2,i=1i=1 201sf(x)%[a,b]p.Page144Zβf2(x)dx=0.1.,.:Bϕ(x)=f(x),&y*%x0∈[α,β],αf(x0)6=0,&Z6e-,*%bx06z[a,b]⊂[α,β],B2(x)>f2(x)/2>0.F6x∈[a,b],f0T,ZβZb222f(x0)0=f(x)dx>f(x)dx>(b−a)>0,αa2)C.℄%[α,β],f(x)≡0.2.p6/[R,Zn2+nZn2+n1−1−1dxlim√exdx=limeξ√n→∞n2xn→∞n2x−12n=limeξ√=1,n→∞n2+n+n2276n<ξ1−sinx>,T222Zππ2dxπαf(x)dx,001,ZZα1(1−α)f(x)dx>αf(x)dx.0αsf(x)T:{Z,_ZαZαZ1Z1f(x)dx>f(α)dx=αf(α),f(x)dx6f(α)dx=(1−α)f(α).00αα)DZZα1(1−α)f(x)dx>(1−α)αf(α)>αf(x)dx.0α5.f(x)%[α,β],&p6/[R-,*%η∈(α,(α+β)/2),5Zα+β2β−αf(x)dx=f(η)·.α2Tf(η)=f(β).%z[η,β]Rolle6/=s5%.;:<0#},.66+x.f(x)%(α,β)13,&Lagrange6/=,B∀x∈(α,β)*%ξ∈(x,β),f(x)−f(β)′=f(ξ),x−βs′f(x)=f(β)+f(ξ)(x−β). 22)DZα+βZα+βZα+β222′f(x)dx=f(β)dx+f(ξ)(x−β)dxαααα+β(x−β)2α+β=f(β)(−α)+f′(ξ)|2α22β−α3′2=f(β)−f(ξ)(α−β).28Zα+β2β−αf(x)dx=f(β),α2/HR53′2f(ξ)(α−β)=0.8_′f(ξ)=0,ξ∈(α,β).Zx6.#F(x)=f(θ)sin(θ)dθ,x∈[0,π],&F(x)∈C[0,π],%(0,π)130;F(0)=F(π)=0,Rolle=-∃α∈(0,π),5F′(α)=0,⇒f(α)sin(α)=0.α∈(0,π),℄sin(α)6=0,"f(α)=0.o,∃β∈(0,π)(β6=α),5f(β)=0,H,G.yf(x)%(0R,π)11r!;x=α,&f(x)%(0,α)f(α,π)1Hπe&2f(θ)sin(θ)dθ=0.Dsin(θ−α)%(0,α)f(α,π)1e0H℄f(θ)sin(θ−α)(Xz1je.TZπf(θ)sin(θ−α)dθ>0.0"
,fh|ZπZπf(θ)sin(θ−α)dθ=f(θ)(sin(θ)cos(α)−cos(θ)sin(α))dθ00ZπZπ=cos(α)f(θ)sin(θ)−sin(α)f(θ)cos(θ)dθ=0.00)Dm#)C."5f(x)%(0,π)12X!;. 237.(1)2tTFZ,&[tf(x)−g(x)]>0,st2f2(x)−2tf(x)g(x)+g2(x)>0.p5ZβZβZβt2f2(x)dx−2tf(x)g(x)dx+g2(x)dx>0.ααα)D^t6E(R63R+,sZβZβZβ[2f(x)g(x)dx]2−4f2(x)dxg2(x)dx60.ααα*5ZZZβββ[f(x)g(x)dx]26f2(x)dxg2(x)dx.αααZxZxZx222[:#h(x)=f(t)dtg(t)dt−[f(t)g(t)dt].ααα(2),G:U,.6Schwarz7R,54ZβZβZβ[f(x)+g(x)]2dx=f(x)[f(x)+g(x)]dx+g(x)[f(x)+g(x)]dxαααZβ
Zβ
21/221/26f(x)dx·[f(x)+g(x)]dxααZβ
Zβ
21/221/2+g(x)dx·[f(x)+g(x)]dx.ααZβ2
1/2Aj$[f(x)+g(x)]dxs5Minkowski7R.α,GE:snZβZβo22121[f(x)dx]2+[g(x)dx]2ααZβZβZβZβ22221=f(x)dx+g(x)dx+2[f(x)dxg(x)dx]2,ααααD(1)-ZβZβZβ222f(x)dxg(x)dx>[f(x)g(x)dx],ααα 24)DnZβZβo22121[f(x)dx]2+[g(x)dx]2ααZβZβZβ>f2(x)dx+g2(x)dx+2f(x)g(x)dxαααZβ=(f2(x)+2f(x)g(x)+g2(x))dxαZβ2=[f(x)+g(x)]dx.α
5nZβo1ZβZβ222121[f(x)+g(x)]dx6[f(x)dx]2+[g(x)dx]2.ααα11[:f,g∈R[a,b],p+q=1,7610),..7,Bpqf(x)g(x)α=R1,β=R1,bppbqq|f(x)|dx|g(x)|dxaa/HYoung7Rj$%[a,b]p*s5.Minkowskipp−17RH¨older7R,.,|f+g|=|f+g|·|f+g|s.Cj,Y#Young7R6,..X-,Zf(x)=lnxsz(0,+∞)6Z,)Dαpβq11ln+>lnαp+lnβq=ln(αβ).pqpq 258.Z11XniXnZniXnZniif(x)dx−f()=f(x)dx−f()dx0nni−1i−1ni=1i=1ni=1nXnZniiXnZniiXnZnii=[f(x)−f()]dx6f(x)−f()dx6Lx−dxi−1ni−1ni−1ni=1ni=1ni=1nXnZinLL6dx6.i−1nni=1n1,···,n.9.}[0,1]zn7;s0,nnf%[0,1]0<{,_B∀x∈[i−1,i](i=1,2,···,n),f(i−1)>f(x)>f(i),nnnnGfZ11XniXnZniXnZniif(x)dx−f()=f(x)dx−f()dx0nni−1i−1ni=1i=1ni=1nXnZniiXnZnihi−1ii=[f(x)−f()]dx6f()−f()dxi−1ni−1nni=1ni=1nXn1i−1if(0)−f(1)=[f()−f()]=.nnnni=110.2(x)−3f(x)+26016f(x)62⇒[f(xZ)−1][f(x−2)]60Z⇒f1121⇒f(x)−3+60⇒f(x)dx−3+2dx60f(x)00f(x)Z1Z1hZ1Z1i1112⇒3>f(x)dx+2dx>22f(x)dxdxZ0Z0f(x)00f(x)1119⇒f(x)dxdx]6.00f(x)8[:SfTG}KantorovichS6:+Zf∈C[a,b],M=maxf(x),m=minf(x),&a6x6ba6x6bZbZb2dx(M+m)2f(x)dx·6(b−a).aaf(x)4Mm11.g(x)%[α,β],_∃M,m(M>m>0),B∀x∈[α,β],m6ϕ(x)6M.f(x0)=maxf(x),x0∈(α,β)(&,j,6!Bα6x6β0),&B∀ε>0,∃δ>0,52x∈[x0−δ,x0+δ]⊂[α,β],εf(x0)−xdx=,βn6xdx=,(n=2,3,···)(2)0202}
2/E
1Z1Z1Z1Z1215213αn6dx+xdx=,βn>xdx+dx=,(n=2,3,···)(3)02180128221531⇒6αn6,6βn6,(n=2,3,···)(4)2882(4)r
15ZβnZ122αn+1=2(βndx+xdx)=1+βn,(5)Z0αZβn(n=2,3,···)n12β=2(xdx+αdx=2α−α2,(6)n+1nnn0αnβn+1−βn⇒αn+2−αn+1=(βn+1−βn),22−αn−αn−1βn+1−βn=(αn−αn−1),(n=2,3,···)2βn+1+βn2−αn−αn−1⇒αn+2−αn+1=·(αn−αn−1),22 27
4⇒|αn+2−αn+1|6|αn−αn−1|,n=2,3,···HR511|α2m+2−α2m+1|64m|α2−α1|,|α2m+3−α2m+2|64m|α3−α2|,m=1,2,···#m→∞,5α2m+2−α2m+1→0,α2m+3−α2m+2→0,,)D5nlim→∞αn*%j-limβn*%.limαn=αlimβn=β,
5
65n→∞n→∞n→∞2α=1+β2,2β=2α−α2(7)√√5:α=2−2,β=2−1.ZβZβ13.ϕ(x)fn+1(x)dx6Mϕ(x)fn(x)dx=MΛ,,Λn+1=nαα76M=maxα6x6βf(x).Λn+1Λn+1⇒6M,sZ{}.$Cauchy-Schwartz7RΛnΛnZβZβ2n+121n+21n2Λn+1=(ϕ(x)f(x)dx)=([ϕ(x)]2[f(x)]2[ϕ(x)]2[f(x)]2dx)ααZβZβ6[ϕ(x)][f(x)]n+2dx[ϕ(x)][f(x)]ndx=Λ·Λ,n+2nααΛn+1Λn+2Λn+1TΛ6Λ,sZ{Λ}T0<"x6℄7q*%.$911fnn+1n-pZβΛn+1nn1lim=limΛn=lim([ϕ(x)][f(x)]dx)n=maxf(x).n→∞Λnn→∞n→∞αα6x6βPage151Z2Z23xn132n+11.(1)limdx=limxndx=lim=0,n→∞01+xn→∞1+ξ0n→∞3n+1(1+ξ)(1+n)76ξ∈[0,2/3],_1/(ξ+1).(2)p96/=,*%ξ∈[n,n+1],5Zn+1Zn+1sinx1n+1limdx=limsinξ·dx=limsinξ·ln=0n→∞nxn→∞nxn→∞n2ex1(3)&Æ,G&5,"R=lim=lim=0.x→∞e2x2x→∞ex2 28(4)2#r=t,&Zx+1Z(x+1)22Z(x+1)221sinrcosr(x+1)1cosrsintdt=√dr=−√−√dr.x2x2r2rx24x2rrs2x>0,22cosxcos(x+1)11−6+→0(x→+∞),xx+1xx+1Z(x+1)2Z(x+1)21cosr1111√dr6√dr=−→0(x→+∞),2x2rr2x2rrxx+1Z(x+1)sint2dt=0._x→lim+∞xZx(5)#S(x)=|cost|dt.|cost|Tπs86686Z,℄%F8066z=p/j.nπ6x<(n+1)π(ns+*Z),&ZnπZ(n+1)π|cost|dt6S(x)<|cost|dt.00ZZππZπ2|cost|dt=cosxdx−cosxdx=2,00π2℄2n6S(x)<2(n+1)."2nS(x)2(n+1)<<.(n+1)πxnπs2x→+∞,n→∞;2n2(n+1)2lim=lim=,n→∞(n+1)πn→∞nππS(x)2℄nlim→∞x=π.XnZ11i112.(1)"R=lim(−)=xdx=.n→∞nnn02i=11XniZ1112(2)"R=limsinπ=sinπxdx=−cosπx=.n→∞nn0π0πi=11XniZ1x31133(3)"R=lim()=xdx==.n→∞nn03+104i=1 291Z1xπZ1x3.(3)"R=xarcsinx−√dx=−√dx.001−x2201−x22#t=1−x,&dt=−2xdx.2x=0,t=1;2x=1,t=0.TZ1π1Z01π√0πarcsinxdx=+√dt=+t=−1.0221t212(4)t#lnx=t,&dx=edt.2x=1,t=0;2x=e,t=1.TZeZ11Z1tttsin(lnx)dx=esintdt=esint−ecostdt,100076Z11Z1tttecostdt=esint−esintdt0001Z1tt=esin1+ecost−ecostdt00Z1=esin1+ecos1−1−etcostdt,0TZ1t11ecostdt=(esin1+ecos1)−.022℄Ze1111sin(lnx)dx=esin1−e(sin1+cos1)+=e(sin1−cos1)+.122222tdt.(5)(fuf,}B."pF)#x=tant,&dx=sec2x=0π.,t=0;2x=1,t=4TZπZππ4sect44"R=tantdt=csctdt=ln|csct−cott|=+∞.000Z11Z11+x2111(6)"R=dx=d(x−).#t=x−,&2x2+1(x−1)2+2xx0x20xx→0+,t→−∞;2x=1,t=0.TZ0√11t02√arctan√"R=t2+2dt==4π.−∞22−∞(7)v"psIn,&1e1Ze11nZe2n2n−12n−1In=xlnx−x·nlnx·dx=e−xlnxdx,2121x221 30s1nI=e2−I.nn−122;4Ze1212I1=xlnxdx=e−(e−1),1245412nIn=e−In−12212n2n(n−1)=e−e+In−2244=···1nn(n−1)n!n!(e2−1)=e2[1−++···+(−1)n−1]+(−1)n22222n−12n+112nn(n−1)n−1n!n+1n!=e[1−++···+(−1)]+(−1).22222n2n+1Z24x2·6x9x2xxx(8)"R=(4+2·6+9)dx=++02ln2ln62ln30157040=++.2ln2ln6ln3√(9)#t=x,&dx=2tdt.2x=0,t=0;2x=1,t=1.TZ11ttt"R=2tedt=2(te−e)=2(e−e+1)=2.00Z1x3ax211α(11)2α60,"R=x(x−α)dx=(−)=−;03203220<α1,"R=x(α−x)dx=(−3+2)=2−3.00Rln2Rln3Rln4Rln5Rln6Rln7R2(12)"R=1dx+2dx+3dx+4dx+5dx+6dx+7dx0ln2ln3ln4ln5ln6ln7=ln2+2(ln3−ln2)+3(ln4−ln3)+4(ln5−ln4)+5(ln6−ln5)+6(ln7−ln6)+7(2−ln7)=ln[2·(3)2·(4)3·(5)4·(6)5·(7)6·(1)7]+14234567=14−ln(7!).RaR0RaR0Ra4.(1)f(x)dx=f(x)dx+f(x)dx=−f(−x)dx+f(x)dx=R−aR−a0a0aa[f(−x)+f(x)]dx=2f(x)dx.00 31RaR0RaR0RaRa(2)f(x)dx=f(x)dx+f(x)dx=f(−x)d(−x)+f(x)dx=f(−x)dx+R−aR−a0a00aaf(x)dx=[f(−x)+f(x)]dx=0.0R0RRRRRa+TTa+TaTa(3)f(x)dx−f(x)dx=f(x)dx+f(x)dx−f(x)dx−f(x)dxRaR0RaRT0Ta+Taa+Ta=f(x)dx−f(x)dx=f(x)dx−f(x+T)d(x+T)RTR0T0a+Ta+T=f(x)dx−f(x)dx=0.TT(4)πR#t=2−x,&πRπRπRπ2f(cosx)dx=2f[cos(π−t)]dt=2f(sint)dt=2f(sinx)dx00200(5)#t=π−x,&RπR0Rπxf(sinx)dx=−(π−t)f[sin(π−t)]dt=(π−t)f(sint)dt0RRπR0Rππππ=πf(sint)dt−tf(sint)dt=πf(sinx)dx−xf(sinx)dx,0R0R00πππT0xfZ(sinx)dx=20f(sinxZ)dx.ππsinxππ1ππ"R=21+cos2xdx=−21+cos2xd(cosx)=−2arctan(cosx)000πππππ2=−[arctan(−1)−arctan1]=−(−−)=.22444√√√5.BDA67R;42k−1x,℄k>Rk√xdx,)D5k−1√√Zn√√21+2+···+n>xdx=n3/2.03√BA7RAy=x%(0,+∞)TÆWk6_√√Zk−1+kk√0,∀x∈[0,1],|f(x)|6M.Z1Z1n+2′′n+2M⇒|xf(x)dx|6Mx=→0(n→∞).00(n+3)(1)5Z1f(1)f(1)+f′(1)limn2xnf(x)dx−[−]=0n→∞0nn2Z1′nf(1)f(1)+f(1)1⇒xf(x)dx=−+o(n→∞).0nn2n2ZxZxZa7.#F(x)=2tf(t)dt−xf(t)dt+af(x)dx,x∈[a,b],&F(a)=0,a00f(x)0<{_ZxZxF′(x)=xf(x)−f(t)dt=[f(x)−f(t)]dt60,00℄F(x)%[a,b]0<{⇒F(b)6F(a)=0,ZbZbZa⇒2xf(x)dx6bf(x)dx+af(x)dx.a00Ra1|f(x)|dx.8.=p96/=-*%ξ∈(0,a),"B|f(ξ)|=a0Tf(x)%[0,2π]3,5ZaZξ1′|f(0)|−|f(x)|dx=|f(0)|−|f(ξ)|6|f(0)−f(ξ)|=f(x)dxa00ZξZa′′6|f(x)|dx6|f(x)|dx.00 33"ZaZa1′|f(0)|6|f(x)|dx+|f(x)|dx.a009.f(x)%[0,1],&f(η)=max|f(x)|,η∈[0,1].p6/=06x61R1-,*%ξ∈[0,1],5|f(x)dx|=|f(ξ)|.0
ξ=η,&7RC.}ξ6=η,&ZξZ1′′|f(η)−f(ξ)|=f(x)dx6|f(x)|dx,η0sZ1|f(ξ)|>|f(η)|−|f′(x)|dx.0"ZZ11′f(x)dx>|f(η)|−|f(x)|dx.00sZZ11′max|f(x)|6f(x)dx+|f(x)|dx.06x6100sB∀x∈[0,1],|f(x)|60max6x61|f(x)|,_Z1Z1Z1′′|f(x)|6f(x)dx+|f(x)|dx6[|f(x)|+|f(x)|]dx.000[:8,9fwb%G}f6:,.:Zf(x)%[a,b]p,&ZbZb1′max|f(x)|6f(x)dx+|f(x)|dx.a6x6bb−aaa,:f(x)%[a,b]-,*%ξ,η∈[0,1],|f(ξ)|=max06x61|f(x)|,|f(η)|=min|f(x)|.T06x61ZξZb′′|f(ξ)|−|f(η)|6|f(ξ)−f(η)|=f(x)dx6|f(x)|dx.ηaZb1p96/=,*%c∈(a,b),f(c)=f(x)dx,)Db−aaZb1|f(η)|6|f(c)|=f(x)dx.b−aa 34"ZbZb1′|f(ξ)|=(|f(ξ)|−|f(η)|)+|f(η)|6f(x)dx+|f(x)|dx.b−aaa10.f∃x1∈[0,1/2],5f(1)−2x1f(x1)(1−1/2),sf(1)=x1f(x1).$BF(x)=xf(x)%z[x1,1]Rolle=s.Ru11.′G(u)=0f(t)dt,&f(x)6-G(u)3;G(u)=f(u).hZ>3G&Zv(x)′f(t)dt=G[v(x)]′=G′[v(x)]v′(x)=f[v(x)]v′(x).0TZv(x)′Zv(x)Zv(x)′′′′F(x)=f(t)dt=f(t)dt−f(t)dt=f[v(x)]v(x)−f[u(x)]u(x).u(x)0012.,.
Zf(x)%(−∞,+∞)6Fz[α,β]p;B∀x,y∈[α,β],f(x+y)=f(x)+f(y),&f(x)=cx,c=f(1).,∀x∈R,x6=0,f(t+y)=f(t)+f(y),Bt)04xp5ZxZxZxZxf(t+y)dt=f(t)dt+f(y)dt=f(t)dt+xf(y),0000oZxZxxf(y)=f(t+y)dt−f(t)dt.00#t+y=u,ZxZx+yZx+yZyf(t+y)dt=f(u)du=f(u)du−f(u)du,0y00Zx+yZyZx⇒xf(y)=f(u)du−f(u)du−f(u)du,000mxy6t4Ap6/Zfsf(x)f(y)xf(y)=yf(x)o=.xyf(x)Tx=c,sf(x)=cx.2x=y=0f(0)=2f(0),⇒f(0)=0,R.#x=1,⇒c=f(1). 3513.Fmt=nx,=p96/=-*%εk∈(2(k−1)π,2kπ),Z2π1Z2nπx1XnZ2kπxf(x)|sinnx|dx=f()|sinx|dx=f()|sinx|dx0n0nn2(k−1)πnk=11XnξZ2kπ4Xnξkk=f()|sinx|dx=f()nn2(k−1)πnnk=1k=1Xn2ξk2π=f(),πnnk=1Xnξk2πDf()Tf(x)}[0,2π]zn76pf,f(x)%[0,2π],nnk=1℄ZXnξ2π2πklimf()=f(x)dx,n→∞nn0k=1)DZZ2π2π2limf(x)|sinnx|dx=f(x)dx.n→∞0π014.,0dt=.kπx0kπ+t0(k+1)π(k+1)πZn+1Zn+1dxdx1x=πxkπx(k+1)ππk+1k=1k=1k=12nX−1Zk+212Zn+112n+1>dx=dx=ln.πk+1xπ2xπ2k=116.1eS2n6=mn;(x,y)%9-n6Aq!Gl._>,psZ2Z2′238A=|y(t)x(t)|dt=|(2t−t)(2−2t)|dt=.0015 38(6)Z2π1′′A=(xyt−yxt)dt20Z2π1=[(2acost−acos2t)·(2acost−2acos2t)20−(2asint−asin2t)·(−2asint+2asin2t)]dtZ2π2=3a(1−costcos2t−sintsin2t)dt0Z2π22=3a(1−cost)dt=6πa.0ααπα2(7)2Ass26#,psA=π(2)=4.(8)SAsq";6n#_s,psZπ2Zπ1pdθ2dθA=2·=p.20(1+εcosθ)20(1+εcosθ)2θ=t,21+ε#tan2va=1−ε,&ZZdθ2(t2+1)dt=(1+εcosθ)2(1−ε)2(t2+a2)2ZZ2dt2(1−a2)dt=+(1−ε)2t2+a2(1−ε)2(t2+a2)22no2t2(1−a)t1t=arctan++arctan+C.a(1−ε)2a(1−ε)22a2(t2+a2)2a3a2θ∈[0,π]t∈[0,+∞),u^52n2t2(1−a2)ht1tio+∞A=parctan++arctana(1−ε)2a(1−ε)22a2(t2+a2)2a3a0πp2=.3(1−ε2)22=4ax2.B~;sqG";4w69sq9.&4wy6qG
s2ar=(0<θ<2π).1−cosθa~;6>sθ=t,B=04w_q6,psZZt+πr21t+π2a
2A(t)=dθ=dθ.t22t1−cosθ 3912a
22a
28a2cosθA′(t)=−=−.21−cos(π+t)1−costsin4θπ′#A(t)=0,5r<;t=2s2q9&._q,pCC,psZπ13π/22a
28a2A()=dθ=.22π/21−cosθ33.4wf#%916;s(2,2),(6,p66sA1,-6sA2,BZ2py2ypyy324A=2(8−y2−)dy=2[8−y2+4arcsin(√)−]=2π+.10222260344A2=8π−(2π+)=6π−.332π+4A133π+2==.A26π−49π−234.X#:,q6g^XG,?Ba6gpT9H0gp68Gl.∀x∈[0,a],ax;&.x965,
9H0g6
T+
√227Ta−x,AgpsZap2V=8(a2−x2)2dx=16a.03Zπ22π5.(1)V=πsinxdx=.0r2Zb2y242(2)V=π(a1−)dy=πab.b23−b 40ZπZπ42(3)V=π(cos2x−sin2x)dx+π(sin2x−cos2x)dx=π.0πZ42ππ8πa3(4)V=[a(1+cosθ)]3sinθdθ=.3036.n#h:q6!^x9B,"1b%t90!Dy9=6gp$2s,Gl.t91n#6:;GT(a,b)ytg-:
Taxby+=1.α2β2√2aa2b2α3β-:ia;(2α,0),α=1α2+β2=1,5:;Gs(2,2).:
T√3x=2α(1−y).2βTS!Dy9=_5=g6gpZb√Zb2232yV=2π4α1−ydy−α1−dy02β0β2Z√b24342=2απ3−y+ydy02ββ2√√234b3=2α2π3y−y2+y3(b=β)β3β202√=3πα2β.7.ZZr1p1161393(1)l=21+y′2dx=21+xdx=[()2−1].004274 41exex(2)y=ln(ex+1)−ln(ex−1),y′=−=−(shx)−1,ex+1ex−1Z2pZ2p2l=1+y′2dx=1+(shx)−2dx=ln(shx)=ln(e2+1)−1.111(3)x=a(cost+tsint),y=a(sint−tcost),x′=atcost,y′=asint,A6kZ2πpZ2πpZ2πl=x′2(t)+y′2(t)dt=a2t2cos2t+a2t2sintdt=atdt=2π2a.000(4)A^xB7l%9.%t=±16B;(3,2)f(3,−2)%5x96:%";%6:5y9,Gl_S.x′(t)=6t,y′(t)=3−3t2,BZ3pZ3pZ3l=2x′2(t)+y′2(t)dt=2(6t)2+(3−3t2)2dt=6(t2+1)dt=72.000′2θθ(5)r=asincos.A6k33Z3πZ3πrZ3πp6θ4θθ3θ3πal=r2+r′2dθ=a2sin+a2sincos2dθ=asindθ=.0033303211(6)Aθ=θ(ρ)=(ρ+)(ρ∈[1,3])6l7HZ6lj72ρ5HZsρ=ρ(θ)(θ∈[1,]),&qG{6A6k[R-3Z5/3pl=ρ2(θ)+ρ′2(θ)dθ.1 4211%Yp6Fmθ=2(ρ+ρ),ρsp&12ρ211ρ′(θ)==,dθ=(1−)dρ.θ′(ρ)ρ2−12ρ2℄sZ5/3pZ32ρ2211l=ρ2(θ)+ρ′2(θ)dθ=ρ2+·(1−)dρ11ρ2−12ρ2Z3111=(ρ+)dρ=(4+ln3).21ρ28.(1)ZπZπ4p4pS=2πy1+y′2dx=2πtanx1+(sec2x)2dx00Zπ4p1=π1+cos4xd()cos2x0√1+cos4xpπ244=π[−ln(cosx+1+cosx)]cos2x0√√√√(2+1)(5−1)=π[5−2+ln].2x33x2′(2)y=,y=a2a2ZZrapax33x2S=2πy1+y′2dx=2π1+()2dxa2a200Z√2πap1010−1=x39x4+a4dx=πa2.a4270(3)Zπ/2pZπ/2S=2·2πy(θ)x′2(θ)+y′2(θ)dθ=36πa2sin3θcos2θdθ00Zπ/2223522!!4!!12πa=36πa(sinθ−sinθ)dθ=36πa(−)=.03!!5!!5(4)ρ=α(1+cosθ),kppθds=ρ2+ρ′2dθ=2αcosdθ,2 433θθy=ρsinθ=α(1+cosθ)sinθ=4αcossin.22ZπZπ24θθ322S=2πyds=2π8αcossindθ=πα.00225VT5.4Page1701.u^}v=p:Z+∞1(1)dx;x2Z1+∞x(2)dx;1+x4Z0+∞−αx(3)esinβxdx;Z0+∞(4)e−xxndx.0ZZ+∞A11:(1)x2dx=A→lim+∞x2dx=1.Z11ZZ+∞AAxx12(2)dx=limdx=limdx=01+x4A→+∞01+x4A→+∞02(1+x4)ZA22111Aπlimdt=limarctant=.A→+∞201+t2A→+∞204Z+∞e−αx+∞β−αx(3)esinβxdx=(−αsinβx−βcosβx)=.0α2+β20α2+β2Z+∞+∞Z+∞+∞−xnn−xn−1−xn−1−x(4)exdx=−xe+nxedx=0−nxe+Z00Z0Z0+∞+∞+∞n−2−xn−2−x−xn(n−1)xedx=n(n−1)xedx=...=n!edx=n!.0002.3}v=p6Z+∞1(1)√dx;34Z01+x+∞xarctanx(2)dx;1+x3Z1+∞1(3)sindx;x2Z1+∞x(4)dx.−∞ex+e−xZ+∞41413√√(1)x→lim+∞x31+x4=1,p=3,λ=1℄31+x4dxV.0 44ππZ+∞Z+∞xarctanxxπ1π16262,(2)%[1,+∞)1+x31+x3x22x2dx=2x2dx=Z11+∞πarctanx.ÆG&-dxV.211+x31Z+∞Z+∞sinx211(3)lim=1,;V_sindxV.x→+∞1x2x2x211Z+∞Z1Z+∞xxx2x(4)dx=dx+dx,limx=−∞ex+e−x−∞ex+e−x1ex+e−xx→−∞ex+e−xZ−1Z−1Z11xx0,;V,_dxV=pdx=0;−∞x2−∞ex+e−x−1ex+e−xZ+∞Z+∞x21xslimx=0,;dxV_dxV℄x→+∞ex+e−x1x21ex+e−xZ+∞xdxV.−∞ex+e−xZ+∞Z+∞sinxcosx3.,.v=pdxdx%p∈(0,1)Th|V6.xpxpZ1Z1+∞+∞sinxcosx,~,xpdxfxpdxV.BFA>1,|F(A)|=Z11A1sinxdx62,;xp2x→+∞,0=−,>=+;xpxp2xp2xpxpxp2xp2xpZ+∞Z+∞1cos2xp∈(0,1),2xpdxF9,6,.-,2xpdxV&ÆZ1Z1Z+∞sinx+∞cosx+∞sinxdxdx3G-,xpfxpF._YxpdxZ111+∞cosxxpdx%p∈(0,1)Th|V6.1Z+∞Z+∞f(x)=024.,.
v=pf(x)dxBV;x→lim+∞&f(x)dxaaV.,x→lim+∞|f(x)|=0-,*%A>a,BFx∈[A,+∞),06|f(x)|61,"Z+∞Z+∞2(x)6|f(x)|.206ff(x)dxBV54f(x)dxV.ZZaZA+∞A+∞R222A2f(x)dx=f(x)dx+f(x)dx,Daf(x)dxs=p,℄aaA 45Z+∞f2(x)dxV.aZ+∞5.,.
Zf(x)%[0,+∞)3;v=pf(x)dxV&0limf(x)=0x→+∞.,H,G.
%_Yh|}x→lim+∞f(x)6=0,&*%ε0>0,BFY=6X>0,*%x0>X,5|f(x0)|>ε0.sf(x)%[0,+∞)3_*%δ0∈(0,ε1),5BF6x1,x2∈(0,+∞),2|x1−x2|<δ0|f(x1)−f(x2)|<.BFY=6A0>0,BX=A0+1,x0>X"B2|f(x0)|>ε0.f(x0)>0,&B"B|x−x0|6δ06Fx,ε0ε0f(x)>f(x0)−>>0.22ε0ε0BA1=x0−2,A2=x0+2,&A2>A1>A0,;ZA2ε0f(x)dx>δ0>0.A12Z∞CauchyV>&,f(x)dxV,-)C.℄x→lim+∞f(x)=0.0Z+∞6.,.
Zf(x)%[a,+∞)p;v=pf(x)dxZa+∞f′(x)dx?V&x→lim+∞f(x)=0.aZ+∞′,sf(x)dxV_BFε>0*%M>02x1,x2>MZax2|f′(x)dx|<ε,s|f(x1)−f(x2)|<ε_x→lim+∞f(x)*%.
x→lim+∞f(x)=x1A6=0AAZA>Z0&Bε=2MZ*%2x>MfZ(x)>2_+∞+∞+∞+∞Af(x)dx>dx=+∞,Tf(x)dxF,)Df(x)dxFMM2Ma.f)C.℄limf(x)=0.x→+∞;:x→lim+∞f(x)*%-,f(x)%[a,+∞)3,$f5,%.Z+∞7.,
v=pf(x)dxV;xf(x)%[a,+∞)0<{&alimxf(x)lnx=0x→+∞ 46.ZZZ+∞1+∞R1,
a<1&f(x)dx=f(x)dx+f(x)dx&af(x)dxs=Raa1+∞p1$1f(x)dx℄a>1.T,BFx>a,xf(x)>0.&,*%x0>a,5x0f(x0)=cx0,+∞+∞c1xf(x)6c<0,5f(x)6,_f(x)dx6cdx=−∞,xxx0x0f)C._ZpxVÆz>&ZBxFε>0*%ZxA>a>1,BF√11x>x>A|f(t)dt|<ε,Df(t)dt>xf(x)dt=xf(x)lnx,√√√t2xxx_x→lim+∞xf(x)lnx=0.Z+∞8.,.
v=pf(x)dxV;f%[a,+∞)0<&limxf(x)=x→+∞a0.,f(x)0{6,&f(x)R.Z&,*%x0,5Zf(x0)<0,TB+∞+∞Fx>x0,f(x)6f(x0)<0,)Df(x)dx6f(x0)dx(ZZx0x0+∞+∞f(x)dxV)C.sf(x)dxV_BFε>0,*%M>a,aRaA2BFA1,A2>MR|A1f(x)dx|<ε.BA1=x/2,A2=x&2x>2Mx06xf(x)/26f(t)dt<ε,_limxf(x)=0.x/2x→+∞Page1761.u^}pZ11(1)√dx;−11−x2Z12x(2)√dx;01−x2Zβ1(3)pdx;α(x−α)(β−x)Z1Z0Z1Z01111√√√√(1)2dx=2dx+2dx=lim+2dx+−11−x−11−x01−xa→−1a1−xZb10bππlim√dx=limarcsinx|a+limarcsinx|0=0−(−)+−0=π.b→1−01−x2a→−1+b→1−22Z1x2Zax2Zap1(2)√dx=lim√dx=lim−[(1−x2+√)dx]=01−x2a→1−01−x2a→1−01−x2θ1ππππ3−(+sin2θ|2)−=−−=−π.0242424x−αβ−xx−α2(3)BFx∈(α,β),0<<1,0<<1.#=sintβ−αβ−αβ−α 47,222Z&x=α+(β−α)sintZ=cost+βsint,dx=2(β−α)sintcostdt,_βπ12pdx=2dt=π.α(x−α)(β−x)02.3}
p6Z11(1)√dx;0xlnxZπ21(2)√dθ;01−sinθZ11(3)pdx;3x2(1−x)0Z1lnx(4)dx.0x2−1Z1ZAZ1111√√√(1)
;x=0,x=1,xlnxdx=xlnxdx+xlnxdx(A∈Z00AA1111(0,1)).limx2√=0,s√dxV,Dlim(x−1)√=1,x→0+xlnx0xlnxx→1−xlnxZ1Z111√√sxlnxdxF,_xlnxdxF.A0ZπZ1211(2)√√#t=sinθ,1−sinθdθ=(1−t)1+tdt,t=1s7
;0√Z0Z1π12121lim(1−t)√=,s√dtF_√dxt→1−(1−t)1+t20(1−t)1+t01−sinθF.(3)x=0,x=1?T
;,BA∈(0,1),$Z1ZAZ1111pdx=pdx+pdx.3x2(1−x)3x2(1−x)3x2(1−x)00AZA21121limx3p=1,spdxV;lim(1−x)3p=x→0+3x2(1−x)3x2(1−x)x→1−3x2(1−x)0Z1Z1111,spdxF,_pdxF.3x2(1−x)3x2(1−x)A0√lnx(4)x=0s7
;,x=1T7
;.limx·=0,_x→0+x2−1Z1lnxdxV.0x2−13.>}ZZ+∞Z1α−1−xp−1q−1Γ(α)=xedxB(p,q)=x(1−x)dx006=!. 48R∞α−1−x(1)Hp0xedxT.8;0(α<1)6v=p.sa6VaXpsZ+∞Z1Z+∞xα−1e−xdx=xα−1e−xdx+xα−1e−xdx00176A9XT8p(α<1)D9EXTv=p.BA9Xps106xα−1e−x=(00p0xedxVBA9EXpZ7Rx2x3xnxnxe>1+x+++···+>(x>0)2!3!n!n!1B+*Zn>α&xα−1n!06xα−1e−x=6(16x<+∞)exx1+n−αR+∞α−1−xR+∞α−1−xZÆz3Gp1xeRdxV."p0xedxBF1xα−1e−xdxα>0?V.2α60%p06e−xe−1α−1−x>(xe=x1−αx1−α;:1−α>1)R1xα−1e−xdxR+∞α−1−xZÆz3G8p0F"p0xedxF._Y=Z!sα>0.1(2)p−1q−1%px(1−x)dx6XZpfq.s;0f;1?02T8;_aXpb%a6VsZ1Z1/2Z1xp−1(1−x)q−1dx=xp−1(1−x)q−1dx+xp−1(1−x)q−1dx(∗)001/22p>0;q>0%A9Xp6
02T8;s
;01)p−1q−1x1−p06x(1−x)=61−qx1−p2(01)p−1q−106x(1−x)=61−p(1−x)1−q2(01)xp−1(1−x)q−1=>x1−px1−p1(q<1)x1−p_A9XpFj2q60A9EXpF.h`:2p>0;q>0pZ1xp−1(1−x)q−1dx0VD2p60oq60pZ1xp−1(1−x)q−1dx0F.℄,=!sp>0,q>0.4.,.(1)Zf(x)%[0,+∞);limf(x)=k&x→+∞Z+∞f(αx)−f(βx)βdx=[f(0)−k]ln(β>α>0).0xαR+∞f(x)(2)
Yh|limf(x)=kTsdx*%&x→+∞0xZ+∞f(αx)−f(βx)βdx=f(0)ln(β>α>0).0xαZ+∞ZMf(αx)−f(βx)f(αx)−f(βx),.(1)xdx=+limxdx=0m→0,M→+∞mZMZMZMαZMβf(αx)f(βx)f(x)f(x)limdx−dx=limdx−dx=m→0+,M→+∞mxmxm→0+,M→+∞mαxmβxZMαZMβf(x)f(x)βlimdx−lim=limf(mα+θ1(mβ−mα))ln−limf(Mα+m→0mαxM→+∞mβxm→0αM→+∞ββθ2(Mβ−Mα))ln=[f(0)−k]ln(0<θ1<1,0<θ2<1)ZααZZ+∞+∞+∞f(αx)−f(βx)f(αx)−f(βx)f(αx)(2)dx=limdx=limdx−Z0xZm→0mZxZm→0mx+∞+∞+∞mβf(βx)f(x)f(x)f(x)dx=limdx−dx=limdx=mxm→0mαxmβxm→0mβxββlimf(θ)ln=f(0)ln.m→0αα'