《信号与线性系统》试题与答案6.doc 36页

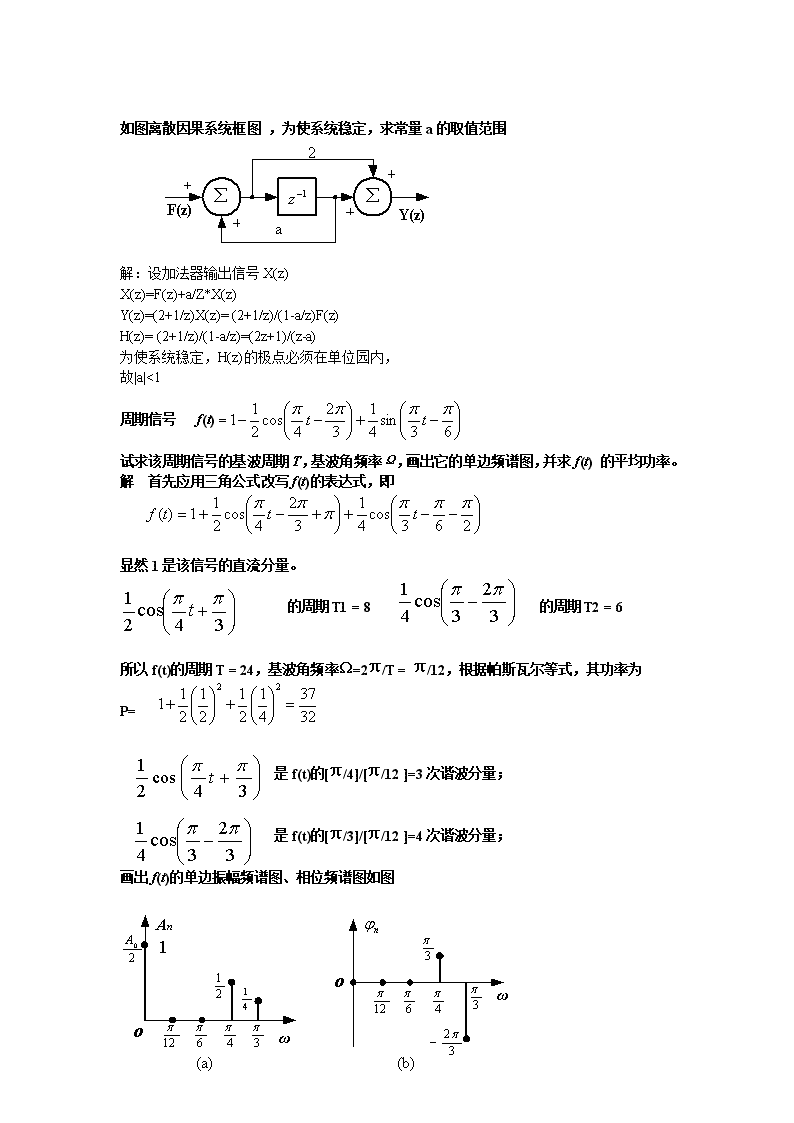
'如图离散因果系统框图，为使系统稳定，求常量a的取值范围解：设加法器输出信号X(z)X(z)=F(z)+a/Z*X(z)Y(z)=(2+1/z)X(z)=(2+1/z)/(1-a/z)F(z)H(z)=(2+1/z)/(1-a/z)=(2z+1)/(z-a)为使系统稳定，H(z)的极点必须在单位园内，故|a|<1周期信号f(t)=试求该周期信号的基波周期T，基波角频率Ω，画出它的单边频谱图，并求f(t)的平均功率。解首先应用三角公式改写f(t)的表达式，即显然1是该信号的直流分量。的周期T1=8的周期T2=6所以f(t)的周期T=24，基波角频率Ω=2π/T=π/12，根据帕斯瓦尔等式，其功率为P=是f(t)的[π/4]/[π/12]=3次谐波分量；是f(t)的[π/3]/[π/12]=4次谐波分量；画出f(t)的单边振幅频谱图、相位频谱图如图 二、计算题（共15分）已知信号1、分别画出、、和的波形,其中。（5分）2、指出、、和这4个信号中，哪个是信号的延时后的波形。并指出哪些信号的拉普拉斯变换表达式一样。（4分）3、求和分别对应的拉普拉斯变换和。（6分）1、（4分）2、信号的延时后的波形。（2分）3、（2分）。（2分）三、计算题（共10分）如下图所示的周期为秒、幅值为1伏的方波作用于RL电路，已知，。1、写出以回路电路为输出的电路的微分方程。2、求出电流的前3次谐波。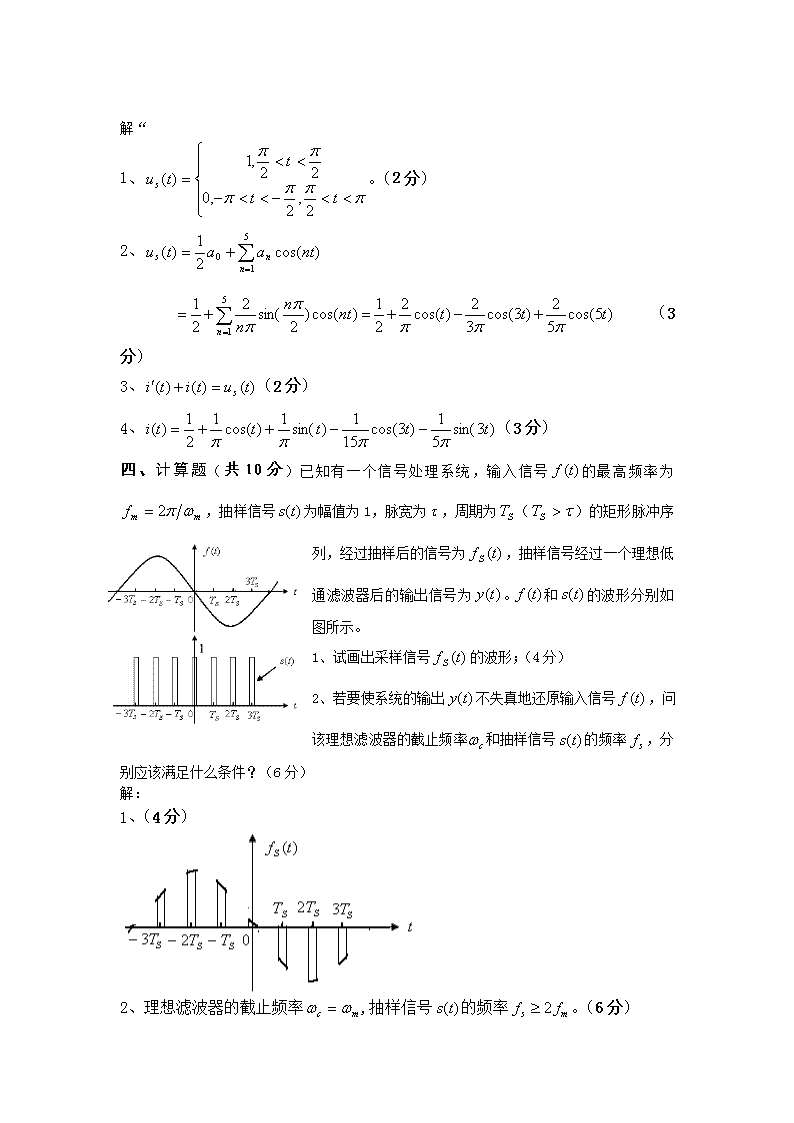 解“1、。（2分）2、（3分）3、（2分）4、（3分）四、计算题（共10分）已知有一个信号处理系统，输入信号的最高频率为，抽样信号为幅值为1，脉宽为，周期为（）的矩形脉冲序列，经过抽样后的信号为，抽样信号经过一个理想低通滤波器后的输出信号为。和的波形分别如图所示。1、试画出采样信号的波形；（4分）2、若要使系统的输出不失真地还原输入信号，问该理想滤波器的截止频率和抽样信号的频率，分别应该满足什么条件？（6分）解：1、（4分）2、理想滤波器的截止频率,抽样信号的频率。（6分） 五、计算题（共15分）某LTI系统的微分方程为：。已知，，。求分别求出系统的零输入响应、零状态响应和全响应、和。解：1、。（2分）2、（3分）3、（5分）4、（5分）六、计算题（共10分）如下图所示的RC低通滤波器网络。已知电容C的初始电压为。（共10分）1、写出该电路的s域电路方程，并画出对应的电路图。（2分）2、写出以电容电压为输出的电路的系统函数的表达式。（2分）3、求出的极点，判断该RC网络的稳定性。（2分）4、求出该RC网络的频率特性。（2分）5、求出该RC网络的幅频特性和相频特性的表达式，并画出频率特性图。（2分） 解：1、或（2分）2、（2分）3、的极点，该RC网络是稳定的。（2分）已知象函数求逆z变换。其收敛域分别为：（1）÷z÷>2(2)÷z÷<1(3)1<÷z÷<2解：部分分式展开为(1)当÷z÷>2，故f(k)为因果序列(2)当÷z÷<1，故f(k)为反因果序列(3)当1<÷z÷<2，已知象函数求逆z变换。其收敛域分别为：（1）÷z÷>3(2)1<÷z÷<2 解：（1）÷z÷>3由收敛域可知，上式四项的收敛域满足÷z÷>3，(2)1<÷z÷<2由收敛域可知，上式前两项的收敛域满足÷z÷>1，后两项满足÷z÷<2。1．系统的激励是，响应为，若满足，则该系统为线性、时不变、因果。（是否线性、时不变、因果？）2．求积分的值为5。3．当信号是脉冲信号时，其低频分量主要影响脉冲的顶部，其高频分量主要影响脉冲的跳变沿。4．若信号的最高频率是2kHz，则的乃奎斯特抽样频率为8kHz。5．信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为一常数相频特性为_一过原点的直线（群时延）。6．系统阶跃响应的上升时间和系统的截止频率成反比。7．若信号的，求该信号的。8．为使LTI连续系统是稳定的，其系统函数的极点必须在S平面的左半平面。9．已知信号的频谱函数是，则其时间信号为。10．若信号的，则其初始值1。得分二、判断下列说法的正误，正确请在括号里打“√”，错误请打 “×”。（每小题2分，共10分）1.单位冲激函数总是满足（√）2.满足绝对可积条件的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。（×）3.非周期信号的脉冲宽度越小，其频带宽度越宽。（√）4.连续LTI系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。（√）5.所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。（×）得分三、计算分析题（1、3、4、5题每题10分，2题5分，6题15分，共60分）1.信号，信号，试求。（10分）解法一：当时，=0当时，当时，解法二：2.已知，，求。（5分）解： ，收敛域为由，可以得到3.若连续信号的波形和频谱如下图所示，抽样脉冲为冲激抽样。（1）求抽样脉冲的频谱；（3分）（2）求连续信号经过冲激抽样后的频谱；（5分）（3）画出的示意图，说明若从无失真还原，冲激抽样的应该满足什么条件？（2分）解：（1），所以抽样脉冲的频谱。（2）因为，由频域抽样定理得到：（3）的示意图如下 的频谱是的频谱以为周期重复，重复过程中被所加权，若从无失真还原，冲激抽样的应该满足若。4.已知三角脉冲信号的波形如图所示（1）求其傅立叶变换；（5分）（2）试用有关性质求信号的傅立叶变换。（5分）解：（1）对三角脉冲信号求导可得：，可以得到。（2）因为5.电路如图所示，若激励信号，求响应并指出响应中的强迫分量、自由分量、瞬态分量与稳态分量。（10分）解：由S域模型可以得到系统函数为 由，可以得到，在此信号激励下，系统的输出为则强迫响应分量：自由响应分量：瞬态响应分量：稳态响应分量：06.若离散系统的差分方程为（1）求系统函数和单位样值响应；（4分）（2）讨论此因果系统的收敛域和稳定性；（4分）（3）画出系统的零、极点分布图；（3分）（4）定性地画出幅频响应特性曲线；（4分）解：（1）利用Z变换的性质可得系统函数为：，则单位样值响应为（2）因果系统z变换存在的收敛域是，由于的两个极点都在z平面的单位圆内，所以该系统是稳定的。（3）系统的零极点分布图 （4）系统的频率响应为当时，当时，得分四、简答题（1、2二题中任选一题解答，两题都做只计第1题的分数，共10分）1.利用已经具备的知识，简述如何由周期信号的傅立叶级数出发，推导出非周期信号的傅立叶变换。（10分）2.利用已经具备的知识，简述LTI连续时间系统卷积积分的物理意义。（10分）1.解：从周期信号FS推导非周期信号的FT 对于非周期信号,T1→∞,则重复频率,谱线间隔，离散频率变成连续频率。在这种极限情况下，但可望不趋于零，而趋于一个有限值，且变成一个连续函数。考察函数,并定义一个新的函数F(w)傅立叶变换：F(w)称为原函数f(t)的频谱密度函数(简称频谱函数).傅立叶逆变换 2.解：线性系统在单位冲激信号的作用下，系统的零状态的响应为单位冲激响应：利用线性系统的时不变特性：利用线性系统的均匀性：利用信号的分解，任意信号可以分解成冲激信号的线性组合：班级：学生学号：学生姓名：适用专业年级：2007物理出题教师：试卷类别：A（√）、B（）、C（）考试形式：开卷（√）、闭卷（）印题份数：利用线性系统的叠加定理：1.。2.=。3.已知f(t)的傅里叶变换为F(jω),则f(2t-3)的傅里叶变换为。4.已知，则;。5.已知，则。6.已知周期信号，其基波频率为rad/s；周期为s。7.已知，其Z变换；收敛域为。8.已知连续系统函数，试判断系统的稳定性：。9．已知离散系统函数，试判断系统的稳定性：。 10．如图所示是离散系统的Z域框图，该系统的系统函数H(z)=。二．(15分)如下方程和非零起始条件表示的连续时间因果LTI系统，已知输入时，试用拉普拉斯变换的方法求系统的零状态响应和零输入响应，以及系统的全响应。三．（14分）①已知,,试求其拉氏逆变换f(t)；②已知，试求其逆Z变换。 四（10分）计算下列卷积：1.；2．。五．（16分）已知系统的差分方程和初始条件为：，1.求系统的全响应y(n)；2.求系统函数H(z)，并画出其模拟框图； 六．（15分）如图所示图（a）的系统，带通滤波器的频率响应如图(b)所示，其相位特性，若输入信号为:试求其输出信号y(t)，并画出y(t)的频谱图。 参考答案一填空题（30分，每小题3分）1.1；2.e-2;3.;4.1，0;5.；6.2л;7.，|z|>0；8.不稳定；9.稳定10.二．（15分）方程两边取拉氏变换： 三．1．（7分）2．（7分）四．1.（5分）2.（5分）五．解：（16分）（1）对原方程两边同时Z变换有： （2）六（15分） （装订线内不准答题）课程名称_______信号与系统（A）1__一填空题（30分，每小题3分）1.10；2.0.707；3.课本1524.；5.0,1/3；6.30kHz；7.，|z|>0.5；8.稳定；9.不稳定；10.二．解：（15分）三．(14分)1．（7分）2．（7分）双边序列；四．1．（5分）（1）2．（6分）湖南工程学院试卷参考答案及评分标准（A卷） 专业班级_电子信息0201/02/03命题老师陈爱萍_2003_至_2004_学年第_2_学期共2页第2页（装订线内不准答题）课程名称信号与系统(A)2五．解：（15分）（3）模拟框图六（15分） 湖南工程学院试卷用纸___2003_____至___2004__学年第__1__学期专业班级姓名_________学号_____共3页第__1__页 （装订线内不准答题）命题教师陈爱萍审核________________________课程名称信号与系统考（试）____A__（A卷）适用专业班级___电子信息0201/02/03_____考试形式_闭__（闭）题号一二三四五六七八九十总分计分一、填空题：（30分，每小题3分）1.2.3.已知则。4.为信号传输无失真，系统的频率响应函数为。5.则;。6.要传送频带为15kHz的音乐信号，为了保证不丢失信息，其最低采样频率应为。7.已知，其Z变换；收敛域为。8．已知连续系统函数，试判断系统的稳定性：。9．已知离散系统函数，试判断系统的稳定性：。10．如图所示是LTI系统的S域框图，该系统的系统函数H(s)=。二．(15分)如下方程和非零起始条件表示的连续时间因果LTI系统，已知输入时，试用拉普拉斯变换的方法求系统的零状态响应和零输入响应，以及系统的全响应。湖南工程学院试卷用纸 专业班级____________姓名______________学号______共__3__页第__2__页（装订线内不准答题）三．（14分）①已知,试求其拉氏逆变换f(t)；②已知，试求其逆Z变换。四．（5分）1．已知；。2．（6分）已知f1(t)、f2(t)、f3(t)的波形如图所示，f2(t)、f3(t)为单位冲激函数，试画出和的波形图。五、（15分）已知描述离散因果系统的差分方程为：求该系统的系统函数H(z)、单位冲激响应h(n)、阶跃响应，并画出它的模拟框图。 共__3__页第__3__页（装订线内不准答题）六．（15分）如图所示图（a）是抑制载波振幅调制的接收系统。若输入信号为，，低通滤波器的频率响应如图(b)所示，其相位特性。试求其输出信号y(t)，并画出x(t)和y(t)的频谱图。图（a）一、选择题（每小题可能有一个或几个正确答案，将正确的题号填入[]内）1．f（5-2t）是如下运算的结果————————（） （A）f（-2t）右移5（B）f（-2t）左移5（C）f（-2t）右移（D）f（-2t）左移2．已知，可以求得—————（）（A）1-（B）（C）（D）3．线性系统响应满足以下规律————————————（）（A）若起始状态为零，则零输入响应为零。（B）若起始状态为零，则零状态响应为零。（C）若系统的零状态响应为零，则强迫响应也为零。（D）若激励信号为零，零输入响应就是自由响应。4．若对f（t）进行理想取样，其奈奎斯特取样频率为fs，则对进行取样，其奈奎斯特取样频率为————————（）（A）3fs（B）（C）3（fs-2）（D）5．理想不失真传输系统的传输函数H（jω）是————————（）（A）（B）（C）（D）（为常数）6．已知Z变换Z，收敛域，则逆变换x（n）为——（）（A）（C）（B）（D）二．（15分）已知f(t)和h(t)波形如下图所示，请计算卷积f(t)*h(t)，并画出f(t)*h(t)波形。三、（15分） 四．（20分）已知连续时间系统函数H(s),请画出三种系统模拟框图(直接型/级联型/并联型)。.五．（20分）某因果离散时间系统由两个子系统级联而成，如题图所示，若描述两个子系统的差分方程分别为：1．求每个子系统的系统函数H1（z）和H2（z）；2．求整个系统的单位样值响应h（n）；3．粗略画出子系统H2（z）的幅频特性曲线； 《信号与系统》试题一标准答案说明：考虑的学生现场答题情况，由于时间问题，时间考试分数进行如下变化：1）第六题改为选做题，不计成绩，答对可适当加分；2）第五题改为20分。一、1．C2.C3.AD4.B5.B6.A二、 三、四．（20分）已知连续时间系统函数H(s),请画出三种系统模拟框图(直接型/级联型/并联型)。. 五、答案：1.Re(z)jIm(z)02.3.一．选择题（共10题，20分）1、，该序列是　　　　　　。 A.非周期序列B.周期C.周期D.周期2、一连续时间系统y(t)=x(sint)，该系统是　　　　　　。A.因果时不变B.因果时变C.非因果时不变D.非因果时变3、一连续时间LTI系统的单位冲激响应，该系统是　　　。A.因果稳定B.因果不稳定C.非因果稳定D.非因果不稳定4、若周期信号x[n]是实信号和奇信号，则其傅立叶级数系数ak是　　　　。A.实且偶B.实且为奇C.纯虚且偶D.纯虚且奇5、一信号x(t)的傅立叶变换，则x(t)为　　　　。A.B.C.D.6、一周期信号，其傅立叶变换为　　　　。A.B.C.D.7、一实信号x[n]的傅立叶变换为，则x[n]奇部的傅立叶变换为　　　　。A.B.C.D.8、一信号x(t)的最高频率为500Hz，则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为　　　　。A.500B.1000C.0.05D.0.0019、一信号x(t)的有理拉普拉斯共有两个极点s=－3和s=－5，若，其傅立叶变换收敛，则x(t)是　　　　。A.左边B.右边C.双边D.不确定10、一系统函数，该系统是　　　　。 A.因果稳定B.因果不稳定C.非因果稳定D.非因果不稳定简答题（共6题，40分）1、（10分）下列系统是否是（1）无记忆；（2）时不变；（3）线性；（4）因果；（5）稳定，并说明理由。(1)y(t)=x(t)sin(2t)；（2）y(n)=2、（8分）求以下两个信号的卷积。3、(共12分，每小题4分)已知，求下列信号的傅里叶变换。（1）tx(2t)（2）(1-t)x(1-t)（3）4.求的拉氏逆变换（5分）5、已知信号，当对该信号取样时，试求能恢复原信号的最大抽样周期Tmax。（5分）四、（10分）求周期矩形脉冲信号的傅立叶级数（指数形式），并大概画出其频谱图。 DCADBACDCC二、简答题（共6题，40分）1、（1）无记忆，线性，时变，因果，稳的；（5分）（2）无记忆，非线性，时不变，因果，稳定（5分）2、3、（3×4分＝12分）（1）（2）（3）4、（5分） 5、（5分）因为f(t)=4Sa(4πt)，所以X(jω)＝R8π(jω),其最高角频率ω=4π。根据时域抽样定理，可得恢复原信号的最大抽样周期为三、（10分）（1）2分3分四、（10分）3分五、（20分）（8分） '