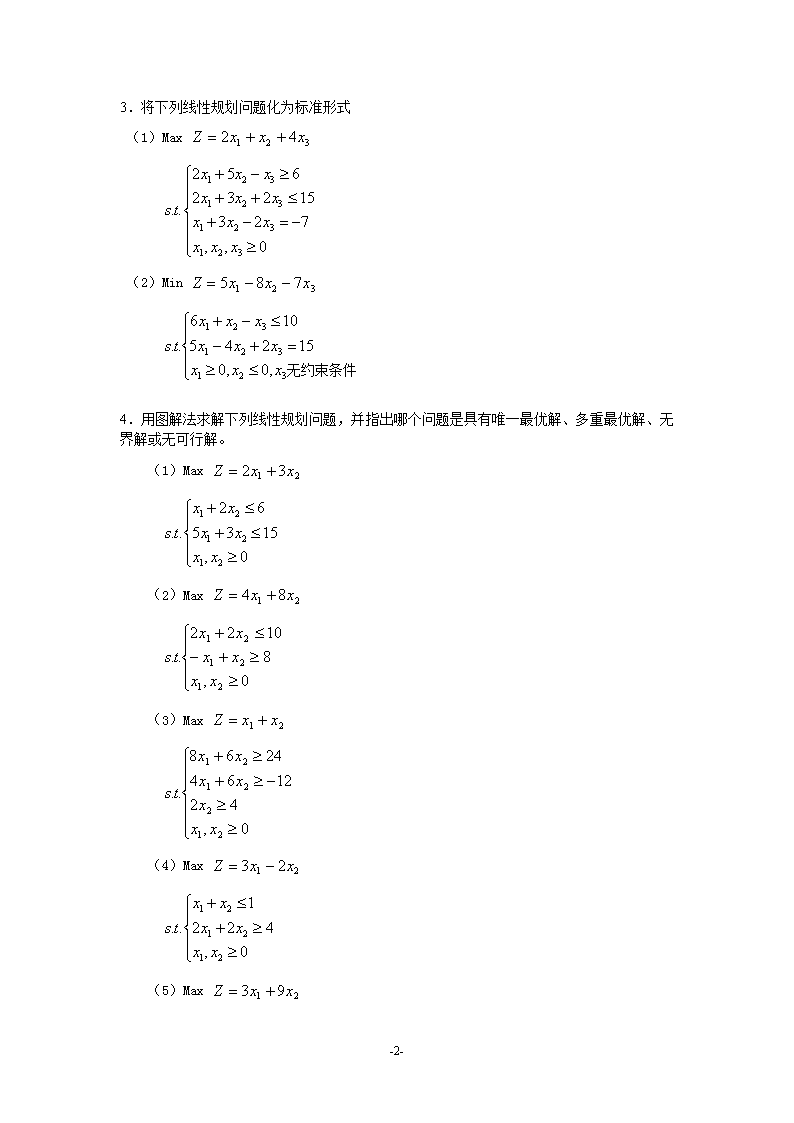《卫生管理运筹学》习题与参考答案.doc 68页

'《卫生管理运筹学》习题与参考答案习题一1．某医学院动物房饲养某种动物供教学与研究使用，设每头该种动物每天至少需700g蛋白质，30g矿物质，100mg维生素。现有5种饲料可供选用，各种饲料每公斤营养成分含量及单价如下表所示。要求确定既满足动物生长的营养需要，又使费用最省的饲料选用方案？只建模不求解。各种饲料营养成分含量及单价表饲料蛋白质（g）矿物质（g）维生素（mg）价格（元/kg）1310.50.2220.510.7310.20.20.446220.35180.50.80.82．某食品厂用原料A、B、C加工成3种不同类型的食品甲、乙、丙。已知各种类型食品中A、B、C的含量，原料成本，各种原料每月的限制用量以及3种食品的单位加工费和售价（如下表所示）。问该厂每月生产这3种类型食品各多少公斤，可得到利润最大？只建模不求解。食品、原料、费用分析表原料食品原料成本（元/kg）每月限制用量（kg）甲乙丙A2.002000B无限制无限制无限制1.502500C1.001200加工费（元/kg）0.500.400.30售价（元/kg）3.402.852.25-68- 3．将下列线性规划问题化为标准形式（1）Max　　　（2）Min　　　4．用图解法求解下列线性规划问题，并指出哪个问题是具有唯一最优解、多重最优解、无界解或无可行解。（1）Max　　　（2）Max　　　（3）Max　　　（4）Max　　　（5）Max-68- 　　　（6）Max　　　5．已知线性规划问题：　　　　Max下表所列的解均满足第1至第3个约束条件，请指出表中那些解是可行解，那些是基本解，哪些是基本可行解。表满足第1至第3个约束条件的解序号A24300B100-504C30274D14.540-0.5E02562F045206．考虑下面线性规划问题：Max-68- 　　　（1）写出该线性规划问题的标准型；（2）在这个线性规划问题的基本解中，将至少有多少个变量的取值为零？为什么？（3）在这个线性规划问题中，共有多少种基本解？（4）图解法求解此线性规划问题的可行域（观察可行域各顶点所对应的基本可行解），并求出最优解和最优值。7．用单纯形法求解下列线性规划问题（1）Max（2）Max8．下表中给出线性规划问题计算过程中某次迭代的单纯形表，目标函数为：Max，约束条件均为，表中为松弛变量，表中目标函数值。某次迭代的单纯形表01130-14/3a05/206d251000ef00-1gbc0-68- （1）求出a-g的值；（2）表中给出的解是否为最优解。9．用大M法求解下列线性规划问题，并指出问题的解属于哪一类？（1）Max　　　（2）Min　　　（3）Max　　　（4）Max　　　习题二1．写出下列线性规划问题的对偶问题：（1）Max-68- s.t.（2）Min无约束s.t.（3）Min无约束s.t.2.已知线性规划问题用单纯形法计算时得到的初始单纯形表与最终单纯形表如下表，请将表中空白处数字填上。表初始与最终单纯形表2-11000xjXB03111006001-1201010011-1001202-11000=0………………-68- 2-11000xjXB01-1-2201/21/2-10-1/21/2*=3.有LP问题Mins.t.已知其对偶问题的最优解为=4/5,=3/5，最优值为=5，试用对偶理论求原问题的解。4.对偶单纯形法求解下列线性规划问题，并指出其对偶问题的最优解。（1）Mins.t.（2）Mins.t.5.根据下列线性规划问题及其最终单纯形表：-68- Maxs.t.表最终单纯形表621200xjXB124/31/311/3080-250-116-10-20-40*=（1）写出线性规划原问题的最优解、最优值、最优基B及其逆B-1。（2）写出原问题的对偶问题，并从上表中直接求出对偶问题的最优解。（3）试求出最优解不变时c3的变化范围。（4）试求出最优基本变量不变时b2的变化范围。（5）在原线性规划的约束条件上，增加下面的约束条件，其最优解是否变化？如变化，试求出最优解？6.某制药公司生产A、B、C三种药品，若设x、y、z分别为A、B、C三种药品的产量，为制定最优生产计划建立如下所示模型：原材料1约束原材料2约束原材料3约束Maxs.t.引入松弛变量s1、s2、s3，利用单纯形法求解可得最终单纯形表如下：-68- 表最终单纯形表423000xjXB20103/4-1/20254102-1/41/2025000-40-112000-5-1/2-10*=150请分别就以下情况进行分析（各问题条件相互独立）：（1）由于市场需求变化，药品B的单位利润可能改变，试求出保持最优生产计划不需改变的药品B单位利润的变化范围；若药品B单位利润由2变为5，求相应最优生产计划。（2）由于原材料市场变化，原材料1的供应从100单位降低至50个单位，此时是否会影响最优生产计划？若影响，求其最优生产计划。（3）由于生产技术改进，每生产1个单位的药品C需消耗原材料1、原材料2和原材料3的量由原来的4、6、2个单位依次变为2、2、1个单位，求相应的最优生产计划。习题三1．已知极小化运输问题的产销平衡及单位运价表如表1至表3所示，用最小元素法求各问题的初始调运方案并用表上作业法求最优解，同时用伏格尔法求各问题的近似最优解。表1运输表（1）销地产地B1B2B3B4产量A1102201115A212792025A321416185销量5151510-68- 表2运输表（2）销地产地B1B2B3B4产量A198121318A21010121424A38911126A41010111212销量614355表3运输表（3）销地产地B1B2B3B4产量A184127A2694725A3534326销量101020152．某药品公司在3个不同的地区分别设有药厂，生产同一种药品，其产量分别为300箱、400箱和500箱。该药厂需要在4个地区供应该种药品，这4个地区该种药品的需求量均为300箱。3个药厂到4个销地的单位运价如下表所示：表药厂到销地的单位运价销地产地甲乙丙丁药厂121172325药厂210153019药厂32321200a.应如何安排运输方案，使得总运费最小？-68- b.如果药厂2的产量从400箱提高到了600箱，那么应如何安排运输方案，使得总运费为最小？c.如果销地甲的需求从300箱提高到450箱，而其他情况与a相同，那么该如何安排运输方案，使得运费为最小？3．已知运输问题的运输表及最优运输方案如下表所示：表运输表及最优运输方案销地产地B1B2B3B4产量A1101201115510A21279202501015A3214161855销量5151510试分析：a.单位运价c22在什么范围变化时，上述最优调运方案不变；b.单位运价c24变为何值时，将有多重最优调运方案。4.格林公司有甲、乙、丙3个分厂生产同一种产品，产量分别为200吨、400吨和300吨，供应Ⅰ、Ⅱ、Ⅲ、Ⅳ4个地区的需要，各地区的需要量分别为300吨、250吨、350吨和200吨。由于原料、工艺、技术的差别，各厂每千克产品的成本分别为1.3元、1.4元、1.5元。又由于行情不同，各地区销售价分别为每千克2.0、2.2、1.9、2.1元。已知从各分厂运往各销售地区的运价如下表所示：-68- 表各分厂到各销地的单位运价（单位：元/千克）销地产地ⅠⅡⅢⅣ甲分厂0.40.50.30.4乙分厂0.30.70.90.5丙分厂0.60.80.40.7由于产品供不应求，因此各地的需求不可能完全充分满足，因此要求第Ⅰ和第Ⅱ销地至少供应150吨；第Ⅳ销地必须全部满足；请确定一个运输方案使该公司获利最多。5.大洋发动机厂按合同规定需于每个季度末分别完成10、15、25、20台同一规格发动机。已知该厂各季度生产能力及生产每台发动机成本如下表所示。如果生产出来的发动机当季不交货，每台每积压一个季度需储存、维护费用0.15万元。要求在完成合同的条件下，制订使该厂全年生产、存贮和维护费用为最小的决策方案。表大洋发动机厂各季度生产能力及生产每台发动机成本季度生产能力（台）单台成本（万元）12510.823511.133011.041011.36．南方飞机制造公司在制造过程的最后一步是生产喷气发动机并把它们安装到已经完成的飞机框架之中去。公司根据订单为未来4个月喷气发动机的生产制定计划。根据订单要求，1至4月要安装的发动机数量分别是10台、15台、25台和20台。而在此期间，根据其他产品制造、保养以及维修工作安排的不同，这种发动机的生产能力及生产成本也有所不同（见表）。此外，如果当月生产的发动机不在当月安装，其储存成本为每台30万元/月。-68- 表发动机的生产能力及生产成本月份最大产量单位生产成本（百万元）正常时间加班时间正常时间加班时间12342030255101510105.405.555.505.655.505.605.555.75生产管理人员需要制订出一个每月生产多少发动机的计划，使制造和存储的总成本达到最小。习题四1．判断下列说法是否正确：（1）整数规划问题解的目标函数值一般优于其相应的松弛问题解的目标函数值。（2）用分枝定界法求解一个极大化的整数规划问题时，任何一个可行解的目标函数值是该问题目标函数值的一个下界。（3）用分枝定界法求解一个极大化的整数规划问题，当得到多于一个可行解时，通常可任取其中一个作为下界值，经比较后确定是否再进行分枝。（4）指派问题成本矩阵的每个元素乘上同一常数k，将不影响最优指派方案。2．用分枝定界法求解下列整数规划问题：（1）Max（2）Max-68- （3）Min3．用隐枚举法求解下列0-1规划：（1）Max（2）Min4．一个旅行者要在其背包里装一些最有用的旅行物品。背包容积为a，携带物品的总重量最多为b。现有物品m种，第i件物品的体积为ai、重量为bi(i=1,2,…,m)。为了比较物品的有用程度，假设第i件物品的价值为ci(i=1,2,…,m)。问旅行者应携带哪几件物品，才能使携带物品的总价值最大（给出数学模型）？5．某城市急救中心考虑为6个区设点配置救护车，6个区中均可设点。从成本和服务社会两方面着想，急救中心希望设置的点尽量少，但必须满足在任何地区有呼救，救护车都能在15分钟内赶到。各区之间救护车的行驶时间见下表（单位：分钟）。请帮助急救中心制定一个设点最少的计划。-68- 表车在各区之间的行驶时间区号1234561010162827202100243217103162401227214283212015255271727150146201021251406．用匈牙利法求解下列指派问题：（1）Min（2）Max7．学生小强、小明、小林组成了一个课程竞赛代表队，他们各门课的成绩如下。竞赛同时进行，每人只能参加一项。问如何参赛才能使他们的总分最高？-68- 表课程成绩表学生课程英语数学基础医学小强859280小明879485小林8897788．某医院6名检验师担当4项检验项目需用的时间矩阵如下，问应如何指派4名检验师去担当这4项检验任务，使总检验时间最少？习题五1.某项任务的各项工序与所需时间以及它们之间的相互关系如下表所示。请根据此表画网络图，并确定关键线路。表某项任务的工序逻辑明细表工序紧前工序工序时间A-2BA3CA4DA5EB6GD、C3HC4IE、H、G22．-68- 今有网络的结构和工时如下图所示，试计算各工序的平均时间，最早开始时间，最早结束时间、最迟开始时间、最迟结束时间以及总时差。16345279－12－3310－20－305.5－11－16.510－10－1012－18－2415－20－5515－20－5510－10－4012-16-24图习题2的网络结构和工时图3.某工程的各项工序所需人员（箭线上方[]内所示数据）以及完成时间如下图所示。试进行人力资源的平衡优化。16853247A[8]2E[8]5B[7]3G[6]4H[4]4F[4]4I[8]4J[4]2C[6]2D[10]316853247A[8]2E[8]5B[7]3G[6]4H[4]4F[4]4I[8]4J[4]2C[6]2D[10]3图习题3的网络结构和工时图-68- 习题六1．某企业为了扩大生产经营业务，准备生产一种新产品，生产这种新产品有3个可行方案：一是改造本企业原有的生产线，二是从国外引进一条高效自动生产线；三是按专业化协作组织生产。由于对未来几年内市场需求状况无法了解，只能大致估计有需求高、需求中等和需求低3种可能，其中需求高这一状况出现的可能性好像偏大。每个方案在各自然状态下的收益估计值如下表所示。试问企业采取哪个方案较好?表3种方案的损益值（单位：万元）方案需求状况需求高需求中等需求低改造生产线1609530引进生产线22012015协作生产10070502．同上题条件，只是未来市场需求低的可能性好像偏大，且各方案在不同自然状态下的收益值如下表所示。试问企业采用哪个方案较好?表3种方案的损益值（单位：万元）方案需求状况需求高需求中等需求低改造生产线17080－70引进生产线220100－100协作生产9050－23．从甲地向乙地运送活螃蟹5000公斤，可以采用五种不同的装运方法，记为至。螃蟹抵达乙地的存活数受沿途气温高低的影响，也因不同装运方法而异。预测高、中、低温度的概率和收益如下表所示。试分析哪一个决策为最优装运方法，以求获利最大。-68- 表各装运方法的损益值（单位：千元）装运方案自然状态高温=0.2中温=0.3低温=0.54060120408060010080－201006050100604．某决策者试图决定究竟签订两个合同中的某一个还是两个合同都不签订。他已经把情况稍微简化了一些，并且认为下表所示的信息已足够用于决定是否签订合同。问：如果该决策者希望将期望利润增加到最大值，那么他应当选择哪个合同?与最佳决策相联系的期望利润是多少?表两份合同的利润及概率合同A合同B利润(元)概率利润(元)概率1000000.2400000.3500000.4100000.400.3－100000.3－300000.15．某出版者打算在市场上出版一种名为《生活顾问》的月刊杂志，这种杂志登载有投资者特别关心的文章和其它信息。根据过去的经验和对这类月刊潜在需求量的感性认识，该出版者制定了收益表（见下表）。试问这位出版者会继续出版这种杂志吗?-68- 表各种方案的损益值（元）方案购买者的反应不好=0.5一般=0.2好=0.3不出版000出版－250000050000030000006．甲经营的公司全部资产有10万元，乙经营的公司总资产为1000万元。现有两个投资方案供他们选择，其损益表如下。问：（1）甲、乙两个公司最大可能会选择哪个方案？（2）若有一个投资者认为收益2万元的效用值为0.5，效用函数为对数函数时，按期望效用决策准则，最优方案是什么？（3）按期望值准则，最优方案是什么？对此最优方案的决策作敏感性分析。表两种投资方案的损益值（单位：万元）投资方案自然状态=0.75=0.2520－10327．考虑一个筹建新医院的10年规划，共有2个方案：一是建大医院；二是先建小医院，如果利用条件好，3年后扩建。根据预测，前3年利用率好的概率为70%，利用率不好的概率为30%。如果前3年利用率好，则后7年利用率好的概率为90%，利用率差的概率为10%；如果前3年利用率差，则后7年利用率肯定差。建大医院需投资300万元，建小医院需投资160万元，扩建投资140万元，扩建后每年的益损与大医院相同。2个方案的年益损值估计如下表。请用决策树法进行决策。-68- 表各方案的年损益值（单位：万元）方案自然状态利用好利用差建大医院100－20建小医院40108．某地区有人口10万，该地区某种疾病的发生率在暴发年为5‰，在常年为0.3‰。平均每例该病患者的治疗费为300元。现在该地区的某一医学院向所在地的卫生局申请经费10000元来研制一种预防该病的疫苗，据初步估计，该疫苗如果制成，则可使该病的发病率在暴发年降为0.5‰，在常年降为0.03‰。该疾病暴发年发生的概率为20%，非暴发年发生的概率为80%。疫苗研制成功的概率为40％。若从费用的角度，卫生局是否应该同意该疫苗的研制？习题七1．一次指数平滑法与一次移动平均法相比，其优点在哪？2．根据本章所学的知识，结合医院管理的实际，试分析其中哪些事件可以运用马尔可夫链方法预测，并给出相应的实例。3.某医院的经营收入如下：月份123456789101112销售收入（万元）430380330410440390380400450420390试用一次移动平均法（N=4）对月经营收入进行预测。4．对第3题运用一次指数平滑法（进行预测。-68- 5．（项目选址问题）某市有一家三级甲等医院为了给当地居民提供高质量的社区基本医疗服务，在该市三个地段设立甲、乙、丙三家社区卫生服务分支机构。由于具有较低的服务价格与较高的医疗服务质量，患者在长期保持相对稳定。在患者的就医意愿进行调查以后，发现患者在三个地段就医的转移概率矩阵为如下，由于资金的原因，该医院打算只对一家社区医疗服务中心加大投入。问应该选择哪一个机构？习题八1．某医院X光室只有一名医生，来检查的患者人数服从泊松分布，平均每小时4人；患者检查时间服从负指数分布，平均每人需12分钟，求：（1）X光室的各项工作指标；（2）患者不必等待的概率。2．某医院门诊部只有一名医生，病人平均20分钟到达一个，医生对每个病人的诊治时间平均为15分钟，上述两种时间均为负指数分布。若该门诊希望到达的病人90%以上能有座位，则该医院至少应设置多少个座位？3．某医院理疗室只有1名医生，且理疗室内最多只能有3位病人等待理疗。设理疗病人按泊松流到达理疗室，平均每小时到达1人，理疗时间服从负指数分布，平均每1.25小时理疗完1位病人。试求：（1）患者到达便可看病的概率；（2）病人流失的概率；（3）病人等待理疗的平均时间和队长。4．设某医院内科危重病房1位护士负责5个床位，病床经常住满。每个病人的需求服从泊松分布，平均每2小时1次，病人每次的护理时间服从负指数分布，平均为20分钟。试求：（1）没有病人需要护理的概率；（2）等待护理的病人平均数；-68- （3）若该护士负责6个病人的护理，其它各项条件不变，则上述（1）和（2）的结果；（4）若希望至少45%时间内所有病人都不需要护理，则该护士最多负责护理的病人数。5．某医院机关文书室有3名打字员，每名打字员每小时能打6份文件。若该室平均每小时收到15份要打的文件。假设该室为M/M/C/∞/∞系统。（1）求3名打字员忙于打字的概率；（2）该室主要运行指标；（3）若打字员分工包打不同科室的文件，每名打字员都平均每小时接到5份文件，试计算此情况下该室的各项工作指标，并与（2）比较。6．某电话交换台的呼叫强度服从平均每分钟4次的泊松分布，最多有6条线同时通话，每次通话时间服从平均0.5分钟的负指数分布。呼叫不通时，呼叫自动消失。试求：（1）系统空闲的概率；（2）呼叫不通的概率；（3）平均通话线路数。7．某院一台血液分析仪每份血样检测时间为3分钟，血样按泊松分布平均每小时到达18份。试求主要工作指标和仪器空闲概率。8．某医院有一个取药窗口，患者按泊松分布平均每小时到达10人。药剂员发药时间（小时）。试求该药房空闲的概率和其它运行指标。9．到达只有一名医生诊所的病人有两类：急诊病人和普通病人。当急诊病人到达时，医生将暂停正在治疗的普通病人而为其服务。同类型病人按FCFS服务规则进行。已知两类病人到达均服从泊松分布，急诊病人平均每天2人，普通病人每天6人；医生为两类病人治疗时间相同且服从负指数分布，平均每小时2人，若一天按8小时工作时间计算，试求：（1）两类病人分别在系统内的平均等待时间；（2）两类病人分别在系统内的平均队长。-68- 10．某工厂设备维修部要求维修的设备按泊松分布到达，平均每天17.5台。维修部工人每人每天平均维修10台，服从负指数分布。已知每名工人工资每天60元，因设备维修而造成的停产损失为每台每天300元。试确定该维修部的最佳工人数（停产损失费和工资支付费总和最小）。习题九1．某医院每年平均需求某种针剂2000盒，每盒价值2元，每盒的月库存费为价值的5%，每订购一次的费用为20元，假设货物为瞬时到货，不允许缺货。试求：（1）最佳经济批量、最佳订购间隔期、最小费用各是多少？（2）当经济批量减少至129盒或增大至387盒时，最小费用分布增长了多少元？（3）当最佳经济批量增加或减少多少盒时，才能使最小费用增长25%？（4）当改变为原来的时，最佳经济批量变为多少?当扩大为原来的2倍时，最佳经济批量变为多少?解释、变化后使最佳经济批量发生变化是否符合实际意义。2．如果上题中，仍为瞬时到货、但允许缺货，每月每盒缺货损失费为价值的25%。求最佳经济批量、最佳订购间隔期、最小费用各是多少？3．通过比较不允许缺货和允许缺货的最小总费用公式，说明为什么允许缺货的总费用比不允许缺货的总费用低，最多只能相等。4．某食品店出售蛋糕，每盒成本为5元，售价7元。若到期卖不完，则削价为每盒4元销售完毕。已知蛋糕销售数量及其相应的概率分布如下表所示。问应如何订货才能使利润最高？表10-7蛋糕销售量及相应的概率（个）90100110120130140-68- 0.050.200.400.200.100.055．某医院青霉素针剂的月需求及备运期情况如下表所示。假设青霉素的需求服从正态分布，=0.1（元/盒/月），=17（元/次）。试求：（1）在服务水平为95%时，定点控制的订购点、订购量各是多少？（2）在服务水平为99%时，以月为周期定期控制的订购量是多少？表10-8某医院青霉素针剂的月需求量与备运期需求量时间（月）123456789101112月需求量（盒）290250320400370350440490340200140550备运期需求量（盒）109114547391101130119124185160140习题十1．A、B两人在互不知道的情况下，各在纸上写{-1，0，1}三个数字中的任意一个。设A所写的数字为s，B所写的数字为t，答案公布后B付给A人民币[s（t-s）+t（t+s）]元，写出此对策问题中A的赢得矩阵。2．设二人有限零和对策G={SA，SB；C}，其中，利用优超原则化简这个对策。3．已知A、B二人零和对策中，A的赢得矩阵如下，求双方的最优纯策略与对策值。（1）C=-68- （2）C=4．A、B矩阵对策中A的赢得矩阵如下，利用图解法求解最优策略与对策值。（1）C=（2）C=5．利用线性规划方法求解矩阵对策G={SA，SB；C}，其中。6．用划线法求解下列二人非零和对策的纯策略纳什均衡。（1）=（2）=7．用图解法或一阶条件求下列二人非零和对策的混合策略纳什均衡。=8．运用对策论知识，结合所学专业，举出一个具有实际意义的对策问题，给出解并讨论其专业意义。习题十一-68- 1．某医院过去一年中住院病人死亡率较往年有较大幅度的提高，试用因果分析图的方法寻找原因。2．假设根据数据统计，某地区过去一年中的死亡病例中有68例死亡和医疗护理不当有关，见下表，试用排列图进行分析。表68例死亡原因原因例数诊断原因7抢救原因23治疗实施原因4手术原因26护理原因83．实验室每天将一已知标本分作两份，分别测定，结果见下表，试作－R图。表平行样本测定结果日次第一次测定第二次测定15.004.9624.985.0034.925.0044.945.0254.984.9864.975.0074.995.0584.974.9995.025.00104.974.95115.005.00124.984.96134.994.96145.004.95154.984.96165.044.95-68- 175.035.00184.974.99195.024.94205.024.943．控图和控制图的差异是什么？习题十二1．常用的综合评价方法有哪几种？各有何优缺点？2．某社区卫生服务中心从服务态度、业务水平与工作量3个方面对医务人员的工作质量进行考评，评判等级为好、中、差3级。该社区卫生服务中心采用问卷评价的方式，共收回100份评估表，指标的权重及评估结果见下表：表社区卫生服务中心考核权重与评估等级分布指标权重好中差合计服务态度0.2065278100业务水平0.4813807100工作量0.3210000100试用模糊评价法对该社区卫生服务中心医务人员的工作质量进行评价。3．某医院有5个临床科室，拟从医疗（包括治愈率、诊断符合率、床位周转率）、科研（包括科研成果、论文专著）、管理（包括服务满意度、出勤率）3个方面进行评价，请用层次分析法比较各科室的工作质量高低。各科室的有关资料见下表：某医院临床科室各指标的状况评价指标临床科室12345治愈率（%）83.690.189.496.098.0诊断符合率（%）90.385.189.988.186.0床位周转率（%）92.692.795.894.693.1科研成果（项）52.040.038.054.048.0-68- 论文专著（数）40.334.030.341.438.2服务满意度（%）95.092.094.795.690.7出勤率（%）93.692.291.796.291.2习题十三1．某仪器设备有两个关键部件A和B，其使用寿命分布如下表所示。假设A、B之中有一个发生故障，则整个仪器就不能使用。试用蒙特卡洛法进行20次模拟试验，以估计该仪器设备的使用寿命。表14-9A、B两部件的使用寿命概率分布使用寿命（周）部件A概率分布部件B概率分布10.020.0520.030.1030.120.3040.200.2050.250.2060.120.1570.1080.0690.05100.052．某医院神经科的每天门诊病人数统计如下表，试用随机数表模拟该科未来10天门诊病人数的随机数列。表14-10门诊病人数的分布门诊病人数4050607080百分比（%）18152922163．某医院有救护车一辆，以往使用161次的情况如下表所示。表中“呼叫救护车的时间间隔”是指两次相邻的间隔时间。“救护车服务时间”是指从应唤出车到把病人送至医院这一段时间。试模拟该救护车未来20次的使用情况，并评价该救护车的利用程度。-68- 表14-11救护车呼叫时间间隔和救护车服务时间时间（分钟）呼叫救护车救护车服务次数频率（%）次数频率（%）2.5—7.5301935227.5—12.53421382412.5—17.52717251517.5—22.52113201222.5—27.51912171127.5—32.515910632.5—37.5749637.5—42.5535342.5—47.5212147.5—52.511合计161100161100假若该医院有两辆相同的救护车，试模拟未来30次救护车的使用情况，并评价车的利用率。-68- 习题参考答案习题一1．设选用第1种、第2种、第3种、第4种、第5种饲料的量分别为。Min2．设xij为生产第i种食品所使用的第j种原料数，i＝1，2，3分别代表甲、乙、丙，j＝1，2，3分别代表A、B、C。其数学模型为：MaxZ=s.t.3．将下列线性规划问题化为标准形式-68- （1）引入剩余变量，松弛变量Max　　　（2）令，，引入松弛变量Max4.（1）唯一最优解=1.7143，＝2.1429，Max=9.8571；（2）无可行解；（3）无界解；（4）无可行解；（5）多重最优解，MaxZ=66，其中一个解为=4，＝6；（6）唯一最优解，为=6.6667，＝2.6667，Max=30.6667。5．可行解：(A),(C),(E),(F)；基本解：(A),(B),(F)；基本可行解：(A),(F)6.（1）标准型为：Max（2）至少有2个变量的值取零，因为有3个基本变量、2个非基本变量，非基本变量的取值为零。（3）在这个线性规划问题中，共有10种基本解。（4）最优解X=（4，6，0，0，1）T，MaxZ=74。-68- 7．单纯形法求解下列线性规划问题（1）0011/3-1/320101/206100-1/31/32000-3/2-136（2）02.51-0.254.7510.500.252.250-10-198．（1）a=7，b=-6，c=0，d=1，e=0，f=1/3，g=0；（2）表中给出最优解X*＝（007050）T。9．用大M法求解结果：（1）无可行解；（2）最优解X*=（44）T，最优值为28；（3）有无界解；（4）最优解为X*=（4，0，0）T，最优值为8。习题二1.（1）原问题的对偶问题为-68- s.t.（2）原问题的对偶问题为s.t.（3）原问题的对偶问题为s.t.2．由教材表3-4与表3-5的对应关系，如图可知B=（x4，x1，x2）列，B=（x4，x5，x6）列,故B=，B-1=因最终单纯形表中非基变量的系数为BN，所以，(x1*，x2*，x3*，b*)=B（N，b）=B-1(x1，x2，x3，b)==-68- 检验数=c-CP=(0,0,-3/2,0,-3/2,-1/2)3．原问题的对偶问题为s.t.由松弛互补性质可知，在最优性条件下，=0和=0，这里（i=1,2），（j=1,2,3,4,5）分别为原问题的剩余变量及对偶问题的松弛变量。由=4/5>0,=3/5>0,利用互补松弛定理==0，得到==0,即原问题的两个约束条件为等式约束条件。将=4/5,=3/5代入对偶问题的约束条件，得到（2）式y1*-y2*=1/5<3，（3）式2y1*+3y2*=17/5<5，（4）式y1*+y2*=7/5<2，（2）、（3）、（4）三式为严格不等式，所以>0，>0，>0，再利用一次互补松弛定理===0，得到===0。根据上述结果，原约束可以转化成二元一次线性方程组：解方程组得x1*=x5*=1综上所得，原问题的最优解为X=(1,0,0,0,1)，相应的目标函数最优值为==5。4.（1）将原问题化为标准形式为-68- s.t.建立这个问题的单纯形表并运算，具体见下表：-2-3-400bxjXBx1x2x3x4x50x4-1-2-110-30x5[-2]1-301-4-2-3-400w=014/30x40[-5/2]1/21-1/2-1-2x11-1/23/20-1/220-4-10-1w=-48/5-22-3x201-1/5-2/51/52/5-2x1107/5-1/5-2/511/500-9/5-8/5-1/5w*=-28/5表中b列数字全为非负，检验数全为非正，故问题的最优解为-68- =(11/5,2/5,0,0,0)若对应两个约束条件的对偶变量分别为y1和y2，则对偶问题的最优解为=(8/5,1/5,0,0,9/5)（2）将原问题化为标准形式为：s.t.建立这个问题的单纯形表并计算，过程见下表:-3-2-1000bxjXBx1x2x3x4x5x60x411110060x5[-1]01010-40x60-11001-3-3-2-1000W=030x40121102-3x110-10-1040x60[-1]1001-300-40-30W=-12-68- 00x4003111-1-3x110-10-104-2x201-100-1300-60-3-2W=-18由上述表格可以看出基变量x4行系数全为正，而其限定向量b却存在负值，在x0,i=的情况下不可能成立，故此题无解。原问题的对偶规划如下：s.t.显然，（0，0，0）为该对偶问题的可行解，则对偶问题为无界解。5.（1）线性规划原问题的最优解X*=（0，0，8，0，6）T最优值==（12，0）=96最优基B=逆B-1=（2）原问题的对偶问题为：-68- s.t.对偶问题的最优解Y*=（4，0，10，2，0）。（3）若最优解不变，c3变化Δc3，则变化后的最终单纯形表为：6212+Δc300bxjXBx1x2x3x4x512+Δc3x34/31/311/3080x5-250-116-10-4/3Δc3-2-1/3Δc30-4-1/3Δc30=由上表可以看出，在最优解不变的情况下，需满足下列不等式：得到因此c3=12+6。（4）由最终单纯形表可知=，而=，易见b+=+=。因最优基变量不变,知6+,故-6,而b2*=b2+=30+24，因此，当b2*24时最优基变量不变。（5）在原线性规划的约束条件上，增加下面的约束条件x1+2x2+2x3,原问题变为：-68- s.t.原最终单纯形表新增一行和一列，见表。此时原最终单纯形表中的x3和x5的系数不再是单位向量了，所以继续进行行变换，保持原基变量不变。在行变换后得到的新单纯形表中，检验数均小于等于零，但右端项出现负值，所以可用对偶单纯形法继续运算。CB6212000bxjXBx1x2x3x4x5x612x34/31/311/30080x5-250-11060x612200112-10-20-400Z=9612x34/31/311/30080x5-250-11060x6[-5/3]4/30-2/301-4-10-20-400Z=9666012x307/51-1/504/524/50x5017/50-1/51-6/554/56x11-4/502/50-3/512/50-10000-6Z*=72-68- 最后得最优解X*=(12/5,0,24/5,0,54/5,0)T，最优值Z*=72。6.（1）设y的系数增加了y，变化后的最优单纯形表为：CB42+3000bxjXBxyzs1s2s32+y0103/4-1/20254x102-1/41/20250s300-40-112000-5-1/2-3/4-1+1/20Z*=150+25因为保持最优生产计划不改变，所以，需满足下列不等式：，故2y，所以，y的系数的变化范围为y+2=（4/3，4）。若产品B单位利润由2变为5，超出了最优解的范围，因此，会影响最优生产计划。将5代入到最优单纯形表，并继续迭代，得：CB453000bxjXBxyzs1s2s35y0103/4-1/20254x102-1/4[1/2]025500s300-40-112000-5-11/41/20Z=2255y1121/200500s2204-1/210500s3200-1/20170-10-7-5/200Z*=250-68- 此时的最优生产计划为（x,y,z）=(0,50,0)（2）由表最后三列可知B-1=，若不影响最优生产计划，则需使+，即-100/3100。因为当原材料1的供应从100单位降低至50个单位，超过了的范围，故会影响最优生产计划。当b1=50时，可算出此时原最优单纯形表中b1*=+=因为此时原问题变为非可行解，而其对偶问题为可行解,对此时的对偶单纯形表继续进行迭代：CB423000bxjXBxyzs1s2s32y0103/4[-1/2]0-25/24x102-1/41/2075/20s300-40-112000-5-1/2-10Z=125020s20-20-3/210254x1121/200250s30-2-4-3/201450-2-5-200Z*=100-68- 此时最优生产计划为（x,y,z）=(25,0,0).（3）当药品C的单位利润消耗原材料1，2，3的工时由原来的4，6，2依次变为2，2，1时，变化后药品C在最优单纯形表中系数变为c3*=B-1c3==此时的单纯形表为：CBcj423000bxjXBxyzs1s2s32y01[1/2]3/4-1/2025→504x101/2-1/41/2025500s300-10-1120000↑-1/2-10Z*=1503z0213/2-10504x1-10-11000s30203/2-2170000-1/2-10Z*=150有非基变量检验数为0，此时最优生产计划为多重最优解，从上表中可得到两个解(x,y,z)=(25,25,0)或(0,0,50)，最优值Z*=150。习题三1．a.表1.1最优运输方案销地产地B1B2B3B4A1A2A3005510001501000-68- 总运费335。表1.2Vogel近似最优运输方案销地产地B1B2B3B4A1A2A3005150001500100总运费375。b.表2.1最优运输方案销地产地B1B2B3B4A1A2A3A44020140000240110041总运费633。表2.2Vogel近似最优运输方案销地产地B1B2B3B4A1A2A3A4402014000024470005总运费633。c.表3.1最优运输方案销地产地B1B2B3B4A1A2A3091001071300015总运费203。-68- 表3.2Vogel近似最优运输方案销地产地B1B2B3B4A1A2A3091001071300015总运费203。2．a.表4最佳决策方案销地产地甲乙丙丁药厂1药厂2药厂3030002001000100020000300总运费14200元。b.表5最佳决策方案销地产地甲乙丙丁药厂1药厂2药厂30300003000100020000300总运费13800。c.表6最佳决策方案销地产地甲乙丙丁药厂1药厂2药厂30300030010000020000300总运费13600。3．a.令c22=k，则对应的检验数为：-68- 运输表销地产地B1B2B3B4A11012011（k-3）5（k+10）10A212792001015（10-k）A321416185（24-k）（17）（18-k）使表中检验数全部大于等于零时有3≤k≤10。b.令c24=l，则对应的检验数为：l-7，即当c24=7时该检验数为零，问题有无穷多最优运输方案。4．最优运输方案销地产地ⅠⅡⅢⅣ甲乙丙0300015000002505010050总利润185。5．设xij表示第i季度生产第j季度交货的发动机数量，则最优方案为：最优生产方案销地产地1234123410000105000025050510总成本773。-68- 6．优生产计划为第一月正常生产10台，加班生产0台；第二月正常生产15台，加班生产0台；第三月正常生产25台，加班生产5台；第四月正常生产5台，加班生产10台；总成本389.75百万元。习题四1．（1）错，（2）对，（3）错，（4）对。2．（1）x1=4，x2=1，MaxZ=14；（2）x1=2，x2=2，或x1=3，x2=1，MaxZ=4;（3）x1=2，x2=1，MinZ=13。3．（1）(x1,x2,x3)=(1,0,1)，MaxZ=8；（2）(x1,x2,x3,x4,x5)=(1,0,1,0,0)，MinZ=12。4．设。数学模型为：5．设，数学模型-68- 最优解(0,1,0,1,0,0)，即只在区2和区4设点便可。6．(1)指派矩阵为：，最优值为：47；(2)指派矩阵为：，最优值为：41。7．派小强、小明、小林分别参加英语、基础医学、数学竞赛，可使他们的总分最高，其最高值为85+85+97＝267分。8．最优指派：序号为一、二、三、六的检验师分别检验项目三、二、一、四可使总时间最短，为8小时。习题五1．-68- 2．平均时间：t(1,2)=18t(1,3)=25t(1,4)=20t(2,5)=15t(3,6)=10t(4,6)=20t(5,7)=15t(4,7)=11t(6,7)=25最早开始时间：TES(1,2)=0TES(1,4)=0TES(1,3)=0TES(2,5)=18TES(5,7)=33TES(4,7)=20TES(4,6)=20TES(3,6)=25TES(6,7)=40最早结束时间：TEF(1,2)=18TEF(1,4)=20TEF(1,3)=25TEF(2,5)=33TEF(5,7)=48TEF(4,7)=31TEF(4,6)=40TEF(3,6)=35TEF(6,7)=65最迟开始时间：TLS(5,7)=50TLS(2,5)=35TLS(6,7)=40TLS(3,6)=30TLS(4,7)=54TLS(4,6)=20TLS(1,2)=17TLS(1,3)=5TLS(1,4)=0最迟结束时间：TLF(1,2)=35TLF(1,4)=20TLF(1,3)=30TLF(2,5)=50TLF(5,7)=65TLF(4,7)=65TLF(4,6)=40TLF(3,6)=40TLF(6,7)=65各工序的总时差：R(1,2)=17R(1,4)=0R(1,3)=5R(2,5)=17R(5,7)=17R(4,7)=34R(4,6)=0R(3,6)=5R(6,7)=03．-68- 天习题六1．①按悲观准则：最优方案是：协作生产。②按乐观准则：-68- 最优方案是：引进生产线。③按等可能准则：最优方案是：引进生产线。④按后悔值准则：后悔值矩阵如下表：方案需求状况需求高需求中等需求低改造生产线602520引进生产线0035协作生产120500三种方案下的最大后悔值：改造生产线：{60，25，20}=60引进生产线：{0，0，35}=35协作生产：{120，50，0}=120最优方案是：引进生产线。2．因为未来市场需求低的可能性好像偏大，因此适合采用悲观准则决策。-68- 按此准则，最优方案为协作生产。3．按期望值准则：方案最优。4．合同A的期望利润为：合同B的期望利润为：该决策者希望期望利润最大，则他应该选择合同A，期望利润是37000元。5．出版这种杂志的期望利润为：（元）因此，不应该出版这种杂志。6．两种方案下的期望收益为：（1）根据甲、乙两个公司的资产看，两个公司的决策者会采取不同的选择：甲公司若选择了方案，则可能要承担破产的风险，因而从效用决策的角度来看，甲公司最大可能会选方案；-68- 乙公司若选择了方案，则可能承担的损失仅为总资产的1%，但却可能获得方案的4.55倍的收益，因而从效用决策的角度来看，乙公司最大可能会选方案。（2）将三个点：（-10，0）、（2，0.5）、（20，1）代入对数函数：解得：，，因此，效用函数为：从而得到效用值表如下：投资方案自然状态=0.75=0.25100.530.50按期望效用准则：因此，方案最优。（3）按期望值准则，最优方案是。敏感性分析：因为：＋=1，故有：若维持方案为最优，则应有：-68- 由此解出：即：当时，方案始终是最优方案。7．根据表7绘制决策树如图1。图1中的结果是收益（万元）。根据决策树，计算出各种方案的期望收益：（万元）（万元）因此，先建小医院，3年后根据利用条件再扩建。图1题7的决策树8．—同意研制—不同意研制绘制决策树如图2。图2中结果是该病的病例数。根据决策树，计算出：①采用方案若疾病暴发：则期望病例数：0.4×50＋0.6×500=320(人)，总费用：320×300＋10000=106000(元)-68- 若疾病不暴发：期望病例数：0.4×3＋0.6×30=19.2(人)总费用：19.2×300＋10000=15760(元)则方案的期望费用：（元）采用方案若疾病暴发：病例数：500(人)总费用：500×300=150000(元)若疾病不暴发病例数：30(人)总费用：30×300=9000(元)则方案的期望费用：（元）从费用的角度，卫生局应该批准该疫苗的研制。图2题8的决策树-68- 习题七1．移动平均法存在两个主要的限制：其一，计算移动平均必须具备N个过去观察值。当需要预测大量的数值时，就需要对大样本数据的占有。其二，N个过去观测值每个权数均相等，而早于t-N+1期的观察值的权数却等于零。但在实际预测中，最新的观察值应包含了比早期观察值更多的信息。基于此，最新观察值应比早期的观察值赋予更大的权数。指数平滑法正是在这一点上是对移动平均法的修正。在具体预测中，指数平滑法只需要两个数据值。因此，预测只需要较少的数据量与较小的计算量。2．略3．某医院的经营收入一次移动平均法预测表:月份销售额一次移动平均值（万元）1430—2380—3330—4410—5440387．563903907380392．584004059450402．51042040511390412．512—4154．一次指数平滑法预测：-68- 5．解：p为正规概率矩阵。因此，存在唯一的固定概率向量，解方程组推出：。得=，则经过长期趋势可见，患者在三个社区卫生服务机构就医的转移达到均衡状态，其中有50%的患者选择在甲社区卫生服务机构就医。故而，该医院应选择在甲投资。习题八1．（1）L=4人Lq=3.2人W=60(min)Wq=48(min)（2）P0=20%2．P1+P2+…+Pn+Pn+1≥0.90n≥63．（1）P0=0.12185（2）P4=0.298（3）L=2.44人Lq=1.56人W=3.47(h)Wq=2.22(h)4．（1）P0=0.3604（2）L=1.162人Lq=0.523人W=0.606(h)Wq=0.272(h)（3）P0=0.2649L=1.590人Lq=0.854人W=0.721(h)Wq=0.387(h)（4）m=45．（1）P（n≥3）=0.70225-68- （2）L=6.01份Lq=3.51份W=0.401(h)Wq=0.234(h)（3）L=5份Lq=4.17份W=1(h)Wq=0.833(h)6．（1）P0=0.136（2）P6=0.012（3）L=1.98条7．P0=0.1L=4.95份Lq=4.05份W=0.275(h)Wq=0.225(h)8．P0=0.5L=1.75人Lq=1.25人W=0.175(h)Wq=0.125(h)9．（1）Wq1=4.28(min)Wq2=38.57(min)（2）Lq1=0.018人Lq2=0.482人10．C=4习题九1．D=2000,T=12,,=20（1）最佳经济批量(盒)最小费用（元）最佳订购间隔期（月）（2）批量变化，总费用增长。因为，258-129=129，387-258=129所以总费用增长（元）-68- （3）由公式得，解出=0.039（=-0.041舍去）。批量变化(盒)即，当最佳经济批量增加或减少10盒时，就能使最小费用增长25%。（4）(盒)(盒)2．D=2000,T=12,,=20，得到最佳经济批量：(盒)最佳间隔期（月）最小总费用3．通过比较不允许缺货和允许缺货的最小总费用公式，说明为什么允许缺货的总费用比不允许缺货的总费用低，最多只能相等。不允许缺货最小总费用公式允许缺货最小总费用公式-68- 比较两式可见，允许缺货比不允许缺货公式多一项，而，当时，。所以，允许缺货的总费用比不允许缺货的总费用低（），最多只能相等（时）。4．临界值又即因此，应订货120支。5．（1）服务水平为95%时，-68- 定购点：（盒）定购量：（盒）（2）服务水平为99%时，习题十1．A的赢得矩阵为：BA-101-12-1-201011-2-122．化简后的对策赢得矩阵为：3．用(ai，bj)与v分别表示双方最优纯策略与对策值（1）(a2，b3)，v=3（2）(a1，b1)，v=04．设为A方最优策略，为B方最优策略，v为对策值（1）（2）先化简为,再求得5．用表示A的混合策略,用表示B的混合策略,表示B的至少赢得,令,,写出求解对策问题的线性规划模型:-68- 利用单纯形法解得:，；，，从而得，，对策值。6．（1）,纯策略纳什均衡为(a2，b2);（2）,纯策略纳什均衡为(a1，b3),(a2，b1).7．设A采用混合策略，B采用混合策略，则A的赢得期望：B的赢得期望：利用一阶条件：，，得与，对应的混合策略纳什均衡:。应用划线法易得该对策的两个纯策略纳什均衡(a1，b1),(a2，b2).8．略。-68- 习题十一1．略2．手术原因和抢救原因是关键原因。3．图：CL＝＝4.98；UCL＝5.05；LCL＝4.91。R图：CL＝＝0.0395；UCL＝0.129；LCL＝（不考虑）。4．略习题十二1．-68- 常用的方法有综合指数法、层次分析法、TOPSIS法、模糊评价法。综合指数法计算比较简单但没有考虑各指标对总评价结果的贡献大小的不同；层次分析法较综合指数法计算比较复杂，但考虑了各指标对总评价结果的贡献大小的不同，却可以分层次比较；TOPSIS法比较容易理解，计算简便，正理想解与负理想解的制定是本法的关键，理想解制定的不同，结果可能出现相反的情况；模糊评价法在处理评价对象不能明确和清晰的描述时，它优于其它各法，但此法的评判矩阵与权重系数矩阵的确定是获得正确结论的关键，当评价集中最大的两个分量较接近时，难于得到结论。2．模糊评判矩阵R考评指标的权重矩阵是结果评定：最大分量所对应的评价等级集合中的等级，因此评价结果为中等。3．（1）建立阶梯层次结构，形成目标树，如下图：医院临床科室综合评价体系医疗0.60科研0.20管理0.200.4290.4290.1420.7500.2500.500.50治愈率诊断符合率床位周转率科研成果论文专著出勤率服务满意度（2）总次矩阵：第一层目标判断矩阵医疗科研管理权重医疗1330.600科研1/3110.200管理1/3110.200-68- 本层3.00、3.00、3.00，CI=0，CR=0<0.10医疗目标判断矩阵治愈率诊断符合率床位周转率权重治愈率1130.429诊断符合率1130.429床位周转率1/31/310.142本层3.00、3.00、3.00，CI=0，CR=0<0.10科研目标判断矩阵科研成果论文专著权重科研成果130.750论文专著1/310.250管理目标判断矩阵出勤率服务满意度权重出勤率110.500服务满意度110.500（3）计算组合权重：治愈率（%）=0.60´0.429=0.257诊断符合率（%）=0.60´0.429=0.257床位周转率（%）=0.60´0.142=0.085科研成果（项）=0.20´0.750=0.150论文专著（数）=0.20´0.250=0.050服务满意度（%）=0.20´0.500=0.100出勤率（%）=0.20´0.500=0.100（4）计算部分科室的综合指数：-68- 评价指标临床科室权重标准值12345治愈率（%）83.690.189.496.098.00.25791.42诊断符合率（%）90.385.189.988.186.00.25787.88床位周转率（%）92.692.795.894.693.10.08593.76科研成果（项）52.040.038.054.048.00.15046.40论文专著（数）40.334.030.341.438.20.05036.84服务满意度（%）95.092.094.795.690.70.10093.60出勤率（%）93.692.291.796.291.20.10092.98综合指数1.0080.9590.9651.0501.013注：标准值为该医院各科室的平均值根据综合指数的大小，将各科排序，由好到劣的顺次是：科室4>科室5>科室1>科室3>科室2习题十三1．根据随机数的不同，可以有不同的模拟结果。下面是一个20次的模拟结果。表20次模拟结果周号机器正常次数故障概率（％）1200.002180.103120.40460.70560.70601.00701.00801.00901.00100　1.002．根据随机数的不同，可以有不同的模拟结果。下面是一个模拟未来10天门诊量的结果。-68- 表某医院神经科未来10天门诊量模拟天数ri门诊量（人次）10.51996020.10284030.76537040.70617050.94118060.73347070.31735080.53546090.060940100.286250合计5903．一辆救护车时，利用率为100％，如下表：表20次模拟救护车呼叫时间间隔和救护车服务时间　　呼叫救护车　　救护车服务时间1辆救护车病人等待时间模拟r1间隔时间达到时刻　r2服务起始时刻服务结束时刻10.1912000.617120020020.490110100.96624020601030.923815250.58881560753540.163635600.0070575801550.52015650.694720801001560.237515800.132551001052070.241510900.162451051101580.6092101000.3681101101201090.1245201200.5173151201350100.835051250.94523513517010110.1898301550.97924017021015120.725851600.87933021024050130.0537251850.0784524024555140.000051900.28821024525555150.159451950.90763525529060160.253352000.91673529032590170.0067102100.891530325355115180.746052150.641220355375140190.8448252400.831625375400135200.6802302700.488515400415130二辆救护车时，救护车的利用率为53.76%，见下表。-68- 表30次模拟救护车呼叫时间间隔和2辆救护车服务时间　　呼叫救护车　第1辆救护车　第2辆救护车　模拟r1间隔时间达到时刻r2服务时间服务起始时刻服务结束时刻r3服务时间服务起始时刻服务结束时刻病人等待时间10.1912000.6171200200.942635020.490110100.9662400.5086151025030.923815250.58881525400.583915040.163635600.0070560650.239910050.52015650.69472065850.221210060.237515800.132550.70002080100070.241510900.1624590950.579615080.6092101000.3681101001100.592215090.1245201200.5173151201350.137850100.835051250.9452350.9611401251650110.1898301550.9792401551950.3883100120.725851600.8793300.9515351652005130.0537251850.078451952000.97884010140.000051900.2882102002100.1982510150.159451950.9076350.134252002055160.253352000.9167350.8008252052305170.0067102100.8915302102400.8374250180.746052150.6412200.28991023024015190.8448252400.8316252402650.2676100200.6802302700.4885152702850.9329350210.193352750.5973150.047252752800220.8967303050.186753053100.9477350230.3020103150.8480303153450.108450240.7884253400.191550.8856303403700250.3253103500.6558203503700.7035200260.8036253750.4412103753850.9302350270.3389103850.4450103853950.6717200280.8086254100.087254104150.3793100290.9422354450.080654454500.108650300.131854500.4616154504650.8180250-68-'