《控制工程导论》(周雪琴 张洪才 著)习题答案-阳光大学生网.pdf 74页

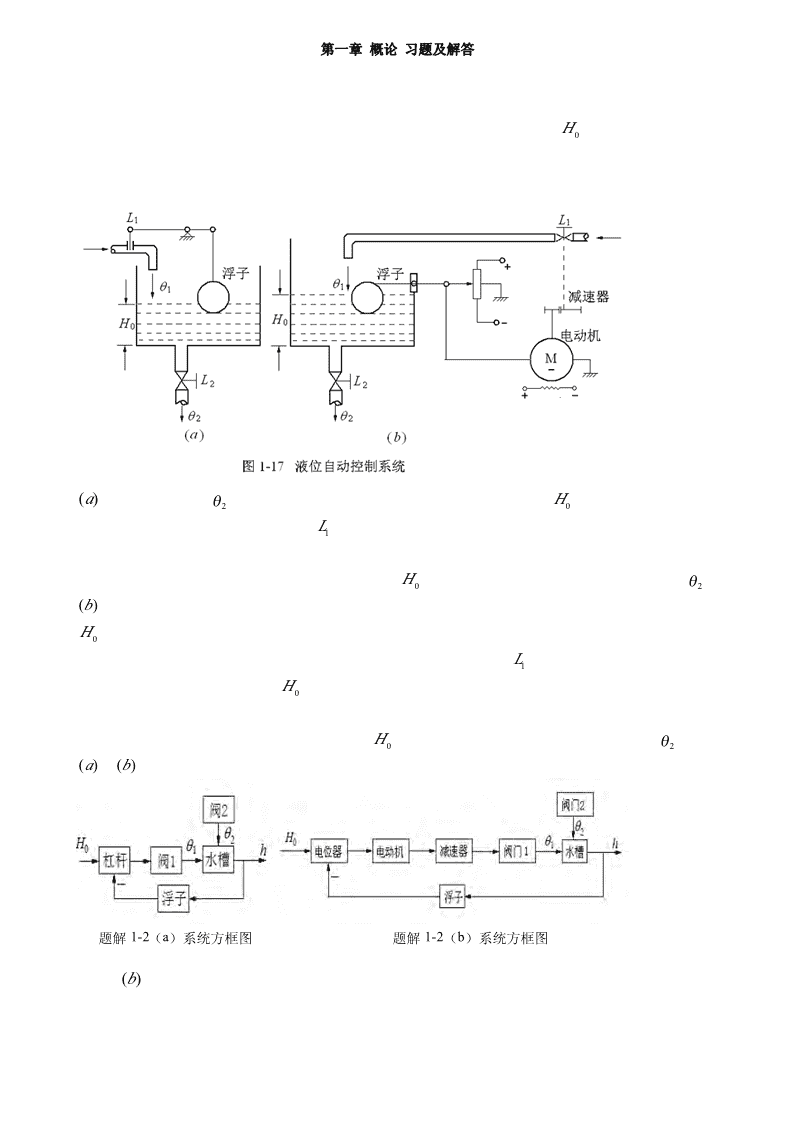
'欢迎光临阳光大学生网,提供最全面的大学生课后习题答案和复习试题免费下载，http://www.sundxs.com/阳光大学生网我们希望呵护您的眼睛，关注您的成长，给您一片绿色的环境，欢迎加入我们，一起分享大学里的学习和生活感悟，免费提供:大学生课后答案，大学考试题及答案，大学生励志书籍。 第一章概论习题及解答1-1试列举几个日常生活中的开环控制和闭环控制系统实例，并说明它们的工作原理。略1-2.图1-17是液面自动控制系统的两种原理示意图。在运行中，希望液面高度H维持不变。01．试说明各系统的工作原理。2．画出各系统的方框图，并说明被控对象、给定值、被控量和干扰信号是什么?()a工作原理：出水量θ与进水量一致，系统处于平衡状态，液位高度保持在H。当出水量大于进水量，20液位降低，浮子下沉，通过连杆使阀门L开大，使得进水量增大，液位逐渐回升；当出水量小于进水量，1液位升高，浮子上升，通过连杆使阀门1关小，液位逐渐降低。其中被控对象是水槽，给定值是液面高度希望值H。被控量是液面实际高度，干扰量是出水量θ。02()b工作原理：出水量与进水量一致系统处于平衡状态，电位器滑动头位于中间位置，液面为给定高度H。当出水量大于（小于）进水量，浮子下沉（上浮）带动电位器滑动头向上（下）移动，电位器输出0一正（负）电压，使电动机正（反）转，通过减速器开大（关小）阀门L，使进水量增大（减小），液面1高度升高（降低），当液面高度为H时，电位器滑动头处于中间位置，输出电压为零，电动机不转，系统0又处于平衡状态。其中被控对象是水槽，给定值为液面高度希望值H，被控量是液面实际高度，干扰量是出水量θ。02()a，()b系统结构图如下图1-3什么是负反馈控制?在图1-17(b)系统中是怎样实现负反馈控制的?在什么情况下反馈极性会误接为正，此时对系统工作有何影响?解：负反馈控制就是将输出量反馈到输入端与输入量进行比较产生偏差信号，利用偏差信号对系统进行题解1-2（a）系统方框图题解1-2（b）系统方框图调节，达到减小或消除偏差的目的。图1-17()b系统的输出量液面实际高度通过浮子测量反馈到输入端与输入信号（给定液面高度）进行比较，如果二者不一致就会在电位器输出一电压值——偏差信号，偏差信号带动电机转动，通过减速器使阀门1开大或关小，从而进入量改变，当输出量——液面实际高度与给定高度一致偏差信号为0，电机，减速器不动，系统又处于平衡状态。 当电位器极性接反（或将电机极反接）此时为正反馈，系统不可能把液面高度维持在给定值。1-4.若将图1-17(a)系统结构改为图1-18。试说明其工作原理。并与图1-17(a)比较有何不同?对系统工作有何影响?解：若将1-17()a系统结构图改为1-18，系统变成了正反馈，当出水量与进水量一致，液面高度为给定值H。当出水量大于进水量，液面位降低，浮子下称，通过连杆使阀门1关小，进水量越来越小，液面高0度不能保持给定高度H，同样当出水量小于进水量，浮子上浮，液位升高，使阀门1开大，进水量增大，0液位越来越高，不可能维持在给定高度H01-5某仓库大门自动控制系统的原理图如图1-19所示。试说明自动控制大门开启和关闭的工作原理并画出系统方框图解当合上开门开关时，电桥会测量出开门位置与大门实际位置间对应的偏差电压，偏差电压经放大器放大后，驱动伺服电动机带动绞盘转动，将大门向上提起。与此同时，和大门连在一起的电刷也向上移动，直到桥式测量电路达到平衡，电动机停止转动，大门达到开启位置。反之，当合上关门开关时，电动机带动绞盘使大门关闭，从而可以实现大门远距离开闭自动控制。系统方框图如图解1-2所示。题解1-5图第二章物理系统的数学模型习题及及解答2-1试建立图2-55所示各系统的动态方程，并说明这些动态方程之间有什么特点。图中电压u和位移x为输11入量，电压u2和位移x2为输出量；k、k1和k2为弹性系数；f为阻尼器的阻尼系数。 解：题解21()−a图⎧11u=idtu+⇒u&=iu+&⎪⎪1C∫21C2⎨u⎪u=iR⇒=i22⎪⎩R1u&+u=u&221RCUs()sRCs2==Us()1RCs+11s+RC题21()−b图及题解21()−b图fx&+kx=fx&221fsXs()fsk2==Xs()fsk+f1s+1k题21()−c图及题解21()−c图 1R⋅1CsUs()=Is()⋅+Us()1c1R+1CsUs()=RIs()22Us()RRCs(+1)221=Us()R+R+RRCs11221(R+Ru)+RRCu&=RRCu&+Ru12212212121R+R112u&+u=u&+u2211RRRC121Us()RRRRCs(+1)22221===Us1()1R1R1+R2+RRCs12R⋅R+12CsRCs+1R+121R+1Cs题21()−d图及题解21()−d图fx&+kx+kx=kx+fx&21222111k⎛f⎞1⎜s+1⎟xs2()fsk+1k1+k2⎝k1⎠＝=xs()fsk++kf112s+1k+k12题21()−e图及题解21()−e图 1R+Us()2CsRCs+122==Us()1(R+RCs)+11R+R+1212Cs题21()−f图及题解21()−f图⎧k2⎪fx&+kx=kx⇒x=x3232232⎨sf+k2⎪⎩kx+kx=kx+kx22121123k2(k+kx)−kx=kx1222211sf+k2(k+ksf)+kk1212x=kx211sf+k2fs+1xksf(+k)k2122==x1(k1+ksf2)+kk12k1+k2fs+1kk122-2.图2-56所示水箱中，Q和Q分别为水箱的进水流量和用水流量，被控量为实际水面高度H。试求出该12系统的动态方程。假设水箱横截面面积为C，流阻为R。1解：H=(Q−Qdt)∫12C Q2=aHa——系数，取决于管道流出侧的阻力，消去中间变量Q，可得2dHC+aH=Q1dt假定系统初始处在稳定点上，这时有：Q=Q=Q，H=H，当信号在该点附近小范围变化时，可102000以认为输出θ与输入H的关系是线性的，。即2⎧Q=Q+∆Q202⎪⎨H=H+∆H0⎪⎩Q=Q+∆Q1011∴∆H=(∆Q−∆Qdt)∫12CdQ12∆Q=∆H=∆H2dHHH=0Rθ2=θ012H0R==_________流阻dQQ20dHHH=0θ2=θ0dH∆CR+∆H=∆RQ1dtdH有时可将∆符号去掉，即CR+H=RQ1dtHs()R=Qs()CRs+112-3求图2-57信号x(t)的象函数X(s)。解：()aΘx(t)=2+(t−t)021−t0s∴X(s)=+e2ss∞−ts()bXs()=∫Xtedt()0t0∞−ts=∫tedt+∫0⋅dt0t01t0−ts=−∫tde()s0=−1⎡−tst0−t0−ts⎤teedts⎢⎣0∫0⎥⎦1⎡−ts1t0−ts⎤=−te0+de()s⎢0s∫0⎥⎣⎦⎡t0⎤1−ts1−ts=−⎢te0+e⎥0s⎢⎣s0⎥⎦ 1⎡−ts1−ts⎤=−te0+(e−1)⎢0⎥s⎣s⎦11−ts0=−(1−tse)220ss44T4T4()cΘx(t)=t−(t−)−(t−)+(t−T)222222TTTT−T4s∴1(22−Ts)X(s)=−e+e22Ts2-4.用拉氏变换求解下列微分方程（假设初始条件为零）1.Tx&(t)+x(t)=r(t)其中r(t)分别为δ(t)，1(t)和·t1(t)。2.x&&(t)+x&(t)+x(t)=δ(t)3.x&&(t)+2x&(t)+x(t)=1(t)解：1.Txt&()+xt()=rt()1Xs()=Rs()Ts+1rt()=δ(),tRs()1=11TXs()==Ts+11s+T11−tXt()=eTT1rt()1(),=tRs()=s1+−ss1T11Xs()===−sTs(+1)1s1ss(+)s+TT1−tXt()1=−eT1rt()=⋅t1(),tRs()=2s11+−ss+−ss11T1TXs()=⋅==−T12121Ts+s2sss(+)ss(+)TT111=−T(−)s2s1s+T1−tXt()=−tT(1−eT) 2-5.一齿轮系如图2-58所示。Z1、Z2、Z3和Z4分别为齿轮的齿数；J1、J2和J3分别表示传动轴上的转动惯量；θ1、θ2和θ3为各转轴的角位移；M是电动机输出转矩。试列写折算到m电机轴上的齿轮系的运动方程。MZ11解：=,MZ22MZZZ3313=⇒M=MM,=M1234MZZZ4424dθZZ121=⇒dθ=dθ21dθZZ212dθZZZZ24341=⇒dθ=dθ=⋅dθ321dθZZZZ33432⎧dθ1M−M=J⋅⎪m11dt⎪⎪dθ2⎨M−M=J⋅232dt⎪⎪dθ3⎪M=J⋅43⎩dtdθZdθZdθdθ111121M=M+J=M+J=(M+J)+Jm112132dtZdtZdtdt22ZZdθdθ1321=(M+J)+J421ZZdtdt24ZZdθdθdθ13321=(J+J)+J321ZZdtdtdt24Z12Z32dθ1Z12dθ1dθ1=J()()+J()+J321ZZdtZdtdt242Z12Z32Z12dθ1[J()()+J()+J]=M321mZZZdt2422-6系统的微分方程组如下：x1(t)=r(t)−c(t)+n1(t)x(t)=Kx(t)211x(t)=x(t)−x(t)325dx4T=x(t)3dtx(t)=x(t)−Kn(t)54222dcdcKx(t)=+052dtdt C(s)C(s)C(s)其中K、K、K、T均为大于零的常数。试建立系统的结构图，并求传递函数、及012R(s)N(s)N(s)12解：xt()=rt()−ct()+nt()Xs()=Rs()−Cs()+Ns()1111x=KxXs()=KXs()211211x=x−xXs()=Xs()−Xs()325325dx14T=x⇒X=X343dtTsx=x−KnX=X−KNs()542254222dcdcK0Kx=+Cs()=X05225dtdts+sCs()求令Ns()=0,Ns()=012Rs()消去中间变量，得Cs()KK01=Rs()ss(+1)(Ts+1)+KK01Cs()求令Rs()=0,Ns()=02Ns()1消去中间变量得Cs()KK01=Ns()ss(+1)(Ts+1)+KK101Cs()求令Rs()=0,Ns()=02Ns()2消去中间变量得Cs()−TKKs01=Ns()ss(+1)(Ts+1)+KK201C(s)2-7.简化图2-59所示系统的结构图，并求系统传递函数。R(s) 解： C(s)2-8.试用梅逊公式列写图2-60所示系统的传递函数。R(s)解：()aL=−GGH,L=−GGH12332344L=−GGGH,L=GGGGH31232412341∆=+1GGH+GGH+GGGH−GGGGH233344123212341P=GGGH,∆=1112341Cs()GGGH1234=Rs()1+GGH+GGH+GGGH−GGGGH233344123212341 ()bL=−GH,L=−GH111232L3=−GGGHHL12312,4=GGHH1312∆=+1GH+GH+GGGHH+GGHH1132123121312P=GGG,∆=111231P=GG,∆=+1GH243211Cs()GGG+GG(1+GH)1234311=Rs()1+GH+GH+GGGHH+GGHH11321231213122-9.C(s)C(s)C(s)C(s)1212求出图2-61所示系统的传递函数、、、。R(s)R(s)R(s)R(s)1122解：()a∆=−1GGGG1234Cs()G11=Rs()1−GGGG11234Cs()−GGG2123=Rs()1−GGGG11234Cs()−GGG1134=Rs()1−GGGG21234Cs()G23=Rs()1−GGGG1234()b∆=−1GG+G+GGGHH−GGG12414512124Cs()GGG(1+G)11234=Rs()∆1Cs()GGGGH214562=Rs()∆1 Cs()−GGGGGH1123451=Rs()∆2Cs()GGG(1−GG)245612=Rs()∆22-10.已知系统结构图2-62所示，图中N(s)为扰动作用，R(s)为输入。C(s)C(s)1.求传递函数和。R(s)N(s)C(s)2.若要消除干扰对输出的影响（即=0），问G(s)=？0N(s)KKK123解：∆=+1sTs(+1)KKK123Cs()sTs(+1)KKK123①==RsKKKTs2sKKK()123++1231+sTs(+1)KKKKKG341230−+Cs()Ts+1sTs(+1)−KKs+KKKG341230==NsKKKTs2sKKK()123++1231+sTs(+1)Cs()②=0Ns()−KKs+KKKG=0341230K4G=s0KK122-11.若某系统在阶跃输入作用r(t)=1(t)时，系统在零初始条件下的输出响应为−2t−tc(t)=1−2e+e试求系统传递函数和脉冲响应。 1解单位阶跃输入时，有R(s)=，依题意s1213s+21C(s)=−+=⋅ss+2s+1(s+1)(s+2)sC(s)3s+2∴G(s)==R(s)(s+1)(s+2)−1[]−1⎡−14⎤−2t−tk(t)=LG(s)=L+=4e−e⎢⎥⎣s+1s+2⎦2-12.已知系统的传递函数C(s)2=2R(s)s+3s+2且初始条件为c)0(=−1，c&)0(=0。试求阶跃响应rt)(=t)(1作用时，系统的输出响应ct)(。解系统的微分方程为2dc(t)dc(t)+3+2c(t)=2r(t)（1）2dtdt考虑初始条件，对式（1）进行拉氏变换，得22sC(s)+s+3sC(s)+3+2C(s)=（2）s2s+3s−2142C(s)=−=−+2s(s+3s+2)ss+1s+2−t−2t∴c(t)=1−4e+2e第三章时域分析法习题及解答13-1.假设温度计可用传递函数描述其特性，现在用温度计测量盛在容器内的水温。发现需要1minTs+1时间才能指示出实际水温的98%的数值，试问该温度计指示出实际水温从10%变化到90%所需的时间是多少?解：4T=1min,=0.25minT1−t1ht()=1-eT=0.1,=t−Tln0.9111−t2ht()=0.9=1-eT，t=−Tln0.1220.9t=t−t=Tln=2.2T=0.55minr210.13-2.系统在静止平衡状态下，加入输入信号r(t)=1(t)+t，测得响应为−10tC(t)=(t+9.0)−9.0e试求系统的传递函数。 10.90.910(s+1)解：Cs()=+−=22sss+10s(s+10)11s+1R(s)=+=22sssCs()10φ()s==Rs()s+103-3.某惯性环节在单位阶跃作用下各时刻的输出值如下表所示。试求环节的传递函数。t01234567∞h()t01.612.973.724.384.815.105.366.00K解：设φ()s=Ts+1K11Cs()=φ()sRs⋅()==K(−)sTs(+1)s1s+T1−tht()=K−KeTh()∞=K=61−161.61−ht()=−66eT=1.61,−=ln=−0.312T66∴T=3.2()φs=3.2s+13-4.已知系统结构图如图3-49所示。试分析参数对输出阶跃响应的影响。aKTs+K解：φ()s=1=Kas(T+Kas)+11+Ts+11KCs()=φ()sRs⋅()=⋅s(T+Kas)+111T+aK=K⋅⋅s1s+T+aK11=(K−)s1s+T+aK 1−th(t)=(1-eKTaK+)当a>0时，系统响应速度变慢；T−ξ>0.707，ω≥2n2.5.0>ξ>0，4≥ω≥2n3..0707>ξ>5.0，ω≤2n解：①0.707<<1,ξω≥2n题解3-5（1）②0<ξ≤0.5,2≤ω≤4n题解3-5（2）③0.5≤ξ≤0.707,ω≤2n3-6.已知某前向通路的传递函数(如图3-50所示)10G(s)=2.0s+1今欲采用负反馈的办法将阶跃响应的调节时间t减小为原来的1.0倍，并保证总放大系数不变。试选择题解3-5(3)sKH和K0的值。解：10K0KGs()10K110+K00Hφ()s===1+KGs()0.2s++110K0.2HHs+1110+KH ⎧K=K=10=10K0⎪φ110+K⎪H⎨0.2⎪T=0.20.10.02×==φ⎪⎩110+KH解得：K=0.9K=10H03-7.设一单位反馈控制系统的开环传递函数为KG(s)=s(1.0s+1)−1−1试分别求出当K=10s和K=20s时系统的阻尼比ξ，无阻尼自然频率ω，单位阶跃响应的超调量nσ%及峰值时间t，并讨论K的大小对系统性能指标的影响。pGs()K10K解：φ()s===221+Gs()0.1s++sKs+10s+10K100K=10,(s)=φ2s+10s+1002⎧ωn=10⎧⎪ω=100⎪n⎨⇒⎨1⎪⎩2ξω=10⎪ξ=n⎩2−ξπ1−ξ2σ%=e×100%16.3%=πt==0.362sp2ω1−ξn200K=20(s)=，φ2s+10s+2002⎧⎪ω=200⎧ω=14.14nn⎨⇒⎨⎪⎩2ξω=10⎩ξ=0.353n−ξπ1−ξ2σ%=e×100%=30%πt==0.237sp2ω1−ξnK增大使σ%,↑t↓，但不影响调节时间。p3-8.设二阶控制系统的单位阶跃响应曲线如图3-51所示。如果该系统属于单位反馈控制系统，试确定其开环传递函数。2ωn解：φ()s=22s+2ξωs+ωnn −ξπ⎧21−ξ⎪σ%=e×100%=30%ξ=0.357⎪⎧⎨π⇒⎨==0.1⎩ω=33.63⎪tpn2⎪⎩ω1−ξn1131φ()s1131φ()s=()Gs==2s+24s+11311−φ()sss(+24)3-9.设系统闭环传递函数C(s)1Φ(s)==22R(s)Ts+2ξTs+1试求1．ξ=2.0；T=.008s；ξ=4.0；T=.008s；ξ=0.8；T=.008s时单位阶跃响应的超调量σ%、调节时间t及峰值时间t。sp2．ξ=4.0；T=.004s和ξ=4.0；T=.016s时单位阶跃响应的超调量σ%、调节时间t和s峰值时间t。p3．根据计算结果，讨论参数、ξT对阶跃响应的影响。122ωTn解：φ()s==2ξ122ξωω22s+s+s+s+nn2TT−ξπ1−ξ2σ%=e×100%π3.5t=t=psω1−ξ2ξωnn1.T=0.08ξ0.20.40.8σ%52%25%0.5%t0.260.27s0.42sspt1.2s0.6s0.38ss2.ξ=0.4T0.040.080.16σ%25%25%25%t0.140.270.55ssspt0.30.61.2ssss3.ξ,T改变使闭环极点位置改变，从而系统动态性能发生变化。T不变,ξ↑,%,σ↓t↑,t↓,ξ不变,T↑,%σ不变t↑,t↑。psps 3-10.已知图3-52(a)所示系统的单位阶跃响应曲线图3-52(b)，试确定K1、K2和的数值。a解:由系统阶跃响应曲线有⎧h(∞)=3⎪⎨tp=1.0⎪⎩σoo=(4−3)3=333.oo系统闭环传递函数为2K1K2K2ωnΦ(s)==(1)222s+as+Ks+2ξωs+ω1nn⎧πt==1.0⎪p⎧ξ=.0332由⎨1−ξωn联立求解得⎨⎪−ξπ1−ξ2⎩ωn=33.28⎩σoo=e=333.oo2⎧K=ω=11081n由式（1）⎨⎩a=2ξωn=221K1K2另外h(∞)=limsΦ(s)⋅=lim=K=322s→0ss→0s+as+K13-11.测得二阶系统图3-53(a)的阶跃响应曲线如图3-53(b)所示。试判断每种情况下系统内、外两个反馈的极性(其中“0”为开路)，并说明其理由。K1Ks2解：Gs()=⋅sK11msKKK211⋅1msssKK12φ()s==Ks2KsKK1m1m12Ks21m⋅sK11ms(1)单位阶跃响应为等幅振荡，故闭环极点为纯虚根，故内回路断开，外回路为负反馈；(2)单位阶跃响应为发散，内回路为正反馈，外回路为负反馈；(3)单位阶跃响应为近似斜坡信号，故外回路断开，内回路为负反馈；(4)单位阶跃响应为加速度信号，闭环极点为原点上2个极点，故内回路开路，外回路也开路。 3-12.试用代数判据确定具有下列特征方程的系统稳定性。321．s+20s+9s+100=0322．s+20s+9s+200=04323．3s+10s+5s+s+2=032解：1.s+20s+9s+100=03Rouths.19220100s1209100×−s=40200100sRouth表第一列系数均大于0，故系统稳定。322.s+20s+9s+200=03Rouths.19220200s1209200×−s=10−200200sRouth表第一列系数有小于0的，故系统不稳定。4323.3s+10s+5s++=s20 4Rouths.3523s10102105-3×47s==4.72101014.71102×−×s=3.26-4.702sRouth表第一列系数有小于0的，故系统不稳定。3-13.设单位反馈系统的开环传递函数分别为∗∗K(s+1)K1．G(s)=；2．G(s)=s(s−1)(s+5)s(s−1)(s+5)1∗试确定使闭环系统稳定的开环增益K的范围(传递函数G(s)中的称为不稳定的惯性环节。K为根轨s−1迹增益)。∗Ks(+1)解：1.(s)=Gss(−1)(s+5)∗Ds()=ss(−1)(s+5)+Ks(+1)32∗∗=s+4s+−+(5KsK)+3∗Rouths.1K−52∗4sK∗∗14×K−20−Ks>040∗sK>0∗∗20K4由Routh表第一列系数>0得K>,K=故当K>时系统稳定。353∗K2.(s)=Gss(−1)(s+5)∗32∗Ds()=ss(−1)(s+5)+K=s+4s−5s+K不满足必要条件，系统不稳定。3-14.试确定图3-54所示系统的稳定性. 10s+1ss(+1)10(s+1)解：().()aGs=⋅=s2s×10ss2(+21)1+ss(+1)232Ds()=(ss+21)10(+s+1)=s+21s+10s+13Rouths.1102211s12101−s>02101s系统稳定。10ss(+2)10().()bφs==10(10s+1)s2+102s+101+ss(+2)2Ds()=s+102s+10满足必要条件，故系统稳定。3-15.已知单位反馈系统的开环传递函数为KG(s)=2s(.001s+2.0ξs+1)试求系统稳定时，参数K和ξ的取值关系。2解：Ds()=s(0.01s+0.2ξs+1)+k=032Ds()=s+20ξs+100s+100k=03Rouths:1100220sξ>0100k12000ξ−100ks>020ξ0100sk>0⎧ξ>0⎪k由Routh表第一列系数大于0得⎨k>0，即<20(ξ>,0k>0)ξ⎪⎩k<20ξ 3-16.设系统结构图如图3-55所示，已知系统的无阻尼振荡频率ωn=3rads。试确定系统作等幅振荡时的K和a值(K、均为大于零的常数a)。1KK1K解：∆=+1+−+⋅s+2ssa(+)(s+2)(sa+)s+2ssa(+)Ds()=ss(+2)(sa+)+ssa(+)+Ksa(+)−KsK+22=s+(3+as)+3as+3K=032Dj(ω)=−jω−(3+a)ω+ja3ω+3K=0nnnn2⎧⎪Re[(Djω)]=−(3+a)ω+3K=0nn⎨3⎪⎩Im[(Djω)]=−ω+3aω=0nnn⎧a=3解得：⎨⎩K=1823-17.已知单位反馈控制系统开环传递函数如下，试分别求出当输入信号为1(t)、和tt时系统的稳态误差。101．G(s)=(1.0s+1)(5.0s+1)7(s+3)2．G(s)=2s(s+4)(s+2s+2)8(5.0s+1)3．G(s)=2s(1.0s+1)10⎧K=10解：1.Gs()=⎨(0.1s+1)(0.5s+1)⎩v=0Ds()=(0.1s+1)(0.5s+1)10+=0经判断系统稳定rt()1()=tA1e=ss1+K11 2rt()=trt()=te=e∞ssss⎧73×217(s+3)⎪K==2.Gs()=⎨42×82ss(+4)(s+2s+2)⎪⎩v=12Ds()=ss(+4)(s+2s+2)7(+s+3)=0经判断：系统不稳定。8(0.5s+1)⎧K=83.Gs()=⎨经判断系统稳定2s(0.1s+1)⎩v=2rt()1()=trt()=tee0ssss2rt()=tA21e==ssK843-18.设单位反馈系统的开环传递函数100G(s)=s(1.0s+1)试求当输入信号r(t)=1+2t时，系统的稳态误差。100⎧K=100解：Gs()=⎨s(0.1s+1)⎩v=12Ds()=s(0.1s+1)100+=0.1s++s100=0满足必要条件，系统稳定。e=0ss1A21e===ss2K100501e=e+e=ssss1ss2503-19.控制系统的误差还有一种定义，这就是无论对于单位反馈系统还是非单位反馈系统，误差均定义为系统输入量与输出量之差，即E(s)=R(s)−C(s)现在设闭环系统的传递函数为mm−1bs+bs+L+bs+bmm−110Φ(s)=n≥mnn−1s+as+L+as+an−110试证：系统在单位斜坡函数作用下，不存在稳态误差的条件是a=b和a=b。0011证明：Es()=Rs()−Cs() Es()Rs()Cs()=−=−1φ()s=φ()seRs()Rs()Rs()mm−1bs+bs+L+bsb+mm−110∴φ()1s=−φ()1s=−enn−1s+as+L+asa+n−110nn−1mm−1s+as+L−bs−bs+L+(a−bsa)+−bn−1mm−11100=nn−1s+as+L+asa+n−1101rt()=tRs()=2se=limsEs⋅()=lims⋅φ()sRs⋅()sses→0s→0nn−1mm−11s+as+L−bs−bs+L+(a−bsa)+−bn−1mm−11100=lim⋅nn−1s→0ss+as+L+asa+n−110要使e=0，只有让a−b=0,a−b=0，即a=ba,=bss110011003-20.具有扰动输入n(t)的控制系统如图3-56所示。试计算阶跃扰动输入n(t)=N·1(t)时系统的稳态误差。K2−Es()Ts+1KTs(+1)221解：φ()s===−enNs()1+K1(Ts2+1)(Ts1++1K1)Tss+1N0nt()=N⋅1()()tNs=0se=lims⋅φ()sNs⋅()ssens→0−KTs(+1)N−KN21020=lims⋅⋅=s→0(Ts++1K)(Ts+1)sK+111213-21.试求图3-57所示系统总的稳态误差。 Es()1s(0.5s+1)解：(a).φ()s===e()2000.52200Rss++s1+s(0.5s+1)Es()1s(0.5s+1)φ()s===en()2000.52200Nss++s1+s(0.5s+1)e=e+e=lims⋅φ()sRs⋅()lim+s⋅φ()sNs⋅()ssss1ss2eens→0s→0s(0.5s+1)1s(0.5s+1)0.1=lims⋅⋅+lims⋅⋅=022s→00.5s++s200ss→00.5s++s200s2s+1ss(+1)(b).φ()s==e121s++s1+ss(+1)1ss(+1)φ()s==en121s++s1+ss(+1)2ss(+1)1ss(+1)1e=e+e=lims⋅⋅+lims⋅⋅=1ssss1ss2222s→0s++s1ss→0s++s1s3-22.系统如图3-58(a)所示，其单位阶跃响应C(t)如图3-58(b)所示，系统的位置误差e=0，试确定ssK、与vT值。sa+解：Gs()=vsTs(+1)Ksa(+)vsTs(+1)Ksa(+)φ()s==sa+Tsv+1+sv++sa1+vsTs(+1)系统是稳定的，故v≤2Ksa(+)1C()∞=lims⋅φ()sRs⋅()=lims⋅⋅=K=10v+1vs→0s→0Ts+s++sasv1sTs(+1)φ()s==esa+Tsv+1+sv++sa1+vsTs(+1) vsTs(+1)1e=lims⋅⋅=0ssv+1vs→0Ts+s++sas∴≥v13-23.系统结构图如图3-59所示。现要求：(1)扰动nt)(=t)(5，稳态误差为零；(2)输入r(t)=2t(rads)，稳态误差不大于2.0(rad)。试：各设计一个零极点形式最简单的控制器G(s)的传递函数，以满足上述各自的要求。并确定cG(s)中各参数可选择范围。c10−(s+1)(s+2)−10解：(1).φ()s==en1+10Gsc()(s+1)(s+2)10+Gsc()(s+1)(s+2)−105e=lims⋅φ()sNs⋅()=lims⋅⋅ssnens→0s→0(s+1)(s+2)10+Gs()sck32取G(s)=，可使e=0，D(s)=s+3s+2s+10k,要使系统稳定由劳斯判据得00及T>，155K−3综合得参数选择范围为K≥2及T>。15第四章根轨迹法习题及解答4-1、已知开环零、极点分布如图4-25所示。试概略绘制相应的闭环根轨迹图。 图解4-1解：根轨迹如图解4-1所示。图解4-14-2、已知系统开环传递函数*K(s+3)G(s)=s(s+1)*试作K从0→∞的闭环根轨迹，并证明在[]s平面内的根轨迹是圆，求出圆的半径和圆心。*Ks(+3)解：Gs()=ss(+1)*2**Ds()=ss(+1)+Ks(+3)=s+(K+1)s+3K=0 ***2−(K+1)±j12K−(K+1)λ==X±jY1,22*K+1*X=−⇒K=−−12X2**22212K−(K+1)12(12)(12−−X−−−X+1)Y==442=−(X+3)+622(X+3)+Y=6图解4-2根轨迹圆心(3,0)−，半径6的圆，如图解4-2所示。。4-3、设单位反馈控制系统开环传递函数如下，试概略绘出系统根轨迹图（要求确定分离点坐标d）。K（1）G(s)=s(2.0s+1)(5.0s+1)*K(s+5)（2）G(s)=s(s+2)(s+3)K10K解⑴G(s)==s(2.0s+1)(5.0s+1)s(s+5)(s+2)系统有三个开环极点：p1=0,p2=−2,p3=−5①实轴上的根轨迹：(−∞,−5],[−0,2]⎧0−2−57σa==−⎪⎪33②渐近线：⎨(2k+1)ππ⎪ϕa==±,π⎪⎩33③分离点：111++=0dd+5d+2解之得：d1=−.088，d2−.37863(舍去)。32④与虚轴的交点：特征方程为D(s)=s+7s+10s+10k=02⎧Re[D(jω)]=−7ω+10k=0令⎨3⎩Im[D(jω)]=−ω+10ω=0⎧ω=10解得⎨⎩k=7与虚轴的交点（0，±10j）。根轨迹如图解4-3(a)所示。 ⑵根轨迹绘制如下：①实轴上的根轨迹：[−,5−3],[−2,0]⎧0−2−3−(−5)σa==0⎪⎪2②渐近线：⎨(2k+1)ππ⎪ϕa==±⎪⎩221111③分离点：++=dd+2d+3d+5用试探法可得d=−0.886。根轨迹如图解4-3(b)所示。4-4、已知单位反馈系统的开环传递函数如下，试概略绘出系统的根轨迹图（要求算出出射角）。*K(s+2)（1）G(s)=(s+1+j2)(s+1−j2)*K(s+20)（2）G(s)=s(s+10+j10)(s+10−j10)*K(s+2)解⑴G(s)=(s+1+j2)(s+1−j2)根轨迹绘制如下：①实轴上的根轨迹：(−∞,−2]111②分离点：+=d+1+j2d+1−j2d+2解之得：d=−4.23③起始角：ooooθ=180+63.435−90=153.43p1o由对称性得另一起始角为−153.43。根轨迹如图解4-4(a)所示。*K(s+20)⑵G(s)=s(s+10+j10)(s+10−j10)系统有三个开环极点和一个开环零点。根轨迹绘制如下：①实轴上的根轨迹：[−20,0]oooo②起始角：θ=180+45−90−135=0°根轨迹如图解4-4(b)所示。4-5、已知系统如图4-26所示。作根轨迹图，要求确定根轨迹的出射角和与虚轴的交点。并确定使系统稳定的K值的范围。 1Kss(+2)K解：Gs()=⋅=2(222)sss+s+1+ss(+2)K=ss(++1j1)(s+−1j1)n=3有3条根轨迹，且3条全趋于无穷远处。①实轴上：(−∞,0]⎧−+1j11−−j12σ==−⎪⎪a33②渐近线：⎨π⎪ϕ=π,±a⎪⎩300③出射角：0(−θ+135+90)=(2k+1)πp1图解4-50θ=−45p10θ=45p2④与虚轴交点：32Ds()=s+2s+2s+K=032Dj(ω)=−jω−2ω+j2ω+K=02⎧⎪Re[(Djω)]=−2ω+K=0则有⎨3⎪⎩Im[(Djω)]=−ω+2ω=0⎪⎧ω=±2解得：⎨⎪⎩K=4∴使系统稳定的K值范围为00)（1）当a=10时，作系统根轨迹，并求出系统阶跃响应分别为单调、阻尼振荡时（有复极点）K的取值范围。（2）若使根轨迹只具有一个非零分离点，此时的取值？并做出根轨迹。a（3）当a=5时，是否具有非零分离点，并做出根轨迹。2解：Ds()=ssa(+)+Ks(+1)=0(a>0)（1）a=102Ds()=ss(+10)+Ks(+1)=0*Ks(+1)做等效开环传递函数Gs()=2ss(+10)n=3有3条根轨迹，有2条趋向无穷远处。①实轴上：[10,1]−−⎧−101+9σ==−⎪⎪a22②渐近线：⎨⎪ϕ=±π图解4-8(1)a⎪⎩2211③分离点：+=dd+10d+1解得：d=−2.51d=−422dd+1011K==31.25d1d+112dd+1022K==32d2d+12当31.25≤K≤32时系统阶跃响应为单调。当032时系统阶跃响应为阻尼振荡。2（2）Ds()=ssa(+)+Ks(+1)=0*Ks(+1)Gs()=2ssa(+)211分离点：+=dd+ad+122d+(a+3)d+2a=0图解4-8(2) 2−(a+3)±(a+3)−16ad=22要使系统只有一个非零分离点，则(a+3)−16a=0即a=9，a=1（舍去）（3）a=52Ds()=ss(+5)+Ks(+1)=0*Ks(+1)作等效开环传递函数Gs()=2ss(+5)n=3有3条根轨迹其中2条趋向无穷远处①实轴上：[5,1]−−⎧−+51σ==−2⎪⎪a2②渐近线：⎨π⎪ϕ=±a⎪⎩2③分离点：211+=dd+5d+12d+4d+=50图解4-8(3)无解，故无分离点。4-9、试作图4-27所示系统K从0→∞时的系统根轨迹图，并确定使系统稳定的K值范围。解根轨迹绘制如下：①实轴上的根轨迹：[7,5.0/4]②渐近线：⎧−1−1+7/4−(−5.0)1σ==a⎪⎪24⎨(2k+1)ππ⎪ϕ==±⎪a⎩22③与虚轴交点：闭环特征方程为431210D(s)=s+s+(2K−)s+K−1=0777把s=jω代入上方程，令图解4-9根轨迹图 ⎧12Re(D(jω))=K−1−ω=0⎪7⎨1043⎪Im(D(jω))=(2K−)ω−ω=0⎩77⎧ω=±2⎧ω=0⎪解得：⎨，⎨9⎩K=1⎪K=⎩7根轨迹如图解4-9所示。由图解4-9可知使系统稳定的K值范围为11132解得：当K<10或25T)212s(Ts+1)2K(5)G(s)=3sK(Ts+1)(Ts+1)12(6)G(s)=3sK(Ts+1)(Ts+1)56(7)G(s)=s(Ts+1)(Ts+1)(Ts+1)(Ts+1)1234K(8)G(s)=,(K>1)Ts−11K(9)G(s)=,(K<1)Ts−11K(10)G(s)=s(Ts−1)解题5-12计算结果列表PNZ=闭环题备开环传递函数P−2N稳定性号注KGs()=1(Ts+1)(Ts+1)(Ts+1)0-12不稳定123 KGs()=2sTs(+1)(Ts+1)000稳定12KGs()=3sTs2(+1)0-12不稳定KTs(+1)1Gs()=(T>T)4sTs2(+1)12000稳定2K5Gs()=30-12不稳定sKTs(+1)(Ts+1)126Gs()=3000稳定sKTs(+1)(Ts+1)56Gs()=sTs(+1)(Ts+1)(Ts+1)(Ts+1)71234000稳定KGs()=(K>1)8Ts−111/20稳定1KGs()=(K<1)9Ts−1101不稳定1KGs()=10sTs(−1)1-1/22不稳定5-13设控制系统的开环传递函数为100(1)G(s)=s(2.0s+1)50(2)G(s)=(2.0s+1)(s+2)(s+5.0)100(s+1)(3)G(s)=s(1.0s+1)(5.0s+1)(8.0s+1)10(4)G(s)=s(1.0s+1)(.025s+1)10(5)G(s)=s(2.0s+1)(s−1)试用奈氏判据或对数判据，判别对应闭环系统的稳定性，并确定稳定系统的相裕量和幅裕量。100100解(1)Gs()==s(02.s+1)ss(+1)5⎧⎪ωC=5×100=22.36画Bode图得：⎨⎪⎩ωg=∞ 000−10γ=180+∠Gj(ω)=180−90−tg02.ω=126.C1h==∞G(ω)g题解5-13(1)Bode图Nyquist图5050（2）Gs()==(02.s+1)(s+2)(s+05.)ss(+1)(+12)(s+1)52画Bode图判定稳定性：Z=P-2N=0-2×(-1)=2系统不稳定。由Bode图得：ω>6c50令：G(jω)=1≈解得ω=6.3cωωcc⋅⋅2ωc52ωω−1g−1g−10令：∠G(jωg)=tg−tg−tg2ωg=−180解得ωg=37.52ωω00−1C−1C−10γ=180+∠G(jω)=180−tg−tg−tg2ω=−29.4C52ωωg2g22()+1()+12(ω)+1g152h===0.391G(ω)50g 100(s+1)100(s+1)（3）Gs()==s(0.1s+1)(0.5s+1)(0.8s+1)ssss(+1)(+1)(+1)1021.25100⋅ωc令Gj(ω)=≈1得ω=13.6cωωωcccω⋅⋅⋅c1021.25ωωωo−1−1g−1g−1go令∠Gj(ω)=−90+tgω−tg−tg−tg=−180得ω≈5ggg1.25210ooo−1−1ωc−1ωc−1ωcoγ=180+∠Gj(ω)180=−90+tgω−tg−tg−tg=−44.3c1.25210222⎛ωg⎞⎛ωg⎞⎛ωg⎞ω⋅⎜⎟+1⎜⎟+1⎜⎟+1g1⎝1.25⎠⎝2⎠⎝10⎠h===0.12=−1842dBG(ω)100ω21g⋅g+系统不稳定。题解5-13(3)图1010(4)Gs()==s(01.s+1025)(.s+1)sss(+1)(+1)104⎧⎪ω=4×10=.6325⎧=00Cγ画Bode图得：⎨⎨系统临界稳定。⎪⎩ωg=4×10=.6325⎩h=1题解5-13(4)Bode图Nyquist图 1010(5)Gs()==s(0.2s+1)(s−1)ss(+1)(s−1)5题解5-13(5)图10令Gj(ω)=1得ω为15之间，即≈1：ω=3.16cccωωccoooωcooγ=180+∠Gj(ω)180=−90−arctan−180+arctanω=−49.8cc5幅相曲线与负实轴无交点h=∞5-14设系统开环对数相频特性曲线如图5-56所示，ω为系统开环对数幅频特性20lg|G(jω|)=0时的频cc率，在第一个转折频率之前的频率范围，都有L(ω)>0，试判别闭环系统的稳定性。 +o解：()a由p=0,υ=1在原曲线上增补ω从00变化时对应得相角变化−90+−在20lgGj(ω)(Hjω)>0的范围内N=0≠N=1故系统不稳定+o()bp=0,υ=4在曲线上增补ω从00变化时对应得相角变化−360+−在20lgGj(ω)(Hjω)>0范围内N==1N=1故系统稳定。5-15设单位反馈系统的开环传递函数as+1(1)G(s)=2s试确定使相裕量等于45°时的a值。K(2)G(s)=3(.001s+1)试确定使相角裕度等于45°时的K值。ooo解：（1）由γ=180+arctan(aω)180−=45：aω=1cc2(aω)+1c又Gj(ω)==1c2ωc44解得：ω=2，a=12=0.84coωco（2）由γ=180−3arctan=45：ω=100c100KGj(ω)==1c322[(0.01)ω+1]c得：K=225-16已知单位反馈系统的开环对数频率特性(数据列表如下)，试画出系统闭环对数频率特性曲线。ω07101520223040∞∞10.55.90−5.3−5−10−15−∞L(dB) −90−125−135−146−1534.−158−161.−166−180ϕ(°)5解：根据表格中的开环对数频率特性数据，查Nichols图线得出比环对数频率特性相应数值，然后描图作出M,α曲线。ωrad07101520223040∞LdB∞10.55.90−3.5−5−10−15−180000000000ϕ()−90−125−135−146−153.4−158−161.5−166−180MdB01.252.754.72.50.5-7−13.3−17α()00000000000−16−30−74−116−132−160−164−180题解5-16图5-17一系统，其实验得到的对数频率特性数据如下表，试确定系统的传递函数。ω0.10.20.4124102030342821135－5－20－31－44L(dB)－93－97－105－123－145－180－225－285－345ϕ(°)解：由ω=0.10.2，2倍频程∆L()ω=−6dB，须有一个积分环节ω=1020，2倍频程∆L()ω=−12dB，须有一个惯性环节 ooω=30时，∠Gj(ω)=−345>−180，须有延迟环节−τs−jωτKeKe故Gs()=，Gj(ω)=sTs(+1)jω(Tjω+1)⎧K120lgω<⎪⎪ωTL()ω=⎨K1⎪20lgω>⎪⎩2TωTK由20lg=34，当ω=0.1时，有K=5ω5ω=30时，20lg=−34，T=0.282Tω−τs5e因此Gs()=s(0.28s+1)o∠Gj(ω)=−ωτ×57.390−−arctan(Tω)0.1so5e由ω=30时，∠Gj(ω)=−345得τ=0.1故Gs()=s(0.28s+1)5-18一单位系统的开环对数渐近线曲线如图5-57所示。试(1)写出系统开环传递函数；(2)判别闭环系统的稳定性；(3)确定系统阶跃响应的性能指标σ%,t；s(4)将幅频特性曲线向右平移10倍频程，求时域指标σ%和t。s解：（1）由系统的对数幅频特性曲线，sK(+1)可设开环传函Gs()=0.2sss(+1)(+1)0.142⎛ωc⎞K⎜⎟+1⎝0.2⎠5K又ω=1，则Gj(ω)===1，K=2cc2210ω⎛⎜ωc⎞⎟+1⎛⎜ωc⎞⎟+1c⎝0.1⎠⎝4⎠s2(+1)0.22(5s+1)故Gs()==sss(10s+1)(0.25s+1)s(+1)(+1)0.14ooo（2）由于γ=180+∠Gj(ω)180=−90−arctan10ω−arctan0.25ω+arctan5ωccco=70.4>0所以闭环系统稳定 ⎛1⎞⎛1⎞（3）σ%=0.160.4+⎜−1⎟=0.160.4+⎜−1⎟=0.184618.46%=0⎝sinγ⎠⎝sin70.4⎠2π⎡⎛1⎞⎛1⎞⎤t=⎢20.15+⎜−1⎟+0.25⎜−1⎟⎥=6.6ssωc⎢⎣⎝sinγ⎠⎝sinγ⎠⎥⎦(4)将幅频特性曲线右移10倍频程,γ不变,ω增大10倍c因此σ%=18.64%t=0.66ss5-19已知二个系统的开环对数幅频特性曲线如图5-58中曲线(1)和(2)所示。试分析闭环系统的稳态性能和瞬态性能。解(1)由系统的对数幅频特性曲线,设两系统的开环传函分别为⎛s⎞⎛s⎞K⎜+1⎟K⎜+1⎟12⎝10⎠⎝4⎠Gs()=，Gs()=11⎛s⎞⎛s⎞⎛s⎞2⎛s⎞⎛s⎞s⎜+1⎟⎜+1⎟⎜+1⎟s⎜+1⎟⎜+1⎟⎝4⎠⎝200⎠⎝1000⎠⎝100⎠⎝400⎠ω=1时,20lgGj(ω)=40则K=100，K=10012由 解得:ω=40c1ooωc1ωc1ωc1ωc1oγ=180−90+arctan−arctan−arctan−arctan=68.1110420010001σ%=0.160.4(+−1)=0.1919%=sinγ12π⎡⎛1⎞⎛1⎞⎤t=⎢20.15+⎜−1⎟+0.25⎜−1⎟⎥=0.17ssωc1⎢⎣⎝sinγ1⎠⎝sinγ1⎠⎥⎦解得:ω=25c2ooωc2ωc2ωc2oγ=180−180+arctan−arctan−arctan=63.3241004001σ%=0.160.4(+−1)=0.209=20.9%sinγ2 2π⎡⎛1⎞⎛1⎞⎤t=⎢20.15+⎜−1⎟+0.25⎜−1⎟⎥=0.26ssωc2⎢⎝sinγ2⎠⎝sinγ2⎠⎥⎣⎦第六章线性系统频率法校正习题及答案6-1对图6－21所示系统，要求具有相角裕量等于45°，幅值裕量等于6dB的性能指标，若用串联超前校正系统以满足上述要求，试确定超前校正装置的传递函数。解：44Gs()==s(0.2s+1)(0.5s+1)11s(s+)(s+1)ω=10=3.16g025ω=8=2.8283.1623.162c03.161(+)⋅1(+)125002.8282.828h0=00=000=1.72γ0=180−90−arctan−arctan=90−Gj35.26(ωg)−29.47=25.274<4535采用超前校正，提供最大超前角00000ξ=45−25.27+510=26m1sin+ξma==2.561sin−ξms+1ω1*Gs()=取校正后截止频率为ω=ω=2.83ccc0s+1ω21*ω=ω=1.81cas+1*1.8ω=aω=4.5,ω()s=αccs+14.5校正后系统开环传递函数s4(+1)Gs′()=1.8ssss(+1)(+1)(+1)24.5502.8302.832.832.8300γ′=180−arctan−90−arctan−arctan−arctan=50>451.824.55解得：ω′=4.8gh′=2.22=6.93dB>6dB6-2对习题6－1系统，若改用串联迟后校正使系统满足要求，试确定迟后校正参数，并比较超前和迟后校正的特点。解： 4Gs()=0sss(+1)(+1)25ω=8=2.82c000γ=25.27<45,h=1.72=4.7dB00*000γ=45+6=510由γ(2.82)=250取γ(1.5)=360做弧线得γ(1)=51取ω′=1radsc过ω′=1作垂直于0dB线交L于A，其镜像点为B，过B作平行于0dB线，取ω=0.1,ω′=0.1过c0ccC作−20dBdec斜率直线交0dB线于D4ωωcc=∴ω==0.025D1ω4Ds+10.1校正装置Gs()=cs+10.025校正后系统开环传递函数s4(+1)Gs′()0.1ssss(+1)(+1)(+1)0.025250−110−11−11−11γ′=180+tg−90−tg−tg−tg0.10.0252500000000=180+84−90−88.6−26.6−11.3=47.5>45算出：ω′=2.8radsgh′=5.53=14.85dB>6dB如图所示 题解6-2图2006-3单位反馈系统的开环传递函数G(s)=试设计一个无源校正网络，使已校s(1.0s+1)正系统的相角裕量不小于45°，截止频率不低于50rad/s，同时要求保持原系统的稳态精度。解：200200Gs()==0s(0.1s+1)ss(+1)10ω=20010×=44.7250Ac0取校正后截止频率为ω=ω′=70radsAc过A点作垂直于0dB线，其镜像点为B，过B作+20dBdec直线交0dB线于C点，取CB=BD，过D作平行于0dB线，即为校正装置频率特性Lc校正装置传递函数为： s+1ω1Gsc()=s+1ω2ω=ω，ω=ω1c2p22ω44.72c0ω===291ω′70c7.82×ω=ω⋅10=1752120s+129Gs()=cs+1175校正后系统开环传递函数s200(+1)Gs′()=29sss(+1)(+1)10175γω′(′)180=0+tg−170−900−tg−170−tg−170c291017500=53.8>45ω′=70>50radsc由于开环增益及系统型别没改变，故稳态精度校正后没改变 题解6-3图6-4设单位反馈系统的开环传递函数7G(s)=11s(s+1)(s+1)26试设计一个串联迟后校正网络，使已校正系统的相角裕量为40°±2°，幅值裕量不低于10dB，开环增益保持不变，截止频率不低于1rad/s。7解：Gs()=011s(s+1)(s+1)26ω=27×=3.74c0003.743.740*0γ=180−90−arctan−arctan=−3.8<γ=40026*0110*00γω()=γ(1)90−−arctan−arctan=54>γ+6=480c0260求得γ(1.23)=470取校正后截止频率为ω′=1.23c过ω′=1.23作垂直于0dB线交L于A，其镜像点为B，过B作平行于0dB线于C点，取c0ω=0.1ω′=0.123过C作−20dBdec线交0dB线于D点。cc7ωωω′1.230.123×ccc=∴ω===0.02Dω′ω77cD s+10.123校正装置传递函数Gs()=cs+10.02s7(+1)校正后开环传递函数Gs′()=0.123ssss(+1)(+1)(+1)0.022601.2301.231.231.23γ′=180+arctan−90−arctan−arctan−arctan0.1230.02260000000=180+84.3−90−89−32−116=41.4算得：ω′=3.45gh′=6.93=16.8dB>10dB题解6-4图6-5图6－22所示为三种串联校正网络的对数幅频特性，它们均由稳定环节组成。若有一单位反馈系统，其开环传递函数为400G(s)=2s(.001+1)试问：（1）这些校正网络特性中，哪一种可使已校正系统的稳定程度最好？（2）为了将12Hz的正弦噪声削弱10倍左右，应采用哪一种校正网络特性？ 解（1）s+1（a）采用迟后校正时，校正装置的传递函数为G(s)=ca10s+1400(s+1)校正后系统开环传递函数为G(s)⋅G(s)=Ca2s(.001s+1)(10s+1)画出对数幅频特性曲线如图题解6-5中曲线L所示：a截止频率ω=4×10=.632ca相角裕度γ=180°+ϕ(ω)=−117.°（系统不稳定）aaca1.0s+1(b)采用超前校正时，校正装置的传递函数为G(s)=cb.001s+1400(1.0s+1)校正后系统开环传递函数为G(s)⋅G(s)=Cb22s(.001s+1)画出对数幅频特性曲线如图题解6-5中曲线L所示：b22ω020截止频率ω===40cb1010相角裕度γ=180°+ϕ(ω)=32.36°bbcb2(5.0s+1)(c)采用迟后-超前校正时，校正装置的传递函数为G(s)=cc(10s+1)(.002s+1)2400(5.0s+1)校正后系统开环传递函数为G(s)⋅G(s)=cc2s(.001s+1)(10s+1)(.0025s+1)画出对数幅频特性曲线如图解5-39中曲线L所示：c22ω020截止频率ω===10ccω40cb相角裕度γ=180°+ϕ(ω)=48.21°cccc可见，采用迟后校正时系统不稳定；采用迟后-超前校正时稳定程度最好，但响应速度比超前校正差一些。 题解6-5图（2）确定使12Hz正弦噪声削弱10倍左右的校正网络f=12Hz时，ω=2πf=75.4(rad/s)对于单位反馈系统，高频段的闭环幅频特性与开环幅频特性基本一致。从Bode图上看，在ω=75.4处，有1L(754.)=20lg=−23dBcαc23衰减倍数α=1020=14.13≈10，可见，采用迟后-超前校正可以满足要求。cK6-6设单位反馈系统的开环传递函数G(s)=试设计一s(.005s+1)(2.0s+1)−1串联超前校正网络，使系统的稳态速度误差系数不小于5s，超调量不大于25%，调节时间不大于1s。KK解：Gs()==0s(0.05s+1)(0.2s+1)sss(+1)(+1)520K=limsGs⋅()=K≥5v0s→0取K=55Gs()=0sss(+1)(+1)520σ%≤25%,t≤1s对应频域指标s09γ≥55,≤1即ω≥9cωcω=<59c0005500γ=180−90−arctan−arctan=31<550520串联超前校正可补偿的最大角度 *000ξm=γ−γ0+510=34查表得10lga=7在−10lga作水平线交L于A′点，过A′作垂直于0dB线，交0dB线于P07ω=ω⋅1040=7.5955 题解6-6图6-7已知单位反馈系统及其串联校正的传递函数G(s)cK(Ts+1)G(s)=cs+1当式中K=10，T=0.1时，系统截止频率ω=5，若要求ω不变，如何改变K、T才能使相裕量提高cc45°。KTs(+1)解：Gs()=cs+1当K=10,T=0.1时，ω=5c10(0.1s+1)Gs()=cs+1ξω()=arctan(0.1)arctanω−ωccc10(1+j0.5)L(ω)=20lgc1+j50若重新选择TK,值，使γ提前45KTs(+1)′=11设Gs()cs+1当ω=5时cξω′()=arctan(Tω)arctan−ωc1cc K1(1+jTωc1)L′(ω)=20lgc1+jωc0由ξω′()=ξω()45+得c0arctan(Tω)=arctan(0.1)45ω+1ccT1ωc−0.1ωc0arctan=45210.1+Tω1cTω−0.1ω1cc∴=⇒1T=0.62110.1+Tω1c另外，在增大的同时要保持γGs()的幅制不变c10(1+j0.5)K(1+jTω)1c1即：20lg=20lg1+j51+jωcK(1+j3)1=20lg1+j5解得：K=3.54116-8已知单位反馈系统的开环传递函数G(s)=，串联微分校正传递函数G(s)为2csK(Ts+1)1G(s)=cTs+12要使校正后系统开环增益为100，ω=31.6rad/s，中频段斜率为-20dB/dec，而且具有两个十倍频程的c宽度。试求（1）校正后系统的开环对数幅频特性曲线；（2）确定G(s)的参数T、T；c12（3）校正后系统的相裕量、幅裕量γh。1解：Gs()=02sKTs(+1)1Gs()=cTs+12KTs(+1)′=1校正后系统开环传递函数Gs()2sTs(+1)2校正后开环增益为100,K=10011中频段斜率为−20dBdec，且有2个十倍频程，故=100T=100T12TT21 1110010010=⋅ω,===3.16cTTω31.611cT=0.31611=316,T=0.003162T2100(0.316s+1)Gs()=c0.00316s+1100(0.316s+1)校正后系统开环传递函数Gs′()=2s(0.00316s+1)校正后对数幅频特性如图所示00γ′=180+arctan0.31631.6180×−−arctan0.0031631.6×00000=180+84.3−180−5.7=78.6⎧⎪ω′=∞g⎨⎪⎩h′=0题解6-8图'