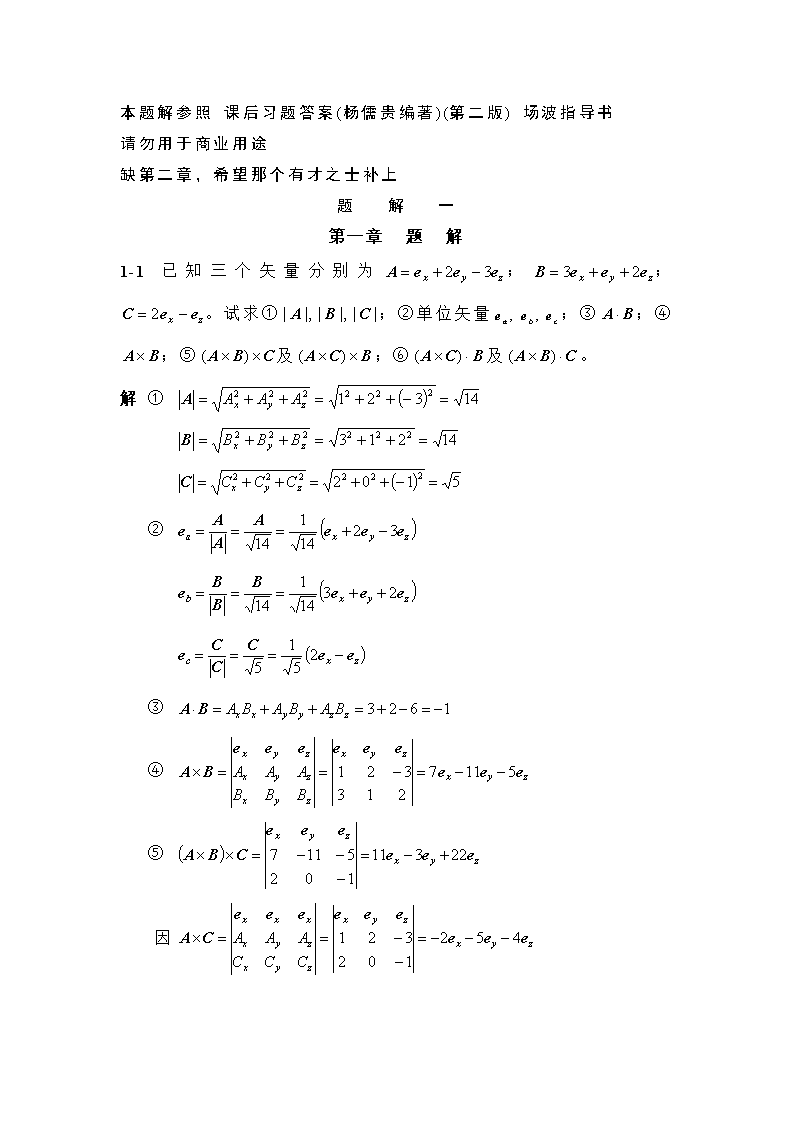- 4.04 MB
- 2022-04-22 11:44:38 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'本题解参照课后习题答案(杨儒贵编著)(第二版)场波指导书请勿用于商业用途缺第二章,希望那个有才之士补上题解一第一章题解1-1已知三个矢量分别为;;。试求①;②单位矢量;③;④;⑤及;⑥及。解①②③④⑤因
则⑥。1-2已知平面内的位置矢量A与X轴的夹角为a,位置矢量B与X轴的夹角为b,试证证明由于两矢量位于平面内,因此均为二维矢量,它们可以分别表示为已知,求得即1-3已知空间三角形的顶点坐标为,及。试问:①该三角形是否是直角三角形;②该三角形的面积是多少?解由题意知,三角形三个顶点的位置矢量分别为;;那么,由顶点P1指向P2的边矢量为同理,由顶点P2指向P3的边矢量由顶点P3指向P1的边矢量分别为因两个边矢量
,意味该两个边矢量相互垂直,所以该三角形是直角三角形。因,所以三角形的面积为1-4已知矢量,两点P1及P2的坐标位置分别为及。若取P1及P2之间的抛物线或直线为积分路径,试求线积分。解①积分路线为抛物线。已知抛物线方程为,,则②积分路线为直线。因,两点位于平面内,过,两点的直线方程为,即,,则。1-5设标量,矢量,试求标量函数F在点处沿矢量A的方向上的方向导数。解已知梯度那么,在点处F的梯度为因此,标量函数F在点处沿矢量A的方向上的方向导数为1-6已知标量函数,试求该标量函数F在点
P(1,2,3)处的最大变化率及其方向。解标量函数在某点的最大变化率即是函数在该点的梯度值。已知标量函数F的梯度为那么将点P(1,2,3)的坐标代入,得。那么,在P点的最大变化率为P点最大变化率方向的方向余弦为;;1-7若标量函数为试求在点处的梯度。解已知梯度,将标量函数F代入得再将P点的坐标代入,求得标量函数F在P点处的梯度为1-8试求距离在直角坐标、圆柱坐标及圆球坐标中的表示式。解在直角坐标系中
在圆柱坐标系中,已知,,,因此在球坐标系中,已知,,,因此1-9已知两个位置矢量及的终点坐标分别为及,试证与之间的夹角g为证明根据题意,两个位置矢量在直角坐标系中可表示为已知两个矢量的标积为,这里g为两个矢量的夹角。因此夹角g为式中因此,1-10若C为常数,A及k为常矢量,试证:
①;②;③。证明①证明。利用公式,则而求得。②证明。利用公式,则再利用①的结果,则③证明。利用公式,则再利用①的结果,则。1-11试证,式中k为常数。证明已知在球坐标系中则
即1-12已知某点在圆柱坐标系中的位置为,试求该点在相应的直角坐标系及圆球坐标系中的位置。解已知直角坐标系和圆柱坐标系坐标变量之间的转换关系为,,因此,该点在直角坐标下的位置为;;z=3同样,根据球坐标系和直角坐标系坐标变量之间的转换关系,;;可得该点在球坐标下的位置为;;1-13已知直角坐标系中的矢量,式中a,b,c均为常数,A是常矢量吗?试求该矢量在圆柱坐标系及圆球坐标系中的表示式。解由于的大小及方向均与空间坐标无关,故是常矢量。已知直角坐标系和圆柱坐标系坐标变量之间的转换关系为;;求得;;;又知矢量A在直角坐标系和圆柱坐标系中各个坐标分量之间的转换关系为
将上述结果代入,求得即该矢量在圆柱坐标下的表达式为直角坐标系和球坐标系的坐标变量之间的转换关系为;;由此求得;;矢量A在直角坐标系和球坐标系中各个坐标分量之间的转换关系为求得即该矢量在球坐标下的表达式为。1-14已知圆柱坐标系中的矢量,式中a,b,c均为常数,A是常矢量吗?试求及以及A
在相应的直角坐标系及圆球坐标系中的表示式。解因为虽然a,b,c均为常数,但是单位矢量er和ef均为变矢,所以不是常矢量。已知圆柱坐标系中,矢量A的散度为将代入,得矢量A的旋度为已知直角坐标系和圆柱坐标系坐标变量之间的转换关系为;;;又知矢量A在直角坐标系和圆柱坐标系中各个坐标分量之间的转换关系为将上述接结果代入,得即该矢量在直角坐标下的表达式为,其中。
矢量A在圆柱坐标系和球坐标系中各个坐标分量之间的转换关系以及,,求得即该矢量在球坐标下的表达式为。1-15已知圆球坐标系中矢量,式中a,b,c均为常数,A是常矢量吗?试求及,以及A在直角坐标系及圆柱坐标系中的表示式。解因为虽然a,b,c均为常数,但是单位矢量er,eq,ef均为变矢,所以不是常矢量。在球坐标系中,矢量A的散度为将矢量A的各个分量代入,求得。矢量A的旋度为
利用矢量A在直角坐标系和球坐标系中各个坐标分量之间的转换关系以及,,求得该矢量在直角坐标下的表达式为利用矢量A在圆柱坐标系和球坐标系中各个坐标分量之间的转换关系求得其在圆柱坐标下的表达式为。
题解三3-1若真空中相距为d的两个电荷q1及q2的电量分别为q及4q,当点电荷位于q1及q2的连线上时,系统处于平衡状态,试求的大小及位置。解要使系统处于平衡状态,点电荷受到点电荷q1及q2的力应该大小相等,方向相反,即。那么,由,同时考虑到,求得可见点电荷可以任意,但应位于点电荷q1和q2的连线上,且与点电荷相距。习题图3-2zo¢xE3E2E13-2已知真空中有三个点电荷,其电量及位置分别为:试求位于点的电场强度。解令分别为三个电电荷的位置到点的距离,则,,。利用点电荷的场强公式,其中为点电荷q指向场点的单位矢量。那么,在P点的场强大小为,方向为。在P点的场强大小为,方向为。在P点的场强大小为,方向为
则点的合成电场强度为3-3直接利用式(3-1-14)计算电偶极子的电场强度。解令点电荷位于坐标原点,为点电荷至场点P的距离。再令点电荷位于+坐标轴上,为点电荷至场点P的距离。两个点电荷相距为,场点P的坐标为(r,,f)。根据叠加原理,电偶极子在场点P产生的电场为考虑到r>>l,=er,,那么上式变为式中以为变量,并将在零点作泰勒展开。由于,略去高阶项后,得利用球坐标系中的散度计算公式,求出电场强度为3-4已知真空中两个点电荷的电量均为C,相距为2cm,如习题图3-4所示。试求:①P点的电位;②将电量为C的点电荷由无限远处缓慢地移至P点时,外力必须作的功。
ÅÅ1cmP1cmqq1cm习题图3-4解根据叠加原理,点的合成电位为因此,将电量为的点电荷由无限远处缓慢地移到点,外力必须做的功为3-5通过电位计算有限长线电荷的电场强度。习题图3-5r0Pzodllq1q2y解建立圆柱坐标系。令先电荷沿z轴放置,由于结构以z轴对称,场强与无关。为了简单起见,令场点位于yz平面。设线电荷的长度为,密度为,线电荷的中点位于坐标原点,场点的坐标为。利用电位叠加原理,求得场点的电位为式中。故
因,可知电场强度的z分量为电场强度的r分量为
式中,那么,合成电强为
当L®¥时,,则合成电场强度为可见,这些结果与教材2-2节例4完全相同。3-6已知分布在半径为a的半圆周上的电荷线密度,试求圆心处的电场强度。习题图3-6ayxoE解建立直角坐标,令线电荷位于xy平面,且以y轴为对称,如习题图2-6所示。那么,点电荷在圆心处产生的电场强度具有两个分量Ex和Ey。由于电荷分布以y轴为对称,因此,仅需考虑电场强度的分量,即考虑到,代入上式求得合成电场强度为3-7已知真空中半径为a的圆环上均匀地分布的线电荷密度为,试求通过圆心的轴线上任一点的电位及电场强度。
习题图3-7xyzProa解建立直角坐标,令圆环位于坐标原点,如习题图2-7所示。那么,点电荷在z轴上点产生的电位为根据叠加原理,圆环线电荷在点产生的合成电位为因电场强度,则圆环线电荷在点产生的电场强度为3-8设宽度为W,面密度为的带状电荷位于真空中,试求空间任一点的电场强度。习题图3-8xyzoryxdx¢x¢(a)(b)P(x,y)
解建立直角坐标,且令带状电荷位于xz平面内,如习题图2-8所示。带状电荷可划分为很多条宽度为的无限长线电荷,其线密度为。那么,该无限长线电荷产生的电场强度与坐标变量z无关,即式中得那么3-9已知均匀分布的带电圆盘半径为a,面电荷密度为,位于z=0平面,且盘心与原点重合,试求圆盘轴线上任一点电场强度。习题图3-9oxyzrdrP(0,0,z)
解如图2-9所示,在圆盘上取一半径为,宽度为的圆环,该圆环具有的电荷量为。由于对称性,该圆环电荷在z轴上任一点P产生的电场强度仅的有分量。根据习题2-7结果,获知该圆环电荷在P产生的电场强度的分量为那么,整个圆盘电荷在P产生的电场强度为3-10已知电荷密度为及的两块无限大面电荷分别位于x=0及x=1平面,试求及区域中的电场强度。解无限大平面电荷产生的场强分布一定是均匀的,其电场方向垂直于无限大平面,且分别指向两侧。因此,位于x=0平面内的无限大面电荷,在x<0区域中产生的电场强度,在x>0区域中产生的电场强度。位于x=1平面内的无限大面电荷,在x<1区域中产生的电场强度,在x>1区域中产生的电场强度。由电场强度法向边界条件获知,即由此求得根据叠加定理,各区域中的电场强度应为
3-11已知空间电场强度,试求(0,0,0)与(1,1,2)两点间的电位差。解设P1点的坐标为(0,0,0,),P2点的坐标为(1,1,2,),那么,两点间的电位差为式中,因此电位差为3-12已知同轴圆柱电容器的内导体半径为a,外导体的内半径为b。若填充介质的相对介电常数。试求在外导体尺寸不变的情况下,为了获得最高耐压,内外导体半径之比。解已知若同轴线单位长度内的电荷量为q1,则同轴线内电场强度。为了使同轴线获得最高耐压,应在保持内外导体之间的电位差V不变的情况下,使同轴线内最大的电场强度达到最小值,即应使内导体表面处的电场强度达到最小值。因为同轴线单位长度内的电容为则同轴线内导体表面处电场强度为令b不变,以比值为变量,对上式求极值,获知当比值时,取得最小值,即同轴线获得最高耐压。3-13若在一个电荷密度为,半径为a的均匀带电球中,存在一个半径为b的球形空腔,空腔中心与带电球中心的间距为d,试求空腔中的电场强度。习题图3-13obaPrdr¢o¢
解此题可利用高斯定理和叠加原理求解。首先设半径为的整个球内充满电荷密度为的电荷,则球内点的电场强度为式中是由球心o点指向点的位置矢量,再设半径为的球腔内充满电荷密度为的电荷,则其在球内点的电场强度为式中是由腔心点指向点的位置矢量。那么,合成电场强度即是原先空腔内任一点的电场强度,即式中是由球心o点指向腔心点的位置矢量。可见,空腔内的电场是均匀的。3-14将一块无限大的厚度为d的介质板放在均匀电场中,周围媒质为真空。已知介质板的介电常数为,均匀电场的方向与介质板法线的夹角为,如习题图2-20所示。当介质板中的电场线方向时,试求角度及介质表面的束缚电荷面密度。Eedq1q1q2q2e0e0E习题图3-14E2en2en1
解根据两种介质的边界条件获知,边界上电场强度切向分量和电通密度的法向分量连续。因此可得;已知,那么由上式求得已知介质表面的束缚电荷,那么,介质左表面上束缚电荷面密度为介质右表面上束缚电荷面密度为3-15已知两个导体球的半径分别为6cm及12cm,电量均为C,相距很远。若以导线相连后,试求:①电荷移动的方向及电量;②两球最终的电位及电量。解设两球相距为d,考虑到d>>a,d>>b,两个带电球的电位为;两球以导线相连后,两球电位相等,电荷重新分布,但总电荷量应该守恒,即及,求得两球最终的电量分别为可见,电荷由半径小的导体球转移到半径大的导体球,移动的电荷量为。两球最终电位分别为
3-16如习题图3-16所示,半径为a的导体球中有两个较小的球形空腔。若在空腔中心分别放置两个点电荷q1及q2,在距离处放置另一个点电荷q3,试求三个点电荷受到的电场力。q1q2rq3a习题图3-16解根据原书2-7节所述,封闭导体空腔具有静电屏蔽特性。因此,q1与q2之间没有作用力,q3对于q1及q2也没有作用力。但是q1及q2在导体外表面产生的感应电荷-q1及-q2,对于q3有作用力。考虑到r>>a,根据库仑定律获知该作用力为3-17已知可变电容器的最大电容量,最小电容量,外加直流电压为300V,试求使电容器由最小变为最大的过程中外力必须作的功。解在可变电容器的电容量由最小变为最大的过程中,电源作的功和外力作的功均转变为电场储能的增量,即式中因此,外力必须作的功为
3-18若使两个电容器均为C的真空电容器充以电压V后,断开电源相互并联,再将其中之一填满介电常数为的理想介质,试求:①两个电容器的最终电位;②转移的电量。解两电容器断开电源相互并联,再将其中之一填满相对介电常数为理想介质后,两电容器的电容量分别为两电容器的电量分别为,且由于两个电容器的电压相等,因此联立上述两式,求得,因此,两电容器的最终电位为考虑到,转移的电量为e2ae1b习题图3-193-19同轴圆柱电容器的内导体半径为a,外导体半径为b,其内一半填充介电常数为的介质,另一半填充介质的介电常数为,如习题图2-27所示。当外加电压为V时,试求:①电容器中的电场强度;②各边界上的电荷密度;③电容及储能。
解①设内导体的外表面上单位长度的电量为,外导体的内表面上单位长度的电量为。取内外导体之间一个同轴的单位长度圆柱面作为高斯面,由高斯定理求得已知,在两种介质的分界面上电场强度的切向分量必须连续,即,求得内外导体之间的电位差为即单位长度内的电荷量为故同轴电容器中的电场强度为②由于电场强度在两种介质的分界面上无法向分量,故此边界上的电荷密度为零。内导体的外表面上的电荷面密度为;外导体的内表面上的电荷面密度为;③单位长度的电容为电容器中的储能密度为
3-20一平板电容器的结构如习题图2-28所示,间距为d,极板面积为。试求:①接上电压V时,移去介质前后电容器中的电场强度、电通密度、各边界上的电荷密度、电容及储能;②断开电源后,再计算介质移去前后以上各个参数。dl/2KVl/2ee0习题图3-20解①接上电源,介质存在时,介质边界上电场强度切向分量必须连续,因此,介质内外的电场强度是相等的,即电场强度为。但是介质内外的电通密度不等,介质内,介质外。两部分极板表面自由电荷面密度分别为,电容器的电量电容量为电容器储能为若接上电压时,移去介质,那么电容器中的电场强度为电通密度为极板表面自由电荷面密度为
电容器的电量为电容量为电容器的储能为②断开电源后,移去介质前,各个参数不变。但是若移去介质,由于极板上的电量不变,电场强度为电通密度为极板表面自由电荷面密度为两极板之间的电位差为电容量为电容器的储能为3-21若平板电容器的结构如习题图2-29所示,尺寸同上题,计算上题中各种情况下的参数。d/2d/2ele0习题图3-21
解①接上电压,介质存在时,介质内外的电通密度均为,因此,介质内外的电场强度分别为;两极板之间的电位差为。则则电位移矢量为;极板表面自由电荷面密度为;介电常数为的介质在靠近极板一侧表面上束缚电荷面密度为介电常数为与介电常数为的两种介质边界上的束缚电荷面密度为此电容器的电量则电容量为电容器的储能为接上电压时,移去介质后:
电场强度为电位移矢量为极板表面自由电荷面密度为电容器的电量电容量为电容器的储能为(2)断开电源后,介质存在时,各个参数与接上电源时完全相同。但是,移去介质后,由于极板上的电量不变,电容器中电场强度为,电通密度为极板表面自由电荷面密度为两极板之间的电位差为电容量为电容器的储能为3-22已知两个电容器C1及C2的电量分别为q1及q2,试求两者并联后的总储能。若要求并联前后的总储能不变,则两个电容器的电容及电量应满足什么条件?解并联前两个电容器总储能为并联后总电容为,总电量为,则总储能为
要使,即要求方程两边同乘,整理后得方程两边再同乘,可得即由此获知两个电容器的电容量及电荷量应该满足的条件为dVte0e0习题图3-23A3-23若平板空气电容器的电压为V,极板面积为A,间距为d,如习题图2-32所示。若将一块厚度为的导体板平行地插入该平板电容器中,试求外力必须作的功。解未插入导体板之前,电容量。插入导体板后,可看作两个电容串联,其中一个电容器的电容,另一个电容器的电容,那么总电容量为根据能量守恒原理,电源作的功和外力作的功均转变为电场能的增量,即
式中则3-24已知线密度的无限长线电荷位于(1,0,z)处,另一面密度的无限大面电荷分布在x=0平面。试求位于处电量的点电荷受到的电场力。xz1Po0.55y习题图3-24解根据题意,两种电荷的位置如图2-33所示。由习题2-10知,无限大面电荷在P点产生的电场强度为无限长线电荷在P点产生的电场强度为因此,P点的总电场强度为所以位于P点的点电荷受到的电场力为3-25已知平板电容器的极板尺寸为,间距为d,两板间插入介质块的介电常数为,如习题图2-34所示。试求:①当接上电压V时,插入介质块受的力;②电源断开后,再插入介质时,介质块的受力。da´bSUee0习题图3-25
解①此时为常电位系统,因此介质块受到的电场力为式中x为沿介质块宽边b的位移。介质块插入后,引起电容改变。设插入深度x,则电容器的电容为电容器的电场能量可表示为那么介质块受到的x方向的电场力为②此时为常电荷系统,因此介质块受到的电场力为式中x为沿介质块宽边b的位移。介质块插入后,极板电量不变,只有电容改变。此时电容器的电场能量可表示为因此介质块受到的x方向的电场力为3-26已知在直角坐标系中四个点电荷分布如习题图3-1所示,试求电位为零的平面。-q3cmYX+q+q-q1cm习题图3-26解已知点电荷q的电位为
,令,,,,那么,图中4个点电荷共同产生的电位应为令,得由4个点电荷的分布位置可见,对于x=1.5cm的平面上任一点,,因此合成电位为零。同理,对于x=0.5cm的平面上任一点,,因此合成电位也为零。所以,x=1.5cm及x=0.5cm两个平面的电位为零。xqP(r,z)hh-qz习题图3-273-27试证当点电荷q位于无限大的导体平面附近时,导体表面上总感应电荷等于。证明建立圆柱坐标,令导体表面位于xy平面,点电荷距离导体表面的高度为,如图3-2所示。那么,根据镜像法,上半空间的电场强度为电通密度为式中;那么,
已知导体表面上电荷的面密度,所以导体表面的感应电荷为则总的感应电荷为3-28根据镜像法,说明为什么只有当劈形导体的夹角为p的整数分之一时,镜像法才是有效的?当点电荷位于两块无限大平行导体板之间时,是否也可采用镜像法求解。答根据镜像法,如果劈形导体的夹角不为的整数分之一时,则镜像电荷不能最终和原电荷重合,这样将会产生无限多个镜像电荷,每个镜像电荷都会产生一定的电位,导致合成电位无限大,因而无解。当点电荷位于两块无限大导体板之间时,可采用镜像法求解。此时虽然也会产生无限多个镜像电荷,但是远处的镜像电荷对于两板之间的场点贡献越来越小,因此可以获得一个有限的解。errlh导体习题图3-29xy3-29一根无限长的线电荷平行放置在一块无限大的导体平面附近,如习题图3-4所示。已知线电荷密度,离开平面的高度m,空间媒质的相对介电常数。试求:①空间任一点场强及能量密度;②导体表面的电荷密度;③当线电荷的高度增加一倍时,外力对单位长度内的线电荷应作的功。解①建立圆柱坐标,令导体表面位于xz平面,导体上方场强应与变量z无关。根据镜像法,上半空间中任一点的场强为
电场能量密度为已知导体表面的电荷面密度,那么单位长度内线电荷受到的电场力可等效为其镜像线电荷对它的作用力,即可见,线电荷受到的是吸引力。所以,当线电荷的高度增加一倍时,外力必须做的功为(J)。dd/3q习题3-303-30已知点电荷q位于两块无限大的接地的平行导体板之间,如习题图3-7所示。两板
间距为d,点电荷位于处,试求两板间的电位分布。解选用圆柱坐标系,令下底板位于z=0平面,点电荷q位于轴,则导体板之间任一点电位与角度q无关。根据镜像法,必须在轴上引入无限多个镜像电荷,zq-q-qqqrx它们的位置分别为:正轴上:,,,...负轴上:,,,...则两板之间任一点的电位为:
题解四4-1已知一根长直导线的长度为1km,半径为0.5mm,当两端外加电压6V时,线中产生的电流为A,试求:①导线的电导率;②导线中的电场强度;③导线中的损耗功率。解(1)由,求得由,求得导线的电导率为(2)导线中的电场强度为(3)单位体积中的损耗功率,那么,导线的损耗功率为4-2已知圆柱电容器的长度为L,内外电极半径分别为a及b,填充的介质分为两层,界面半径为c。在区域中,填充媒质的参数为;在区域中,媒质参数为。若接上电动势为的电源,试求:①各区域中的电流密度;②内外导体表面上以及介质表面上的驻立电荷密度。解(1)建立圆柱坐标系,则电位应满足的拉普拉斯方程为忽略边缘效应,设媒质①和媒质②内的电位分别为j1和j2,那么根据边界条件,得知;
联立上式,求得;;代入上式,得(2)r=a表面上面电荷密度为r=b表面上面电荷密度为r=c表面上面电荷密度为
4-3已知环形导体块尺寸如习题图4-5所示。试求与两个表面之间的电阻。YXdabfr(r,f)0习题图4-3解建立圆柱坐标系,则电位应满足的拉普拉斯方程为该方程的解为令求得常数。那么,电场强度为电流密度为电流强度为由此求得两个表面之间的电阻为
4-4若两个同心的球形金属壳的半径为及,球壳之间填充媒质的电导率,试求两球壳之间的电阻。解对于恒定电流场,因,可令。将其代入,得建立球坐标系,上式展开为该方程的解为那么,求得电流密度为两球壳之间的电流为两球壳之间的恒定电场为两球壳之间的电位差为求得两球壳之间的电阻为4-5已知截断的球形圆锥尺寸范围为,,电导率为,试求及两个球形端面之间的电阻。解由于两个球形端面之间的导电媒质是均匀的,因此由上例获知那么
;求得电流密度;电场强度那么,电流电位差因此电阻4-6若上题中电导率,再求两球面之间的电阻。解由于媒质是非均匀的,那么由,求得电流密度电场强度电流电位差因此电阻4-7若两个半径为及的理想导体球埋入无限大的导电媒质中,媒质的电参数为及
,两个球心间距为,且,,试求两导体球之间的电阻。解设两球携带的电荷分别为Q和-Q,考虑到两球相距很远,,两球表面电荷分布可视为均匀。因此,两球的电位分别为,则两球之间的电位差为那么,两球之间的电容根据静电比拟,两球之间的电阻应为4-8知半径为25mm的半球形导体球埋入地中,如习题图4-10所示。若土壤的电导率,试求导体球的接地电阻(即导体球与无限远处之间的电阻)。s=10-6S/me02a习题图4-8解已知半径为a的孤立导体球与无限远处之间的电容为,那么根据静电比拟,埋地导体球的电阻R为对于埋地的导体半球,表面面积减了一半,故电阻加倍,即W4-9恒定电流通过无限大的非均匀电媒质时,试证任意一点的电荷密度可以表示为
解已知恒定电流场是无散的,即,那么又由于介质中电通密度在某点的散度等于该点自由电荷的体密度,即由上两式求得4-10若一张矩形导电纸的电导率为,面积为,四周电位如习题图4-12所示。试求:①导电纸中电位分布;②导电纸中电流密度。baj=0sj=V0XY习题图4-10解(1)建立直角坐标,根据给定的边界条件,得导电纸区域中电位的通解为
由边界条件及得由此求得常数:,其中,其中代入上式,得由边界条件,得由此求得常数:那么,导电纸中的电位分布为(2)由,求得导电纸中电流密度为
题解五5-1在均匀线性各向同性的非磁性导电媒质(即)中,当存在恒定电流时,试证磁感应强度应满足拉普拉斯方程,即。证在均匀线性各向同性的非磁性导电媒质中,由及,得对等式两边同时取旋度,得但是,考虑到恒等式,得又知,由上式求得。5-2设两个半径相等的同轴电流环沿x轴放置,如习题图5-2所示。试证在中点P处,磁感应强度沿x轴的变化率等于零,即Paaaz习题图5-2xy①②o解设电流环的半径为a,为了求解方便,将原题中坐标轴x换为坐标轴z
,如图示。那么,中点P的坐标为(z,0,0),电流环①位于处,电流环②位于处。根据毕奥—沙伐定律,求得电流环①在P点产生的磁感应强度为取圆柱坐标系,则,,,因此同理可得,电流环②在P点产生的磁感应强度为那么,P点合成磁感应强度为由于和均与坐标变量z无关,因此P点的磁感应强度沿z轴的变化率为零,即aoaaPxyACB习题图5-35-3已知边长为a的等边三角形回路电流为I,周围媒质为真空,如习题图5-3所示。试求回路中心点的磁感应强度。
解取直角坐标系,令三角形的AB边沿x轴,中心点P位于y轴上,电流方向如图示。由毕奥—沙伐定律,求得AB段线电流在P点产生的磁感应强度为式中,,,即由于轴对称关系,可知BC段及AC段电流在P点产生的磁感应强度与AB段产生的磁感应强度相等。因此,P点的磁感应强度为5-4两条半无限长直导线与一个半圆环导线形成一个电流回路,如习题图5-4所示。若圆环半径r=10cm,电流I=5A,试求半圆环圆心处的磁感应强度。rI①②③0X习题图5-4Y解根据毕奥—沙伐定律,载流导线产生的磁场强度为设半圆环圆心为坐标原点,两直导线平行于X轴,如图所示。那么,对于半无限长线段①,,因此,在圆心处产生的磁场强度为
同理线段③在圆心处产生的磁场强度为对于半圆形线段②,,因此,它在半圆心处产生的磁场强度为那么,半圆中心处总的磁感应强度为5-5若在处放置一根无限长线电流,在y=a处放置另一根无限长线电流,如习题图5-5所示。试YZ-aaI0IX习题图5-5求坐标原点处的磁感应强度。解根据无限长电流产生的磁场强度公式,求得位于处的无限长线电流在原点产生的磁场为位于处的无限长线电流产生的磁场为因此,坐标原点处总磁感应强度为
yz-w/2w/2IodxJxP5-6已知宽度为W的带形电流的面密度,位于z=0平面内,如习题图5-6所示。试求处的磁感应强度。dyyzyo习题图5-6(a)习题图5-6(b)解宽度为,面密度为的面电流可看作为线电流,其在P点产生的磁场为由对称性可知,z方向的分量相互抵消,如习题图5-6(b)所示,则因此,在处的磁感应强度为YZPah0IX习题图5-75-7已知电流环半径为a,电流为I,电流环位于z=0平面,如习题图5-7所示。
试求处的磁感应强度。解由毕奥—沙伐定律得因为处处与正交,则即由对称性可知,P点磁场强度只有分量,所以因此,处的磁感应强度为zzdr05-8当半径为a的均匀带电圆盘的电荷面密度为,若圆盘绕其轴线以角速度旋转,试求轴线上任一点磁感应强度。解如习题图5-8所示,将圆盘分割成很多宽度为的载流圆环dI,它在处产生的磁感应强度,根据题5-9结果,得知因为
习题图5-8因此0XYZ习题图5-95-9已知位于y=0平面内的表面电流,试证磁感应强度B为解有两种求解方法。解法一:将平面分割成很多宽度为的无限长线电流,那么由题5-8结果获知,当时因此,积分求得同理,当时,那么,积分求得解法二:由题5-8知,即令y<0的区域中磁场强度为H1,而y>0的区域中磁场强度为H2,那么,在的边界上,。由此求得,因此
5-10已知N边正多边形的外接圆半径为a,当通过的电流为I时,试证多边形中心的磁感应强度为IIIO习题图5-10式中为正多边形平面的法线方向上单位矢量。若时,中心B值多大?解如习题图5-10所示,载流线圈每边在中心O处产生的磁感应强度为所以,N条边在中心O处产生的磁场为当时,此结果即是半径为的电流环在中心处产生的磁感应强度。5-11若无限长的半径为a的圆柱体中电流密度分布函数,试求圆柱内外的磁感应强度。解取圆柱坐标系,如习题图5-11所示。当时,通过半径为r的圆柱电流为
oxyz习题图5-11由求得当时由求得xyo习题图5-125-12已知空间y<0区域为磁性媒质,其相对磁导率区域为空气。试求:①当空气中的磁感应强度时,磁性媒质中的磁感应强度B;②当磁性媒质中的磁感应强度时,空气中的磁感应强度B0。
解根据题意,建立的直角坐标如图5-17所示。①设磁性媒质中的磁感应强度为已知在此边界上磁感应强度的法向分量连续,磁场强度的切向分量连续。因此,求得,即②设空气中的磁感应强度为则由边界条件获知,求得,即5-13已知均匀绕制的长螺线管的匝数为N,长度为L,半径为a,电流为I,如习题图5-13(a)所示。试求:①螺线管内部中点o处的磁感应强度;orRxzyPIdl习题图5-13(b)f②螺线管外部P点的磁感应强度,图中。PoNL2ad习题图5-13(a)
解①螺线管可看作是线密度为的圆柱面电流,如图习题图5-13(b)所示。由题的结果得知,电流为的电流环在中点o处产生的磁感应强度为那么,螺线管在中点o处产生的总磁感应强度为②为了计算螺线管外的场强,可将螺线管看作为由N个同轴电流环组成。已知在xoy平面内,单个电流环I在点产生的矢量磁位为式中,。考虑到,那么因此当电流环位于xoy平面时,,r¢=d,那么,在处产生的磁感应强度为考虑到,对于P点而言,可以认为每个电流环均处于xoy平面内。因此,P
点磁感应强度增加N倍,即5-14当磁矩为25Am2的磁针位于磁感应强度B=2T的均匀磁场中,试求磁针承受的最大转矩。解当磁矩方向与磁感应强度方向垂直,即夹角时,磁针承受的转矩最大,因此磁针承受的最大转矩为5-15已知体积为1m3的均匀磁化棒的磁矩为10Am2,若棒内磁感应强度,为轴线方向。试求棒内磁场强度。解由磁化强度定义,求得棒内磁化强度为那么,棒内磁场强度为5-16已知位于坐标原点的磁化球的半径为a,若球内的磁化强度,式中A,B均为常数,试求球内及球面上的磁化电流。解球内的磁化电流密度为因此,球内的磁化电流为零。球面上的表面磁化电流密度为位于处宽度为的环形电流为因此,球面上的总磁化电流为
5-17已知双导线中的电流,导线半径a远小于间距d,计算单位长度内双导线的内电感与外电感。解建立直角坐标,且令一根导线位于x=0处。在双导线中取出单位长度,沿长度方向形成一个矩形回路,该回路方向与正y方向构成右旋关系,如习题图5-17(a)所示。令,习题图5-17(a)axI2I1XYa0×d那么,两个电流在两导线间产生的磁感应强度为该磁场形成的外磁通为由于此时磁通链等于磁通,即,故外电感为如习题图5-17(b)所示,导体内的磁感应强度为xyr0odrr习题图5-17(b)a该磁场形成的内磁通链为
即故内电感为xyI1I2adzydy习题图5-185-18若无限长直导线与半径为a的圆环导线平行放置,电流方向如习题图5-18所示。计算直导线与圆环之间的互感。解建立的直角坐标如图5-18所示,令长直导线位于z轴。那么,无限长z向电流在平面内+y轴一侧产生的磁感应强度为B1产生的磁通与线圈电流交链的磁通链为因此,直导线与线圈之间的互感为可见,为负,这是因为产生的磁通方向与互磁通方向相反导致的。I1adI2aaydyzxy习题图5-195-19若无限长直导线与边长为a的等边三角形线框平行放置,电流方向如习题图5-19所示。计算直导线与三角形线框之间的互感。
解建立的直角坐标如图5-19所示,令长直导线位于z轴。那么,无限长z向电流在平面内y>0区域中产生的磁感应强度为B1产生的磁通与线框电流交链的磁通链为因此,直导线与线框之间的互感为5-20已知同轴线的内导体半径为a,外导体的内外半径分别为b及c,内外导体之间为空气,当通过恒定电流I时,计算单位长度内同轴线中磁场储能及电感。解由安培环路定律,求得内导体中的磁场感应强度为那么,内导体单位长度内的磁场能量为在内外导体之间单位长度内的磁感应强度及磁场能量分别为在外导体中单位长度内的磁感应强度及磁场能量分别为
因此,同轴线单位长度内的磁场能量为那么,单位长度的自感5-21已知两根平行导线中电流分别为,,线间距离,试求当电流与同向及反向时,单位长度导线之间的作用力。⊙zyI1I2xd习题图5-21解建立的直角坐标如图5-21所示,令电流位于z轴。那么,电流在平面内y>0区域中产生的磁感应强度为当和方向相同时,电流上的电流元受到磁场B1的作用力为则单位长度电流②受到磁场B1的力为可见,当电流同向时,单位长度导线间的作用力为吸力。当电流和反向时,同理可以求出单位线电流受到磁场B1的力为
可见,当电流同向时,单位长度导线间的作用力为斥力。5-22若宽度为w的无限IJszyxwdo习题图5-22长带状电流与无限长线电流平行放置,如习题图5-22所示。若带状电流密度,线电流为I,试求两者之间的作用力。解已知无限长线电流产生的磁感应强度为将无限长的带状电流分为很多宽度为dx,长度为无限长的条形电流,这些条形电流强度为JS0dx。那么,根据题6-11结果,线电流对位于x处的反向条形电流的斥力为由对称关系可知,x方向上的合力为零。那么,两者之间的作用力为即
题解六6-1已知真空平板电容器的极板面积为S,间距为d,当外加电压时,计算电容器中的位移电流,且证明它等于引线中的传导电流。解在电容器中电场为,则,所以产生的位移电流为
;已知真空平板电容器的电容为,所带电量为,则传导电流为;可见,位移电流与传导电流相等。6-2已知正弦电磁场的频率为100GHz,试求铜及淡水中位移电流密度与传导电流密度之比。解设电场随时间正弦变化,且,则位移电流,其振幅值为传导电流,振幅为,可见;在海水中,,,则;在铜中,,,则。6-3设真空中的磁感应强度为试求空间位移电流密度的瞬时值。解由麦克斯韦方程知,而真空中传导电流,则位移电流为,
求得e1m1s1e2m2s2d1d2V习题图6-46-4若平板电容器中填充两层媒质,第一层媒质厚度为d1,第二层媒质厚度为d2,极板面积为S,电容器的外加电压,试求两种媒质参数分别为下列两种情况时:①;。②;。电容器中的电场强度,损耗功率及储能。解①设两种媒质中的电场强度分别为和,由于两种媒质均为非理想介质,则电容器中将有传导电流,且其在两媒质的分界面上应该连续,即,而,则有:即得,损耗功率为系统的储能为②当时,则电容器中传导电流中断,媒质①
中存在位移电流,两媒质之间的分界面上逐渐积累表面电荷,最后导致媒质②中的电场为零。此时,,。损耗功率为零,系统能量仅储藏在媒质①中,即。6-5已知电磁波的合成电场的瞬时值为式中。试求合成磁场的瞬时值及复值。解根据题意,电场分量E1的复值为。电场分量E2的瞬时值可写为对应的复值为那么,合成电场的复值为由,得求得对应的磁场分量的瞬时值分别为
6-6已知某真空区域中时变电磁场的时变磁场瞬时值为试求电场强度的复数形式、能量密度及能流密度矢量的平均值。解由,可得其复值为因真空中传导电流为零,,得即能量密度的平均值能流密度的平均值6-7已知真空中正弦电场的复矢量为①试证电场强度E的等相面为平面;②试求磁感应强度B、平均储能密度w及复能流密度矢量Sc。解①令空间相位因子,即显然这是一个平面方程。因此,等相面为平面。②由麦克斯韦方程,求得磁感应强度和磁场强度分别为
平均能量密度为复能流密度矢量为。6-8若真空中正弦电磁场的电场复矢量为试求电场强度的瞬时值E(r,t),磁感应强度的复矢量B(r)及复能流密度矢量Sc。解由可知求得,,则(rad/s)那么电场强度的瞬时值为同上题,由麦克斯韦方程,求得磁感应强度为复能流密度矢量为。6-9已知真空中时变电磁场的电场强度在球坐标系中的瞬时值为
式中,试求磁场强度的复数形式、储能密度及能流密度的平均值。解由获知电场的复数形式为同理由,得那么,储能密度及能流密度的平均值分别为6-10若真空中两个时变电磁场的电场强度分别为试证总平均能流密度等于两个时变场的平均能流密度之和。证明令合成电场强度和磁场强度分别为;根据给定的电场强度两个分量,由麦克斯韦方程,可以分别求得磁场强度的两个分量为;对应的瞬时值分别为;;则总能流密度的瞬时值为
式中的周期为;的周期为。而及也是周期函数,但是它们的周期为。因此,总能流密度的时间平均值为由此可见,第一项为第一个时变电磁场的能流密度的时间平均值,第二项为第二个时变电磁场的能流密度的时间平均值。但是式中第三项积分值为零,因为由于T12既是正弦函数的周期的整倍数,又是正弦函数的周期的整倍数,因此对于周期T12的平均值一定为零。积分演算的结果也会是零。这就证实6-11已知及,试证此时复能量定理为并解释其物理意义。证明已知又知及,那么,
则即其物理意义是,流进有源区内的复能流密度矢量通量的实部等于内的损耗功率以及源区本身的损耗功率。因此,复能流密度矢量的实部代表单向流动的能量,虚部表示能量的转换。6-12若考虑媒质极化和磁化损耗,认为,。试证无外源区中的能量定理为并解释其物理意义。证明同上题,由于,,,则,代入中得则其物理意义是,流进无源区内的复能流密度矢量通量的实部等于内的热损耗功率以及磁化损耗和极化损耗功率的和。复能流密度矢量的实部代表单向流动的能量,虚部表示能量的转换。
题解七7-1导出非均匀的各向同性线性媒质中,正弦电磁场应该满足的波动方程及亥姆霍兹方程。解非均匀的各向同性线性媒质中,正弦电磁场应该满足的麦克斯韦方程如下:,分别对上面两式的两边再取旋度,利用矢量公式,得则相应的亥姆霍兹方程为7-2设真空中平面上分布的表面电流,试求空间电场强度、磁场强度及能流密度。解平面上分布的表面电流将产生向和方向传播的两个平面波,设z>0区域中的电场和磁场分别为,,传播方向为;而z<0区域中的场强为
和,传播方向为。显然,各个场分量均与边界平行。由于表面电流的存在导致磁场强度在边界上不连续,但是电场强度仍然连续。由此求得下列方程:式中。考虑到;求得,,获知因此,那么,,z>0同理可得,z<0因此,两边的电场强度分别为,z>0,z<0能流密度分别为,z>0,z<07-3已知理想介质中均匀平面波的电场强度瞬时值为(V/m)试求磁场强度瞬时值、平面波的频率、波长、相速及能流密度。解已知电场强度瞬时值为(V/m)可见这是向+x方向传播的平面波。因此,磁场强度的瞬时值为(A/m)
式中为媒质的波阻抗。根据题意,获知平面波的角频率,波数。由此求出频率:;波长:相速:(m/s)能流密度:7-4设真空中平面波的磁场强度瞬时值为(A/m)试求该平面波的频率、波长、相位常数、相速、电场强度复矢量及能流密度。解根据题意,获知平面波的角频率,相位常数。由此求出频率:;波长:相速:(m/s)已知磁场强度瞬时值为(A/m)可见这是向-y方向传播的平面波。因此,电场强度的瞬时值为(V/m)式中为真空的波阻抗。那么,电场强度的复矢量为(V/m)能流密度矢量:7-5当频率分别为10kHz与10GHz的平面波在海水中传播时,求此平面波在海水中的波长、传播常数、相速及特性阻抗。
解当时,,,故可视为良导体。那么相位常数:;衰减常数:波长:;相速波阻抗:当时,,,故可视为非理想的电介质,则相位常数:衰减常数:波长:;相速:波阻抗:7-6推导式(7-3-9)。解若媒质的电导率为,则无源区中的麦克斯韦方程为令,代入下述齐次亥姆霍兹方程再令,显然为复数。设,将代入得该方程两端对应的实部和虚部应该相等,即
求解上述联立方程即可求得式(8-3-9),即7-7试证一个线极化平面波可以分解为两个旋转方向相反的圆极化波。证明令一个x方向的线极化平面波为那么可将上式改写为显然上式右端两项均为圆极化平面波,而且旋转方向恰好相反。这就证实一个线极化平面波可以分解为两个旋转方向相反的圆极化波。7-8试证一个椭圆极化平面波可以分解为两个旋转方向相反的圆极化平面波。证明由教材8-4节可见,通过坐标轴旋转,任一椭圆极化平面波均可表示为令,,即,那么前式可展开为此式又可改写为显然,上式代表两个旋转方向相反的圆极化波。7-9试证圆极化平面波的能流密度瞬时值与时间及空间无关。证明设圆极化波电场强度的瞬时值为
上式可改写为相应的磁场强度为那么,能流密度瞬时值为可见,圆极化波的能流密度瞬时值与时间及空间无关。7-10设真空中圆极化平面波的电场强度为(V/m)试求该平面波的频率、波长、极化旋转方向、磁场强度以及能流密度。解由电场强度的表示式可见,,那么波长:;频率:因传播方向为+x方向,z分量又导前y分量,因此该圆极化平面波是左旋的。磁场强度为(A/m)能流密度为(W/m2)7-11当平面波自第一种理想介质向第二种理想介质垂直投射时,若媒质波阻抗,证明边界处为电场驻波最大点;若,则边界处为电场驻波最小点。证明设入射波的传播方向为+z方向,z<0一侧媒质波阻抗为Z1,z>0一侧媒质波阻抗为Z2,那么,入射波和反射波可以分别表示为入射波:;反射波:
边界上的反射系数为由于两种介质均为理想介质,和为实数,且。媒质①中合成电场可表示为媒质①中合成电场的振幅为显然,绝对值的最大值为,而最小值为。当时,,那么在z=0的边界上可见边界上为电场驻波最大点。当时,,那么在z=0的边界上可见边界上为电场驻波最小点。实际上,当时,,由于边界上反射波和入射波的相位相同,因而形成电场驻波的最大点。当时,,边界上反射波和入射波的相位相反,因而形成电场驻波的最小点。7-12当均匀平面波自真空向理想介质平面边界垂直投射时,测得驻波比为2.7,试求该理想介质的介电常数。解由题可知,,求得。若取,则由及,求出。显然,此结果不合理。因此,应取,则求得。7-13当右旋圆极化平面波自真空沿正Z方向向位于z=0
平面的理想导电体平面垂直投射时,若其电场强度的振幅为E0,试求:①电场强度的瞬时形式及复数形式;②反射波电场强度的表示式;③理想导电体表面的电流密度。解由题意知,可设该右旋圆极化平面波的电场强度的复数形式为其瞬时值为反射波为,因,则。令真空中的合成磁场为因为;那么合成磁场为已知表面电流密度为式中,为理想导电体表面的合成磁场。因此,求得表面电流为。7-14试证式(7-6-14)。证明已知均匀平面波表示式为,式中代入无源区中的麦克斯韦方程
考虑到式中显然,上式可改写为因此求得同理可证第二方程。对于散度方程,考虑到可见,,求得。同理可证第四方程。yxzEy+EzExk习题图7-157-15已知平面波的电场强度为试求:①传播常数k;②极化特性;③是否是TEM波?解已知平面波的表示式为,由题获知可见,,即传播常数为
传播方向位于yz平面,如习题图7-15所示。Ey分量与Ez分量构成线极化波,它和相位不同振幅不等的Ex分量合成后,构成椭圆极化波。由于Ex分量相位导前,因此形成右旋椭圆极化波。因,故为TEM波。7-16当以及e和m均不等时,试求垂直极化平面波斜投射时的布鲁斯特角和临界角。解已知,当时,要使,发生无反射,则应满足可见,布鲁斯特角。当时,,发生全反射。那么,由求得临界角。显然,只有时才会发生全发射。当e和m均不等时,要使,发生无反射,则由
求得布鲁斯特角。当时,,发生全反射。那么,由求得临界角。7-17当平面波向理想介质边界斜投射时,试证布鲁斯特角与相应的折射角之和为。证明考虑到大多数介质的磁导率相同,此时只有平行极化波才可能发生全反射和无反射。已知平行极化波的反射系数为又由折射定律,对平行极化波而言要使,则,即,解得,因,可见7-18当平面波自空气向无限大的介质平面斜投射时,若平面波的电场强度振幅为1(V/m),入射角为60°,介质的电磁参数为,试求对于水平和垂直两种极化平面波形成的反射波及折射波的电场振幅。解对于平行极化波,因,可见,故此时发生无反射,即折射波的电场振幅为1(V/m)。对于垂直极化波
故反射波和折射波的电场振幅均为0.5(V/m)。7-19当均匀平面波由空气向位于平面的理想导电体表面斜投射时,已知入射波电场强度(V/m)试求:①平面波的频率;②入射角;③反射波的电场强度和磁场强度;④空气中的合成场及能流密度矢量。解由入射波的电场强度表示式可知因此波数:;波长:频率:;入射角:入射波的磁场强度为由于入射方向位于xz平面,电场方向垂直于入射面,因此,入射波为垂直极化波。已知垂直极化波在理想导电体表面上的反射系数,则反射波的电场强度和磁场强度分别为合成波的电场强度和磁场强度分别为
能流密度矢量。7-20已知区域为理想导电体,区域为空气,若入射波的磁场强度为(A/m)试求:①平面波的频率;②入射角;③离开导体表面1m处的合成波电场强度及能流密度。解①由入射波的磁场强度表示式获知,可见,,则频率:②根据传播方向与分界面的关系,得入射角。③入射波的磁场强度可分解为两个分量,即式中对应的电场强度为已知传播方向位于xy平面,因此为平行极化波,它在理想导电体边界上的反射系数,故反射波的电场强度和磁场强度分别为因为为垂直极化波,它在理想导电体边界上的反射系数,故反射波的电场强度和磁场强度分别为
那么,合成波的电场强度和磁场强度分别为离开导体表面1m处的合成波电场强度磁场强度分别为能流密度为d习题图7-21q¢qtqi7-21当平面波向位于空气中厚度为d的无限大介质层斜投射时,若介质层的介电常数为e,入射角为,试求介质中以及空气中的折射角。解平面波在边界上满足相位匹配条件,即而由于第一种介质和第三种介质均为空气,相位常数,可见空气中的折射角,如图8-25所示。由,求得介质层中折射角为er习题图7-221327-22当平面波向等腰直角玻璃棱镜的底边垂直投射时,如习
题图8-26所示。若玻璃的相对介电常数,试求反射功率与入射功率之比。解当该平面波进入玻璃棱镜后,在边界2上的入射角为但是在此边界上发生全反射的临界角为可见,,因此在边界2上发生全反射。同样在边界3上也将发生全反射,所以到达稳态后,没有能量越过边界2和3。因此,可以认为反射功率等于入射功率。qiqrqte1m1e2m2ZXEtErEi习题图7-237-23当右旋圆极化平面波以入射角自媒质①向媒质②斜投射时,如习题图8-29所示。若两种媒质的电磁参数为,平面波的频率为300MHz,试求入射波、反射波及折射波的表示式及其极化特性。解已知平面波的频率,求得媒质①中的波长,相位常数。又知入射角为,则媒质①中的传播矢量为设入射波的电场强度振幅为E0,则右旋圆极化入射波可表示为
那么,该入射波可分解为一个平行极化波和一个垂直极化波,分别表示如下:其中平行极化波的反射系数和透射系数分别为垂直极化波的反射系数和透射系数分别为则反射波的电场强度为显然,该反射波为左旋椭圆极化波。根据折射定律,求得折射角为折射波在媒质②中的波长,相位常数,则折射波的传播矢量为
因此,折射波为显然,折射波为右旋椭圆极化波。7-24已知区域中媒质参数,;区域中,,若第一种媒质中入射波的电场强度为(V/m)试求:①平面波的频率;②入射角;③反射波和透射波的磁场强度及其极化特性。解①由入射波的电场强度表示式获知,,则频率②根据入射方向与x轴的关系可知,入射角。③已知入射面为xy平面,因此入射波电场可分解为一个平行极化波和一个垂直极化波,分别如下:对于平行极化波,由于,反射系数,,反射波消失。透射系数为垂直极化波的反射系数和透射系数分别为
因此,反射波的电场强度为显然,反射波为线极化波,其磁场强度为其中为媒质1中的波阻抗。根据折射定律,获知折射角为又知折射波在媒质②中的波长,相位常数,则折射波的传播矢量为那么,折射波的电场强度为显然,折射波为左旋椭圆极化波,其磁场强度为其中为媒质②中的波阻抗。
题解八8-1推导式(8-1-4)。解已知在理想介质中,无源区内的麦克斯韦旋度方程为,令,则将上式代入旋度方程并考虑到,可得整理上述方程,即可获得式(9-1-4)。8-2推导式(9-8-17)。
解对于波,。应用分离变量法,令由于满足标量亥姆霍兹方程,得此式要成立,左端每项必须等于常数,令;显然,。由上两式可得原式通解为根据横向场与纵向场的关系式可得因为管壁处电场的切向分量应为零,那么,TE波应该满足下述边界条件:;将边界条件代入上两式,得故的通解为其余各分量分别为
8-3试证波导中的工作波长、波导波长与截止波长之间满足下列关系解已知波导中电磁波的波长为则即8-4已知空气填充的矩形波导尺寸为,若工作频率,给出可能传输的模式。若填充介质以后,传输模式有无变化?为什么?解当内部为空气时,工作波长为,则截止波长为那么,能够传输的电磁波波长应满足,若令,则k应满足。满足此不等式的m,n数值列表如下:
0.2512.25411.2523.2544.25由此可见,能够传输的模式为填充介质以后,已知介质中的波长为,可见工作波长缩短,传输模式增多,因此除了上述传输模式外,还可能传输其它高次模式。8-5已知矩形波导的尺寸为,若在区域中填充相对介电常数为的理想介质,在区域中为真空。当TE10波自真空向介质表面投射时,试求边界上的反射波与透射波。解已知波导中沿轴传输的波的电场强度为那么,反射波和透射波的电场强度可分别表示为;式中;考虑到边界上电场强度与磁场强度的切向分量必须连续的边界条件,因而在处,获知根据波阻抗公式,获知z<0和z>0区域中的波阻抗分别为将场强公式代入,得
,;,根据上述边界条件,得那么,处的反射系数及透射系数分别为;反射波与透射波的电场强度分别为;根据,可得反射波的磁场强度为根据,可得透射波的磁场强度8-6试证波导中时均电能密度等于时均磁能密度,再根据能速定义,导出式(8-3-9)。解在波导中任取一段,其内复能量定理式(7-11-14)成立。考虑到波导为理想导电体,内部为真空,因此内部没有能量损耗。因此式(7-11-14)变为因为流进左端面的能量应该等于流出右端面的能量,故上式左端面积分为零,因而右端体积分为零。但是右端被积函数代表能量,只可能大于或等于零,因此获知
已知能速的定义为,对于TE波,波导中平均能量密度为波导中能流密度平均值仅与场强的横向分量有关。对于TE波,能流密度的平均值为波导中电场和磁场的横向分量关系为将上述结果代入,求得TE波的能速为同理对于TM波也可或获得同样结果。8-7当比值为何值时,工作于主模的矩形波导中波导壁产生的损耗最小?(指获得最小衰减常数)。解当矩形波导传播波时,其衰减常数为式中A仅与波导的参数有关。令,则求k¢¢的最小值问题转化为求函数
的最小值问题。由,得,解此方程,得若取,则。由于,则。故不合理。应取即得8-8已知空气填充的铜质矩形波导尺寸为,工作于主模,工作频率。试求:①截止频率、波导波长及衰减常数;②当场强振幅衰减一半时的距离。解当工作于主模波时,则截止频率为波导波长为因矩形波导为空气填充,故仅需考虑波导壁产生的衰减,则衰减常数为
对于铜制波导,波导壁表面电阻,则设场强衰减一半时的距离为d,由,求得8-9已知空气填充的矩形波导尺寸为,工作频率。若空气的击穿场强为,试求该波导能够传输的最大功率。解由于波导是空气填充,故工作波长为已知,为了满足,该波导只能传播波,其截止波长为此时,矩形波导能够传输的最大功率为,式中为波导中空气的击穿强度,。又知该矩形波导的波阻抗求得该矩形波导能够传输的最大功率为8-10若波导中填充介质的参数为,试证由于填充介质产生的衰减常数为
解当波导中填充的媒质具有一定的电导率时,可以引入等效介电常数,即令。因此,波导中的波数。已知,那么考虑到通常s<
您可能关注的文档
- 《电气与可编程控制技术》课后习题答案.doc
- 《电气工程基础》(熊信银 张步涵 华中科技大学)习题答案全解.doc
- 《电气工程基础》(熊信银_习题答案全解.doc
- 程基础》(熊信银_张步涵_华中科技大学)习题答案全解 2.doc
- 程基础》(熊信银_张步涵_华中科技大学)习题答案全解.doc
- 《电气工程基础》习题集(2版).doc
- 《电气工程基础习题答案》陈慈萱 2003.doc
- 《电气控制系统设计》习题解答.doc
- 工》判断题_706T_(带答案).doc
- 《电磁场与电磁波》(陈抗生)习题解答选.doc
- 第4版(谢处方_编)课后习题答案_高等教育出版社.pdf
- 《电磁场与电磁波》试题含答案.pdf
- 《电网调度自动化厂站端调试检修员》技能鉴定题库 2016(无答案版).doc
- 《电路与模拟电子技术》第二版(殷瑞祥主编) 课后习题答案 高等教育出版社.doc
- 《电路与模拟电子技术》课后习题答案.doc
- 《电路分析》习题讲解.pdf
- 《电路分析基础》习题解答.pdf
- 《电路分析基础》试题及答案.doc
相关文档
- 施工规范CECS140-2002给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程
- 施工规范CECS141-2002给水排水工程埋地钢管管道结构设计规程
- 施工规范CECS142-2002给水排水工程埋地铸铁管管道结构设计规程
- 施工规范CECS143-2002给水排水工程埋地预制混凝土圆形管管道结构设计规程
- 施工规范CECS145-2002给水排水工程埋地矩形管管道结构设计规程
- 施工规范CECS190-2005给水排水工程埋地玻璃纤维增强塑料夹砂管管道结构设计规程
- cecs 140:2002 给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程(含条文说明)
- cecs 141:2002 给水排水工程埋地钢管管道结构设计规程 条文说明
- cecs 140:2002 给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程 条文说明
- cecs 142:2002 给水排水工程埋地铸铁管管道结构设计规程 条文说明