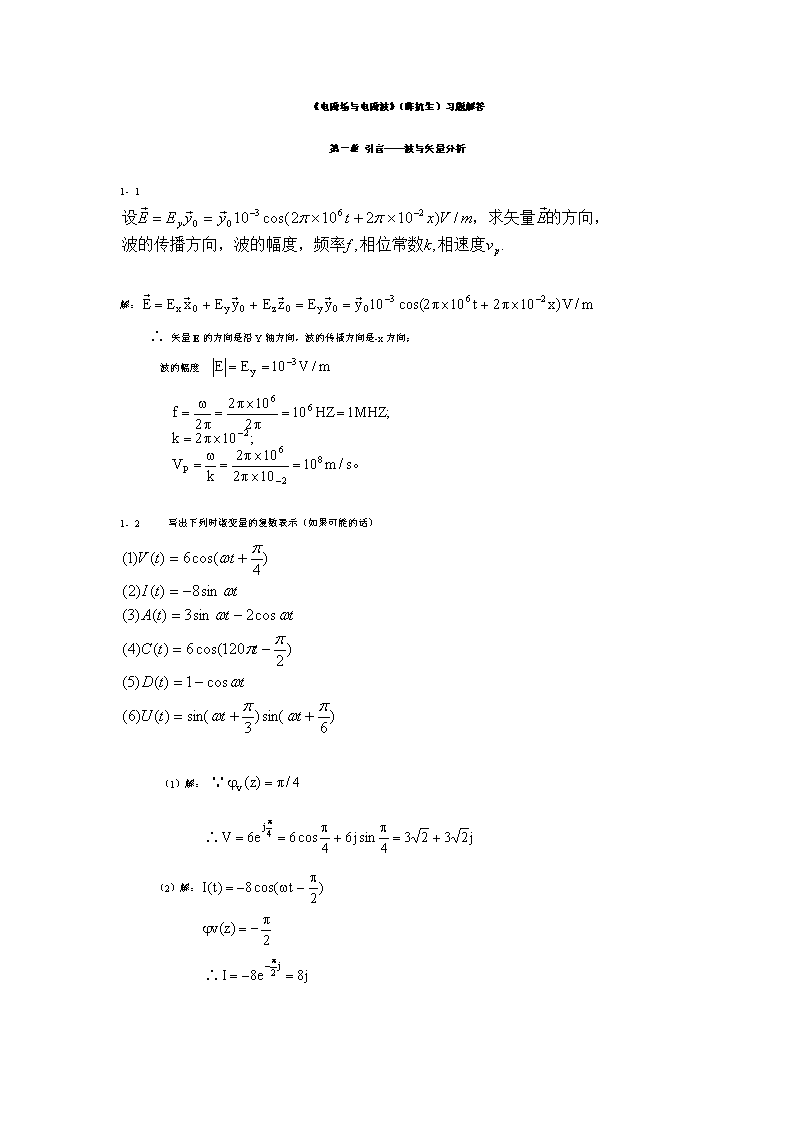《电磁场与电磁波》(陈抗生)习题解答选.doc 46页

'《电磁场与电磁波》（陈抗生）习题解答第一章引言——波与矢量分析1．1解：矢量E的方向是沿Y轴方向，波的传播方向是-x方向；波的幅度1．2写出下列时谐变量的复数表示（如果可能的话）（1）解：（2）解： （3）解：（4）解：(5)(6)两个分量频率不同，不可用复数表示1．3由以下复数写出相应的时谐变量]（1）解：（2）解：（3）解：得：1．4解： 1．5计算下列标量场的梯度（1）解：（2）解：(3)解：(4)解：（5）解：1．6 解：梯度的方向就是电位变化最陡的方向令则法线方向与同向1．7求下列矢量场的散度，旋度（1）解：（2）解：div(A)=0curl(A)=0(3)解：div(A)=1+2y(4)解：div(A)=6z1.11 解：由散度定理可得：1．12证明：1．13（1）证明： （2）证明：1．14证明：（1）证明： （2）证明： 第二章传输线基本理论与圆图2．1解：将数据代入解得（以50Hz代入，不是很正确）：2．2ZcZL解：（1）由题意可锝： （2）（3）(4)可得：2．3解： 2．4解：（1）（2）（3）2．6解：终端开路时： 2．8解：2．9ZcZLdl解：归一化阻抗： 2.10ZcZLdl解：归一化阻抗： 2．13解：为了不引起介质反射 第三章麦克斯韦方程3．1求以下几个量的量纲解：（1）（2）（3）解：3．2写出以下时谐矢量的复矢量表示解：（1）（2）（3）3．3从下面的复矢量写出相应的时谐矢量解：（1）（2） （3）3．4解：3．5假定满足麦克斯韦方程的解。求源为时麦克斯韦方程的解。解：由题意可得：分别将（1）+（5），（2）+（6），（3）+（7），（4）+（8）可以得到：3.6解：由斯托克斯定理，在此表面上 3.7解：同3.6证明方法也不能得出3.8解：由题可得：3．9 Va解：由题意可得：穿过圆盘的磁通量不发生变化由法拉第电磁感应定律可得整个圆盘是一个等势体3．10解：设t=0时3．11解： 3．12证明：3．13证明： 第四章均匀平面波4．1解：4.2。解：4．3解：（1） （2）（3）4．4解：4．5解：（1） 4．6商用调幅广播电台覆盖地域最低信号场强为25Mv/m，问与之相联系的最小功率密度是多少？最小磁场是多大？解：4．7解： 4．8求下列场的极化性质（1）（2）（3）（4）解：（1）(2)是左手椭圆极化（3） 是右手圆极化（4）是线极化4.10解：讨论z=0的情况：4.11解： 4.12解：4.13用上例数据，设地球表面电场强度为1V/m，求地球表面功率密度。解： 4.14解：4.15 解：（1）由于雪中电磁波有损耗，所以雷达测得的高度与实际有差别（2）4.16解：低频时海水是良导体 第五章波的反射与折射及多层介质中波的传播5.1解：5.2两无限大平板间有电场，式中A为常数，平行板外空间电磁场为零，坐标如图所示。试求：(1)；(2)E能否用一位置的标量函数的负梯度表示，为什么？(3)求与E相联系的H；(4)确定两板面上面电流密度和面电荷密度.解：（2）（3）（4） 5.3有一均匀平面波垂直入射到z=0处的理想导电平面，其电场强度，试确定：(1)入射波和反射波的极化方式；(2)导电平面上面电流密度；(3)写出z≤0区域合成电场强度的瞬时值。解：（1）（2）（3）此入射波可看成是两个平面波的叠加。 在这个坐标系下两个均为TEM波，对平面波1，在z≤0区域合成电场强度对平面波2，在z≤0区域合成电场强度所以z≤0区域合成电场强度的瞬时值5.4计算从下列各种介质斜入射到它与空气的平面分界面时的临界角：解：（1）（2）（3）（4）5.5一圆极化均匀平面波自空气投射到非磁性媒质表面z=0，入射角，入射面为x-z面。要求反射波电场在y方向，求媒质的相对介电系数。解：将该圆极化波分解为TE，TM，如果 5.7介质1介质2介质3如题图所示三介质系统，解：由SNELL定理可得：5.8ka,Yak水,Y水空气水k解：以TE模为例： 5.9均匀平面波由介质I（空气）以45°角投射到无损介质II，已知折射角为30°，如图频率为300MHz。求：(1)(2)反射系数解：（1） （2）5.10两个各向同性介质组成的交界面，求入射波平行极化、垂直极化两种情形下的布儒斯特角。解：对于TE模 5.11垂直极化平面波由媒质I倾斜投射到媒质II，如图，求：(1)产生全反射时的临界角；(2)当=60°时，求(用表示)；(3)求(用表示)(4)在媒质II，求场衰减到1/e时离开交界面的距离；(4)求反射系数Γ。解：（1） （2）（3）（4）（5）5.14一均匀平面电磁波由空气向理想介质垂直入射。已知z=5米处毫安/米（设介质分界面处为z=0，初相0°）。试求：（1）此平面电磁波的工作频率；（2）写出介质区域及空气区域的的表示式；（3）在介质区域中再求：a.由复数振幅写成复数或瞬时的表示式；b.坡印廷矢量瞬时表示式S及；c.电场与磁场能量密度的瞬时表示式及其最大的能量密度的大小d.能量密度的平均值。解：（1）由题意（2） （3）（注意：TEM波即可以用TE波的公式，也可以用TM波的公式） 5.15均匀平面波垂直投射到介质板，介质板前电场的大小示于下图，求（1）介质板的介电常数ε（2）入射波的工作频率。 解：5.16在介电系数分别为的介质中间放置一块厚度为d的介质板，其介电常数为，三种介质的磁导率均为，若均匀平面波从介质1以0°垂直投射到介质板上，（1）试证明：当，且时，没有反射。（2）如果，导出没有反射时的d的表达式。解：每一层介质可等效为传输线，如果均匀平面波从介质1以垂直投射到介质板上，对TE波，传输线的特征参数为: 当，即介质板相当于传输线，当时，传输线匹配，即没有反射，把波阻抗公式代入即可得，所以得证。5.19在玻璃基片上涂复多层介质膜，试从原理上说明，只要适当选择每层膜的厚度及膜材的介电系数，该多层膜系统即可制作成增透膜系统（），也可做成全反射膜（）。解：如果作增透膜，选择每一层介电系数、厚度使 第六章波导6.3矩形波导BJ-100的宽边尺寸为a=22.86mm,窄边尺寸为b=10.16mm，传输频率为10GHz的信号。求截止波长，导波波长，相速和特征阻抗。当频率f稍微上升时，上述个参量如何变化？当宽边a稍微变化时，上述各参量如何变化？当窄边b稍微增大时，它们又怎么变化？解：6.4上题中信号频率由10GHz逐步增大到30GHz，写出在波导中依次可能出现的高次模式。解： 6.8解：6.9 解：6.11 解：6.17脉冲光信号沿着多模和单模光纤传输时所引起的色散效应有什么不同？以什么因素为主？答：多模光纤以模间色散为主。单模光纤以模内色散为主，即以波导色散为主。模间色散>>模内色散6.20解： 6.23答：圆波导，场全部限制在波导内传播。介质圆波导，包层中，在横向没有波的传播，但包层中接近界面有高频能量储存。金属圆波导截止条件，kz为虚数即截止，kz=0是截止与非截止的临界点。介质圆波导，包层中横向有能量传播就截止，kt2=0，是截止与非截止的临界点，但此时kz可以是实数。金属圆波导有高通滤波特性，介质圆波导对于LP01模到DC也能传播。 第八章天线8.1解：8.3解：8.7解： 8.14解：8.16解：（1）（2） 8.20解：'