《离散数学》课程习题与解答(2011级使用)中山大学计算机科学系.pdf 58页

'第一章TheFoundations:LogicandProofs1.1PropositionalLogic作业1.1【习题1.1第8题】：设p是“你有流感”；q是“你错失期末考试”；r是“你通过课程”，翻译下列公式成自然语句：a)p→qb)¬q↔rc)q→¬rd)p∨q∨re)(p→¬r)∨(q→¬r)f)(p∧q)∨(¬q∧r)解答：a)若你有流感，则你会错失期末考试；b)你没错失期末考试，则你通过课程，反之亦然；c)若你错失期末考试，则你没通过课程；d)若你有流感，则你没通过课程；或者若你错失期末考试，则你没通过课程；e)或者你有流感，或者你错失期末考试，或者你通过课程；f)你有流感且错失期末考试，或者你没错失期末考试且通过课程。作业1.2【习题1.1第10题】：设p是“你期末考试得A”；q是“你完成本书所有练习”；r是“你课程得A”。使用p,q,r及逻辑联结词符号化下面的自然语句：a)你课程得A，但你没完成本书所有练习；b)你期末考试得A，你完成本书所有练习，而且你课程得A；c)你期末考试得A是你课程得A的必要条件；d)你期末考试得A，但你没完成本书所有练习，然而你课程得A；e)你课程得A的充分条件是你期末考试得A且你完成本书所有练习；f)你课程得A当且仅当要么你完成本书所有练习要么你期末考试得A。解答：a)r∧¬qb)p∧q∧rc)r→pd)p∧¬q∧re)(p∧q)→rf)r↔(p∧q)点评1.1这一题出现错误最多的是(c)，不少同学将“期末考试得A”是“课程得A”的必要条件，理解成了“期末考试得A”蕴含“课程得A”，这是错误的。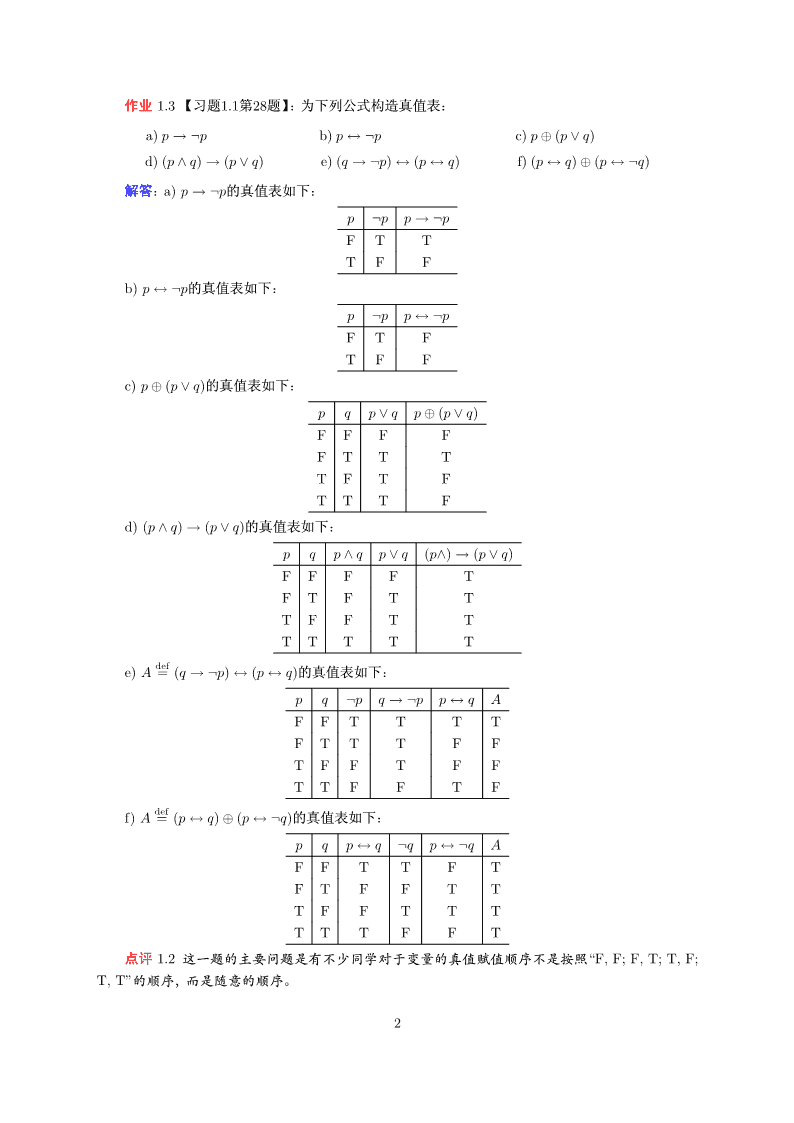1 作业1.3【习题1.1第28题】：为下列公式构造真值表：a)p→¬pb)p↔¬pc)p⊕(p∨q)d)(p∧q)→(p∨q)e)(q→¬p)↔(p↔q)f)(p↔q)⊕(p↔¬q)解答：a)p→¬p的真值表如下：p¬pp→¬pFTTTFFb)p↔¬p的真值表如下：p¬pp↔¬pFTFTFFc)p⊕(p∨q)的真值表如下：pqp∨qp⊕(p∨q)FFFFFTTTTFTFTTTFd)(p∧q)→(p∨q)的真值表如下：pqp∧qp∨q(p∧)→(p∨q)FFFFTFTFTTTFFTTTTTTTdefe)A=(q→¬p)↔(p↔q)的真值表如下：pq¬pq→¬pp↔qAFFTTTTFTTTFFTFFTFFTTFFTFdeff)A=(p↔q)⊕(p↔¬q)的真值表如下：pqp↔q¬qp↔¬qAFFTTFTFTFFTTTFFTTTTTTFFT点评1.2这一题的主要问题是有不少同学对于变量的真值赋值顺序不是按照“F,F;F,T;T,F;T,T”的顺序，而是随意的顺序。2 1.2PropositionalEquivalence作业1.4【习题1.2第10题】：利用真值表说明下面的公式都是永真式：a)(¬p∧(p∨q))→qb)((p→q)∧(q→r))→(p→r)c)(p∧(p→q))→qd)((p∧q)∧(p→r)∧(q→r))→r解答：利用真值表判断一个公式是否是永真式只要看该公式在任意的变量真值赋值下的真值是否都是T，或者更简单地，该公式真值表的最后一行（这一行给出的就是该公式的真值）是否都是T。defa)公式A=(¬p∧(p∨q))→q的真值表如下，根据该真值表，此公式是永真式。pqp∨q¬p¬p∧(p∨q)AFFFTFTFTTTTTTFTFFTTTTFFTdefb)A=((p→q)∧(q→r))→(p→r)的真值表如下，根据该真值表，此公式是永真式。pqrp→qq→r(p→q)∧(q→r)p→rAFFFTTTTTFFTTTTTTFTFTFFTTFTTTTTTTTFFFTFFTTFTFTFTTTTFTFFFTTTTTTTTTc)(p∧(p→q))→q的真值表如下，根据该真值表，此公式是永真式。pqp→qp∧(p→q)(p∧(p→q))→qFFTFTFTTFTTFFFTTTTTTdefdefd)A=((p∧q)∧(p→r)∧(q→r))→r的真值表如下，其中B==((p∧q)∧(p→r)∧(q→r))，根据该真值表，此公式是永真式。3 pqrp∧qp→r(p∧q)∧(p→r)q→rBAFFFFTFTFTFFTFTFTFTFTFFTFFFTFTTFTFTFTTFFFFFTFTTFTFFFTFTTTFTTTFFTTTTTTTTTT作业1.5【习题1.2第26题】：证明¬p→(q→r)与q→(p∨r)逻辑等值。证明可使用等值演算证明这两个公式等值：¬p→(q→r)≡p∨(q→r)//蕴含等值式≡p∨(¬q∨r)//蕴含等值式≡¬q∨p∨r//交换律≡q→(p∨r)//蕴含等值式作业1.6【习题1.2第33题】：证明(p→q)→(r→s)与(p→r)→(q→s)不逻辑等值。证明若p的真值为假,q的真值为假,r的真值为真，而s的真值为假，则(p→q)的真值为真，而(r→s)的真值为假，所以(p→q)→(r→s)的真值为假，而(p→r)的真值为真，(q→s)的真值为真，所以(p→r)→(q→s)的真值为真，两个公式不等值。点评1.3这一题有学生列出两个公式的真值表来说明这两个公式不等值，实际上只要给出对变量的一种真值赋值说明这两个公式不等值即可。有同学使用等值演算来说明公式的不等值，通常来说这是错误的，等值演算只能证明两个公式等值，无法证明两个公式不等值。作业1.7【习题1.2第50题】：这个练习证明逻辑联结词↓是完备集：a)证明p↓p与¬p逻辑等值；b)证明(p↓q)↓(p↓q)与p∨q逻辑等值c)证明逻辑联结词↓是完备集。证明根据↓的定义，即当p和q都为假时p↓q为真，其他情况p↓q为假。即↓的真值表如下：pqp↓qFFTFTFTFFTTF这样我们可利用真值表证明(a)，4 pp↓p¬pFTTTFF上述真值表表明p↓p与¬p逻辑等值。类似地，也可使用真值表证明(b)，pqp↓q(p↓q)↓(p↓q)p∨qFFTFFFTFTTTFFTTTTFTT上述真值表表明(p↓q)↓(p↓q)与p∨q逻辑等值。由于{¬,∨}是完备集，而(a)与(b)表明任何使用¬和∨的逻辑公式都可使用↓表达，因此{↓}也是完备集。1.3PredicatesandQuantifiers作业1.8【习题1.3第10题】：设C(x)表示“x有只猫”；D(x)表示“x有只狗”；E(x)表示“x有只白鼬”。使用这些谓词符号化下面的句子（设所有变量的论域都是你们班所有学生）：a)你们班有学生有只猫、狗和白鼬；b)你们班所有学生都有只猫、狗或白鼬；c)你们班有学生有只猫和白鼬，但没有狗d)你们班没有学生同时有猫、狗和白鼬；e)对于猫、狗和白鼬这三种动物，你们班都有人将它们之中的一种动物作为宠物。解答：a)∃x(C(x)∧D(x)∧E(x))b)∀x(C(x)∧D(x)∧E(x))c)∃x(C(x)∧E(x)∧¬D(x))d)¬∃x(C(x)∧D(x)∧E(x))e)∃xC(x)∧∃xD(x)∧∃xE(x)作业1.9【习题1.3第20题】：设谓词P(x)的论域是{−5,−3,−1,1,3,5}，请展开下面的公式：a)∃xP(x)b)∀xP(x)c)∀x((x6=1)→P(x))d)∃x((x≥0)∧P(x))e)∃x(¬P(x))∧∀x((x<0)→P(x))解答：a)P(−5)∨P(−3)∨P(−1)∨P(1)∨P(3)∨P(5);b)P(−5)∧P(−3)∧P(−1)∧P(1)∧P(3)∧P(5);c)P(−5)∧P(−3)∧P(−1)∧P(3)∧P(5);d)P(1)∨P(3)∨P(5);5 e)∃x(¬P(x))∧∀x((x<0)→P(x))≡(P(−5)∨P(−3)∨P(−1)∨P(1)∨P(3)∨P(5))∧(P(−5)∧P(−3)∧P(−1))≡(¬(P(−5)∧P(−3)∧P(−1))∨(P(1)∨P(3)∨P(5)))∧(P(−5)∧P(−3)∧P(−1))≡(P(1)∨P(3)∨P(5))∨(P(−5)∧P(−3)∧P(−1))作业1.10【习题1.3第22题】：对下面每个句子找一个域使得该句子真值为真，再找一个域使得该句子真值为假。a)每人都说印地语；b)有人超过21岁；c)任意两人都有相同名字d)有人认识多于两个（其他的）人解答：定义论域D={MichaelJordan}，且MichaelJordan会说印地语，年龄超过21岁，则在该论域下(a),(b),(c)为真，若MichaelJordan不会说印地语，年龄小于21岁，则(a),(b)为假。要使得(c)为假，则可另论域D={MichaelJordan,KobeJordan}。要使得(d)为真，可令论域D={Jordan,Bryant,Jeremy}，而要使得(d)为真，只要令论域D={Jordan}即可。作业1.11【习题1.3第44题】：判断∀x(P(x)↔Q(x))和∀xP(x)↔∀xQ(x)是否逻辑等值，并说明理由。解答：这两个公式不等值，设论域D={1,2}，且P(1),Q(2)为真，而P(2),Q(1)为假，则显然∀x(P(x)↔Q(x))为假，而∀xP(x)和∀xQ(x)都为假，因此∀xP(x)↔∀xQ(x)的真值为真，从而∀x(P(x)↔Q(x))和∀xP(x)↔∀xQ(x)不等值。点评1.4不少同学认为这两个公式逻辑等值，但其证明显然不会正确，实际上当∀x(P(x)↔Q(x))为真时，∀xP(x)↔∀xQ(x)一定为真，但反之却不一定成立，即∀xP(x)↔∀xQ(x)为真，而∀x(P(x)↔Q(x))却不一定为真。1.4NestedQuantifiers作业1.12【习题1.4第10题】：设F(x,y)表示“x可以愚弄y”。使用这些谓词符号化下面的句子（设变量的论域是全世界所有人）：a)每个人都可以愚弄Fred；b)Evelyn可以愚弄所有人；c)每个人都可以愚弄某些人；d)没有人可以愚弄每个人；e)每个人都可能被别人愚弄；f)没有人可以既愚弄Fred又愚弄Jerry；g)Nancy恰好可以愚弄两个人；h)恰好有这么一个人可以被所有人愚弄；i)没有人可以愚弄他（她）自己；j)有人可以恰好愚弄除了他自己之外的另一个人。6 解答：a)∀xF(x,Fred)b)∀xF(Evelyn,x)c)∀x∃yF(x,y)d)¬∃x∀yF(x,y)e)∀y∃xF(x,y)f)¬∃x(F(x,Fred)∧F(x,Jerry))g)∃x∃y[F(Nancy,x)∧F(Nancy,y)∧x6=y∧∀z(F(Nancy,z)→(z=x∨z=y))]h)∃y(∀xF(x,y)∧∀z(∀xF(x,z)→z=y))i)¬∃xF(x,x)j)∃x∃y[x6=y∧F(x,y)∧∀z((F(x,z)∧z6=x)→z=y)]作业1.13【习题1.4第16题】：一个离散数学班级里面有1个主修数学的大一新生，12个主修数学的大二学生，15个主修计算机的大二学生，两个主修数学的大三学生，两个主修计算机的大三学生，和一个主修计算机的大四学生，使用谓词符号化下面的句子并判定它们的真假：a)班里面有有一个学生是大三的；b)班里面每个学生都是主修计算机；c)有一个学生在班级里既不是主修数学专业也不是大三的；d)每个学生在班里要不就是大二的要不就是主修计算机专业的；e)有这么一个专业，有学生每年都在这个专业进修。解答：设谓词P(x,y,z)表示y年级的学生x主修z专业，其中x的论域是这个离散数学班级所有学生构成的集合，而y的论域是{freshman(大一),sophomore(大二),junior(大三),senior(大四)}z的论域是{ComputerScience(计算机),Mathematics(数学)}上述公式可符号化为：a)∃x∃yP(x,junior,y)，真值为真，班里有两个主修数学的大三学生；b)∀x∀yP(x,y,ComputerScience)，真值为假，班里有12个主修数学的大二学生；c)∃x∃y∃z(P(x,y,z)∧(y6=junior)∧(z6=Mathematics))，真值为真，班里有1个主修数学的大一新生；d)∀x∀y∀z(P(x,y,z)→(y=sophomore∨z=ComputerScience))，其真值为假，因为班里有1个主修数学的大一新生，既不是大二学生，也没有主修计算机；e)∃z∀y∃x(P(x,y,z))，真值为假，因为没有主修计算机的大一新生，而且没有主修数学的大四学生。作业1.14【习题1.4第24题】：把下面的谓词逻辑翻译成中文的数学事实，论域是所有实数：a)∃x∀y(x+y=y)；b)∀x∀y(((x≥0)∧(y<0))→(x−y>0))；c)∃x∃y(((x≤0)∧(y≤0))∧(x−y>0))；d)∀x∀y((x6=0)∧(y¬0)↔(xy6=0))；7 解答：a)有实数加任意实数都等于那个实数b)非负数减负数大于0c)有两个负数之差大于0d)两非负数相乘仍然是非负数。作业1.15【习题1.4第30题】：否定后置，使得所有的否定都置于全称和指代量词的后面。a)¬∃y∃xP(x,y)；b)¬∀x∃yP(x,y)；c)¬∃y(Q(y)∧∀x¬R(x,y))；d)¬∃y(∃xR(x,y)∨∀xS(x,y))；e)¬∃y(∀x∃zT(x,y,z)∨∃x∀zU(x,y,z))解答：a)∀x∀y¬P(x,y)b)∃x∀y¬P(x,y)c)∀y(¬Q(y)∨∃xR(x,y))d)∀y(∀x¬R(x,y)∧∃x¬S(x,y))e)∀y(∃x∀z¬T(x,y,z)∧∀x∃z¬U(x,y,z))1.5RulesofInference作业1.16【习题1.5第4题】：下面的语句用到了哪些推理规则？a)袋鼠住在澳大利亚是有袋动物，所以袋鼠是有袋动物；b)要不今天超过100度，要不污染就是危险的，今天外面不超过100度，所以污染是危险的；c)琳达是一个优秀的游泳者。如果琳达是一个优秀的游泳者，她就可以从事救生员工作，所以琳达可以从事救生员工作；d)史蒂文今年夏天将在电脑公司工作，因此，今年夏天，史蒂文会在电脑公司工作，或者成为一个海滨迷；e)如果我整晚上都在做这个作业，我就可以回答所有的问题，如果回答了所有的问题，我就能理解本质，因此，如果我整晚都在做这份作业，我就能理解本质；解答：每个语句使用的推理规则如下：a)简化b)析取三段论c)假言推理d)附加律e)假言三段论作业1.17【习题1.5第14题】：对每个语句，解释每一步骤使用了那些推论法则。a)这个班的学生琳达(Linda)，有一个红色的敞篷车，每一个有敞篷车的人都至少得到过一次超速罚单，因此这个班有人得到过超速罚单；b)寝室里面的五个人，Meslissa,Aaron,Ralph,Veneesha和Keeshawn都选修了离散数学，每个选修了离散数学的人都可以选修算法，因此，寝室所有人都可以在下一年选修算法；8 c)所有JohnSayles拍摄的电影都很棒，JohnSayles拍摄了一部关于煤矿工的电影，所以有一部关于煤矿工的很棒的电影；d)这个班有学生在法国呆过，每个在法国呆过的人都参观过卢浮宫，因此，这个班有人参观过卢浮宫。解答：a)D(x)表示x有敞篷车，C(x)表示x得到过超速罚单，则(1)∀x(D(x)→C(x))//前提引入(2)D(Linda)→C(Linda)//(1)全称例化(3)D(Linda)//前提引入(4)C(Linda)//(2)(3)的假言推理(5)∃xC(x)//(4)存在推广b)D(x)表示x有离散数学课程，C(x)表示x可以选修算法课程，则(1)D(Meslissa)∧D(Aaron)∧D(Ralph)∧D(Veneesha)∧D(Keeshawn)//前提引入(2)∀xD(x)//(1)的全称推广(3)∀x(D(x)→C(x))//前提引入(5)D(a)→C(a)//(3)全称例化(6)D(a)//(2)全称例化(7)C(a)//(5),(6)假言推理(8)∀xC(x)//(7)全称推广c)D(x)表示x是JohnSayles拍摄的电影，C(x)表示电影x很棒，a表示一部关于煤矿工的电影，则(1)∀x(D(x)→C(x))//前提引入(2)D(a)→C(a)//(1)的全称例化(3)D(a)//前提引入(5)C(a)//(2)(3)假言推理(6)∃C(x)//(5)存在推广d)D(x)表示x去过法国，C(x)表示x去过卢浮宫，则(1)∃xD(x)//前提引入(2)D(a)//(1)存在例化(3)∀xD(x)→C(x)//前提引入(4)C(a)//(2)(3)假言推理(5)∃xC(x)//(4)存在推广9 作业1.18【习题1.5第16题】：判断下列语句的正误，并给出解释：a)每个被大学录取的人都住过宿舍，Mia从没住过宿舍，因此，Mia没有被大学录取；b)敞篷车开起来很有趣，Isaac的车不是敞篷车，因此，Isaac的车开起来不是很有趣；c)Quincy喜欢所有的动作电影，Quincy喜欢电影八面威风，因此八面威风是动作电影；d)所有捕龙虾的渔夫都至少打了一个陷阱，Hamilton是一个捕龙虾的渔夫，因此Hamilton至少打了一个陷阱；解答：a)正确b)错误，敞篷车开起来有趣不代表别的车开起来没有趣味。c)错误，Quincy喜欢所有的动作电影不代表Quincy喜欢的电影都是动作电影。d)正确。作业1.19【习题1.5第24题】：找出下面证明如果∀x(P(x)∨Q(x))是正确的，则∀xP(x)∨∀xQ(x)也是正确的过程中的错误。(1)∀x(P(x)∨Q(x))//前提引入(2)P(c)∨Q(c)//(1)全称例化(3)P(c)//(2)化简(4)∀xP(x)//(3)全称推广(5)Q(c)//(2)化简(6)∀xQ(x)//(5)全称推广(7)∀xP(x)∨∀xQ(x)//(4)(6)合取解答：第(3),(5),(7)句都是错的：其中(3),(5)中使用的化简规则对析取使用而非合取（化简规则应对合取使用）；(7)中的合取规则是对析取使用而非合取。1.6IntroductiontoProofs作业1.20【习题1.6第16题】：证明若m和n是整数，且mn是偶数，则m或者n是偶数；解答：利用反证法。若是m和n都是奇数，设m=2k+1，n=2q+1，k,q为非负整数,则mn=(2k+1)(2q+1)=4kq+2k+2q+1，显然4kq，2k，2q都是偶数，所以4kq+2k+2q+1是奇数，这与mn是偶数矛盾！所以m,n中至少有一个是偶数。证毕。1.7ProofMethodsandStrategy作业1.21【习题1.7第5题】：证明三角不等式|x|+|y|≥|x+y|,其中x和y是实数，|x|表示当x大于等于零的时候，取x自身，当x小于零的时候，取x的相反数。解答：分三种情况讨论：当x和y都是大于等于零的时候，|x|+|y|=|x+y|；当x和y都是小于零的时候，左边为−(x+y)，右边也是−(x+y)，二者相等；当x和y中一个为非负一个为负时，不妨设x≥0，则y小于零，此时左边为x−y,若|x|≥|y|,右边为x+y,因为y小于零，所以x−y≥x+y,即|x|+|y|≥|x+y|，若|x|≤|y|，右边为−x−y，因为x大于等于零，则x−y≥−x−y,即|x|≤|y|。命题得证。10 点评1.5这一题在分情况证明时，有些同学并没有将所有情况都列出来，常见的是分x>0,y>0;x<0,y>0;x>0,y<0;x<0,y<0等几种情况，而忽略了x=0或y=0这种情况。作业1.22【习题1.7第7题】：证明存在100个连续的正整数，他们都不是完全平方数。你的证明是构造性的还是非构造性的？解答：我们知道一个完全平方数一定可以表示成k2的形式，其中k是整数。现在我们只需要找到这样的k，使得k2和(k+1)2之间存在连续一百个正整数即可，即2k≥100，不难解出此时k≥50，事实上我们任取大于等于50的k，则在k2和(k+1)2之间存在连续一百个正整数。这是一个构造性的证明。p作业1.23【习题1.7第22题】：实数x和y的二次均值可以表示成(x2+y2)/2，通过利用几组正实数计算二次均值和算数均值，对他们的大小关系进行猜想，并证明你的猜想。p解答：(x2+y2)/2≥(x+y)/2，证明如下：(x+y)2≥0则x2+y2≥2xy，则4(x2+y2)≥2(x2+y2)+4xy，则4(x2+y2)≥2(x+y)2，则(x2+y2)/2≥(x+y)2/4，对上式两边开根号即得所求结论。作业1.24【习题1.7第33题】：证明任意两个有理数之间必存在无理树。解答：不失一般性，我们可假设两个有理数可表示成有共同分母的两个分数a/b和c/b，且a0do2:n:=2n3:endwhileb)proceduredivide(n:positiveinteger)Ensure:1:whilen≥0do2:m:=1/n3:n:=n−14:endwhilec)proceduresum(n:positiveinteger)Ensure:1:sum:=02:whilei<10do3:sum:=sum+i4:endwhiled)procedurechoose(a,b:positiveinteger)Ensure:1:x:=eitheraorb解答：a)缺少有限性(finiteness)，循环没有终止条件。b)缺少正确性(correctness)，因为存在n=0的情况，而n作为分母是不能为零的。c)缺少明确性(definiteness)，i的值从未给出。18 d)缺少明确性(definiteness)，程序无法判定x究竟选择a还是b的值。作业3.2【习题3.1第8题】：设计一个算法，找到n个不同的输入的整数中的最大的偶数并返回它的位置，若不存在偶数，则返回0。解答：Algorithm1largestevenlocationRequire:Setk=0;largest=−∞;i=1Ensure:1:whilei≤ndo2:ifaiisevenandai>largestthen3:k←i;largest←ai;4:endif5:i←i+1;6:endwhile7:returnkisthedesiredlocation(or0iftherearenoevens)3.2TheGrowthofFunctions作业3.3【习题3.2第20题】：给出下面函数的大O估计，对每个使得f(x)为O(g(x))的函数g，用最小的值表达函数g。a)(n3+n2logn)(logn+1)+(17logn+19)(n3+2);b)(2n+n2)(n3+3n);c)(nn+n2n+5n)(n!+5n)解答：a)可以表示为O(n3logn+n3logn),等于O(n3logn);b)可以表示为O(2n·3n)=O(6n);c)可以表示为O(nn·n!);点评3.1由于n!属于O(nn)，因此有的同学将c)写成O(nn·nn)，也就是O(n2n)，并进一步认为是O(nn)，这最后一步是错误的，因为n2n不属于O(nn)!3.3ComplexityofAlgorithms作业3.4【习题3.3第8题】：这里有一个比传统方法更有效的计算当x=c时，多项式axn+naxn−1+...ax+a的值的方法。它被称之为Horner方法。Horner方法可以用如下的算法描述：n−110procedureHorner(c,a0,a1....an:realnumbers)Ensure:1:y:=an2:fori:=1tondo19 3:y:=y∗c+an−i;4:endfornn−15:returny=anx+an−1x+...a1x+a0a)计算当x=2时3x2+x+1通过Horner方法计算出的每一步的值;b)用这种方法当多项式最高次为n,x=c时，用了多少次乘法和加法呢？（循环的变量自加不计算在加法中）解答：a)初始时y=3,i=1时，y=3·2+1=7,i=2时，y=7·2+1=15;b)每次循环使用了一次加法和乘法，所以当多项式最高项为n时，共使用了n次加法和n次乘法;3.4TheIntegersandDivision作业3.5【习题3.4第24题】：证明若n是奇数，则n2≡1(mod8)。解答：若n是奇数，设n=2k+1,k为自然数，则n2=4k2+4k+1=4k(k+1)+1，不难证明，k和k+1中有且只有一个偶数，则k(k+1)可以被2整除，则4k(k+1)可以被8整除。所以，n2≡1(mod8)。3.5PrimesandGreatestCommonDivisors3.6IntegersandAlgorithms作业3.6【习题3.6第22题】：用算法5计算1231001mod101。解答：首先有1001=(1111101001)，然后开始计算123mod101=22,1232mod101=280,1234mod101=37,1238mod101=56,12316mod101=5,12332mod101=23,12364mod101=19,123128mod101=58,123256mod101=31,123512mod101=52,所以我们要计算的结果从22,56,25,19,58,31,52中产生，将它们的乘积模11,两两相乘不停地除以11,最后结果为22.作业3.7【习题3.6第24题】：用辗转相除法计算下列各式。a)gcd(1,5);b)gcd(100,101);c)gcd(123,277);d)gcd(1529,14039);e)gcd(1529,14038);f)gcd(11111,111111);解答：a)gcd(1,5)=gcd(1,0)=1;b)gcd(100,101)=gcd(100,1)=gcd(1,0)=1;c)gcd(123,277)=gcd(123,31)=gcd(30,1)=gcd(1,0)=1;d)gcd(1529,14039)=gcd(1529,278)=gcd(278,139)=gcd(139,0)=139;20 e)gcd(1529,14038)=gcd(1529,277)=gcd(277,144)=gcd(144,133)=gcd(133,11)=gcd(11,1)=gcd(0,1)=1;f)gcd(11111,111111)=gcd(11111,1)=gcd(1,0)=1;点评3.2上面两题最大的问题是有不少人不愿意按照相应的算法写出过程，这就无法检验他是否真的弄懂了算法本身。3.7ApplicationsofNumberTheory作业3.8【习题3.7第18题】：求下列问题解的同余系。解答：由中国剩余定理知，答案一定是以3·4·5=60为模；我们有a1=2,m1=3,a2=1,m2=4,a3=3,m3=5,M1=60/3=20,M2=60/4=15,M3=60/5=12,而M1,M2,M3的逆为y1=2,y2=3,y3=3，所以x=80+45+108=233≡53(mod60)所以，解为所有的形如53+60k的整数。点评3.3有的同学在求yi时，是直接令yi=Mimodmi，从而得到结果是17。这是错误的，表明这些学生没有仔细看中国剩余定理的证明!yi是Mi的逆，即使得yiMi≡1(modmi)。21 第四章InductionandRecursion4.1MathematicalInduction作业4.1【习题4.1第18题】：让P(n)解释成语句n!21时，若对每一个18≤k≤n的k,P(k)成立.c)n=k+1时，P(n)成立;d)n=k+1时，n−4=k−3≥18由归纳假设知P(n−4)成立，由于P(n)=P(n−4)+4,所以P(n)可以由四分和七分的邮戳表示，所以P(n)成立；e)由我们的归纳假设和归纳的步骤知道，21≤k≤n成立就可以推导出n=k+1成立，即当之前的归纳假设全部成立，就可以推导出下一个公式成立，进而可以推到n=k+2,n=k+3....都是成立的，又由于n=18,19,20,21的归纳基成立，那么对于所有的n≥18，语句都是成立的，故命题得证;23 作业4.4【习题4.2第12题】：用强数学归纳法证明每个正整数都可以表示成不同的2的幂指数的和。证明实际上，要证明的命题P(n)是：存在m及0≤a1a>...a)则k+1一定可以唯一表示12i成2a1+1+2a2+1+...2ai+1(a>a>...a)，命题成立！若k+1为奇数，则k为偶数，则k可以表示12i为2a1+2a2+...2ai(a>a>...aanda6=0)，那么k+1可以表示成2a1+2a2+...2ai+20(a>a>12ii12...aiandai6=0)，故命题得证！作业4.5【习题4.2第40题】：用well-ordering原则证明在实数x,y,x1/(y−x)。定义集合+S={j∈Z|x1。记r=bxc+j0/A。由于j0是S的最小元素，所以x≥bxc+(j0−1)/A，即x≥r−1/A，即1/A≥r−x，而A>1/(y−x)，即y−x>1/A，从而y−x>r−x，即y>r。从而x1/(y−x),现在关注bxc+(j/A)，（其中j是一个正整数）显然每个形如这个形式的数字都是有理数，我们总可以选择适当的并且最小的j,使得这样的数大于x,由well-ordering原则我们知这样的j是存在的，那么我们有：r=bxc+(j/A)>x但是bxc+((j−1)/A)=r−(1/A)1）：建立一个新的序列l，它是把与an相同的项目全部从L中删除后得到的序列，这样我们可以清楚的得到an的个数，不放设为k,设原有的前n−1项的mode为m，mode为ai,比较k,m大小，若k>m，则mode为an,并记录k，反之前n项与前n−1项的mode相同，mode出现次数为m。作业4.12【习题4.4第18题】：当n是非负整数时，证明算法1对计算n!是正确的;解答：n=0时算法得到的结果为1，并且实际结果也为1，基本步正确；当n=k时，假设算法正确，则当n=k+1时，算法执行else部分，是把第k+1项乘到前k项的乘积（有前面提到的，我们假设这个是正确的）上，所到的的数与实际相符合，所以第k+1次也正确，故算法正确。作业4.13【习题4.4第32题】：设计一个递归算法，来找到序列的第n项，序列用如下的形式定义：a0=1,a1=2,a2=3并且an=an−1+an−2+an−3(n=3,4,5....);解答：Algorithm3sequence(n)Ensure:1:ifn<3then2:sequence(n):=n+1;3:else4:sequence(n):=sequence(n−1)+sequence(n−2)+sequence(n−3)5:endif6:returnsequence(n)作业4.14【习题4.4第33题】：用迭代算法来求上题中的第n项;解答：Algorithm4sequence(n)Ensure:1:ifn=0then2:z:=1;3:elseifn=1then4:z:=25:else6:x:=1,y:=2,z:=37:fori=1ton−2do8:w:=x+y+z9:x:=y10:y:=z11:z:=w12:endfor13:endif14:returnz27 第五章Counting5.1TheBasicsofCounting作业5.1【习题5.1第14题】：有多少个以1开头并结尾，且长度为n（n是正整数）bit的二进制串;解答：当n=1，时，只有一个；当n≥2时，剩下的n−2位，每一位都有两种选择，所以共有2n−2个。作业5.2【习题5.1第20题】：有多少个小于1000的正整数a)可以被7整除;b)能被7整除而不能被11整除;c)能同时被7和11整除;d)能被7或者11整除;e)只能被7或者11中的一个整除;f)既不能被7又不能被11整除;g)有不同的数字;h)有不同的数字并且是偶数;解答：a)b999/7c=142,所以有142个;b)b999/7c=142，b999/11c=90，b999/77c=12，欲求能被7整除而不能被11整除的数字，只需要142−12=130,所以共有130个。c)由上面b计算知，本题答案为12;d)由上面b计算和容斥原理知，本题答案为142+90−12=220;e)在计算这一部分时，应该由能被7或者11整除的数字中再减去能同时被7和11整除的数字，由上面计算知，本题答案为220−12=208;f)只需要用总数减去能被7或者11整除的数字即可，由上面计算知，本题答案为999−220=799;g)我们把数字分成三种，一位数，两位数和三位数，对于一位数而言，他们本身就是独特的数字，共有9个，两位数中十位有9中选择，当选定十位后，对应每种选择，个位也有9中选择（因为十位数是不能选0而个位数却可以）所以共有81种;三位数的话按照上面的选择方式共有9·9·8=648种，所以共有9+81+648=738。作业5.3【习题5.1第52题】：用树图去寻找长度为4的二进制字符串中的没有连续三个0的字符串;解答：28 5.2ThePigeonholePrinciple作业5.4【习题5.2第14题】：a)证明从前十个正整数中挑选七个正整数，一定有至少两对的和为11;b)若是把(a)部分中，挑选的数字的数目变成六，结论是否成立？解答：a)我们按照两数字求和为11进行分组，可以得到1,10,2,9,3,8,4,7,5,6,现在选择七个数字的话一定会有两组被全部选中，故命题得证。b)不成立，不妨选择1,2,3,4,5,6，则只存在一组5,6的和为11，故命题不成立;5.3PermutationsandCombinations作业5.5【习题5.3第12题】：长度为12的二进制字符串包含多少：a)恰好只有三个1;b)至多有三个1;c)至少有三个1;d)有一样多的0和1;解答：a)恰好只有三个1时为，C(12,3)=220;b)至多有三个1可以表示成C(12,3)+C(12,2)+C(12,1)+C(12,0)=299;c)至少有三个1可以理解成用所有的情况减去字符串中只有0,1,2个1的这些情况，所有的情况可能为212=4096,所以答案为4096−C(12,0)−C(12,1)−C(12,2)=4017;d)有一样多的0和1，说明字符串中恰好有六个1，所以答案为C(12,6)=924;作业5.6【习题5.3第24题】：有多少种排队方法，使得10个女士和6个男士站成一排，并且两个男人不相邻;29 解答：先对女士进行全排列，共有P(10,10)种可能，男士可以站的位置就是女士之间的空隙，共有11个位置，选择其中6个并且考虑顺序关系，这是一个P(11,6)种可能的排列问题，所以一共有P(11,6)P(10,10)=120708403200种排队方式。作业5.7【习题5.3第38题】：有多少种方法可以从联合国中选出12个理事国，其中三个是从45个国家选择，另外四个从另外57个国家选择，剩下的从剩下的69个国家选择;解答：直观的有C(45,3)C(57,4)C(69,5)=14190·395010·11238513≈6.3×10165.4BinomialCoefficients作业5.8【习题5.4第20题】：假设k,n为正整数且i≤k2时，Kn中包含一个三角形，故无法被二分。b)首先n≥3时，Cn才有定义，当n是奇数时，他不是可二分的，当n是偶数时，它可以被二分。c)每个wheel都含有三角形，所以没有一个Wn是可二分的。d)对所有的n≥1，Qn都是可二分的。我们总可以把点分成两类，一类有奇数个1，另一类有偶数个1。9.3RepresentingGraphsandGraphIsomorphism作业9.5【习题9.3第6题】：用邻接矩阵表示练习2中的图。0101010011解答：000111110001100作业9.6【习题9.3第26题】：用incidence矩阵表示练习1，2中的图。47 1100001110010110010010解答：练习1：，练习2：0000110100101101000111000101作业9.7【习题9.3第38题】：判断下列的一对图是否是同构的。解答：他们是同构的，两个图形都包含K4,并且第五个点都和K4中的两个点相连。许多同构都是可以的，这里列举一个可行的：f(v1)=v1,f(v2)=v3,f(v3)=v2,f(v4)=v5,f(v5)=v4.9.4Connectivity作业9.8【习题9.4第2题】：从下面的图中找出的这些点序列是否能构成路径？那些路径是简单路径？那些是回路？路径长度分别是多少？a)a,b,e,c,b。b)a,d,a,d,a。c)a,d,b,e,a。d)a,b,e,c,b,d,a.解答：a)这是长度为4的路径，但不是回路，因为它始于a点儿终止于b点，是简单路径，因为没有边重复。b)这是一个长度为4的路径，是回路，不是简单路径，因为存在边被使用了两次。48 c)不是路径，因为没有d到b的边。d)不是路径，因为没有b到d的边。作业9.9【习题9.4第12题】：判断下列的图是否是强连通的，是否是弱连通的。a)b)c)解答：a)他不是强连通的，因为a到c没有可达的有向路径，但它是弱连通的。b)它是强连通的，因为任意两个点之间都有到达彼此的路径。显然，它一定是弱连通的。c)既不是强连通的，也不是弱连通的。因为没有a到b的可达路径。作业9.10【习题9.4第30题】：找出下图中的割点。解答：c,d是割点，移除其中的任意一个都会使得图变成两部分。49 作业9.11【习题9.4第48题】：用理论2找出练习2中的有向图从a到c的最短路径的长度。解答：首先我们可以写出练习2的邻接矩阵如下：0101010001A=010001000000110关注矩阵中的(1,3)（第一行第三列），它为0，代表不存在a到c的长度为1可达路径，紧接着计算A2，2000101120A2=100010101010110关注矩阵中的(1,3)（第一行第三列），它为0，代表不存在a到c的长度为2可达路径，紧接着计算A3，A3的第一行第三列为1，故存在1条a到c的距离为3的可达路径。所以最短距离为3.9.5EulerandHamiltonPaths作业9.12【习题9.5第2题】：判断下图是否存在欧拉回路，若存在则构建这个回路。若不存在欧拉回路，判断是否包含欧拉道路并构建。解答：所有点的度数都为偶数，所以存在欧拉回路。一个可行的欧拉回路为a,b,c,f,i,h,g,d,e,h,f,e,b,d,a。作业9.13【习题9.5第28题】：当m,n为何值时，全二分图Km,n包含a)欧拉回路？b)欧拉道路？解答：a)考虑到二分图两边的点的度数分别为m和n，当且仅当m,n同时为偶数的时候才能包含欧拉回路。b)所有包含欧拉回路的情况，一定都包含欧拉道路，所以m,n同时为偶数时，包含欧拉道路。另外，K1,1明显包含欧拉道路。还有一种情况为Kn,2,其中n为奇数，则图中仅有两个点的度数为奇数，其余的都为偶数，满足欧拉道路的判别条件，此时包含欧拉道路，其余的情况都不满足条件。50 作业9.14【习题9.5第40题】：判断练习33中的图是否包含哈密顿道路，若有，则找到他，若没有，指明原因。解答：图中有三个结点的度数为1，都可以作为哈密顿的终点，但是一条路径最多两个终点，所以不存在哈密顿道路。9.6Shortest-PathProblems作业9.15【习题9.6第5题】：找出练习3的带权图中从a到z的最短路径。解答：a,c,d,e,g,z.9.7PlanarGraphs作业9.16【习题9.7第6题】：判断下图是否为平面图，若是，以边不相交的形式画出该平面图。解答：它是平面图.图如下：51 作业9.17【习题9.7第12题】：假设一个平面的连接图有八个顶点，每个顶点的度数为3，则该图将平面分成多少个区域？解答：由欧拉公式知：v−e+r=2,其中v=8，由常识知，度数的和应为边的两倍，所以e=(3·8/2)=12，代入公式，所以r=6。52 第十章Trees10.1IntroductiontoTrees作业10.1【习题10.1第4题】：回答下列关于树的问题。a)哪个结点是根节点。b)哪些结点是内部结点。c)哪些结点是叶子结点。d)哪些结点是j的孩子结点。e)哪个结点是h的父结点。f)o的兄弟结点有哪些。g)m的祖先有哪些。h)b的后代有哪些。解答：a)a是根节点，因为在树的顶端。b)a,b,c,d,e,g,h,i,o是内部结点。c)c,f,j,k,l,m,n,p,q,r,s是叶子结点。d)没有结点是j的孩子结点。e)d是h的父结点。53 f)o的兄弟结点有i。g)m的祖先有g,b,a。h)b的后代有e,f,g,j,k,l,m。作业10.2【习题10.1第6题】：练习4中的结点是否满足某个m的满m叉树？解答：不是，因为有的结点有3个孩子，所以m最小为3，但是有的结点有一个或者两个孩子，故不是满3叉树，所以他不是满m叉树。作业10.3【习题10.1第16题】：m,n为何值时，完全可二分的Km,n是树。解答：若m,n，都至少为2，那么显然存在一个长度为4的环路，所以他们至多有一个大于等于2，另一方面若m=1,则对于任意的n,Km,n都是树。所以Km,n是树当且仅当m=1或者n=1。作业10.4【习题10.1第22题】：这是一个寄信链。他开始于一个人发送出去五封信件（每封信件对应一个接受者，下同），收到的人每人再给没有发送过信件或者没有收到过信件的人发送五封信件，假设有10000个人在链结束前发送出去了信件，并且每个人至多只收到了一封信件，请问：有多少人收到了信件？有多少人没法送信件？解答：这是一棵满五叉树。发送者个数为10000个，对应于10000个有分叉的内结点，由理论4可知，共有n=mi+1=10000∗5+1=50001个结点，共有l=(m−1)i+1=40001叶子结点，对应了只接受到了信件，而未发送信件的人。除了最先发送信件的人，所有人都收到了信件，所以共有50000人收到了信件。10.2ApplicationofTrees作业10.5【习题10.2第20题】：用前缀码表示下面代码序列，构建二进制树。a)a:11,e:0,t:101,s:100b)a:1,e:01,t:001,s:0001,n:00001c)a:1010,e:0,t:11,s:1011,n:1001,i:10001解答：a)54 b)c)作业10.6【习题10.2第24题】：对下面的的特征序列构建哈夫曼编码。A:0.10,B:0.25,C:0.05,D:0.15,E:0.30,F:0.07,G:0.08。解答：先将最小权重的C，F结合，我们称之为T1,求和得到0.05+0.07=0.12，比G,A的权重要大，紧接着将G和A结合，得到0.1+0.08=0.18,比D以及T1权重要大，我们称之为T2，按照将最小两个权重相加的原则，依次类推，将D与T1结合，得到和为0.27的T3,讲B与T2结合，得到和为0.43的T4,E和T3结合得到T5,T4,T5的结合就是最后的哈夫曼树,用0−1将分叉结点编码即可。（具体编码可参考下图），加权求和知3·0.10+2·0.25+4·0.05+3·0.15+2·0.30+4·0.07+3·0.08=2.57，所以平均需要2.57bit来表示每个字母。55 10.3TreeTraversal作业10.7【习题10.3第8题】：给出下图的前序遍历结果。解答：前序遍历结果如下：a,b,d,e,i,j,m,n,o,c,f,g,h,k,l,p.作业10.8【习题10.3第11题】：给出练习8的中序遍历结果。解答：中序遍历结果如下：d,b,i,e,m,j,n,o,a,f,c,g,k,h,p,l作业10.9【习题10.3第14题】：给出练习8的后序遍历结果。56 解答：后序遍历结果如下：d,i,m,n,o,j,e,b,f,g,k,p,l,h,c,a作业10.10【习题10.2第20题】：a)用二进制树表示((x+2)↑3)∗(y−(x+3))−5b)求他的前序表达式c)求他的后序表达式d)求他的中序表达式解答：a)结果图如下b)−∗+↑+x23−y+3x5.c)x2+3↑y3x+−∗5−.d)中序表达式即为题目表述的本身：(((x+2)↑3)∗(y−(x+3))−5)10.4SpanningTrees10.5MinimumSpanningTrees作业10.11【习题10.5第4题】：用Prim算法找出下图中的最小生成树。57 解答：边按照下列的顺寻添加到最少生成树中：{a,b},{a,e},{a,d},{c,d},{d,h},{a,m},{d,p},{e,f},{e,i},{g,h},{l,p},{m,n},{n,o},{f,j},{k,l}.最小生成树长度为28.作业10.12【习题10.5第8题】：用Kruskal算法找出练习4中的最小生成树。解答：边按照下列的顺寻添加到最少生成树中：{a,b},{a,e},{c,d},{d,h},{a,d},{a,m},{d,p},{e,f},{e,i},{g,h},{l,p},{m,n},{n,o},{f,j},{k,l}.最小生成树长度为28.58'