《金属学原理》各章习题及解答(第一章晶体题解).pdf 17页

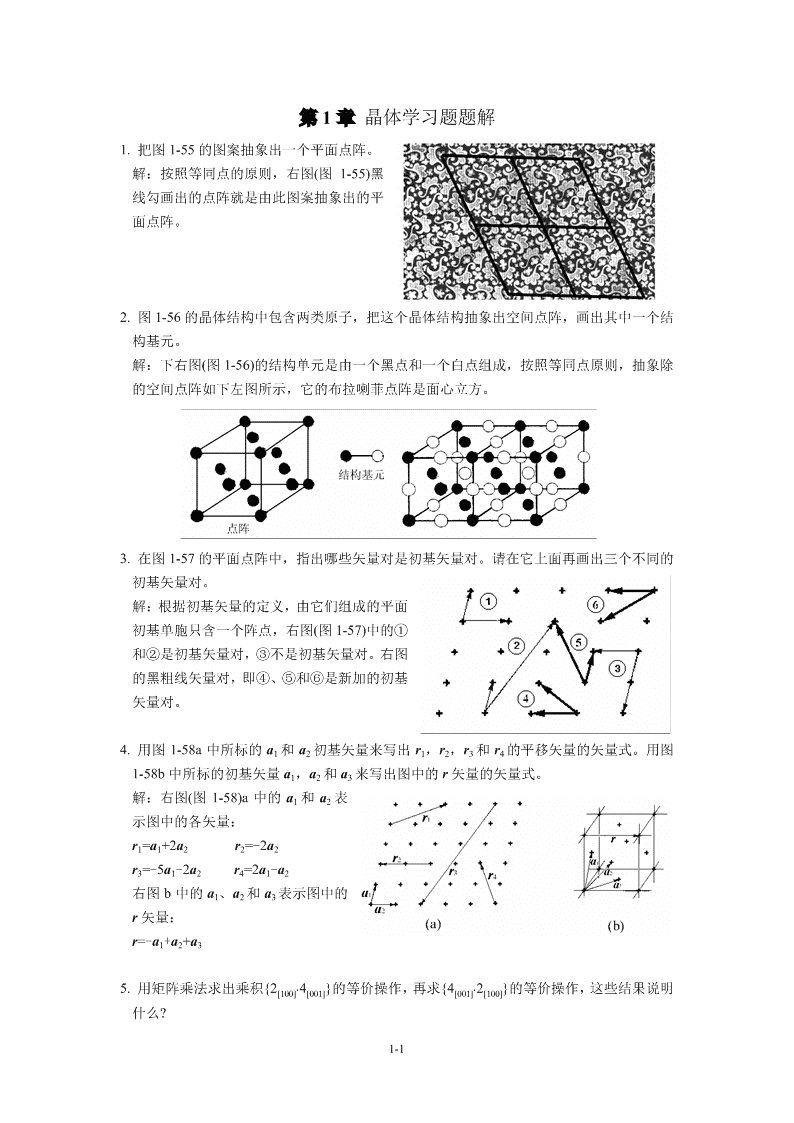
'第1章晶体学习题题解1.把图1-55的图案抽象出一个平面点阵。解：按照等同点的原则，右图(图1-55)黑线勾画出的点阵就是由此图案抽象出的平面点阵。2.图1-56的晶体结构中包含两类原子，把这个晶体结构抽象出空间点阵，画出其中一个结构基元。解：下右图(图1-56)的结构单元是由一个黑点和一个白点组成，按照等同点原则，抽象除的空间点阵如下左图所示，它的布拉喇菲点阵是面心立方。3.在图1-57的平面点阵中，指出哪些矢量对是初基矢量对。请在它上面再画出三个不同的初基矢量对。解：根据初基矢量的定义，由它们组成的平面初基单胞只含一个阵点，右图(图1-57)中的①和②是初基矢量对，③不是初基矢量对。右图的黑粗线矢量对，即④、⑤和⑥是新加的初基矢量对。4.用图1-58a中所标的a1和a2初基矢量来写出r1，r2，r3和r4的平移矢量的矢量式。用图1-58b中所标的初基矢量a1，a2和a3来写出图中的r矢量的矢量式。解：右图(图1-58)a中的a1和a2表示图中的各矢量：r1=a1+2a2r2=-2a2r3=-5a1-2a2r4=2a1-a2右图b中的a1、a2和a3表示图中的r矢量：r=-a1+a2+a35.用矩阵乘法求出乘积{2[100]⋅4[001]}的等价操作，再求{4[001]⋅2[100]}的等价操作，这些结果说明什么?1-1 解：因⎡100⎤⎡0−10⎤⎢⎥⎢⎥{2}=0−10{4}=100[100]⎢⎥[001]⎢⎥⎢⎣00−1⎥⎦⎢⎣001⎥⎦{2[100]⋅4[001]}的等价操作为⎡100⎤⎡0−10⎤⎡0−10⎤⎢⎥⎢⎥⎢⎥{2}⋅{4}=0−10⋅100=−100[100][001]⎢⎥⎢⎥⎢⎥⎢⎣00−1⎥⎦⎢⎣001⎥⎦⎢⎣00−1⎥⎦这组合的操作和{2}操作等效。{4[001]⋅2[100]}的等价操作为[110]⎡0−10⎤⎡100⎤⎡010⎤⎢⎥⎢⎥⎢⎥{4}⋅{2}=100⋅0−10=100[001][100]⎢⎥⎢⎥⎢⎥⎢⎣001⎥⎦⎢⎣00−1⎥⎦⎢⎣00−1⎥⎦这组合的操作和{2}操作等效。对比上面两个结果，操作的顺序不同，所得的操作结果[110]不同。6.画出图1-59中各个形体所有的对称元素。其中a)是立方体，b)是四面体，c)是八面体，d)是正六面柱体。解：下图是立方体和八面体的对称元素示意图。立方体有4个3次轴，它们是4个体对角线，即过立方体中心的3个<111>方向；有3个4次轴，它们是立方体三对平行面的中点连线，即过立方体中心的3个<100>方向；有6个2次轴，它们是过立方体中心的6个<110>方向；有9个镜面，即过立方体中心的3个{100}面和过立方体中心的6个{110}面；有一个对称中心，它就是立方体的中心。立方体顶面和底面中心与过立方体中心并平行于顶面（和底面）的四边形四个顶点连接起来就是一个八面体，所以八面体的对称性质与立方体的相同。它有4个3次轴，3个4次轴，见上图右2图；有6个2次轴，见上图的右3图；有9个镜面，上面最右边的图只画出了四个镜面，它们是过E、F点与ABCD四边形的两条中线连成的两个面以及EAFC面和EBFC面，按同样方法以A、C顶点和B、D顶点也可各得四个镜面，但是其中有三个是重复的，所以共有9个镜面；八面体中心是对称中心。下右图是六面柱体和四面体的对称元素的示意图。六面柱体有1个6次轴，它是过六面柱体中心并垂直顶面和底面的轴；有6个2次轴，它们是过六面柱体中心的六边形的三个对角线和这个六边形对边中点连线；有7个镜面，它们是是过六面柱体中心的六边形面、六1-2 面柱体三对棱连成的三个面以及六面柱体三对柱面中线连成的三个面；有一个对称中心，它是六面柱体的中心。四面体有四个3次轴，它们是四个顶点与其对面的三角形中心的连线；有3个2次轴，它们是六条边两两中点的连线；有6个镜面，它们是每一个面(等边三角形)三条中线与这个面所对的顶角连成的三角形面，这样四个面共作出12个面，但它们有一半是重复的，所以共有6个镜面；四面体没有对称中心。7.画出适当的图形证明：在平行的2次轴通过的两个相邻阵点之间的中点上有另一个2次轴；在平行的镜面通过的两个相邻阵点之间的中点上有另一个镜面。解：右图a是在平行的2次轴通过的两个相邻阵点之间的中点上有另一个2次轴的例子。图中只画出这个平面点阵的一个单胞，在讨论时应记住整个点阵是由这个单胞无限重复平移得出的。可以看出，在原来的阵点上有2次轴，显然，阵点间的中点也是2次轴，如图a左边的图所示。右图b是在平行的镜面通过的两个相邻阵点之间的中点上有另一个镜面的例子。同样，图中只画出这个平面点阵的一个单胞。图中通过阵点的线是镜面(图中的黑线)，可以看出，在这些镜面的中点上，仍有平行于原来镜面的镜面存在，图b左图的虚线。8.画出图1-60中四种平面点阵（它是无限大的）除平移外的所有对称元素及其所在位置（在有限个阵点画出就可以了）。解：把对称元素直接画在图1-60中，如下图所示。图a中过每个阵点并垂直纸面的轴都是2次轴；根据上题的结果，在平行的2次轴中间又有2次轴，所以在四个相邻阵点中间出现新的2次轴；因为α=90°，所以过a1以及过a2轴并垂直纸面的面是镜面，根据上题的结果，在平行的2个镜面中间应是镜面，故在那里又出现新的镜面。图c中过每个阵点并垂直纸面的轴都是2次轴；因在平行的2次轴中间应是2次轴，所以在阵点中间出现新的2次轴，在这些新的2次轴之间又出现新的2次轴；在图中看到一个复式单胞的轴之间夹角是90°，所以过复式单胞两根轴并垂直纸面的两个面是镜面，同样在每一组平行镜面之间又应是新的镜面。图b中a1=a2，并且α=90°，所以过每个阵点并垂直纸面的轴都是4次轴，4次轴隐含2次轴，因在平行的2次轴中间应是2次轴，故在两个4次轴的中间出现1-3 新的2次轴；因为a1和a2构成正四边形，所以过四边形的边并垂直纸面的面以及过四边形对角线并垂直纸面的面都是镜面，同样在平行的镜面的中间又出现新的镜面；在过四边形中心有4个镜面，它们的夹角是45°，根据定理，两个镜面的交线必是旋转对称轴，它的旋转角度是夹角的两倍，所以这交线是4次轴，结果过四边形中心又有一个新的4个次轴。图d中过每个阵点并垂直纸面的轴都是6次轴；6次轴隐含2次轴，在平行的2次轴中间应是2次轴，所以在两个6次轴的中间出现2次轴；根据6次轴对称的性质，每三个阵点构成一个等边三角形，过这三角形的边并垂直纸面的面是镜面，过等边三角的三条中线并垂直纸面的面也是镜面；在等边三角形的中心有三个镜面通过，它们的夹角是60°，根据定理，两个镜面的交线必是旋转对称轴，它的旋转角度是夹角的两倍，所以这交线是3次轴，结果过等边三角形的中心又有一个新的3个次轴。9.立方P、I和F点阵，单胞轴长为a，给出这三种点阵的每一个阵点的最近邻、次近邻的点数，求出最近邻、次近邻的距离。解：立方P、I和F点阵的阵点最近邻、次近邻的点数如右图所示。图中以影线的阵点作为中心，黑点是最近邻的阵点，带有×的阵点是次近邻阵点。P点阵有4个最近邻，阵点与最近邻间的距离是a；有12个次近邻，阵点与次近邻的距离是a2。1-4 I点阵有8个最近邻，阵点与最近邻间的距离是a32，6个次近邻，阵点与次近邻的距离是a；F点阵有12个最近邻，阵点与最近邻间的距离是a2/2，6个次近邻，阵点与次近邻的距离是a。10.对于立方P、I和F点阵，如果每个阵点放上硬球，证明可以填充的最大体积依次为0.52、0.68和0.74。解：如果每个阵点放上硬球，最近邻之间的硬球是相切的，它们中心的距离是硬球的直径。3P点阵的硬球半径是a/2，硬球体积是4π(a/2)/3，每个P点阵含1个阵点硬球，单胞的体3积是a，故P点阵的填充率为34π(a2)填充率==0.523533aI点阵的硬球半径是a34，每个P点阵含2个阵点硬球，故I点阵的填充率为32×4π(a34)填充率==0.680233aF点阵的硬球半径是a24，每个P点阵含4个阵点硬球，故F点阵的填充率为34×4π(a24)填充率==0.740433a11.某正交晶系单胞中，在如下位置有单原子存在：①(0,1/2,0)，(1/2,0,1/2)两种位置都是同类原子；②([1/2,0,0])，(0,1/2,1/2)上是A原子，(0,0,1/2)，(1/2,1/2,0)是B原子。问上两种晶胞各属于哪一种布喇菲点阵？解：①右图a中黑实线是一个正交单胞，a和b分别是两个晶轴，两个带影线的圆代表给定的原子位置，应该注意到在与此等效的所有位置都有原子。根据题意，一个单胞含两个原子，如果把黑线所定的晶轴向-b平移b/2，把现在的ABCDD"A"B"C"六面体看成是单胞，可以知道这是I点阵。②右图b中黑实线是一个正交单胞，a和b分别是两个晶轴，两个带影线的圆代表A原子位置，两个黑色的圆代表B原子位置，应该注意到在与这些位置等效的所有位置都有相应的各类原子。如果把黑线所定的晶轴向-a平移a/2，把现在的CDEFF"C"D"E"六面体看成是单胞，看出这是I单胞，其中结构基元由一个A原子和一个B原子构成。12．图1-61给出Al、W、Nacl、ZnS、MoSi2和BiLi3结构的晶胞，图中每种结构右边的图是投影图，其中数字表示原子的坐标位置。指出它们的结构基元（用坐标位置写出）和布拉维点阵。1-5 解：下左图是Al的晶胞，它的结构基元是一个Al原子；因为三个晶轴的长度相等，轴之间的夹角为90°，根据原子的分布位置知它的布喇菲点阵是面心立方点阵；每个晶胞有4个原子(结构基元)，它们的位置分别是[0,0,0]、[0,1/2,1/2]、[1/2,0,1/2]和[1/2,1/2,0]。下右图是W的晶胞，它的结构基元是一个W原子；因为三个晶轴的长度相等，轴之间的夹角为90°，根据原子的分布位置知它的布喇菲点阵是体心立方点阵；每个晶胞有2个原子(结构基元)，它们的位置分别是[0,0,0]和[1/2,1/2,1/2]。下左图是NaCl的晶胞，它的结构基元由相邻的一个Na原子和一个Cl原子构成，例如在[0,0,0]位置的Na原子和在[0,1/2,0]的Cl原子构成一个结构基元；因为三个晶轴的长度相等，轴之间的夹角为90°，根据结构基元的分布位置知它的布喇菲点阵是面心立方点阵；每个晶胞有4个结构基元(8个原子)，结构基元的位置分别是[0,0,0]、[0,1/2,1/2]、[1/2,0,1/2]和[1/2,1/2,0]。下右图是ZnS的晶胞，它的结构基元由相邻的一个他Zn原子和一个S原子构成，例如在[1,0,0]位置的Zn原子和在[3/4,1/4,1/4]的S原子构成一个结构基元；根据结构基元的分布位置知它的布喇菲点阵是面心立方点阵；每个晶胞有4个结构基元(8个原子)，结构基元的位置分别是[0,0,0]、[0,1/2,1/2]、[1/2,0,1/2]和[1/2,1/2,0]。13.在单胞中画出(010)、(110)、()121、(312)等晶面，画出[]111、[]123、[]110和[211]等晶向。解：在右图左边的单胞画出各个晶面；右边的单胞画出各个晶向，有两个晶向给出了箭头处的坐标数。1-6 14.用四轴坐标系画出六方晶系的()1120、()1012、()1011等晶面及[]1120、[]2113、[]3125等晶向。解：在右图左边的单胞画出各个晶面；右边的单胞画出各个晶向，有1个晶向给出了箭头处相应图中Z坐标轴的坐标数。15.写出图1-62中晶向的四轴坐标晶向指数。解：为了方便地定出四轴坐标晶向指数，先定出三轴坐标的晶向指数，然后再换算成四轴坐标的晶向指数。晶向1，三轴坐标指数是[021]，根据三轴坐标指数[UVW]与四轴坐标指数[uvtw]的换算关系，得u=(2U-V)/3=(0-2)/3=-2/3v=(2V-U)/3=(2×2-0)/3=4/3t=-(u+v)=-(-2/3+4/3)=2/3w=1故晶向1的四轴坐标指数是[2423]。晶向2，三轴坐标指数是[111]，根据三轴坐标指数[UVW]与四轴坐标指数[uvtw]的换算关系，得u=(2U-V)/3=(2-1)/3=1/3v=(2V-U)/3=(2-1)/3=1/3t=-(u+v)=-(1/3+1/3)=-2/3w=1故晶向1的四轴坐标指数是[1123]。晶向3，三轴坐标指数是[112]，根据三轴坐标指数[UVW]与四轴坐标指数[uvtw]的换算关系，得u=(2U-V)/3=(-2+1)/3=-1/3v=(2V-U)/3=(-2+1)/3=-1/3t=-(u+v)=-(-1/3-13)=2/3w=2故晶向1的四轴坐标指数是[1126]。晶向4，三轴坐标指数是[120]，根据三轴坐标指数[UVW]与四轴坐标指数[uvtw]的换算关系，得u=(2U-V)/3=(-2+2)/3=0v=(2V-U)/3=(-4+1)/3=-1t=-(u+v)=-(0-1)=1w=0故晶向1的四轴坐标指数是[0110]。16.列出三斜、单斜、正交及四方系中{210}面族包含面的数目及其指数；列出六方系中{}2130面族包含面的数目及其指数。解：对于{210}面族，①三斜系的对称性最低，{210}面族只含一个(210)晶面。②单斜系的a≠b≠c，α=β=90°≠γ，{hkl}晶面族中的等效晶面指数遵守的规则是：h和k可以同时换号，三个指数不能交换位置；(210)面中2和1同时换号的结果是一样的，所以{210}面族只含1-7 一个(210)晶面。③正交系的a≠b≠c，α=β=γ=90°，{hkl}晶面族中的等效晶面指数遵守的规则是：三个指数不能交换位置，但可以单独换号；又因0的正号和负号是相同的，所以{210}面族含2个晶面：(210)和(210)。④四方系的a=b≠c，α=β=90°≠γ，{hkl}晶面族中的等效晶面指数遵守的规则是：h和k可以交换位置，三个指数可以单独换号；又因0的正号和负号是相同的，所以{210}面族含4个晶面：(210)、(210)、(120)和(120)。对于六方系中{hkil}面族中的等效晶面指数遵守的规则是：h、k和i三个指数可以交换位置，但仍要保持h+k+i=0的条件。{}2130面族中的l=0，其正号和负号相同，故{}2130面族含6个晶面：(2130)、(2310)、(3120)、(3210)、(1230)和(1320)。17.(110)、(112)、(312)面是否同属一个晶带？如是，求出晶带轴的方向指数。解：因为下面的行列式为0：1−1011−2=0−312所以(110)、(112)、(312)面同属一个晶带。它的晶带轴[uvw]的三个指数是−10011−1u:v:w=::=−1:−1:−1−21111−2即其晶带轴的方向指数为[111]，利用晶带定律检验知道，它确实是这三个面的晶带轴。18.下列的晶面：(234)、(201)、(111)、(241)、(221)、(432)、(101)、(010)和(432)中有哪些面属于同一个晶带？求出晶带轴。解：两个晶面一定有交线，交线一定是这两个晶面的晶带轴，这些情况在这里不讨论。不用计算的方法，可以用晶带定律试探求出晶带轴。试探得[102]是(201)、(221)、(432)和(010)面的晶带轴。19.画出面心立方点阵的P初基单胞，写出复式单胞的(110)和(011)在初基单胞中的面指数。从这个例子你能否看出为什么这种点阵通常采用复式单胞来描述解：下图中的粗线是面心立方点阵的F单胞，细线是面心立方点阵的P初基单胞，a"、b"和c"是F单胞的晶轴，a、b和c是P初基单胞的晶轴。下图a画出F单胞的(220)面，它和(110)面平行，实际上也是(110)面。这个面和P单胞的三个晶轴相交构成图中影线三角形，它在a、b和c轴的截距分别是1、1/2和1，因此它在P单胞中的面指数是(212)。下图b画出F单胞的(011)面，这个面和P单胞的三个晶轴相交构成图中影线所示的平行四1-8 边形，它平行于c轴。如果把P单胞的原点平移b，得出此面在晶轴的截距分别为1、-1和∞，因此它在P单胞中的面指数是(110)。由次看出，这两个面本质是等同的，在F单胞它们的面指数的三个数字相同，F单胞反映了晶体的对称性，然而在P单胞的面指数的三个数字不相同，P单胞不能反映晶体的对称性，所以一般采用F单胞而不采用P单胞。20.四方点阵的初基单胞轴长a=2.5nm、c=7.5nm，画出(h0l)的倒易阵点（h和l≤±4）。解：四方点阵a=b≠c，α=β=γ=90°。(h0l)面平行与(010)面，即其晶带轴是[010]，它们的倒易阵点构成的倒易面与正点阵的[010]轴垂直。下图左边是四方点阵(正点阵)初基单胞的(010)面，左边是(h0l)的倒易阵点（h和l≤±4），因为正点阵的b轴垂直于纸面，所以倒易*点阵的a轴在纸面上与正点阵的c轴垂直，长度是正点阵(100)面间距(即a)的倒数，**a=1/2.5nm=0.4/nm；c轴在纸面上与正点阵的a轴垂直，长度是正点阵(001)面间距(即c)***的倒数，c=1/0.75nm=0.133/nm。画出[(100)]及[(001)]倒易点后，把它们周期平移，直到h和l到±4为止。21.画出体心立方点阵[123]晶带的倒易点（各指数≤10），画出面心点阵[]111晶带的倒易点（各指数≤10）。解：立方点阵的倒易点阵也是立方点阵。设立方点阵的点阵常数a=1。**(1)体心立方点阵[123]晶带的倒易点都在(123)倒易面上。在倒易点阵中，(123)倒易面在＊三个轴相截均为阵点时在三个轴的截距分别是6、3和2，即它们的阵点分别是[(600)]、＊＊＊**＊**[(030)]和[(002)]。为了画出过[(000)]的(123)倒易面，把此面在c平移-2c(c=a)，这＊＊＊时，三个阵点的坐标变成：[(602)]、[(032)]和[(000)]。求出正点阵(602)面与(032)＊＊＊面的夹角以及(602)和(032)的面间距的倒数，就可以获得[(602)]、[(032)]和[(000)]三个倒易点，把它们周期平移，并考虑其消光效应，就可得出所求的倒易面。(602)面与(032)面的夹角为−2×−2ocosθ==0.1754θ=79.922226+23+21-9 (602)面的面间距d是60212212=(6+2)=6.32，d602(032)面的面间距d是03212212=(3+2)=3.60d032右图a是根据上面计算的结＊＊果画出[(602)]、[(032)]＊和[(000)]三个倒易点再把它们周期地平移所得的倒易点阵，图中各线的交点都是阵点。仔细分析这一点阵，＊＊在[(000)]和[(602)]阵点＊之间应该还有[(301)]阵＊点；另外，体心立方的倒易点阵的三个指数之和不等于偶数的阵点应消失，[(032)]阵点不*＊＊＊应存在，所以，(123)倒易面的阵点应由[(000)]、[(301)]和[(064)]阵点周期平移所得出，如上图b所示，图中各线的交点都是阵点。**(2)面心点阵[111]晶带的倒易点都在(111)倒易面上。在倒易点阵中，(111)倒易面在三＊个轴相截均为阵点时在三个轴的截距分别是1、1和-1，即它们的阵点坐标分别是[(100)]、＊＊＊**＊**[(010)]和[(001)]。为了画出过[(000)]的(111)倒易面，把此面在c平移c(c=a)，这＊＊＊时，三个阵点的坐标变成：[(101)]、[(011)]和[(000)]。因为面心立方的倒易点阵中阵＊＊＊点的三个指数必须同奇或同偶，否则阵点会消失，所以应以[(202)]、[(022)]和[(000)]作为倒易点阵的基点来讨论。求出正点阵(202)面与(022)面的夹角以及(202)和(022)面的＊＊＊面间距，就可以获得[(202)]、[(022)]和[(000)]三个倒易点，把它们周期平移，并进一步考虑消光效应，就可得出所求的倒易面。(202)面与(022)面的夹角为2×2ocosθ==0.5θ=6022222+22+21-10 (202)面和(022)的面间距是相等的，d的倒数是20212212=(2+2)=2.828d202＊＊＊上图是根据上面计算的结果画出[(202)]、[(022)]和[(000)]三个倒易点，再把它们周期地平移所得的倒易点阵，图中各线的交点都是阵点。仔细分析这一点阵，全部阵点都没有符合消光条件，所以都是倒易阵点。22.求Be（六方系，c/a=1.57）的(1123)与(1120)的夹角和这两种面的面间距。解：(1123)和(1120)面的三轴坐标指数是(113)和(110)。根据六方系(hkl)与(hkl)111222晶面夹角θ的余弦cosθ的式子：22[hh+(hk+hk)2+kk]4c3a+ll1212211212cosθ=[]2222212[]2222212(h+hk+k)4c3a+l(h+hk+k)4c3a+l1111122222(113)和(110)面的夹角θ的余弦cosθ为2[−1+(−1+−1)/2−1]×4×(1.57)/3cosθ==−0.7232212212[(1+1+1)×4×(1.57)/3+3][(1+1+1)×4×(1.57)/3]故θ=136.3°。根据六方系(hkl)面间距的式子22214(h+k+hk)l=+222d3achkl计算(113)面间距d113214(1+1+1)311=+=7.65d=a=0.362a2222211312d3a(1.57)aa(7.65)113计算(113)面间距d11014(1+1+1)41==d=a=0.5a22211012d3aa(4)11023.证明P单胞中的(hkl)面在单胞各轴长上分别各有h、k和l个面截过。解：设(hkl)面的法线单位矢量为n，(hkl)面的面间距为dhkl，a轴在a长度截出(hkl)面的数目m应等于a⋅nm=dhkl***因为n与倒易点阵的Hhkl=ha+kb+lc平行，并且Hhkl的模等于1/dhkl，故∗∗∗(ha+kb+lc)n=H/H=hklhkl1dhkl把它代回前面式子，得∗∗∗a⋅na⋅(ha+kb+lc)m===hdd(1/d)hklhklhkl同理可证明在b和c长度上各有k和l个(hkl)截过。1-11 22224.证明立方系中的(hkl)面是按每隔(h+k+l)个面重复堆垛的。解：立方系(hkl)面法线方向指数与面同名，即为[hkl]，法线从原点遇到第一个阵点，含这个阵点并平行于(hkl)的面就是(hkl)堆垛遇到的第一个重复的面。所以法线从原点遇到第一个阵点间的长度除以(hkl)面的面间距dhkl所得的数目m，它就是重复堆垛之间的面数。根2221/2据方向指数的定义，法线[hkl]从原点遇到第一个阵点间的长度为(h+k+l)，故2221222212(h+k+l)(h+k+l)222m===(h+k+l)22212dhkl1(h+k+l)25.编制一个电算程序计算和画出任一种晶系的任一晶带的倒易阵点。解：（略）26.四方系点阵的(111)面与(110)面的夹角为26.81°，求它的轴比；再求(111)与(101)面的夹角。解：四方晶系(h1k1l1)面与(h2k2l2)面的夹角式子为22(hh+kk)ca+ll121212cosθ=[]2222212[]2222212(h+k)ca+l(h+k)ca+l111222把(111)面与(110)面以及其夹角θ=26.81°代入上式，得2222o(1+1)ca2cacos26.81==[]2212[]2212[222+1]122(1+1)ca+1(1+1)cacaca把上式整理，得122oc⎡−cos26.81⎤=⎢2⎥=1.399a⎣2(cos26.81−1)⎦把(111)面与(101)面指数代入上面给出的夹角式子，得它们的夹角θ"余弦为222ca+11.399+1cosθ"===0.7757[]2212[]2212[2×1.3992+1]12[1.3992+1]12(1+1)ca+1ca+1即θ"=39.132°。27.某点在极射赤面投影图上的坐标用从投影圆中心开始量的纬度和经度来表示。例如：N极为90°N，0°E；E极为0°N、90°E；余类推。A面的大圆通过N、S极，并通过0°N，60°E，B面的极点为20°N，70°W。求两个面的夹角。画出A和B面大圆的投影，量这两个投影的夹角，验证极射赤面投影的保角性。解：用吴氏网找出0°N,60°E极点，过这一极点并通过N、S极点得出A面，同时找出20°N,70°W极点，如下右图所示。因为A面通过N、S极点，所以A面的极点是在W-N极连线上，从0°N,60°E极点向左数90°就获得A面的极点，它是0N,30W。把B极点在吴氏网上转到W-E极的连线上，向右数出90°得出一个极点，过这一极点以及N和S极的大圆就是B极点所对应的B面。得出的A面和B面如下右图所示。过A面和B面的交点1-12 作切线，两切线的交角为40°，同吴氏网量A极点和B极点的夹角也是40°，这就说明极射赤面投影有保角性质。28.极点A的坐标为20°N，50°E，把它绕投影图的法线顺时针转动70°；从N向S看，以逆时针方向绕N-S轴转动80°；绕坐标为20°S，40°W的极点顺时针转动60°。在上列每一种情况求出极点A转动后的位置，并画出转动路线。解：用吴氏网找出坐标为20°N,50°E极点A以及坐标为20°S，40°W的极点B，如下左图所示。A极点绕投影图的法线顺时针转动70°的操作是：以投影圆中心为圆心，把A极点顺时针转动70°获得A"极点，如下中图所示。A极点N-S轴转动80°的操作是：把A极点沿A极点所在的吴氏网纬线向E方向转动，转动40°后到达大圆边上，然后再向反方向转动40°，因为此时极点在投影面下侧，以其反方向的极点表示，即下中图的A""点。A极点绕B极点转动60°的操作(上右图)是：把B极点转向投影图中心，相应A极点沿极点所在的吴氏网纬线向E方向转动，转动了38°后到达大圆边上，再反转4°转到投影圆的下侧，以其反的极点A"点表示；以投影圆中心为圆心，把A"点顺时针方向转动60°，到达A""位置；最后把中心的B"点转回原来B极点位置，相应A""点沿所在的吴氏网纬线向W方向转动，转动了4°后到达大圆边上，再反转38°转到投影圆的下侧，以其反的极点A"""点表示，A"""极点就是A极点绕B极点转动60°的位置。29.画一张立方系晶体的标准(011)投影图，在图上标出{100}、{110}和{111}的所有晶面的极点以及这些晶面构成的晶带的晶带圆。在画出的图中，若(100)极点为N极，(011)极点为E极，求坐标为17°W，24.1°S的晶面的面指数。1-13 解：①以立方系的(011)面作为极射赤面的投影面，[011]为晶带轴的晶带的极点都在基圆圆周上。在(011)面上找出两个互相垂直的低指数方向，如[100]和[011]，这两个晶向的迹点一定在投影图的圆周上(如下图所示)。立方系晶面的法线方向指数与晶面指数同名，所以这两个方向的迹点也是(100)和(011)面的极点，以(011)、(100)和(011)三个互相垂直的面的极点作为参考坐标极点。因为垂直(011)面的晶向[011]是2次对称轴，所以只要标出投影面上由(011)、(100)和(100)三个极点连成的直径的一侧的极点，通过[011]2次轴操作得出另一半的极点。在定出(hkl)极点的一般方法是，计算(hkl)面与三个参考坐标(011)、(100)和(011)极点的夹角，再用吴氏网找出这个极点的位置。先标出除(100)以外的{100}的极点。(010)属于[100]晶带，所以它的极点一定在(011)与(011)相连的投影圆的直径上，计算(010)与(011)及(011)的夹角都为45°，用吴氏网从(011)极点沿上述直径向(011)极点方向量出45°就得出(010)极点。讨论{111}面的极点。(111)属于[011]晶带，所以它的极点一定在(100)与(011)相连的投影圆的直径上，计算知(111)与(100)间的夹角为54.73°，用吴氏网从(100)极点沿上述直径量出54.73°就得出(111)极点；(111)属于[011]晶带，所以它的极点一定在投影圆的圆周上，计算(111)与(100)及(011)的夹角分别为54.73°和35.27°，用吴氏网从(100)极点沿圆周向(011)极点方向量出54.73°就得出(111)极点。因为(111)极点应是(111)极点的反向，所以它的极点位置是在过(111)极点的直径在圆周的另一端的交点。最后讨论除(011)和(011)以外的{110}极点。(110)极点与三个参考坐标(011)、(100)和(011)极点的夹角分别是60°、45°和60°，用吴氏网可量出它的位置；(101)极点与三个参考坐标(011)、(100)和(011)极点的夹角分别是60°、45°和135°，用吴氏网可量出它的位置。上面已标出了半个投影圆的{100}、{110}和{111}晶面的极点，通过[011]2次轴操作得出另一半的极点。上面给出标准(011)投影图，图中的投影大圆以及一些大圆的迹径投影都分别属于一个晶带。②在右图中以(100)极点为N极，(011)极点为E极，用吴氏网量出坐标为17°W，24.1°S的极点位置，如右图所示。这个极点为(hkl)，用吴氏网量出该极点与(100)、(010)和(001)三个极点间的夹角，它们分别为65.9°、65.9°和34°，则1-14 oooh:k:l=cos65.9:cos65.9:cos34=0.4083:0.8043:0.829≈1:1:2这个极点的面指数是(112)。30.画一张Be（六方晶系，c/a=1.57）的标准(0001)极射赤面投影图。在图上标出{2110}、{1010}、{2111}和{1011}所有晶面的极点以及它们构成的晶带圆。解：(0001)面的三轴指数是(001)，六方系在面族中的四轴指数中第三个指数的位置不能改变，所以[001]轴{1010}面族和{2110}面族是的晶带轴。{1010}面族包含的面的三轴指数是(100)、(010)和(110)，它们的极点全部都在标准(0001)极射赤面投影图的大圆圆周上。先在圆周上任意定出(100)极点，计算(100)和(010)面间的夹角是60°，(100)和(110)面间的夹角是-60°，选定(100)极点作为起始极点，沿大圆圆周量出相应的角度就可以定出(010)和(110)以及它们反向的极点。{2110}面族包含的面的三轴指数是(210)、(110)和(120)，和上面讨论的道理相同，[001]轴也是它们的晶带轴，计算(100)和(110)面间的夹角是30°，(100)和(210)面间的夹角是-30°，(100)和(120)面间的夹角是90°，这样，以(100)极点作为起始极点，沿大圆圆周量出相应的角度就可以定出(210)、(110)和(120)以及它们反向的极点。{2111}面的三轴指数是(211)、(111)和(121)，根据六方晶系的面与面间夹角式子，并注意到c/a=1.57，计算(211)面和(001)面间夹角为72.3°、(211)面和(100)面间夹角为34.4°、(211)面和(121)面间夹角为61.5°，用吴氏网在上面定出的极点量出相应的角度，定出(211)极点及其反向极点的位置；因为[001]是六次轴，所以，以投影圆为中心，把(211)极点转动60°得到这个面族的另一个极点(111)及其反向极点的位置；再转动60°又得到这个面族的另一个极点(121)及其反向极点的位置。{1011}面的三轴指数是(101)、(111)和(011)，计算(101)面和(001)面间夹角为61.1°、(101)面和(100)面间夹角为28.9°，在(001)及(100)极点连线上量出上述角度，得(101)极点及其反向极点位置，以投影圆为中心，把(101)极点转动60°得到这个面族的另一个极点(011)及其反向极点的位置；再转动60°又得到这个面族的另一个极点(111)及其反向极点的位置。31.测得一个立方晶系单晶体的三个低指数晶面的极点，设Z轴为投影面的法线，X和Y轴在投影面上，X、Y、Z构成右手坐标系，α是极点方向在投影面上与Y轴的夹角，从投影图上看，顺时针方向转动为正，γ是晶面极点方向(晶面法线方向)与X-Y面的夹角，极1-15 点方向在投影图上方为正。三个极点的α和γ角为：124°，10°；215°，9°及350°，16°。查看标准极图的低指数面间的夹角关系定出三个极点的面指数。（答案：(001)、(100)、(110)）解：下左图是按题意定义的α和γ角的示意图。以A、B和C表示α和γ角为：124°，10°；215°，9°及350°，16°的极点。找出A的极点位置的操作是：用吴氏网从y极点沿大圆圆周顺时针方向量出124°，这点与圆中心连线，把它与吴氏网的赤道重叠，沿赤道线向中心量出10°所得的极点就是所求的极点位置；按同样办法找出B和C极点，如下右图所示。用吴氏网量出A-B极点间的夹角为90°；B-C极点间夹角为135°；C-A极点间夹角为120°。一些立方晶体{h1k1l1}面族与{h1k1l1}面族的夹角(度)在下表列出：{hkl}{h1k1l1}11110011011110009011045090609011154.735.309070.5109.5从上表看出，{100}面族与{110}面族各面之间的夹角可能是45°(或135°)，也可能是90°；{110}面族中各面之间的夹角可能是60°(或120°)，所以A极点会是属于{100}面族，B极点和C极点会是属于{110}面族。再在面族之中考虑，若确定A极点为(100)，则B极点应为(110)，C极点应为(011)。32.图1-63是一个立方系单晶体，它的取向是上题标定的取向。晶体的A面和投影面平行，B面和Y轴成70°(如图示)，pq是A面和B面的交线，与X轴平行。一个晶面和A面及B面相交的迹痕与pq的夹角分别是α=55°和β=157.5°，求此面的面指数(hkl)。1-16 解：因为A面是投影面，而Z轴是A面的法线，所以投影圆的中心是Z轴的极点；在投影圆的圆周上定出X和Y轴的极点。1)先找出A和B面在投影图中的迹线。投影圆是A面的投影，其迹线就是大圆；从右图看出，B面的与Z轴夹角为20°，把XX"与吴氏网的N-S轴重合，B面的迹线应是从N-S轴向负Y方向量20°的经线，如下图所示。2)找出所求的晶面与A面相交的痕迹(α线)的迹点。因α线在A面(投影面)上并与X轴成55°，从X极点开始在大圆周顺时针量出55°，这点就是α线的迹点。3)找出所求的晶面与B面相交的痕迹(β线)的迹点。因β线在B面上，所以它的迹点一定在B面的迹线上，同时β线和X轴夹角为180°-157°=22.5°。从X点开始在B面的迹线上量出22.5°，它就是β线的迹点(见右图)。4)因α线和β线都在所求的晶面上，所求的晶面的法线必与α线和β线垂直，所以，过α线的迹点和β线的迹点的大圆迹痕所对应的极点就是所求面的极点，右图中的Ｃ极点。5)量出所求晶面(hkl)的极点Ｃ与上题定出的(100)、(110)和(011)极点间的角度，分别为∼55°、90°和90°。根据立方晶系计算晶面间夹角的关系，cos90°=0，由(hkl)与(011)间夹角为90°得：k+l=0；由(hkl)与(110)间夹角为90°得：h+k=0；这就得出所求晶面为(111)。另外，因[111]也是(011)的晶带轴，所以，(011)极点也在过α线的迹点和β线的迹点的大圆迹痕上1-17'