中南大学传递过程原理--习题---解答.docx 43页

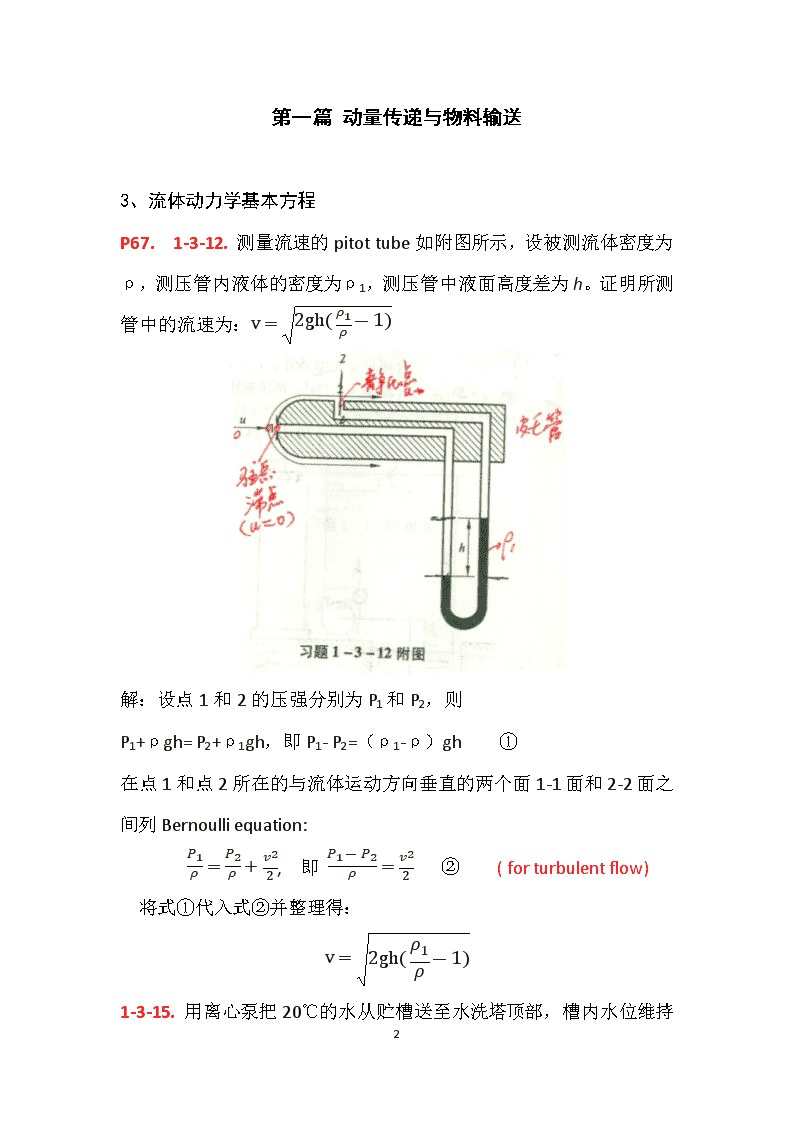
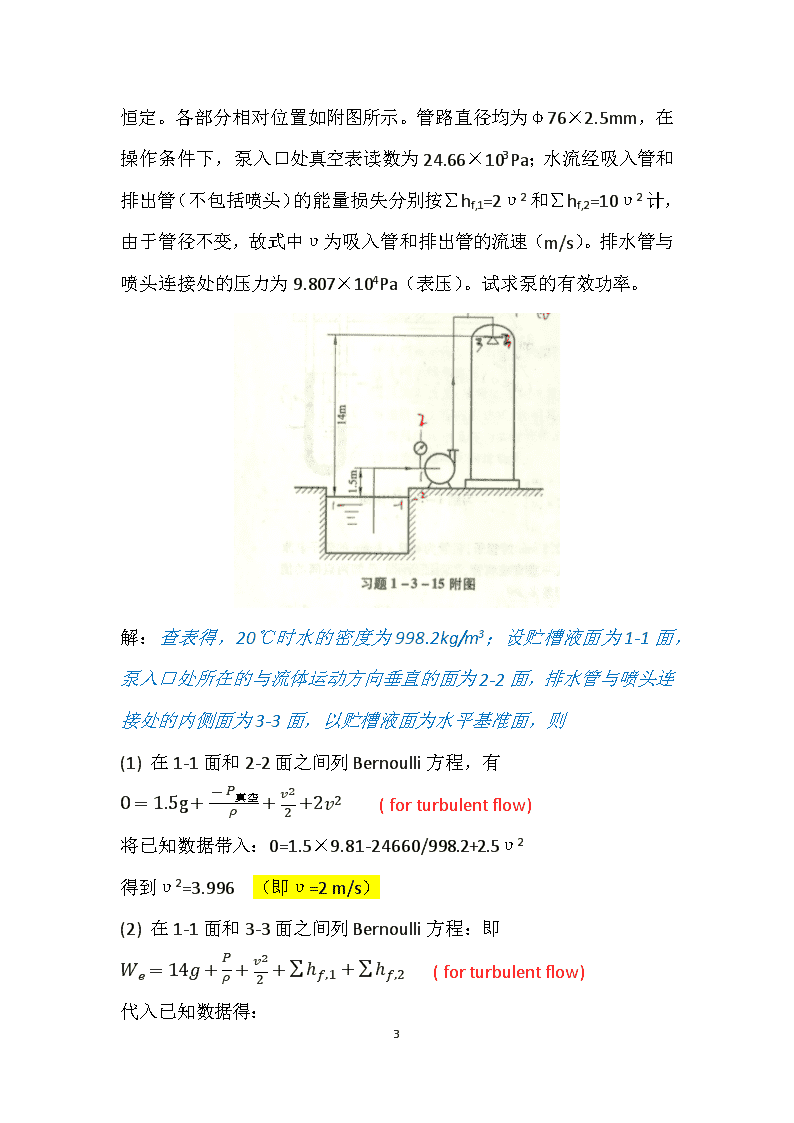
'《传递过程原理》习题（部分）解答2014-12-1943 第一篇动量传递与物料输送3、流体动力学基本方程P67.1-3-12.测量流速的pitottube如附图所示，设被测流体密度为ρ，测压管内液体的密度为ρ1，测压管中液面高度差为h。证明所测管中的流速为：v=2gh(ρ1ρ-1)解：设点1和2的压强分别为P1和P2，则P1+ρgh=P2+ρ1gh，即P1-P2=（ρ1-ρ）gh①在点1和点2所在的与流体运动方向垂直的两个面1-1面和2-2面之间列Bernoulliequation:P1ρ=P2ρ+v22,即P1-P2ρ=v22②(forturbulentflow)将式①代入式②并整理得：v=2gh(ρ1ρ-1)1-3-15.用离心泵把2043 ℃的水从贮槽送至水洗塔顶部，槽内水位维持恒定。各部分相对位置如附图所示。管路直径均为φ76×2.5mm，在操作条件下，泵入口处真空表读数为24.66×103Pa；水流经吸入管和排出管（不包括喷头）的能量损失分别按∑hf,1=2υ2和∑hf,2=10υ2计，由于管径不变，故式中υ为吸入管和排出管的流速（m/s）。排水管与喷头连接处的压力为9.807×104Pa（表压）。试求泵的有效功率。解：查表得，20℃时水的密度为998.2kg/m3；设贮槽液面为1-1面，泵入口处所在的与流体运动方向垂直的面为2-2面，排水管与喷头连接处的内侧面为3-3面，以贮槽液面为水平基准面，则(1)在1-1面和2-2面之间列Bernoulli方程，有0=1.5g+-P真空ρ+v22+2v2(forturbulentflow)将已知数据带入：0=1.5×9.81-24660/998.2+2.5υ2得到υ2=3.996（即υ=2m/s）(2)在1-1面和3-3面之间列Bernoulli方程：即We=14g+Pρ+v22+hf,1+hf,2(forturbulentflow)代入已知数据得：43 We=14×9.81+98070/998.2+12.5×3.996=285.54J/kg(3)根据泵的有效功率Ne=ρQvWe=ρ×υA×We=998.2×2×(3.14×0.0712/4)×285.54=2255.80J/sRe=duρ/μ=0.071×2×998.2/(100.42×10-5)=1.41×105湍流假设成立！1-3-16.用压缩空气将密度为1100kg/m3的腐蚀性液体自低位槽送到高位槽，设两槽的液面维持恒定。管路尺寸均为φ60×3.5mm，其他尺寸见附图。各管段的能量损失为∑hf,AB=∑hf,CD=υ2，∑hf,BD=1.18υ2。两压差计中的指示液均为水银。试求当R1=45mm、h=200mm时：（1）压缩空气的压力P1为若干？（2）U形管压差计读数R2为多少？解：设低位贮槽液面为1-1面，B点所在的与流体运动方向垂直的面为2-2面，C点所在的与流体运动方向垂直的面为3-3面，高位槽的液面为4-4面。(1)PB+ρgR1=PC+5ρg+ρHggR1，代入数据后得到：43 PB-PC=5×1100×9.81+13600×9.81×0.045-1100×9.81×0.045=59473Pa①(2)在2-2面和3-3面之间列Bernoulli方程，有：PBρ=5g+PCρ+0.18v2②将式②整理、并将式①代入后，得：59473/1100=5×9.81+0.18υ2由此得出：υ2=27.866(υ=5.28m/s)(3)在1-1面和4-4面之间列Bernoulli方程，有：P1ρ=10g+2.18v2由此得:P1=(10×9.81+2.18×27.866)×1100=174733Pa=1.74×105pa(gaugepressure)(4)在2-2面和4-4面间列Bernoulli方程，有：PBρ+v22=7g+1.18v2由此可得出：PB=[7×9.81+(1.18-0.5)×27.866]×1100=96382Pa(5)根据流体静力学原理，由图可知，PB=ρHggR2+ρgh，代入数据得：96382=13600×9.81×R2+1100×9.81×0.2得出：R2=0.706m=706mm1-3-19.在图示装置中，水管直径为φ57×3.5mm。当阀门全闭时，压力表读数为0.3大气压，而在阀门开启后，压力表读数降至0.243 大气压，总压头损失为0.5。求水的流量为若干m3/h?解：据题意，设水槽液面为1-1面，出水管出水端内侧面为2-2面，以出水管中轴线为水平基准面。（1）当阀门全闭时，据流体静力学原理，可得：水槽液面的高度为3米；阀门开启后，在1-1面和2-2面之间列Bernoulliequation:3=Pρg+v22g+0.5，代入数据得：3=20000/(1000×9.81)+υ2/(2×9.81)+0.5得出：υ=3m/s（2）水的流量Qv=υA=3×0.25×3.14×0.052×3600=21.20m3/h（3）Re=duρ/μ=0.05×3×1000/(100.42×10-5)=1.5×105＞2300属于湍流1-3-21.本题附图所示的贮槽内径为2m，槽底与内径为32mm的钢管相连，槽内无液体补充，其液面高度h1为2m（以管子中心线为基准）。液体在管内流动时的全部能量损失可按∑hf=20υ2公式计算，式中υ为液体在管内的流速（m/s）。试求当槽内液面下降1m43 时所需的时间。解：属于不稳定流动。设在某时刻t，贮槽液面下降至高度为h处。在贮槽的瞬时液面1-1面与管子出口内侧截面2-2面间列Bernoulli方程，设液体在管内流动为湍流，速度的校正系数为1，则：（1）在1-1面和2-2面间列Bernoulli方程，得gh=v22+20v2，即9.81h=20.5υ2由此得出u=0.69h①（2）由瞬时物料衡算，有-π4d2udt=π4D2dh，即dt=-(Dd)2dhu②将式①代入式②，得：dt=-(Dd)2dh0.69h=-（20.032）2dh0.69h=-5661dhh③确定边界条件：t=0时，h0=h1=2m,t=t时,h1=1m，对式③积分得：t=-5661×2(1-2)=4687s(约1.3h)43 5.流体流动阻力与管路计算P99.1-5-2.某输水管路，水温为10℃，求：（1）当管长为6m，管径为φ76×3.5mm，输水量为0.08L/s时的阻力损失；（2）当管径减小为原来的1/2时，若其他条件不变，则阻力损失又为多少？解：(1)据题意，l=6m,d=76-7=69mm=0.069m,Qv=0.08L/s=0.08/1000m3/s=8×10-5m3/s,查表得10℃水的密度和粘度分别为999.7kg/m3和130.53×10-5Pa.s,则Qv=0.25×3.14×0.0692×u,得出：流速u=8×10-5/(0.25×3.14×0.0692)=2.14×10-2m/sRe=ρud/μ=999.7×2.14×10-2×0.069/(130.53×10-5)=1131laminarflow因此，直管沿程阻力系数λ=64/Re=64/1131=0.057阻力损失为：hf=λldu22=0.057×(6/0.069)×0.5×(2.14×10-2)2=1.13×10-3J/kg(2)当管径缩小为原来的一半,其他条件不变时，流速将变为原来的4倍，Re将变为原来的2倍，即Re=1131×2=2262<2300laminarflow此时沿程阻力将变为原来的16倍，即hf=1.13×10-3×16=0.018J/kg1-5-7.某冶金炉每小时产生20×104m3（标准）的烟气，通过烟囱排至大气，烟囱由砖砌成，内径为3.5m，烟气在烟囱中的平均温度为260℃，密度为0.6kg/m3，粘度为0.028×10-3Pa.s。要求在烟囱下端维持160Pa的真空度，试求烟囱的高度。已知在烟囱高度范围内，43 大气的平均密度为1.10kg/m3，地面处大气压力为常压（砖砌烟囱内壁粗糙度较大，其摩擦阻力系数约为光滑管的4倍。）解：据题意得：烟气平均流速u=20×104/(3600×0.25×3.14×3.52)=5.78m/sRe=3.5×5.78×0.6/(0.028×10-3)=4.34×105>4000查摩狄摩擦系数图中流体力学的光滑管曲线得，Re数为4.34×105时，摩擦系数λ光滑=0.014，由此得：λ=4λ光滑=0.056设烟囱的高度为H，则烟气的沿程阻力损失为：hf=0.056×(H/3.5)×0.5×5.782×[1+(1/273)×260]=0.53H烟囱顶端大气的压力P=1.1×9.81×H=10.79HPa真空度设烟囱下端截面为1-1面，烟囱顶端截面为2-2面，烟囱下端所在平面为基准面，在1-1面和2-2面间列Bernoulli方程：P1ρ=gH+P2ρ+hf，代入数据得：-160/0.6=9.81H-10.79H/0.6+0.53H,整理得：H≈35m1-5-8.水塔每小时供给车间90m3的水。输水管路为φ114×4mm的有缝钢管，总长为160m（包括各种管件及阀门的当量长度，不包括进出口损失）。水温为25℃，水塔液面上方及出水口均为常压。问水塔液面应高出管路出水口若干米才能保证车间用水量。设水塔液面恒定不变，管壁粗糙度ε为0.1mm。43 解：据题意得：水温为25℃，查表得其密度为ρ=996.9kg/m3,粘度μ=90.27×10-5Pa.s,输水管直径d=114-8=106mm=0.106m,l=160m,Qv=90m3/h=90m3/3600s=0.025m3/s,则流速u=0.025/(0.25×3.14×0.1062)=2.83m/s则：Re=0.106×2.83×996.9/(90.27×10-5)=3.31×105,相对粗糙度ε/d=0.1/106=0.000943查图1-5-2得：摩擦系数λ=0.019水输送过程中能量损失总计为:∑hf=0.019×(160/0.106)×(0.5×2.832)=114.84J/kg设水塔液面上方需超出管路出水口H米，水塔液面为1-1面，出水口内截面为2-2面（设为水平基准面），在此两截面间列Bernoulli方程，得：gH=v22+hf,数据得：H=(4+114.84)/9.81=12.11m43 1-5-10.为测定90°弯头的局部阻力系数ξ，可采用本题附图所示的装置。已知AB段总管长为10m，管内径d为50mm，摩擦系数λ为0.03，水箱液面恒定。实验数据为：AB两截面测压管水柱高差Δh为0.425m；水箱流出的水量为0.135m3/min。求弯头局部阻力系数ξ。解：据题意得：Qv=0.135m3/min=0.135m3/60s=0.00225m3/s,则管内水的流速u=0.00225/(0.25×3.14×0.052)=1.15m/s沿程阻力损失为：0.03×（10/0.05）×(0.5×1.152)=3.97J/kg设点A、B所在的截面分别为1-1面和2-2面，在1-1面和2-2面间列Bernoulli方程，有PAρ=PBρ+hf,(忽略弯管的高度)而PA-PB=ρgΔh,由此得到：∑hf=gΔh=9.81×0.425=4.17ξ×(0.5×1.152)+3.97=4.17,整理后得到:ξ=(4.17-3.97)/0.66=0.3043 43 6、流体输送机械(p131)1-6-12.欲用一离心泵将贮槽液面压力为157kPa，温度为40℃，密度为1100kg/m3，饱和蒸汽压为7390Pa的料液送至某一设备，已知其允许吸上真空高度为5.5m，吸入管路中的动压头和能量损失为1.4m液柱，当地大气压为10.34mH2O柱。试求其安装高度（已知其流量和扬程均能满足要求）。解：已知：Pa=10.34mH2O，P0=157kPa，Pv=7390Pa，ρ料液=1100kg/m3，Hs=5.5m液柱，(υ12/2g)+∑hf=1.4m液柱由于被输送料液的温度为40℃，则应对允许吸上真空高度Hs进行修正，以换算成实际操作条件下的Hs’，即Hs’=[Hs+（Ha-10）-(Hv-0.24)]×998.21100=[5.5+(10.34-10)-(7390/(998.2×9.81)-0.24)]×998.21100=[5.5+0.34-(0.75-0.24)]×0.907=4.83mHg=P0-Paρg+Hs-υ122g-ΣHf=157000-10.34×9.81×998.29.81×1100+4.83-1.4=8.60一般地，为了安全起见，泵的实际安装高度比允许安装高度8.60米小0.5~1.0米。1-6-13.用泵将贮槽中的有机试剂以40m3/h的流速，经φ108×4mm的管子输送到高位槽，如附图所示。两槽的液面差为20m，管子总长（各种阀件的当量长度均计算在内）为450m。试分别计算泵输送43 15℃和50℃的有机试剂所需的有效功率。设两槽液面恒定不变，已知有机试剂在15℃和50℃下的密度分别为684kg/m3和662kg/m3，粘度分别为6.21×10-2Pa.s和5.20×10-2Pa.s。解：要求泵的有效功率Ne=QρgH=QρWe，则要求先求出扬程H或We。已知：d=108-8=100mm=0.1m,Q=40m3/h，则：流速u=(40/3600)/(0.25×3.14×0.12)=1.42m/sRe15℃=duρ/μ=0.1×1.42×684/(6.21×10-2)=1563λ15℃=64/1563=0.041∑hf15℃=λ15℃×(l/d)×(u2/2)=0.041×(150/0.1)×(1.422/2)=62J/kgRe50℃=duρ/μ=0.1×1.42×662/(5.20×10-2)=1807λ50℃=64/1807=0.035∑hf=λ50℃×(l/d)×(u2/2)=0.035×(150/0.1)×(1.422/2)=52.9J/kg在1-1面（设为水平基准面）和2-2面之间列Bernoulli方程，有：We=20g+∑hf15℃，即We=20×9.81+62=258.2J/kg,43 则泵的有效功率Ne15℃=QρWe=(40/3600)×684×258.2=1.96KW同理，可求出Ne50℃=1.83KW1-6-14.用泵将池中水（25℃）送至30m高的水塔。泵安装在水面以上5m处。输水管道采用φ114×4mm、长1700m的钢管（包括管件的当量长度，但未包括进、出口能量损失）。已知该泵的输水能力为35m3/h，设管道的相对粗糙度为0.02，泵的总效率为0.65，试求泵的轴功率。解：已知Q=35m3/h=35/3600=0.0097m3/s管道内径d=114-8=106mm=0.106m,则流速u=0.0097/(0.25×3.14×0.1062)=1.1m/s已知：ε/d=0.02,η总=0.65，∑L=1700m查表得25℃下，水的动力粘度μ=（100.42+80.12）/2=90.27×10-5Pa.s,水的密度为ρ=（998.2+995.7）/2=996.95kg/m343 则:Re=duρ/μ=0.106×1.1×996.95/(90.27×10-5)=128,774>2300，turbulentflow！由ε/d=0.02，Re=128,774，查摩擦系数图得：摩擦阻力系数λ=0.048因此，∑hf=λ×(L/d)×(u2/2)=0.048×(1700/0.106)×(1.12/2)=465.7J/kg设水池中水和水塔中水的液面分别为1-1面和2-2面，且设水池中水的液面为水平基准面，在1-1和2-2面间列Bernoulli方程，有We=35g+∑hf=35×9.81+465.7=809.05J/kg则泵的总功率N=(QρWe)/η总=(0.0097×996.95×809.05)/0.65=12037W≈12KW43 第二篇热量传递1.导热(Conductiveheattransfer)P185.2-1-13.燃烧炉的内层为460mm厚的耐火砖，外层为230mm厚的绝缘砖。若炉的内表面温度t1为1400℃，外表面温度t3为100℃。试求导热的热流密度及两砖间的界面温度。设两层砖接触良好，已知耐火砖的导热系数为λ1=0.9+0.0007t，绝缘砖的导热系数为λ2=0.3+0.0003t。两式中的t可分别取各层材料的平均温度，单位为℃，λ单位为W.m-1.℃-1。Solution:设两层砖间的界面温度为t2=600℃，则λ1=0.9+0.0007×(1400+600)/2=1.6①λ2=0.3+0.0003×(600+100)/2=0.405②q=∆tδ1λ1+δ2λ2=t1-t3δ1λ1+δ2λ2=1400-1000.461.6+0.230.405=1520.5W/m2③1520.5=1400-t2δ1λ1=1400-t20.461.6=1400-t20.2875④求得t2=963℃。计算所得值963℃与设定值600℃相差较大，因此设定t2=963℃，重新按照①~④进行计算。此时，λ1=1.727，λ2=0.459，q=1695W/m2,t2=949℃。计算所得值949℃与设定的963℃仍然相差14℃，可考虑再设定t2=949℃，重复计算①~④得：t2=949.2℃，与前一次设定值仅相差43 0.2℃，假设成立，计算结束。因此，导热的热流密度为1688.3W/m2，两砖间的界面温度为949℃。Anothersolution：直接解方程！2-1-14.厚200mm的耐火砖墙，导热系数λ1=1.3W.m-1.℃-1。为使每平方米炉墙热损失不超过600W.m-2，在墙外覆盖一层导热系数λ2=0.11W.m-1.℃的绝热材料。已知炉墙两侧的温度分别为1300℃和60℃，试确定覆盖材料层的厚度。Solution:据题意得，δ1=200mm=0.2m，λ1=1.3W.m-1.℃-1设覆盖层材料厚度为δ2，λ2=0.11W.m-1.℃-1热流密度q=600W.m-2q=∆tδ1λ1+δ2λ2=1300-600.21.3+δ20.11=600求得，δ2=0.21m=210mm2-1-17.某燃烧炉的平壁由下列三种砖依次砌成：耐火砖：δ1=230mm，λ1=1.05W.m-1.℃-1绝热砖：δ2=230mm，λ1=0.151W.m-1.℃-1普通砖：δ3=240mm，λ3=0.93W.m-1.℃-1若已知耐火砖内侧温度为1000℃，耐火砖与绝热砖接触处的温度为940℃，而绝热砖与普通砖接触处的温度不超过138℃。试问：（143 ）绝热层需几块绝热砖？（2）普通砖外侧温度为若干？Solution:本题属于多层平壁的一维稳定导热问题。（1）设绝热层需要n快绝热砖，则有：1000-9400.231.05=940-1380.23n0.151解之得：n=1.92（2）由（1）可知，需要2块绝热砖，材料满足设计要求，设此时普通砖外侧温度为t3℃，则有：1000-9400.231.05=1000-t30.231.05+0.23×20.151+0.240.93解之得：n=34℃2-1-19.一炉墙平壁面积为12m2，由两层耐火材料组成，内层为镁砖，其导热系数为λMg=4.3-0.48×10-3tW.m-1.℃-1，外层为粘土砖，其导热系数为λ粘土=0.698+0.58×10-3tW.m-1.℃-1，两层厚度均为0.25m，假设两层紧密接触，已知炉墙内壁温度为t1=1000℃，外表面温度为t2=100℃，求热流密度q及热流量Q。Solution:（1）属于多层平壁稳定一维导热问题。设两层耐火材料界面温度为600℃，则λMg=4.3-0.48×10-3×（1000+600）/2=3.916λ粘土=0.698+0.58×10-3×（600+100）/2=0.90143 q=1000-1000.253.916+0.250.901q=2637W.m-2，Q=2637×12=31644W验算界面温度：1000-31644×[0.25/(3.916×12)]=831.7℃（2）设界面温度为831.7，重复上述步骤：λMg=4.3-0.48×10-3×（1000+831.7）/2=3.86λ粘土=0.698+0.58×10-3×（831.7+100）/2=0.968q=1000-1000.253.86+0.250.968q=2786W.m-2，此时界面温度为：1000-2786×（0.25/3.86）=819.6℃（3）与假定的831.7℃仍相差较大，再重复计算一次：λMg=4.3-0.48×10-3×（1000+819.6）/2=3.863λ粘土=0.698+0.58×10-3×（819.6+100）/2=0.965q=1000-1000.253.863+0.250.965q=2779.5W.m-2，此时界面温度为：1000-2779.5×（0.25/3.863）=820.1℃试算结束。Q=2779.5×12=33354W2-1-20.某热风管道，管壁导热系数λ=58W.m-1.℃-1，内径d1=85mm，外径d2=100mm，内表面温度t1=150℃，现拟用硅酸铝纤维毡保温，其导热系数λ=0.0526W.m-1.℃-1，若要求保温层外壁温度不高于40℃，允许的热损失为QL=52.3W.m-1，试求硅酸铝纤维毡保温层的最小厚度。Solution:本题属于圆筒壁的一维稳定导热问题，据题意有：43 圆筒壁：d1=85mm，d2=100mm，λ1=58W.m-1.℃，t1=150℃硅酸铝纤维毡：设其最小厚度为δ2，λ2=0.0526W.m-1.℃，t3=40℃线热流量QL=52.3W.m-1，则,由圆筒壁的线热流量计算公式：QL=t1-t312πλ1lnr2r1+12πλ2lnr3r2=2π(150-40)158ln5042.5+10.0526lnr350由此求得r3=100mm硅酸铝纤维毡保温层的最小厚度为：r3-r2=100-50=50mm2-1-24.某工厂用φ170×5mm的无缝钢管输送水蒸气。为了减少沿途的热损失，在管外包覆两层绝热材料，第一层为厚30mm的矿渣棉，其导热系数为0.065W.m-1.℃-1，第二层为厚30mm的石灰棉，其导热系数为0.21W.m-1.℃-1。管内壁温度为300℃，保温层外表面温度为40℃，管道长为50m。试求该管道的散热量。Solution:本题属于多层圆筒壁的一维稳定导热问题，据题意有：t1=300℃,t4=40℃,无缝钢管（碳钢）的导热系数为~52W.m-1.℃-1Q=t1-t412πλ1Llnr2r1+12πλ2Llnr3r2+12πλ3Llnr4r3=2π×50×300-401λ1ln8580+10.065ln11585+10.21ln145115=816400.001+4.650+1.104=816405.755=14186WResults:金属的导热系数λ很大（通常金属材料的导热系数λ为43 2.3~420W.m-1.℃-1）。由上述计算可知，若金属壁不太厚时，其热阻可以忽略不计。2-1-27.一双层玻璃窗，宽1.1m，高1.2m，玻璃（热导率λ1=1.03W.m-1.℃-1）厚3mm，中间空气隙（λ2=2.60×10-2W.m-1.℃-1）厚7mm。求其导热热阻，并与单层玻璃窗比较（设空气隙仅起导热作用）。Solution:1）双层玻璃窗：最外层玻璃的热阻：Rλ1=δ/λ1A=0.003/(1.03×1.1×1.2)=0.002206℃.W-1中间空气隙的热阻：Rλ1=δ/λ2A=0.007/(0.026×1.1×1.2)=0.204℃.W-1因此，总导热热阻为：0.002206×2+0.204=0.2084℃.W-12）单层玻璃窗：导热热阻即为Rλ1=0.002206℃.W-1单层玻璃窗的热阻仅相当于双层玻璃窗热阻的(0.002206/0.2084)×100=1.06%43 2.对流传热(Convectiveheattransfer)P219.2-2-12.水流过长l=5m的直管时，从入口温度tf’=15℃被加热到出口温度tf’’=45℃。管子内径d=20mm，水的流速u=2m.s-1。求对流传热系数α。Solution:管内流动时，取流体进、出口温度的算术平均值，即水的定性温度为t=(tf’+tf’’)/2=30℃。查表得，水的密度为ρ=995.7kg/m3，水的粘度μ=80.12×10-5Pa.s，导热系数λ=0.6176W.m-1.℃-1，普兰特数Pr=5.42则：雷诺数Re=duρ/μ=0.02×2×995.7/(80.12×10-5)=49710>104,属于管内强制紊流故可选用经验公式公式：α=0.023×（λ/d）×Re0.8×Pr0.4=0.023×(0.6176/0.02)×497100.8×5.420.4=0.023×30.88×5716.87×1.97=7998.9W.m-2.℃-1因l/d=5/0.02=250>50,不要考虑εL;题中未告知管壁温度tw，可不考虑热流方向的修正εt！2-2-16.冷却水在φ19×2mm，长为2m的钢管中以1m.s-1的流速通过。水温由288K升至298K。求管壁对水的对流传热系数α。Solution:定性温度t=(15+25)/2=20℃查表得：ρ水=998.2μ=100.42×10-5Pa.s，λ=0.5985W.m-1.℃-143 ，普兰特数Pr=7.01则：雷诺数Re=duρ/μ=0.015×1×998.2/(100.42×10-5)=14910>104,属于管内强制紊流。故可选用经验公式公式：α=0.023×（λ/d）×Re0.8×Pr0.4=0.023×(0.5985/0.015)×149100.8×7.010.4=0.023×39.9×2181.64×2.18=4365W.m-2.℃-1因l/d=2/0.015=133>50,不要考虑εL；管壁与流体温度差不知道，不考虑热流方向的修正εt。2-2-18.常压下，45℃的空气以1.2m.s-1的流速流过内径为25mm、长2m的圆管。管壁外侧利用蒸汽冷凝加热使管内壁面维持恒温100℃。试计算管内壁与空气之间的平均对流传热系数α和热流密度q，并计算空气出口温度。Solution:雷诺数Re=duρ/μ=0.025×1.2×1.11/(1.91×10-5)=1743<2300,属于管内强制层流100℃的空气的粘度μw=2.19×10-5Pa.s。设定空气的出口温度为t出=75℃，则定性温度t=（45+70）/2=60℃，有：μ=2.01×10-5Pa.s，ρ=1.06kg.m-3,Pr=0.698,Re=0.025×1.2×1.06/(2.01×10-5)=1582，λ=0.02893因Re<2300,RePr(d/l)=1582×0.698×(0.025/2)=15.2,l/d=80>60Nu=1.86×(Re.Pr)1/3×(d/l)1/3×(μ/μw)0.14=1.86×(1582×0.698)1/3×(0.025/2)1/3×(2.01/2.19)0.1443 =1.86×10.33×0.232×0.99=4.41对流传热系数α=Nu×（λ/d）=4.41×0.02893/0.025=5.10W.m-2.℃-1又由：αA△t=ρQvCp△t’即α△t=ρuA’Cp△t’,代入数据得：5.10×(3.14×0.025×2)×（100-60）=1.06×1.2×(0.25×3.14×0.0252)×1005×△t’得△t’=51℃，即t’出=96℃[△t’:空气进、出口温度差；△t：壁面温度100℃与流体主流区温度的平均值（定性温度）之差]以t’出=96℃替代前面的t出，即设定t出=96℃，重复上述各步骤。定性温度为70℃，μ=2.06×10-5Pa.s，ρ=1.029kg.m-3,Pr=0.701,Re=0.025×1.2×1.029/(2.06×10-5)=1499，λ=0.02963Nu=1.86×(Re.Pr)1/3×(d/l)1/3×(μ/μw)0.14但[Re.Pr.(d/l)]1/3<100????=1.86×(1499×0.701)1/3×(0.025/2)1/3×(2.06/2.19)0.14=1.86×10.16×0.232×0.991=4.34α=Nu×（λ/d）=4.34×0.02963/0.025=5.15W.m-2.℃-1得△t’=40℃，即t’出=85℃还可再返回算一次。2-2-20.空气以4m.s-1的流速通过一φ75.5×3.75mm的钢管，管长20m，空气入口温度为32℃，出口为68℃。试计算空气与管壁间的对流传热系数。如果空气流速增加一倍，其他条件均不变，对流传热系数又为多少？（设管壁温度为90℃）Solution:43 1）据题意，d=75.5-3.75×2=68mm=0.068m,u=4m/s,l=20m定性温度t=(32+68)/2=50℃,t壁=90℃,查表得定性温度50℃下空气的物性参数：μ=1.96×10-5Pa.s，ρ=1.093kg.m-3,Pr=0.697,λ=0.02824则有：Re=0.068×4×1.093/(1.96×10-5)=15168>104,属管内强制紊流α=0.023×（λ/d）×Re0.8×Pr0.4=0.023×(0.02824/0.068)×151680.8×0.6970.4=0.023×0.415×2211.8×0.866=18.28W.m-2.℃-1因l/d=20/0.068=294>50、壁温与定性温度之间的温差=90-50=40℃<50℃，两者均无需校正。2）如果空气流速增加一倍，其他条件均不变，Re’=2Reα’=20.8α=31.83W.m-2.℃-1AnotherSolution：先求出单位时间内空气流经钢管所吸收的热量Q，即Q=ρQVCP∆t=1.093×(π4d2u)×Cp×∆t=1.093×(0.25×3.14×0.0682×4)×1005×(68-32)=574.16W再由Q=αA∆t"=α×(πdl)×(tw-tf)α=Qπdl∆t=574.163.14×0.068×20×(90-50)=3.36W.m-2.℃-1Why？？？？43 3、RadiativeheattransferP234.2-3-4.将一外径为50mm，长为10m的氧化钢管敷设在与管径相比很大的车间内，车间内石灰粉刷壁面的温度为27℃，石灰粉刷壁ε=0.91。求钢管的外壁温度为250℃时的辐射热损失。解：氧化钢管1的黑度ε1=0.80，壁面2的黑度为ε2=0.91，T1=523K,T2=300K,据题意得，φ12=1，由于钢管的辐射面积<<壁面面积，可用简化的辐射传热公式进行计算，即Q=ε1CbA1[(T1100)4-(T2100)4]=0.8×5.67×(3.14×0.05×10)×[5.234-34]=0.8×5.67×1.57×667.18=4751.3W2-3-5.两平行的大平板，放置在空气中相距5mm，其中一平板的黑度为0.1，温度为350K；另一平板的黑度为0.05，温度为300K。若将第一板加涂层，使其黑度变为0.025，试计算由此引起的传热量变化的百分率。假设两平板间对流传热可以忽略。解：因两平板相距很近，可近似为两无限大平板间的辐射传热问题。1）加涂层前，两平板间的传热量为：Q12=Cb1ε1+1ε2-1A1[T11004-T21004]=Cb29A1[T11004-T21004]2）加涂层后，两平板间的传热量为43 Q12"=Cb1ε1"+1ε2-1A1[T11004-T21004]=Cb59A[T11004-T21004]则传热量的变化率为：Q12-Q12"Q12×100%=(129-159)/(129)=50.85%2-3-6.两块平行放置的无限大灰体平板，温度分别为T1和T2，表面黑度均为0.9。在两灰体间插入一块薄的金属板，使辐射传热量减为原来的1/20。问此金属板的表面黑度应为多少？解：设薄金属薄板3的表面黑度为ε3、平板1侧表面的温度为T3，平行板1和2的黑度为ε1=ε2=0.9，据题意得：放置薄板前辐射传热量为：Q12=Cb1ε1+1ε2-1A1[T11004-T21004]=911CbA1[T11004-T21004]（1）插入平板后的传热量为：Q13=Cb1ε1+1ε3-1A1[T11004-T31004](2)忽略金属薄板3两侧的温度降，则有Q32=Cb1ε1+1ε3-1A3[T31004-T21004](3)假设A1=A3，由Q32=Q13可导出：T31004=12[T11004+T21004](4)将式（4）代入式（2）得：Q13=12×Cb1ε1+1ε3-1A1[T11004-T21004]（5）43 因Q13=120Q12则12×119+1ε3=120×911得出：ε3=9/109=0.08262-3-7.两个平行放置的无限大平板1和2，表面温度和黑度分别为t1=300℃、t2=100℃和ε1=0.5、ε2=0.8。在板1、2之间插入导热系数很大的板3。当板3的A侧面向板1时，板3的平衡温度为279℃；当板3的B侧面向板1时，其平衡温度为139℃。试求板3两侧的黑度。解：设板3的A、B两侧的表面黑度分别为ε3A和ε3B，据题意，板3的导热热阻可忽略不计，即板3两侧的温度相等。ε1=0.5、ε2=0.8；t1=300℃=573K、t2=100℃=373K，t3A=279℃=552K，t3B=139℃=412K1）当A侧面向板1时，有Q1-3A=Cb10.5+1ε3A-1A[5731004-5521004]=149.55ACb1+1ε3A43 Q3B-2=Cb10.8+1ε3B-1A[5521004-3731004]=734.88ACb0.25+1ε3B因Q1-3A=Q3B-2,则有：149.551+1ε3A=734.880.25+1ε3B①2）当板3的B侧面向板1时，同理有：Q1-3B=Cb10.5+1ε3B-1A[5731004-4121004]=789.87ACb1+1ε3BQ3A-2=Cb10.8+1ε3A-1A[4121004-3731004]=94.56ACb0.25+1ε3AThen,789.871+1ε3B=94.560.25+1ε3A②Combinedrelation①withrelation②,wegetε3A=0.96,ε3B=0.10Indication:??2-3-9.黑度ε1=0.3和ε2=0.8相距很近的两块大平行平板之间进行辐射换热。试问当其间设置ε3=0.04的磨光铝制隔热板后，换热量减少为原有换热量的百分之几？解：无隔热铝板时的换热量：43 Q12=Cb10.3+10.8-1A[T11004-T21004]=0.279CbA[T11004-T21004]放置隔热板后，辐射传热量为：Q13=Cb10.3+10.04-1A[T11004-T31004]=0.037CbA[T11004-T31004]①Q32=Cb10.04+10.8-1A[T31004-T21004]=0.0396CbA[T31004-T21004]由于Q13=Q32即：0.037[T11004-T31004]=0.0396[T31004-T21004]得出：T31004=0.483T11004+0.517T21004②将式②代入①得：Q13=0.0191CbA[T11004-T21004]因此，换热量减少百分数为：Q12-Q13Q12=0.279-0.01910.279×100%=93.15%减少为原来换热量的1-93.15%=6.85%2-3-10.烟气流过辐射换热器内管，其直径d=1m，内管黑度ε2=0.9，温度t2=700℃；烟气温度t1=1200℃，烟气成分为：CO2=14.5%,H2O=4%,若忽略端头辐射的影响，试计算单位管长上的辐射传热量。解：1）已知：ε2=0.9，t2=700℃；tg=1200℃，εg=？43 将换热器视为无限长圆柱体，查表2-3-3得其平均射线行程为L=0.9D=0.9m,若烟气的总压力为1atm,则PCO2L=101325×0.145×0.9=13223Pa.mPH2OL=101325×0.04×0.9=3648Pa.m查附录III，Tg=1473K时,εCO2=0.087,εH2O=0.04,CCO2=1.0,CH2O=1.0[查表时，CCO2以气体的总压力为横坐标；而CH2O以气体总压力和水分压的平均值为横坐标]忽略△ε，得出烟气的黑度为:εg=CCO2×εCO2+CH2O×εH2O=0.087×1.0+0.04×1.0=0.1272）又Tw=973K,Tg=1473KPCO2LTwTg=13223×(973/1473)=8735PH2OLTwTg=3648×(973/1473)=2410查附录III，以Tw为横坐标、PCO2LTwTg为参量，得：εCO2‘=0.12εH2O‘=0.054aCO2=CCO2.εCO2"(TgTw)0.65=1.0×0.12×(1473/973)0.65=0.157aH2O=CH2O.εH2O"(TgTw)0.65=1.0×0.054×(1473/973)0.65=0.071ag=aCO2+aH2O=0.157+0.071=0.228则辐射传热速率为：QL=5.6710.9+10.228-1×πD[0.1270.22814731004-(973100)4]=1.261×3.14×(0.557×47077.24-8962.96)=68338W.m-2若直接以气体的黑度εg=0.127计算，得43 QL"=5.6710.9+10.127-1×πD[14731004-(973100)4]=0.71×3.14×（47077.24-8962.96）=84972W.m-23）与用烟气活度计算所得结果相比，偏大~24%。2-3-12保温（热水）瓶瓶胆是一夹层结构，且夹层表面镀银，银层的黑度ε=0.04。瓶内存放t1=100℃的开水，周围环境温度t2=20℃。设瓶胆内外层的温度分别与水和周围环境温度大致相同。求瓶胆的散热量。如用导热系数λ=0.04W.m-1.℃-1的软木代替瓶胆夹层保温，问需用多厚的软木才能达到保温瓶原来的保温效果？解：可将瓶胆内外层看成是两无限大平板，则瓶胆的辐射传热速率q为：q=Cb10.04+10.04-1[3731004-2931004]=0.1157×(193.569-73.701)=13.97W.m-2若用导热系数λ=0.04W.m-1.℃-1的软木代替瓶胆夹层保温,则有qcond=∆tδλ=100-20δ0.04=13.97得出：δ=0.23m43 2.4Steadycomprehensiveheattransferandheatexchanger2-4-8.一外径为80mm、壁厚为3mm的水蒸气管道，外包厚40mm、导热系数λ2=(0.065+0.000105t)W.m-1.℃-1的水泥珍珠岩保温层，管内水蒸气温度t1=150℃，环境温度t0=20℃；保温层外表面的表面传热系数α0=7.6W.m-2.℃-1。管道壁的导热系数为λ1=53.7W.m-1.℃-1。求每米管道的热损失。解：设管道内壁温度近似于150℃，管道外壁温度为t2，珍珠岩保温层外壁温度为t3,则有：QL1-vapor-wall-cond.=Δt12πλlnr2r1=150-t216.28×53.7ln4037=48.39-0.3226t2①QL2=150-2016.28×53.7ln4037+16.28×(0.065+0.000105(t2+t3)2ln8040+17.6×3.14×0.16=1300.000231+0.11040.065+0.0000525(t2+t3)+0.2619=1300.26213+0.11040.065+0.0000525(t2+t3)②QL2-保温层=t2-t316.28×(0.065+0.000105(t2+t3)2ln8040=t2-t30.11040.065+0.0000525(t2+t3)②QL3-保温层-air=t3-2017.6×3.14×0.16=t3-200.2619=3.818t3-76.365③由QL1=QL2=QL3得：2-4-9.一根外径为30mm、外侧表面温度为10043 ℃的管道，以对流方式向温度为20℃的空气散热，对流传热系数为30W.m-2.℃-1。为了使每米管道的热损失不超过50W.m-1，现有A、B两种保温材料可供采用。材料A的导热系数为0.5W.m-1.℃-1，其数量足够按3.14×10-3m3.m-1的用量使用。材料B的导热系数为0.1W.m-1.℃-1，其数量足够按4.0×10-3m3.m-1的用量使用。假定覆盖保温层后，管道外侧壁面与空气之间的对流传热系数与管道裸露时相同，试问哪种保温材料放在内层时能满足提出的保温要求？解：据题意得：(1)若材料A放内层、B放外层，则：对于保温材料A，有πr22-0.0152=3.14×10-3得出，r2=35mm，即其最大厚度只能为20mm。对于保温材料B有：πr32-0.0352=4×10-3得出，r3=0.05m=50mm，即此时材料B的最大厚度只能为50-35=15mm则由稳态综合传热得出：QL=100-2016.28×0.5ln3515+16.28×0.1ln5035+130×3.14×0.100=800.27+0.568+0.106=84.8W.m-1>50W.m-1不能满足要求。（2）若材料B放在内层、A放外层，则对于保温材料B，有43 πr22-0.0152=4×10-3得出，r2=38.7mm，即其最大厚度只能为38.7-15=23.7mm。对于保温材料A有：πr32-0.03872=3.14×10-3得出，r3=0.05m=50mm，即此时材料B的最大厚度只能为50-38.7=11.3mmQL=100-2016.28×0.1ln38.715+16.28×0.5ln5038.7+130×3.14×0.100=801.509+0.0816+0.106=47.14W.m-1QL<50W.m-1,因此，材料B放内层时能满足要求。2-4-11.一炉壁由三层材料组成，内层是厚度δ1=0.23m，λ1=1.2W.m-1.℃-1的粘土砖；外层是δ3=0.24m、λ3=0.5W.m-1.℃-1的红砖；两层中间填以厚度为δ2=0.03m，λ2=0.1W.m-1.℃-1的石棉作为隔热层。炉墙内侧烟气温度为tf1=1200℃，烟气侧传热系数αT1=40W.m-2.℃-1，厂房室内空气温度tf2=20℃，空气侧传热系数αT2=15W.m-2.℃-1。试求通过该炉墙的散热损失和炉墙内外表面的温度t1和t4。解：据题意得：属稳态综合传热问题，由q=1200-201αT1+δ1λ1+δ2λ2+δ3λ3+1αT2=1180140+0.231.2+0.030.1+0.240.5+115=11800.025+0.1917+0.3+0.48+0.06667=1109.7W.m-2q=1200-t1140=1109.65,得t1=1172℃43 q=t4-20115=1109.65,得t4=94℃2-4-12.在并流换热器中，用水冷却油。水的进、出口温度分别为15℃和40℃，油的进、出口温度分别为150℃和100℃。现因生产任务要求油的出口温度降至80℃，假设油和水的流量、进口温度及物性均不变，若原换热器的管长为1m，试求此换热器的管长增加至若干米才能满足要求。设换热器的热损失可忽略。解：由题意得：1)设总传热系数为K，则水进口15℃出口40℃Δt1=135油进口150℃出口100℃Δt2=60Q1=KA1×∆t=kA1×∆t2-∆t1ln∆t2∆t1=kA1×-75ln60135=kA1×-75-0.8109=92.49KA1由于：QM油×cp×150-100=92.49KA1得出：K=QM油×cp×0.5406/A12）若要求油的出口温度降至80℃，油和水的流量、进口温度及物性均不变，则由Q油放=Q水吸有：QM油×cp油×150-100=QM水×cp水×40-15QM油×cp油×150-80=QM水×cp水×t水出口-15得：水出口温度应为：t水出口=25×（7/5）+15=50℃水:进口15℃出口50℃油:进口150℃出口80℃43 Δt1=135Δt2=30Q2=KA2×∆t=KA2×∆t2-∆t1ln∆t2∆t1=KA2×-105ln30135=KA2×-105-1.504=69.81KA2由于：QM油×cp×150-80=69.81KA2把上面的K值代入得：QM油×cp×150-80=69.81×(QM油×cp×0.5406/A1)×A2得出：A2/A1=70/(69.81×0.5406)=1.85亦即长度应增加至1.85米才能满足要求。2-4-14.在一列管式换热器中，某液体在管内流过被加热，其进口温度为20℃，出口温度为70℃，流量为1800kg.h-1，比热为2.5kJ.kg-1.℃-1。管外为压力为176.5kPa的饱和水蒸气冷凝。试求蒸汽用量。解：由题意得：液体的质量流量为QM=1800/3600=0.5kg/s则该液体从20℃加热到70℃时所吸收的热量为：Q=QM×CP×∆t=0.5×2500×70-20=62500W管外饱和水蒸汽的压力为176.5kPa，查表得其温度约为115℃，其汽化热为2219000J/kg则所需蒸汽用量为：62500/2219000=0.0282kg/s=101.4kg/h2-4-15.在一套管式换热器中，内管为φ165×4.5mm的钢管，内管中热水被冷却，热水流量为3000kg.h-1，进口温度为90℃，出口温度为60℃，环隙中冷却水进口温度为20℃，出口温度为4543 ℃，总传热系数K=1600W.m-2.℃-1，试：（1）冷却水用量；（2）并流流动时的平均温度差及所需的管子长度；（3）逆流流动时的平均温度差及所需的管子长度。解：1)热水被冷却：其定性温度取（90+60）/2=75℃，查表得，Cp=4191J.kg-1.K-1QM=30003600=0.833kg.s-1QM×cp×∆t=0.833×4191×90-60=104770.8J/S冷却水被加热：其定性温度为（20+45）/2=32.5℃Cp=4174J.kg-1.k-1则QM×Cp×∆t=QM×4174×(45-20)=104770.8得出QM=1kg.S-12）并流流动时：热水：进口90出口60冷却水：进口20出口45△t1=70△t2=15平均温度差为:∆t2-∆t1ln∆t2∆t1=15-70ln1570=-55-1.54=35.7℃Q=KA∆t=1600×3.14×0.165L×35.7=104770.8得出：L=3.54m3）逆流流动时：热水：进口90出口60冷却水：出口45进口20△t1=45△t2=40平均温度差为:∆t2-∆t1ln∆t2∆t1=40-45ln4045=-5-0.1178=42.5℃43 Q=KA∆t=1600×3.14×0.165L×42.5=104770.8得出：L=2.97m43 第三篇质量传递3-1-2.（1）应用式（3-1-14）：查表得：V(SO2)=40.4V（空气）=29.9D=4.36×10-5×（38+273）1.598.07×（40.413+29.913）2164+129=1.29×10-5m2.s-1（2）应用式3-1-4查的：σ（空气）=3.617δ(SO2)=4.29所以σ（AB）=3.617+4.292=3.95(εK)SO2=252(εK)空气=97所以(εK)=252×97=156.3（KTε）=311156.3=1.99由表3-1-3的数据估算Ω（D）=1.075由式（3-1-15）得：D=1.88×10-5×3111.598.07×3.952×1.075164+129=1.404×10-5m2.s-1（3）应用式（3-1-15）与（3-1-18）计算：常数=【21.7-4.98164+129】×10-6=2.06×10-5由此可计算扩散系数D：D=1.54×10-5m2.s-13-1-3水的缔合度是2.6水的分子量是18由表（3-1-2）可知甲醇的分子体积为37该温度下的水的μ=72.5×10-5Pa.s代入公式中：D=7.4×10-12（2.6×18）0.5×30872.5×10-5×370.6=2.507×10-6m2.s-143 3-2-2N(A)=c（AL）dZdt其中c（AL）为水的摩尔浓度。根据式（3-2-14）N(A)=DABρzRTPBm（PA1-P(A2)）313K下水的饱和蒸汽压P(A1)=7.38KPa出口处的水蒸汽压P（A2）=69.63KPaC（AL）=992.2/18=55.12kmol/m3P（Bm）=98.07-（98.07-7.38）ln98.0798.07-7.38=94.6KPa代入原始公式中即可得出答案，由于条件不足，没有给出具体的时间t和水的高度变化h，故无法得出最后答案。3-2-3（1）应用式（3-1-14）：查表得:V(SO2)=40.4V（空气）=29.9D=4.36×10-5×（425+273）1.598.07×（40.413+29.913）2164+129=4.31×10-5m2.s-1（2）应用式3-1-4查的：σ（空气）=3.617δ(so2)=4.29所以σ（AB）=3.617+4.292=3.95(εK)SO2=252(εK)空气=97所以(εK)=252×97=156.3（KTε）=698156.3=4.47由表3-1-3的数据估算Ω（D）=0.865由式（3-1-15）得：43 D=1.88×10-5×3111.598.07×3.952×0.865164+129=1.745×10-5m2.s-1（3）应用式（3-1-15）与（3-1-18）计算：常数=【21.7-4.98164+129】×10-6=2.06×10-5由此可以计算:D=1.91×10-5m2.s-13-2-4由于碳在钢中的扩散系数非常小，可以将钢视为半无限体，利用3-2-20，其中ω（c∞）=0.002ω(c’)=0.012代入公式ωc-ωc∞ωc’-ωc∞=1-erf（x2Dt）ωc-0.0020.012-0.002=1-erf（0.523.59×10-7×3.5×3600）由误差函数表对应于函数值代入以上公式即可算出答案。由于本书没有给出函数误差表，故无法算出具体的答案。43'