信息编码习题答案或提示.doc 37页

'第二章部分习题2.1试问四进制、八进制脉冲所含信息量是二进制脉冲的多少倍?答：2倍，3倍。2.2一副充分洗乱了的牌(含52张牌)，试问(1)任一特定排列所给出的信息量是多少？(2)若从中抽取13张牌，所给出的点数都不相同,能得到多少信息量？解：(1)(2)任取13张，各点数不同的概率为，信息量：9.4793(比特/符号)2.3居住某地区的女孩子有是大学生，在女大学生中有是身高160厘米上的，而女孩子中身高160厘米以上的占总数的一半。假如我们得知“身高160厘米以上的某女孩是大学生”的消息，问获得多少信息量？答案：1.415比特/符号。提示：设事件A表示女大学生，事件C表示160CM以上的女孩，则问题就是求p(A|C)，2.4设离散无忆信源，其发出的消息为，求(1)此消息的自信息量是多少？(2)在此消息中平均每个符号携带的信息量是多少？解：(1)87.81比特，(2)1.951比特。提示：先计算此消息出现的概率，再用自信息量除以此消息包含的符号总数(共45个)。2.5从大量统计资料知道，男性中红绿色盲的发病率为，女性发病率为，如果你问一位男士：“你是否是色盲？”他的回答可能是“是”，可能是“否”，问这两个回答中各含有多少信息量?平均每个回答中含有多少信息量？如果问一位女士，则答案中含有的平均自信息量是多少？(1)男性回答是的信息量为，回答否的信息量是0.104737 比特，平均每个回答含的信息量(即熵)是0.36596比特。(2)0.045425比特2.1设信源，求这信源的熵，并解释为什么不满足信源熵的极值性。提示：信源的概率之和大于1。2.2同时掷两个正常的骰子，也就是各面呈现的概率都为，求：(1)“3和5同时出现”这事件的自信息量；(2)“两个1同时出现”这事件的自信息量；(3)两个点数的各种组合(无序对)的熵或平均信息量；(4)两个点数之和(即构成的子集)的熵；(5)两个点数中至少有一个是1的自信息量。解：(1)4.17(比特/符号)，提示：3和5同时出现的概率为=1/18(2)5.17(比特/符号)，提示：两个1同时出现的概率1/36(3)“两个点数相同”的概率:1/36,共有6种情况;“两个点数不同”的概率:1/18,共有15中情况.故平均信息量为:4.337比特/符号(4)3.274(比特/符号)。提示：信源模型(5)1.711(比特/符号)。提示：至少有一个1出现的概率为2.3证明提示：见教材式(2.1.26)和(2.1.28)2.4证明，并说明等式成立的条件。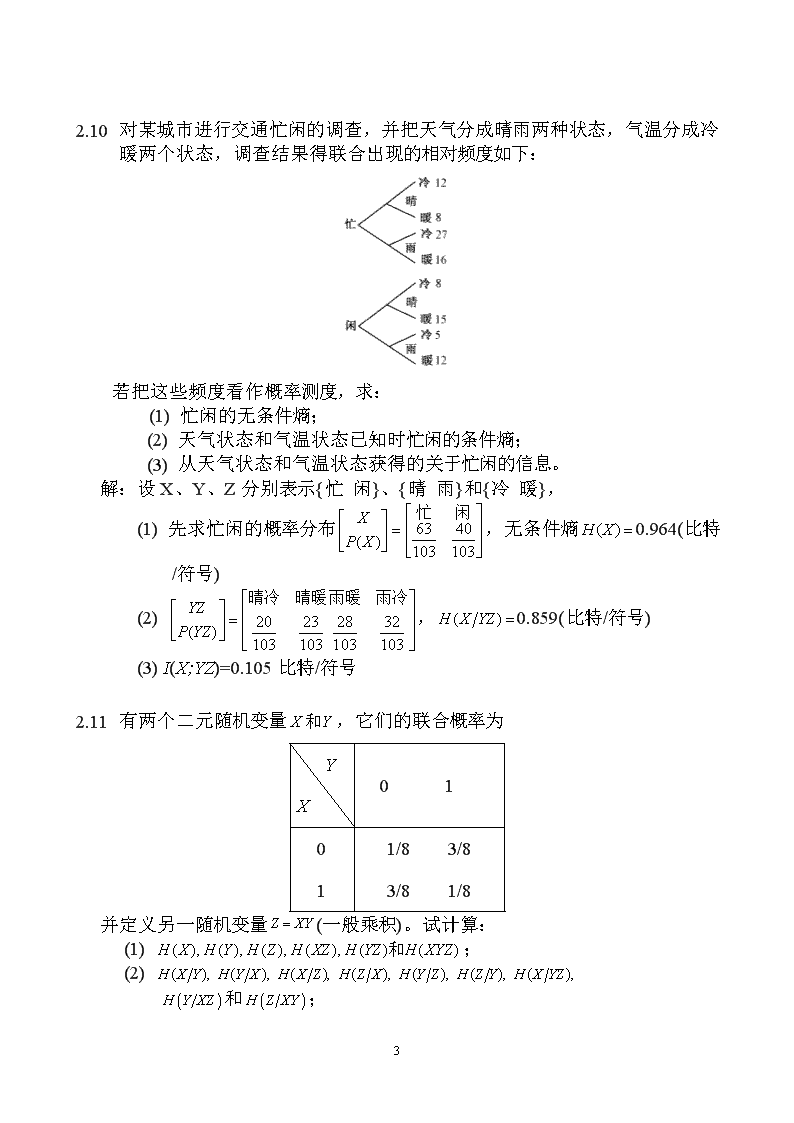提示：见教材第38页37 2.1对某城市进行交通忙闲的调查，并把天气分成晴雨两种状态，气温分成冷暖两个状态，调查结果得联合出现的相对频度如下：若把这些频度看作概率测度，求：(1)忙闲的无条件熵；(2)天气状态和气温状态已知时忙闲的条件熵；(3)从天气状态和气温状态获得的关于忙闲的信息。解：设X、Y、Z分别表示{忙闲}、{晴雨}和{冷暖}，(1)先求忙闲的概率分布，无条件熵0.964(比特/符号)(2)，0.859(比特/符号)(3)I(X;YZ)=0.105比特/符号2.2有两个二元随机变量，它们的联合概率为YX01011/83/83/81/8并定义另一随机变量(一般乘积)。试计算：(1)；(2)和；37 (3)。解：提示：的联合概率分布XZ的联合概率分布YZ的联合概率分布Z的概率分布(1)1比特/符号，1比特/符号，0.543比特/符号，1.406比特/符号，1.406比特/符号，1.811比特/符号(2)0.811比特/符号，0.811比特/符号，0.863比特/符号，0.406比特/符号，0.863比特/符号，0.406比特/符号，0.405比特/符号(3)0.189比特/符号，0.137比特/符号，0.137比特/符号，0.458比特/符号，0.406比特/符号，0.406比特/符号2.1略2.2设有一个信源，它产生序列的信息。它在任意时间而且不论以前发生过什么符号，均按的概率发出符号。(1)试问这个信源是否是平稳的？(2)试计算；(3)试计算并写出信源中可能有的所有符号。解：(1)是(2)信源熵0.971比特/信源符号，比特/信源符号，由题设知道这个信源是无记忆信源，因此条件熵和极限熵都等于信源熵。(3)比特/信源符号，信源中可能的符号共16个。2.3设是平稳离散有记忆信源，试证明：。提示：见教材第44页37 2.1略2.2一阶马尔可夫信源的状态图如题2.16图所示。信源的符号集为。(1)求平稳后信源的概率分布；(2)求信源的熵。题2.16图解：(1)由图得一步转移概率矩阵，状态极限概率(2)2.17黑白气象传真图的消息只有黑色和白色两种，即信源。设黑色出现的概率为p(黑)=0.3，白色的出现概率p(白)=0.7。(1)假设图上黑白消息出现前后没有关联，求熵；(2)假设消息前后有关联，其依赖关系为p(白/白)=0.9，p(黑/白)=0.1，p(白/黑)=0.2，p(黑/黑)=0.8，求此一阶马尔可夫信源的熵；(3)分别求上述两种信源的剩余度，比较的大小，并说明其物理意义。解：(1)0.881比特/信源符号;(2)=0.5533比特/符号;(3)11.9%，44.67%37 2.18每帧电视图像可以认为是由个像素组成的，所有像素均是独立变化，且每像素又取128个不同的亮度电平，并设亮度电平是等概率出现，问每帧图像含有多少信息量？若有一个广播员，在约10000个汉字中选1000个汉字来口述这电视图像，试问若要恰当地描述此图像，广播员在口述中至少需要多少汉字？解：(1)每帧图象包含的信息量比特(2)每1000个汉字提供的信息量(3)需要个汉字。2.19略2.20连续变量的联合概率密度为：，求。(提示：)解：令，则同理，由函数对称性利用分部积分法、三角函数性质、习题提示并注意自然对数与以2为底对数的换算关系可得：(比特/符号)37 (比特/符号)(比特/符号)2.21略2.22略37 第三章习题3.1设信源通过一干扰信道，接收符号为，信道传递矩阵为，求(1)信源中事件分别含有的自信息量。(2)收到消息后，获得的关于的信息量。(3)信源和信宿的信息熵。(4)信道疑义度和噪声熵。(5)接收到信息后获得的平均互信息量。解：(1)(比特/符号)，比特/符号，(2)，(比特/符号),(比特/符号),(比特/符号),(比特/符号)(3)0.971(比特/符号)，0.971(比特/符号)，(4)(比特/符号)，，(5)0.2564比特/符号3.2设二元对称信道的传递矩阵为(1)若；(2)求该信道的信道容量及其达到信道容量时的输入概率分布。解：(1)0.8113比特/符号，0.7498比特/符号，0.9183比特/符号，0.0615比特/符号，(2)0.0818比特/符号，p(0)=p(1)=1/237 3.1设有一批电阻，按阻值分70%是，30%是；按瓦分64%是1/8W，其余是1/4W。现已知阻值的电阻中80%是1/8W。问通过测量阻值可以得到的关于瓦数的平均信息量是多少？解：设随机变量X表示电阻的瓦数，Y表示电阻的阻值，则其概率分布为，已知，由概率的归一性：由，得再由,得:.代入条件熵计算公式得:(比特/符号)3.4参见教材第二章相关内容。3.5参见教材第二章相关内容。3.6有一个二元对称信道，其信道矩阵为。设该信源以1500的速度传输输入符号。现有一消息序列共有14000个二元符号，并设，问从信息传输的角度来考虑，10秒钟内能否将这消息序列无失真地传递完？解：信道容量C=0.8586比特/信道符号，则每秒钟可传送的信息量为1500×0.859=1288.5比特，10秒钟最大可传送的信息量为12885比特，而待传送的信息量为14000比特，因此，10秒钟内不能无失真的传送完毕。3.7仿教材例题3.2.1和3.2.2。37 3.8已知一个高斯信道，输入信噪比(比率)为3。频带为3kHz，求最大可能传送的信息率。若信噪比提高到15，理论上传送同样的信息率所需的频带为多少？提示：由式(3.5.13)可得。(1)最大可能传送的信息率是比特/秒(2)1.5kHZ3.9略3.10略3.11已知离散信源，某信道的信道矩阵为试求：(1)“输入，输出”的概率；(2)“输出”的概率；(3)“收到的条件下推测输入”的概率。解：由信道矩阵的概念和概率论可得(1)；(2)=0.19；(3)3.12略3.13试证明：当信道每输入一个值，相应有几个值输出，且不同的值所对应的值不相互重合时，有。证明：因为，并且由已知可得37 ，所以有3.12试求以下各信道矩阵代表的信道的容量：(1)(2)(3)解：2比特/信道符号，1.585比特/信道符号，1.585比特/信道符号3.13此题很简单，略。3.14参见教材相关问题的证明过程。3.15见教材证明。3.16设加性高斯白噪声信道中，信道带宽3kHz，又设{(信号功率+噪声功率)/噪声功率}=10dB。试计算该信道的最大信息传输速率。提示：的dB数:。解:由题意,,故=9.96kbit/s。3.17略3.18略37 第四章习题4.1一个四元对称信源，接收符号，其失真矩阵为求函数，并画出其曲线(取4至5个点)。解：，。4.2若某无记忆信源，接收符号，其失真矩阵为求信源的最大失真度和最小平均失真度，并求选择何种信道可达到该的失真度。解：4.3某二元信源其失真矩阵为求这信源的函数。提示：见公式(4.2.41)。4.4已知信源，信宿37 。设信源输入符号为等概率分布，而且失真函数为，求信源的率失真函数。解：。提示：注意参量S<0,求4.3略，4.4略4.5参见教材p110.4.6略4.7设某地区的“晴天”概率，“雨天”概率，把“晴天”预报为“雨天”，把“雨天”预报为“晴天”造成的损失均为元。又设该地区的天气预报系统把“晴天”预报为“晴天”，“雨天”预报为“雨天”的概率均为0.9；把“晴天”预报为“雨天”，把“雨天”预报为“晴天”的概率均为0.1。试计算这种预报系统的信息价值率(元/比特)。解：，预报结果：，提示：天气信源：，预报信道矩阵：，失真矩阵：4.8设离散无记忆信源其失真度为汉明失真度。(1)求，并写出相应试验信道的信道矩阵；(2)求，并写出相应试验信道的信道矩阵；(3)若允许平均失真度，试问信源的每一个信源符号平均最少由几个二进制码符号表示？解：(1)(2)(3)由教材例题可知，，因此每个信源符号最少要用0.331个二进制码表示。4.11见教材例题。37 第五章习题5.1设有信源(1)求信源熵；(2)编二进制香农码；(3)计算其平均码长及编码效率。解：(1)2.609比特/信源符号(2)码字：(3)平均码长3.14比特/符号，编码效率83.09%5.2对题5.1的信源编二进制费诺码，计算其编码效率。解：(1)码字：，(2)平均码长2.74比特/符号，编码效率95.22%5.3对题5.1的信源分别编二进制和三进制赫夫曼码，计算各自的平均码长及编码效率。解：二进制码码字：，平均码长2.72比特/符号，编码效率95.92%三进制码码字：，平均码长1.8比特/符号，编码效率91.45%5.4设信源(1)计算信源熵；(2)编二进制香农码和二进制费诺码；(3)计算二进制香农码和费诺码的平均码长和编码效率；(4)编三进制费诺码；(5)计算三进制费诺码的平均码长和编码效率。解：(1)(比特/符号)(2)二元香农码：37 信源符号概率累加概率累加概率小数表示码字1/20110.001/41/2220.10101/83/4330.1101101/167/8440.111011101/3215/16550.11110111101/6431/32660.1111101111101/12863/64770.111111011111101/128127/128770.11111111111111(3)(比特/符号)，编码效率：二元费诺码码字与香农码相同，顾二者平均码长和编码效率相同。(4)三元费诺码：信源符号概率码字1/2001/4111/820201/161211/32202201/6412211/1282022201/12812221(5)，(比特/符号)，编码效率：5.3略5.4有二元平稳马氏链，已知，，求它的符号熵。用三个符号合成一个来编二进制哈夫曼码，求新符号的平均码字长度和编码效率。（略）5.5对题5.6的信源进行游程编码。若“0”游程长度的截止值为16，“1”游程长度的截止值为8，求编码效率。（略）37 5.3选择帧长=63(1)对001000000000000000000000000000000100000000000000000000000000000编码；(2)对100001000010110000000001001000010100100000000111000001000000001编码，再译码；(3)对000000000000000000000000000000000000000000000000000000000000000编码；(4)对10100011010111000110001110100110000111101100101000110101011010010编码；(5)对上述结果进行讨论。解：(1)值：2；的长度：，的编码：000010,；的长度：的编码：01000010010码：00001001000010010(2)(a)编码：值：15；的长度：，的编码：0011111234567891011121314151611131424273234374647485463的长度：的编码：010,1011,0111,1110,1011,1111,1110,0000,0000,0000,0000,0000L-D码：0,0111,1010,1011,0111,1110,1011,1111,1110,0000,0000,0000,0000,0000(b)译码：Q码001111，Q=15，显然，，故，，所以QK15626314535437 1347190,039,465,350192,928,249,26948124649,362,616,90552,251,400,85147114510,451,999,25013,340,783,196461036301,403,340348,330,1363793347,216,48452,451,256348318,649,38410,518,30032726760,659888,03027623102,859134,596245131,9122,0021441262571513310130165112510156100011译码：100001000010110000000001001000010100100000000111000001000000001(3)的编码：000000；的编码：无。L-D码：000000(4)略(5)L-D编码适合于冗余位较多或较少的情况。N一定,Q的长度确定。T的长度取决于，当Q=[1/2N]时，最大，T的位数最长。5.3将幅度为3.25、频率为800的正弦信号输入采样频率为8采样保持器后通过一个如题图5.1所示量化数为8的中升均匀量化器。试画出均匀量化器的输出波形。题图5.1解：采样频率是正弦信号频率的10倍，每个正弦周期内有10个采样点，采样值及其量化值如下表所示：37 012345678901.913.093.091.910-1.91-3.09-3.09-1.910.51.53.53.51.5-0.5-1.5-3.5-3.5-1.5均匀量化器输出如下图示：5.10已知某采样时刻的信号值的概率密度函数如题图5.2所示，将通过一个量化数为4的中升均匀量化器得到输出。试求：(1)输出的平均功率；(2)量化噪声的平均功率；(3)量化信噪比。题图5.2解：依题意，均匀量化器的4个量化区间是、、、，4个量化电平是37 、、、。由图示概率密度函数可知，采样值落入4个区间的概率是、因此(1)输出的平均功率(2)量化噪声的平均功率在第一个积分中令，在第二个积分中令，得(3)量化信噪比换算成分贝值37 5.11在CD播放机中，假设音乐是均匀分布，采样频率为44.1，采用16比特的中升均匀量化器进行量化。试确定50分钟音乐所需要的比特数，并求量化信噪比。解：(1)(2)量化级数，对于均匀量化器，当输入为均匀分布时，其量化信噪比换算成分贝值5.12采用13折线A律非均匀量化编码，设最小量化间隔为，已知某采样时刻的信号值。(1)试求该非均匀量化编码，并求其量化噪声；(2)试求对应于该非均匀量化编码的12位均匀量化编码。解：(1)由于，极性码；取第1段与第8段的中位第5段进行比较，由于，所以；取第5段与第8段的中位第7段进行比较，由于，所以；取第7段与第8段的中位第8段进行比较，由于，所以，段落码；第7段的起始量化值为，量化间隔为；与段内码最高位权值比较，由于，所以；与段内码次高位权值比较，由于，所以；与段内码次高位和第三位权值之和比较，由于，所以；与段内码次高位和最低位权值之和比较，由于，所以，段内码；因此，非均匀量化编码；量化噪声；37 (2)12位均匀量化编码。5.13将正弦信号输入采样频率为8采样保持器后通过A律13折线非均匀量化编码器，设该编码器的输入范围是[-1，1]。试求在一个周期内信号值的非均匀量化编码。解：采样频率是正弦信号频率的10倍，每个正弦周期内有10个采样点，采样值及其非均匀量化编码如下表所示：绝对值的量化单位极性码段落码段内码非均匀量化编码000100000001000000010.58782048111100101111001020.95113896111111101111111030.95113896111111101111111040.5878240811110010111100105-0000000000000000006-0.5878204801110010011100107-0.9511389601111110011111108-0.9511389601111110011111109-0.5878240801110010011100105.14将正弦信号进行增量调制，量化增量和采样频率的选择既要保证不过载，又要保证不致因振幅太小而无法工作。试证明。证：为保证不过载，，即为保证振幅足以分辨，故，即5.15将正弦信号输入采样频率为4采样保持器后通过增量调制器，设该调制器的初始量化，量化增量。试求在半个周期内信号值的增量调制编码和量化值。解：采样频率是正弦信号频率的20倍，半个周期内有10个采样点，采样值、增量调制编码及量化值如下表所示：37 预测值量化增量调制编码量化值000-0.1250-0.12510.0773-0.1250.1251020.146900.12510.12530.20230.1250.12510.2540.23780.25-0.12500.12550.250.1250.12510.2560.23780.25-0.12500.12570.20230.1250.12510.2580.14690.25-0.12500.12590.07730.125-0.125005.16将正弦信号输入采样频率为4采样保持器后通过差分脉冲编码调制器，设该调制器的初始值，，采用码长为4的均匀量化编码，量化间隔。试求在半个周期内信号值的差分脉冲编码和量化值。解：采样频率是正弦信号频率的20倍，半个周期内有10个采样点，采样值、差分调制编码及量化值如下表所示：预测值量化差分调制编码量化值00001000010.077300.062510100.062520.14690.06250.093810110.156330.20230.15630.031310010.187640.23780.18760.062510100.250150.250.2501-000000.250160.23780.2501-000000.250170.20230.2501-0.062500100.187680.14690.1876-0.031300010.156390.07730.1563-0.093800110.06255.17的子带编码如题图5.3所示。试证明要求的低通滤波器和高通滤波器满足：……×题图5.337 ……×证：设、、、如图：由抽取，得由内插，得令故37 第六章习题6.1奇校验码码字是,其中奇校验位满足方程证明奇校验码的检错能力与偶奇校验码的检错能力相同，但奇校验码不是线性分组码。证明提示：奇数个差错的发生总导致校验方程不满足。全0向量不是奇校验码码字。6.2一个线性分组码的一致校验矩阵为(1)求使该码的最小码距。(2)求该码的系统码生成矩阵及其所有4个码字。解题提示：(1)对H作行初等变换得要使最小码距等于3，有中任意两项为1，其余为零。当要使最小码距大于3，有中三项或四项均为1，其余为零。有上述关系可以求得一组或多组关于的解。(2)对作行初等变换得6.3一个纠错码消息与码字的对应关系如下：37 (00)—(00000)，(01)—(00111)，(10)—(11110)，(11)—(11001)(1)证明该码是线性分组码(2)求该码的码长，编码效率和最小码距。(3)求该码的生成矩阵和一致校验矩阵。(4)构造该码BSC上的标准阵列。(5)若在转移概率的BSC上，消息等概发送，求用标准阵列译码后的码字差错概率和消息比特差错概率。(6)若在转移概率的BSC上消息0发送概率为，消息1发送概率为，求用标准阵列译码后的码字差错概率和消息比特差错概率。(7)若传送消息0出错的概率为，传送消息1出错的概率为，消息等概发送，求用标准阵列译码后的码字差错概率和消息比特差错概率。解题提示：(1)任意两个码字的和是另一个码字且全零向量为码字。(2)码长为向量长，即。码字数为4，故。最小非零码字的重量为。(3)因为码字数为4，任意两非零码字构成生成矩阵的行向量。按G与H正交的条件，解得H的一种可能情况等于。(4)标准阵列见题表(3.1)。题表(3.1)标准阵列＝00000＝00111＝11110＝11001＝0000000000001111111011001＝0000100001001101111111000＝0001000010001011110011011＝0010000100000111101011101＝0100001000011111011010001＝1000010000101110111001001＝1001010010101010110001011＝101001010010011010100110137 (5)按题解(4)的标准阵列译码，记是标准阵列中码字c对应的列，是包括无错图案和全部可纠正差错图案的集合，那么码字差错概率为记消息比特差错概率为，消息向量差错概率为，注意到该码是非系统码以及消息向量长为2，则应有(6)码字差错概率计算中，，消息比特差错概率：(7)码字差错概率计算中消息比特差错概率：码字差错概率和消息比特差错概率相等。6.4证明最大长度码(simplex码)可以由1阶Reed-Muller码缩短(shortening)构成。证明提示：证明一阶RM缩短码是极长码等价于证明一阶RM缩短码是汉明码的对偶码。37 汉明码的校验矩阵是其对偶码的生成矩阵，可表为H，在汉明码的对偶码基础上构造一阶RM码生成矩阵为G，，显然RM码的一位缩短码就是对偶汉明码的校验矩阵，所以命题得证。6.5证明线性分组码的码字重量或者为偶数(包括0)或者恰好一半为偶数(包括0)另一半为奇数。证明提示：若码字重量全为奇数，则码不含全零码字，故不是线性码。若码字重量全为偶数，则任意两偶数重量的码字c与相加仍为偶数重码字，故所有码字均可以是偶数重码字。若个偶数重量的码字集合{c}和个奇数重量码字为集合，则根据二元线性分组码的任意码字重量满足可得：对固定的奇数重码字有，所以。又对任意奇数重码字，，由而有，，所以，由此证明。6.6一个通信系统消息比特速率为，信道为衰落信道，在衰落时间(最大为)内可以认为完全发生数据比特传输差错。(1)求衰落导致的突发差错的突发比特长度。(2)若采用Hamming码和交织编码方法纠正突发差错，求Hamming码的码长和交织深度。(3)若用分组码交织来纠正突发差错并限定交织深度不大于256，求合适的码长和最小码距。(4)若用BCH码交织来纠正突发差错并限定交织深度不大于256，求合适的码长和BCH码生成多项式。解题提示：(1)突发长度为bits。(2)汉明码可纠正t＝1个差错，所以交织深度为。由于没有延迟限制，所以任何码长汉明码均可。37 (3)由，以及设计。6.7若循环码以为生成多项式，则(1)证明可以构成任意长度的循环码；(2)求该码的一致校验多项式；(3)证明该码等价为一个偶校验码。解题提示：(1)由，总是的因子。(2)一致效验多项式为。(3)对生成矩阵作行初等变换总能获得偶校验码的生成矩阵形式。6.8已知循环码生成多项式为，分别做(1)求该码的最小码长，相应的一致校验多项式和最小码距；(2)求该码的生成矩阵，一致校验矩阵，系统码生成矩阵；(3)画出该码的级系统码编码电路图，给出编码电路的编码工作过程；(4)若消息为，分别由编码电路和代数计算求其相应的码式；(5)画出该码的伴随式计算电路图，给出伴随式计算电路的工作过程；(6)若错误图样为，分别由伴随式计算电路和代数计算求其相应的伴随式；(7)若消息长度大于，由(2)小题给出的编码电路产生的输出是什么？仍可以用(5)小题给出的伴随式计算电路判断是否有传输差错吗？解题提示：(1)最小码长为15。最小码距为3。(3)电路图题图(8.1)所示。37 题图(8.1)工作时序题表(8.1)所示。题表(8.1)时钟t门控信号G1/G2输入m(x)输出c(x)1/00/1m(x)0(6)代数计算得。6.9已知线性分组码的生成矩阵为，(1)证明该码为循环码；(2)求该码的生成多项式，一致校验多项式和最小码距。解题提示：(1)行等价生成矩阵为(2)生成多项式为，校验多项式为，最小码距为2。37 6.10已知Hamming码生成多项式为，证明用此码进行交织深度为3的交织后为生成多项式为的循环码。证明提示：交织后的码字为以及多项式。6.11一通信系统信道为转移概率的BSC，求下列各码的重量分布和不可检差错概率。(1)Hamming码。(2)最大长度码(simplex码)。(3)扩展Hamming码。(4)重复码。(5)偶校验码。解题提示：(1)二元Hamming码的重量分布多项式为：(2)最大长度码是等重码，。(3)扩展Hamming码扩展后，(4)因为只有两个码字00000000和11111111所以。(5)因为是偶校验，可知码字重量为偶数6.12证明循环码可以检测出所有长度不大于的突发差错。证明提示：假设错误图样,,次数等于或小于，则除不尽。又和互素。所以不能被除尽。37 6.13Fire(法尔)码是常用于检测或纠正突发差错的循环码，其生成多项式为其中为次数(次数与互素)的不可约多项式，即不能分解为次数更低的多项式的乘积。(1)证明Fire码码长，这里表示两数的最小公倍数。(2)证明Fire码可以检测出长度的单个突发差错。证明提示(参考第12题)。6.14以太网协议所用的CRC码是生成多项式如下的二进制码(1)估计该码的不可检差错概率。(2)如果分组长度限制为1024，如何改造此码最佳？解题提示：(1)不可检错概率。6.15ATM协议对帧头4字节(32比特)地址和路由信息校验所用的8比特CRC码生成多项式为在实际应用中是以此码构造一个最小码距为的码，讨论其构造方法。解题提示：利用循环码缩短方法。6.16对如下由子生成元或生成序列确定的(A)(B)(C)(D)4个卷积码，(A)，(B)，(C)，(D)，分别做(1)求多项式生成矩阵，生成矩阵，渐进编码效率，约束长度37 ，状态数。(2)画出简化型的编码电路图。(3)画出开放型的状态转移图，栅格图。(4)求自由距离。(5)求消息的卷积码码字序列。(6)在栅格图上画出消息的编码路径。解题提示：(1)(A)，=1/2，，，(B)，=1/2，，，(2)简化型的编码电路图见题图(16-1A)和题图(16-1B)题图(16-1A)题图(16-1B)(3)开放型的状态转移图和栅格图见题图(16-2A1)、图(16-2A2)和题图(16-2B1)图(16-2B2)。题图(16-2A1)37 题图(16-2A2)题图(16-2B1)题图(16-2B2)(4)自由距离分别为：A-3，B-4，C-8，D-2。(5)考虑补零，A：110100111001；B：11100111011101。6.17举例说明(16)题(B)码是一个恶性码，即少数差错可能导致无穷多差错。解题提示：考查寄存器状态为全1时输入导致的输出。37 6.18对题图(18)中的(A)，(B)两卷积码分别做码字码字消息消息码字题图(6.18-A)题图(6.18-B)(1)求卷积码的生成序列，多项式生成矩阵，生成矩阵，渐进编码效率，约束长度，状态数。(2)求自由距离。(3)画出开放型的状态转移图，栅格图。(4)求消息的卷积码码字序列。(5)在栅格图上画出消息的编码路径。(6)若消息的相应码字序列在BSC上传送，差错图案是，给出Viterbi译码的译码过程和输出与。(7)判断是否是恶性码。解题提示：(1-A)，，，，，。(2-A)自由距离为2。6.19第三代移动通信(3GPP)建议的码率，约束长度的卷积码(八进制表示)为(1)写出此码的正规多项式表示式，求状态数。(2)画出此码的电路图。(3)求此码的标准Viterbi译码在一个时隙内要做的ACS操作数。37 (4)若信道为转移概率的BSC，估计采用此码和Viterbi译码后的误码率。(5)若信道采用的调制方式为双极PSK，估计信道转移概率为时的编码增益。解题提示：(1)(2)(3)译码深度比特6.20解释卷积码译码(如Viterbi译码)为什么在译码端所用的记忆单元数越多(大大于发送端的记忆单元数)，则获得的译码差错概率越小(越逼近理想最佳的最大似然译码)。解题提示：当译码译码端所用的记忆单元数大于发送端的记忆单元数时，译码序列就有充足的空间回到全零状态，如果发生错误译码，则错误序列也会汇合到全零状态。37 第七章习题7.1用维吉尼亚密码加密，已知p=polyalphabeticcipher，密钥K=RADIO，试求密文。解：设a~z的编码分别是0~25。根据加密算法，其中,,分别表示第个明文、密文和密钥字母编码公式，可以得到：密钥：RADIORADIORADIORADIO明文：polyalphabeticcipher密文：GOOGOCPKIPVTLKQZPKMF7.2描述DES数据加密算法的流程。解：DES对64位的明文分组进行操作。通过一个初始置换，将明文分组分成左半部分和右半部分，各32位长。然后进行16轮完全相同的运算，这些运算被称为函数f。分别用16个不同的子密钥（由外部密钥产生）控制每一轮变换。一轮变换有4个操作步骤：扩展、密钥加、s盒代替、p盒置换。这4个步骤仅对右半部分的32位进行操作，结果与左半部分的32位混合后作为本轮右半部分的输出，而左半部分的输出直接复制右半部分的输入。经过16轮后，左、右半部分合在一起，经过一个末置换(初始置换的逆置换)，这样该算法就完成了。7.3明文p=themachineisnotbreakable，若用密钥的希尔密码加密，求密文。解：设a~z的编码分别是0~25。根据希尔密码加密公式：=其中,,分别表示第个明文、密文和密钥字母编码，然后把明文p=37 themachineisnotbreakable三个一组分别计算，明文the，字母编码为19、7、4，那么三个字母被表示为向量[19 7 4]计算为：=运算结果为(215251386)(mod26)=(7 17 22)=HRW同理计算第2组明文mac，字母编码为12、0、2，然后计算，取模，转化成相关字母，接着计算后面的三个明文字母，以此类推。密文：HRWKQGASDWWAUSZZXCGKELXK7.4古典密码体制和现代密码体制的主要区别是什么？解：古典密码体制和现代密码体制的主要区别是：古典密码体制数据的加密基于加密算法的保密，而现代密码体制的数据的加密基于密钥保密，而不是加密算法的保密。7.5公钥密码体制的一般定义是什么？解：1976年W.Diffie和M.E.Hellman提出的一种新型密码体制，即公钥密码体制。在公钥体制中，加密密钥不同于解密密钥，加密密钥公之于众，谁都可以使用；解密密钥只有解密人自己知道，分别称为公钥(Publickey)和私钥(Privatekey)。这种体制能够奏效的关键是利用了某些函数的单向性。要求设计的体制满足：（1）密钥产生容易，且密钥空间足够大；（2）合法用户解密容易，非法用户由公钥和密文不能推知明文；（3）已知密文和生成该密文的公钥，不能推知对应的私钥，并且在已知公钥、任选明文和对应的密文情况下仍不能推知用户私钥。满足上述条件的体制称为公钥密码体制。若还满足加解密变换的交换性，则体制可进行数字签名。7.6在RSA公钥密码系统中，如果截取了发送给其他用户的密文C=10，如果此用户的公钥为e=5，n=35，请问明文的内容是什么？解：利用幂剩余的周期性：=5所以37'