同济大学结构力学习题答案-朱慈勉.pdf 118页

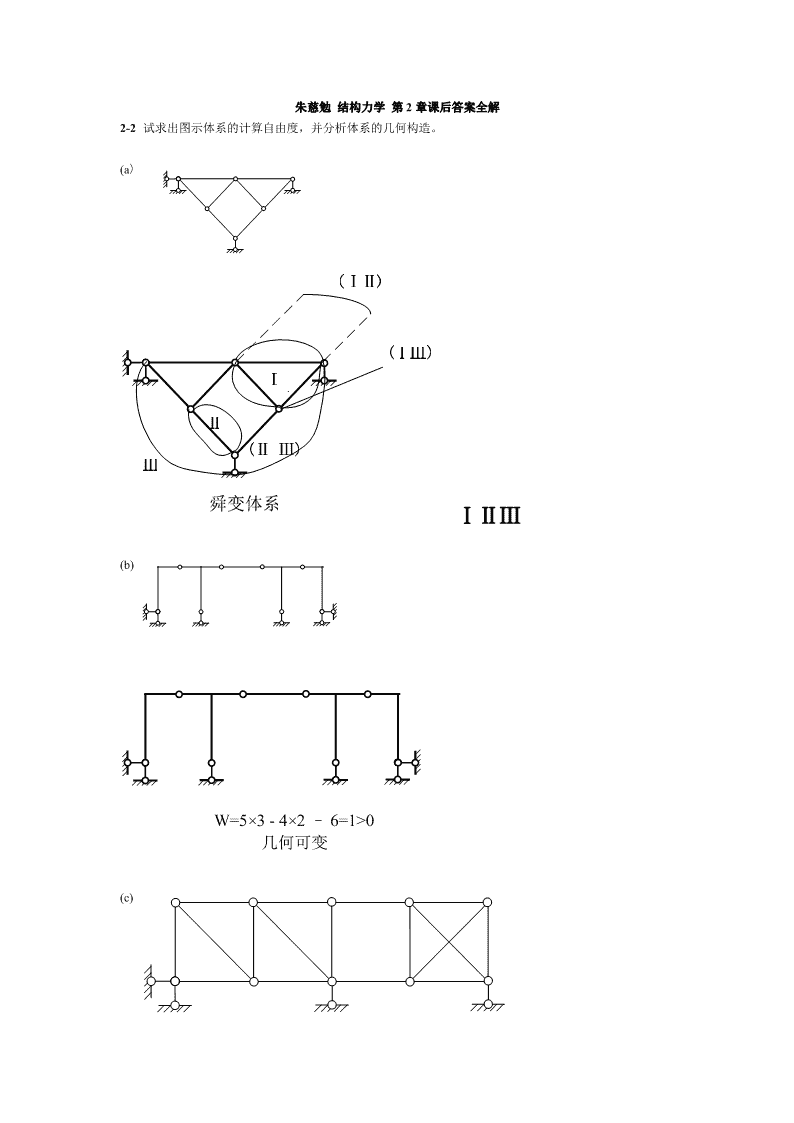
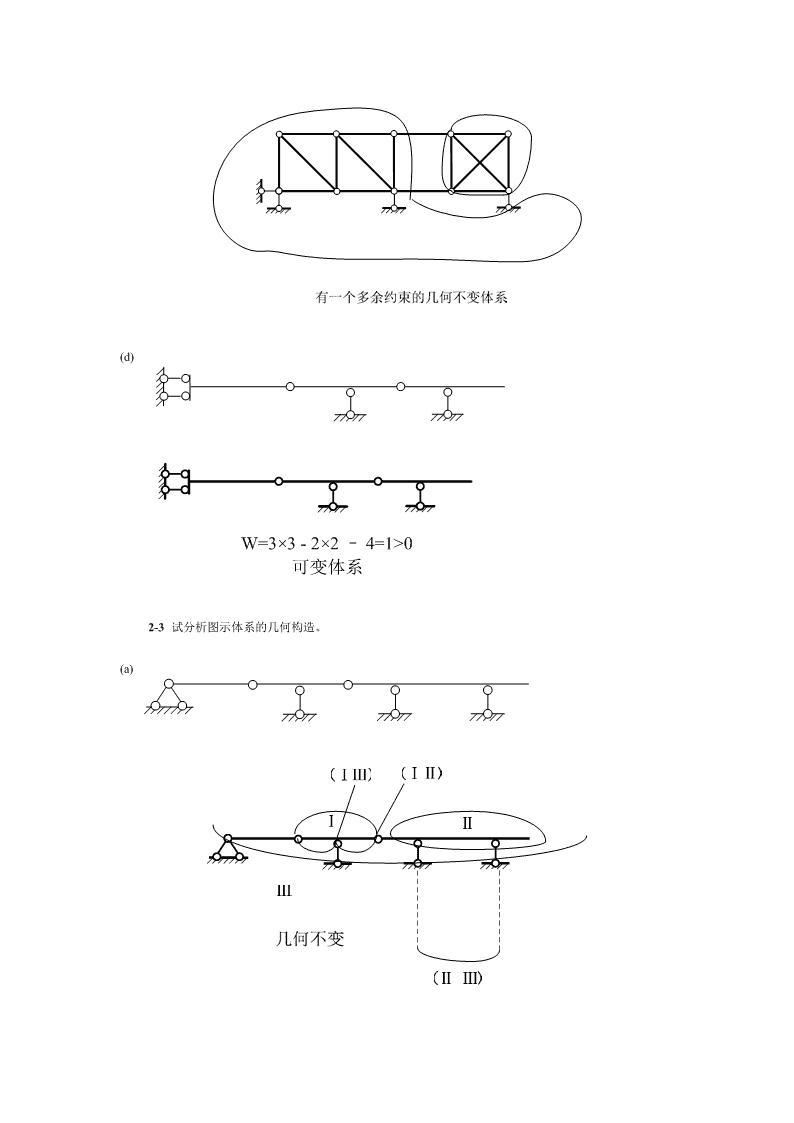
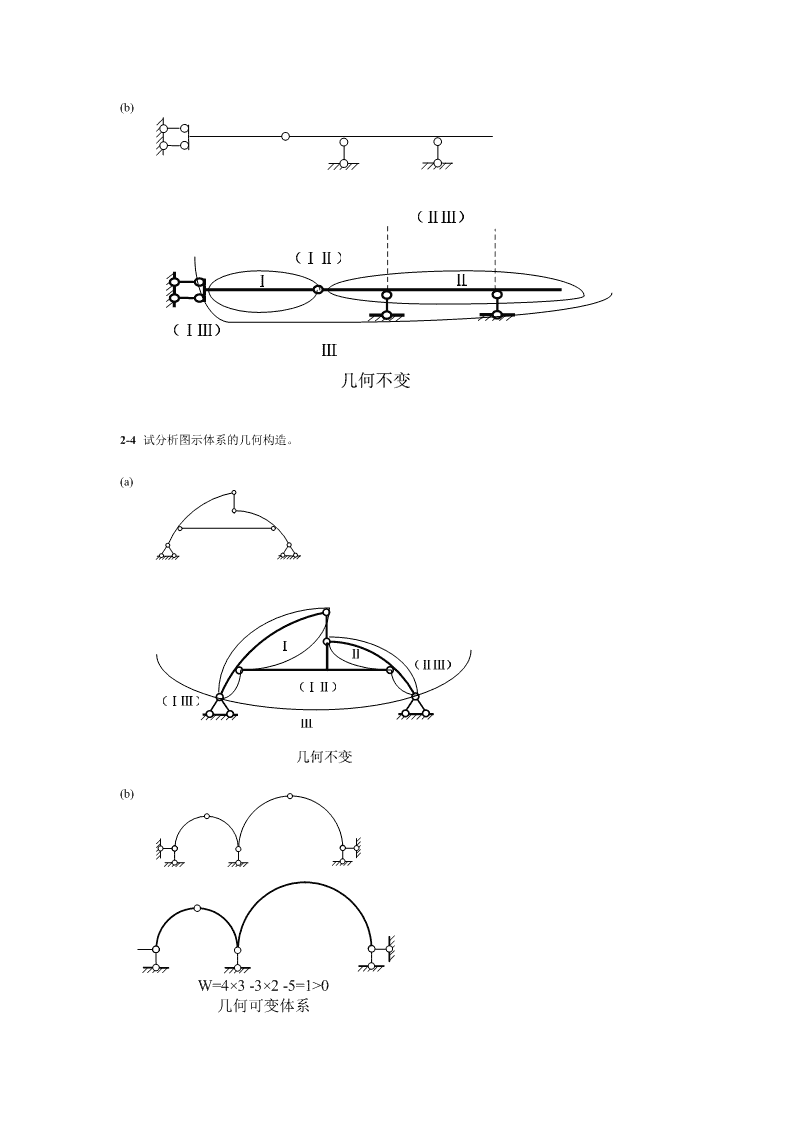
'朱慈勉结构力学第2章课后答案全解2-2试求出图示体系的计算自由度，并分析体系的几何构造。(a)ⅠⅡⅢ(b)W=5×3-4×2–6=1>0几何可变(c) (d)W=3×3-2×2–4=1>0可变体系2-3试分析图示体系的几何构造。(a) (b)2-4试分析图示体系的几何构造。(a)(b)W=4×3-3×2-5=1>0几何可变体系 (c)(d) (e)(f) (g)(h) 2-5试从两种不同的角度分析图示体系的几何构造。(a)(b) 同济大学朱慈勉结构力学第3章习题答案3-2试作图示多跨静定梁的弯矩图和剪力图。(a)FPFPaAFBCDEaaaaaFaFaPP22ＭFaP4FPFP243FP4(b)2kN/m10kNABCD2m2m2m6m4m (c)15kN20kN/mABCDEF2m2m3m3m3m4m180M4018070210Q401540604kN(d)6kN·m4kN·mABCDEFGH2m2m2m2m2m2m2m3m 3-3试作图示刚架的内力图。(a)2kN4kN·mBC6m1kN/mAD3m3m(b)BC3m10kND3mA40kN·m6m (c)2kN/m4kNBC3m6kN3mAD6m(d)4kN·m2kNCD2m2kNE2mAB6m MQN(e)C4m1kN/mABD4m4m(f)4kNC2kN/mB4mA3m2m4m 3-4试找出下列各弯矩图形的错误之处，并加以改正。(a)(b)(c) (d)M(e)(f)3-5试按图示梁的BC跨跨中截面的弯矩与截面B和C的弯矩绝对值都相等的条件，确定E、F两铰的位置。qADEBCFxxl 2qlM8ADEBCFq12qlM=()l-xx+=qxxcFD222QM==MMBC中BC12=MqlqC()lx-162ql12=xql2161=xl83-6试作图示刚架的弯矩和剪力图。(a)对B点求矩20´9´(4.5-3)=RR´6=45()FF2MR=0.5´20´9-45´9=405,=135()EEMM=45´3=135,=0.5´20´=990CFCDM=0.5´20´=990BA (b)113.75MQ12.12.95.754.25M=4.25´4-24´´=21EM=3.5´1.5+0.25´=25.75K对A点求矩：RR´7+24´´2=5´2.5®=-¯0.5()BB对C点求矩：2´4´2+0.5´2=HH´4®=®4.25()BBVH=3.5(),=¬0.25()AA5.75QQ==2.1,=2´4-=4.253.75K左EF2.5(c)160QM80/33016016401008080601608080MM=´3=80,=´=6160DAED33H=¬30()C对FV点求矩:=(20´2´3+30´4)/2=120()C对AV点求矩:´6+120´10=30´4+20´´211B320V=-¯()B380V=()A3 (d)435435203588M=´4-1´42´=DA33对A点求矩:41´´6+1´4´2=VV´8®=4()BB4对C点求矩:4´4-1´4´2=HH´6®=¬()BB38HV=(¬=),0AA3(e)ååMC=0®VB=2Fp(),ME=02®=HVBFåMB=0®3FP´2a+2a´HH=2FPF´22a+´VaH=F(¬),VF=¯2()HPFPH=4FV(®=),0DPD(f) 848844++--44+-4488-+848利用对称性8进一步简化HIVIHB88VB可知:H=4KN(®),V=¯4KN()BBH=-4KN(¬),V=-4KN(),M=4´2=·810NmIIA(g) qq2qa对H点求矩：2DEFGHIJ2qaqa+=HCC´a®H=®1.5qa()a2ABC对F点求矩：qa´1.5a+H´a=0®H=-¬1.5qa()AAaaaaaa22H=0,M==qa,M1.5qa2DGFGH23qaqa2222qa2qa23qa3qa222qaqa22qa22qa2qa1.5qa1.5qa 同济大学朱慈勉结构力学第5章习题答案5-1试回答：用单位荷载法计算结构位移时有何前提条件？单位荷载法是否可用于超静定结构的位移计算？FPFPDEaABCaaaa由对称性分析知道F=F=0,RR==FF=F=2FF=F=FFF=-NCDNCEABPNBENADPNBCNACPPDE-122--22222211221112212´F´2a-´(-´2Fa)2FNFNPl22PP-1´(-´FaP)26.83DcxP=å=´2+´2+=¯Fa()EAEAEAEAEA2625-4已知桁架各杆截面相同，横截面面积A＝30cm，E＝20.6×10N/cm，FP＝98.1kN。试求C点竖向位移ΔyC。 -5F-5FPP-5FP5F5F-5FPPP442F52FPFPP4由节点法知：对A节点F=-5FFF2=NADPPNAE55对E节点FF==FFNECPPNEF44由节点法知：5对A节点F=-F1=NADNAE2FNFl155NPDyc=å=(1´2FP´2´5+1´FFPP´6+(-)´(-55)´´24)EAEA42=¯11.46cm()5-5已知桁架各杆的EA相同，求AB、BC两杆之间的相对转角ΔqB。-4242424242-421421-4221-48414111424411DqB=åFNFlNP=-(1242)EAEA5-6试用积分法计算图示结构的位移：（a）ΔyB；（b）ΔyC；（c）qB；（d）ΔxB。 (a)q2q1AEIBl以点B为原点，向左为正方向建立坐标。qq-21q()x=+xq1l123qq21-M()x=+qxxp126l显然，M()xx=ll11134qq21-D=M(x)´M(x)dx=+()qxxdxyc1òòpEIEIl26001q241114=()l+qlEI30120(b)qBClEI=常数A3ll4q2l2l5q2l47l4MPM211qlq3152325124315127D=(l´´l+´ql´l+ql´´l+´l´l+l´´l)=¯ql()ycEI3242443422434EI16 (c)1kN/m2kNBR=2m4mAO12M(j)=(RRsinjj)´1-2´-(1cos)2M(j)1=p2112q=1´[(Rsinj)´1-2´-R(1cosjj)]RdBòEI20(8-3p)-1.42==()逆时针EIEI(d)AqREI=常数OBqds=qRdqjqj2M(j)=òqRdq´Rsin(j-qj)=-qR(1cos)0MR(jj)=sinp211124D=M(j)M(j)ds=qR(1-cosj)RsinjjRd=¬qR()xBòòEIEI2EI05-7试用图乘法计算图示梁和刚架的位移：（a）ΔyC；（b）ΔyD；（c）ΔxC；（d）ΔxE；（e）qD；（f）ΔyE。(a) 1113222以Ax为原点，向右为正方向建立坐标2M(x)5=-xxì1x(0££x3)ïï2Mx()=í1ï3-x(3££x6)ïî26181D=M(x)´M(x)dx=¯()ycòEIEI0(b) 2kN/m6kNEABCDEI=常数1m2m2m6mMPM611211D=(2´3´)-´´6´´2´´36yD6EI2EI384311+´(´3´2+1´6´2+(-3)+´-(6))6EI2225+´6´1´2=¯()62EIEI(c)2kN2kN1B2EIC6EIEI6m2kN/m1AD3m3m3m22336MPM3D=(2´18´2+2´18´2+2´30´4+2´30+18´4+2´30´+42´36´6+4´36+´630)xc62´EI26122´6918+(2´36´6)+´´6´´3=®()6EIEI38EI(e)2kN/m4kNEICDkEI6mAB M1812MM11110PqDP=åòds+FF=(´12´3´1)+(2´´121)EIkEI26EI12141111311-(´10´16´)-(2´´26)-(´4´16´´)+´´13.5EI326EI2EIk32486227=-+()顺时针3EIk165-9图示结构材料的线膨胀系数为α，各杆横截面均为矩形，截面高度为h。试求结构在温度变化作用下的位移：（a）设h＝l/10，求ΔxB；（b）设h＝0.5m，求ΔCD（C、D点距离变化）。（a）+25℃CD+25℃+35℃+25℃lABl 1LL11MNtt12+60oot===30CCDt=t-=t1002122aDtDkt=+ååat0òòFNdsMdsha´10122=a´30´1´l+´(ll´+2)h22l=30al+(10aa´=2ll)/23010(b)11CD5543340000--3m44A000B+t+t+t-1-1-14m4m4mN图aDt5Dkt=ååaat0òòFNds+Mdst=´´5h451tta+aat´´5+´´(-1)´12+´(´4´3´+´243)422hM图=54.5at()®¬5-10试求图示结构在支座位移作用下的位移：（a）ΔqC；（b）ΔyC，ΔqC。(a)CDEE′D′C′ΔqChABB′blla22 11hh1aDqC=-åFRCa=-[(-)´=]()方向与图示一致hh(b)ABCDc132cA′cB′D′C′ΔqC2aa2aFR图1331Dyc=-åFRC=-[C1-C2]=CC21-¯()2222351531D=-[]C-C+C=C--CCqC1232134a4a2a4a42aa3514a4a2a 习题6-1试确定图示结构的超静定次数。(a)2次超静定(b)6次超静定(c)4次超静定(d)3次超静定(e)II去掉复铰，可减去2（4-1）=6个约束，沿I-I截面断开，减去三个约束，故为9次超静定(f)沿图示各截面断开，为21次超静定(g)所有结点均为全铰结点刚片I与大地组成静定结构，刚片II只需通过一根链杆和一个铰与I连接即可，故为4次超静定III (h)题目有错误，为可变体系。6-2试回答：结构的超静定次数与力法基本结构的选择是否有关？力法方程有何物理意义？6-3试用力法计算图示超静定梁，并绘出M、FQ图。(a)FPA2EIEIBC2ll233lFpF3p解：上图=+lX1=1M1MpdX+D=01111p其中：2l31æ1lll2ö3ælllö14ld11=ç´´´´÷+ç2´´+2´l´l+´l´2÷=EIè23333ø2´6EIè333ø81EI2l33æ22lö-7FplD1p=ç-2´lFp´l-lFp´÷=6EI´2è333ø81EI37Fl314lpX-=0181EI81EI1X=F1p2M=M1X1+Mp1Flp6M图1Flp6 Q=QX+Q11p1Fp2Q图Å1Fp2(b)FPABECDFEI=常数lllll2222FP解：基本结构为：X1X2lM1l3lM21Flp2FPMp1Flp3ìïd11X1+d12X2+D1p=0íïîd21X1+d22X2+D2p=0M=M1X1+M2X2+MpQ=QX+QX+Q1122p6-4试用力法计算图示结构，并绘其内力图。(a) 20kN/mB1.75EICDEI6mA6m3m解：基本结构为：20kN/mX161M16810810MpdX+D=01111pM=M1X1+Mp(b)Ea2CDqa4EI=常数AB4a4a解：基本结构为： X1计算M1，由对称性知，可考虑半结构。112a122M1计算M：荷载分为对称和反对称。p对称荷载时：qa2q22qaqa22226qa6qa6qa反对称荷载时：q2aqa2q22qaqa22228qa8qa8qa22qa22M14qa2qap dX+D=01111pM=M1X1+Mp6-5试用力法计算图示结构，并绘出M图。(a)CEI6m11kNDBEI2EI6mA3m3m解：基本结构为：X111KNX2111KN336112633M1M2Mp用图乘法求出d,d,d,D,D1112221p2pìïd11X1+d12X2+D1p=0íïîd21X1+d22X2+D2p=0(b) EDEI=常数6m20kN/mACB6m6m解：基本结构为：X2X1X2X120kN/m111163633M1M21503090180150MMp6108d=(2´3´3+2´3´3+2´6´6)=116EIEI6d=(2´3´3-2´3´3)=0126EI6108d=(2´3´3+2´3´3+2´6´6)=226EIEI1æ122æ12ö312ö2700D1p=çç´6´180´3´+´6´ç´20´6÷´+´6´180´3´÷÷=EIè233è8ø223øEI1æ122æ12ö312ö540D2p=çç´6´180´3´+´6´ç´20´6÷´-´6´180´3´÷÷=EIè233è8ø223øEI ì1082700X+=0ïï1ìX=-25EIEI1íÞíï108X+540=0îX2=-5ïîEI1EIM=180-3´25-5´3=90KN×mCAM=180-3´25+5´3=120KN×mCBM=6´(-5)=-30KN×mCD(c)CEA=∞DII3m10kN·m10kN·m5I5I6mAB12m解：基本结构为：X110kN·m10kN·m11Å3310kN·m10kN·m10kN·m991010N1M1Mpé1æ3ö6ù558d11=êç´2´3´3÷+(2´3´3+2´9´9+2´3´9)ú´2=ëEIè6ø6E´5Iû5EIé6()ù144D=-2´10´3+2´9´10+9´10+3´10´2=-1pê´úë6E5IûEIdX+D=0ÞX=1.291111p1M=9´1.29-10=1.61KN×mAC M=3´1.29-10=-6.13KN×mDAM=3´1.29=3.87KN×mDC3.876.136.133.871.611.61M(d)DEA=∞EII3mEA=∞FG10kN/m5I5I2I6mABCX2解：基本结构为：X110kN/m11339966M1M245405Mp36111.6d=(2´3´3)´2+(2´3´3+2´9´9+2´3´9)´2=116EI6E´5IEI 625.2d=-(2´6´9+3´6)=-126E´5IEI6650.4d=(2´6´6)+(2´6´6)=226E´5I6E´2IEI1æ13ö6()1æ2ö1721.25D1p=ç´3´45´3´÷+2´3´45+2´9´405+3´405+45´9-ç´6´45´6÷=EIè34ø6E´5I5EIè3øEID=02pì111.625.21721.25X-X+=0ïïEI1EI2EIìX=-17.391íÞíï-25.2X+50.4X=0îX2=-8.69ïîEI1EI2M=405-9´17.39=248.49KN×mADM=6´(-8.69)-9´17.39=104.37KN×mBFM=3´(-17.39)=-52.17KN×mFEM=6´(-8.69)=-52.14KN×mCG52.17M248.49104.3752.146-6试用力法求解图示超静定桁架，并计算1、2杆的内力。设各杆的EA均相同。(a)(b)11a21.5m2FPFP30kNaaa2m2m题6-6图6-7试用力法计算图示组合结构，求出链杆轴力并绘出M图。(a) FPABEI12EIkθ=l2EIlEA=2lCll解：基本结构为：FP12lFlFpP1M1Mp3l2l2l7ld=+(2´2l´2l)+2l=11EA6EIk2EIq3l()FplFplD=2´Fl´2l+Fl´l+2l=1ppp6EIk2EIq2dX+D=0ÞX=-F1111p1p723M=Fl-F´2l=FlAppp773Flp72FlMp7(b)qqaEFGaEAC2DEA=EI/aaEI=常数ABaa 6-8试利用对称性计算图示结构，并绘出M图。(a)FPDEA=∞EEA=∞FEI2EIEI9mABC6m6m解：FFpFpFpp原结构=22+22①②①中无弯矩。②取半结构：Fp2基本结构为：FFppX1122999Fp2M1Mp2æ12ö243´2d11=´ç´9´9´9´÷=EIè23øEI1æ192ö243D1p=´ç´9´Fp´9´÷=FpEIè223ø2EI1dX+D=0ÞX=-F1111p1p4 9999FpF9FFpFp4pp4244M图整体结构M图(b)60kNCDEI=常数3mAB4m5m4m(c)qCDEI=常数lABql解：根据对称性，考虑1/4结构：q基本结构为：q2qX1l181M1Mp1ælöld11=ç1´´1´2÷=EIè2øEI2221æ1lqllqlöqlD=ç´´´1+´´1÷=1pç÷EIè32828ø12EI 2qldX+D=0ÞX=-1111p112M=M1X1+Mp222qlqlql2424242ql2ql12ql2121222qlqlM2424(d)qDEFEI=常数lABCqll解：取1/4结构：q基本结构为：qX2X11q2l2l11M11M2Mp 231æl2öld=ç´l´÷=11ç÷EIè23ø3EI21æ12öld12=-ç´l´1÷=-EIè2ø2EI1ælö3ld22=ç´1´1+l´1´1÷=EIè2ø2EI241æ1ql3öqlD=-ç´l´´l´÷=-1pç÷EIè324ø8EI231æ1qlöqlD=ç´l´´1÷=2pç÷EIè32ø6EI324ìllqlì5X-X-=0X=qlï121ï3EI2EI8EIïï12íÞí231ïl3lqlïX=ql2ï-X1+X2+=0ï236î2EI2EI6EIî22qlql92922qlqlql36363622qlqlM36362ql(e)950kNE2IFII6mC2IDII6mAB9m (f)4FPHGIa2EDFa2ABC(BEH杆弯曲刚度为2EI，其余各杆为EI)aaaa取1/2结构：2FFFpppFpFp=+2FFpFpFpFpp①②②中弯矩为0。考虑①：反对称荷载作用下，取半结构如下：FpFFpFpp2222=+FpFpFpF2FpFp2p22③④④中无弯矩。考虑③：FFFpppa222ÞFpaF2p2弯矩图如下：FpFpaa22FpFaaFpap2FFppaa22FpaFpFap2a2Fpa2 (g)3EIk=3k4aEFaFPCGDaAEI=常数Baa解：原结构=+FpFpFpFp2222①②①弯矩为0。反对称荷载下：Fp2基本结构为：X1Fp21Fp2Fpa2a2M1Mp31æ12ö8ad11=ç´2a´2a´2a´÷=EIè23ø3EI 3aæFpFpö5FpaD=ç-2´2a´a-a´a÷=-1pç÷6EIè22ø12EI35F3X18ap34a5dX+D=-ÞX-a=-XÞX=F1111p111pk3EI12EI3EI48M图如下：5Fpa485Fap4877FpaFa24p24(h)4FPBDFIIIII2I2I2IIhACEllll6-9试回答：用力法求解超静定结构时应如何恰当地选取基本结构？6-10试绘出图示结构因支座移动产生的弯矩图。设各杆EI相同。(a)ABCDEEI=常数D2Dllll(b)22CDa3AEI=常数BDB′4a4a4a题6-10图6-11试绘出图示结构因温度变化产生的M图。已知各杆截面为矩形，EI=常数，截面高度h=l/10，材料线膨胀系数为α。(a)(b)B-15℃CA+15℃B-15℃℃℃℃+25℃l10-l10-+15C+15℃DA+5℃lll 题6-11图6-12图示平面链杆系各杆l及EA均相同，杆AB的制作长度短了D，现将其拉伸（在弹性范围内）拼装就位，试求该杆轴力和长度。FPABCDABl题6-12图题6-13图6-13刚架各杆正交于结点，荷载垂直于结构平面，各杆为相同圆形截面，G=0.4E，试作弯矩图和扭矩图。6-14试求题6-11a所示结构铰B处两截面间的相对转角ΔqB。6-15试判断下列超静定结构的弯矩图形是否正确，并说明理由。(a)(b)(c)qFPFP(d)qFP题6-15图6-16试求图示等截面半圆形两铰拱的支座水平推力，并画出M图。设EI=常数，并只考虑弯曲变形对位移的影响。FPCRABRR题6-16图 同济大学朱慈勉结构力学第7章位移法习题答案7-1试确定图示结构的位移法基本未知量数目，并绘出基本结构。(a)(b)(c)EIEIEI2EI2EI1个角位移3个角位移，1个线位移4个角位移，3个线位移(d)(e)(f)EIEI1=∞1=∞EIEA3个角位移，1个线位移2个线位移3个角位移，2个线位移(g)(h)(i)k一个角位移，一个线位移一个角位移，一个线位移三个角位移，一个线位移7-2试回答：位移法基本未知量选取的原则是什么？为何将这些基本未知位移称为关键位移？是否可以将静定部分的结点位移也选作位移法未知量？7-3试说出位移法方程的物理意义，并说明位移法中是如何运用变形协调条件的。7-4试回答：若考虑刚架杆件的轴向变形，位移法基本未知量的数目有无变化？如何变化？7-5试用位移法计算图示结构，并绘出其内力图。(a)qAiDiCliBll 解：（1）确定基本未知量和基本结构有一个角位移未知量，基本结构见图。12ql3iZ=131Rr1p114iii12ql62iM1图Mp图（2）位移法典型方程rZR+=01111p（3）确定系数并解方程12r=8i,R=-ql111p3128iZ-ql=0132qlZ=124i（4）画M图721qlql224812ql652ql24M图(b)2.5kN/m10kNA2EIBEIDEI4mC4m4m解：（1）确定基本未知量1个角位移未知量，各弯矩图如下 390EIZ112r511EI1EI2M图M图1p（2）位移法典型方程rZR+=01111p（3）确定系数并解方程5r=EIR,=-35111p25EIZ-=3501214Z=1EI（4）画M图4026147M图()KNm×(c)FPDEA=∞EEA=∞FEI2EIEI9mABC6m6m解：（1）确定基本未知量一个线位移未知量，各种M图如下 Z=11r11FpR1pEI2EIEI272727M图112EIEI1243243EIMp图243（2）位移法典型方程rZR+=01111p（3）确定系数并解方程4r=EI,RF=-111pp2434EIZF-=01p243243Z=14EI（4）画M图999FpFpF424p(d)EFEAEAa2ABCDEI1=∞FPFPaa2aa解：（1）确定基本未知量一个线位移未知量，各种M图如下 24EAa/2EAa/255r11Z1=1M图122EAa/2EAa/2255EA简化5r11M图1R1p143aaFa5F5p5pMp（2）位移法典型方程rZR+=01111p（3）确定系数并解方程26r=EA/,aRF=-111pp5526EAZF-=01p55a3aZ=1EA（4）画M图0.6F1.2Fpp0.6FaFappM(e)DCFPEAlEAEABAl 解：（1）确定基本未知量两个线位移未知量，各种M图如下r21EAlZ1=1r11EAæö2Þr=+ç÷111lèø4EA2l2EAr=214lM图1r22Z2=1r12EAEAæö2EAÞr=+ç÷1l22lèø42lM2FpR1pÞRF=-1pp0R=2pMp（2）位移法典型方程rZ+rZR+=01111221prZ+rZR+=02112222p（3）确定系数并解方程 EAæö22EAr=ç÷1,+rr==111221llèø44EAæö2r=+ç÷122lèø4R=-=FR,012ppp代入，解得1+22lZF=××1p2(12+)EA1lZF=-××2p2(12+)EA（4）画M图1+22Fp2(12+)2Fp1-F2(12+)p2(12+)M图7-6试用位移法计算图示结构，并绘出M图。(a)10kN/mACEF6mEI=常数BD6m6m6m解：（1）确定基本未知量两个角位移未知量，各种M图如下22EIEI332Þ=r2EIEI111EI313r=EI2131EI3M1 2EI321EI111EIÞ=rEI3EI223361EI3M2Þ=R301p0R=1pMp（2）位移法典型方程rZ+rZR+=01111221prZ+rZR+=02112222p（3）确定系数并解方程1r=2,EIr==rEI111221311r=EI226RR==30,012pp代入，解得ZZ=-=15.47,2.8112（4）画最终弯矩图35.1619.699.383.2710.311.871.40M图(b)AB10kN/mEI=常数6mCDE6m6m解：（1）确定基本未知量两个位移未知量，各种M图如下 r11r21M1i/2iri12ri22M图23030R1pR2pMp图（2）位移法典型方程rZ+rZR+=01111221prZ+rZR+=02112222p（3）确定系数并解方程r=11i,0rr==1112213ir=-224R=30KN,R=-30KN12pp代入，解得3011ZZ=-×,=×401211ii（4）画最终弯矩图M(c) C30kN2mAEFDEI=常数2mB2m2m2m解：（1）确定基本未知量两个位移未知量，各种M图如下ir4i113i2i3ir21M图13i3ir1222r22M2图30KNR1pR2pMp图（2）位移法典型方程rZ+rZR+=01111221prZ+rZR+=02112222p（3）确定系数并解方程 3ir=11,irr==-11122126ir=224R=0,R=-30KN12pp代入，解得6.31646.316ZZ==,12EIEI（4）求最终弯矩图4.2125.2612.639.476.32M图(d)ElqqlGBDFlEI=常数AClll2解：（1）确定基本未知量两个位移未知量，各种M图如下2EIl3EIZ=11lr4EI11l3EIr21l3EIlM1图 6EI2l6EIr12l2Z2=13EIr222l3EI2lM212ql812ql16R1pR2pMp（2）位移法典型方程rZ+rZR+=01111221prZ+rZR+=02112222p（3）确定系数并解方程133EIEIr=,rr==1112212ll18EIr=222l12R=ql,R=-ql12pp16代入，解得3466ql211qlZZ=-×,=×123600EI3600EI（4）求最终弯矩图20.315ql20.125ql220.278ql0.008ql20.231ql20.055ql20.176qlM(e)20kN50kN·m80kN·m10kN·mDA2EIBEICEI4m4m4m4m8m 解：（1）确定基本未知量两个角位移未知量，各种M图如下3EIZ=1411rEIr114211EI2M11EIZ=1r1222r2213EIEI48M图225252020252050M图p（2）位移法典型方程rZ+rZR+=01111221prZ+rZR+=02112222p（3）确定系数并解方程51r=EI,r==rEI111221447r=EI228R=45KN×=mR,012pp代入，解得ZZ=-=38.18,10.9112（4）求最终弯矩图M7-7试分析以下结构内力的特点，并说明原因。若考虑杆件的轴向变形，结构内力有何变化？(a)(b)(c)FPFPFP (d)(e)(f)MFPqFPEI1=∞EI7-8试计算图示具有牵连位移关系的结构，并绘出M图。对称轴(a)20kNEBEI1=∞3EI3mDEI1=∞G3EI3EIEI6mACF8m8m解：（1）画出M,M,M图12pr11r11Z=14EI122EIEI44399EIEI813rr21212EI9由图可得：1124r=EI,r==rEI111221813r2114EIEI6Z2=131EIrr221222EI1136EIEIEI618212EI1EI2EI96M2由图可知：14r=EI229 R1pR2pMpÞR1p=-20KNR=02p（2）列方程及解方程组ì1124EIZ+EIZ-=200ïï81312í414ïEIZ+=EIZ012ïî39解得：11ZZ=83.38,=-71.4712EIEI（3）最终弯矩图(b)D6mBC10kN4m10kNEI=常数4mA8m35解：C点绕D点转动，由Cy=1知，Cx=,C^CD=44知 EI9EI3EI3EIr11=EI,r12=r21=,r31=r13=-=-4128321284EI4EI93327r22=+=EI,r23=r32=-EI-EI=-EI108103240160R1p=10KN×m,R2p=0,R3p=-6.25KN求r33åMD=0知273399EIEI+EI+EI-EI+´1416040128128128´8r33==0.055EI8ìEI3ïEIZ1+Z2-EIZ3+10=04128ïìZ1=-17.9/EIïEI9EI27ïíZ1+Z2-EIZ3=0ÞíZ2=58.5/EIï410160ïï327îZ3=285.6/EIï-EIZ1-Z2+0.055EIZ3-6.25=0î128160(c)FPCBEI1=∞EIEIaDAaaa22解：（1）作出各M图o瞬心10EI2a9EI264EIEIa+22aa42EI2a42EI62EIEI2a+22aaM1图 9EI18EIåM0=02Þr11´a=33´aa+´aa(92+18)EI=r113ao瞬心PR1p1Pa4M图paåM01=00ÞP×+Rap×=2PR=-1p2（2）列出位移法方程rZR+=01111p解得：3PaZ=12(92+18)EI（3）最终M图5Pa92+185Pa92+181Pa452Pa2(92+18)22Pa92+184Pa92+18(d)qEI1=∞AB4EICEIDk=3llll22解：基本结构选取如图所示。作出M1及Mp图如下。 9EI8EI22l2l10EIZ=121lr11M图11ql2121ql2ql12812M图pæ10EI8EIöæ10EI9EIö29EIr=ç+÷l+ç-÷l/2=1122223èlløèl2lølæ112ö7R1p=-çql+ql/l÷=-qlè212ø12由位移法方程得出：47qlrZ+R=0ÞZ=1111p1348EI作出最终M图852ql34852ql76841122qlql3488M图7-9试不经计算迅速画出图示结构的弯矩图形。(a)BθAAC(b)ByBDB′AC题7-9图7-10试计算图示有剪力静定杆的刚架，并绘出M图。qqaFCGaqqaDEBaEI=常数Aaa 解：（1）画出M,M,M图12pZ=111r11rql212ql1282i3i12Z1qlr2821rql22212ql23ii2qlM1图M2图Mp图由图可知，得到各系数：r=7i,r=r=-i,r=8i1112212252132R=-qa,R=-qa1p2p885312求解得：Z=,Z=1244055（2）求解最终弯矩图1592ql4402632ql4401042ql440362ql55432ql551772ql4402382ql440672ql55M图7-11试利用对称性计算图示刚架，并绘出M图。(a)20kN/mABCDEEI=常数6mFG6m6m6m6m解：（1）利用对称性得： 2EI3Z=11r112R1EIEI31p31EI3M图M图1p4（2）由图可知：r=EI,R=-300KN×m111p34EIZ-300=0133225可得：Z=300´=14EIEI（3）求最终弯矩图M图(b)CEIEI20kN3mABEI4m4m解：（1）利用对称性，可得：EI10KNEI2EI5Z1=1r11EI44EI5M1图Mp（2）由图可知，各系数分别为：EI421r=+EI=EI114520R=-20KN×m1p21EIZ-20=0120 400解得：Z=121EI（3）求最终弯矩图如下7.6215.2424.76M图(c)FPABEI12IEAA=2llEIEICDEll解：（1）在D下面加一支座，向上作用1个单位位移，由于BD杆会在压力作用下缩短，所以先分析上半部分，如下图。1Pl8P1x512EIN=-425lN=-Pl5R1pM图p3EI12EI4D点向上作用1个单位，设B向上移动x个单位，则x=(1-x)，得x=个单位。33ll5（2）同理可求出Mp图。12EI212EI132EI4r=x+=,R=Pl113331pl5l5l53Pl可得：Z=-133（3）求最终弯矩图 3Pl118N=-Pl1122PlPl11112Pl11M图(d)10kNC3mDBEIEIB′D′EIEI2EI2EI4mAA′4m4m4m4m(e)EIDEICC′EIEIEI3mBEB′EI1=∞EI1=∞EI50kNEI3mAA′3m3m解：（1）利用对称性，取左半结构 Z=1221EIEI4EIr113r123R1p32EI94EI23EI34EI29EI43EI98rEIZ=1219225KNr22R2pM1图M2图Mp图（2）由图可知：8420r=EI,r=r=EI,r=EI112112223927R=0,R=25KN1p2p2575解得：Z=,Z=-124EI3EI（3）求得最终弯矩图50503312522562256650503312512566252533M图(f)10kNABC2m10kNDEEI=常数2mF2m2m解：由于Ⅱ不产生弯矩，故不予考虑。只需考虑（Ⅰ）所示情况。对（Ⅰ）又可采用半结构来计算。如下图所示。 Z=1Z22rr21225kNZ=11Z1r11r125kN11M1图M2图R2pR1p7-12试计算图示结构在支座位移作用下的弯矩，并绘出M图。(a)AEIBEICDEIDlll (b)BC3EIEIEIlADjΔ=ljl解：（1）求M,M,M,M图。123p12ir116ir21r12r22rr13234ir314ir326ir336il6i12il6i6i2i2illM1图M2图M3图（2）由图可知：6i24ir=16i,r=r=6i,r=r=-,r=16i,r=11122123322233ll18ifR=0,R=8if,R=1p2p3pl代入典型方程，得：Z=0.426,Z=-0.374,Z=0.763l123（3）求最终弯矩图EI2.87flEI1.93flEIEI4.67f3.73fllM图7-13试用位移法求作下列结构由于温度变化产生的M图。已知杆件截面高度h＝0.4m，EI＝2×42－510kN·m，α＝1×10。+20℃A0℃B0℃+20℃4mC6m题7-13图解：（1）画出M,M¢,M¢¢图。t1tt 4EI20lEIa3r11R1t¢R1t¢¢4EI45EIa2EIl3l10EIa2EIlM1图M1t¢图Mt¢¢图595（2）求解各系数，得，r=EI,R¢=-EIa,R¢¢=0111tt36595典型方程：EIZ-EIa=013619解得：Z=a12（3）求最终弯矩图M图7-14试用混合法作图示刚架M图。DFlPACFEI=常数lBEll题7-14图 同济大学朱慈勉结构力学第8章矩阵位移法习题答案8-1试说出单元刚度矩阵的物理意义及其性质与特点。8-2试说出空间桁架和刚架单元刚度矩阵的阶数。8-3试分别采用后处理法和先处理法列出图示梁的结构刚度矩阵。(a)ABCD2EIEIEIlll解：（a）用后处理法计算（1）结构标识y①②③x1234单元局部坐标系（i®j）杆长cosasina各杆EI①1®2l102EI②2®3l10EI③3®4l10EI（2）建立结点位移向量，结点力向量[]TD=nqnqnqnq11223344q[]TF=FMFMFMFMy11y22y33y44（3）计算单元刚度矩阵12é126l-126lùék①k①ù2EIê6l4l2-6l2l2úk①=1112=êúêúk①k①l3ê-12-6l12-6lúêë2122úûêú22êë6l2l-6l4lúû12é63l-63lùék②k②ùê3l2l2-3ll2ú②22232EIêúk=êú=k②k②l3ê-6-3l6-3lúêúë3233ûêú22êë3ll-3l2lúû 12é63l-63lùék③k③ùê3l2l2-3ll2ú③33342EIêúk=êú=k③k③l3ê-6-3l6-3lúêúë4344ûêú22êë3ll-3l2lúû（4）总刚度矩阵12341234é126l-126l0000ùê22úê6l4l-6l2l0000ú①①ék11k1200ùê-12-6l18-3l-63l00úêúêú①①②②222qêk21k22+k22k230ú2EIê6l2l-3l6l-3ll00úk=ê②②③③ú=3êúê0k32k33+k33k34úlê00-6-3l120-63lúê③③úê003ll204l2-3ll2ú00kkë4344ûêúê0000-6-3l6-3lúê22úë00003ll-3l2lû（5）建立结构刚度矩阵支座位移边界条件[νθθθ]=[0000]1134将总刚度矩阵中对应上述边界位移行列删除，得刚度结构矩阵。é18-3l3l0ùê22ú2EI-3l6ll0qêúk=l3ê3ll24l2l2úêú22êë00l2lúû(b)用先处理法计算（1）结构标识yx12345单元局部坐标系（i®j）杆长cosasina各杆EI①1®2l012EI②2®3l01EI③3®4l01EI（2）建立结点位移向量，结点力向量TTD=[nqnn]=[0000]1145 T故D=[nqqqq]22345（3）计算单元刚度矩阵nq222EIé12-6lù①k=3ê2úlë-6l4lûnqq234é126l6lù②EIê22úk=6l4l2l3êúlê6l2l24l2úëûqq4522EIé4llù③k=3ê22úlêël4lúû（4）建立结构刚度矩阵（按对号入座的方法）nqqqq22345é18-6l3l3l0ùê2úê-6l4l000ú2EIkq=ê3l02l2l20ú3êúl222ê3l0l4llúêú22êë000l2lúû(b)ABCD2EIEIEIlll8-4试分别采用后处理法和先处理法分析图示桁架，并将内力表示在图上。设各杆的EA相同。yFP1①2l③④⑤⑥EA=常数34x②l解：（1）结构标识如图 单元局部坐标系（i®j）杆长cosasina①1®2l10②3®4l10③1®3l0-1④2®4l0-1⑤2®3222l--22⑥1®4222l22（2）建立结点位移向量，结点力向量[]TD=mnmnmnmn11223344[]TF=FF0-FFF00x1y1px3y3（3）计算单元刚度矩阵1234é10-10ùé10-10ùêúêú①EAê0000ú同理②①EAê0000úk=k=k=lê-1010úlê-1010úêúêúë0000ûë0000û1324é0000ùé0000ùêúêú③EAê010-1ú同理④③EAê010-1úk=k=k=lê0000úlê0000úêúêúë0-101ûë0-101û2314é1111ùé1111ù----ê2222úê2222úêúêúê11-1-1úê11-1-1ú⑤EAê2222ú同理⑥⑤EAê2222úk=êúk=k=êú2l11112l1111ê--úê--úê2222úê2222úê1111úê1111úê--úê--úë2222ûë2222û（4）形成刚度矩阵，刚度方程 1234é4+2222ùê--1000-ú4444êúê24+222úê-000-1-ú4444êúê4+2222úê-10--00ú4444êúê24+222úê00--0-1úqEA4444k=êúlê224+22úê00---10ú4444êúê2224+2úê0-1--00ú4444êúê224+22úê-00-10-ú4444êúê2224+2úê-0-100-úë4444û刚架总刚度矩阵方程：TTk[mnmnmnmn]=[FF0-FFF00]11223344x1y1px3y3（5）建立结构刚度矩阵，结构刚度方程ém1ùé0ùêúêúéD1ùên1úê0ú制作位移边界条件为：êú==Dêmúê0úë2û3êúêúën3ûë0û将刚度矩阵中对应上述边界位移的行、列删除，即得结构刚度矩阵，相应结构刚度方程为：é4+22ùê00ú44êúê24+2úém2ùé0ùê0-1úêúê-FúEAê44úên2úêpú=lê4+22úêm4úê0úê00-úêúêúê44úën4ûêë0úûê24+2úê0-1-úë44û（6）计算节点位移，得： -1é4+22ùê00ú44êúém2ùê24+2úé0ùé0.5578ùêú-1ê0-1úê-FúêúD=ên2ú=æEAöê44úêpú=ê-2.1354úç÷êm4úèløê4+22úê0úê-0.4422úêúê00-úêúêúën4ûê44úêë0úûë-1.6928ûê24+2úê0-1-úë44û（7）计算各杆内力23é1111ù--êú2222ê1111úé0.5578ùé-0.7888ùê--úêúêú{}5EAê2222úê-2.1354úFplê-0.7888úFpF=êú=2l1111ê0úEAê0.7888ú2ê--úêúêúê2222úë0ûë0.7888ûê1111úê--úë2222ûé1100ùé-0.7888ùé-0.7888Fpùêúêúêú{}5[]{}52ê-1100úê-0.7888úFpê0úF=TF==2ê0011úê0.7888ú2ê0.7888Fpúêúêúêúë00-11ûë0.7888ûêë0úû同时可得其他杆内力。FP0.5578Fp0.6253Fp-0.7888Fp-0.4422Fp-0.4422Fp（b）采用先处理法（1）步与后处理法相同。（2）建立结点位移向量，结点力向量TD=[mnmn]2244[]TF=0-F00p 24①EAé10ù②①EAé10ùk=êúk=k=êúlë00ûlë00û2444é0000ùé11ùé11ùEAê010-1úEAê-úEAê-úk④=êúk⑤=22k⑥=22êúêúlê0000ú2lê11ú2lê11úêú--ë0-101ûêë22úûêë22úû（4）形成总刚度矩阵，结构刚度方程é4+22ùê00ú44êúê24+2úém2ùé0ùê0-1úêúê-FúEAê44úên2úêpú=lê4+22úêm4úê0úê00-úêúêúê44úën4ûêë0úûê24+2úê0-1-úë44û（5）结点位移及内力计算同上。8-5试列出图示刚架的结构刚度方程。设杆件的E、A、I均相同，结点3有水平支座位移s，弹簧刚度系数为k。ys20kN30kN·m33′1m②2k①2mE、A、I=常数1x3m解：（1）结构标识y3②2③①1x单元局部坐标系（i®j）杆长cosasina①1®2201②2®323122 （2）建立结点位移向量，结点力向量TD=[mnqq]2223TF=[200-300]（3）建立单元刚度矩阵（l=2m）mnq222é12EI6EIù0ê33úllêúEA①êúk=00êlúêú6EI4EIê0ú2êëllúûmnqnq22233é3EA3EIù+0000ê3ú4llêúê3æEA12EIöEA9EIúç-÷+000ê33ú4èllø4llêú②ê3EI33EI4EIúk=ê2200úêlllúêæ3EA3EIö3æEA12EIö3EIæ3EA3EIöúê-ç+3÷-ç-3÷2ç+3÷0úêè4llø4èllølè4lløúêú3EI33EI2EI3EI4EIê-ú222êëlllllúû③k=k（4）建立结构刚度方程（对号入座的原则写出保留支座位移n在内的刚度方程）3é3EA15EIù++k0000ê3ú4llêúê3æEA12EIö5EA9EIúêç-3÷+3000úém2ùé20KNùê4èllø4llúêúêún0ê3EI33EI8EIúê2úêúê2200úêq2ú=ê-30KNúêlllúêúêúnFêúê3úêx3úæ3EA3EIö3æEA12EIö3EIæ3EA3EIöê-ç+÷-ç-÷ç+÷0úêqúêë0úû3323ë3ûêè4llø4èllølè4lløúêú3EI33EI2EI3EI4EIê-ú222êëlllllúû由已知，支座位移n=c，将以上刚度矩阵n的行删除，并将n与刚度矩阵第4列乘333 积移至方程右端与荷载向量合并。é3153æEA3EIö33ùéæ33öùêEA+EI+kç-÷EI-EIúêçEA+EI÷cúê884è22ø44úêè88øúê3æEA3EIö593333úém2ùêæEA3EIö3úêç-÷EA+EIEIEIúênúêç-÷´cúê4è22ø8844úê2ú=êè22ø4úê333úêq2úê3úêEIEI4EIEIúêúê-30KN×m-EIcúê44úëq3ûê4úê333úê3úê-EIEIEI2EIúê-EIcúêë44úûë4û8-6试采用先处理法列出图示刚架的结构刚度方程，并写出CG杆杆端力的矩阵表达式。设各杆的EI=常数，忽略杆件的轴向变形。50kN50kN10kN②5FG6①315kN2⑤③D6m④EI=常数3mABC1474m6m解：（1）结构标识如上图。单元局部坐标系（i®j）杆长cosasina①2®354/53/5②3®5610③6®760-1④1®2301⑤4®3601（2）建立结点位移向量，结点力向量TD=[nqqqq]22356TF=[15+100000]（3）建立单元刚度矩阵（考虑杆件①及②两端点无相对水平位移，故水平位移可以不考虑）qq23é4EI2EIù①êllú其中l=5mk=êúê2EI4EIúêëllúû qq35é4EI2EIù②êllú其中l=6mk=êúê2EI4EIúêëllúûnq26é12EI6EIùêl3l2ú其中l=6m③k=êúê6EI4EIúêël2lúûnq22é12EI6EIùêl3l2ú其中l=3m④k=êúê6EI4EIúêël2lúûnq23é12EI6EIùêl3l2ú其中l=6m⑤k=êúê6EI4EIúêël2lúû（4）建立结构刚度方程（按对号入座的方式）nqqqq22356é5211ùEIEIEI0EIêú9366êúê2EI32EI2EI00úén2ùé25ùê3155úêúêúq0ê12321úê2úêúêEIEIEIEI0úêqú=ê0ú3ê65153úêúêúê12úêq5úê0úê00EIEI0úêqúêë0úûê33úë6ûê12úêEI000EIúë63û(方程中已省去单位)én2ùé82.06ùêúêúq-25.31ê2úêú1解得：êqú=ê-1.81ú3êúêúEIq0.90ê5úêúêqúêë-20.52úûë6û （5）写出CG杆杆端力的矩阵表达式é126126ùé1111ù0--0-0--0-ê366366úê186186úém6ùê000000úé82.06ùê000000úé82.06ùêúêúêúêúêúên6úê66úê0úê1211úê0úêqúê-0402úê-20.52úê-00úê-20.52ú{}36EIê66ú1ê6363úF=êú=×êú=êúm6ê126126úEI0ê1111ú0ê7ú-00êú-00êúênúê366366úê0úê186186úê0ú7êúêúêúêúêúêëq7úûê000000úêë0úûê000000úêë0úûêúêú661112ê-0204úê-00úë66ûë6363û28-7试采用矩阵位移法分析图示刚架，并作出刚架的内力图。设各杆件E、A、I相同，A=1000I/l。qCBl45E、A、I=常数A3ll5解：（1）结构标识yx②32①11000IA=2l单元局部坐标系（i®j）杆长cosasina①1®2l3/54/5②2®3l10（2）建立结点位移向量，结点力向量[]TD=mnq222T2éqlqlùF=ê0--úë212û（3）建立单元刚度矩阵mnqmnq22222222éEAæ3ö12EIæ4öæEA12EIö126EI4ùê´ç÷+´ç÷ç-÷-´úé91921185624ùl5l35ll325l25-êèøèøèøúê25l325l35l2úê22úêúk①=êæçEA-12EIö÷12EA´æç4ö÷+12EI´æç3ö÷-6EI´3ú=EIê1185616108-18úêèll3ø25lè5øl3è5øl25úê25l325l35l2úêúêúê6EI46EI34EIúê-24184ú-2´-2´ê5l25l2lúêl5l5lúëûëû mnq222é1000EIù00ê3ú25lêú②ê12EI6EIúk=0êl3l2úêú6EI4EIê0ú2êëllúû(4)建立结构刚度矩阵é341921185624ù-ê332ú25l25l5lêúê118561640818úk=EI-ê25l325l35l2úêú24128ê-ú22êë5l5llúû(5)结构刚度方程éùê0úém2ùêúêúêqlúkn=-ê2úê2úêëq2úûê2úêqlú-êë12úûém2ùé0.0003ùêúêú解得：n=-0.0009ê2úêúêqúê-0.0100úë2ûëû8-8试利用对称性用先处理法分析图示刚架并作出M、FQ图。忽略杆件的轴向变形。(a)10kNDEIEEIF2EI3mAEIBEIC4m4m解：（1）结构标识（取半结构）y5KN1①2x②3③4 单元局部坐标系（i®j）杆长cosasina①1®2410②2®330-1③5®4410TD=[nq]24TF=[-5KN0](2)建立单元刚度矩阵n2①é12EIùl=4mk=ê3úëlûnq24é12EI6EIù-êl3l2úl=4m③k=êúê6EI4EIú-êël2lúû(3)建立结构刚度矩阵nq24é24EI6EIù-êl3l2úk=êúê6EI4EIú-êël2lúû(4)建立结构刚度方程é24EI6EIù-êl3l2úén2ùé-5ùêúêú=êúê6EI4EIúëq4ûë0û-êël2lúûé64ùén2ùê-ú1解得：êú=3qêúEIë4û-8ëû(5)计算杆件内力é1212ù6-6é0ùêllúêúé1ùéQ5ùêú0êúêú{}3{}3EIê64l-62lúêú1ê4úêM5úF=F=2êúê64ú==l-12-612-6ê-úEIê-1úêQ4úêú3êúêúêllúêúë0ûëM4ûêúêë-8úûë62l-64lû é1212ù6-6é0ùêllúêúé4ùéQ1ùêú0êúêú{}1{}1EIê64l-62lúêú1ê8úêM1úF=F=2êúê64ú==l-12-612-6ê-úEIê-4úêQ2úêú3êúêúêllúêúë8ûëM2ûêúêë0úûë62l-64lû(6)作出M、F图Q8KN×m8KN×m4KN8KN×m4KN×m4KN×m1KNMN(b)30kND3EIE3EIF2EI2EI2EI4m10kN/mABC3m3m解：原结构等效为下面结构：15kN15kN15kN15kN+5kN/m5kN/m5kN/m5kN/m正对称反对称1.正对称结构(1)结D2构标识如图所示D2①3y2②D2D11x(2)结构位移向量éq1ùéD1ùD=êú=êúëq2ûëD2û (3)等效结点荷载2020331025KN10KN10202033Té2020ùF=-,êúë33û(4)建立单元刚度矩阵D(q)D(q)2211é4EI2EIùé1ù1①êllúê2úk=2´êú=2EIêúê2EI4EIúê1ú1êëllúûêë2úûD(q)22②é4EIùé4ùk=3´=3EIêúêúëlûë3û(5)建立结构刚度方程é20ù-é21ùéD1ùê3úEIêúêú=êúë16ûëD2ûê20úêë3úû14020解得：D=-，D=-1233EI11EI(6)求杆端力é3333ùé-10ùê-úé-130ù168168êúéFy2ùê20úê331úé0ùê11úêúê-úê1-úêúê80ú①êM2úê3úê882úêD2ú-F=êú=êú+2EIêú=ê11úêFy1ú-10ê3333úê0úêúêú---êúê90úêMúê20úê168168úëD1û-ë1ûêúê11úêë3úûê313úê0ú-1ëûë828û é4242ùé40ù-ê9393úê11úê2432úé0ùê80úê-úêúêú②ê3383úêD2úê11úF=3EIêú=êú4242ê0ú40ê---úêúê-úê9393úDê11úë1ûê2224úê40úê-úêúë3333ûë11û80804013011111301111114040111190901111M图Q图2．反对称结构D2(1)结构标识如图所示DD23①3D2yD2D24②③D2D11x(2)结构位移向量2020331025KN10KN10202033é20ù-éq1ùéD1ùê3úéM1ùêúêúêúêúqD20MD=ê2ú=ê2ú,F=êú=ê2úêqúêDúê3úêMú333êúêúê0úêúëy3ûëD4ûêúëy3ûêë25úû(3)计算单元刚度矩阵 D(y)D(q)D(q)432211é333ùêú844êú3①êúk=EI21ê4úêú3ê12úêë4úûD(q)D(q)2233②é42ùk=EIêúë24ûD(y)D(q)4333é33ù③ê168úk=EIêúê3ú1êë8úû(4)建立刚度方程é3ù210ê4úé20ùêúéDùê-úê3ú1ê3ú162êúê4úêD2úê20úEIêú=êú3êDú3ê025ú3êúê8úêú0ëD4ûêúê3339úêë25úûêúë44816û1111解得：D=-43.54，D=-3.21，D=-7.08，D=111.501234EIEIEIEI(5)求杆端力é3333ù-é-10ùê168168úéFy2ùê20úê331úéD4ùé-3.25ùêúê-úê1-úêúêú①êM2úê3úê882úêD2úê27úF=êú=êú+2EIêú=êFy1ú-10ê3333úê0úê-16.75úêú---êúêúêëM1úûê20úê168168úëD1ûë0ûêë3úûê313úê-1úë828û é4242ù-êú9393éFy2ùê2432úé0ùé-20.58ùêúê-úêúêú②êM2úê3383úêD2úê-27úF=êú=3EIêú=êFy3úê4242úê0úê20.58ú---êúêúêëM3úûê9393úëD3ûë-34.73ûê2224úê-úë3333ûé3333ù-êú168168éFy3ùê331úéD4ùé18.25ùêúê1-úêúêú③êM3úê882úêD3úê34.73úF=êú=EIêú=êFy4úê3333úê0úê-18.25ú---êúêúêM4úê168168úë0ûë38.27ûëûêú313ê-1úë828û34.7320.582769.46273.253.2534.7336.576.5416.7516.75M图Q图整体受力图为：31.0916.9424.2219.7369.4634.2715.0738.3736.58.5776.5424.93M图Q图8-9设有如图两杆件刚结组成的特殊单元ij（或称为子结构），试直接根据单元刚度矩阵元素的物理意义，求出该特殊单元在图示坐标系中的刚度矩阵元素k33和k31。yEIEIaxijaa 解：将单元在3方向转动单位角度视为主动力作用情况：（加一个刚臂）2iR=2i4i1pr=8i114i2i2i4iEIi=2aMM1p18iZ+2i=0ÞZ=-114得出在3方向转动单位角度的弯矩图如下：i1i27i277EI72EIk=i==33222a4aæ7öç+1÷/2aè2ø92EIk=k==3113228a8-10试采用先处理法列出图示刚架的结构刚度方程。设各杆的EI=常数，忽略杆件的轴向变形。8kN·m4kN·mCD6kN6mEI=常数AB6m6m解：(1)结构标识如图 y23D②1①D③414x显而易见，D=-D41(2)建立结构位移向量和结构荷载向量[]T[]TD=mqqn=DDDD22321234[]TF=6KN,-8KN×m,4KN×m,0(3)建立单元刚度矩阵142é22222ùêEA+EIEA-EIEIú241442414424êú①ê2222-2úk=êEA-EIEA+EIEIú241442414424êúê2-22úêEIEIEIúë24243û423éEIEIEIùêú1866êú②êEI2EIúk=EIê633úêúEIEI2êEIúêë633úû13éEIEIù③ê186úk=êúêEI2úEIêë63úû(4)建立结构刚度方程将上述单元刚度矩阵的元素，按照其对应的未知节点位移序号对号入座，即可得到结构刚度矩阵，据此可列出结构的刚度方程。 é28+22122ùêEA+EIEIEIEA-EIú2414424624144êúê22+214-2úéD1ùé6KNùêEIEIEIEIúêDúê-8KN×múê243324úê2ú=êúê1141úêD3úê4KN×múêEIEIEIEIúêúêúê6336úëD4ûë0ûê224-2128+2úêEA-EIEIEIEA+EIúë2414424624144û将D=-D带入上式，然后将结构刚度矩阵第一列减去第四列得方程。41é8+221ùêú144246êúê2-22+21úDé6KNùêúé1ùê-8KN×múEIê1233úêDú=êúê2úê4KN×múê14úê0úêëD3úûêúê33úë0ûê8+24-21úê-úë144246û上述方程组四个方程，三个未知数，为了获得位移解的存在性，以及刚度矩阵的对称性，我们将第一个方程减去第四个方程，得：é8+22-2ùê0ú1212êúém1ùé6KNùê2-22+21úêúêúEIêúêq2ú=ê-8KN×múê1233úêqúê4KN×múê14úë3ûëû0êú33ëû 同济大学朱慈勉结构力学第9章超静定结构的实用计算方法与概念分析习题答案9-1试说出何为杆端转动刚度、弯矩分配系数和传递系数，为什么弯矩分配法一般只能用于无结点线位移的梁和刚架计算。9-2试用弯矩分配法计算图示梁和刚架，作出M图，并求刚结点B的转角φB。(a)20kN/m40kNAEIBEIC6m2m2m解：设EI=6，则i=1,i=1.5ABBC4´1m==0.47BA4´1+3´1.53´1.5m==0.53BC4´1+3´1.5结点ABC杆端ABBABC分配系数固端0.470.53绞支固端弯矩-6060-300分配传递-7.05-14.1-15.90最后弯矩-67.0545.9-45.901é1()ùq=M-m-M-mB3iêBABA2ABABúëû2é1()ù=45.9-60--67.05+60EIêë2úû21.152()=-KN×m逆时针方向EI(b)D40kN3m2EIABC3mEIEI2EI6mE20kN/m9m9m解：设EI=9，则 i=1,i=1ABBCi=3,i=3BDBE3´3m=m==0.36BDBE3´3+3´3+3´1+4´14´1m==0.16BA3´3+3´3+3´1+4´13´1m==0.12BC3´3+3´3+3´1+4´1结点ABC杆端ABBABCBDBE分配系数固端0.160.120.360.36绞支固端弯矩00045-900分配传递3.67.25.416.216.20最后弯矩3.67.25.461.2-73.801é1()ùq=M-m-M-mB3iêBABA2ABABúëû3é1()ù=7.2-0-3.6-0EIêë2úû16.22=KN×m(顺时针方向)EI607.261.23.65.473.8909-3试用弯矩分配法计算图示刚架，并作出M图。(a)32kN8kN/m6kNAEIBEIC100kN·m2m4m4m8m解：Ｂ为角位移节点设EI=8,则i=i=1，m=m=0.5ABBCBABCPab(l+b)32´4´4´12固端弯矩M===48KN×mBA222l2´829l1M=-+6×2=-58KN×mBC82结点力偶直接分配时不变号结点ABC杆端ABBABC分配系数铰接0.50.5固端弯矩048-5812 5050分配传递05512最后弯矩0103-312(b)60kN60kN40kN40kN/mABCDEEI=常数2m2m2m6m6m2m解：存在B、C角位移结点设EI=6，则i=i=i=1ABBCCD4´1m=m==0.5BABC4´1+4´14´14m==CB3´1+4´173m=BC7固端弯矩：M=-80KN×mABM=-80KN×mBAM=M=0BCCB240´61M=-+80´=-140KN×mCD82结点ABC杆端ABBABCCBCD分配系数固结0.50.54/73/7固端弯矩-808000-140-20-40-40-2047.591.468.6-11.4-22.8-22.8-11.4分配传递3.256.54.9-0.82-1.63-1.63-0.820.60.45最后弯矩-112.2215.57-15.4866.28-66.05 (c)24kN/mBEICEIDEI3mA4m5m5m解：B、C为角位移结点1144m==,m==BABC1+451+454411m==,m==CBCD1+451+45固端弯矩：224´4M==64KN×mAB6224´4M==128KN×mBA3224´5M=-=-50KN×mBC12224´5M==50KN×mCB12224´5M=-=-200KN×mCD3224´5M=-=-100KN×mDC6结点ABCD杆端ABBABCCBCD滑动分配系数滑动0.20.80.80.2-100固端弯矩64128-5050-20015.6-15.6-62.4-31.272.48144.9636.24-36.2414.5-14.5-58-29分配传递11.623.25.8-5.82.32-2.32-9.28-4.643.70.93-0.93 最后弯矩96.4295.58-95.6157.02-157.03-142.97(d)20kN×m2kN/mCDE4mEI=常数AB4m4m解：4´1m==m=0.5CACD4´1+4´14´14m==m=DCDE4´1+4´1+3´1113´13m==DB4´1+4´1+3´111固端弯矩：22´48M=-=-KN×mDE1238M=KN×mED3结点ACDE杆端ACCACDDCDBDEED分配系数固结0.50.54/113/114/11固结固端弯矩00000-2.672.67-5-10-10-546/3392/3369/3392/3346/33分配传递-0.35-23/33-23/33-0.350.1270.0960.1270.064最后弯矩-5.35-10.7-9.3-2.442.190.254.129.34.122.090.2510.72.445.35(e)3kN/mEI1=∞CD2EIEk=EIEIEI4m316mAB EI-2解：当D发生单位转角时：Y=K´(4´1)=(m)C4EI-1则M=´4=EI(m)(假设=12）DC4S=12,S=9,S=16,S=12,S=16DCDADEEBDE1291643m=,m=,m=,m=,m=DCDADEEDEB37373777结点DEB杆端DCDADEEDEBBE分配系数12/379/3716/374/73/7固结固端弯矩00-9900-2.57-5.14-3.86-1.933.752.815-2.5分配传递-0.72-1.43-1.07-0.540.230.180.310.16最后弯矩3.982.99-6.985-5-2.47(f)2kN/mAA′1.5EIEIEI4m2kN/mBB′1.5EI6m解：截取对称结构为研究对象。SAA¢¢=0.5EIEIS=4´=EIAB41/21m==AA¢¢2/332m=AB321同理可得：mm==,BB¢¢BA33另 CCAA¢=BB¢¢=-11CC==ABBA2ABAA¢¢AA¢¢BABB¢¢BB¢¢M图9-4试用弯矩分配法计算图示梁，并作出M图。设图a梁含无限刚性段；图b梁B支座处含转动弹簧，刚度系数为kθ=4i。(a)MEI1=∞AEIBEICll3l443l44解：4iBB¢¢BB¢C¢16i6i28i4i33 i1EIMB¢C=3i+3´3´l=4i(其中i=3)l4l44M=0CB16iM=BC316iMBCS=,C==0BCBC3MCB11MB¢A=4i+6i´3´l=6il4411M=2i+6i´´l=4iAB3l4428S=M=iBABA3M3ABC==BAM7BA结点ABC杆端ABBABCCB分配系数固结7/114/11铰结固端弯矩00分配传递3M/117M/114M/110最后弯矩3M/117M/114M/1107M1143MM1111M图(b)32kNkθAiBiC4m2m2m解：首先在B点偏右作用一力矩，如图所示。M根据杆BC端，可得M=4iq+kq(q-q)①BCBCBA根据杆BA端，可得kq(q-q)=4iq②BCBABA4i+kθ由②式得：θ=θ③BCBAkθ将②式代入①式得：M=4iθ+4iθ④BCBA 4iθθ4i+kq4i+4i2BCBCm=====BC4iθ+4iθθ+θ4i+2kq4i+8i3BCBABCBAkq1μ=1-μ==BABC4i+2kq39-5试用弯矩分配法计算图示剪力静定刚架，并作出M图。(a)EI1=∞CE2EIlqDBEI2EIlAll解：作出M图（在B处加刚臂）S=3i,S=0,S=2iBDBABCm=0.6,m=0,m=0.4BDBABC结点ABCE杆端ABBDBABCCBCEEC分配系数铰结0.600.4铰结222固端弯矩0-2ql-ql/3-ql/600222分配传递021ql/15014ql/15-14ql/1502222最后弯矩021ql/15-2ql3ql/5-33ql/3000(b)10kN10kNEFGH3mABCDEI=常数4m4m4m解：提取左半部分分析FEG¢ABC¢ （a）图中结构不产生弯矩，（b）图中结构为反对称结构，因此可以取下半部分分析得：S¢=3Ei/1.5=2EIAE1S=EI/4=EIAB41æ1ö1mAB=ç+2÷=4è4ø98mAE¢=1-mAB=91S=S=EIBAAB4S=S=2EIBF¢AE¢1SBC¢=EI/2=EI21æ11ö1mBA=ç+2+÷=4è42ø111æ11ö2mBC¢=ç+2+÷=2è42ø118mBF¢=1-mBA-mBC¢=11ABAE¢5kNA1/98/9E¢-101.118.89-1.010.110.9-9.799.795kNBABC¢BF¢1/11B2/118/11F¢-10-1.111.012.028.08-0.110.010.020.08-10.22.048.16C¢9.798.162.0410.2M图9-6试回答：剪力分配法的适用范围如何？什么叫柱子的并联和串连？由并联和串连所构成的合成柱，其剪切刚度和剪切柔度应如何计算？9-7试用剪力分配法计算图示结构，并作出M图。(a)10kNBDFHEA=∞EA=∞EA=∞EI3EI3EIEI10m6kN/m10kN/mACEG解：AB、CD、EF、GA均为并联结构。①首先转化结间荷载F5ql()F3ql()F()Q==62.5KN¬Q=-=-37.5KN¬Q=-22.5KN¬ABBAAG88 2Fql固端弯矩：M=-=-125KN×mAB83EI9EI9EI3EI24ik=k+k+k+k=+++=并ABCDEFGH33332lllll13于是边柱和中柱的剪力分配系数为r=,r=1288转化后的荷载为：37.5+22.5+10=70KN边柱和中柱的剪力分别为：70F=r´70=KNQ118210F=r´70=KNQ22870边柱柱脚弯矩为：´10+125=212.5KN×m8210中柱柱脚弯矩为：´10=262.5KN×m8M图(KNm×)(b)EI1=∞EI1=∞EI1=∞BD10kNFHEI3EI3EIEI10m8mACEG13解：同上题，边柱和中柱的剪力分配系数为r=,r=1288转化结间荷载2()F10×810+4Q=-=-8.96KNFE310边柱和中柱的剪力分别为：2F10×8×2F=r´8.96=1.12KN,M=-=-3.2KN×mQ1EF11002FP×8×2F=r´8.96=3.36KN,M==12.8KN×mQ22FE100边柱柱脚弯矩为：1.12´5=-5.6KN×m中柱CD柱脚弯矩为：3.36´5=-16.8KN×m中柱EF柱脚弯矩为：-3.2-16.8=-20KN×m M图(KNm×)(c)BEH30kNEI1=∞EI1=∞dEIEIe4m30kNa4EIDEI1=∞G4mbEIEIcACF解：当顶层横梁没有水平位移时，d、e、b、c并列R=45KN1r=r=r=r=bced4F=F=F=F=7.5KNQbQcQdQe单位：KNm× 12EI设k==1d34则k=k=k=k=1bcde12´4EI1k==a382k(de)=kd+ke=2üï1ýÞk(bcde)==1k(bc)=kb+kc=2ïþ1+122æ1ö21r(bcde)=1ç1+÷=ra=1-r(bcde)=è2ø33FQa=45/3=15KNFQ(de)=FQ(bc)=30KN1FQb=FQc=FQd=FQe=FQ(de)=15KN2M图(KNm×)(d)AaCbEdGEIEIEIEI1=∞EI1=∞ceFBEIDEI20kN2m2m2m解：结构分析：bc并联与de并联，经串联后的结合柱与a并联。3EI1159EIk=+=并3113l13l+12EI3EI12EI12EI++3333llll39120120241r=,r=,r=r=´´abcdebc159159159392120151120154r=´´,r=´´de159395159395Q=4.97KN,Q=Q=4.64KN,Q=1.16KN,Q=4.64KNabcde M图(KNm×)9-8图示刚架设各柱的侧移刚度如括号内所示，试用剪力分配法计算，并作出M图。30kNFEI1=∞JEI1=∞Mg(1)h(1)i(1)4m55kNEEI1=∞IEI1=∞Ld(2)e(2)4mBHf(3)EI1=∞DEI1=∞a(2)b(3)c(3)4mACGK解：g、、hi三杆并联1r=rr==gni3F=F==F10KNQgQhQiR=+=305585KN ab并c串d并并fek=2+3+=38(abc)k=2+=24(de)18k==(abcde)113+8488æö17m=ç÷+=3(abcde)33èø889m=1-=f17179F=85´=45KNQf178F=85´=40KNQ(abcde)171F=F=´=4020KNQdQe22F=´=4010KNQa83F=F=´=4015KNQbQc8将（a）、（b）两图叠加得： M图(KNm×)9-9试运用力学基本概念分析图示结构，并作出M图的形状。(a)qEI=常数lll解：对于跨间均布荷载的等截面连续梁。其变形曲线如图所示。C点角位移应是顺时针方向。2C支座处承受负弯矩，数值应小于C端为固定端时的弯矩ql/3MC>M=2MBA2(b)q2EI2EIl2qlEIEIl2ll2Plql解：若D点固定，则M==DC222ql实际结点的转动受到弹性约束MMEDDEMMDBBA>M,=MBDAB22(c)EI1=∞aEIFPEIEIaEIEI2aa解：对于仅有结点线位移的刚架B端若为固定端则A、B两点固端弯矩为F/4paB端若为自由端，则B端弯矩为-F/4paB端实际弯矩应介于两者之间。根据柱的侧移刚度，B端弯矩为左边受拉。MBD且>M=2MDBCD2(d)FlFP34lEI=常数ll（a）解： 3Flp811FlFlpp82（b）（c）B点没有线位移，于是考虑两种极端情况，如（b）、（c）所示。æ11ö可以看出MABÎçFpl,Fpl÷è82ø1且M+M=FlABBAp2我们还应注意BD杆没有剪力。M图(e)+tEI=常数，正六边形(f)Ma2EI=常数aa解：1111MMMM2222 反对称：可知AB杆和ED杆没有剪力，因为如果有，则剪力方向相同，结构水平方向的里无法平衡。所以AB杆与ED杆的弯矩与杆平行。1M23M17M143EIS=BCaEIS=BA2a6m=BC71m=BA73M711MM223M171MM1414(a)对称：C铰只能提供水平力，忽略轴向变形。11MM221M411MM1221MM221M14M4（b）（a）、（b）两图叠加，得 3M73M74M73M759MM2828M图(g)FP2EIEIEIhFP2EIEIEIhl解：忽略轴向变形，则竖直方向的Fp不产生弯矩，可略去。1111FFFFpppp2222对称结构不产生弯矩。反对称：1M=Fh1p4b图中因BC杆的m比较大，所以M接近于M。BCBC1 FDGBAHM图其中MM>，所以反弯点偏上，这是考虑节点转动的原因。ABBA(h)Mqh2EI1=∞EIEIhqEI1=∞EIEIhl解：单独考虑力矩和竖向荷载。力矩：MMMM2222反对称：M2EDM2BCA(a) AB，BD杆中无剪力，又因为M，所以AB杆中无弯矩，又因为DE杆的EI=¥，DAB=01点无转角，对于剪力静定杆而言，无转角则无弯矩，所以DB杆中无弯矩。对称：M2M2这是结点无线位移结构，又因为DE杆与BC杆的EI=¥，所以结点又无转角，所以AB杆、1BD杆、BC杆无弯矩。（a）、（b）图叠加：竖向荷载：ED12ql8CB12ql8A(d)本结构无线位移，D、B两结点又无转角，DB杆、BA杆上又无荷载，所以DB杆、BA杆无弯矩。(c)(d)两图叠加得： 12ql812ql8M图9-10试用静力法求图a所示超静定梁B支座反力FyB的影响线方程，并绘制它的影响线。设取基本结构如图b所示。(a)FP＝1xABEIl22Px(23l+l--x)Px(xl)解：由力法求出：F=-=yB3322ll故影响线为：(b)FP＝1xABFyBLR9-11试用机动法绘制图示等截面连续梁FyB、FQB、FQB、M2和MC的影响线形状。FP=1A1B2C3DEEI=常数llll2解：①FyB F=1yBL②FQBR③FQB④M2d=1f⑤MCd=1f'