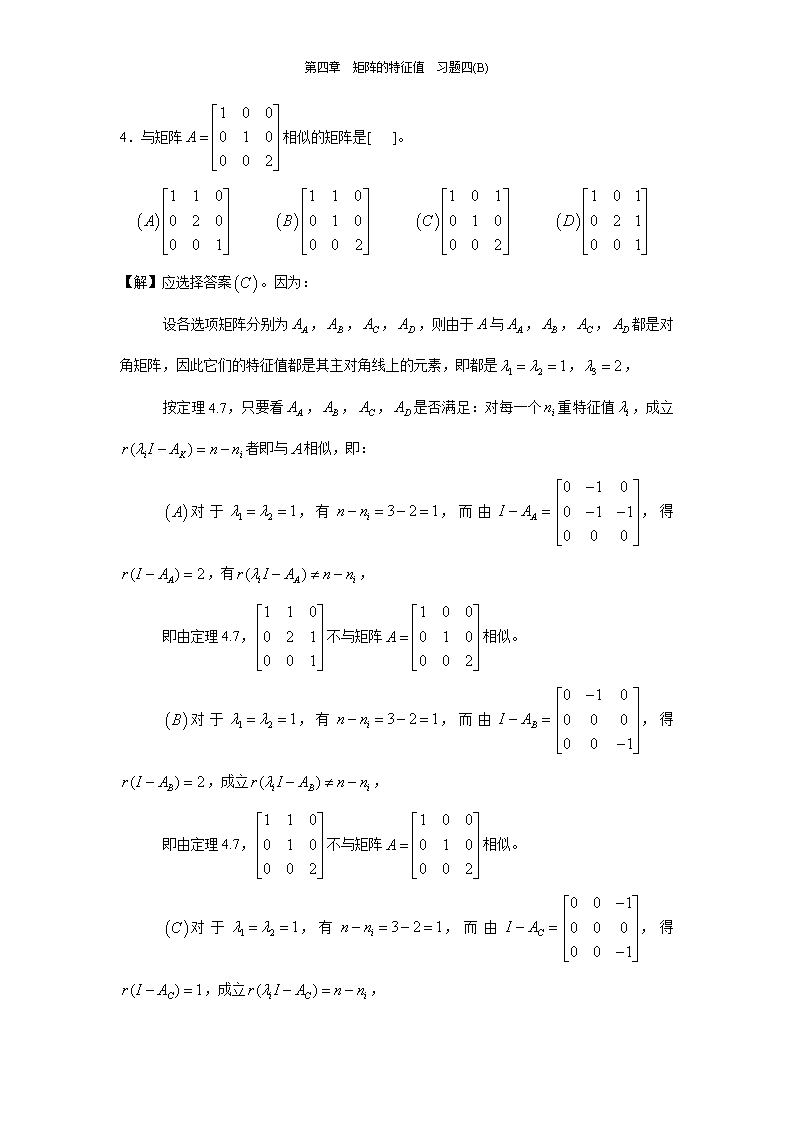赵树源线性代数习题四(B)题目和答案.doc 9页

'第四章矩阵的特征值习题四(B)1．三阶矩阵的特征值为－2，1，3，则下列矩阵中非奇异矩阵是[]。【解】应选择答案。因为：由已知及特征值定义，的特征方程的根为－2，1，3，应有，即有，知为奇异矩阵；由知为奇异矩阵；，知为奇异矩阵；而三阶矩阵只能有三个特征值，故2不可能是的特征值，从而，即为非奇异矩阵。2．设是可逆矩阵的一个特征值，则矩阵必有一个特征值为[]。【解】应选择答案。因为：是矩阵的一个特征值，即有，于是，亦即，对上式两端左乘，得，亦即，整理得，这说明是矩阵的一个特征值。3．设，都是阶矩阵的特征值，，且与分别是的对应于与 第四章矩阵的特征值习题四(B)的特征向量，则[]。且时，必是的特征向量且时，必是的特征向量时，必是的特征向量而时，必是的特征向量【解】应选择答案。因为：当且时，为零向量，不可成为任一阶矩阵的特征向量；反设是的特征向量，对应的特征值为，于是有,亦即为，由定理4.3，不同特征值对应的特征向量线性无关，由上式应有，而题设且，于是只能有，亦即为，但这与题设相矛盾，从而且时，不可能是的特征向量；当时，有可能与同时为0，因为此时为零向量，所以“必”是的特征向量的说法是错误的；综上知，正确。事实上：当而时，，而已知是的对应于的特征向量，即有，知此时是的对应于的特征向量。 第四章矩阵的特征值习题四(B)4．与矩阵相似的矩阵是[]。【解】应选择答案。因为：设各选项矩阵分别为，，，，则由于与，，，都是对角矩阵，因此它们的特征值都是其主对角线上的元素，即都是，，按定理4.7，只要看，，，是否满足：对每一个重特征值，成立者即与相似，即：对于，有，而由，得，有，即由定理4.7，不与矩阵相似。对于，有，而由，得，成立，即由定理4.7，不与矩阵相似。对于，有，而由，得，成立， 第四章矩阵的特征值习题四(B)又对于，有，而由，得，成立，综上，由定理4.7，与矩阵相似。对于，有，而由，得，有；由定理4.7，不与矩阵相似。5．矩阵与相似的充分必要条件是[]。与有相同的特征多项式阶矩阵与有相同的特征值且个特征值互不相同【解】应选择答案。因为：是与相似的充分但不必要条件。如与矩阵有，但由上面4题知，与不相似。是与相似的充分但不必要条件。如与矩阵 第四章矩阵的特征值习题四(B)有，但由上面4题知，与不相似。与有相同的特征多项式，是与相似的充分但不必要条件。如与矩阵具有相同的特征多项式，但由上面4题知，与不相似。矩阵与相似的充分必要条件是“阶矩阵与有相同的特征值且个特征值互不相同”。这是定理4.6的推论。6．设，为阶矩阵，且与相似，则[]。与有相同的特征值和特征向量与都相似于一个对角矩阵对任意常数，与相似【解】应选择答案。因为：～时，不一定有。如～，但，，对比可见。与相似，由定义4.3，有可逆阵，使，亦即， 第四章矩阵的特征值习题四(B)由定理4.5，与相似则有相同的特征值。于是可设与有相同的特征值，并设对应于的特征向量为，即应有，于是在等号两端左乘，得，由于本小题的第一步所得的，上式因此变化为，这说明对应于的特征向量为，而与未必相等，即说明与对应于相同的特征值未必有相同的特征向量。由课本P183页末知，与约当矩阵相似，而由课本P180页末又知，不存在相似的对角矩阵，因此，与相似，则与都相似于一个对角矩阵的判断未必正确。综上知，正确。事实上：由于与相似，由定义4.3，有可逆阵，使，于是，对任意常数，亦即为，由定义4.3，这说明与相似。7．设三阶矩阵有三个线性无关的特征向量，则[]。【解】应选择答案。因为： 第四章矩阵的特征值习题四(B)由，得的特征值，，由定理4.6，有三个线性无关特征向量的三阶矩阵必与对角矩阵相似，从而由定理4.7，对于2重特征值，由于，应有，而由于，即应有。8．设矩阵与相似，其中，已知矩阵有特征值1，2，3，则[]。【解】应选择答案。因为：题设，由定理4.5知，与有相同的特征值1，2，3，再由定理4.4，的所有特征值之和等于的主对角线上元素之和，即有解之得。9．下述结论中，不正确的是[]。若向量与正交，则对任意实数，，与也正交若向量与向量，都正交，则与，的任一线性组合也正交若向量与正交，则，中至少有一个是零向量若向量与任意同维向量正交，则是零向量【解】应选择答案。因为： 第四章矩阵的特征值习题四(B)若向量与正交，由定义4.7，成立，于是，对任意实数，，有，即由定义4.7知，与也正交。命题正确而非不正确。若向量与向量，都正交，由定义4.7，成立，，于是，对，的任一线性组合，成立，由定义4.7知，与，的任一线性组合也正交。命题正确而非不正确。若向量与正交，由于正交定义4.7并未指定与是否为零向量，因此本命题肯定说正交向量，中至少有一个是零向量不正确。事实上，当，中至少有一个是零向量时，必成立，而当，中都不是零向量时，仍可能成立，如而时，它们都不是零向量，但成立。若向量与任意同维向量正交，不妨设为维向量，则与初始单位向量组，，…，正交，即有（），亦即（），从而的个分量都为零，即是零向量。命题正确而非不正确。10．设为阶实对称矩阵，则[]。的个特征向量两两正交的个特征向量组成单位正交向量组的重特征值，有的重特征值，有【解】应选择答案。因为： 第四章矩阵的特征值习题四(B)关于实对称矩阵的特征向量的正交判断定理仅有定理4.12，而且定理指明：对应于不同特征值的特征向量才是正交的，因此，本题的正交条件不足，仅为“实对称矩阵”，难以保证特征向量两两正交。事实上，课本P191例5中，实对称矩阵有特征值，。其中对应于的特征向量为，，显见，说明与就不是正交的；由知，的个特征向量尚且不一定两两正交，那就更不一定能组成单位正交向量组了；“的重特征值，有”是阶实对称矩阵与对角矩阵相似的充分必要条件——定理4.7，而本题已知“为阶实对称矩阵”，由定理4.13知其必与对角矩阵相似，从而本判断是正确的；由定理4.7及的判断，的重特征值，应有成立而不是成立。*11．为3阶矩阵，，，为其特征值，的充分条件是[]。，，，，，【解】应选择答案。因为：由定理4.14，阶矩阵成立的充分必要条件为的一切特征值的模小于1。可知仅有条件可选。'