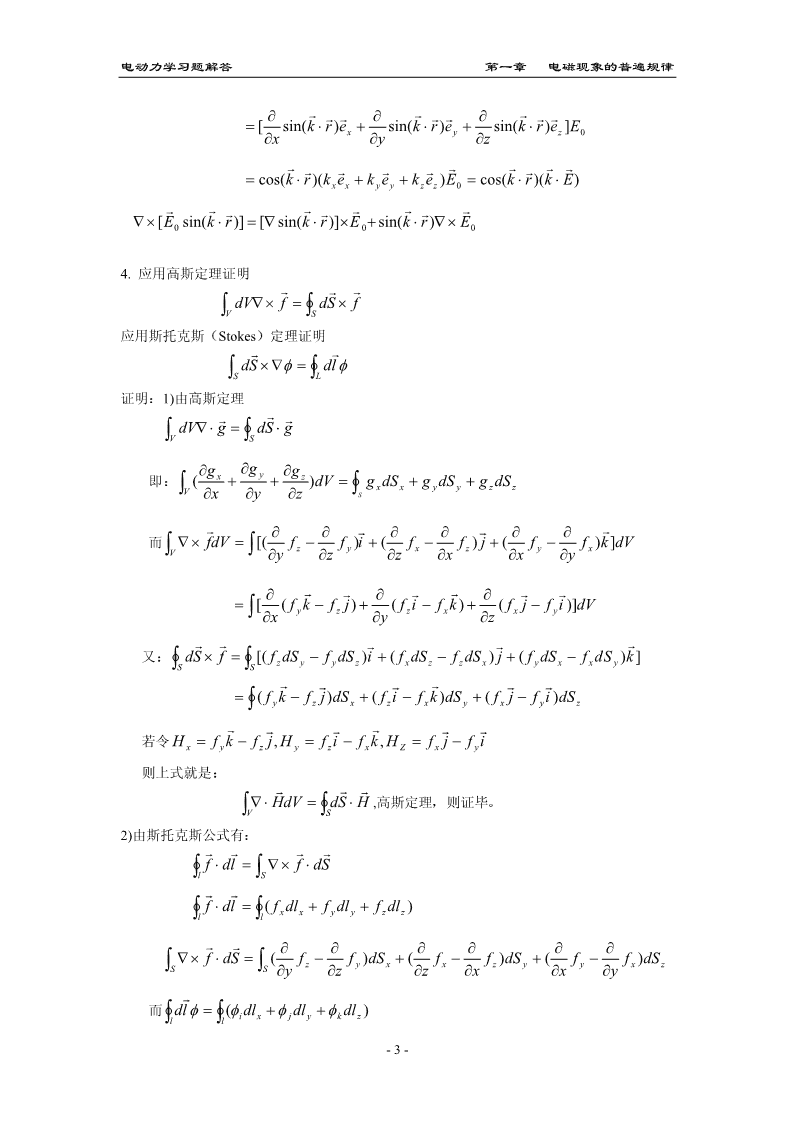郭硕鸿《电动力学》习题解答完全版(1-6章).pdf 98页

'电动力学习题解答第一章电磁现象的普遍规律1.根据算符∇的微分性与矢量性推导下列公式rrrrrrrrrr∇(A⋅B)=B×(∇×A)+(B⋅∇)A+A×(∇×B)+(A⋅∇)Brr1r2rrA×(∇×A)=∇A−(A⋅∇)A2vvvvvvvvvv解1∇(A⋅B)=B×(∇×A)+(B⋅∇)A+A×(∇×B)+(A⋅∇)B首先算符∇是一个微分算符其具有对其后所有表达式起微分的作用对于本题vv∇将作用于A和B又∇是一个矢量算符具有矢量的所有性质vvvvvvvvv因此利用公式c×(a×b)=a⋅(c⋅b)−(c⋅a)b可得上式其中右边前两项是∇作用于vvA后两项是∇作用于Bvv2根据第一个公式令AB可得证2.设u是空间坐标xyz的函数证明df∇f(u)=∇udurrdA∇⋅A(u)=∇u⋅durrdA∇×A(u)=∇u×.du证明1∂f(u)r∂f(u)r∂f(u)rdf∂urdf∂urdf∂urdf∇f(u)=ex+ey+ez=⋅∂xex+⋅ey+⋅ez=∇u∂x∂y∂zdudu∂ydu∂zdu2rrrrrrrr∂Ax(u)∂Ay(u)∂Azz(u)dAx(u)∂udAy(u)∂udAz(u)∂udA∇⋅A(u)=++=⋅+⋅+⋅=∇u⋅∂x∂y∂zdu∂xdu∂ydz∂zdu3rrreeexyzrrrrrrr∂∂∂∂Az∂Ayr∂Ax∂Azr∂Ay∂Axr∇×A(u)==(−)e+(−)e+(−)e=xyz∂x∂y∂z∂y∂z∂z∂x∂x∂yrrrAA(u)A(u)x(u)yz-1- 电动力学习题解答第一章电磁现象的普遍规律rrrrrrrdAz∂udAy∂urdAx∂udAz∂urdAy∂udAx∂urdA=(−)e+(−)e+(−)e=∇u×xyzdu∂ydu∂zdu∂zdu∂xdu∂xdu∂ydu"2"2"2"3.设r=(x−x)+(y−y)+(z−z)为源点x到场点x的距离r的方向规定为从源点指向场点"r∂r∂r∂1证明下列结果并体会对源变数求微商(∇=e+e+e)与对场变数求x"y"z"∂x∂y∂zr∂r∂r∂微商(∇=e+e+e)的关系xyz∂x∂y∂zrrrrr"r1"1rrr"r∇r=−∇r=,∇=−∇=−,∇×=0,∇⋅=−∇=0.(r≠0)3333rrrrrrr(最后一式在人r0点不成立见第二章第五节)2求rrrrrrrrrrrrrrr∇⋅r,∇×r,(a⋅∇)r,∇(a⋅r),∇⋅[Esin(k⋅r)]及∇×[Esin(k⋅r)],其中a,k及E均为常矢量000"""r∂(x−x)∂(y−y)∂(z−z)证明∇⋅r=++=3∂x∂y∂zrrreeexyzr∂∂∂∇×r==0∂x∂y∂z"""x−xy−yz−zvrvvv∂v∂v∂vvrv(a⋅∇)r=[(ae+ae+ae)⋅(e+e+e)][(x−x")e+(y−y")e+(z−z")e]xxyyzzxyzxyz∂x∂y∂z∂∂∂vrv=(a+a+a)[(x−x")e+(y−y")e+(z−z")e]xyzxyz∂x∂y∂zvvvv=ae+ae+ae=axxyyzzvvvvvvrvvv∇(a⋅r)=a×(∇×r)+(a⋅∇)r+r×(∇×a)+(r⋅∇)⋅avvvvvrv=(a⋅∇)r+r×(∇×a)+(r⋅a)⋅avvvvv=a+r×(∇×a)+(r⋅∇)⋅arrrrrrrrr∇⋅[Esin(k⋅r)]=[∇(sin(k⋅r)]⋅E+sin(k⋅r)(∇⋅E)000-2- 电动力学习题解答第一章电磁现象的普遍规律∂rrr∂rrr∂rrr=[sin(k⋅r)e+sin(k⋅r)e+sin(k⋅r)e]Exyz0∂x∂y∂zrrrrrrrrrr=cos(k⋅r)(ke+ke+ke)E=cos(k⋅r)(k⋅E)xxyyzz0rrrrrrrrr∇×[Esin(k⋅r)]=[∇sin(k⋅r)]×E+sin(k⋅r)∇×E0004.应用高斯定理证明rrr∫dV∇×f=∫dS×fVS应用斯托克斯Stokes定理证明rr∫dS×∇φ=∫dlφSL证明1)由高斯定理rrr∫dV∇⋅g=∫dS⋅gVS∂g∂g∂gxyz即(++)dV=gdS+gdS+gdS∫V∫xxyyzz∂x∂y∂zSr∂∂r∂∂r∂∂r而∇×fdV=[(f−f)i+(f−f)j+(f−f)k]dV∫V∫zyxzyx∂y∂z∂z∂x∂x∂y∂rr∂rr∂rr=[(fk−fj)+(fi−fk)+(fj−fi)]dV∫yzzxxy∂x∂y∂zrrrrr又dS×f=[(fdS−fdS)i+(fdS−fdS)j+(fdS−fdS)k]∫S∫Szyyzxzzxyxxyrrrrrr=(fk−fj)dS+(fi−fk)dS+(fj−fi)dS∫yzxzxyxyzrrrrrr若令H=fk−fj,H=fi−fk,H=fj−fixyzyzxZxy则上式就是rrr∫∇⋅HdV=∫dS⋅H,高斯定理则证毕VS2)由斯托克斯公式有rrrr∫f⋅dl=∫∇×f⋅dSlSrrf⋅dl=(fdl+fdl+fdl)∫l∫lxxyyzzrr∂∂∂∂∂∂∇×f⋅dS=(f−f)dS+(f−f)dS+(f−f)dS∫S∫Szyxxzyyxz∂y∂z∂z∂x∂x∂yr而dlφ=(φdl+φdl+φdl)∫l∫lixjykz-3- 电动力学习题解答第一章电磁现象的普遍规律r∂φ∂φr∂φ∂φr∂φ∂φrdS×∇φ=(dS−dS)i+(dS−dS)j+(dS−dS)k∫S∫Syzzxxy∂z∂y∂x∂z∂y∂x∂φr∂φr∂φr∂φr∂φr∂φr=(k−j)dS+(i−k)dS+(j−i)dS∫xyz∂y∂z∂z∂x∂x∂y若令f=φ,f=φ,f=φxiyjzk则证毕5.已知一个电荷系统的偶极矩定义为rr"r""P(t)=∫ρ(x,t)xdV,Vr∂ρr利用电荷守恒定律∇⋅J+=0证明P的变化率为∂trdPrr""=∫J(x,t)dVdtVrr"∂P∂ρr"""r"r""证明=∫xdV=−∫∇jxdV∂tV∂tVr∂P"r"""""r"""r"""""r""()=−∇jxdV=−[∇⋅(xj)−(∇x)⋅j]dV=(j−∇⋅(xj)dVx∫V∫∫Vx∂trr"=jdV−xj⋅dS∫∫xSrrr若S→∞,则∫(xj)⋅dS=0,(jS=0)rr∂ρ"∂ρ"同理()=jdV,()=jdVy∫yz∫z∂t∂trdPrr""即=∫j(x,t)dVdtVrrrrrrm×Rm⋅R6.若m是常矢量证明除R0点以外矢量A=的旋度等于标量ϕ=的梯33RR度的负值即r∇×A=−∇ϕ其中R为坐标原点到场点的距离方向由原点指向场点证明vvvm×R)v1v1v11v1v∇×A=∇×(=−∇×[m×(∇)]=(∇⋅m)∇+(m⋅∇)∇−[∇⋅(∇)]m−[(∇)⋅∇]m3RRrrrr-4- 电动力学习题解答第一章电磁现象的普遍规律v1=(m⋅∇)∇,(r≠0)rvvm⋅Rv1v11vv1∇ϕ=∇()=−∇[m⋅(∇)]=−m×[∇×(∇)]−(∇)×(∇×m)−(m⋅∇)∇3Rrrrr1vv1−[(∇)⋅∇]m=−(m⋅∇)∇rrv∴∇×A=−∇ϕ7有一内外半径分别为r1和r2的空心介质球介质的电容率为ε使介质内均匀带静止自由电荷ρf求1空间各点的电场2极化体电荷和极化面电荷分布rr解1∫SD⋅dS=∫ρfdV,(r2>r>r1)24π33即D⋅4πr=(r−r1)ρf333r(r−r1)ρfr∴E=3r,(r2>r>r1)3εrrrQf4π33由∫E⋅dS==(r2−r1)ρf,(r>r2)Sε3ε0033r(r2−r1)r∴E=3ρfr,(r>r2)3ε0rrrr>r1时∫lH⋅dl=2πrH=∫Sjf⋅dS=jfπ(r−r1)vµj(r2−r2)µ22rf1(r−r1)rB==jf×r2r22r22当r>r2时2πrH=πjf(r2−r1)22rµ0(r2−r1)rrB=jf×r22r22rrµ−µ0)rµrrr−r1JM=∇×M=∇×(χMH)=∇×()H=(−1)∇×(jf×r2)µ0µ02rµrµr=(−1)∇×H=(−1)jf,(r1R0且ϕ0是未置入导体球ϕ外R=R0=φ0前坐标原点的电势∞nnb根据有关的数理知识可解得ϕ外∑anRn1Pncosθ)n0R由于ϕ=−ERcosθϕ即外00R→∞∞b∞bn0b1nϕ外a0+a1Rcosθ+∑anRPn(cosθ)++2cosθ+∑n+1Pn(cosθ)R→∞=−E0Rcosθ+ϕ0n=2RRn=2R故而有a=ϕ,a=−E,a=0(n>1),b=0(n>1)0010nnbb01∴ϕϕERcosθ+cosθ外002RR-2- 电动力学习题解答参考第二章静电场bb01又ϕ=φ,即ϕ=ϕ−ERcosθ+cosθ=φ外R=R00外R=R000R200R0b0ϕ+=φ00R0故而又有∴b−ERcosθ+1cosθ=0002R02得到b=(φ−ϕ)R,b=ER0000100最后得定解问题的解为3(φ−ϕ)RER00000ϕ=−ERcosθ+ϕ++cosθ(R>R)外000RR2当导体球上带总电荷Q时定解问题存在的方式是2∇φ0(RR0)φ有限内R→0φ外R→∞E0Rcosθ+ϕ0(ϕ0是未置入导体球前坐标原点的电势φ内φ外RR0∂φ外−εdsQ(R=R)∫00∂Rs解得满足边界条件的解是nbnϕ内∑anRPncosθϕ外ϕ0E0Rcosθ∑n1Pncosθn=0n=0R由于ϕ的表达式中只出现了P(cosθcosθ项故b=0(n>1)外R→∞1nbb01∴ϕϕERcosθ+cosθ外002RR又有ϕ是一个常数导体球是静电平衡外R=R0bb01ϕ=ϕ−ERcosθ+cosθ=C外R=R00002RR00b13∴−ERcosθ+cosθ=0即b=ER002100R0-3- 电动力学习题解答参考第二章静电场3bER000ϕϕERcosθ++cosθ外002RR∂φ外Q又由边界条件−εdsQ∴b=∫00∂r4πεs0Q∴ϕ−ϕRR外2004πεRR03均匀介质球的中心置一点电荷Q球的电容率为ε球外为真空试用分离变数法求f空间电势把结果与使用高斯定理所得结果比较Q提示空间各点的电势是点电荷Q的电势f与球面上的极化电荷所产生的电势的f4πεR叠加后者满足拉普拉斯方程解一.高斯法rr在球外R>R0,由高斯定理有ε0∫E⋅ds=Q总Qf+QP=Qf对于整个导体球而言束缚电荷Q=0)PrQf∴E=24πε0RQf积分后得ϕ+C.(C是积分常数外4πεR0又由于ϕ=0,∴C=0外R→∞Qf∴ϕ=(R>R)外04πεR0rr在球内RR外04πε0R∴QQQϕff−f,RR0)4πε1R4πε1(ε1+2ε2)R4πε1R4πε1(ε1+2ε2)R4π(ε1+2ε2)R-6- 电动力学习题解答参考第二章静电场球面上的极化电荷密度rσP=P1n−P2n,n从2指向1如果取外法线方向则σp=P外n−P球n=[(ε2−ε0)∇φ外)]n−[(ε1−ε0)∇φ内)]n∂φ外∂φ内=−(ε2−ε0)+(ε1−ε0)RR∂R∂R0−6ρfcosθ6(ε0−ε2)ρfcosθ2(ε1−ε2)−2(ε1+2ε2)=(ε2−ε0)3−(ε1−ε0)[3−3ρfcosθ]4π(ε1+2ε2)R04π(ε1+2ε2)R04πε1(ε1+2ε2)R06ε1(ε0−ε2)+6ε2(ε1−ε0)3ε0(ε1−ε2)=3ρfcosθ=−3ρfcosθ4πε1(ε1+2ε2)R02πε1(ε1+2ε2)R0求极化偶极子rrPf=ql可以看成两个点电荷相距l对每一个点电荷运用高斯定理就得到在每个点电荷旁边有极化电荷ε0ε0qP=(−1)qf,−qP=(−1)(−qf)两者合起来就是极化偶极子ε1ε1rεr0PP=(−1)Pfε1r5.空心导体球壳地内外半径为R1和R2球中心置一偶极子P球壳上带电Q求空间各点电势和电荷分布解R2φ23φR∇φ3=0,φ3r→∞=011φ2=C,φ2r→0=∞φ2rrP⋅r""φ1=3+φ1,φ1r→0为有限值4πεr0Blφ3∑l+1Pl(cosθ),φ3r−R2=Crφ2=C,φ2r=R=C1rrPf⋅rl∂φ3∂φ1Qφ1=3+∑AlrPl(cosθ)−∫dSr=R2+∫dSr=R1=4πε0r∂r∂rε0-7- 电动力学习题解答参考第二章静电场B0B1B2+2cosθ+3P2+L=CR2R2R2Pfcosθ2+A0+A1R1cosθ+L=C4πε0R1B0Pf即A0==C,(A1R1+2)cosθ=0,Bl=0(l=1.2.3L),Al=0(l=2.3.4L)R24πεR1∂φ12Pfcosθl−1Pfcosθ又=−3+∑lAlR1PL=−3+A1cosθ+L∂r4πε0R12πε0R1∂φ3BlB0B1=∑(−l−1)l+2Pl=−2−23cosθ+L∂rrR1R1∂φ3B0B02B0则−∫∫∫dS=2dS=2dS=4πR12=4πB0∂rR1R1R1∂φ12ππPf22ππ−Pf2∫dS=∫∫00−3cosθR1sinθdθdϕ+∫∫003cosθR1sinθdθdϕ=0+0=0∂r2πε0R14πε0R1∂φ3∂φ1Q故−∫∫dS+=4πB0=∂r∂rε0QQ−PfB0=,A0=,A1=34πε04πε0R24πε0R1最后有rrrrP⋅rPf⋅rQφ1=2−3+,(rR2)4πε0rQφ2=,(R1R03rε0r(ε+2ε0)r得ρf22113ε0E0φr±Rρ(rcosθ,r>σ及112σ>>σ两种情况的电流分布特点21先求空间电势2∇φ内02φ内φ外r=R0∇φ0外因为δδ(r=R)稳恒电流认为表面无电流堆积即流入=流出内n外n0nn2φ2φ内外故σ=σ122r2r并且δ=δ即φ=−Ercosθ(j=σE)外r→∞0外r→∞0f020φ有限可以理解为在恒流时r→0的小封闭曲面流入流出内r→∞-10- 电动力学习题解答参考第二章静电场3σ2φErcosθ,rR外00020σ+2σr12rr2φer2φeθ12φr求内外电场E=−∇φ=−(++e)φ2r2θrsinθ2Φrr2φ内er12φ内r3σ2rrE(+e)=E(cosθe−sinθe)内θ0rθ2rr2θσ+2σ123σ2r=E0ezσ1+2σ23rrE0R0σ1−σ2rrEE(cosθe−sinθe)+()[]2cosθe+sinθe外0rθ3rθrσ+2σ123rrE0R0σ1−σ2rrrE(cosθe−sinθe)+()[]3cosθe−cosθe+sinθe0rθ3rrθrσ+2σ12v3σ1−σ23E0cosθvE0E+R()e−003r3σ+2σrr12求电流rvvv根据jσEjσE内1内外2外vvjf0=σ2E0vrv及(jf⋅r)rσ2E0rcosθrr0=e55rrrrrrr3σ1rrσ1σ233(jf0⋅r)rjf0得j内jf0,j外=j内R0[5−3]σ12σ2σ12σ2rr3ε0E0cosθωf=ε0(E2n−E1n)=ε0(E外n−E内n)=(σ1−σ2)σ1+2σ2-11- 电动力学习题解答参考第二章静电场8.半径为R的导体球外充满均匀绝缘介质ε导体球接地离球心为a处(a>R)置一点00电荷Q试用分离变数法求空间各点电势证明所得结果与镜像法结果相同f提示∞111Rn==∑()Pn(cosθ).(R>a)rR2+a2−2aRcosθan=0a解1分离变数法由电势叠加原理球外电势Qf""φ+φ,φ是球面上感应电荷产生的电势且满足定解条件外4πεR∇2φ"=0,(r>R)0z"φr→∞=0QfPφ外r=R0=0ar根据分离变数法得∞BO"lφ=∑l+1Pl(cosθ),(r>R0)l=0rQ1∞Bfl∴φ外+∑l+1Pl(cosθ)*4πεa2+r2−2arcosθl=0rQ1∞r∞Bfnl=∑()Pn(cosθ)+∑l+1Pl(cosθ),(ra).外4πεr4πεr4πεa2+r2−2arcosθRR212r2+(0)2+2r0cosθaa将分离变数法所得结果展开为Legend级数可证明两种方法所求得的电势相等9接地的空心导体球的内外半径为R1和R2在球内离球心为a(aR)外πε24R0QR11Qaφ=[−]+φ.(RR)外02rQ+Q0当φ=时两种情况的解相同04πεR0211在接地的导体平面上有一半径为a的半球凸部如图半球的球心在导体平面上点电荷Q位于系统的对称轴上并与平面相距为bb>a试用电象法求空间电势解如图利用镜像法根据一点电荷附近置一P无限大接地导体平板和一点电荷附近置一接地导体Q球两个模型可确定三个镜像电荷的电量和位置aR2−QaarbQ=−Q,r=r11Obba2QaarQ2=Q,r2=−rbbb-QrQ=−Q,r=−br33Q11aφ=[−+4πεR2+b2−2RbcosθR2+b2+2Rbcosθa4a202bR++2Rcosθ2bb-14- 电动力学习题解答参考第二章静电场a+],(0≤θ<π,R>a)4222aabR+−2Rcosθ2bb12.有一点电荷Q位于两个互相垂直的接地导体平面zP(x,y,z)所围成的直角空间内它到两个平面的距离为a和ba-QQ(x0,a,b)求空间电势(x0,-a,b)b解可以构造如图所示的三个象电荷来代替y两导体板的作用+Q-Q(x0,a,-b)(x0,-a,-b)Q11φ=[−−4πε(x−x)2+(y−a)2+(z−b)2x−x2+y−a2+z+b200(0)()()11−+],(y,z>0)222222(x−x)+(y+a)+(z−b)(x−x)+(y+a)+(z+b)0013.设有两平面围成的直角形无穷容器其内充满电导率为的液体取该两平面为xz面和yz面在x0,y0,z0和x0,y0,-z0两点分别置正负电极并通以电流I求导电液体中的电势解本题的物理模型是由外加电源在AB两点间建立电场使溶液中的载流子运动形r∂ρ∂ρz成电流I,当系统稳定时是恒定场即∇⋅j+=0中=0∂t∂trj对于恒定的电流可按静电场的方式处理A(x0,y0,z0)于是在A点取包围A的包围面rrσrrQI=∫i⋅ds}1∫rr∫E⋅ds=而又有rr⇒I=E⋅dsyεni=E⋅σσ1QIε1r∴有I=⇒Q=xjσε1σB(x0,y0,z0)Iε1z对BQQB=−Q=−σQ(-x0,-y0,z0)Q(x0,y0,z0)r又在容器壁上jn=0,即元电流流入容器壁Q(x-yz)Q(x0,y0,z0)0,0,0rrrr由j=σE有jn=0时En=0y∴可取如右图所示电像-Q(-x0,y0,z0)-Q(-x0,y0,-z0)-Q(x0,-y0,z0)-Q(x0,y0,-z0)x-15- 电动力学习题解答参考第二章静电场dδ(x)rr14.画出函数的图说明ρ=−(P⋅∇)δ(x)是一个位于原点的偶极子的电荷密度dxdδ(x)0,x≠0dx解δ(x)=∞,x=0dδ(x)δ(x+∆x)−δ(x)=limdx∆x→0∆xxdδ(x)1x≠0时=0dxdδ(x)0−∞2x=0时a∆x>0,=lim=−∞dx∆x→0∆xdδ(x)0−∞b)∆x<0,=lim=+∞dx∆x→0∆x15证明11δ(ax)=δ(x).(a>0)若a<0,结果如何a2xδ(x)=0δ(x−xkδ(x)证明1根据δ[φ(x)]=∑所以δ(ax)="aφ(x)k2从δ(x)的定义可直接证明有任意良函数f(x),则f(x)⋅x=F(x)也为良函数∫f(x)xδ(x)dx=f(x)⋅xx=0=0rr"16一块极化介质的极化矢量为P(x)根据偶极子静电势的公式极化介质所产生的静电势为rr"rP(x)⋅r"ϕ=∫dVV4πεr30rrrr另外根据极化电荷公式ρr=−∇"⋅P(x")及σr=n⋅P,极化介质所产生的电势又可表为PPrrrrrP∇"⋅P(x")P(x")⋅dS""ϕ=−∫dV+∫V4πε0rS4πε0rr试证明以上两表达式是等同的’XO-16- 电动力学习题解答参考第二章静电场证明rr"r1P(x)⋅r"1rr""1"ϕ=∫3dV=∫P(x)⋅∇dV4πε0Vr4πε0Vr"pr1"r1r"1又有∇(P)=∇⋅P+P⋅∇rrrrrrr""1∇⋅P""P"1∇⋅P"Pr则ϕ=[−dV+∇⋅()dV]=[−dV+⋅dS]∫V"∫V"∫V"∫S4πε0rr4πε0rr"rrrρsσr1∇⋅P"P⋅n1P"P=[−∫V"dV+∫SdS]=[∫VdV+∫SdS]4πε0rr4πε0rr刚好是极化体电荷的总电势和极化面电荷产生的总电势之和17证明下述结果并熟悉面电荷和面偶极层两侧电势和电场的变化1在面电荷两侧电势法向微商有跃变而电势是连续的2在面偶极层两侧电势有跃变1rrϕ2−ϕ1=n⋅Pε0而电势的法向微商是连续的各带等量正负面电荷密度±σ而靠的很近的两个面形成面rr偶极层而偶极矩密度P=limσl.)σ→∞l→0zσ⋅∆sE证明1如图可得2E⋅∆s=,ε01+xσσσ∴E=,φ1−φ2=z−z=02S2ε2ε2ε000E∂φ1rσr∂φ2rσr面=E1=ez=E2=(−ez)∂n12ε0∂n22ε0∂φ1∂φ2σ∴−=∂n∂nε120rσr+2)可得E=erznrr1ε0Elrrrrrr⋅2σnP-∴φ2−φ1=limE⋅l=limn⋅l=l→0l→0εε00∂φ1r∂φ2r又=E,=Ez∂n∂n-17- 电动力学习题解答参考第二章静电场∂φ∂φ21∴−=0.∂n∂nππ18.一个半径为R0的球面在球坐标0<θ<的半球面上电势为ϕ0在<θ<π的半22球面上电势为−ϕ0求空间各点电势1Pn+1(x)−Pn−1(x)1∫Pn(x)dx=0,02n+1提示Pn(1)=10,(n=奇数)Pn(0)=n1⋅3⋅5⋅⋅⋅(n−1)(−1)22⋅4⋅6,(n=偶数)解∇2φ0内2∇φ=0外φ内r→0<∞φ外r→∞=0πφ0,0≤θ<2φr=R=f(θ)=0π−φ0,<θ≤π2llφ内=∑AlrPl(cosθ)这是φ内按球函数展开的广义傅立叶级数Alr是展开系数1l2l+12l+1πAlR0=fl=[∫φ内R0Pl(cosθ)dcosθ]=[−∫0φ内R0Pl(cosθ)⋅sinθdθ]22−1π2l+1π=[−∫2φ0Pl(cosθ)sinθdθ+∫πφ0Pl(cosθ)sinθdθ]2022l+10−1=[φ0∫Pl(x)dx−φ0∫Pl(x)dx]2102l+101=φ0[−∫−1Pl(x)dx+∫0Pl(x)dx2l由Pl(−x)=(−1)Pl(x)l2l+1l+111则AlR0=φ0[(−1)∫P(x)dx+∫P(x)dx]200-18- 电动力学习题解答参考第二章静电场2l+1l+11=φ0[(−1)+1]∫Pl(x)dx20l当l为偶数时AlR0=0当l为奇数时有l2l+1l+11Pl+1(x)−Pl−1(x)1AlR0=φ0[(−1)+1]∫0Pl(x)dx=(2l+1)φ0022l+1l+1l−11⋅3⋅5⋅⋅⋅l1⋅3⋅5⋅⋅⋅(l−2)=−φ0[(−1)2−(−1)2]2⋅4⋅6⋅⋅⋅(l+1)2⋅4⋅6⋅⋅⋅(l−1)l−1l−11⋅3⋅5⋅⋅⋅l1⋅3⋅5⋅⋅⋅(l−2)=φ0[(−1)2+(−1)2]2⋅4⋅6⋅⋅⋅(l+1)2⋅4⋅6⋅⋅⋅(l−1)l−1l−11⋅3⋅5⋅⋅⋅(l−2)l1⋅3⋅5⋅⋅⋅(l−2)=φ0(−1)2(+1)=φ0(−1)2(2l+1)2⋅4⋅6⋅⋅⋅(l−1)l+12⋅4⋅6⋅⋅⋅(l+1)l−1φ021⋅3⋅5⋅⋅⋅(l−2)则A=(−1)(2l+1)ll2⋅4⋅6⋅⋅⋅(l+1)R0l−121⋅3⋅5⋅⋅⋅(l−2)rlφ内=∑φ0(−1)(2l+1)()Pl(cosθ),(l取奇数rR0)2⋅4⋅6⋅⋅⋅(l+1)r-19- 电动力学习题解答参考第三章静磁场rrr1.试用A表示一个沿z方向的均匀恒定磁场B写出A的两种不同表示式证明两者之0差是无旋场rrrrr解B是沿z方向的均匀的恒定磁场即B=Be且B=∇×A00z0r∂Az∂Ayr∂Ax∂Azr∂Ay∂Axr在直角坐标系中∇×A=(−)e+(−)e+(−)exyz∂y∂z∂z∂x∂x∂y∂Az∂Ay−=0∂y∂zrr∂A∂Axz如果用A在直角坐标系中表示B0即−=0∂z∂x∂A∂Ayx−=0∂x∂yr由此组方程可看出A有多组解如解1A=A=0,A=−By+f(x)yZx0rr即A=[−By+f(x)]e0x解2A=A=0,A=Bx+g(y)xzY0rr即A=[Bx+g(y)]e0yrrr解1和解2之差为∆A=[−By+f(x)]e−[Bx+g(y)]e0x0y则r∂(∆A)z∂(∆A)yr∂(∆A)x∂(∆A)zr∂(∆A)y∂(∆A)xr∇×(∆A)=[−]e+[−]e+[−]exyz∂y∂z∂z∂x∂x∂y0这说明两者之差是无旋场2.均匀无穷长直圆柱形螺线管每单位长度线圈匝数为n电流强度为I试用唯一性定理求管内外磁感应强度B解根据题意得右图取螺线管的中轴线为z轴rrrµJ×rr0本题给定了空间中的电流分布故可由B=dV"求解磁场分布又J在导∫34πrrrrµ0Jdl×r线上所以B=∫34πr1螺线管内由于螺线管是无限长理想螺线管故由电磁学的有关知识知其内部磁-1- 电动力学习题解答参考第三章静磁场场是均匀强磁场故只须求出其中轴线上的磁感应强度即可知道管内磁场由其无限长的特性不妨取场点为零点以柱坐标计算rrrrr=−acosϕ"e−asinϕ"e−z"exyxrrrdl=−adϕ"⋅sinϕ"e+adϕ"⋅cosϕ"exyrrrrrrr∴dl×r=(−adϕ"⋅sinϕ"e+adϕ"⋅cosϕ"e)×(−acosϕ"e−asinϕ"e−z"e)xyxyxrr2r=−az"cosϕ"dϕ"e−az"sinϕ"dϕ"e+adϕ"exyz取由z"−z"+dz"的以小段此段上分布有电流nIdz"rr2rrµ0nJdz"(−az"cosϕ"dϕ"ex−az"sinϕ"dϕ"ey+adϕ"ez)∴B=∫34π[a2+(z")2]2z"2π∞2+∞d()µ0adz"rnIµ0a=dϕ"⋅nIe==nµI4π∫∫223z2∫z"300−∞[a+(z")]2−∞[()2+1]2a2)螺线管外部:由于是无限长螺线管不妨就在xoy平面上任取一点P(ρ,ϕ.0)为场点(ρ>a)rr222∴r=x−x"=(ρcosϕ−acosϕ")+(ρsinϕ−asinϕ")+z"222=ρ+a+z"−2aρcos(ϕ−ϕ")rrrrrrr=x−x"=(ρcosϕ−acosϕ")e(ρsinϕ−asinϕ")e−z"exyzrrrdl=−adϕ"⋅sinϕ"e+adϕ"⋅cosϕ"exyrrrr2r∴dl×r=−az"cosϕ"dϕ"e−az"sinϕ"dϕ"e+[a−aρcos(ϕ"−ϕ)]dϕ"exyz2π∞2π∞rµ0az"cosϕ"dϕ"raz"sinϕ"dϕ"r∴B=⋅nI[dϕ"−edz"+dϕ"−edz"+∫∫3x∫∫3y4πrr0−∞0−∞2π∞2a−aρcos(ϕ"−ϕ)r+dϕ"dz"e]∫∫3zr0−∞由于磁场分布在本题中有轴对称性而螺线管内部又是匀强磁场且螺线管又是无限r长故不会有磁力线穿出螺线管上述积分为0所以B=0-2- 电动力学习题解答参考第三章静磁场3.设有无穷长的线电流I沿z轴流动以z<0空间充满磁导率为µ的均匀介质z>0区域为真空试用唯一性定理求磁感应强度B然后求出磁化电流分布解本题的定解问题为rr2∇A=−µJ,(z>0)10rr2∇A2=−µJ,(z<0)rrA=A12z=01r1r∇×A=∇×Aµ2z=0µ1z=00由本题具有轴对称性可得出两个泛定方程的特解为rrrµ0IdlA(x)=1∫4πrrrrµIdlA(x)=2∫4πrµ0Ire,(z>0)rπθ2r由此可推测本题的可能解是B=µIre,(z<0)2πrθrrrrr验证边界条件1A=A,即n⋅(B−B)=012z=021rrrr题中n=e,且e⋅e=0所以边界条件1满足zzθ1r1rrrr2∇×A=∇×A,即n×(H−H)=02z=01z=021µµ0本题中介质分界面上无自由电流密度又rrBIr1H==e1θµ2πr0rrBIr2H==e2θµ2πrrrrrr∴H−H=0,满足边界条件n×(H−H)=02121µ0Ire,(z>0)rπθ2r综上所述由唯一性定理可得本题有唯一解B=µIre,(z<0)2πrθrrrBrrBr2在介质中H=−M故在z<0的介质中M=−H2µµ00-3- 电动力学习题解答参考第三章静磁场rIµrIrIµr即M=⋅e−e=(−1)eθθθ2πrµ2πr2πrµ00∴介质界面上的磁化电流密度rrrIµrrIµrα=M×n=(−1)e×e=(−1)eMθzr2πrµ2πrµ002πrrIµrrµ总的感应电流J=M⋅dl=(−1)e⋅r⋅dϕ⋅e=I(−1)电流M∫∫θθ2πrµµ000在z<0的空间中沿z轴流向介质分界面4.设x<0半空间充满磁导率为µ的均匀介质x>0空间为真空今有线电流I沿z轴流动求磁感应强度和磁化电流分布解假设本题中得磁场分布仍呈轴对称则可写作vµ′IvB=eϕ2πrvvvn⋅(B−B)=021其满足边界条件vvvvn×(H−H)=α=021即可得在介质中vvBµ′IvH==e2ϕµ2πrµvvBvµ′Ivv而H=−M=e−M2ϕµ2πrµ00vµ′Iµ−µ0v∴在x<0的介质中M=eϕ2πrµµ0vv则I=Mdl取积分路线为B→C→A→B的半圆M∫vQAB⊥e,∴AB段积分为零ϕIµ′(µ−µ)0I=M2µµ0vµ0(I+IM)v∴B=eϕ2πrµ0(I+IM)vvµ′Iv2µµ0∴由e=B=−e可得µ′=ϕϕ2πr2πrµ+µ0-4- 电动力学习题解答参考第三章静磁场vµµ0Iv∴空间B=eϕµ+µπr0µ−µ0I=I沿z轴Mµ+µ02125.某空间区域内有轴对称磁场在柱坐标原点附近已知B≈B−C(z−ρ)其中z02B0为常量试求该处的Bρrr提示用∇⋅B=0,并验证所得结果满足∇×H0vvvv212解由B具有轴对称性设B=Be+Be其中B=B−c(z−ρ)ρρzzz02vQ∇⋅B=01∂∂∴(ρB)+B=0ρzρ∂ρ∂z1∂2即(ρB)−2cz=0∴ρB=czρ+A(常数)ρρρ∂ρ取A=0得B=czρρvv212v∴B=czρe+[B−c(z−ρ)]e1ρ0z2vvv∂Bρ∂BzvQj=0,D=0∴∇×B=0即(−)e=02θ∂z∂ρ代入1式可得2式成立∴B=czρc为常数ρ6.两个半径为a的同轴线圈形线圈位于z=±L面上每个线圈上载有同方向的电流I1求轴线上的磁感应强度2求在中心区域产生最接近于均匀的磁场时的L和a的关系2∂提示用条件B=02z∂z解1由毕萨定律L处线圈在轴线上z处产生得磁感应强度为-5- 电动力学习题解答参考第三章静磁场vvvvµIdl×rµIa200B=Be,B=sinα=dθ11zz1z∫∫334πr4π[a2+(z−L)2]2121=µIa032[(L−z)2+a2]2同理L处线圈在轴线上z处产生得磁感应强度为121vvB=µIaB2=B2zez2z20223[(L+z)+a]2∴轴线上得磁感应强度vv1211vB=Bzez=µ0Ia3+3ez2[(L−z)2+a2]2[(L+z)2+a2]2v2Q∇×B=0vvv2∴∇×(∇×B)=∇(∇⋅B)−∇B=0vv∂22又∇⋅B=0∴∇B=0,B=0代入1式中得2z∂z115−−[(L−z)2+a2]2(L−z)2−[(L−z)2+a2]2[(L−z)2+a2]3+6(L−z)2[(L−z)2+a2]2226[(L−z)+a]115−[(L+z)2+a2]2(L+z)2+[(L+z)2+a2]2[(L+z)2+a2]3−6(L−z)2[(L+z)2+a2]2−226[(L−z)+a]0取z0得115−22322222222222(L+a)[−2(L+a)L−2(L+a)]+12(L+a)L=0222∴5L=L+a-6- 电动力学习题解答参考第三章静磁场1∴L=a2r7.半径为a的无限长圆柱导体上有恒定电流J均匀分布于截面上试解矢势A的微分方程设导体的磁导率为µ导体外的磁导率为µ0解定解问题为vv∇2A=−µJ,(ra)外vA内0<∞vvA=A外a内a1v1v∇×A=∇×A内外µµ0选取柱坐标系该问题具有轴对称性且解与z无关令vvA=A(r)e内内zvvAA(r)e代入定解问题得外外z1∂∂A内(r)(r)=−µJ0r∂r∂r1∂∂A外r)(r)=0r∂r∂r12A(r)=−µJr+Clnr+C内12得4A(r)=Clnr+C外34由A(r)<∞得C=0内r=011v1vµ2由∇×A=∇×A得C=−Ja内外3µµ20-7- 电动力学习题解答参考第三章静磁场vvvv12µ2由A=A令A=A=0得C=µJa,C=Jalna外a内a外a内a20442v1v22A=µJ(a−r)内04∴vµv2aAJaln外2rrrQrm8.假设存在磁单极子其磁荷为Qm它的磁场强度为H=给出它的矢势的34πµr0一个可能的表示式并讨论它的奇异性vvQmrQm1v解H==e32r4πµr4πµr00vvvQmv由∇×A=B=µH=e得02r4πr1∂∂AθQm[(sinθA)−]=φ2rsinθ∂θ∂φ4πr11∂Ar∂[−(rAφ)]=0(1)rsinθ∂φ∂r1∂∂Ar[(rAθ)−]=0r∂r∂θ∂Qmsinθ令A=A=0,得(sinθA)=rθφ∂θ4πrθQsinθm∴sinθA=dθφ∫04πrQm1−cosθ∴A=φ4πrsinθ显然A满足1式φvQm1−cosθv∴磁单极子产生的矢势A=eφ4πrsinθ-8- 电动力学习题解答参考第三章静磁场v讨论当θ→0时A→0πvQmv当θ→时A→eφ24πrvvv当θ→π时A→∞故A的表达式在θ=π具有奇异性A不合理rr9.将一磁导率为µ半径为R0的球体放入均匀磁场H0内求总磁感应强度B和诱导r磁矩mvv解根据题意以球心为原点建立球坐标取H的方向为e此球体在外界存在的磁场0z的影响下极化产生一个极化场并与外加均匀场相互作用最后达到平衡保持在一个静止的状态呈现球对称本题所满足的定解问题为2∇ϕ=0,RR02∂ϕm∂ϕmϕ=ϕ,µ1=µ2,(R=R)m1m200∂R∂Rϕ<∞m1R=0ϕm2R=∞=−H0Rcosθ由泛定方程和两个自然边界条件得∞nϕm1=∑anRPn(cosθ)n=0∞dnϕm2=−H0Rcosθ+∑n+1Pn(cosθ)n=0R由两个边界条件有∞∞dnn∑anR0Pn(cosθ)=−H0R0cosθ+∑n+1Pn(cosθ)n=0n=0R0∞∞n−1(n+1)dnµ∑annR0Pn(cosθ)=−H0µ0cosθ−µ0∑n+2Pn(cosθ)n=1n=0R0得-9- 电动力学习题解答参考第三章静磁场3µ0H0a=−1µ+2µ0µ−µ03d1=H0R0µ+2µ0a=d=0,(n≠1)nn3µ0ϕ=−HRcosθ,RRm20µ+2µR2000v3µ0v3µ0v3µ0vH=−∇ϕ=Hcosθe−Hsinθe=H1m10r0θ0µ+2µ0µ+2µµ+2µvv3µµvB=µH=0H110µ+2µ033vµ−µ02R0vµ−µ0R0vH2=−∇ϕm2=[1+⋅3]H0cosθer−[1−⋅3]H0sinθeθµ+2µRµ+2µR00vvvvvµ−µ033(H0⋅R)RH0=H0+R0[5−3]µ+2µRR0vvvvvvvµ−µ3(H⋅R)RH0300B=µH=µH+µR[−]202000053µ+2µRR03µµ0vH,(RR)0000530µ+2µ0RRv当B在R>R0时表达式中的第二项课看作一个磁偶极子产生的场3µ−µ0R0v∴ϕ中⋅Hcosθ可看作偶极子m产生的势m220µ+2µR0vv331m⋅Rµ−µ0R0µ−µ0R0vv即⋅=⋅Hcosθ=⋅H⋅R320204πRµ+2µ0Rµ+2µ0Rvµ−µv03∴m=4π⋅RH0µ+2µ0r10.有一个内外半径为R1和R2的空心球位于均匀外磁场H0内球的磁导率为µ求空-10- 电动力学习题解答参考第三章静磁场r腔内的场B讨论µ>>µ时的磁屏蔽作用0vvv解根据题意以球心为原点取球坐标选取H的方向为e在外场H的作用下球0z0v壳极化产生一个附加场并与外场相互作用最后达到平衡B的分布呈现轴对称定解问题2∇ϕ=0,RR33ϕm1=ϕm2R=R1,ϕm2=ϕm3R=R2∂ϕ∂ϕ∂ϕ∂ϕµm1=µm2,µm3=µm20∂R∂RR=R10∂R∂RR=R2ϕ<∞m1R=0ϕ=−HRcosθm3R=∞0由于物理模型为轴对称再有两个自然边界条件故三个泛定方程的解的形式为∞nϕm1=∑anRPn(cosθ)n=0∞cnnϕm2=∑(bnR+n+1)Pn(cosθ)n=0R∞dnϕm3=−H0Rcosθ+∑n+1Pn(cosθ)n=0Rv因为泛定方程的解是把产生磁场的源H做频谱分解而得出的分解所选取的基本函数0系是其本征函数系{P(cosθ)}在本题中源的表示是n−HRcosθ=−HRP(cosθ)001所以上面的解中a=b=c=d=0,(n≠0)nnnn故解的形式简化为ϕ=aRcosθm11c1ϕ=(bR+)cosθm212Rd1ϕ=−HRcosθ+cosθm302R-11- 电动力学习题解答参考第三章静磁场代入衔接条件得c1aR=bR+11112R1cd11bR+=−HR+122022R2R22caµ=µ(b−11013R12d2c11−µH−µ=µ(b−)00313RR22解方程组得333µ(2µ+µ)HR+3µ(µ−µ)HR00020002a=12332(µ−µ)R−(2µ+µ)(2µ+µ)R0100233µ(2µ+µ)HR0002b=12332(µ−µ)R−(2µ+µ)(2µ+µ)R01002333µ(µ−µ)HRR00021c=12332(µ−µ)R−(2µ+µ)(2µ+µ)R010026333µ0(2µ+µ0)H0R2+3µ0(µ−µ0)H0R2R13d=+HR1233022(µ−µ)R−(2µ+µ)(2µ+µ)R01002vv而B=µH=−µ∇ϕ,(i=1,2,3)i0i0mivv∴B=−µae101zR131−()Rv2=[1−]µH00(µ+2µ0)(2µ+µ0)R13−()22(µ−µ)R02当µ>>µ时0(µ+2µ)(2µ+µ)00≈122(µ−µ)0v∴B=01即球壳腔中无磁场类似于静电场中的静电屏障rrr11.设理想铁磁体的磁化规律为B=µH+µM,M是恒定的与H无关的量今将一个000-12- 电动力学习题解答参考第三章静磁场理想铁磁体做成均匀磁化球M为常值浸入磁导率为µ"的无限介质中求磁感应0强度和磁化电流分布vv解根据题意取球心为原点做球坐标以M的方向为e本题具有球对称的磁场分布0z满足的定解问题为2∇ϕ=0,RR02ϕm1=ϕm2R=R0,∂ϕ∂ϕµm1−µ′m2=MµcosθR000∂R∂Rϕ<∞m1R=0ϕ=0m2R=∞∞n∴ϕm=∑anRPn(cosθ)1n=0∞bnϕm2=∑(n+1)Pn(cosθ)n=0R代入衔接条件对比P(cosθ)对应项前的系数得nµM00µMa=003a=b=0,(n≠1)1b=Rnn2µ′+µ102µ′+µµM00∴ϕ=Rcosθ,(RR)m2202µ′+µRvvvr2µ′µM00由此RR,B=−µ′∇ϕ=[−]02m2532µ′+µRRv2µ′µM00,(RR)2µ′+µR5R30-13- 电动力学习题解答参考第三章静磁场vvvvvv又n×(B−B)=µ(α+α)其中α021R00Mv代入B的表达式得v3µ′vαMsinθeM0ϕ2µ′µ0r12.将上题的永磁球置入均匀外磁场H中结果如何0vv解根据题意假设均匀外场H的方向与M的方向相同定为坐标z轴方向00定解问题为2∇ϕ=0,RR02ϕm1=ϕm2R=R0,∂ϕ∂ϕm1m2µ−µ=Mµcosθ0R000∂R∂Rϕ<∞m1R=0ϕ=−HRcosθm2R=∞0解得满足自然边界条件的解是ϕ=aRcosθ,(RR)m2020R代入衔接条件d1aR=−HR+10002R02d1µH+µ+µa=µM0003100R0µM−3µH0000得到a=1µ+2µ0µ0M0+(µ−µ0)H03d=R10µ+2µ0µM−3µH0000∴ϕ=Rcosθ,(RR)m2020µ+2µR0vµ0M0−3µ0H0vµ0M0−3µ0H0v∴H=−∇ϕ=−[cosθe−sinθe]1m1rθµ+2µµ+2µ00vvµM−3µH0000=−2µ+µ0vvvv2v3µµ2µ00B=µH+µM=H+M,(RR021∂ϕm2∂ϕm1Qωsinθ(−)=−R=R0R∂θ∂θ4πR00∂ϕm∂ϕmµ1=µ2,(R=R)00∂R∂Rϕm1R=0<∞ϕm2R=∞=0Qωsinθ其中σ=是球壳表面自由面电流密度4πR0解得满足自然边界条件的解为-15- 电动力学习题解答参考第三章静磁场ϕ=aRcosθ,(RR)m220Rb1QωaR−=−102R04πR0代入衔接条件2ba+1=013R02QωQωR0解得a=−b=116πR12π0Qω∴ϕ=−Rcosθ,(RR)m22012πRvvQωvQωvQω∴H=−∇ϕ=cosθe−sinθe=1m1rθ6πR6πR6πR000vrQµ0vB=µH=ω1016πR022vvvrv2QωR0vQωR0v13(m⋅R)RmH=−∇ϕ=cosθe+sinθe=[−]其中2m23r3r5312πR12πR4πRR2vQR0vm=ω3vvvrvvµ03(m⋅R)RmB=µH=[−]202534πRR14.电荷按体均匀分布的刚性小球其总电荷为Q半径为R0它以角速度ω绕自身某以直径转动求1它的磁矩2它的磁矩与自转动量矩之比设质量M0是均匀分布的v1vvv解1磁矩m=∫x×J(x)dV2-16- 电动力学习题解答参考第三章静磁场vvvvvvQvv又x=R=ReJ(x)=ρv=(ω×R)r43πR03v13Qrvv213Qωvv42∴m=R×(ω×R)Rsinθdrdθdφ=(e×e)Rsinθdrdθdφ3∫3∫rφ24πR24πR00vvvvvv又e×e=−e=sinθe+cosθ(−cosφe−sinφe)rφθzxyv3Qω2ππR0vvv42∴m=[sinθe+cosθ(−cosφe−sinφe)Rsinθdrdθdφ3∫∫∫000zxy8πR023Qωv2ππR034QR0v=esinθRdrdθdφ=ω3z∫∫∫0008πR50vvvvvv3Mvvv02)自转动量矩L=dL=R×dP=R×vdm=R×(ω×R)dV∫∫∫3∫4πR03M02vvv2=Rω(e×e×e)Rsinθdrdθdφ3∫rzr4πR03M02vv2=Rω(−sinθe×e)Rsinθdrdθdφ3∫φr4πR03M02v2=Rωsinθ(−e)Rsinθdrdθdφ3∫θ4πR03M0ω2ππR0vvv42=[sinθe+cosθ(−cosφe−sinφe)Rsinθdrdθdφ3∫∫∫000zxy4πR0v2v3M0ω2ππR0432M0R0ω=Rsinθdrdθdφ=4πR3∫∫∫000502QR0vvω∴mv=5=Q22ML2M0R0v0ω5r15.有一块磁矩为m的小永磁体位于一块磁导率非常大的实物的平坦界面附近的真空中r求作用在小永磁体上的力F.-17- 电动力学习题解答参考第三章静磁场v解根据题意因为无穷大平面的µ很大则可推出在平面上所有的H均和平面垂直rr类比于静电场构造磁矩m关于平面的镜像m′则外场为vB=−µ∇ϕe0mvvm⋅Rmcosθϕm=3=24πR4πrvm2cosθvsinθrµ0mvv∴B=−µ[−e−e]=(αcosθe+sinθe)e03r3θ3rθ4πrr4πrv∴m受力为2vvv3mµ02vF=(m⋅∇)⋅B=−(1+cosα)eer=2a4zθ=α64πa-18- 电动力学习题解答第四章电磁波的传播1.考虑两列振幅相同的偏振方向相同频率分别为ω+dϖ和ω−dω的线偏振平面波它们都沿z轴方向传播1求合成波证明波的振幅不是常数而是一个波2求合成波的相位传播速度和振幅传播速度rrrrE(x,t)=E(x)cos(kx−ωt)1011解rrrrE(x,t)=E(x)cos(kx−ωt)2022rrrrrrrE=E(x,t)+E(x,t)=E(x)[cos(kx−ωt)+cos(kx−ωt)]1201122rrk+kω+ωk−kω−ω12121212=2E(x)cos(x−t)cos(x−t)02222其中k1=k+dk,k2=k−dk;ω1=ω+dω,ω2=ω−dωrrr∴E=2E(x)cos(kx−ωt)cos(dk⋅x−dω⋅t)0rrri(kx−ωt)用复数表示E=2E(x)cos(dk⋅x−dω⋅t)e0相速kx−ωt=0ω∴vp=k群速dk⋅x−dω⋅t=0dω∴vg=dko2一平面电磁波以θ=45从真空入射到εr=2的介质电场强度垂直于入射面求反射系数和折射系数r解n为界面法向单位矢量,,分别为入射波反射波和折射波的玻印亭矢量的周期平均值则反射系数R和折射系数T定义为r"2⋅nE0R=r=2⋅nE0r2⋅nn2cosθ2E""T=r=2⋅nncosθE10又根据电场强度垂直于入射面的菲涅耳公式可得2ε1cosθ−ε2cosθ2R=ε1cosθ+ε2cosθ2-1- 电动力学习题解答第四章电磁波的传播4ε1ε2cosθcosθ2T=2(ε1cosθ+ε2cosθ2)又根据反射定律和折射定律oθ=θ1=45ε2sinθ2=ε1sinθ由题意ε1=ε0,ε2=ε0εr=2ε0o∴θ2=3023−22222−3∴R=()=232+3+222234ε022223T==2322+3(ε0+ε02)223有一可见平面光波由水入射到空气入射角为60证明这时将会发生全反射并求折射波沿表面传播的相速度和透入空气的深度设该波在空气中的波长为−5λ=6.28×10cm水的折射率为n1.3301解由折射定律得临界角θc=arcsin()=48.75所以当平面光波以60入射时1.33将会发生全反射折射波k′′=ksinθω′′ω3相速度v===cpk′′k2sinθ−5λ16.28×10−5投入空气的深度κ==≈1.7×10cm2212πsinθ−n212πsin260−()21.33vvvvvvvi(k⋅x−ωt)4频率为ω的电磁波在各向同性介质中传播时若E,D,B,H仍按e变化但Dvvv不再与E平行即D=εE不成立vvvvvvvvvv1证明k⋅B=k⋅D=B⋅D=B⋅E=0,但一般k⋅E≠0-2- 电动力学习题解答第四章电磁波的传播v1vvvv22证明D=[kE−(k⋅E)k]2ωµvv3证明能流S与波矢k一般不在同方向上证明1由麦氏方程组vv∂B∇×E=−∂tvv∂D∇×H=∂tv∇⋅D=0v∇⋅B=0得vvvvvvvvvvi(k⋅x−ωt)i(k⋅x−ωt)∇⋅B=B⋅∇e=ik⋅Be=ik⋅B=000rv∴k⋅B=0vv同理k⋅D=0vvvvvvvi(k⋅x−ωt)∇×H=[∇e]×H=ik×H=−iωD0vvv∴ik×B=−iµωDvv1vvv∴B⋅D=−B⋅(k×B)=0µωvvvvvvvi(k⋅x−ωt)∇×E=[∇e]×E=ik×E=iωB0vv1vvvvvv∴B⋅E=(k×E)⋅E=0∇⋅E=ik⋅EωvvvvvQD≠εE∴∇⋅E一般≠0即k⋅E一般≠0-3- 电动力学习题解答第四章电磁波的传播vv∂Bv1vv2由∇×E=−得B=(k×E)∂tωvv∂Dv1vv另由∇×H=得D=−(k×B)∂tµωv1vvv1vvv12vvvv∴D=−[k×(k×E)]=[(k×E)×k]=[kE−(k⋅E)k]222µωµωµωv1vvv1vv3由B=(k×E)得H=(k×E)ωµωvvr1vvv12vvvv∴S=E×H=E×(k×E)=[Ek−(k⋅E)E]µωµωvvv1vvv2Qk⋅E一般≠0∴S一般≠Ek即S一般不与k同向µω5有两个频率和振幅都相等的单色平面波沿z轴传播一个波沿x方向偏振另一个沿yπ方向偏振但相位比前者超前求合成波的偏振2反之一个圆偏振可以分解为怎样的两个线偏振解偏振方向在x轴上的波可记为x=Acos(ωt−kz)=Acos(ωt+ϕ)000x在y轴上的波可记为πy=Acos(ωt−kz+)=Acos(ωt+ϕ)000y2π∆ϕ=ϕ−ϕ=0y0x2合成得轨迹方程为22222x+y=A[cos(ωt+ϕ)+cos(ωt+ϕ)]00x0y222=A[cos(ωt+ϕ)+sin(ωt+ϕ)]00x0x2=A0222即x+y=A0所以合成的振动是一个圆频率为ω的沿z轴方向传播的右旋圆偏振反之一个圆偏-4- 电动力学习题解答第四章电磁波的传播振可以分解为两个偏振方向垂直同振幅同频率相位差为π的线偏振的合成26平面电磁波垂直直射到金属表面上试证明透入金属内部的电磁波能量全部变为焦耳热证明设在z>0的空间中是金属导体电磁波由z<0的空间中垂直于导体表面入射已知导体中电磁波的电场部分表达式是vv−αzi(βz−ωt)E=Eee0于是由z0的表面单位面积进入导体的能量为vvvv1vv1vvS=E×H其中H=k×E=(β+iα)n×Eωµωµv1v*vβ2其平均值为S=Re(E×H)=E022ωµvvv−αzi(βz−ωt)在导体内部J=σE=σEee0所以金属导体单位面积那消耗的焦耳热的平均值为1v*v12−2αzdQ=Re(J×E)=σEe02212∞−2αzσ2作积分Q=σEedz=E即得单位面积对应的导体中消耗的平均焦0∫0204α耳热ωµσ又Qαβ=2σ2β2∴Q=E=E原题得证.004α2ωµ−1697已知海水的µ=1,σ=1S⋅m试计算频率ν为50,10和10Hz的三种电磁波在海r水中的透入深度解取电磁波以垂直于海水表面的方式入射12透射深度δ==αωµσQµ=1r−7∴µ=µµ=µ=4π×100r022∴1>ν=50Hz时:δ===72m1−7ωµσ2π×50×4π×10×1-5- 电动力学习题解答第四章电磁波的传播6222>ν=10Hz时δ≈0.5m267ωµσ2π×10×4π×10×19223>ν=10Hz时:δ==≈16mm39−7ωµσ2π×10×4π×10×18平面电磁波由真空倾斜入射到导电介质表面上入射角为θ求导电介质中电磁波的1相速度和衰减长度若导电介质为金属结果如何vvvv提示导电介质中的波矢量k=β+iα,α只有z分量为什么解根据题意如图所示入射平面是xz平面zvvvvvv−α⋅xi(β⋅x−ωt)导体中的电磁波表示为E=Eee0vv""vvθ3k""k=β+iα介质x与介质中的有关公式比较可得真空v222vθ1θ2k"β−α=ωµεkvv1α⋅β=ωµσ2""根据边界条件得k=β+iα=实数∴α=0xxxx""ω又k=k=ksinθ=sinθxx11cω∴β=sinθx1cvv""而入射面是xz平面故k,k无y分量∴α=0,β=0yyvvω∴α只有α存在β有β与β其中β=sinθzxzx1cω2222(sinθ)+β−α=ωµε1zzc∴有1αβ=ωµσzz2解得22212ω21ω2222221β=(µεω−sinθ)+[(sinθ−ωµε)+ωµσ]2z21212c2c22212ω212ω222221α=−(µεω−sinθ)+[(ωµε−sinθ)+ωµσ]2z21212c2c-6- 电动力学习题解答第四章电磁波的传播ω其相速度为v=衰减深度为1βα2ω222sinθ+β−α=021zzc如果是良导体则1αβ=ωµσzz2242ω1ω422212∴β=−sin2θ+[sinθ+ωµσ]z21412c2c242ω21ω422212α=sinθ+[sinθ+ωµσ]z21212c2c9无限长的矩形波导管在在z0处被一块垂直地插入地理想导体平板完全封闭求在z=−∞到z0这段管内可能存在的波模解在此中结构得波导管中电磁波的传播依旧满足亥姆霍兹方程rr22∇E+kE=0k=ωµ0ε0v∇⋅E=0方程的通解为E(x,y,z)=(Csinkx+Dcoskx)⋅(Csinky+Dcosky)⋅(Csinkz+Dcoskz)1x1x2y2y3z3z根据边界条件有E=E=0,(x=0,a)E=E=0,(y=0,b)yzxz∂Ex∂Ey∂Ez=0,(x=0,a)=0,(y=0,b)=0,(z=0)∂x∂y∂zE=Acoskxsinkysinkzx1xyz故Ey=A2sinkxxcoskyysinkzzE=Asinkxsinkycoskzz3xyzmπ其中k=,m=0,1,2Lxanπk=,n=0,1,2Lyb222222ωmπnπk+k+k=k=ωεµ=且A+A+Ak=0xyz002123zcab-7- 电动力学习题解答第四章电磁波的传播综上即得此种波导管种所有可能电磁波的解vv10电磁波E(x,y,z,t)=E(x,y)ei(k2z−ωt)在波导管中沿z方向传播试使用vvvv∇×E=iωµH及∇×H=−iωεE证明电磁场所有分量都可用E(x,y)和H(x,y)这两00xz个分量表示证明沿z轴传播的电磁波其电场和磁场可写作vvvvE(x,y,z,t)=E(x,y)ei(kzz−ωt)H(x,y,z,t)=H(x,y)ei(kzz−ωt)vv∂Bv∇×E=−=iωµH0∂t由麦氏方程组得vv∂Ev∇×H=ε=−iωεE00∂t∂E∂E∂Ezyz写成分量式−=−ikE=iωµH1zy0x∂y∂z∂y∂E∂E∂Exzz−=ikE−=iωµH2zx0y∂z∂x∂x∂E∂Eyx−=iωµH0z∂x∂y∂H∂H∂Hzyz−=−ikH=−iωεE3zy0x∂y∂z∂y∂H∂H∂Hxzz−=ikH−=−iωεE4zx0y∂z∂x∂x∂H∂Hyx−=−iωεE0z∂x∂y1∂Hz∂Ez由23消去Hy得Ex=2(−ωµ0−kz)ω2∂y∂xi(−k)2zc-8- 电动力学习题解答第四章电磁波的传播1∂H∂Ezz由14消去Hx得Ey=2(ωµ0−kz)ω2∂x∂yi(−k)2zc1∂H∂Ezz由14消去Ey得Hx=2(−kz+ωε0)ω2∂x∂yi(−k)2zc1∂H∂Ezz由23消去Ex得Hy=2(−kz−ωε0)ω2∂y∂xi(−k)2zcv11写出矩形波导管内磁场H满足的方程及边界条件vvvv−iωt解对于定态波磁场为H(x,t)=H(x)evv∂Dv∇×H==−iωεE由麦氏方程组∂tv∇⋅H=0vvvvv22得∇×(∇×H)=∇(∇⋅H)−∇H=−∇H=−iωε∇×Evv∂Bv又∇×E=−=iωµH∂tvvv22∴−iωε∇×E=ωµεH=−∇Hv2222(∇+k)H=0,k=ωεµv∴v即为矩形波导管内磁场H满足的方程∇⋅H=0vvvv由n⋅B=0得n⋅H=0H=0nvv∂Ht利用∇×E=iωµH和电场的边界条件可得=0∂n-9- 电动力学习题解答第四章电磁波的传播Hn=0∴边界条件为∂Ht∂n12论证矩形波导管内不存在TMm0或TM0n波v证明已求得波导管中的电场E满足E=Acoskxsinkyeikzzx1xyikzE=Asinkxcoskyezy2xyikzE=Asinkxsinkyezz3xyviv由H=−∇×E可求得波导管中的磁场为ωµiikzH=−(Ak−iAk)sinkxcoskyezx3y2zxyωµiikzH=−(iAk−Ak)coskxsinkyezy1z3xxyωµiH=−(Ak−Ak)coskxcoskyeikzzz2x1yxyωµ本题讨论TM波故Hz0即A2kx−A1ky=0nπ故1若n=0,则k==0,Ak=0y2xbmπ又k=≠0,那么A0x2a∴H=H=0xymπ2若m=0,则k==0,Ak=0x1yanπ又k=≠0,那么A=0y1b∴H=H=0xy∴波导中不可能存在TMm0和TM0n两种模式的波913频率为30×10Hz的微波在0.7cm×0.4cm的矩形波导管中能以什么波模传播在0.7cm×0.6cm的矩形波导管中能以什么波模传播9解1ν=30×10Hz波导为0.7cm×0.4cm-10- 电动力学习题解答第四章电磁波的传播ωcm2n2由ν==()+()2m2ab−2−2当a=0.7×10m.,b=0.4×10m时10m=1,n=1时,ν=4.3×10Hz10m=1,n=0时ν=2.1×10Hz10m=0,n=1时,ν=3.7×10Hz∴此波可以以TM10波在其中传播92ν=30×10Hz波导为0.7cm×0.6cm10m=1,n=1时,ν=2.1×10Hz10m=1,n=0时ν=2.5×10Hz10m=0,n=1时,ν=3.3×10Hz∴此波可以以TE10和TE01两种波模传播14一对无限大的平行理想导体板相距为b电磁波沿平行与板面的z方向传播设波在x方向是均匀的求可能传播的波模和每种波模的截止频率解在导体板之间传播的电磁波满足亥姆霍兹方程rr22∇E+kE=0k=ωµ0ε0v∇⋅E=0vv令Uxyz是E的任意一个直角分量由于E在x方向上是均匀的∴U(x,y,z)=U(y,z)=Y(y)Z(z)又在y方向由于有金属板作为边界是取驻波解在z方向是无界空间取行波解∴解得通解U(x,y,z)=(Csinky+Dcosky)eikzz1y1yvv∂E由边界条件n×E=0,和=0定解∂nnπi(kzz−ωt)E=Asin(y)ex1b2nπi(kzz−ωt)2ωnπ22E=Acos(y)e且k==()+k,n=0,1,2Ly22zbcbnπi(kzz−ωt)E=Asin(y)ez3bvnπ又由∇⋅E=0得A1独立与A2,A3无关A2=ikzAzb-11- 电动力学习题解答第四章电磁波的传播nπc令kz0得截止频率ωc=b15证明整个谐振腔内的电场能量和磁场能量对时间的平均值总相等v证明在谐振腔中电场E的分布为E=Acoskxsinkyeikzzx1xyikzE=Asinkxcoskyezy2xyikzE=Asinkxsinkyezz3xyviv由H=−∇×E可求得波导管中的磁场为ωµiikzH=−(Ak−iAk)sinkxcoskyezx3y2zxyωµiikzH=−(iAk−Ak)coskxsinkyezy1z3xxyωµiH=−(Ak−Ak)coskxcoskyeikzzz2x1yxyωµ1vvvr由ω=(E⋅D+H⋅B)有谐振腔中21电场能流密度1rvω=E⋅DE211r*v1v*v∴ω=[Re(E⋅D)]=Re(E⋅D)E224ε222222222222=[Acoskxsinkysinkz+Asinkxcoskysinkz+Asinkxsinkycoskz]1xyz2xyz3xyz42)磁场能流密度1vvω=H⋅BB21vv*ω=Re(H⋅B)B412222=[(Ak−Ak)sinkxcoskkycoskz+23yzzxyz4µω2222+(Ak−Ak)coskxsinkycoskz+1z3xxyz2222+(Ak−Ak)coskxcoskysinkz]2x1yxyz-12- 电动力学习题解答第四章电磁波的传播22222有k+k+k=k=ωµε且Ak+Ak+Ak=0xyz1x2Y3zmπnπpπ其中k=,k=,k=,m,n,p=0,1,2Lxyzabcabc是谐振腔的线度不妨令x:0a,y:0b,z:0c于是谐振腔中电场能量对时间的平均值为abcε22222222W=ωdV=(Acoskxsinkysinkz+Asinkxcoskysinkz+E∫E∫∫∫1xyz2xyz40002222+Asinkxsinkycoskz)dxdydz3xyzabcε222=(A+A+A)12332谐振腔中磁场能量的时间平均值为1abc222W=ωdV=⋅[(Ak−Ak)+(Ak−Ak)(Ak−Ak)]B∫B23y2z1z3x2x1y4µω8QAk+Ak+Ak=01x2y3z2222222∴(Ak+Ak+Ak)=Ak+Ak+Ak+2AAkk+2AAkk+2AAkk=01x2y3z1x2y3z12xy13zx23yzabc222222∴W=[(A+A+A)(k+k+k)]B2123xyz32µω2abck222abcε222=(A+A+A)=(A+A+A)212312332µω32∴W=WEB-13- 电动力学习题解答参考第五章电磁波的辐射v1.若把麦克斯韦方程组的所有矢量都分解为无旋的(纵场)和无散的(横场)两部分写出E和vB的这两部分在真空所满足的方程式并证明电场的无旋部分对应于库仑场解在真空中的麦克斯韦方程组是vvv∂Bvv∂E∇×E=−∇×B=µJ+εµ000∂t∂tvρv∇⋅E=,∇⋅B=0ε0如果把此方程组中所有的矢量都分解为无旋的纵场用角标L表示无散的横场用角标T表示vvvvv那么E=E+E且∇×E=0∇⋅E=0LTLTvvvJ=J+JLTvvvvvB=B+B由于∇×B=0即B无源场不存在纵场分量亦是说LTvvvB,则B=BLT代入上面麦氏方程组vv∂B1>∇×E=−∂tvvvvvv∂BT∇×(E+E)=∇×E+∇×E=∇×E=−LTLTT∂tvρvvvvvρ2>∇⋅E=∇⋅(E+E)=∇⋅E+∇⋅E=∇⋅E=εLTLTLε00vvv∂Evvv∂vv3>∇×B=µJ+εµ∇×B=µ(J+J)+εµ(E+E)000T0LT00LT∂t∂tvvv∂Ev∂ETL=(µJ+εµ)+(µJ+εµ0T000L00∂t∂tv若两边同时取散度∇⋅(∇×B)=0Tvv∂ET∇⋅(µJ+εµ)=00T00∂t-1- 电动力学习题解答参考第五章电磁波的辐射vv∂EL∴当且仅当µJ+εµ0时上式方成立0L00∂t综上得麦氏方程的新表示方法vv∂BTvρ∇×E=−∇⋅E=TLε∂t0vvvv∂Ev∂EvTL∇×B=µJ+εµµJ+εµ0B=0T0=T000L00L∂t∂t证明电场的无旋部分对应库仑场vρ电场的无旋部分表达式为∇⋅E=Lε0vρ2引入E=−∇ϕ于是有∇ϕ=−此泊松方程的解即是静止Lε0v电荷在真空中产生的电势分布那么E即对应静止电荷产生的库仑场Lr2.证明在线性各向同性均匀非导电介质中若ρ=0,J=0,则E和B可完全由矢势A决定若取ϕ=0,这时A满足哪两个方程v解在线性各向同性均匀非导电介质中如果令J=0,ρ=0麦氏方程表示为vvv∂Bv∂Dvv∇×E=−;∇×H=∇⋅D=0∇⋅B=0∂t∂tvvvvB其中D=εEH=µvvvv由∇⋅B=0引入矢势A使B=∇×Avvvv则∇⋅B=∇⋅(∇×A)=0故B由矢势A完全决定vvvv∂B把B=∇×A代入∇×E=−;有∂tvvvv∂Av∂Av∂A∇×(E+)=0令E+=−∇ϕ则∇×(E+)=∇×(−∇ϕ)=0∂t∂t∂tvv∂Avv则E=−∂ϕ−故E有标势A完全决定∂t-2- 电动力学习题解答参考第五章电磁波的辐射vvvv∂D如果取ϕ=0有B=∇×A代入方程∇×H=∂tvv∂AvE=−∇⋅D=0∂tvvv∂Dv∂E有1>∇×H=∇×B=εµ∂t∂tvv∂∂A⇒∇×(∇×A)=−εµ()∂t∂tvv∂2A⇒∇×(∇×A)+εµ=02∂tv∂v2>∇⋅D=0(∇⋅A)=0∂tvv1∂ϕ由于取ϕ=0库仑规范∇⋅A=0与洛伦兹规范∇⋅A+=0相同2c∂tv∴由1>2>得A满足的方程有v∇⋅A=0vv∂2A2∇A−εµ=0∂tv3.证明沿z轴方向传播的平面电磁波可用矢势A(ωτ)表示其中τ=t−zA垂直于zc轴方向vv证对于沿z轴传播的任意一平面电磁波E,B可写作vvi(kz−ωt)E=Eee0xvvi(kz−ωt)B=Bee0yvvv满足1E,B均垂直于传播方向ezvvvvv2E,B相互垂直E×B沿k方向vv3E,B同相振幅比为υ真空中为czvv−iω(t−)vi(kz−ωt)ω故不妨取A=Aeec=Aee,k=0x0xc-3- 电动力学习题解答参考第五章电磁波的辐射vv∂Axvvi(kz−ωt)∴B=∇×A=e=ikAee1y0y∂zv∂Avi(kz−ωt)E=−=iωAee20x∂t可见如果令kA=B,ωA=E表达式12可表示的波正是符合条件的平面波0000所以命题得证vvvvikv⋅xv*−ikv⋅xv4.设真空中矢势A(x,t)可用复数傅立叶展开为A(x,t)=∑[ak(t)e+ak(t)e],其中kv*va是a的复共轭kk2vvdak(t)22v1证明a满足谐振子方程+kca(t)=0k2kdtvvv2当选取规范∇⋅A=0,ϕ=0时证明k⋅a=0kvvvv*3把E和B用a和a表示出来kkvvvikv⋅xvv*−ikv⋅xv解1证明QA(x,t)=∑[ak(t)e+ak(t)e]k∴根据傅立叶级数得正交性必有vvvikv⋅xvva(t)=A(x,t)edxk∫22vvdak(t)∂A(x,t)ikv⋅xvv∴=edx12∫2dt∂tvvv1∂2Av2而洛仑兹变换时矢势A满足方程∇A−=−µJ220c∂tvvv1∂2A2在真空中J=0故∇A=22c∂t2vdak(t)ikv⋅xv22vv∴1式化为=e(c∇A)dx2∫dt22v22vvikv⋅xvv而kca(t)=kcA(x,t)edxk∫2vdak(t)22v22vv22vvikv⋅xvv于是+kca(t)=[c∇A(x,t)+kcA(x,t)]edx22k∫dtvvvikv⋅xvv*−ikv⋅xvQA(x,t)=∑[ak(t)e+ak(t)e]k-4- 电动力学习题解答参考第五章电磁波的辐射2vv2vv∴∇A(x,t)=−kA(x,t)∴2式右边的积分式中被积函数为0积分为02vdak(t)22vv∴+kca(t)=0亦即a满足谐振子方程2kkdtv2选取规范∇⋅A=0,ϕ=0于是有vvikv⋅xvv−ikv⋅xvvikv⋅xvv*−ikv⋅xv∇⋅A=∇⋅∑[ak(t)e+ak(t)e]=∑[ak(t)∇⋅e+ak(t)∇⋅e]kkvvikv⋅xvvv*−ikv⋅xv=∑[k⋅ak(t)⋅ie−k⋅ak(t)⋅ie]=0kvv*Qa(t),a(t)是线性无关的正交组kkvvvv*∴要使上式成立仅当k⋅a=k⋅a=0时kkvvv∴故证得当取∇⋅A=0,ϕ=0时k⋅a=0kvvvikv⋅xvv*−ikv⋅xv3已知A(x,t)=∑[ak(t)e+ak(t)e]kvvvvikv⋅xvv*−ikv⋅xv∴B=∇×A=∑[ikak(t)e−ikak(t)e]kv∂Avdav(t)vvdav*(t)vvvkik⋅xk−ik⋅xE=−∇ϕ−=−∑[e+e]取规范∇⋅A=0,ϕ=0)∂tkdtdtv5.设A和ϕ是满足洛伦兹规范的矢势和标势vvvvv1∂Z1引入一矢量函数Z(x,t)赫兹矢量若令ϕ=∇⋅Z证明A=2c∂tvvvv1∂2Zv222若令ρ=−∇⋅P证明Z满足方程∇Z−=−cµP写出在真空中的推220c∂t迟解vvvvv2vv1∂v3证明E和B可通过Z用下列公式表出E=∇×(∇×Z)−cµP,B=∇×Z02c∂tvv1∂ϕ解1证明A与ϕ满足洛仑兹规范故有∇⋅A+=02c∂tvQϕ=−∇⋅Ζ代入洛仑兹规范有vv1∂vv1∂Ζ∇⋅A+⋅(−∇⋅Ζ)=0即∇⋅A=∇⋅()22c∂tc∂t-5- 电动力学习题解答参考第五章电磁波的辐射vv1∂Ζ∴A=2c∂t221∂ϕρ2证明Q标势ϕ在满足洛仑兹规范得条件下有方程∇ϕ−=−22c∂tε0vvv222而ϕ=−∇⋅Ζ故∇ϕ=∇(−∇⋅Ζ)=−∇⋅(∇Ζ)v∂2ϕ∂2v∂2Ζ=(−∇⋅Ζ)=−∇⋅()222∂t∂t∂t代入原方程vv1∂2Ζρ2−[∇⋅(∇Ζ)−∇⋅()]=−22c∂tε0v令ρ=−∇⋅P则上式化为vv1∂2Ζ1v2∇⋅(∇Ζ)−∇⋅()=−∇⋅P22c∂tε0vv1∂2Ζv22即∇Ζ−=−cµP2220c∂tvvv1∂2Av2由于矢势A∇A−=−µJ在真空中的推迟势为220c∂tvvrJ(x′,t−)vvµ0cA(x,t)=∫dV′4πr故可类比得出方程2在真空中的推迟势解为vvr2P(x′,t−)vvcµ0cΖ(x,t)=∫dV′4πrvvv∂Avv1∂Ζ3QE=−∇ϕ−代入ϕ=−∇⋅Ζ,A=有2∂tc∂tvvvv1∂2Ζv1∂2Ζvv22E=∇(∇⋅Ζ)−=∇×(∇×Ζ)+∇Ζ−=∇×(∇×Ζ)−cµP22220c∂tc∂tvv1∂v同理B=∇×A=∇×Ζ2c∂t-6- 电动力学习题解答参考第五章电磁波的辐射vvv2∴E=∇×(∇×Ζ)−cµP0v1∂vB=∇×Ζ2c∂t6.两个质量电荷都相同的粒子相向而行发生碰撞证明电偶极辐射和磁偶极辐射都不会发生证明电偶极矩与磁偶极矩产生的辐射场分别是ikREv=e(&pv&×nv)×nv24πεcR01>由电偶极矩产生的辐射场ikRBv=µ0eiknv×&pv&4πRikREv=−µ0e(m&v&×nv)4πcR2>由磁偶极矩产生的辐射场ikRBv=µ0e(m&v&×nv)×nv24πcR现有两个质量电荷都相同的粒子相向而行发生磁撞在此过程中取两个电荷的连线为x轴于是此系统的电偶极矩是vvvvvp=qx+qx=q(x+x)12122由此可发现&pv&=d[q(xv+xv)]=q(&xv&+&xv&)21212dt&v&v由于两个粒子质量相同电量也相同故当其运动时x=−&x&牛顿第二定律12v即&p&=0于是系统的电偶极矩辐射场为0v又由于此系统的磁偶极矩m=0于是系统的磁偶极矩辐射场为0综上两个质量电荷都相同的粒子同向而行发生磁撞不会发生电偶极辐射和磁偶极辐射7.设有一个球对称的电荷分布以频率ω沿径向做简谐振动求辐射场并对结果给以物理解释z解设球面上均匀分布了总电量为Q的电荷dS2此假设满足题目中的球对称分布于是球面电荷密度与球面半径的关系是yQσ=dS12x4πR取如图相对的两块小面元dS,dS由于两块小面元对应相同的立体角故有相同的面积12-7- 电动力学习题解答参考第五章电磁波的辐射dS=dS12QQ于是∆Q=σdS=dS=dS=σdS=∆Q112122224πR4πR考虑到两电荷元∆Q,∆Q由于是球对称又以相同的频率ω作沿径向的简谐振动12vvv∴p=∆Q⋅R⋅e+∆Q⋅R⋅(−e)=01r1rvvm=I⋅∆S=0故此两电荷元的振动不能产生辐射场根据场的叠加原理整个球对称分布的电荷体系沿径向的简谐振荡是不能产生辐射场的振动辐射场为08.一飞轮半径为R并有电荷均匀分布在其边缘上总电量为Q设此飞轮以恒定角速度ω旋转求辐射场解Q设飞轮边缘的厚度为d,于是边缘上的电荷面密度σ=2πRdvQvQv体系的电偶极矩为p=∫∫⋅d⋅dl⋅x=x⋅dl2πRd2πR2π2πQvv=[sinθ⋅dθ⋅e+cosθ⋅dθ⋅e]=0∫x∫y2π002vvQω2vQωRv体系的此偶极矩m=I⋅∆S=⋅πR⋅e=ezz2π2vv由此得&p&=0m&&=0故辐射场为0v9.利用电荷守恒定律验证A和ϕ的推迟势满足洛伦兹条件证明如右图所示O是坐标原点Q是源点P是场点v于是A与ϕ的推迟势可写作vrvvvvvvµ0J(r′,t′)or−r′A(r,t)=∫rvdV′4πr−r′vV′r′vvvQv1ρ(r′,t′)vr−r′ϕ(r,t)=∫vvdV其中t′=t−4πεvr−r′c0V∂∂因为在空间中有一个固定点有=,故∂t∂t′-8- 电动力学习题解答参考第五章电磁波的辐射dϕ11∂v=∫rvρ(r′,t′)dV′dt4πεr−r′∂t′0V′vvvµ0J(r′,t′)而∇⋅A=∫∇⋅[vv]dV′4πr−r′V′µv1µ1v00=∫J⋅(∇vv)dV′+∫vv∇⋅JdV′*4πr−r′4πr−r′V′V′vv当算符∇作用于r−r′的n次幂时可写作vvnvvn∇r−r′=−∇′r−r′vvvvvr−r′v其中∇′只作用于r′因为J(r′,t′)中的变量t′=t−其中含有r故cvvvv∂J1∂Jvv1∂Jvv∇⋅J=⋅(∇t′)=−⋅(∇r−r′)=⋅(∇′r−r′)∂t′c∂t′c∂t′vvv1∂Jvv另一方面有∇′⋅J=(∇′⋅J)−⋅(∇′r−r′)t′=constc∂t′vvv对此上两式有∇′⋅J=(∇′⋅J)−∇⋅Jt′=constvvv即∇⋅J=(∇′⋅J)−∇′⋅Jt′=const代入*式有wµv1µ1vv00∇⋅A=∫J⋅(∇vv)dV′+∫vv(∇′⋅J)t′=const−∇′⋅J)dV′4πr−r′4πr−r′V′V′µv1µ1v00=∫J⋅(∇vv)dV′−∫vv∇′⋅JdV′+4πr−r′4πr−r′V′V′µ1v0+∫vv(∇′⋅J)t′=const)dV′4πr−r′V′vvµ0J(r′,t)µ01v=−∫∇′⋅[vv]dV′+∫vv(∇′⋅J)t′=constdV′4πr−r′4πr−r′V′V′vvvvJ(r′,t′)J(r′,t′)v因为∫∇′⋅[vv]dV′=∫S′vvdS′r−r′r−r′V′vv只要把V′取得足够大就可以使J(r′,t′)在V′的边界面上处处为零结果上式便为零-9- 电动力学习题解答参考第五章电磁波的辐射vµ1v0于是∇⋅A=∫vv(∇′⋅J)t′=constdV′4πr−r′V′v∂ϕv1∂ϕµ01v∂ρ∴∇⋅A+ε0µ0=∇⋅A+2=∫vv[(∇′⋅J)t′=const+]dV′∂tc∂t4πr−r′∂tV′由电荷守恒定律有v∂ρv(∇′⋅J)+=0式中t′是r′点的局域时间由以上两式有t′=const∂t′v1∂ϕ∇⋅A+=02c∂tv由此可见只要电荷守恒定律成立则推迟势A和ϕ就满足洛仑兹规范v10.半径为R0的均匀永磁体磁化强度为M0求以恒定角速度ω绕通过球心而垂直于vM的轴旋转设Rω<求B在x方向作简谐振荡的分量-10- 电动力学习题解答参考第五章电磁波的辐射vµ0ikR432−iωtvvvB=⋅e⋅πRMωe(e×e)×ex20xrr4πcR323µ0ωR0M0vvvi(kR−ωt)=(e×e)×e⋅e2xrr3cR在y方向的分量Oy23vµ0ωR0M0vvvi(kR−ωt)tB=(e×e)×e⋅ey2yrr3cRvvxexsinθcosφcosθcosφ−sinφeRvv根据e=sinθsinφcosθsinφcosφevyvθecosθ−sinφ0ezφ23vµ0ωR0M0vvi(kR−ωt+φ)得B=(ecosθ+ie)eθφ3cR23vµ0ωR0M0vvi(kR−ωt+φ)同理可得E=(ie−ecosθ)eθφ3cR462vµ0ωR0M02vS=(1+cosθ)e32r18cR11.带电粒子e作半径为a的非相对论性圆周运动回旋频率为ω求远处的辐射电磁场和辐射能流解由题意得右图v本题所研究的系统的磁偶极矩m是一个常量因此不产生电磁辐射但此系统的电偶极矩是一旋转的变化量vvp=eaer同10题的解法把此旋转量分解到xy方向上的两个简谐振荡是vv−iωtvp=eacosωte=eaeexxxπvv−i(ωt+)vp=eacos(ωt−π2)e=eae2eyyy−iωtv=−eaieeyviµkvv.0ikR根据公式B=e(n×p)4πRviµ0kcikRvv.rE=e(n×p)×n4πR-11- 电动力学习题解答参考第五章电磁波的辐射2v..pvvS=sinθn23232πεcR0v.vv..v−iωt2−iωt有p=−iωeaee,p=ωeaeexxxxr.vv..v−iωt2−iωtp=iωeaiee,p=−ωeaieeyyyy分别代入上式可得2vµ0ωeavvi(kR−ωt+φ)B=(ecosθ−ie)eφθ4πcR2vµ0ωeavvi(kR−ωt+φ)E=(ecosθ+ie)eθφ4πR422vµ0ωea2vS=(1+cosθ)e22r32πcRvv12.设有一电矩振幅为p频率为ω的电偶极子距理想导体平面为a/2处p平行于导00体平面设a<<λ求在R>>λ处电磁场及辐射能流zP解由题如图所示设平面xoy式导体平面vR1利用镜像法构造图中的像电偶极子p0Rv−iωtvp0=p0eexR2由图vv−iωtvp"=−p=−peeo00xyvx分别计算它们在场点P处产生的辐射场Bv"p0v..v2−iωt1p=−ωpee00xa..kacosθ2v1ik(R−cosθ)vv−iωp0vvi(kR−ωt)B=e2⋅p×e=−e2⋅⋅e×e⋅d130r3xr4πεcR4πεcR00..v"2−iωtv2p=ωpee00xa..kacosθv1ik(R+cosθ)v"vi2ω2p0vvi(kR−ωt)B=⋅e2⋅p×e=e⋅⋅e×e⋅d230r3xr4πεcR4πεcR00vvv故B=B+B122kacosθkacosθωp0rvi(kR−ωt)i−i=⋅e×e⋅e⋅[e2−e2]3xr4πεcR0-12- 电动力学习题解答参考第五章电磁波的辐射2ikaωp0i(kR−ωt)vv≈e⋅cosθ(−cosθcosφe−sinφe)3φθ4πεcR03i(kR−ωt)iµ0ωp0aev2v=−⋅(cosθsinφe+cosθcosφe)3θφ4πcR3i(kR−ωt)vviµ0ωp0aev2v∴B(R,t)=−⋅(cosθsinφe+cosθcosφe)3θφ4πcR3i(kR−ωt)vvvviµ0ωp0aev2vE(R,t)=cB×e=⋅(cosθsinφe−cosθcosφe)rφθ4πcR622vcv2vµ0ωp0a2242vS=Bn=(cosθsinφ+cosθcosφ)e232r2µ32πcR0vvvi(kx−ωt)13.设有线偏振平面波E=Ee照射到一个绝缘介质球上E在z方向引起介00v质球极化极化矢量P是随时间变化的因而产生辐射设平面波的波长2π远大于球k半径R0求介质球所产生的辐射场和能流解本题相当于电偶极矩v4πε0(ε−ε0)3−iωtvp=REee的辐射00zε+2ε0v..4πε(ε−ε)23−iωtv00∴p=−ωREee00zε+2ε0∴介质球产生的辐射场为v1ikR4πε0(ε−ε0)3−iωtvvB=⋅e⋅REe(−e)×e00zr4πεcRε+2ε0023ωR0E0(ε−ε0)i(kR−ωt)v=−sinθee3φ(ε+2ε)cR023vvvωR0E0(ε−ε0)2vE=cB×e=−sinθer52r2µ(ε+2ε)cR004622v1v2vωR0E0(ε−ε0)2vS=cBe=sinθer52r2µ02µ0(ε+2ε0)cR-13- 电动力学习题参考第六章狭义相对论1证明牛顿定律在伽利略变换下是协变的麦克斯韦方程在伽利略变换下不是协变的证明根据题意不妨取如下两个参考系并取分别固着于两参考系的直角坐标系且令t0时两坐标系对应轴重合计时开始后Σ′系沿Σ系的x轴以速度v作直线运动根据伽利略变换有z’vzvΣΣ′x′=x−vtvry′=yyvy’r′z′=zt′=toxx’o’1牛顿定律在伽利略变换下是协变的vd2xv以牛顿第二定律为例F=m2dtvd&xv&在Σ系下F=m2dtQx′=x−vt,y′=y,z′=z,t′=tvd2[x′+vt,y′,z′]d2xv′r∴F=m=m′=F′22dt′dt′vd2xv′可见在Σ′系中牛顿定律有相同的形式F′==m′2dt′所以牛顿定律在伽利略变换下是协变的2麦克斯韦方程在伽利略变换下不是协变的vv∂B以真空中的麦氏方程∇×E=−为例设有一正电荷q位于O′点并随Σ′系运动∂tvqvv在Σ′中q是静止的故:E′=2er′,B′=04πεr′0rv∂B′于是方程∇′×E′=−成立∂t′vqv将E′=2er′写成直角分量形式;4πεr′0vqx′vy′vE′=[3ex′+3ey′+4πε222222220(x′+y′+z′)(x′+y′+z′)z′v+3ez′](x′2+y′2+z′2)2-1- 电动力学习题参考第六章狭义相对论由伽利略变换关系有在Σ中vqx−vtvyvE={e+e+3x3y4πε222222220[(x−vt)+y+z][(x−vt)+y+z)zv+e3z[(x−vt)2+y2+z2)2vq3v∴∇×E=−[(y−z)e+3x4πε22220[(x−vt)+y+z]vv+(z−x+vt)e+(x−vt−y)e]yzv可见∇×E不恒为零vvv又在Σ系中观察q以速度ve运动故产生电流J=qvexxµqv0于是有磁场B=R是场点到x轴的距离2πRv∂B此时有=0∂tvv∂B于是∇×E≠−∂t故麦克斯韦方程在伽利略变换下不是协变的2设有两根互相平行的尺在各自静止的参考系中的长度均为l它们以相同的速率v相0对于某一参考系运动但运动方向相反且平行于尺子求站在一根尺子上测量另一根尺子的长度′解根据相对论速度交换公式可得Σ系2Z′′′z1vvz2v相对于Σ的速度大小是v1′′Σ1Σ2v2v′=2v1+2c′′o′′′′o1x12x2∴在Σ系中测量Σ系中静长为l的120OX尺子的长度为-2- 电动力学习题参考第六章狭义相对论2v′2vl=l1−代入v′=022cv1+2c2v1−2′′c即得l=l此即是在Σ系中观测到的相对于Σ静止的尺子的长度0212v1+2c3静止长度为l的车厢以速度v相对于地面s运行车厢的后壁以速度u向前推出一00个小球求地面观测者看到小球从后壁到前壁的时间解根据题意取地面为参考系S车厢为参考系S′于是相对于地面参考系S2vu0+v车长l=l1−车速v球速u=02uvc01+2c故在地面参考系S中观察小球在此后由车后壁到车前壁2vuvl1−0l02l0(1+2)cc∆t===u−vu0+vv2−vu1−uv021+0c2c4.一辆以速度v运动的列车上的观察者在经过某一高大建筑物时看见其避雷针上跳起一脉冲电火花电光迅速传播先后照亮了铁路沿线上的两铁塔求列车上观察者看到的两铁塔被电光照亮的时间差设建筑物及两铁塔都在一直线上与列车前进方向一致铁塔到建筑物的地面距离已知都是l0解由题意得右示意图取地面为静止的参考系Σ列车为运动的参考系Σ′取x轴与x′轴平行同向与列车车速方向一致令t=0时刻为列车经过建筑物时并令此处为Σ系与Σ′的原点如图l0在Σ系中光经过t=的时间后同时照亮左右两塔Z(z’)c左cc右但在Σ′系中观察两塔的位置为l0vx′=lv−βvl=(1−)右00v2c1−2cx=−lox=l00xvΣ′o’x’-3- 电动力学习题参考第六章狭义相对论l0vx′=−lv−βvl=−(1+)左00v2c1−2cl0v∴d′=x′−o′=(1−)右右v2c1−2cl0vd′=x′o′=(1+)左左v2c1−2c时间差为d左′d右′l01vv2vl0∆t=−=(1+)−(1−)=ccv2cccv221−c1−22cc5.有一光源S与接收器R相对静止距离为lSR装置浸在均匀无限的液体介质静止折射率n中试对下列三种情况计算光源发出讯号到接收器收到讯号所经历的时间1液体介质相对于SR装置静止2液体沿着SR连线方向以速度v运动3液体垂直于SR连线方向以速度v运动解1液体介质相对于SR装置静止时nl0∆t=1c2液体沿着SR连线方向以速度v运动取固着于介质的参考系Σ′Σ′系沿x轴以速度v运动在Σ′系中测得光速在c各个方向上均是n由速度变换关系得在Σ系中沿介质运动方向的光速c+vnv′=v1+cnv(1+)l0cn∴R接收到讯号的时间为∆t=2c+vn3液体垂直于SR连线方向以速度v运动同2中取相对于S-R装置静止的参考系为Σ系相对于介质静止的系为Σ′系如下建立坐标-4- y电动力学习题参考第六章狭义相对论y’vux′=−vR可见u′=−vxvcu′y2nc2u′=−vty2noxo’sx’∴在Σ系中测得y方向上的速度2222vc2vc2u′1−−v1−−vy2222cncnu===yu′v(−v)⋅v21+x1+v1−ccc22vl1−02∴∆t=c32c2−v2n6.在坐标系Σ中有两个物体都以速度u沿x轴运动在Σ系看来它们一直保持距离l不变今有一观察者以速度v沿x轴运动他看到这两个物体的距离是多少解根据题意Σ′系取固着于观察者上的参考系又取固着于AB两物体的参考系为Σ′′系在Σ中A,B以速度u沿x轴运动相距为l在Σ′′系中AB静止相距为l0有2ul=l01−2cl∴l0=2u1−2c又Σ′系相对于Σ以速度v沿x轴运动Σ′′系相对于Σ系以速度u沿x轴运动由速度合成公式Σ′′系相对于Σ′系以速度u−vv′=沿x轴运动uv1−2c∴在Σ′系中看到两物体相距2v2l1−v′c2l′=l1−=02uvc1−2c7.一把直尺相对于Σ系静止直尺与x轴交角θ今有一观察者以速度v沿x轴运动他看到直尺与x轴交角θ′有何变化-5- 电动力学习题参考第六章狭义相对论解取固着于观察者上的参考系为Σ′在Σ系中l=lcosθl=lsinθxy22′vv在Σ′系中l=l1−=lcosθ1−xx22cc′l=l=lsinθyy′lytgθ∴tgθ′==′2lvx1−2c8.两个惯性系Σ和Σ′中各放置若干时钟同一惯性系的诸时钟同步Σ′相对于Σ以速度′v沿x轴运动设两系原点相遇时t=t=0问处于Σ系中某点xyz处的时钟00与Σ′系中何处时钟相遇时指示的时刻相同读数是多少解根据变换关系得yy’x−vtΣvx′=LL(1)Σ′Q2v1−2Pcy′=yLLLL(2)z′=zLLLL(3)oo’vt−x2xx’ct′=LL(4)2vz1−z’c2设Σ系中P(x,y,z,t)处的时钟与Σ′系中Q(x′,y′,z′,t′)处时钟相遇时指示时间相同22cv∴在4式中有t=t′解得x=t(1−1−)代入1式2vc22cv得x′=−t(1−1−)=−x2vc2xxv相遇时t=t′==(1+1−)22vc2cv(1−1−2vc即为时钟指示的时刻v−29火箭由静止状态加速到v=0.9999c设瞬时惯性系上加速度为v&=20m⋅s问按-6- 电动力学习题参考第六章狭义相对论照静止系的时钟和按火箭内的时钟加速火箭各需要多少时间解1在静止系中加速火箭vv&v令静止系为Σ系瞬时惯性系为Σ′系且其相对于Σ系的速度为u可知v,v,u同向并令此方向为x轴方向由x轴向上的速度合成有v′+uv=v′是火箭相对于Σ′系的速度uv1+2c2dvu3a′dv′∴在Σ系中加速度为a==(1−)2a′=)dtc2uv′dt′3(1+)2c−2本题中a′=20m⋅s而Σ′系相对于火箭瞬时静止∴u=v,v′=02dvv3∴a==a′(1−)22dtc0.9999ctdv∴=a′dt∫2∫v30(1−)202c1000.9999c得t==47.5年a′10一平面镜以速度v自左向右运动一束频率为ω与水平线成θ夹角的平面光波自00左向右入射到镜面上求反射光波的频率ω及反射角θ垂直入射的情况如何解1平面镜水平放置取相对于平面镜静止的参考系为Σ′系取静止系为Σ系并令入射光线在平面xoy内在Σ系中有入射光线k=kcosθ,k=ksinθ,k=0,ω=ωix0iy0izi0由变换关系得Σ′系中的入射光线-7- 电动力学习题参考第六章狭义相对论′vk=ν(kcosθ−ω)ix020ck′=−ksinθiy0′k=0iz′ω=ν(ω−vkcosθ)i00在Σ′系中平面镜静止由反射定律可得反射光线满足′v′k=ν(kcosθ−ω);k=ksinθrx020ry0c′′k=0;ω=ν(ω−vkcosθ)rzr00代入逆变换关系得Σ系中的反射光线满足vvk=ν[ν(kcosθ−ω)+ν(ω−vkcosθ)]=kcosθrx0202000cck=ksinθry0k=0rzvω=ν[vν(kcosθ−ω)+ν(ω−vkcosθ)]=ωr020000cπ∴在Σ系中观察到入射角−θ=反射角ω=ω=ω0ir02π若垂直入射θ=以上结论不变023镜面垂直于运动方向放置同1选择参考系并建立相应坐标系在Σ系中入射光线满足k=−kcosθ,k=−ksinθ,k=0,ω=ωix0iy0izi0由变换关系得Σ′系中的入射光线′vk=ν(−kcosθ−ω)ix020ck′=−ksinθiy0′k=0iz′ω=ν[ω−v(−kcosθ)]=ν(ω+vkcosθ)i0000在Σ′系中平面镜静止由反射定律可得反射光线满足′vv′k=−ν(−kcosθ−ω)=ν(kcosθ+ω);k=−ksinθrx020020ry0cc′′k=0;ω=ν(ω+vkcosθ)rzr00代入逆变换关系得Σ系中的反射光线满足-8- 电动力学习题参考第六章狭义相对论vvk=ν[ν(kcosθ+ω)+ν(ω+vkcosθ)]rx020200cck=−ksinθry0k=0rzvω=ν[vν(kcosθ+ω)+ν(ω+vkcosθ)]r02000cω0v其中k=.并令β=cckrysinθ0∴反射光满足反射角tgθ==2kν[(β+cosθ)+β(1+βcosθ)]rx002反射光频率ω=νω[(1+βcosθ)+β(β+cosθ)]000如果垂直入射θ=0于是Σ系中会观察到θ=θ=00ir22反射光频率ω=νω(1+β)011.在洛仑兹变换中若定义快度y为tanhy=β1证明洛仑兹变换矩阵可写为chy00ishy0100a=µν0010−ishy00chyβ′+β′′2对应的速度合成公式β=可用快度表示为y=y′+y′′1+β′β′′γ00iβγ0100证明1a=µν0010−iβγ00γ-9- 电动力学习题参考第六章狭义相对论1111chy其中γ=====22thy2shy22ω1−β1−()2(chy)−(shy)1−1−()2chyc22x−xx−x22e+ee−eQ(chy)−(shy)=−=122∴γ=chy又βγ=thy⋅chy=shychy00ishy0100∴a=µν0010−ishy00chyβ′+β′′thy′+thy′′2速度合成公式β=可写为thy=1+β′β′′1+thy′thy′′2y′2y′e−1e−1由定义thy′,thy′′=2y′2y′e+1e+12(y′+y′)thy′+thy′′e−1得==th(y′+y′′)+′′′2(y′+y′)1thythye+1∴thy=th(y′+y′′),y=y′+y′′vvvvv12.电偶极子P以速度v作匀速运动求它产生得电磁势和场ϕ,A,E,B0vv解选随动坐标系Σ′P⊥v0vv~v1P⋅Rv0在Σ′系中P产生的电磁势ϕ′=~,A=0034πε0R-10- 电动力学习题参考第六章狭义相对论v~v~vvv13(P0⋅R)RP0v电磁场E′=[~−~],B′=0534πε0RRvi′四维势A=(A,ϕ)由逆变换A=aAµµµννcAxγ00−iβγ0Ay01000得A=0z0010i1ϕiβγ00γϕ′ccvv~γP0⋅RΣ系中电磁势ϕ=γϕ′=~34πεR0vvvβγvvvvA=Ae=ϕ′e=γϕ′e=ϕxxx2x2cccvvvvvvv电磁场EE′,EγE′v×B′)=γE′平行平行⊥⊥⊥rvvrvvvvvvvvvBB=0,B=γ(B′+×E′)=γ(×E′)=×E平行平行⊥e2⊥2⊥2⊥ccc由坐标变换x′=ax得µµννx′γ00iβγxy′0100y=z′0010zict′−iβγ00γictx′=γx−vγt∴y′=yz′=zx′=γxv~取t=0得y′=y∴R=(x′,y′,z′)=(γx,y.,z)z′=z-11- 电动力学习题参考第六章狭义相对论vvvv13.设在参考系Σ内E⊥BΣ′系沿E×B的方向运动问Σ′系应以什么样的速度相对于Σ系运动才能使其中只有电场或只有磁场v解如图Σ′系以v沿x轴方向相对于Σ系运动由电磁场变换公式v′vvvvvvvvE=E0E′γEv×B)=γ(E+v×B)平行平行⊥⊥vrvvvvvvvvvB′=B=0B′=γ(B−×E)=γ(B−×E)平行平行⊥2⊥2ccvvvv令E=0则E+v×B=0⊥v两边同时叉乘B并利用矢量分析公式得vv1vvEEv=(E×B),取模v==v2BBBvvQvcBvvvc2vvv即若E>cB则当v=(E×B)时B′=02E14做匀速运动的点电荷所产生的电场在运动方向发生压缩这时在电荷的运动方向上v电场E与库仑场相比较会发生减弱如何理解这一减弱与变换公式EE′的关系平行平行v解设点电荷e以速度v沿Σ系x轴方向运动选Σ′系为e的随动系ex′在Σ′系中E′为库仑场平行34πεr′0ex′由变换EE′得E=此场在Σ系中并非静电库仑场平行平行平行34πεr′0-12- 电动力学习题参考第六章狭义相对论x′=xγ由坐标变换y′=yz′=z22vexv得E=(1−)=(1−)EE为Σ系中库仑场平行23200c4πεrc0当v≈c时E<cB)内的运动xy规律设粒子初速度为零v解设Σ′系o′−x′y′z′以u沿z轴运动t0时o′,o重合QE>cBvc2vvv∴当u=E×B时在Σ′内B′=02Evvvvvvvvv此时E′E0E′=γ(E+u×B)=γ(E+u×B)平行平行⊥u⊥uvvB2vvu2E2=γ(E−cE)=γE(1−)=u2u2EcγuvvE即E′=γu由21题结果粒子e在Σ′系中的运动轨迹与时间的关系为2mceE′2x′=[1+(t′)−1],y′=0,z′=0eE′mczγu00−iβγuz′x0100x′由洛仑兹变换=0010′得yyictiβγ00γict′uuz=γuz′+βcγut′=utx=x′y=y′=0t=γt′u∴e在互相垂直得均匀电磁场中的运动规律为22mcγueE2c1x=[1+(t)−1],y=0,z=ut,其中u=B,γ=2ueEγmcEu2u1−2c23.已知t0时点电荷q位于原点q静止于y轴(0,y,0)上q以速度v沿x轴匀速1201运动试分别求出qq各自所受的力如何解释两力不是等值反向12解选参考系Σ′固定在粒子q上在Σ′系观察时粒子静止只有静电场电磁场强度1-20- 电动力学习题参考第六章狭义相对论vvex′v为E′=,B′=01314πεr′0v在Σ系中观察q以速度v沿x轴方向运动由速度变换关系得1ex′ex′ez′E=,E=γE=γ1x′31y′31z′34πεr4πεr4πεr000vez′vey′B=0B=−γB=γ1x1y2′31z2′3c4πεrc4πεr00vvvv2exvv×E1∴E=(1−γ)vvB=13122v⋅x22c4πε[(1−β)r+()]0cvvvvq1eyvv×E1在q处E=,B=2112224πε1−βyc00vvvvvqqe12yq受力F=q(E+0×B)=212211224πε1−βy00vvqxv2同理q产生场E=,B=022324πεr0vvqev2y在q处E=−,B=012224πεy00vvvvvqqe12y∴q受力F=q(E+v×B)=−1211224πεy0024.试比较下列两种情况下两个电荷的相互作用力1两个静止电荷q位于y轴上相距v为l2两个电荷都以相同的速度v平行于x轴匀速运动解1此属于静电场情况两电荷之间的静电库仑为2qF=为排斥力24πεl0由上题求得原点处q在yl处产生的电磁场为vvvvqeyvv×E1vE=B==vEe22z4πε1−β2l2cc0yl处q受洛仑兹力为-21- 电动力学习题参考第六章狭义相对论22vvvvvvqvv2vq1−βeyF=q(E+v×B)=qE+vEv×e=q(1−β)E=2z2c4πεl0vq2F<24πεl0v25.频率为ω的光子能量为hω动量为hk碰在静止的电子上试证明1电子不可能吸收光子否则能量和动量守恒定律不能满足2电子可以散射这个光子散射后光子频率ω′比散射前光子频率ω小不同于经典理论中散射光频率不变的结论v证明1设电子可以吸收这个光子反应后它的动量为p反应前光子能量hω电子22422能量mc反应后能量为mc+pceevv由动量守恒hk=p∴hk=p122422能量守恒hω+mc=mc+pc2ee1式代入2式得2242242hω+mc=mc+(hkc)=mc+(hω)eee2∴2hωmc=0显然此式不成立所以电子不可能吸收光子否则能量和动量守e恒定律不能满足v2)电子可散射这个光子散射后的频率为ω′电子的动量变为pvvv由动量守恒定律得hk=hk′+p2222∴p=(hk)+(hk′)−2hkk′cosθ22422由能量守恒定律得hω+mc=mc+pc+hω′ee24222∴h(ω−ω′)=mc+pc−mceeQp>0∴h(ω−ω′)>0即ω>ω′散射后频率降低v26.动量为hk能量为hω的光子撞在静止的电子上散射到与入射方向夹角为θ的方向2h2θ上证明散射光子的频率变换量为ω−ω′=ωω′sin亦即散射光波长2mc20-22- 电动力学习题参考第六章狭义相对论λλ4πh2θ2πm′=+sinλ为散射前光子波长为电子的静止质量mc2k00vv解设碰撞后光子动量变为hk′能量变为hω′电子碰撞后动量为p能量为2224viw=pc+mc四维动量p=(p,ω)0µc由碰撞前后动量守恒得p=pµ1µ2vvvhk=hk′+p,(1)22224hω+m0c=hω′+pc+m0c,(2)2222对1式由余弦定理p=(hk)+(hk′)−2hkk′cosθ222hωhω2ωω′=+−2hcosθ222ccc222242代入2式得hω−hω′=(hω)+(hω′)−2hωω′cosθ+mc−mc00平方整理得2hωω′2θω−ω′=sin2mc202πc2πc4πh2θ代入ω=,ω′=得λ′=λ+sinλλ′mc2027.一个总质量为M的激发原子对所选定的坐标系静止它在跃迁到能量比之低∆w的0v基态时发射一个光子能量为hω动量为hk同时受到光子的反冲因此光子的频∆w∆w∆w率不能正好是ν=而要略小一些证明这个频率ν=(1−)2hh2Mc0v证明设基态原子静止质量为M跃迁后基态原子反冲动量为p12跃迁前四维动量为p=(0,Mc)µ10vv2224跃迁后四维动量为p=(p+hk,hω+pc+Mc)µ21rvp+hk=0,(1)由四维动量守恒22224M0c=hω+pc+M1c,(2)-23- 电动力学习题参考第六章狭义相对论ω2222由1得p=hk=h∴pc=hω3c222422又Mc−Mc=∆w∴Mc=(Mc−∆w)401102222223(4)代入2得(Mc−hω)=hω+(Mc−∆w)002222整理得2Mchω=2Mchν=2Mc∆w−∆w000∆w∆w∴光子频率ν=(1−)2h2Mc028.一个处于基态的原子吸收能量为hν的光子跃迁到激发态基态能量比激发态能量低∆w求光子的频率解设原子基态静止质量为M激发态静止质量为M光子能量为hν=hω动量为10vvhk原子吸收光子后动量为p设原子基态时静止v2吸收前四维动量为p=(hk,Mc+hω)µ11v2224吸收后四维动量为p=(p,pc+Mc)µ20rvp=hk,(1)由四维动量守恒22224M1c+hω=pc+M1c,(2)ω2222由1得p=hk=h得pc=hω3c222422又Mc−Mc=∆w得Mc=(Mc+∆w)401012222223(4)代入2得(Mc+hω)=hω+(Mc+∆w)112222整理得2Mchω=2Mchν=2Mc∆w+∆w111∆w∆w∴光子频率ν=(1+)2h2Mc1-24-'