新编概率论与数理统计 (夏宁茂 秦衍 倪中新 著) 华东理工大学出版社 课后答案 27页

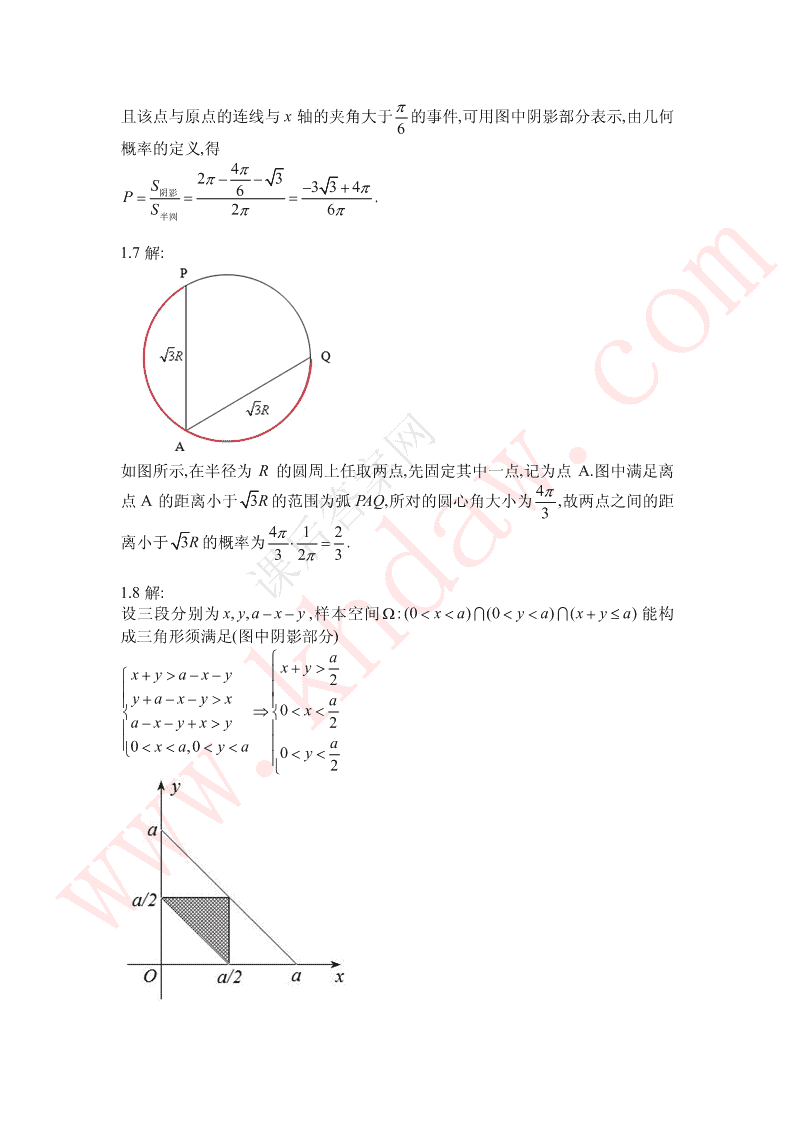
'课后答案网，用心为你服务！大学答案---中学答案---考研答案---考试答案最全最多的课后习题参考答案，尽在课后答案网（www.khdaw.com）！Khdaw团队一直秉承用心为大家服务的宗旨，以关注学生的学习生活为出发点，旨在为广大学生朋友的自主学习提供一个分享和交流的平台。爱校园（www.aixiaoyuan.com）课后答案网（www.khdaw.com）淘答案（www.taodaan.com） 1.1解:(1)Ω={(正,正),(正,反),(反,正),(反,反)},A={(正,正),(反,反)}.(2)Ω={(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5)},A={(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5)}.(3)Ω={(,,)|xyzxyz++=1,,,0}xyz>.1.2解:(1)A={2,4,6},B={3,6}.(2)A={1,3,5}表示“出现奇数点”,B={1,2,4,5}表示“出现的点数不能被3整除”,ABU={2,3,4,6}表示“出现的点数能被2或3整除”,AB={6}表示“出现的点数能被2和3整除”,ABU={1,5}表示“出现的点数不能被2或3整除”.1.3解:(1)ABC.(2)ABC.(3)ABC.(4)ABCUU.(5)ABUUACBC或ABAUUCBC.1.4解:ABCD===≥=={ξ1},{ξξξ1},{2},=={0},互相不相容的事件为:A与C,A与D,B与D,C与D,对立的事件为:B与D.1.5证:由于A与B互为对立事件,故AB=∅=,AUBΩ,因此就有ABU=Ω=,AB∅,所以A与B也互为对立事件.1.6解:2样本空间Ω为半圆{(,)|0xyyx<<4−x},而随机事件A表示点落在半圆区域 π且该点与原点的连线与x轴的夹角大于的事件,可用图中阴影部分表示,由几何6概率的定义,得4π23π−−S阴影6−+334πP===.S26ππ半圆1.7解:如图所示,在半径为R的圆周上任取两点,先固定其中一点,记为点A.图中满足离4π点A的距离小于3R的范围为弧PAQ,所对的圆心角大小为,故两点之间的距3412π离小于3R的概率为⋅=.323π1.8解:设三段分别为x,,yaxy−−,样本空间Ω:(0<⎧xyaxy+>−−⎪2⎪⎪⎪⎪yaxyx+−−>a⎨⎨⇒<<0x⎪⎪axyxy−−+>2⎪⎪⎩0,<<<>,0,0,2p41∫∫dqdp100所以,所求的概率为=.4481.10解:10本书任意放置有10!种方法,指定的3本书放在一起的方法数:○13本书放在一起的方法数:3!,○27本书任意放的方法数:7!,○3剩下的7本书固定好之后,3本书作为一个整体可放的位置有8个,83!7!1××因此,总的方法数为83!7!××,故P==.10!151.11解:2(1)若选取是不放回的,则总方法数为Pn=(1n−),设两张标签分别为i和i+1,则in可取的方法数有n−1,再考虑两张标签可对调顺序,因此方法数为2(n−1),所以2(n−1)2P==.nn(1−)n22(n−1)(2)若选取是放回的,则总方法数为n,有利事件数`同(1),所以P=.2n 1.12解:432CCC2521043该问题为多维超几何分布,故P==.9C2431171.13解:1(1)6个人的生日可从星期一到星期天中任取,故P=.16766(2)6个人的生日可从除星期天外的任何一天中任取,故P=.2671(3)该问题为(1)的对立事件,故P=1−.3671.14解:3总方法数为4.3(1)球的最大个数为1,即每个杯子里至多只有一个球,则方法数为C3!(先从4个杯433!C34子里选3个放球,再把球任意放入这3个杯子里),故P==.1348(2)球的最大个数为2,即有一个杯子里有2个球,另有一个杯子里有1个球,则方法121121CCC4339数为CCC,故P==.433234161(3)球的最大个数为3,即有一个杯子里有3个球,其余三个杯子为空,则方法数为C,41C14故P==.334161.15解:nn只球放入n个盒子的方法数为n,恰有一个空盒子的方法数为:1○1从n个盒子中选取一个空盒子:C,n○2从剩下的n−1个盒子选一个用于放2只球,从n只球中选2只球放入这个盒12子:CC,nn−1○3剩下的n−2只球任意放入剩下的n−2个盒子里:(2n−)!112CCCn(2−)!(1nn−−)(1)!nn−1n故P==.nn−2nn21.16解:210只产品中不放回地取2只的方法数为C.1022C828(1)取出的两只都是正品的方法数为C,故P==.812C451022C21(2)取出的两只都是次品的方法数为C,故P==.222C451011CC1682(3)取出一只是正品,一只是次品,该问题为超几何分布,故P==.32C4510 1.17解:利用PABPAPBPAB()(U=+−)()(),得PABPAPBPAB()=+−()()(U)=pqr+−,PAB()(=∪−=PABPBrq)()−,PABPABPArp()(=∪−=)()−,PAB()1(=−PABU)1=−r.1.18答:45不相等,掷一颗骰子4次至少出现1次6点的概率为1−,而掷两颗骰子24次至4624⎛⎞5少出现1次双6点的概率为1−⎜⎟.4⎝⎠61.19解:设A表示牌号从1到k的车辆,A表示牌号从1到k−1的车辆,且AA⊂,所以抄1221nnkk−−(1)到的最大牌号为k的概率为PAA()−=−PA()PA()=.1212nN1.20解:PABPAPAB()=−−()()=−=0.70.30.4,PAB()1()10=−PAB=−=.40.6. 1.21证:因为PBC()(U=+−=PBPCPBC)()()51ab−≤,又PAB()()()=−=PAPABab−≥0,1结合以上两式得ba≤≤.41.22解:设A=“第i次拨通”,B=“不超过三次拨通”,则iPBPA()=++()(PAA)(PAAA)112123=+PA()(|)()(|)(|)()PAAPA+PAAAPAAPA1211312211111=++=0.3,101010若最后一位是奇数,则PBPA()=++()(PAA)(PAAA)112123=+PA()(|)()(|)(|)()PAAPA+PAAAPAAPA1211312211114134=+×+××=0.6.6453451.23解:设A=“第i次通过考试”,B=“表示通过考试”,则iPB()=+PA()(PAA)122=+PA()(|)()PAAPA12222p3pp=+⋅−=−pp(1).2221.24解:PA()1=−PA()10.3=−=0.7,PABPAPAB()=−=−=()()0.70.50.2,PABPBPAB()=−()()=−=0.40.20.2,PBAB[(U)]PAB()0.2PBAB(|U)====0.25.PAB()1(U−−PAB)10.21.25解:设A=“有i件不合格品”,则i22PAA()CC12410PAA(|)===0.2.211122PA()(CCCC+)1464101.26证:由于PABC[(−=)](PABC)()()()=PAPBPC,PABPC(−=)()()()()PAPBPC,故PABCPABPC[(−=−)]()()即AB−与C相互独立. 1.27解:(1)由于A、B、C两两独立,则满足2PABPAPBx()==()(),2PBC()()(),==PBPCx2PAC()==PAPC()()x,又ABC=∅则PABC()=0,2PABC()−−=PAPABPACPABC()−()−()+()=−≥⇒≤≤x2x00x0.5,故x的最大值为0.5.(2)PABC(UU)=++−−−+PAPBPCPABPBCPACPABC()()()()()()()92⇒=3()3[()]PA−PA⇒PA()=0.25,16而另外的一个解PA()=>0.750.5舍去.1.28解:设A=“第i个零件合格”,则iP(2ξ==)(PAAA)(+PAAA)(+PAAA)123123123⎛⎞11⎛⎞⎛⎞⎛⎞⎛⎞1111111⎛⎞=−×−×+−××−+×−×−⎜⎟11⎜⎟⎜⎟⎜⎟⎜⎟1111⎜⎟⎝⎠23⎝⎠⎝⎠⎝⎠⎝⎠4234234⎝⎠11=.241.29解:设A出现的概率为p,A=“第i次出现A”,则i6541PAAAA()=−=−1(1p)⇒=p.12348131.30解:(1)设S=“系统正常工作”,C=“第i个开关开启”,又开关闭合与否相互独立,iPS()==PCC(U)PC()()(+PC−PCC)1212122=+−=0.960.960.960.9984.(2)当n=3时,PS()==PCC(UUC)PC()()()(+PC+PC−PCC)(−PCC)(−PCC)(+PCCC)12312312132312323=×30.9630.96−×+0.96=0.999936>0.9999.故n=3.1.31解:设A=“甲进i个球”,B=“乙进i个球”,则有iiii33−−iiiiPA()==C(0.7)(0.3),()PBC(0.6)(0.4),i=1,2,3,ii3333iii23−(1)PP(两人进球相等)==∑∑()()AiiPB(C3)(0.42)(0.12)≈0.321.ii==00 (2)ii33−−ijjjPP(甲比乙进球数多)==∑∑()(AijPB)C33(0.7)(0.3)C(0.6)(0.4)≈0.436.03≤<≤ji03≤<≤ji1.32解:设B=“任意取出的零件合格”,A=“由第i台机床加工”,则i21PB()=+=PBAPA(|)()PBAPA(|)()0.97×+0.98×=0.973,112233PAB()PA()−−PAB()130.9813×222PAB(|)===≈0.247.2PB()1−−PB()10.9731.33解:本题符合抽签原理(见例1.2.6),故概率皆为0.1.1.34解:设D=“感染此病”.(1)PD()=++PDAPAPDBPBPDCPC(|)()(|)()(|)()1111111=×+×+×=.6343334PBD()(|)()1PDBPB31×41(2)PBD(|)====.PD()PD()1431.35解:设AAAA,,,分别表示车床、钻床、磨床、刨床,而B表示“需要修理”,利用贝1234叶斯公式,得PABPA()()17915×911PAB(|)===.14173527153721517115×+×+×+×22∑PBAPA(|)()iii=11.36解:设B=“从该器皿中取出一个白球”,A=“器皿中有i个白球”,1,2,...,in=，根i据题意有1i+1PA()=，PBA(|)=；iin+1n+1利用全概率公式和得nn+1in++112PB()==∑∑PBAPA(|)()ii⋅=.ii==10nn+112++(1n)1.37解:设B=“取出两个球都是白球”,A=“从第i个袋中取”,利用全概率公式和贝叶i斯公式,得n+122C411C52⎛⎞n1PB()==∑PBAPA(|)()iin×22×+×=⎜⎟+.i=1CnCnn10++1110+1⎝⎠159 2C15×2PAB()Cn+11n+110PA(|)B===⇒n=10.n+1PB()21⎛⎞n7⎜⎟+n+1159⎝⎠1.38解:设B=“第2次取出3个新球”,A=“从第1次取出i个新球”,利用全概率公式,i得3333ii−CCC99−i3(1)PB()==∑∑PBAPA(|)()ii33⋅≈0.1458.ii==00CC1212PBAPA(|)()533(2)PAB(|)==.3PB()211.39解:属于匹配问题.n⎛⎞(1)令Ai={第i只球恰好放入第i只盒子},则所求得概率为PA⎜⎟Ui,易知有⎝⎠i=1n1(1n−)!PA()ii==,∑PA()1=nn!i=11(2n−)!PAA()==()ij≠ijnn(1−)n!2C1n∑PAA()ij==0≤<≤ijnnn(1−)2!同理可得3C1n∑PAAA()ijk==0≤<<≤ijknnn(1−−)(2n)3!LLLLnC1nPAA()LA==ijnnn!!由概率的一般加法公式我们得到nnk−1⎛⎞(1)−PA⎜⎟Uk=∑.⎝⎠k=1k=1k!nr−k−11(⎛⎞−1)(2)⎜⎟1−∑.rk!!⎝⎠k=11.40解:设A表示“缺陷在第i个过程被检查出”(1in=,2,,)L,()PA=p,ii2(1)PAAA()+=p+(1−=pp)2pp−.112nn−1(2)PAAA(++LL+AA)=p+(1)−+pp+(1)−=pp1(−1)−p.112nn−13(3)PAAA()=−(1p).123 (4)设B表示“元件有缺陷”,则3PBAAAB(+=−+)0.1(1p)0.9.1233(1−×p)0.1(4)P(|)有缺陷通过=,将p=0.5代入,得3(1−×+p)0.10.93(10.5)−×0.1P(有缺陷通过|)==0.0317.3(10.5)−×+0.10.9 2.1解:1572738−(1)组距d==139,我们人为地取d=140,6频率分布表组序分组区间频数频率累积(%)1(737,877]60.20202(877,1017]80.27473(1017,1157]90.30774(1157,1297]40.13905(1297,1437]20.07976(1437,1577]10.03100合计301(2)直方图.2.2解:36.533.7−(1)组距d==0.3110.32≈,9组序分组区间频数频率累积(%)1(33.66,33.98]10.0112(33.98,34.3]60.0663(34.3,34.62]150.15154(34.62,34.94]210.21215(34.94,35.26]270.27276(35.26,35.58]160.16167(35.58,35.9]100.1108(35.9,36.22]10.0119(36.22,36.54]30.033合计1001 (2)直方图.2.3解:(1)第1题:接收频率累积%7370.00%877620.00%1017846.67%1157976.67%1297490.00%1437296.67%15771100.00%其他0100.00% 直方图10120.00%9100.00%8780.00%6560.00%频率频率累积%440.00%3220.00%10.00%73787710171157129714371577其他接收第2题:接收频率累积%33.660.00%33.9811.00%34.367.00%34.621522.00%34.942143.00%35.262770.00%35.581686.00%35.91096.00%36.22197.00%36.543100.00%其他0100.00% 直方图30120.00%25100.00%2080.00%1560.00%频率频率累积%1040.00%520.00%0.00%33.6633.9834.334.6234.9435.2635.5835.936.2236.54其他接收(2)第1题:统计量均值1044.333中位数1034.5众数950极差834标准差182.8891方差33448.44第2题:统计量均值35.043中位数35众数35.2极差2.8标准差0.517619844方差0.2679303032.4解:ξ的分布列为:ξ2345678910111212345654321P363636363636363636363611115151111化简3618129366369121836 12由于Pii(ξ=≥=)0(2,3,?,12),故分布列满足非负性;而∑Pi()1ξ==,则规范性i=2也成立.2.5解:ξ的分布列为:ξ01239393293219P⋅⋅⋅⋅⋅⋅12121112111012111093991化简444220220随机变量ξ分布函数为:⎧0,x<0,⎪34,0≤=−=−=,3313PF(1ξ≥=−−=−=)1(10)1.442.7解:利用规范性,有135737+++=⇒=1c.2481cccc616因此,构成ξ的分布列为:ξ－1012812107P37373737P(1ξ=−)8378P(1ξξ<≠=|0)==.1(0−=−Pξ)11237252.8解:首先,必须满足规范性,故+∞52225241(==∫∫ϕxdx)cxxdx(2)−=cc⇒=,−∞024255242而当0<=∫(21+=x)dx.⎝⎠6161082.13解:5Exξ==∑iip1.9.i=02.14解:ξ的分布列为:ξ1234能被除尽的整数12,3,5,74,96,8,101213P1055104所以,Exξ==∑iip2.7.i=12.15解:ξ的分布列为:ξ12?n−1n00pqn0−2pqqnn00−1+Pppq?其中,1qp=−,所以,Eξ=⋅+⋅++−⋅12ppq?(1n)pqnn00−−21+npq(+qn0)00⎛⎞qq−n0+1′=+++p(12qn?qnnn00−1)+=qp⎜⎟+nqn0.000⎝⎠1−q11−−qpnn00(1−)==.1−qp2.16解:由于ξ∼B(10,0.4),因此Eξ==np4,Dξ==npq2.4,222故EDEξξξ=+()=+=2.4418.4.2.17解:Eξ=−×(2)0.400.320.3+×+×=−0.2,2222Eξ=−×+×+×(2)0.400.320.3=2.8, 2E(ξ+=+=2)2.824.8,222DEEξξξ=−=−()2.8(0.2)−=2.76. 2.18解:(1)利用规范性,有+∞+∞2+∞+∞⎧⎫x222−−xx22σσ222−x222σ21(==−=ptdt)Axexp⎨⎬dx()−Aσede()=()−Aσσe=A∫∫−∞002σ2∫0⎩⎭1⇒=A.2σ(2)22+∞xx⎧⎫+∞−x222σEdξ=−exp⎨⎬x=−xd(e)∫∫00σσ222⎩⎭⎡⎤22+∞+∞22−−xx22σσ=−⎢⎥⎣⎦xe+∫edx002注意到积分号下的函数是N(0,σ)的密度函数,故利用密度的规范性,得21πσπ+∞−x222σEeξ==∫dxσ.22−∞2πσ2π⎛⎞π+∞xx⎧⎫−x222σ+∞−4Pd⎜⎟⎜⎟ξσ>=∫π22exp⎨⎬−=x−eπ=e.22σσσσ⎝⎠2⎩⎭2(3)+∞32+∞+∞+∞22xx⎧⎫−−xx222σσ⎡2222−x222σ⎤Edξ=−exp⎨⎬x=−xd(e)=−+xe2xedx∫∫00σσ222⎢⎣0∫0⎥⎦⎩⎭22+∞22−xσ2=−(2)σσe=2,02⎛⎞ππ⎛⎞2222DEEξ=−=−ξξσ()2⎜⎟σ=−⎜⎟2σ.⎜⎟⎝⎠22⎝⎠2.19解:设误差为ξ(单位:度)且ξ∼−U(0.5,0.5),故2[0.5(0.5)]−−160′EDξσξ===0,===17.3′.1212122.20解:+∞π22x2Exξ==∫∫p()xdxcosxdx,由于被积函数为奇函数,故Eξ=0,−∞−π2π2222π221x2πDEEEξξξξ=−==()∫cosxdx=−.−π2π1222.21解:1显然TE∼(0.02),故ET()==50.0.022.22解:(1)Eξ=×+×+×+×=100.4110.3120.2130.111. (2)EEη=−[50(13ξ)]50(1311)100=−=.(3)Eξ=×+×+×=100.5110.4120.110.6,EEη=−[50(13ξ)]50(1310.6)120=−=,增加利润∆=−=12010020.2.23解:ππ11x⎛⎞1设A=“观察值大于”,PA()=∫cosdx=,而η∼B⎜⎟4,,所以3π3222⎝⎠21Enη==×=p42.22.24解:34π⎛⎞ξ设球的直径长为ξ,且ξ∼Uab[,],球的体积为η,与直径ξ的关系为η=⎜⎟,那32⎝⎠33224(πξπ⎛⎞3πbxπabab++)()么,EEηξ=⋅⎜⎟=⋅=E∫dx=.326⎝⎠6aba−242.25解:由于弧长服从均匀分布的,故圆心角θ也服从均匀分布,即θ∼U[0,2]π,设横坐标为ξ,满足ξ=Rcosθ,所以2πERξθθ=⋅E(cos)=R∫cosdθ=0,022πR22222DERξξ==E(cosθ)=R∫cosθdθ=.022.26解:22DD(13)−==ξξξξ99[E−(E)]=−=9(54)9.2.27证:因为ab≤≤ξ,所以aEb≤≤ξ.又因为ab−+++abababba−=−ab≤−ξ≤−=22222ab+ba−⇒−ξ≤,22222⎛ab+−−⎞⎛⎞⎛⎞baba利用性质2.4.4，有DEξξ≤−⎜⎟⎜⎟⎜⎟≤E≤.⎝222⎠⎝⎠⎝⎠2.28解:设白细胞数为ξ,利用切比雪夫不等式,有27008PP(5200<<ξξ9400)=(−7300<2100)1=−P(ξ−7300≥2100)1≥−=,2210098所以下界为.9 2.29证:x1+∞Eξ因为P(ξ≥=a)∫∫pxdx()≤pxdx()≤∫xpxdx()=,xa≥≥xaaa−∞aEξ所以Pa()ξ<≥−1.a2.30证:gx()+∞gx()Eg(())ξP(ξε>=)dFx()≤dFx()≤dFx()=.∫∫xx>>εεξξξ∫−∞ggg()ε()εε()2.31解:⎛⎞2设5个人中能活30年的人数为ξ,且ξ∼B⎜⎟5,.⎝⎠35⎛⎞232(1)P(5ξ==)⎜⎟=.⎝⎠32435ii5−i⎛⎞⎛⎞21808032192(2)PC(3ξ≥=)∑5⎜⎟⎜⎟=++=.i=3⎝⎠⎝⎠33243243243243232⎛⎞⎛⎞2140(3)PC(2ξ==)⎜⎟⎜⎟=.5⎝⎠⎝⎠332435⎛⎞1242(4)PP(1)1(0)1ξξ≥=−==−⎜⎟=.⎝⎠32432.32解:⎛⎞111212⎛⎞1Pp⎜⎟ξ≤=∫∫()xdx=2xdx=,于是η∼B⎜⎟3,,所以⎝⎠24−∞0⎝⎠422⎛⎞⎛⎞139PC(2η==)⎜⎟⎜⎟=.3⎝⎠⎝⎠44642.33解:因为ξ∼B(,)np,所以⎧⎧Enξ==p2.4,n=6,⎨⎨⇒⎩⎩Dξ==npq1.44,p=0.4.2.34解:282因为ξ∼B(,)np,所以PP(1)1(0)1(1)ξξ≥=−==−−=p,得p=,934⎛⎞280故PP(1)1(0)11ηη≥=−==−−=⎜⎟.⎝⎠381 2.35解:设ξ=“作出正确决策的人数”,则ξ∼B(,)np,55ii5543−i当n=5时,PPiC15==∑∑(ξ)=−=ppppp(1)6−+1510,ii==3322333232当n=3时,PP==+==(2ξξ)(3P)CppCpp(1)−+(1)23−=−+pp,255543321要使PP>,即61pppppp−+>51023−+⇒>.1222.36解:设ξ=“λt时间内汽车数”,则ξ∼Pt()λ,kt−λ()λte那么Pk()ξ==(0k=,1,2,"),k!0−λ()λe由已知,得P(0ξλ==)=⇒=0.2ln5,0!所以02−−λ12λ(2)λλee(2)PP(1ξξ>=)1(0−=−==)(1Pξ)1−−0!1!−−22λλ242ln5−=−1(ee−2λ)=.252.37解:设ξ=“每秒钟呼唤次数”,则ξ∼P(4),84−4e(1)P(ξ==8)≈0.0298.8!8k−44e(2)P(ξ>=−8)1∑≈0.0214.k=0k!2.38解:设η=“一年内恰有r位司机丧生”,那么+∞+∞n−λrrnr−λePPn()ηη==∑∑(|ξξ)(⋅P=nC)=npqnr==nrn!+∞rnrn−−λpqλe=−∑(令nrk=)nr=rnr!(−)!rk−−λλ+∞rλqr()λλpe()()qλλpee()p−λp==∑=e.rkrr!!!!k=02.39解:+∞1Ekξ=⋅∑k+1k=02+∞+∞′′11−k⎛⎞1因为∑∑kx⋅=k+−11−()=−⎜⎟=2,kk==00xx⎝⎠1(−−x1) 1所以Eξ==1.2(21)−2.40解:他7点ξ分到达车站,能被带到甲地,则他到达车站的时间需满足4022ξ∈(5,15](20,30](35,45](50,60]∪∪∪,所以P==,同理可得P=.1260332.41解:23111先解ξξ−+≥⇒≤0ξ或ξ≥,又01<ξ<,4842⎛⎞231⎛1⎞⎛1⎞113所以,PP⎜⎟ξξ−+≥=<≤+≤<=+=00⎜ξ⎟P⎜ξ1⎟.⎝⎠48⎝4⎠⎝2⎠2442.42解:2211x602EW()(2)2==EI∫dx=.9232.43解:(1){TtNt>=}{()=0}即在两次故障之间,设备发生故障的次数为0,又08−t(8)te−t8−t8⎛⎞1PNt(()0)===e,所以PTt()≤=−>=−1()PTt1e,即TE∼⎜⎟.0!⎝⎠8−1(2)利用指数分布的无记忆性,有PT(1>>6|8T)(8=>PT)=e.2.44解:设发射管的寿命为ξ.901−−180t12(1)Pe(ξ<=90)∫dt=1−≈e0.393.0180+∞1−−180t2(2)Pe(ξ>=360)∫dt=≈e0.135.3601803601−−180t12−2(3)Pe(90<<ξ360)=∫dt=e−≈e0.472.901802.45解:⎛⎞⎛⎞104−−24−(1)P(2−<≤ξ10)=Φ⎜⎟⎜⎟−Φ=Φ−=×2(2)120.977210.9544−=.⎝⎠⎝⎠33⎛⎞⎛34−1⎞(2)PP(ξξ>=−≤=−3)1(3)1Φ⎜⎟⎜=Φ=⎟0.6306.⎝⎠⎝33⎠⎛⎞dd−−44⎛⎞(3)Pd(ξξ>≥⇒≤=)0.9Pd()Φ⎜⎟≤⇒0.1Φ⎜⎟≥0.9,查附表5,得⎝⎠33⎝⎠4−d≥⇒1.2816d≤0.1552.32.46解: 设车门的高度为x,则要求⎛⎞x−170Px(ξξ≥≤⇒<=)0.01Px()Φ⎜⎟≥0.99,查附表5,得⎝⎠6x−170≥⇒2.3263x≥183.96.62.47解:⎛⎞9672−设外语成绩为ξ,那么P(ξ>=⇒96)2.3%Φ⎜⎟=0.977,查附表5,得⎝⎠σ9672−=⇒1.9954σ≈12.028,而σ⎛⎞8472−−⎛⎞6072P(60<<=Φξ84)⎜⎟−Φ⎜⎟=Φ2()0.9977−=×120.840810.6816.−=⎝⎠12.028⎝⎠12.0282.48解:⎡⎤⎛⎞19.6先求出PPP(ξξξ>=>+<19.6)(19.6)(−=−19.6)21⎢⎥Φ⎜⎟=0.05.⎣⎦⎝⎠10设100次独立重复测量中,测量误差的绝对值大于19.6的次数为η,显然满足η∼B(100,0.05),100199PP(ηη≥=−=−==−2)1(0)P(η1)1(0.95)−C(0.05)(0.95)≈0.9629.1002.49解:µµ−−xx−−()2xxµσ22+∞µ−−()2µσ22Eeξµ−=∫∫dx+edx,作变换x−=µt,得−∞22πσµπσ+∞2+∞t−−tt2222σσ22σ22Eeξµ−=2∫dt=−e=σ.022πσπσ0π2.50解:(1)设进货量为a,η=“获利”,有满足如下关系式⎧500aa+−≤300(ξξ),a≤30,η=⎨⎩500ξξξ−−≤100(aa),10<,所以a1130Exη=−∫∫[500100(a−x)]⋅dxa++[500300(x−a)]⋅dx1020a2011a30=−∫∫(600x100)adt++(200a300)xdx201020a2=−75aa+3500+5250≥9280,解得21≤≤a26.(2)(Eaη)′=−150+3500=⇒=0a23.33,由于22−×75(23)+3500235250×+>−×75(24)+3500245250×+,故a=23.2.51解: 设η=“获利”,有满足如下关系式⎧100,ξ>1,η=⎨⎩−≤200,0ξ≤1,11−200−−tt44+∞100−4所以Eeη=+=∫∫dxe300e−200≈33.64.0144'