高等数学课后习题答案--第一章.pdf 15页

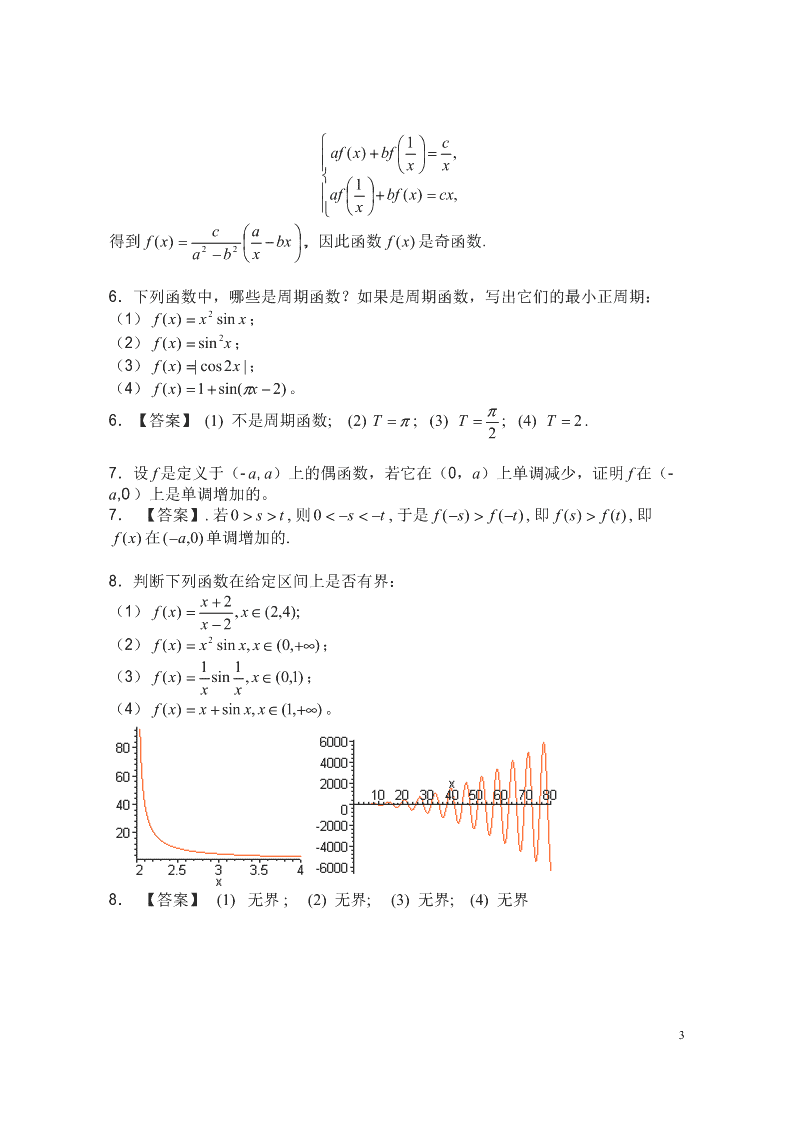
'《高等数学》习题参考资料第一篇一元函数微积分第一章极限与连续§1函数习题1.确定下列初等函数的定义域：x+12(1)f(x)=；(2)f(x)=x−4；2x−x−2x−1lg(5−x)(3)f(x)=arcsin；(4)f(x)=；22x2(5)f(x)=lg(5x−x)−lg4；(6)f(x)=sinx−cosx。1．【答案】(1)D:={x|x∈(−∞,−1)∪(−1,2)∪(2,+∞)}(2)D:={x|x∈(−∞,−2]∪[2,+∞)}(3)D:;={x|x∈[−1,3]}(4)D:={x|x∈(−∞,0)∪(0,5)}(5)D:={x|x∈[1,4]}+∞15(6)D:=x|x∈U2k+π,2k+π.k=−∞442.作出下列函数的图象：（1）f(x)=sinx−|sinx|；(2)f(x)=2−|x−1|；21−x,|x|≤1,（3）f(x)=x−1,1s>t,则0<−s<−t,于是f(−s)>f(−t),即f(s)>f(t),即f(x)在(−a,0)单调增加的.8．判断下列函数在给定区间上是否有界：x+2（1）f(x)=,x∈(2,4);x−22（2）f(x)=xsinx,x∈(0,+∞)；11（3）f(x)=sin,x∈(0,1)；xx（4）f(x)=x+sinx,x∈(1,+∞)。8．【答案】(1)无界;(2)无界;(3)无界;(4)无界3 2x9．设f(x)=x,g(x)=2,求fog,gof,fof,gog。2x2xx429．【答案】fog=2;gof=2;fof=x;gog=210．下列函数分别是由哪几个较简单的函数复合而成：（1）f(x)=3x−5；（2）f(x)=lgx；2（3）f(x)=sin(lg(x+1)).10.【答案】（1）f=u，u=3x−5;(2)f=uu=lgv,v=x2(3)f=sinuu=lgv,v=x+1.11．求下列函数的反函数，并指出反函数的定义域：（1）f(x)=2sin3x;xa（2）f(x)=;xa+1x−xa−a（3）f(x)=;22（4）f(x)=4arcsin1−x,D(f)=[0,1].1xx11.【答案】(1)y=arcsin,D:−2≤x≤2;(2)y=log,)D=(0,1;(3)a321−x22xy=log(x+x+1),)D=(−∞,+∞;(4)y=cos,]D:=[0,2π.a4§2数列的极限习题1111.证明：数列1,,,L,,L为无穷小量。23n4 1111.【答案】对于任意给定的ε>0,<ε,解得n>,于是取N=,当22nεε111n>N时,成立<ε,因此lim=0,即是无穷小量.nn→∞nn2.证明：若数列{a}收敛于a，则数列{|a|}收敛于|a|。并问其逆命题是否成nn立？2.【答案】若对任意给定的ε>0，总存在整数N>0，当n>N时，都有|a−a|<ε.对于任意给定的ε>0,由于|a|−|a|≤a−a,于是当n>N时，nnnn都有|a|−|a|<ε,因此{|a|}收敛于|a|.但反之不一定成立,例如a=(−1).nnn3.求下列极限：2223n−1nn（1）lim;（2）lim−;n→∞n2+nn→∞n−1n+1nn(−2)+3nsin(n!)（3）lim;（4）lim;nn2n→∞(−1)+3n→∞n+12n1+a+a+L+a（5）lim（|a|<1,|b|<1）;2nn→∞1+b+b+L+b12n−1（6）lim++L+;222n→∞nnn111（7）lim++L+;n→∞1⋅22⋅3n(n+1)n−na−a（8）lim(a＞0).n−nn→∞a+an3【答案】(1)3;(2)1;(3)分子分母同除以3,极限为1;(4)利用|sin(n!)|有界,1−b1111极限为0;(5);(6);(7)利用=−,极限为1;1−a2n(n+1)nn+1−1,014.下列命题是否正确？正确的请给予证明，不正确的请举出反例。（1）若{a}收敛，{b}发散，则{a+b}与{ab}均发散；nnnnnn（2）若{a}，{b}均发散，则{a+b}，{ab}也均发散。nnnnnn4.【答案】(1){a+b}发散,用反证法证明;{a}不收敛于零时{ab}发散,用nnnnn1n反证法证明,当{a}收敛于零时,不一定.例a=,b=(−1),则{ab}收敛,但nnnnnn5 n2b=(−1)n时,}{ab发散.(2)不一定;nnn132n−115.设a=⋅L，证明a＜,并求出lima。nnn242n2n+1n→∞5.【提示】22221⋅3⋅L⋅(2n−1)(2n+1)1⋅33⋅5(2n−1)(2n+1)11a==L2=u,设u>u21nn−1成立,则uu=+2>2+=uu也成立,因此数列是单调增加的.其次nn+1nn−1证明它有上界.仍用归纳法来证明.对于u=2<2+1,设对于n成立1u<2+1，则n2uu=+<++<++=22212221(21)+=+21,nn+1因此由归纳假设可知，对一切n,有u<21+.这样数列{u}有上界.因此nn数列收敛.注意,在此题有界性的证明中,归纳假设的界不是唯一的,可以假设an)11111(1)|a−a|≤++L+≤<ε,只要n>log;mnnn+1mn22222ε1111111(2)|a−a|≤++L+<−<<ε,只要n>;mnn(n+1)(n+1)(n+2)m(m−1)nmnε111111(3)|a−a|=++L+≤++L+mn222222(n+1)(n+2)m(n+1)(n+1)(n+1)n11=<<ε,只要n>.2(n+1)nε§3函数的极限习题1.验证下列极限：1−2（1）lim1+x=2;（2）limex=0。x→3x→0|x−3||x−3|1.【解】（1）对于任意给定的ε>0,1+x−2=≤<ε,取x+1+22δ=min{1,2ε},则当x适合不等式0<|x−3|<δ时，1+x−2<ε，因此limx+1=2.x→3−1（2）假定0<ε<1，取δ=min{0.5,−(lnε)}.则当x适合不等式0<|x|<δ11−−22时，ex<ε，因此.limex=0.x→02.设limf(x)=A＞0，证明limf(x)=A。x→ax→a2【证明】由于limf(x)=A>0,则对于任意给定的ε>0,存在δ>0,当1x→a0<|x−x|<δ时,|f(x)−A|<ε,存在δ>0,当0<|x−x|<δ01202A时,f(x)>>0,取δ=min{δ,δ},则当x适合不等式0<|x−x|<δ时,12027 |f(x)−A|1εf(x)−A=≤|f(x)−f(x)|≤,0|f(x)+A|AA因此成立limf(x)=A.x→x03.求极限：2nnx−4x−a（1）lim;（2）lim（n是正整数）;2x→2x−3x+2x→ax−a111(1+x)(1+2x)(1+3x)−1（3）lim(−);（4）lim;h→0x+hxhx→0x2n12x+x+L+x−n（5）lim(−);（6）lim。2x→11−x1−xx→1x−1n11213【答案】(1)4;(2)na;(3)−;(4)6;(5)lim−=−;22xx→111−−xx22n2n(6)利用x+x+L+x−n=(x−1)+(x−1)+L+(x−1),x+x2+L+xn−nnxi−1ni−1nnn(1+)k=∑=∑∑x,极限为∑i=;.x−1i=1x−1i=1k=0i=124.求极限：sinmx1−cos2x（1）lim;（2）lim;x→0sinnxx→0xsin2xcos(x+h)−cosxcosmx−cosnx（3）lim;（4）lim;2h→0hx→0xnxπ（5）lim2sin;（6）lim(x−)tanx;n→∞2nπ2x→2sin3xπ（7）lim;（8）limtan2x⋅tan(−x).x→πtan5xx→π4422mnm−4【答案】(1),(2)1;(3)−sinx;(4);n231(5)x;(6)–1;(7);(8).525.讨论函数1,x∈(0,1],2x2f(x)=x,x∈(1,2],2x,x∈(2,3)在x=0,1,2三个点的单侧极限。8 15.【答案】limf(x)=+∞，limf(x)=，limf(x)=1，limf(x)=4，x→0+0x→1−02x→1+0x→2−0limf(x)=4.x→2+0116.讨论f(x)=−在各整数点处的单侧极限。x[x]116.【解】limf(x)=lim−=0，n≠0，x→n+0x→n+0xn111limf(x)=lim−=,n≠0,1.x→n−0x→n−0xn−1n(n−1)7.求极限：2x415x（1）lim1+；（2）lim(1−)；x→∞xx→∞xxx3−2xx（3）lim（)；（4）lim().x→∞1+xx→∞2−2x1−7.【答案】(1)e8;(2)e−5;(3)e−1;(4)e2.2x+18.求曲线y=的渐近线.x+18.【答案】x=−1,y=x−1.29.求曲线y=x−x+1的渐近线。119.【答案】y=x−,y=−x+.如下图.229 2x10.求曲线y=的渐近线。2x+x−210【解】0x=−2,x=1,y=.§4连续函数习题1．下述命题是否正确，请对正确的给予证明，并对错误的举出反例：（1）设函数f在x=x连续，则|f|在x=x也连续；00（2）设|f|在x=x连续，则f在x=x也连续；0010 （3）设f在x=x连续，g在x=x间断，则f+g在x=x间断；000（4）设f和g在x=x都间断，则f+g在x=x一定间断。001.【答案】(1)正确;利用|x|−|x|≤|x−x|由极限定义证明.001x>0(2)不正确;例f(x)=,在x=0.−1x≤0(3)正确;反证法,不然g=(f+g)−f应该连续.1x>01x<0(4)不正确.例f(x)=,g(x)=,在x=0.−1x≤0−1x≥02．确定下列函数的间断点及其类型：4x+1（1）f(x)=;（2）f(x)=;32(x+1)x+1x1−x−1n（3）f(x)=(1-e);（4）f(x)=sgn(sin);x1（5）f(x)=[x]+[-x];（6）f(x)=(1+2x)x.2.(1)x=3无穷间断点;(2)在R上的连续函数;(3)x=0无穷间断点,x=1跳跃间断点(如图);n(4)【答案】x=,k=±1,±2,L跳跃间断kπ点,x=0间断点.(5)x=n6樱桃沟把5间断a点;(6)x=0可去间断点.注意:x的定义域1x>0,因此本函数的定义域x>−,因此不考21虑点x=−.211 3．如果limf(x)＞0，limg(x)也存在。证明x→x0x→x0limg(x)limf(x)g(x)=[limf(x)]x→x0.x→x0x→x0xg(x)g(x)lnf(x)3．【答案】利用y=e及y=lnx的连续性，f(x)=e，limg(x)lnf(x)limg(x)limlnf(x)limg(x)lnlimf(x)limf(x)g(x)=limf(x)g(x)=ex→x0=ex→x0x→x0=ex→x0x→x0x→x0x→x0limg(x)x→x0=limf(x)x→x04．利用上题结果，求极限：nπ11x（1）limtan(+),（2）lim(1+).2n→∞4nx→∞x24.【答案】(1)e;(2)1.5．求极限：331+x−2x−2（1）lim;（2）lim;x→3x−3x→2x−22x+x+122（3）lim;（4）lim(x+1−x−1);x→∞33x→∞x+222cotx（5）lim(x+2x−x−2x);（6）lim(1+sinx);x→−∞x→0x+ax+b(x+a)(x+b)（7）limx[ln(x−2)−lnx];（8）lim;2x+a+bx→+∞x→∞(x+a+b)πcotx11x（9）lim[tan(−x)];（10）lim(sin+cos).x→04x→∞xx1135.【答案】(1);(2)2;(3)1;(4)0;(5)−2;(6)e;46−(a+b)−2(7)−2;(8)e;(9)e;(10)e.x1111(10)的计算过程:limsin+cos=lim()sint+costt=lim()cost(1+tant)tx→∞xxt→0t→01111tt2t=lim()costt⋅lim()1+tantt,lim(cost)=lim(1−2sin)=0,t→0t→0t→0t→0211tant⋅lim(1+tant)t=lim(1+tant)tantt=e,t→0t→0x11于是limsin+cos=e.x→∞xx12 6．利用等价无穷小替代的方法计算：x[(1+x)−1]lncosx（1）lim;4x→0xα+β1−sinx（2）lim，其中α>0,β>0（提示：令sinx=1−t)。παβx→(1−sinx)(1−sinx)21xxln(1+x)26.【答案】(1)−;(1+x)−1=e−1~xln(1+x)~x,2142x−x2xx[()1+x−1]lncosx21ln(cosx)=ln1−2sin~−lim=lim=−4422x→0xx→0x2α+βππ(2).sinx=cos−x，记−x=t，于是sinx=cost,αβ22α+βα+β1−sinx1−costklim=lim，而1−cosxπαβt→0αβx→()1−sinx()1−sinx()1−cost()1−cost2α+β2kα+βt()2k21−cost2α+β=1−1−sint2~t，于是lim=lim=2t→0()1−cosαt()1−cosβtt→0αβαβ22tt227．当x→0时，用x的幂函数表示下列函数的等价无穷小量：23523（1）4x+6x−x;（2）x+x;3（3）1+2x−1+3x;（4）ln(1+x)−ln(1−x);（5）xsin;x（6）1+tanx−1+sinx.17.【答案】(1)4x2;(2)x3;1233(3)x;事实上，1+2x−1+3x=(1+2x−1)−(1+3x−1)22x3x23=−=x−1+2x+13()1+3x2+31+3x+11+2x+13()1+3x2+31+3x+123()1+3x2+31+3x+1−3()1+2x+1=x3()1+3x2+31+3x+1()1+2x+123()1+3x2−1+31+3x−1−3()1+2x−1=x，3()1+3x2+31+3x+1()1+2x+113 23()1+3x2−1+()31+3x−1−3()1+2x−1而limx→0x23()1+3x2−1+2()31+3x−1()31+2x−1=lim−lim=3x→0xx→0x于是23()1+3x2−1+31+3x−1−3()1+2x−131+2x−1+3x2×3lim=lim2==1，x→012x→0x3()1+3x2+31+3x+1()1+2x+16x2312因此1+2x−1+3x~x21+x2x2x(4)ln(1+x)−ln(1−x)=ln=ln1+~~2x;(5)|x|;1−x1−x1−x1+tanx−1−sinx(6)1+tanx−1+sinx=1+tanx+1+sinx1sinx−1tanx−sinxcosxsinx(1−cosx)===1+tanx+1+sinx1+tanx+1+sinx(1+tanx+1+sinx)cosx2xsinx⋅2sin213=~x(1+tanx+1+sinx)cosx48．设f在(−∞,+∞)上连续，且limf(x)=A，试证明f在(−∞,+∞)上有界。x→∞8.【答案】本题给出了判别函数在(−∞,+∞)上有界的一个准则,其证明需运用极限的分析定义.因为limf(x)=A,取ε=1,则存在X>0,当|x|>X时,0x→∞|f(x)−A|<ε=1,即A−10,使|f(x)|