- 3.70 MB
- 2022-04-22 11:28:26 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'机械原理课后习题参考答案机械原理课程组编武汉科技大学机械自动化学院
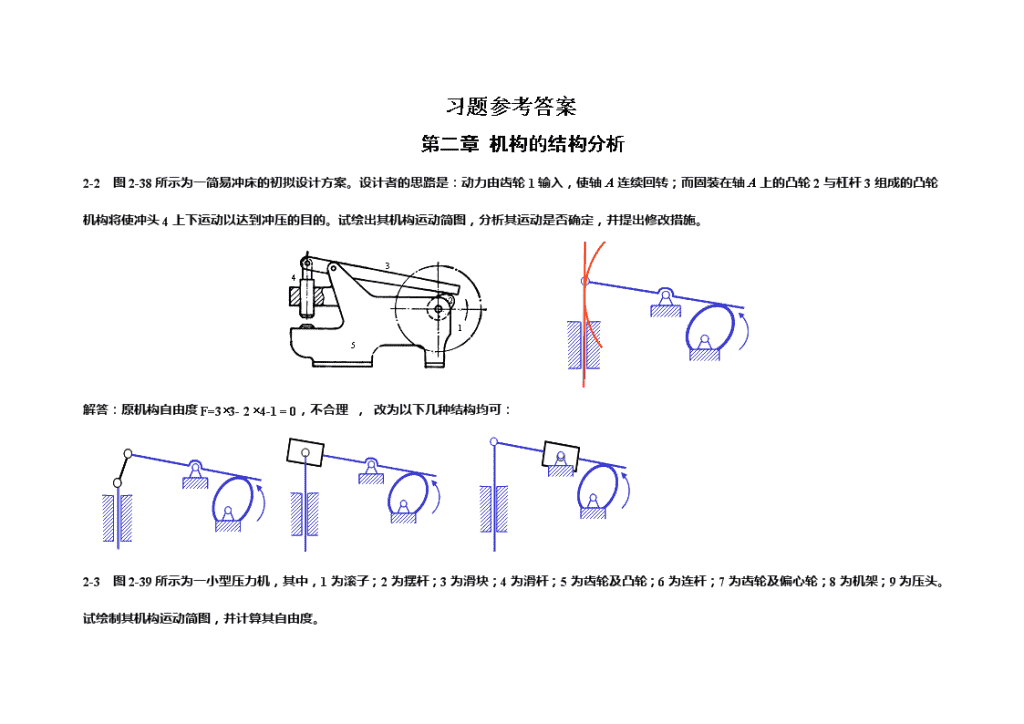
习题参考答案第二章机构的结构分析2-2图2-38所示为一简易冲床的初拟设计方案。设计者的思路是:动力由齿轮1输入,使轴A连续回转;而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。试绘出其机构运动简图,分析其运动是否确定,并提出修改措施。解答:原机构自由度F=3´3-2´4-1=0,不合理,改为以下几种结构均可:2-3图2-39所示为一小型压力机,其中,1为滚子;2为摆杆;3为滑块;4为滑杆;5为齿轮及凸轮;6为连杆;7为齿轮及偏心轮;8为机架;9为压头。试绘制其机构运动简图,并计算其自由度。
解答:n=7;Pl=9;Ph=2,F=3´7-2´9-2=12-6试计算图2-42所示凸轮—连杆组合机构的自由度。解答:a)n=7;Pl=9;Ph=2,F=3´7-2´9-2=1L处存在局部自由度,D处存在虚约束b)n=5;Pl=6;Ph=2,F=3´5-2´6-2=1E、B处存在局部自由度,F、C处存在虚约束
2-7试计算图2-43所示齿轮—连杆组合机构的自由度。解答:a)n=4;Pl=5;Ph=1,F=3´4-2´5-1=1A处存在复合铰链b)n=6;Pl=7;Ph=3,F=3´6-2´7-3=1B、C、D处存在复合铰链2-8试计算图2-44所示刹车机构的自由度。并就刹车过程说明此机构自由度的变化情况。
解答:①当未刹车时,F=3´6-2´8=2②在刹车瞬时,F=3´5-2´7=1,此时构件EFG和车轮接触成为一体,位置保持不变,可看作为机架。③完全刹死以后,F=3´4-2´6=0,此时构件EFG、HIJ和车轮接触成为一体,位置保持不变,可看作为机架。2-9先计算图2-45~图2-50所示平面机构的自由度。再将其中的高副化为低副,确定机构所含杆组的数目和级别,以及机构的级别。机构中的原动件用圆弧箭头表示。解答:a)n=7;Pl=10;Ph=0,F=3´7-2´10=1C、E处存在复合铰链由3个Ⅱ级杆组构成。b)n=7;Pl=10;Ph=0,F=3´7-2´10=1由3个Ⅱ级杆组构成的Ⅱ级机构。
c)n=3;Pl=3;Ph=2,F=3´3-2´3-2=1D处存在局部自由度,由2个Ⅱ级杆组构成Ⅱ级机构。d)n=4;Pl=5;Ph=1,F=3´4-2´5-1=1由1个Ⅲ级杆组构成的Ⅲ级机构。e)n=6;Pl=8;Ph=1,F=3´6-2´8-1=1B处存在局部自由度,G、G"处存在虚约束,由1个Ⅱ级杆组加上1个Ⅲ级杆组构成的Ⅲ级机构。f)n=9;Pl=12;Ph=2,F=3´9-2´12-2=1C处存在局部自由度,I处存在复合铰链,由5个Ⅱ级杆构成的Ⅱ级机构。杆组拆分如下图所示。
++++
第三章平面机构的运动分析3-1如图3-20所示曲柄滑块机构中若已知a,b,e,当给定后,试导出滑块位移s和连杆转角的表达式。解:由得到或写成3-2如图3-20,若已知,设经计算得到:,s=149.81mm,请导出和的表达式,并求出其数值。解:,得:3-12如图3-30所示,曲柄摆动导杆机构中各杆长,已知,构件1以等角速度绕A顺时针方向转动,求此时及角速度比。
解:,其中2式除以1式可得故得:求导得上式中对2式用旋转坐标系法,按逆时针方向旋转角得:所以,又求导得或写成如下等价形式:求导得解得:VDx=-0.4*(-20)*sin(60*pi/180)-0.25*(-8.5244)*sin((63.6705-120)*pi/180)=2.2264m/sVDy=0.4*(-20)*cos(60*pi/180)+0.25*(-8.5244)*cos((63.6705-120)*pi/180)=-8.1097m/s合成可得:VD=sqrt(2.2264^2+8.1097^2)=8.4098m/s,bVD=-74.6485°3-12题解法二(瞬心法):1234P24由余弦定理:,得由,得:
3-15如图3-33所示为采煤康拜因的钻探机构。已知,,构件2绕构件1上的B点以等角速度逆时针方向转动,求C、D两点的速度及加速度。解:(1)求C、D两点的速度(2)求C、D两点的加速度由上面2式可得:840*ε1*cos(15*pi/180)-840*(0.278^2)*sin(15*pi/180)=280*ε2*cos(50.93*pi/180)-280*(1.278^2)*sin(50.93*pi/180)811.3777ε1-16.8022=176.4754ε1-355.0521得ε1=ε2=-0.5328rad/s2求D点加速度的方法有两种:第一种按书上的方法列出运动方程式,按步骤求解;第二种方法求出法向加速度和切向加速度的合成。①对D点列出位置方程式求导得速度方程式
再求导得加速度方程式,则aDx=-1300*(-0.5328)*sin(15*pi/180)-1300*(0.278^2)*cos(15*pi/180)=82.2226mm/s2aDy=1300*(-0.5328)*cos(15*pi/180)-1300*(0.278^2)*sin(15*pi/180)=-695.0422mm/s2故D点的加速度为:aD=sqrt(aDx^2+aDy^2)=699.8887mm/s2,baD=-83.2533°②C点的加速度为:aC=-280*(-0.5328)*sin(50.9373*pi/180)-280*(1.278^2)*cos(50.9373*pi/180)+840*(-0.5328)*sin(15*pi/180)+840*(0.278^2)*cos(15*pi/180)=-225.4828mm/s23-17在图3-35所示凸轮机构中,,,指出速度瞬心,并用瞬心法求及时构件2的速度。解:凸轮形状为圆形,因此凸轮和平底从动件的公法线既垂直于从动件的平底又过凸轮的圆心。速度瞬心P12如图所示,从动件的速度可表示为:;;
3-18如图3-36所示曲柄滑块机构中,已知。指出速度瞬心,并用瞬心法求构件1的角速度。解:速度瞬心P13如图所示。,又故得出3-19如图3-28所示凸轮机构,指出速度瞬心,并用速度瞬心法求从动件的角速度。解:速度瞬心P12如图所示。,所以得
3-21如图3-38所示为铰链四杆机构,试用瞬心法分析欲求构件2和构件3上任何重合点的速度相等时的机构位置,此时解:构件3上任意点的速度方向为:该点与构件3的回转中心D点(瞬心P34)的连线垂直的方向;其大小为构件3的角速度与该点与瞬心P34距离的乘积。构件2上任意点的速度方向为:该点与构件2和4的速度瞬心P24的连线垂直的方向;其大小为构件2的角速度与该点与瞬心P24距离的乘积。要使构件2和构件3上任何重合点的速度相等,即应使瞬心P34与瞬心P24重合(此时AB与AD连线重合)。此时构件2和3都相对于D点做纯转动,且构件2和3的角速度相同(从两者的重合点C可推导出),重合点距离D点的距离也相同,故任何重合点的速度相等。故当时,满足题目要求。
第四章机构的力分析R21R31xR31yMdR31R32全4-4在图4-23所示的对心尖顶直动推杆盘形凸轮机构中,已知,,12mm,(为常数)。又机构在图示位置时,推杆以等加速度垂直向上运动,该处凸轮的压力角。推杆重力,重心位于其轴线上。凸轮的质心与回转中心A相重合。若加于凸轮上的驱动力矩,试求各个运动副反力和推杆所能克服的生产阻力。解:构件2推杆的受力简图如上,其中惯性力对构件2列出力和力矩平衡方程式:注:也可以由图中虚线所示,将机架对推杆的两个支反力合成为一个全反力,这样根据三力汇交理论,可以更方便的求出结果。对构件1列出力平衡方程式:
也可直接由构件1只受两力平衡直接得出:4-10在如图4-29所示摆动导杆机构中,已知,加于导杆上的力矩,求机构各运动副的反力及应加于曲柄1上的平衡力矩。R43R23M3MbR21R41R32R12解:对于构件3,由力矩平衡可得:由力平衡得:对于构件2滑块,由力平衡可得:对于构件1,由力平衡可得:由力矩平衡得:
F2R32R12R21R31Mb4-11在如图4-30所示偏心轮凸轮机构中,已知且OA位于水平位置,外载。求运动副反力和凸轮1上的平衡力矩。解:根据三力汇交理论,画出构件2受力图。列出力平衡方程:解得图中机架对推杆的支反力也可以看作虚线所示两个力的合成,此时也可以按照推杆在四个力的作用下平衡来求解,解法可参考题4-4。由构件1凸轮的受力图可得:
R1FR2Ff4-19如图4-38所示,构件1为一凸轮机构的推杆,它在力F的作用下,沿导轨2向上运动,设两者的摩擦因数f=0.2,为了避免发生自锁,导轨的长度L应满足什么条件(解题时不计构件1的质量)?解:力矩平衡可得:,得:,其中R正压力产生的磨擦力为:要使推杆不自锁,即能够上升,必须满足:,即解得:4-22图4-41所示为一胶带运输机,由电动机1经过平型带传动及一个两级齿轮减速器,带动运输带8。设已知运输带8所需的曳引力F=5500N,运输带8的运送速度,滚筒直径D=900mm,平型带传动(包括轴承)的效率,每对齿轮(包括其轴承)的效率,运输带8的机械效率。试求该传动系统的总效率及电动机所需的功率P。
解:串联机组,总效率输出功率故电机输入功率应为:4-23如图4-42所示,电动机通过三角带传动及圆锥、圆柱齿轮传动带动工作机A及B,设每对齿轮的效率,每个轴承的效率,带传动的效率,工作机A、B的功率分别为,,效率分别为,试求电动机所需的功率。解:电机功率Pd为:第四章
第四章机构的型综合5-1运动链。请画出其运动链的结构图。若以四元连杆为机架,其中一个三元连杆作转动并为原动件,要求机构的执行构件为两个完全对称运动的滑块。试进行机构变换。解:图1运动链结构图图2机构变换方案一图3机构变换方案二图4机构变换方案三5-2运动链。请画出运动链的结构图。分别取不同构件为原动件,三元连杆为机架。试综合出一个II级机构和一个高级别机构。解:运动链的结构图如下。ABCDEFG①以AB或CD杆为原动件得到II级机构;②以FG杆为原动件得到Ш级机构。5-3指出代号中有几个二、三、四元连杆。若以四元连杆为机架,取回转构件为原动件。试变换出一个连架杆为导杆,另两个连架杆为滑块的机构。解:1个四元连杆,2个三元连杆,5个二元连杆。变换机构如下,理论上可以有6种以上方案。
5-4代号为的运动链。请画出其运动链的结构图。问有几个二、三、四元连杆。变换机构后其自由度F=?。解:1个四元连杆,2个三元连杆,6个二元连杆。总构件数N=1+2+6=9,自由度F=3(N-1)-2P=2,变换机构后其自由度不应改变,依然为2。解题注意事项:1.画出运动链结构图后,对比代号进行检验;2.机构变换后检查其中的多元连杆连接是否正确,多元连杆画对的话,机构一般不会有错;3.机构变换后其自由度不应改变。第四章平面连杆机构6-1如图6-48所示,设已知四杆机构各机构的长度为,。试问:1)当取杆4为机架时,是否有曲柄存在?2)若各杆长度不变,能否以选不同杆为机架的方法获得双曲柄和双摇杆机构?如何获得?解:1),满足杆长之和条件,且最短杆为连架杆,故有曲柄存在。2)以a为机架,得双曲柄机构;
以c为机架,得双摇杆机构。6-4在图6-48所示的铰链四杆机构中,各杆的长度为,试求:1)当取杆4为机架时,该机构的极位夹角、杆3的最大摆角和最小传动角。2)当取杆1为机架时,将演化成何种类型机构?为什么?并说明这时C、D两个转动副是周转副还是摆动副?解:1)由曲柄与连杆拉直共线和重叠共线两位置计算极位夹角和杆3的摆角:由曲柄与机架内共线和外共线两位置计算连杆和摇杆的夹角:故2)满足杆长之和条件,A、B为全转副,C、D为摆动副,此时取a为机架得到双曲柄机构。6-8图6-52所示为一牛头刨床的主传动机构,已知行程速比系数K=2,刨头5的行程H=300mm,要求在整个行程中,推动刨头5有较小的压力角,试设计此机构。
解:由已知行程速度变化系数K=2,得极位夹角为:BACD"E"DEαα0.5Hδh——导杆摆角已知,则要使压力角最小,须使滑块导轨线位于D和D"两位置高度中点处,此时在滑块的整个行程中机构的最大压力角最小。此时,压力角。由已知条件,行程,即导杆从中心位置D运动到左边极限位置D"时滑块的行程为,可得:,化简得:,解得:刨头导轨线距离C点的高度为:此时最大压力角为:6-14如图6-57所示,设要求四杆机构两连架杆的三组对应位置分别为;;,试设计此四杆机构。解:对照书上(6-41)式,此处可简化为:分别代入题目中已知3组数据得:
其中解得:故6-16如图6-59所示曲柄摇杆机构,已知摇杆长,摆程角,行程速比系数K=1.25,若远极位时机构的传动角,求各杆长a,b,d,并校验机构最小传动角。解:机构的极位夹角和近极位传动角为:根据课本内容列出投影方程式:解得:其中由式(6-48)解得:
由实际尺寸。得绝对杆长尺寸为:此时机构的最小传动角为,不符合要求。6-22如图6-60所示,已知某刚体上P点的三位置及其上某标线的位置角分别为:;,,,若已知两固定支座A、D的位置坐标为:,求实现P点给定位置的四杆机构的各杆长度。解:,首先根据式(6-13)写出刚体位移矩阵:先计算运动副的坐标值。由式(6-19)解得:将代入式(6-18)有再计算运动副的坐标值。同理将位移矩阵代入式(6-19)解得:将代入式(6-18)有可得各杆长为:
6-27如图6-64所示,砂箱翻转台与连杆BC固结,为使翻转台作平面运动并翻转,B、C两点的坐标值为:,,,,试用代数解析法设计一四杆机构实现以上要求。解:设A、D点的坐标值()及(),由式(6-38)可得:和故得各杆长为:6-28如图6-65所示液压缸翻斗机构,已知翻斗摆角,位置对位置作用于BD上的力矩比为,若摇臂BD的长度,求时的机构尺寸及液压缸行程H。解:设机构的相对尺寸为由式(6-50):可得由式(6-52):故由式(6-54):故:行程。第八章凸轮机构
8-3在尖顶对心直动从动件盘形凸轮机构中,图8-33所示从动件的运动规律尚不完整。试在图上补全各段的曲线,并指出哪些位置有刚性冲击?哪些位置有柔性冲击?解:在凸轮转角处存在刚性冲击;在凸轮转角处存在柔性冲击;8-9在图8-35所示对心直动滚子从动件盘形凸轮机构中,已知,实际基圆半径,滚子半径,推程角,推杆按正弦加速度规律运动。当凸轮转动时,试计算凸轮廓线与滚子接触点处的坐标值。解:(1)首先计算凸轮理论廓线坐标理论基圆半径时,推杆的行程s为:(根据正弦加速度规律方程)由于是对心,,故理论廓线方程中(2)计算凸轮实际廓线坐标处理论廓线点处的法线斜率为:
(其中)则得故实际廓线坐标值为:8-11与题8-9条件相同。试计算对心平底从动件的盘形凸轮当时,平底与凸轮廓线接触点处的坐标值。若推程与回程运动相同,试确定平底应有的最小长度L。解:(1)计算平底与凸轮廓线接触点坐标(2)计算平底从动件的最小长度L上式对求导并令其为0,可得出时上式取得最大值。此时所以
8-17现需设计一对心直动滚子推杆盘形凸轮机构,设已知凸轮以等角速度沿顺时针方向回转,推杆的行程,推程运动角,推杆位移运动规律为,试确定推程所要求的最佳基圆半径。又如该机构为右偏置直动滚子推杆盘形凸轮机构,偏距,试求其最小基圆半径。解:(1)由于是对心直动滚子推杆盘形凸轮机构,偏距e=0因此,基圆半径的计算公式可简化为:对上式求导,并令导数为0,求出极值时对应的凸轮转角。,,,得:,化简为:,取得:,故代入基圆半径计算公式,求得(2)当凸轮机构推杆为右偏置时,偏距e=10mm,得:,即分子为0,与(1)中式子相同,求得代入基圆半径计算公式,求得。
第九章直齿圆柱齿轮机构9-4在图9-43中,已知基圆半径,现需求:1)当时,渐开线的展角、渐开线上的压力角和曲率半径。2)当时,渐开线上的压力角及向径的值。解:1)根据渐开线方程,得:压力角展角曲率半径2)当时,查表9-1,查表计算时可采用插值法9-5一根渐开线在基圆上发生,试求渐开线上哪一点的曲率半径为零?哪一点的压力角为零?解:基圆上的压力角、曲率半径均为0。
9-9若渐开线直齿圆柱标准齿轮的,试求基圆与齿根圆重合时的齿数。又当齿数大于以上求出的数值时,试证明此时基圆与齿根圆哪个大?解:当基圆与齿根圆重合时,由可得:若可导出:,即。9-14在T616镗床主轴箱中有一直齿圆柱渐开线标准齿轮,其压力角齿数z=40,齿顶圆直径。现发现该齿轮已经损坏,需要重做一个齿轮,试确定这个齿轮的模数及齿顶高系数(提示:齿顶高系数只有两种情况,和)。解:,即若,则有:;若,则有:,此为非标准值。所以,,9-17设有一对外啮合齿轮的齿数,压力角,齿顶高系数。试求当中心距a"=725mm时,两轮的啮合角。又当时,试求其中心距a"。解:标准中心距为:
由当时,中心距。9-19设有一对按标准中心距安装的外啮合渐开线齿轮,已知,欲使其重合度,试求这对齿轮的齿顶高系数。解:,且按标准中心距安装,有故有,解得:,有,解得:实际设计时,取,此时重合度可计算得。9-22在某牛头刨床中,有一对外啮合渐开线直齿圆柱齿轮传动,已知,。现已发现小齿轮严重磨损,拟将其报废。大齿轮磨损较轻(沿齿厚方向的磨损量为0.75mm),拟修复使用,并要求新设计小齿轮的齿顶厚尽可能大些,为应如何设计这对齿轮?解:标准中心距为:,此时修复大齿轮,即对大齿轮采用负变位,使其齿厚s变小,小齿轮采用正变位,保证齿厚尽可能大,整个齿轮传动为等变位齿轮传动:,中心距不变。由大齿轮磨损量为0.75mm,可得:,解得。可取进行齿轮设计。
以下计算略,可参见书上公式。9-26在图9-49所示的齿轮变速箱中,两轴中心距为90mm,各轮齿数为、、、、、,模数均为m=2mm,试确定各对齿轮传动的类型。解:实际中心距,各对齿轮的标准中心距为:,采用负传动;,采用标准或等变位传动;,采用正传动;(1)对齿轮1和2传动:啮合角大小齿轮不发生根切需满足:,因两轮齿数分别为41和51,相差不多,故取可使两齿轮接近等强度。(注:选取方式不唯一,满足总体要求即可)(2)对齿轮3和4传动:
啮合角,标准齿轮传动,取(3)对齿轮5和6传动:啮合角,且应满足故取(注:选取方式不唯一,满足总体要求即可)。以下计算略,可参见书上公式。
第十章其它齿轮机构10-2在某设备中有一对渐开线直齿圆柱齿轮,已知。在技术改造中,提高了原动机的转速。为了改善齿轮传动的平稳性,要求在不降低强度、不改变中心距和传动比的条件下,将直齿轮改为斜齿轮,并希望将分度圆螺旋角限制在以内,重合度,试确定、、和齿宽B。解:原直齿轮标准中心距斜齿轮中心距为:,要使齿轮强度不降低,即模数不变,初取螺旋角,则有,取,则此时可计算得:,,满足要求。根据重合度要求计算齿宽:,解得则:,由,可得:,所以得综上,取取,,,。
10-3设有一对外啮合齿轮传动,已知不用变位而用斜齿圆柱齿轮传动来凑中心距,试问螺旋角应多大?解:斜齿轮中心距所以故10-4一蜗轮的齿数,与一单头蜗杆啮合,试求:1)蜗轮端面模数及蜗杆轴面模数;2)蜗杆的轴面齿距及导程l;3)蜗杆的分度圆直径;4)两轮的中心距。解:1)由可得端面模数,蜗杆轴面模数。2)蜗杆轴面齿距,导程3)因模数,故直径系数,根据取较小值且满足为标准值的原则,取,则。4)两轮中心距。第十一章齿轮系11-1图11-36所示为一时钟轮系,S、M、H分别表示秒针、分针、时针。图中数字表示该轮的齿数。假设B和C的模数相等,试求齿轮A、B、C的齿数。解:此轮系为一个定轴轮系。,解得……(1)
又B和C模数相等,即齿轮4、C、5、B的模数均相等,由中心距相等条件可得:,即……(2)联立(1)、(2)两式可得,化成方程式为:,解得(舍去负值)。11-7图11-41所示为一装配用气动一字旋具齿轮减速部分的传动简图。已知各轮齿数为,。若,试求一字旋具的转速。解:该复合轮系由2个行星轮系串联而成。,则由图中几何条件可得:即:,同理故,11-10图11-44所示的差动轮系是各轮模数相同的标准齿轮传动。设已知各轮的齿数又,,试求系杆H转速的大小和方向。1)当、转向相同时;2)当、转向相反时。解:该轮系为一个周转轮系。
得:1)当、转向相同时有:,得:(与转向相同)1)当、转向相同时有:,得:(与转向相反)11-11在图11-45所示的电动三爪自定心卡盘传动轮系中,设已知各轮的齿数为,,,试求传动比。解:该轮系为3K-H型周转轮系,固定系杆H,转化为定轴轮系。对1-2-3-H可得:对3-2-2"-4-H可得:所以轮1与轮4转向相反。
11-19用于自动化照明灯具上的一周转轮系图11-53所示。已知输入转速,组成轮系的各齿轮均为圆柱直齿轮。各轮齿数为。试求箱体的转速。解:该轮系为一行星轮系,其中齿轮1和5为中心轮,箱体为系杆,其它齿轮均为行星轮。'
您可能关注的文档
- 《有机化学》傅建熙 第三版 课本答案.doc
- 《有机电子学》思考题及答案1.doc
- 《机械优化设计》复习题答案.pdf
- 《机械优化设计》孙靖民哈尔滨工业大学课后答案.pdf
- 《机械几何精度设计》习题参考答案.doc
- 《机械制造技术基础》下册习题答案 2.doc
- 《机械制造技术基础》复习题答案.doc
- 《机械制造装备设计》关慧贞第三版课后习题答案.doc
- 《机械制造装备设计》关慧贞第三版课后习题答案.pdf
- 《机械原理》复习题及答案.doc
- 《机械基础》习题答案.doc
- 《机械工程测试技术基础》(第三版熊诗波_黄长艺)课后习题及答案详解.doc
- 《机械工程测试技术基础》第三版课后习题答案.pdf
- 《机械工程测试技术基础》课后习题及答案详解.doc
- 《机械设计-吴昌林》课后习题答案(部分).pdf
- 《机械设计》(第八版)课后习题答案(全共32页).doc
- 《机械设计基础》试题及答案.doc
- 《机械设计基础》课程课后作业.doc
相关文档
- 施工规范CECS140-2002给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程
- 施工规范CECS141-2002给水排水工程埋地钢管管道结构设计规程
- 施工规范CECS142-2002给水排水工程埋地铸铁管管道结构设计规程
- 施工规范CECS143-2002给水排水工程埋地预制混凝土圆形管管道结构设计规程
- 施工规范CECS145-2002给水排水工程埋地矩形管管道结构设计规程
- 施工规范CECS190-2005给水排水工程埋地玻璃纤维增强塑料夹砂管管道结构设计规程
- cecs 140:2002 给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程(含条文说明)
- cecs 141:2002 给水排水工程埋地钢管管道结构设计规程 条文说明
- cecs 140:2002 给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程 条文说明
- cecs 142:2002 给水排水工程埋地铸铁管管道结构设计规程 条文说明