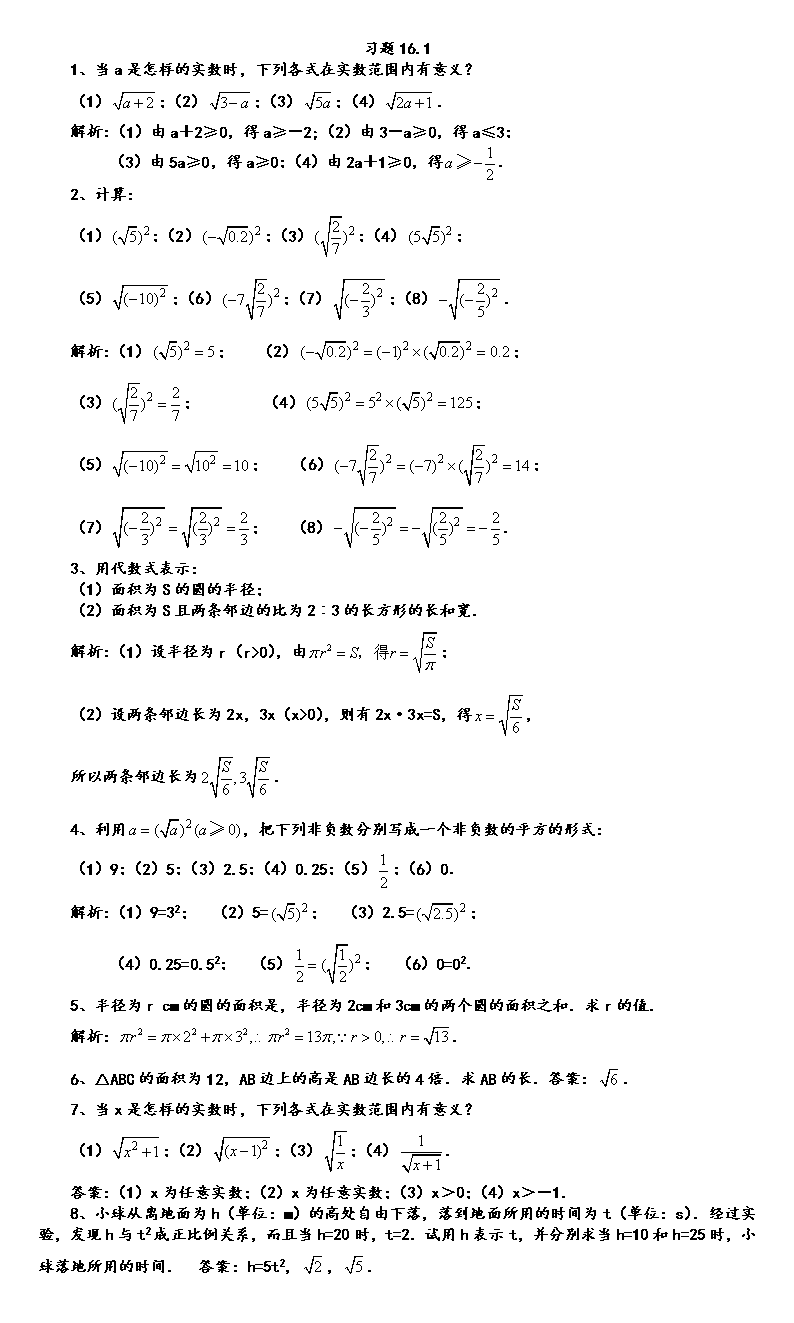八年级数学下学期课后习题与答案.doc 35页

'习题16.11、当a是怎样的实数时，下列各式在实数范围内有意义？（1）；（2）；（3）；（4）．解析：（1）由a＋2≥0，得a≥－2;（2）由3－a≥0，得a≤3；（3）由5a≥0，得a≥0；（4）由2a＋1≥0，得．2、计算：（1）；（2）；（3）；（4）；（5）；（6）；（7）；（8）．解析：（1）；（2）；（3）；（4）；（5）；（6）；（7）；（8）．3、用代数式表示：（1）面积为S的圆的半径；（2）面积为S且两条邻边的比为2︰3的长方形的长和宽．解析：（1）设半径为r（r>0），由；（2）设两条邻边长为2x，3x（x>0），则有2x·3x=S，得，所以两条邻边长为．4、利用，把下列非负数分别写成一个非负数的平方的形式：（1）9；（2）5；（3）2.5；（4）0.25；（5）；（6）0．解析：（1）9=32；（2）5=；（3）2.5=；（4）0.25=0.52；（5）；（6）0=02．5、半径为rcm的圆的面积是，半径为2cm和3cm的两个圆的面积之和．求r的值．解析：．6、△ABC的面积为12，AB边上的高是AB边长的4倍．求AB的长．答案：．7、当x是怎样的实数时，下列各式在实数范围内有意义？（1）；（2）；（3）；（4）．答案：（1）x为任意实数；（2）x为任意实数；（3）x＞0；（4）x＞－1．8、小球从离地面为h（单位：m）的高处自由下落，落到地面所用的时间为t（单位：s）．经过实验，发现h与t2成正比例关系，而且当h=20时，t=2．试用h表示t，并分别求当h=10和h=25时，小球落地所用的时间．答案：h=5t2，，． 9、（1）已知是整数，求自然数n所有可能的值；（2）已知是整数，求正整数n的最小值．答案：（1）2，9，14，17，18；（2）6．因为24n=22×6×n，因此，使得为整数的最小的正整数n是6．10、一个圆柱体的高为10，体积为V．求它的底面半径r（用含V的代数式表示），并分别求当V=5π，10π和20π时，底面半径r的大小．答案：习题16.21、计算：（1）；（2）；（3）；（4）．答案：（1）；（2）；（3）；（4）．2、计算：（1）；（2）；（3）；（4）．答案：（1）；（2）；（3）；（4）．3、化简：（1）；（2）；（3）；（4）．答案：（1）14；（2）；（3）；（4）．4、化简：（1）；（2）；（3）；（4）；（5）；（6）．答案：（1）；（2）；（3）；（4）；（5）；（6）．5、根据下列条件求代数式的值；（1）a=1，b=10，c=－15；（2）a=2，b=－8，c=5．答案：（1）；（2）．6、设长方形的面积为S，相邻两边分别为a，b．（1）已知，，求S；（2）已知，，求S．答案：（1）；（2）240;7、设正方形的面积为S，边长为a．（1）已知S=50，求a；（2）已知S=242，求a．答案：（1）；（2）．8、计算：（1）；（2）；（3）；（4）． 答案：（1）1.2；（2）；（3）；（4）15．9、已知，求与的近似值．答案：0.707，2.828．10、设长方形的面积为S，相邻两边长分别为a，b．已知，求b．答案：．11、已知长方体的体积，高，求它的底面积S．答案：．12题图12、如图，从一个大正方形中裁去面积为15cm2和24cm2的两个小正方形，求留下部分的面积．答案：．13、用计算器计算：（1）；（2）；（3）；（4）．观察上面几题的结果，你能发现什么规律？用你发现的规律直接写出下题的结果：答案：（1）10；（2）100；（3）1000；（4）10000．．习题16.31、下列计算是否正确？为什么？（1）；（2）；（3）；（4）．答案：（1）不正确，与不能合并；（2）不正确，2与不能合并；（3）不正确，；（4）不正确，．2、计算：（1）；（2）；（3）；（4）．答案：（1）；（2）；（3）；（4）．3、计算：（1）；（2）；（3）；（4）．答案：（1）0；（2）；（3）；（4）．4、计算：（1）；（2）； （3）；（4）．答案：（1）；（2）－6；（3）；（4）．5、已知，求的近似值（结果保留小数点后两位）．答案：7.83．6、已知，求下列各式的值：（1）x2＋2xy＋y2；（2）x2－y2．答案：（1）12；（2）．7、如图，在Rt△ABC中，∠C=90°，CB=CA=a．求AB的长．答案：．8、已知，求的值．答案：．9、在下列各方程后面的括号内分别给出了一组数，从中找出方程的解：（1）2x2－6=0，；（2）2（x＋5）2=24，．答案：（1）；（2）．复习题161、当x是怎样的实数时，下列各式在实数范围内有意义？（1）；（2）；（3）；（4）．答案：（1）x≥－3；（2）；（3）；（4）x≠1．2、化简：（1）；　　（2）；　　（3）；　　（4）；（5）；　　（6）．答案：（1）；（2）；（3）；（4）；（5）；（6）．3、计算：（1）；（2）；（3）；（4）；（5）；（6）．答案：（1）；（2）；（3）6；（4）；（5）；（6）．4、正方形的边长为acm，它的面积与长为96cm，宽为12cm的长方形的面积相等．求a的值． 答案：．5、已知，求代数式x2＋5x－6的值．答案：．6、已知，求代数式的值．答案：．7、电流通过导线时会产生热量，电流I（单位：A）、导线电阻R（单位：Ω）、通电时间t（单位：s）与产生的热量Q（单位：J）满足Q=I2Rt．已知导线的电阻为5Ω，1s时间导线产生30J的热量，求电流I的值（结果保留小数点后两位）．答案：2.45A．8、已知n是正整数，是整数，求n的最小值．答案：21．9、（1）把一个圆心为点O，半径为r的圆的面积四等分．请你尽可能多地设想各种分割方法．（2）如图，以点O为圆心的三个同心圆把以OA为半径的大圆O的面积四等分．求这三个圆的半径OB，OC，OD的长．答案：（1）例如，相互垂直的直径将圆的面积四等分；（2）设OA=r，则，，．10、判断下列各式是否成立：类比上述式子，再写出几个同类型的式子．你能看出其中的规律吗？用字母表示这一规律，并给出证明．答案：规律是：．只要注意到，再两边开平方即可．习题17.11、设直角三角形的两条直角边长分别为a和b，斜边长为c．（1）已知a=12，b=5，求c；（2）已知a=3，c=4，求b；（3）已知c=10，b=9，求a．答案：（1）13；（2）；（3）．2、一木杆在离地面3m处折断，木杆顶端落在离木杆底端4m处．木杆折断之前有多高？答案：8m．3、如图，一个圆锥的高AO=2.4，底面半径OB=0.7．AB的长是多少？答案：2.5．4、已知长方形零件尺寸（单位：mm）如图，求两孔中心的距离（结果保留小数点后一位）．答案：43.4mm．5、如图，要从电线杆离地面5m处向地面拉一条长7m的钢缆．求地面钢缆固定点A到电线杆底部B的距离（结果保留小数点后一位）．答案：4.9m．5题图4题图2题图6、在数轴上作出表示的点．答案：略．7、在△ABC中，∠C=90°，AB=c．（1）如果∠A=30°，求BC，AC； （2）如果∠A=45°，求BC，AC．答案：（1），；（2），．8、在△ABC中，∠C=90°，AC=2.1，BC=2.8．求：（1）△ABC的面积；（2）斜边AB；（3）高CD．答案：（1）2.94；（2）3.5；（3）1.68．9、已知一个三角形工件尺寸（单位：mm）如图，计算高l的长（结果取整数）．答案：82mm．10、有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面．水的深度与这根芦苇的长度分别是多少？答案：12尺，13尺．11、如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=2．求斜边AB的长．答案：．12、有5个边长为1的正方形，排列形式如图．请把它们分割后拼接成一个大正方形．答案：分割方法和拼接方法分别如图（1）和图（2）所示． 13、如图，分别以等腰Rt△ACD的边AD，AC，CD为直径画半圆．求证：所得两个月形图案AGCE和DHCF的面积之和（图中阴影部分）等于Rt△ACD的面积．答案：，，．因为∠ACD=90°，根据勾股定理得AC2＋CD2=AD2，所以S半圆AEC＋S半圆CFD=S半圆ACD，S阴影=S△ACD＋S半圆AEC＋S半圆CFD－S半圆ACD，即S阴影=S△ACD．14、如图，△ACB和△ECD都是等腰直角三角形，△ACB的顶点A在△ECD的斜边DE上．求证：AE2＋AD2=2AC2．证明：证法1：如图（1），连接BD．∵△ECD和△ACB都为等腰直角三角形，∴EC=CD，AC=CB，∠ECD=∠ACB=90°．∴∠ECA=∠DCB．∴△ACE≌△DCB．∴AE=DB，∠CDB=∠E=45°．又∠EDC=45°，∴∠ADB=90°．在Rt△ADB中，AD2＋DB2=AB2，得AD2＋AE2=AC2＋CB2，即AE2＋AD2=2AC2．证法2：如图（2），作AF⊥EC，AG⊥CD，由条件可知，AG=FC．在Rt△AFC中，根据勾股定理得AF2＋FC2=AC2．∴AF2＋AG2=AC2．在等腰Rt△AFE和等腰Rt△AGD中，由勾股定理得AF2＋FE2=AE2，AG2＋GD2=AD2． 又AF=FE，AG=GD，∴2AF2=AE2，2AG2=AD2．而2AF2＋2AG2=2AC2，∴AE2＋AD2=2AC2．习题17.21、判断由线段a，b，c组成的三角形是不是直角三角形：（1）a=7，b=24，c=25；（2），b=4，c=5；（3），b=1，；（4）a=40，b=50，c=60．答案：（1）是；（2）是；（3）是；（4）不是．2、下列各命题都成立，写出它们的逆命题．这些逆命题成立吗？（1）同旁内角互补，两直线平行；（2）如果两个角是直角，那么它们相等；（3）全等三角形的对应边相等；（4）如果两个实数相等，那么它们的平方相等．答案：（1）两直线平行，同旁内角互补．成立．（2）如果两个角相等，那么这两个角是直角．不成立．（3）三条边对应相等的三角形全等．成立．（4）如果两个实数的平方相等，那么这两个实数相等．不成立．3、小明向东走80m后，沿另一方向又走了60m，再沿第三个方向走100m回到原地．小明向东走80m后是向哪个方向走的？答案：向北或向南．4、在△ABC中，AB=13，BC=10，BC边上的中线AD=12．求AC．答案：13．5、如图，在四边形ABCD中，AB=3，BC=4，CD=12，AD=13，∠B=90°．求四边形ABCD的面积．答案：36．6、如图，在正方形ABCD中，E是BC的中点，F是CD上一点，且．求证∠AEF=90°．答案：设AB=4k，则BE=CE=2k，CF=k，DF=3k． ∵∠B=90°，∴AE2=（4k）2＋（2k）2=20k2．同理，EF2=5k2，AF2=25k2．∴AE2＋EF2=AF2．根据勾股定理的逆定理，△AEF为直角三角形．∴∠AEF=90°．7、我们知道3，4，5是一组勾股数，那么3k，4k，5k（k是正整数）也是一组勾股数吗？一般地，如果a，b，c是一组勾股数，那么ak，bk，ck（k是正整数）也是一组勾股数吗？答案：因为（3k）2＋（4k）2=9k2＋16k2=25k2=（5k）2，所以3k，4k，5k（k是正整数）为勾股数．如果a，b，c为勾股数，即a2＋b2=c2，那么（ak）2＋（bk）2=a2k2＋b2k2=（a2＋b2）k2=c2k2=（ck）2．因此，ak，bk，ck（k是正整数）也是勾股数．复习题171、两人从同一地点同时出发，一人以20m/min的速度向北直行，一人以30m/min的速度向东直行．10min后他们相距多远（结果取整数）？答案：361m．2、如图，过圆锥的顶点S和底面圆的圆心O的平面截圆锥得截面△SAB，其中SA=SB，AB是圆锥底面圆O的直径．已知SA=7cm，AB=4cm，求截面△SAB的面积．答案：．3、如图，车床齿轮箱壳要钻两个圆孔，两孔中心的距离是134mm，两孔中心的水平距离是77mm．计算两孔中心的垂直距离（结果保留小数点后一位）．答案：109.7mm．4、如图，要修一个育苗棚，棚的横截面是直角三角形，棚宽a=3m，高b=1.5m，长d=10m．求覆盖在顶上的塑料薄膜需多少平方米（结果保留小数点后一位）． 答案：33.5m2．5、一个三角形三边的比为，这个三角形是直角三角形吗？答案：设这个三角形三边为k，，2k，其中k＞0．由于，根据勾股定理的逆定理，这个三角形是直角三角形．6、下列各命题都成立，写出它们的逆命题．这些逆命题成立吗？（1）两条直线平行，同位角相等；（2）如果两个实数都是正数，那么它们的积是正数；（3）等边三角形是锐角三角形；（4）线段垂直平分线上的点到这条线段两个端点的距离相等．答案：（1）同位角相等，两直线平行．成立．（2）如果两个实数的积是正数，那么这两个实数是正数．不成立．（3）锐角三角形是等边三角形．不成立．（4）与一条线段两个端点距离相等的点，在这条线段的垂直平分线上．成立．7、已知直角三角形的两条直角边的长分别为和，求斜边c的长．答案：．8、如图，在△ABC中，AB=AC=BC，高AD=h．求AB．答案：．9、如图，每个小正方形的边长都为1．（1）求四边形ABCD的面积与周长；（2）∠BCD是直角吗？ 答案：（1）14.5，；（2）由，，BD=5，可得BC2＋CD2=BD2．根据勾股定理的逆定理，△BCD是直角三角形，因此∠BCD是直角．10、一根竹子高1丈，折断后竹子顶端落在离竹子底端3尺处．折断处离地面的高度是多少？（这是我国古代数学著作《九章算术》中的一个问题．其中的丈、尺是长度单位，1丈=10尺．）答案：4.55尺．11、古希腊的哲学家柏拉图曾指出，如果m表示大于1的整数，a=2m，b=m2－1，c=m2＋1，那么a，b，c为勾股数．你认为对吗？如果对，你能利用这个结论得出一些勾股数吗？答案：因为a2＋b2=（2m）2＋（m2－1）2=4m2＋m4－2m2＋1=m4＋2m2＋1=（m2＋1）2=c2，所以a，b，c为勾股数．用m=2，3，4等大于1的整数代入2m，m2－1，m2＋1，得4，3，5；6，8，10；8，15，17；等等．12、如图，圆柱的底面半径为6cm，高为10cm，蚂蚁在圆柱表面爬行，从点A爬到点B的最短路程是多少厘米（结果保留小数点后一位）？答案：21.3cm．13、一根70cm的木棒，要放在长、宽、高分别是50cm，40cm，30cm的长方体木箱中，能放进去吗？答案：能．14、设直角三角形的两条直角边长及斜边上的高分别为a，b及h．求证：．答案：由直角三角形的面积公式，得，等式两边平方得a2b2=h2（a2＋b2），等式两边再同除以a2b2c2，得，即.习题18.11、如果四边形ABCD是平行四边形，AB=6，且AB的长是□ABCD周长的，那么BC的长是多少？答案：10． 2、如图，在一束平行光线中插入一张对边平行的纸板．如果光线与纸板右下方所成的∠1是72°15′，那么光线与纸板左上方所成的∠2是多少度？为什么？答案：72°15′，平行四边形的对角相等．3、如图，□ABCD的对角线AC，BD相交于点O，且AC＋BD=36，AB=11．求△OCD的周长．答案：29．4、如图，在□ABCD中，点E，F分别在BC，AD上，且AF=CE．求证：四边形AECF是平行四边形．答案：提示：利用AFCE．5、如图，□ABCD的对角线AC，BD相交于点O，且E，F，G，H分别是AO，BO，CO，DO的中点．求证：四边形EFGH是平行四边形．答案：提示：利用四边形EFGH的对角线互相平分．6、如图，四边形AEFD和EBCF都是平行四边形．求证：四边形ABCD是平行四边形．答案：提示：利用ADEFBC．7、如图，直线l1∥l2，△ABC与△DBC的面积相等吗？为什么？你还能画出一些与△ABC面积相等的三角形吗？ 答案：相等．提示：在直线l1上任取一点P，△PBC的面积与△ABC的面积相等（同底等高）．8、如图，□OABC的顶点O，A，C的坐标分别是（0，0），（a，0），（b，c）．求顶点B的坐标．答案：B（a＋b，c）．9、如图，在梯形ABCD中，AB∥DC．（1）已知∠A=∠B，求证AD=BC；（2）已知AD=BC，求证∠A=∠B．答案：提示：过点C作CE∥AD，交AB于点E，可得四边形AECD为平行四边形．10、如图，四边形ABCD是平行四边形，∠ABC=70°，BE平分∠ABC且交AD于点E，DF∥BE且交BC于点F．求∠1的大小．答案：35°．11、如图，A′B′∥BA，B′C′∥CB，C′A′∥AC，∠ABC与∠B′有什么关系？线段AB′与线段AC′呢？为什么？答案：由四边形ABCB′是平行四边形，可知∠ABC=∠B′，AB′=BC；再由四边形C′BCA是平行四边形，可知C′A=BC．从而AB′=AC′． 12、如图，在四边形ABCD中，AD=12，DO=OB=5，AC=26，∠ADB=90°．求BC的长和四边形ABCD的面积．答案：因为AD=12，DO=5，利用勾股定理可得AO=13，从而四边形ABCD的对角线互相平分，它是一个平行四边形．所以BC=AD=12，四边形ABCD的面积为120．13、如图，由六个全等的正三角形拼成的图中，有多少个平行四边形？为什么？答案：6个，利用对边相等的四边形是平行四边形．14、如图，用硬纸板剪一个平行四边形，作出它的对角线的交点O，用大头针把一根平放在平行四边形上的直细木条固定在点O处，并使细木条可以绕点O转动．拨动细木条，使它随意停留在任意位置．观察几次拨动的结果，你发现了什么？证明你的发现．答案：设木条与□ABCD的边AD，BC分别交于点E，F，可以发现OE=OF，AE=CF，DE=BF，△AOE≌△COF，△DOE≌△BOF等．利用平行四边形的性质可以证明上述结论．15、如图，在□ABCD中，过对角线BD上一点P作EF∥BC，GH∥AB．图中哪两个平行四边形面积相等？为什么？答案：□AEPH与□PGCF面积相等．利用△ABD与△CDB，△PHD与△DFP，△BEP与△PGB分别全等，从而□AEPH与□PGCF面积相等．习题18.21、如图，四边形ABCD是平行四边形，对角线AC，BD相交于点O，且∠1=∠2．它是一个矩形吗？为什么？ 答案：是．利用∠1=∠2，可知BO=CO，从而BD=AC，□ABCD的对角线相等，它是一个矩形．2、求证：四个角都相等的四边形是矩形．答案：由于四边形的内角和为360°，四个角又都相等，所以它的四个角都是直角．因此这个四边形是矩形．3、一个木匠要制作矩形的踏板．他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次，就能得到矩形踏板．为什么？答案：能．这时他得到的是一个角为直角的平行四边形，即矩形．4、在Rt△ABC中，∠C=90°，AB=2AC．求∠A，∠B的度数．答案：∠A=60°，∠B=30°．5、如图，四边形ABCD是菱形，∠ACD=30°，BD=6．求：（1）∠BAD，∠ABC的度数；（2）AB，AC的长．答案：（1）∠BAD=60°，∠ABC=120°；（2）AB=6，．6、如图，AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD．求证：四边形ABCD是菱形．答案：提示：由∠ABD=∠DBC=∠ADB，可知AB=AD，同理可得AB=BC．从而ADBC，四边形ABCD是一组邻边相等的平行四边形，它是菱形．7、如图，把一个长方形的纸片对折两次，然后剪下一个角．要得到一个正方形，剪口与折痕应成多少度的角？ 答案：45°．8、如图，为了做一个无盖纸盒，小明先在一块矩形硬纸板的四角画出四个相同的正方形，用剪刀剪下．然后把纸板的四边沿虚线折起，并用胶带粘好，一个无盖纸盒就做成了．纸盒的底面是什么形状？为什么？答案：矩形，它的四个角都是直角．9、如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，∠ACD=3∠BCD，E是斜边AB的中点．∠ECD是多少度？为什么？答案：45°．提示：∠BCD=∠EAC=∠ECA=22.5°．10、如图，四边形ABCD是菱形，点M，N分别在AB，AD上，且BM=DN，MG∥AD，NF∥AB；点F，G分别在BC，CD上，MG与NF相交于点E．求证：四边形AMEN，EFCG都是菱形．答案：提示：四边形AMEN，EFCG都是一组邻边相等的平行四边形．11、如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于点H．求DH的长．答案：DH=4.8．提示：由AB·DH=2AO·OD=2S△ABD可得．12、（1）如下图（1），四边形OBCD是矩形，O，B，D三点的坐标分别是（0，0），（b，0），（0，d）．求点C的坐标．（2）如下图（2），四边形ABCD是菱形，C，D两点的坐标分别是（c，0），（0，d），点A，B在坐标轴上．求A，B两点的坐标． （3）如下图（3），四边形OBCD是正方形，O，D两点的坐标分别是（0，0），（0，d）．求B，C两点的坐标．答案：（1）C（b，d）；（2）A（－c，0），B（0，－d）；（3）B（d，0），C（d，d）．13、如图，E，F，M，N分别是正方形ABCD四条边上的点，且AE=BF=CM=DN．试判断四边形EFMN是什么图形，并证明你的结论．答案：正方形．提示：△BFE≌△CMF≌△DNM≌△AEN，证明四边形EFMN的四条边相等，四个角都是直角．14、如图，将等腰三角形纸片ABC沿底边BC上的高AD剪成两个三角形．用这两个三角形你能拼成多少种平行四边形？试一试，分别求出它们的对角线的长．答案：3种．可以分别以AD，AB（AC），BD（CD）为四边形的一条对角线，得到3种平行四边形，它们的对角线长分别为h，；m，m；n，．15、如图，四边形ABCD是正方形．G是BC上的任意一点，DE⊥AG于点E，BF∥DE，且交AG于点F．求证：AF－BF=EF．答案：提示：由△ADE≌△BAF，可得AE=BF，从而AF－BF=EF． 16、如图，在△ABC中，BD，CE分别是边AC，AB上的中线，BD与CE相交于点O．BO与OD的长度有什么关系？BC边上的中线是否一定过点O？为什么？答案：BO=2OD，BC边上的中线一定过点O．利用四边形EMND是平行四边形，可知BO=2OD；设BC边上的中线和BD相交于点O′，可知BO′=2O′D，从而O与O′重合．17、如图是一块正方形草地，要在上面修建两条交叉的小路，使得这两条小路将草地分成的四部分面积相等，你有多少种方法？并与你的同学交流一下．答案：分法有无数种．只要保持两条小路互相垂直，并且都过正方形的中心即可．复习题181、选择题．（1）若平行四边形中两个内角的度数比为1︰2，则其中较小的内角是（）．A．90°B．60°C．120°D．45°（2）若菱形的周长为8，高为1，则菱形两邻角的度数比为（）．A．3︰1B．4︰1C．5︰1D．6︰1（3）如图，在正方形ABCD的外侧，作等边三角形ADE，则∠AEB为（）A．10°B．15°C．20°D．125°答案：（1）B；（2）C；（3）B．2、如图，将□ABCD的对角线BD向两个方向延长，分别至点E和点F，且使BE=DF．求证：四边形AECF是平行四边形．答案：提示：连接AC，利用对角线互相平分的四边形是平行四边形．3、矩形对角线组成的对顶角中，有一组是两个50°的角．对角线与各边组成的角是多少度？ 答案：65°和25°．4、如图，你能用一根绳子检查一个书架的侧边是否和上、下底都垂直吗？为什么？答案：可以．通过测量对边以及对角线是否分别相等来检验．5、如图，矩形ABCD的对角线AC，BD相交于点O，且DE∥AC，CE∥BD．求证：四边形OCED是菱形．答案：提示：一组邻边相等的平行四边形是菱形．6、如图，E，F，G，H分别是正方形ABCD各边的中点．四边形EFGH是什么四边形？为什么？答案：正方形．提示：证明四边形EFGH四边相等、四个角都是直角．7、如图，四边形ABCD是平行四边形，BE∥DF，且分别交对角线AC于点E，F，连接ED，BF．求证∠1=∠2．答案：由△ABE≌△CDF，可知BE=DF．又BE∥DF，所以四边形BFDE是平行四边形．所以DE∥BF，从而∠1=∠2．8、如图，ABCD是一个正方形花园，E，F是它的两个门，且DE=CF．要修建两条路BE和AF，这两条路等长吗？它们有什么位置关系？为什么？答案：由△ABE≌△DAF可知，BE和AF等长，并且互相垂直．9、我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形． （1）任意四边形的中点四边形是什么形状？为什么？（2）任意平行四边形的中点四边形是什么形状？为什么？（3）任意矩形、菱形和正方形的中点四边形分别是什么形状？为什么？答案：（1）平行四边形，利用三角形中位线定理可证一组对边平行且相等，或两组对边分别平行；（2）平行四边形；（3）菱形、矩形、正方形．10、如果一个四边形是轴对称图形，并且有两条互相垂直的对称轴，它一定是菱形吗？一定是正方形吗？答案：一定是菱形，不一定是正方形．11、用纸板剪成的两个全等三角形能够拼成什么四边形？要想拼成一个矩形，需要两个什么样的全等三角形？要想拼成菱形或正方形呢？动手剪拼一下，并说明理由．答案：平行四边形；要拼成一个矩形，需要两个全等的直角三角形；要拼成一个菱形，需要两个全等的等腰三角形；要拼成一个正方形，需要两个全等的等腰直角三角形．12、如图，过□ABCD的对角线AC的中点O作两条互相垂直的直线，分别交AB，BC，CD，DA于E，F，G，H四点，连接EF，FG，GH，HE．试判断四边形EFGH的形状，并说明理由．答案：菱形．提示：先证明△AOE≌△COG，△AOH≌△COF，可得OE=OG，OF=OH，所以四边形EFGH是平行四边形．又EG⊥FH，从而□EFGH是菱形．13、如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=26cm．点P从点A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以3cm/s的速度向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．从运动开始，使PQ∥CD和PQ=CD，分别需经过多少时间？为什么？答案：6s；6s或7s．提示：设经过ts，四边形PQCD成为平行四边形，根据PD=QC，可列方程24－t=3t，解得t=6．若PQ=CD，则四边形PQCD为平行四边形或梯形（腰相等），为平行四边形时有t=6；为梯形（腰相等）时，有QC=PD＋2（BC－AD），可列方程3t=24－t＋4，解得t=7．14、如图，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角的平分线CF于点F．求证AE=EF．答案：提示：证明△AGE≌△ECF．15、求证：平行四边形两条对角线的平方和等于四条边的平方和．答案：提示：如图，在□ABCD中，设AD=a，AB=b，BD=m，AC=n，DE=h，AE=x，则分别有h2=a2－x2 ①，h2=n2－（b＋x）2②，h2=m2－（b－x）2③，由①×2=②＋③，化简可得m2＋n2=2a2＋2b2．习题19.11、购买一些铅笔，单价为0.2元/支，总价y元随铅笔支数x变化．指出其中的常量与变量，自变量与函数，并写出表示函数与自变量关系的式子．答案：常量0.2，变量x，y，自变量x，函数y，y=0.2x．2、一个三角形的底边长为5，高h可以任意伸缩．写出面积S随h变化的解析式，并指出其中的常量与变量，自变量与函数，以及自变量的取值范围．答案：常量5，变量h，S，自变量h（h＞0），函数S，．3、在计算器上按下面的程序操作：填表：x13－40101－5.2y显示的计算结果y是输入数值x的函数吗？为什么？答案：7，11，－3，5，207，－5.4，y是x的函数，符合函数定义．4、下列式子中的y是x的函数吗？为什么？（1）y=3x－5；（2）；（3）．请再举出一些函数的例子．答案：y是x的函数，符合函数定义．例子略．5、分别对上一题中的各函数解析式进行讨论：（1）自变量x在什么范围内取值时函数解析式有意义？（2）当x=5时对应的函数值是多少？答案：（1）y=3x－5，x可为任意实数；，x≠1；，x≥1．（2）y=3x－5，x=5，y=10；，x=5，；，x=5，y=2． 6、画出函数y=0.5x的图象，并指出自变量x的取值范围．答案：自变量x的取值范围是全体实数．7、下列各曲线中哪些表示y是x的函数？答案：图（1）（2）（3）中y是x的函数，图（4）中y不是x的函数．8、“漏壶”是一种古代计时器．在它内部盛一定量的水，水从壶下的小孔漏出．壶内壁有刻度，人们根据壶中水面的位置计算时间．用x表示漏水时间，y表示壶底到水面的高度．下列哪个图象适合表示y与x的对应关系？（不考虑水量变化对压力的影响．）答案：图（2）．9、下面的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后散步走回家．图中x表示时间，y表示张强离家的距离． 根据图象回答下列问题：（1）体育场离张强家多远？张强从家到体育场用了多少时间？（2）体育场离文具店多远？（3）张强在文具店停留了多少时间？（4）张强从文具店回家的平均速度是多少？答案：（1）2.5km，15min；（2）1km；（3）20min；（4）．10、某种活期储蓄的月利率是0.06%，存入100元本金．求本息和y（本金与利息的和，单位：元）随所存月数x变化的函数解析式，并计算存期为4个月时的本息和．答案：y=100＋0.06x，100.24元．11、正方形边长为3．若边长增加x，则面积增加y．求y随x变化的函数解析式，指出自变量与函数，并以表格形式表示当x等于1，2，3，4时y的值．答案：y=x2＋6x，自变量x，函数y，x1234y716274012、甲、乙两车沿直路同向行驶，车速分别为20m/s和25m/s．现甲车在乙车前500m处，设xs（0≤x≤100）后两车相距ym．用解析式和图象表示y与x的对应关系．答案：y=500－5x（0≤x≤100）．13、甲、乙两车从A城出发前往B城．在整个行程中，汽车离开A城的距离y与时刻t的对应关系如下图所示．（1）A，B两城相距多远？（2）哪辆车先出发？哪辆车先到B城？（3）甲、乙两车的平均速度分别为多少？（4）你还能从图中得到哪些信息？ 答案：（1）300km；（2）甲先出发，乙先到达；（3）甲60km/h，乙100km/h；（4）6:00～7:30甲在乙前，7:30乙追上甲，7:30～9:00乙在甲前．14、在同一直角坐标系中分别画出函数y=x与的图象．利用这两个图象回答：（1）x取什么值时，x比大？（2）x取什么值时，x比小？答案：（1）－1＜x＜0或x＞1；（2）x＜－1或0＜x＜1．15、四边形有两条对角线，五边形、六边形分别有多少条对角线？n边形呢？多边形对角线的条数是边数的函数吗？答案：五边形有5条对角线，六边形有9条对角线，n边形有条对角线，多边形对角线的条数是边数的函数．习题19.21、一列火车以90km/h的速度匀速前进．求它的行驶路程s（单位：km）关于行驶时间t（单位：h）的函数解析式，并画出函数图象．答案：s=90t（t≥0）．图象略．2、函数y=－5x的图象在第__________象限内，经过点（0，__________）与点（1，__________），y随x的增大而__________．答案：二，四，0，－5，减小．3、一个弹簧不挂重物时长12cm，挂上重物后伸长的长度与所挂重物的质量成正比．如果挂上1kg的物体后，弹簧伸长2cm．求弹簧总长y（单位：cm）关于所挂物体质量x（单位：kg）的函数解析式． 答案：y=12＋2x（0≤x≤m，m是弹簧能承受物体的最大质量）．4、分别画出下列函数的图象：（1）y=4x；（2）y=4x＋1；（3）y=－4x＋1；（4）y=－4x－1．答案：（1）（2）（3）（4） 5、在同一直角坐标系中，画出函数y=2x＋4与y=－2x＋4的图象，并指出每个函数中当x增大时y如何变化．答案：y=2x＋4随x增大而增大，y=－2x＋4随x增大而减小．6、已知一次函数y=kx＋b，当x=2时y的值为4，当x=－2时y的值为－2，求k与b．答案：，b=1．7、已知一次函数的图象经过点（－4，9）和点（6，3），求这个函数的解析式．答案：．8、当自变量x取何值时，函数与y=5x＋17的值相等？这个函数值是多少？答案：，y=－15．9、点P（x，y）在第一象限，且x＋y=8，点A的坐标为（6，0）．设△OPA的面积为S．（1）用含x的式子表示S，写出x的取值范围，画出函数S的图象．（2）当点P的横坐标为5时，△OPA的面积为多少？（3）△OPA的面积能大于24吗？为什么？答案：（1）S=－3x＋24（0＜x＜8）；（2）9；（3）不能大于24，因为0＜x＜8，所以0＜S=－3x＋24＜24．10、不画图象，仅从函数解析式能否看出直线y=3x＋4与y=3x－4具有什么样的位置关系？答案：平行．11、从A地向B地打长途电话，通话时间不超过3min收费2.4元，超过3min后每分加收1元．写出通话费用y（单位：元）关于通话时间x（单位：min）的函数解析式．有10元钱时，打一次电话最多可以通话多长时间？（本题中x取整数，不足1min的通话时间按1min计费．）答案：由函数解析式得x=10.6．由不足1min的通话时间要按1min计算可知，有10元钱最多通话10min．12、（1）当b＞0时，函数y=x＋b的图象经过哪几个象限？（2）当b＜0时，函数y=－x＋b的图象经过哪几个象限？ （3）当k＞0时，函数y=kx＋1的图象经过哪几个象限？（4）当k＜0时，函数y=kx＋1的图象经过哪几个象限？答案：（1）第一、二、三象限；（2）第二、三、四象限；（3）第一、二、三象限；（4）第一、二、四象限．13、在同一直角坐标系中，画出函数和y=5x＋17的图象．并结合图象比较这两个函数的函数值的大小关系．答案：当时，14、图中的折线表示一骑车人离家的距离y与时间x的关系．骑车人9:00离开家，15:00回家．请你根据这个折线图回答下列问题：（1）这个人何时离家最远？这时他离家多远？（2）何时他开始第一次休息？休息多长时间？这时他离家多远？（3）11:00～12:30他骑了多少千米？（4）他在9:00～10:30和10:30～12:30的平均速度各是多少？（5）他返家时的平均速度是多少？（6）14:00时他离家多远？何时他距家9km？答案：（1）12:30～13:30，45km；（2）10:30，30min，30km；（3）15km；（4）20km/h，7.5km/h；（5）30km/h；（6）18km，14:30．15、甲、乙两家商场平时以同样价格出售相同的商品．春节期间两家商场都让利酬宾，其中甲商场所有商品按8折出售，乙商场对一次购物中超过200元后的价格部分打7折． （1）以x（单位：元）表示商品原价，y（单位：元）表示购物金额，分别就两家商场的让利方式写出y关于x的函数解析式；（2）在同一直角坐标系中画出（1）中函数的图象；（3）春节期间如何选择这两家商场去购物更省钱？答案：（1）甲商场y=0.8x（x≥0），乙商场（2）（3）当购物金额按原价小于600元时，在甲商场购物省钱；当购物金额按原价大于600元时，在乙商场购物省钱；当购物金额按原价等于600元时，在两商场购物花钱一样多．复习题191、小亮现已存款100元．为赞助“希望工程”，他计划今后三年每月存款10元．存款总金额y（单位：元）将随时间x（单位：月）的变化而改变．指出其中的常量与变量，自变量与函数，并写出函数解析式．答案：常量100，10，变量x，y，自变量x，函数y，y=100＋10x（0≤x≤36，x为整数）．2、判断下列各点是否在直线y=2x＋6上．这条直线与坐标轴交于何处？（－5，－4），（－7，20），，．答案：（－5，－4）和在直线y=2x＋6上，这条直线与坐标轴交于点（0，6），（－3，0）．3、填空：（1）直线经过第__________象限，y随x的增大而__________；（2）直线y=3x－2经过第__________象限，y随x的增大而__________．答案：（1）二、一、四，减小；（2）三、四、一，增大． 4、根据下列条件分别确定函数y=kx＋b的解析式：（1）y与x成正比例，当x=5时，y=6；（2）直线y=kx＋b经过点（3，6）与点．答案：（1）；2（2）．5、试根据函数y=3x－15的性质或图象，确定x取何值时：（1）y＞0；（2）y＜0．答案：（1）x＞5；（2）x＜5．6、在某火车站托运物品时，不超过1kg的物品需付2元，以后每增加1kg（不足1kg按1kg计）需增加托运费0.5元．设托运pkg（p为整数）物品的费用为c元．试写出c的计算公式．答案：c=0.5p＋1.5（p为正整数）．7、某水果批发市场规定，批发苹果不少于100kg时，批发价为2.5元/kg．小王携带现金3000元到这市场采购苹果，并以批发价买进．设购买的苹果为xkg，小王付款后还剩余现金y元．试写出y关于x的函数解析式，并指出自变量x的取值范围．答案：y=3000－2.5x（100≤x≤1200）8、匀速地向一个容器内注水，最后把容器注满．在注水过程中，水面高度h随时间t的变化规律如图所示（图中OABC为一折线）．这个容器的形状是下图中哪一个？匀速地向另两个容器注水时，你能画出水面高度h随时间t变化的图象（草图）吗？答案：图（3）．（1）（2） 9、已知等腰三角形周长为20．（1）写出底边长y关于腰长x的函数解析式（x为自变量）；（2）写出自变量取值范围；（3）在直角坐标系中，画出函数图象．答案：（1）y=20－2x（5＜x＜10）；（2）5＜x＜10；（3）10、已知点A（8，0）及在第一象限的动点P（x，y），且x＋y=10．设△OPA的面积为S．（1）求S关于x的函数解析式；（2）求x的取值范围；（3）当S=12时，求P点坐标；（4）画出函数S的图象．答案：（1）S=－4x＋40；（2）0＜x＜10；（3）P（7，3）；（4）图象略．11、（1）画出函数y=|x－1|的图象．（2）设P（x，0）是x轴上的一个动点，它与x轴上表示－3的点的距离为y．求y关于x的函数解析式，并画出这个函数的图象．答案：（1）（2）y=|x＋3|． 12、A，B两地相距25km．甲8:00由A地出发骑自行车去B地，平均速度为10km/h；乙9:30由A地出发乘汽车也去B地，平均速度为40km/h．（1）分别写出两个人的行程关于时刻的函数解析式；（2）乙能否在途中超过甲？如果能超过，何时超过？答案：（1）甲：y=10x－80，8≤x≤10.5；乙：y=40x－360，9.5≤x≤10.125．（2）10点以后乙超过甲．13、一个有进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分的进水量和出水量是两个常数．容器内的水量y（单位：L）与时间x（单位：min）之间的关系如图所示．（1）当0≤x≤4时，求y关于x的函数解析式．（2）当4＜x≤12时，求y关于x的函数解析式．（3）每分进水、出水各多少升？答案：（1）y=5x（0≤x≤4）；（2）；（3）进水5L/min；出水3.75L/min．14、一次越野赛跑中，当小明跑了1600m时，小刚跑了1450m．此后两人分别以am/s和bm/s匀速跑．又过100s时小刚追上小明，200s时小刚到达终点，300s时小明到达终点．这次越野赛跑的全程为多少米？答案：2050m．15、A城有肥料200t，B城有肥料300t．现要把这些肥料全部运往C，D两乡．从A城往C，D两乡运肥料的费用分别为20元/t和25元/t；从B城往C，D两乡运肥料的费用分别为15元/t和24元/t．现C乡需要肥料240t，D乡需要肥料260t，怎样调运可使总运费最少？答案：最佳方案：从A往D运200t，从B往C运240t，从B往D运60t．习题20.11、某公司有15名员工，他们所在部门及相应每人所创年利润如下表所示．部门人数每人所创年利润/万元A110 B38C75D43这个公司平均每人所创年利润是多少？答案：5.4万元．2、在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示．成绩/m1.501.601.651.701.751.80人数232341分别计算这些运动员成绩的平均数、中位数、众数（结果保留小数点后两位）．答案：1.67，1.70，1.75．3、为了检查一批零件的质量，从中随机抽取10件，测得它们的长度（单位：mm）如下：22.36　　22.35　　22.33　　22.35　　22.3722.34　　22.38　　22.36　　22.32　　22.35根据以上数据，估计这批零件的平均长度．答案：22.351mm．4、在一次青年歌手演唱比赛中，评分办法采用10位评委现场打分，每位选手的最后得分为去掉最低分、最高分后的平均数．已知10位评委给某位歌手的打分是：9.5　　9.5　　9.3　　9.8　　9.4　　8.8　　9.6　　9.5　　9.2　　9.6求这位歌手的最后得分．答案：9.45分．5、某商场招聘员工一名，现有甲、乙、丙三人竞聘．通过计算机、语言和商品知识三项测试，他们各自成绩（百分制）如下表所示．应试者计算机语言商品知识甲705080乙907545丙506085（1）若商场需要招聘负责将商品拆装上架的人员，对计算机、语言和商品知识分别赋权2，3，5，计算三名应试者的平均成绩．从成绩看，应该录取谁？（2）若商场需要招聘电脑收银员，计算机、语言、商品知识成绩分别占50%，30%，20%，计算三名应试者的平均成绩．从成绩看，应该录取谁？答案：（1）丙；（2）乙．6、某地某个月中午12时的气温（单位：℃）如下：22　　31　　25　　13　　18　　23　　13　　28　　30　　2220　　20　　27　　17　　28　　21　　14　　14　　22　　1218　　21　　29　　15　　16　　14　　31　　24　　26　　29（1）求这个月中午12时的平均气温（结果取整数）；（2）请以4为组距对数据分组，作出频数分布表，根据频数分布表计算这个月中午12时的平均气温，与（1）中的结果比较，你有什么发现，谈谈你的看法．答案：（1）21℃；（2）频数分布表： 根据频数分布表计算这个月中午12时的气温为22℃．这个结果与（1）中的结果（近似值）相差不大．平均数反映的是一组数据的平均水平，是一个统计估计值．7、为了提高农民收入，村干部带领村民自愿投资办起了一个养鸡场．办场时买来的1000只小鸡，经过一段时间精心饲养，可以出售了．下表是这些鸡出售时质量的统计数据．质量/kg1.01.21.51.82频数11222632324198（1）出售时这些鸡的平均质量是多少（结果保留小数点后一位）？（2）质量在哪个值的鸡最多？（3）中间的质量是多少？答案：（1）1.5kg；（2）1.5kg；（3）1.5kg．8、下图是交警在一个路口统计的某个时段来往车辆的车速情况．应用你所学的统计知识，写一份简短的报告让交警知道这个时段路口来往车辆的车速情况．答案：车速的平均数、中位数、众数分别为52.4，52，52．（答案不唯一，使用统计量描述了实际情境即可）．9、下表是某班学生右眼视力的检查结果．视力4.04.14.24.34.44.54.64.74.84.95.0人数12543511596分析上表中的数据，你能得出哪些结论？答案：本班学生的平均视力是4.6，视力是4.9的学生人数最多，一半以上的学生视力不超过4.65．习题20.21、甲、乙两台机床同时生产一种零件．在10天中，两台机床每天出次品的数量如下表．甲0102203124乙2311021101（1）分别计算两组数据的平均数和方差；（2）从计算的结果看，在10天中，哪台机床出次品的平均数较小？哪台机床出次品的波动较小？答案：（1）甲、乙两组数据的平均数分别为1.5和1.2，方差分别为1.65和0.76；（2）乙机床出次品的平均数较小，且出次品的波动较小．2、甲、乙两台包装机同时包装糖果．从中各抽出10袋，测得它们的实际质量（单位：g）如下表．甲501506508508497508506508507499乙505507505498505506505505506506（1）分别计算两组数据的平均数和方差；（2）哪台包装机包装的10袋糖果的质量比较稳定？答案：（1）甲、乙两组数据的平均数分别为504.8和504.8，方差分别为15.76和5.56；（2）乙包装机．3、为了考察甲、乙两种小麦的长势，分别从中随机抽取10株麦苗，测得苗高（单位：cm）如下表．甲12131415101613111511乙111617141319681016 （1）分别计算两种小麦的平均苗高；（2）哪种小麦的长势比较整齐？答案：（1）甲、乙两种小麦的平均苗高都是13cm；（2）甲种．4、在体操比赛中，往往在所有裁判给出的分数中，去掉一个最高分和一个最低分，然后计算余下分数的平均分．6个B组裁判员对某一运动员的打分数据（动作完成分）为：9.4，8.9，8.8，8.9，8.6，8.7．（1）如果不去掉最高分和最低分，这组数据的平均数和方差分别是多少（结果保留小数点后两位）？（2）如果去掉一个最高分和一个最低分，平均数和方差又分别是多少（结果保留小数点后两位）？（3）你认为哪种统计平均分的方法更合理？答案：（1）平均数为8.88，方差为0.06；（2）平均数为8.83，方差为0.01；（3）去掉一个最高分与一个最低分进行统计平均数的方法更合理，因为方差更小，减少了数据受极端值的影响．复习题201、某水库为了解某种鱼的生长情况，从水库中捕捞了20条这种鱼，称得它们的质量（单位：kg）如下：1.15　1.04　1.11　1.07　1.10　1.32　1.251.191.151.211.181.141.091.251.211.291.161.241.121.16计算样本平均数（结果保留小数点后两位），并根据计算结果估计水库中这种鱼的平均质量．答案：样本平均数约为1.17kg，估计水库中这种鱼的平均质量约为1.17kg．2、在一次智力抢答比赛中，四个小组回答正确的情况如下图．这四个小组平均正确回答多少道题目（结果取整数）？答案：这四个小组平均正确回答约12道题．3、为了解某一路口的汽车流量，调查了10天中同一时段通过该路口的汽车数量（单位：辆），结果如下：183　209　195178204215191208167197在该时段中，平均约有多少辆汽车通过这个路口？答案：平均约有195辆汽车通过这个路口．4、一家公司14名员工的月薪（单位：元）是：8000　6000　2550　1700　25504599　42002550　5100　2500　4400　25000124002500（1）计算这组数据的平均数、中位数和众数；（2）解释本题中平均数、中位数和众数的意义．答案：（1）这组数据的平均数为6003.5，中位数为4300，众数为2550；（2）14名员工的月平均工资是6003.5元，约有一半员工的月薪在4300元以下，月薪为2550元的员工最多．5、某年A，B两座城市四季的平均气温（单位：℃）如下表．城市春夏秋冬A－4199－10 B16302411（1）分别计算A，B两座城市的年平均气温（结果取整数）；（2）哪座城市四季的平均气温较为接近？答案：（1）A，B两座城市的年平均气温分别约为4℃和20℃；（2）城市B四季的平均气温较为接近．6、下表是两种股票一周内的交易日收盘价格（单位：元/股）．星期一星期二星期三星期四星期五A股票11.6211.5111.3911.9411.17B股票13.5314.0713.4913.8414.80计算它们的平均数和方差（结果保留小数点后两位），比较这两种股票在这段时间内的涨跌变化情况．答案：A，B两种股票在某周的交易日收盘价格的平均数分别是11.53和13.95，方差分别是0.07和0.23，在这段时间内B种股票的涨、跌幅度更大．7、甲、乙两门大炮在相同条件下向同一目标各发射50发炮弹，炮弹落点情况如下表．炮弹落点与目标的距离/m403020100甲炮发射的炮弹个数013739乙炮发射的炮弹个数132341（1）分别计算两门大炮所发射的炮弹落点与目标的距离的平均数；（2）哪门大炮射击的准确性好？答案：（1）甲、乙两门大炮所发射的炮弹落点与目标距离的平均数分别是3.2m和4m；（2）甲炮．'