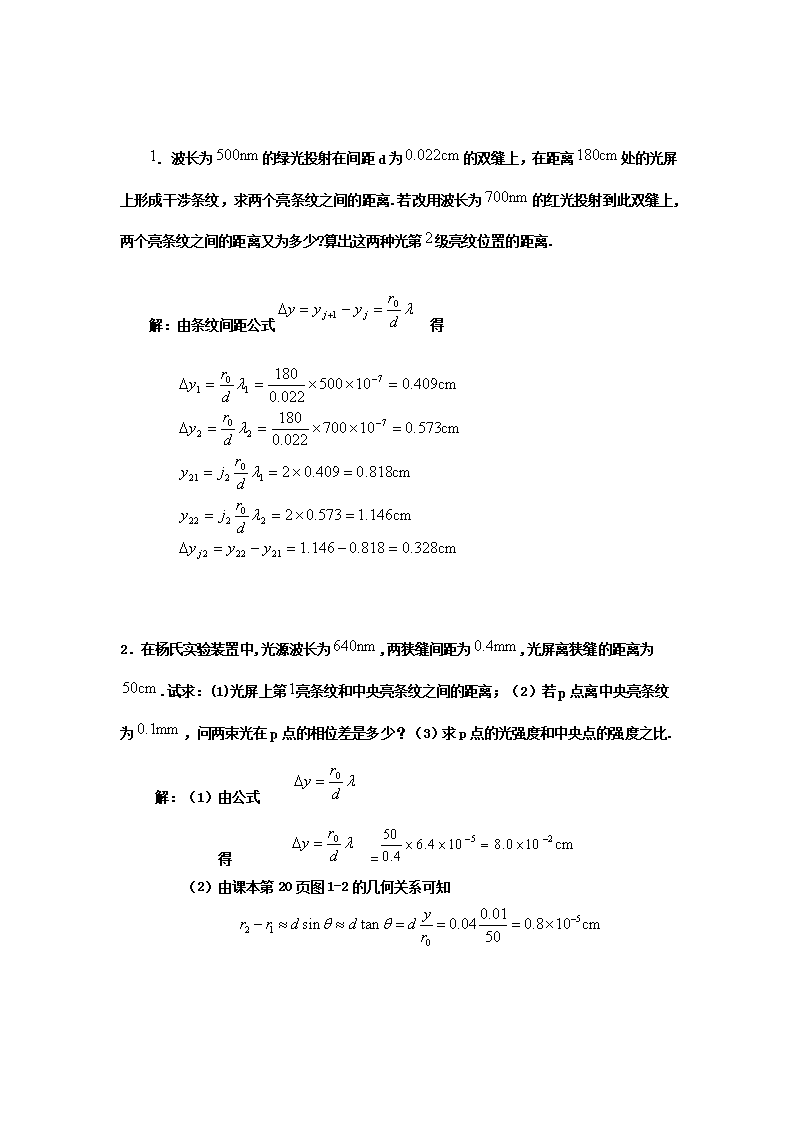姚启钧编著的《光学教程》(第四版)课后习题答案.doc 12页

'                       .波长为的绿光投射在间距d为的双缝上，在距离处的光屏上形成干涉条纹，求两个亮条纹之间的距离.若改用波长为的红光投射到此双缝上,两个亮条纹之间的距离又为多少?算出这两种光第级亮纹位置的距离.解：由条纹间距公式 得 2．在杨氏实验装置中,光源波长为,两狭缝间距为,光屏离狭缝的距离为.试求：(1)光屏上第亮条纹和中央亮条纹之间的距离；（2）若p点离中央亮条纹为，问两束光在p点的相位差是多少？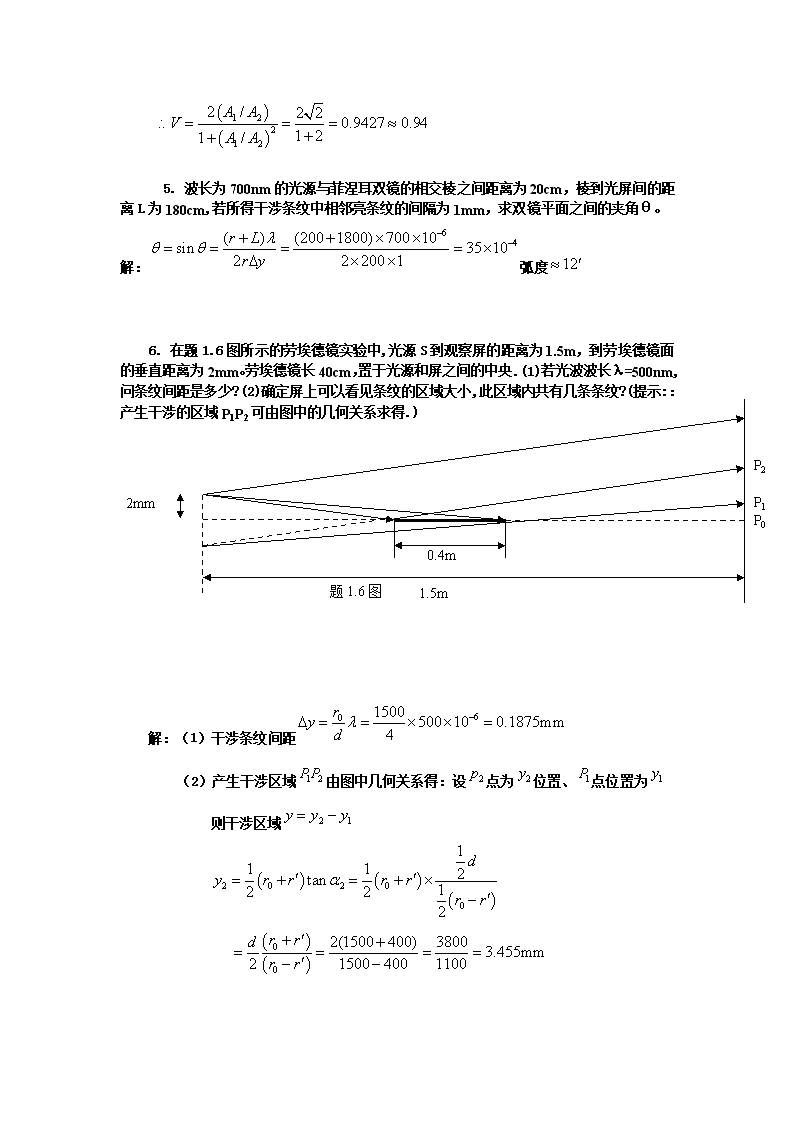（3）求p点的光强度和中央点的强度之比.解：（1）由公式 得  =（2）由课本第20页图1-2的几何关系可知     由公式 得         .把折射率为1.5的玻璃片插入杨氏实验的一束光路中,光屏上原来第5级亮条纹所在的位置为中央亮条纹,试求插入的玻璃片的厚度.已知光波长为6×10-7m.解：未加玻璃片时，、到点的光程差，由公式可知为Δr=现在发出的光束途中插入玻璃片时，点的光程差为所以玻璃片的厚度为4.波长为500nm的单色平行光射在间距为0.2mm的双狭缝上.通过其中一个缝的能量为另一个的2倍,在离狭缝50cm的光屏上形成干涉图样.求干涉条纹间距和条纹的可见度.解：            　5.波长为700nm的光源与菲涅耳双镜的相交棱之间距离为20cm，棱到光屏间的距离L为180cm,若所得干涉条纹中相邻亮条纹的间隔为1mm，求双镜平面之间的夹角θ。解：弧度6.在题1.6图所示的劳埃德镜实验中,光源S到观察屏的距离为1.5m，到劳埃德镜面的垂直距离为2mm。劳埃德镜长40cm，置于光源和屏之间的中央.(1)若光波波长λ=500nm,问条纹间距是多少?(2)确定屏上可以看见条纹的区域大小,此区域内共有几条条纹?(提示:：产生干涉的区域P1P2可由图中的几何关系求得.)2mm0.4m1.5mP2P1P0题1.6图          　　解：（1）干涉条纹间距（2）产生干涉区域由图中几何关系得：设点为位置、点位置为则干涉区域           （3）劳埃镜干涉存在半波损失现象暗  亮暗条亮纹7.试求能产生红光(λ=700nm)的二级反射干涉条纹的肥皂膜厚度.已知肥皂膜折射率为1.33,且平行光与发向成30°角入射.解：根据题意8.透镜表面通常镀一层如MgF2（n=1.38）一类的透明物质薄膜，目的是利用干涉来降低玻璃表面的反射．为了使透镜在可见光谱的中心波长（550nm）处产生极小的反射,则镀层必须有多厚?解：可以认为光是沿垂直方向入射的。即   由于上下表面的反射都由光密介质反射到光疏介质，所以无额外光程差。因此光程差如果光程差等于半波长的奇数倍即公式 ，则满足反射相消的条件因此有         所以        当时厚度最小   9.在两块玻璃片之间一边放一条厚纸,另一边相互压紧.玻璃片l长10cm,纸厚为0.05mm,从60°的反射角进行观察,问在玻璃片单位长度内看到的干涉条纹数目是多少?设单色光源波长为500nm.解：由课本49页公式（1-35）可知斜面上每一条纹的宽度所对应的空气尖劈的厚度的变化量为           如果认为玻璃片的厚度可以忽略不记的情况下，则上式中。而厚度h所对应的斜面上包含的条纹数为                   故玻璃片上单位长度的条纹数为            条/厘米10.在上题装置中,沿垂直于玻璃片表面的方向看去,看到相邻两条暗纹间距为1.4mm。—已知玻璃片长17.9cm,纸厚0.036mm,求光波的波长。解:依题意,相对于空气劈的入射角    11.波长为400760nm的可见光正射在一块厚度为1.2×10-6m,折射率为1.5玻璃片上,试问从玻璃片反射的光中哪些波长的光最强.解：依题意，反射光最强即为增反膜的相长干涉，则有： 故     当时， 当时，     当时，   当时，当时，当时，当时，当时，当时，当时，所以，在的可见光中，从玻璃片上反射最强的光波波长为12.迈克耳孙干涉仪的反射镜M2移动0.25mm时，看到条纹移过的数目为909个，设光为垂直入射，求所用光源的波长。解：根据课本59页公式可知，迈克耳孙干涉仪移动每一条条纹相当h的变化为：现因， 故 所对应的h为     故    13.迈克耳孙干涉仪平面镜的面积为４×４cm2，观察到该镜上有20个条纹。当入射光的波长为589nm时，两镜面之间的夹角为多大？解：因为 所以 所以 又因为 所以 14.调节一台迈克耳孙干涉仪，使其用波长为500nm的扩展光源照明时会出现同心圆环条纹。若要使圆环中心处相继出现1000条圆环条纹，则必须将移动一臂多远的距离？若中心是亮的，试计算第一暗环的角半径。（提示：圆环是等倾干涉图样。计算第一暗环角半径是可利用θ≈sinθ及cosθ≈1－θ2/2的关系。）解：（1）因为光程差δ每改变一个波长λ的距离，就有一亮条A纹移过。所以 又因为对于迈克耳孙干涉仪光程差的改变量（Δd为反射镜移动的距离）所以 所以 （2）因为迈克耳孙干涉仪无附加光程差并且     它形成等倾干涉圆环条纹，假设反射面的相位不予考虑所以光程差   即两臂长度差的2倍若中心是亮的，对中央亮纹有：   （1）对第一暗纹有：     （2）（2）-（1）得： 所以 这就是等倾干涉条纹的第一暗环的角半径，可见是相当小的。15.用单色光观察牛顿环，测得某一亮环的直径为3mm，在它外边第5个亮环的直径为4.6mm，所用平凸透镜的凸面曲率半径为1.03m，求此单色光的波长。解：对于亮环，有  （）所以       所以 16.在反射光中观察某单色光所形成的牛顿环。其第2级亮环与第3级亮环间距为1mm，求第19和20级亮环之间的距离。解：对于亮环，有  （）所以           又根据题意可知      两边平方得      所以  故                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                      17牛顿环可有两个曲率半径很大的平凸透镜之间的空气产生（图）。平凸透镜A和B的曲率半径分别为和，在波长为600nm的单射光垂直照射下观察到第10个暗环半径。若另有曲率半径为的平凸透镜C（图中未画出），并且B、C组合和A、C组合产生的第10个暗环半径分别为和，试计算、和。解：RARBOAOBrABdAB题1.17图又对于暗环： 即        (1)       (2)       (3) (1)(2)(3)联立并代入数据得：=6.28m =4.64m =12.4m18菲涅尔双棱镜实验装置尺寸如下：缝到棱镜的距离为5cm，棱镜到屏的距离为95cm，棱镜角为构成棱镜玻璃材料的折射率，采用的是单色光。当厚度均匀的肥皂膜横过双冷静的一半部分放置，该系统中心部分附近的条纹相对原先有0.8mm的位移。若肥皂膜的折射率为,试计算肥皂膜厚度的最小值为多少？解：如图所示：光源和双棱镜系统的性质相当于相干光源和，它们是虚光源。由近似条件 和   得 (1)SS1S2dθαA1l1n’(a)y∙∙dS1S2r0n(b)题1.18图 按双棱镜的几何关系得     所以   (2) 肥皂膜插入前，相长干涉的条件为    (3)由于肥皂膜的插入，相长干涉的条件为   (4)由(3)和(4)得  代入数据得 19将焦距为50cm的会聚透镜中央部分C切去（见题图），余下的A、B两部分仍旧粘起来，C的宽度为1cm。在对称轴线上距透镜25cm处置一点光源，发出波长为692nm的红宝石激光，在对称轴线上透镜的另一侧50cm处置一光屏，平面垂直于轴线。试求：ABC题1.19图(1)干涉条纹的间距是多少？(2)光屏上呈现的干涉图样是怎样的？解：(1)   透镜由A、B两部分粘合而成，这两部分的主轴都不在该光学系统的中心轴线上，A部分的主轴在中心线上0.5cm处，B部分的主轴在中心线下0.5cm处，由于单色点光源P经凸透镜A和B所成的像是对称的，故仅需考虑P经B的成像位置即可。由  得由因为 所以 即所成的虚像在B的主轴下方1cm处，也就是在光学系统对称轴下方0.5cm处，同理，单色光源经A所成的虚像在光学系统对称轴上方0.5cm处，两虚像构成相干光源，它们之间的距离为1cm，所以 (2)光屏上呈现的干涉条纹是一簇双曲线。ABPLALB•题1.20图20 将焦距为5cm的薄透镜L沿直线方向剖开（见题图）分成两部分A和B，并将A部分沿主轴右移至2.5cm处，这种类型的装置称为梅斯林对切透镜。若将波长为632.8nm的点光源P置于主轴上离透镜LB距离为10cm处，试分析：(1)成像情况如何？(2)若在LB右边10.5cm处置一光屏，则在光屏上观察到的干涉图样如何？               解：（1）如图（b）所示,该情况可以看作由两个挡掉一半的透镜LA和LB构成,其对称轴为PO,但是主轴和光心却发生了平移.对于透镜LA,其光心移到OA处,而主轴上移0.01cm到OAFA;对于透镜LB,其光心移到OB处,而主轴下移0.01cm到OBFB.点光源P恰恰在透镜的对称轴上二倍焦距处.由于物距和透镜LA、LB的焦距都不变,故通过LA、LB成像的像距也不变。根据物像公式将p=-10cm和=5cm代入上式，得=5cm==-1 故=-0.01cm由于P点位于透镜LA的光轴下方0.01cm,按透镜的成像规律可知,实像PA应在透镜LA主轴上方0.01cm处;同理,P点位于透镜LB主轴上方0.01cm处,实像PB应在主轴下方0.01cm处.两像点的距离为上方0.01cm处.PAPB=d=2||+   =0.04cm(2)由于实像PA和PB构成了一对相干光源,而且相干光束在观察屏的区域上是相互交叠的,故两束光叠加后将发生光的干涉现象,屏上呈现干涉花样.按杨氏干涉规律,两相邻亮条纹的间距公式为          将数据代入得=1.582mm21 如图所示，A为平凸透镜，B为平玻璃板，C为金属柱，D为框架，A、B间有空隙，图中绘出的是接触的情况，而A固结在框架的边缘上。温度变化时，C发生伸缩，而假设A、B、D都不发生伸缩。以波长632.8nm的激光垂直照射。试问：(1)在反射光中观察时，看到牛顿环条纹移向中央，这表示金属柱C的长度在增加还是减小？(2)若观察到有10个亮条纹移向中央而消失，试问C的长度变化了对少毫米？ 解：（1）因为:在反射光中观察牛顿环的亮条纹，及干涉级j随着厚度h的增加而增大，即随着薄膜厚度的增加，任意一个指定的j级条纹将缩小其半径，所以各条纹逐渐收缩而在中心处消失，膜厚h增加就相当于金属的长度在缩短。所以，看到牛顿环条纹移向中央时，表明C的长度在减少。（2）由CBAD题1.21图    得. '