清华版《运筹学》(第三版)课后习题详解、....pdf 51页

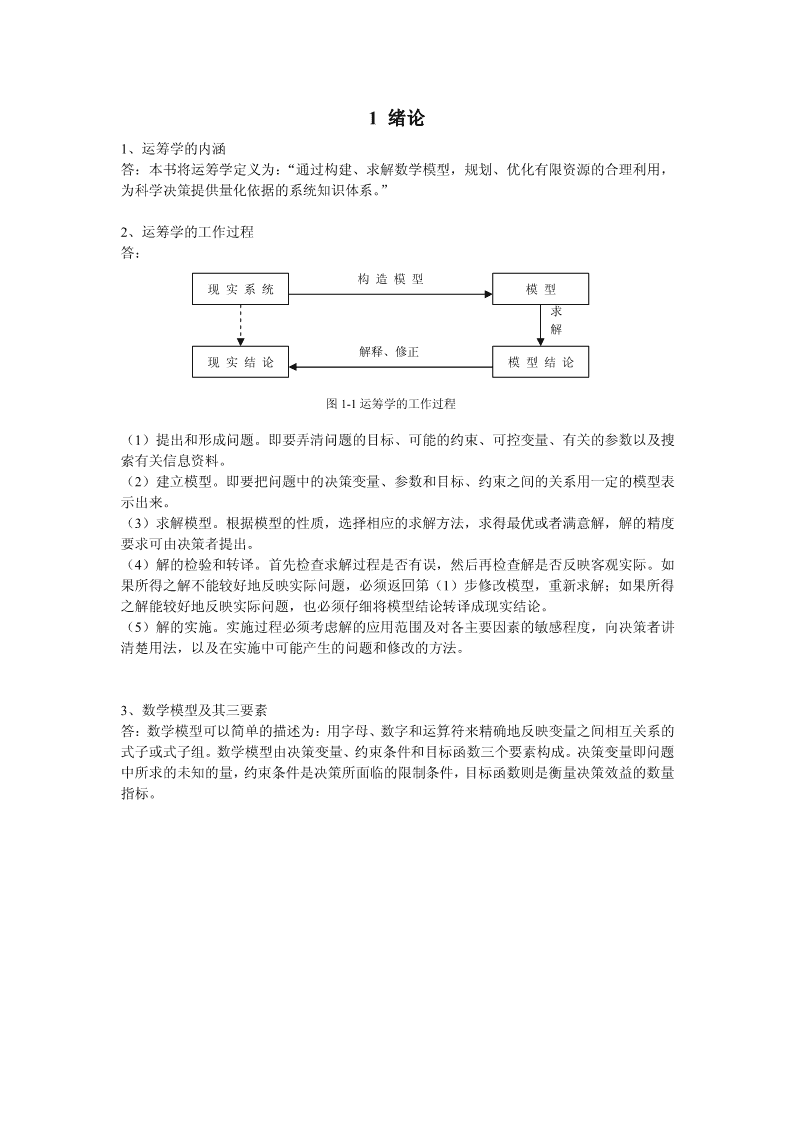
' 1绪论1、运筹学的内涵答：本书将运筹学定义为：“通过构建、求解数学模型，规划、优化有限资源的合理利用，为科学决策提供量化依据的系统知识体系。”2、运筹学的工作过程答：构造模型现实系统模型求解解释、修正现实结论模型结论图1-1运筹学的工作过程（1）提出和形成问题。即要弄清问题的目标、可能的约束、可控变量、有关的参数以及搜索有关信息资料。（2）建立模型。即要把问题中的决策变量、参数和目标、约束之间的关系用一定的模型表示出来。（3）求解模型。根据模型的性质，选择相应的求解方法，求得最优或者满意解，解的精度要求可由决策者提出。（4）解的检验和转译。首先检查求解过程是否有误，然后再检查解是否反映客观实际。如果所得之解不能较好地反映实际问题，必须返回第（1）步修改模型，重新求解；如果所得之解能较好地反映实际问题，也必须仔细将模型结论转译成现实结论。（5）解的实施。实施过程必须考虑解的应用范围及对各主要因素的敏感程度，向决策者讲清楚用法，以及在实施中可能产生的问题和修改的方法。3、数学模型及其三要素答：数学模型可以简单的描述为：用字母、数字和运算符来精确地反映变量之间相互关系的式子或式子组。数学模型由决策变量、约束条件和目标函数三个要素构成。决策变量即问题中所求的未知的量，约束条件是决策所面临的限制条件，目标函数则是衡量决策效益的数量指标。 2线性规划1、试述线性规划数学模型的组成部分及其特性答：线性规划数学模型由决策变量、约束条件和目标函数三个部分组成。线性规划数学模型特征：（1）用一组决策变量表示某一方案，这组决策变量均为非负的连续变量；（2）存在一定数量（m）的约束条件，这些约束条件可以用关于决策变量的一组线性等式或者不等式来加以表示；（3）有一个可以用决策变量加以表示的目标函数，而该函数是一个线性函数。2、一家餐厅24小时全天候营业，在各时间段中所需要的服务员数量分别为：2：00~6：003人6：00~10：009人10：00~14：0012人14：00~18：005人18：00~22：0018人22：00~2：004人设服务员在各时间段的开始时点上上班并连续工作八小时，问该餐厅至少配备多少服务员，才能满足各个时间段对人员的需要。试构造此问题的数学模型。解：用决策变量x,x,x,x,x,x分别表示2：00~6：00，6：00~10：00，10：00~14：12345600，14：00~18：00，18：00~22：00，22：00~2：00时间段的服务员人数。其数学模型可以表述为：minZ=xxxxxx+++++123456xx+>=316xx+>=912xx+>=1223xx+>=534xx+>=1845xx+>=456xxxxxx,,,,,≥01234563、现要截取2.9米、2.1米和1.5米的元钢各100根，已知原材料的长度是7.4米，问应如何下料，才能使所消耗的原材料最省。试构造此问题的数学模型。解：圆钢的截取有不同的方案，用θ表示每种切割方案的剩余材料。其切割方案如下所示：2.92.11.5θ1"1110.92"2000.13"1200.34"10305"0130.86"0041.47"0220.28"0301.1目标函数为求所剩余的材料最少，即 minZ=+++++++0.9xxxxxxx0.10.300.81.40.21.1x12345678xxxx+++>2=1001234xxxxx++++>223=10013578xxxxxx+++++>3342=100124567xxxxxxxx,,,,,,,0≥123456784、某糖果厂用原料A、B、C加工成三种不同牌号的糖果甲、乙、丙。已知各种牌号糖果中A、B、C三种原料的含量要求、各种原料的单位成本、各种原料每月的限制用量、三种牌号糖果的单位加工费及售价如表1所示。问该厂每月生产这三种牌号糖果各多少千克，才能使该厂获利最大？试建立这个问题的线性规划模型。表1甲乙丙原料成本限制用量A60%以上15%以上2.002000B1.502500C20%以下60%以下50%以下1.001200加工费0.500.400.30售价3.402.852.25解：以甲表示甲产品中的A成分，甲表示甲产品中的B成分，甲表示甲产品中的CABC成分，依此类推。据表2-16，有：31331甲甲>=，甲甲<=，乙乙>=，乙乙<=，丙<=丙．．．．．．①ACACA552052其中：甲+甲甲甲+=，乙+乙乙乙+=，丙+丙丙丙+=．．．．．．②ABCABCABC把②逐个代入①并整理得：217−+甲+甲甲<=0，−+甲-甲40甲<=，-乙+乙乙+<=0ABCABCABC332-乙-乙+<乙=0，-丙-丙+丙<=0ABCABC3原材料的限制，有以下不等式成立：甲+乙丙+<=2000，甲+乙丙+<=2500，甲+乙丙+<=1200AAABBBCCC在约束条件中共有9个变量，为方便计算，分别用x,x．．．x表示，即令x=甲，1291Ax=甲，x=甲，x=乙，x=乙，x=乙，x=丙，x=丙，x=丙2B3C4A5B6C7A8B9C由此约束条件可以表示为： 2-xxx++<=01233-x-x+<4x=012317-xxx0++<=45632-x-x+=0123456789我们的目的是使利润最大，即产品售价减加工费再减去原材料的价格为最大。目标函数为MaxZ=+++++−++0.9x1.4x1.9x0.45x0.95x1.45x0.05x0.45x0.95x1234567895、某厂在今后4个月内需租用仓库存放物资，已知各个月所需的仓库面积如表2所示。租金与租借合同的长短有关，租用的时间越长，享受的优惠越大，具体数字见表3。租借仓库的合同每月初都可办理，每份合同具体规定租用面积数和期限。因此该厂可根据需要在任何一个月初办理租借合同，且每次办理时，可签一份，也可同时签若干份租用面积和租借期限不同的合同，总的目标是使所付的租借费用最小。试根据上述要求，建立一个线性规划的数学模型。表2月份12342所需面积（100m）15102012表3合同租借期限1个月2个月3个月4个月2单位（100m）租金（元）2800450060007300解：设x（i＝1,2,3,4;j=1,2．．．4-i+1）为第i个月初签订的租借期限为j个月的合同租借面ij22积（单位：100m）；r表示第i个月所需的面积（j表示每100m仓库面积租借期为j个月i的租借费）；则线性规划模型为：441−+iMinZ=∑∑CXjijij==11 ki41−+∑∑Xrij>=k(k=1,2,3,4)ij==−11ki+Xi>=0(=1,2,3,4;j=1,2...4−+i1)ij6、某农场有100公顷土地及25万元资金可用于发展生产。农场劳动力情况为秋冬季4500人日，春夏季6000人日，如劳动力本身过剩可外出打工，春夏季收入为20元／人日，秋冬季12元／人日。该农场种植三种作物：大豆、玉米和小麦，并饲养奶牛和鸡。种作物不需要专门投资，而饲养动物时每头奶牛投资8000元，每只鸡投资2元。养奶牛时每头需拨出1.5公顷土地种饲草，并占用人工秋冬季为100人日，春夏季为50人日，年净收入3000元／每头奶牛。养鸡不占土地，需人工为每只鸡秋冬季0.3人日，春夏季0.1人日，年净收入为每只8元。农场现有鸡舍允许最多养5000只鸡，牛栏允许最多养50头奶牛，三种作物每年需要的人工及收入情况如表4所示。试决定该农场的经营方案，使年净收入最大。表4大豆玉米麦子每公顷秋冬季所需人日数203510每公顷春夏季所需人日数507540年净收入（元/公顷）11001500900解：设x,x,x分别代表大豆、玉米、麦子的种植数（公顷）；x,x分别代表奶牛和鸡的12345饲养数；x,x分别代表秋冬季和春夏季多余的劳动力（人．日数）则有67MaxZ=++++1100x1500x900x3000x8x++12x20x1234567xx++1.5x<=100(土地限制)1248000xx+<2=250000(资金限制）4520xxxxxx+++++<35101000.3=4500(劳动力限制）12345650xxxxxx+++++<7540500.1=4500(劳动力限制）123457x<=50(牛栏限制）4x<=5000（鸡栏限制）5x,x,x,x,x,x,x>=01234567 7、用图解法求解下列线性规划问题（1）maxz=2x+x（2）maxz=3x+2x12124x+3x≤12−x+2x≤412122x+x≤83x+2x≤1412124x−x≤8x−x≤31212x,x≥0x,x≥01212（3）maxz=2x+3x（4）maxz=x+x1212x−x≤2x−x≥01212−3x+x≤43x−x≤−31212x,x≥0x,x≥01212解：（1）（2）8844*9Q(,1)4234234此题有唯一最有解，此题有无穷多最有解，其*9T*TX=(,1)中一个是X=(4,1)4 （3）（4）432424找不到可行域，此题为无此题为无界解可行解8、考虑线性规划：maxz=2x−x+x+x1234−x+x+x+x=51234x+x+x=21252x+x+x+x=61236x,Λ,x≥016（1）通过观察写出初始的基可行解并构造初始单纯形表；（2）在保持x和x为零的情况下，给出非基变量x增加一个单位时的可行解，并231指出目标函数的净增量是多少?（3）在模型约束条件的限制下，x的最大增量是多少？1（4）在x有其最大增量时，给出一个新的基可行解。1T解：（1）因存在初始可行基(x,,xx)，故可令x,x,x全为0,则可得初始可行解为456123T(0,0,0,5,2,6)，Z＝5。初始单纯行表为：cj2-11100bCBXBx1x2x3x4x5x61x4-11110050x51100102 0x62110016σj3-20000z=0(2)非基变量x,x仍然取零，x由0变为1,即x＝1,x＝0,x=0,代入约束条件得一个可231123T行解X=(1,0,0,6,1,4)。其目标函数值为Z＝8因此，随着x增加1个单位目标函数值的净增量为△Z＝8-5=3.1（3）因为决策变量全非负所以由约束条件①知x增加可以引起x,x,x增加，即条件①对1234x无约束；由约束条件②知x增加可引起x,x减少，由非负约束知x最大增量为2；同理11251可得约束条件③的x最大增量为3，综合得x的最大增量为2。11T（4）x＝2，非基变量x=0,x＝0,代入约束条件得基可行解X=(2,0,0,7,2,2)，目标函123数值为Z＝11。9、将线性规划模型转化为标准形式maxZ=2x+x+3x+x1234x+x+2x+x≤1012342x−3x+5x−x=−81234x+x−6x+4x≥121234x,x,x≥0，x无约束1234解：（1）令x＝x－x并代入模型，这里x>=0,x>=0；45656（2）第二个约束条件方程两侧同乘“-1”；（3）第一个约束条件引入松弛变量x，第三个约束条件引入x作为松弛变量。78（4）目标函数同乘“-1”，即可实现最少化。minZ=−−−−+2xxxxx312356 xxxxxx+++−+=210123567−+−+=235xxxx81236xxxxxx+−+−−=64412123568xxxxxxxx,,,,,,,≥01234567810、用单纯形法求解下述线性规划问题（1）minw=3x+x+x+x（2）maxZ=4x+5x+x1234123−2x+2x+x=43x+2x+x≥181231233x+x+x=62x+x≤412412x,x,x,x≥0x+x−x=51234123x,x,x≥0123（1）解：构造初始单纯行表，并进行初等变换，得：cj3111bCBXBx1x2x3x41x3-2（2）1041x431016σj2-200w=101x2-111/2021x440-1/214σj0010w=6*T最优解X=(0,2,0,4)，由非基变量x的检验数为0,知此问题有无穷多最有解，所以该解1为无穷多最优解中的一个，最优值为w＝6。（2）解：此问题用大M法求解，先把问题标准化为：minZ=−4xxxM−5−+xM+x1236732xxxxx++−+=181234624xxx++=125xxxx+−+=51237xxxxxxx,,,,,,≥01234567构造初始单纯行表，并进行初等变换，得： cj-4-5-100MMbCBXBx1x2x3x4x5x6x7Mx6321-1010180x5(2)1001004Mx711-100015σj-4-4M-5-3M-1M000Mx601/21-1-2/31012-4x11(1/2)001/2002Mx701/2-10-1/2013σj0-5-1M2M+200Mx6-10(1)-1-21010-5x221001004Mx7-10-10-1011σj2M-40-1M3M+500-1x3-101-1-21010-5x221001004Mx7-200-1-31111σj2M+500M-13M+310因为所有检验数均为非负，但人工变量x仍为基变量，故此问题无解。711、求解线性规划问题并给出其中三个最优解：minw=3x+x+x+x1234−2x+2x+x=41233x+x+x=6124x,x,x,x≥01234解：构造初始单纯行表，并进行初等变换，得：cj3111bCBXBx1x2x3x41x3-2（2）1041x431016σj2-200w=10 1x2-111/2021x4(4)0-1/214σj0010w=61x2013/81/433x110-1/81/41σj0010w=6*T*T从单纯形表可以找到两个顶点，X=(0,2,0,4)，X=(1,3,0,0)。可以找到变量之间12存在以下关系：x＝x＋2；x＝－4x＋4；x=021413*T令x＝1/2则有X=(1/2,5/2,0,2)，从而找到了LP问题的三个最优解。1312、（1）如为唯一最优解则要求非基变量的检验数全少于零，从而有β<0，β<0。并且要12令表中的解为最优解，则要求原问题可行，这只要满足ρ>=0即可。（2）要令表中解为无穷多最优解中的一个，则有以下关系成立：β<=0，β<=0，且ββ=01212若β=0，则∂>0。21（3）要使表中的解为退化的基可行解，则必有ρ=0；当β>β且β>0时，∂>0。2121（4）若为无界解，则满足能找到入基变量，但找不到出基变量的条件。即满足：ρ>=0；β>β，且β>0；∂<=0。2121（5）以x代替x，即x入基，x出基，则有以下关系成立：β>β，且β>0；∂>=0；161612133ρρ>=0，且0<<。∂43 3线性规划的对偶问题1．试从经济角度解释对偶变量的含义。答：假设有一企业欲将另一个企业拥有的资源收买过来，至少应付出多少代价，才能使此企业愿意放弃生产活动，出让资源。显然后者放弃自己组织生产活动的条件时，对同等数量资源出让的代价不低于该企业自己组织生产活动是的产值。2．判断下列说法是否正确（1）任何线性规划问题都存在其对偶问题（正确）（2）如果原问题存在可行解，则其对偶问题也一定存在可行解；（错）（3）当原问题为无界解时，对偶问题也为无界解；（错）（4）当对偶问题无可行解时，原问题一定具有无界解；（错）（5）若原问题有无穷多最优解，则对偶问题也一定具有无穷多最优解（错）3写出下列线性规划问题的对偶问题：（1）minw=2x+2x+4x123x+2x+x≥21232x+x+3x≤6123x+4x+6x≤5123x,x,x≥0123解：maxwyyy=++65123yyy++≤2212324yyy++≤2123yyy++≤364123yyy≥≥≥0,0,0123（2）max=2x+3x+x123x+2x+x≥101233x+2x≤1513x+2x+x=12123x≥,0x≤,0x无约束123 解：minwyy=10++1512y123yyy++≥32123223yy+≤13yyy++=21123yyy≤≥0,0,无约束1234.用对偶单纯形法求解下述线性规划问题（1）minw=4x+12x+18x（2）minw=x+2x+3x+4x1231234x+3x≥3x+2x+2x+3x≥301312342x+2x≥52x+x+3x+2x≥20231234x,x,x≥0x,x,x,x≥01231234（1）转换化成标准形式：minwxxx=++41218123xxx+−=3313422xxx+−=5235x≥01~5cj4121800bCBXBx1x2x3x4x50x4-10-310-30x50-2-201-5σj412180018x31/301-11/30112x2-1/3101/3-1/22/3σj201026W=36X=(0,2/3,1,0,0)(2)转化为标准形式minwxxxx=+++231234xxxxx+++−=223301234523xxxxx+++−=22012346x≥01~6cj123400b CBXBx1x2x3x4x5x60x5-1-2-2-310-300x6-2-1-3-201-20σj1234001x11223-1010x60314-212/3σj001110W=30X＝(30,0,0,0,0,40)minz=305（1）由最终单纯形表可知，为保持原最优解不变应有：σ=−−−1(3C−≥5)0211σ=−(1C+≥)0解不等式组得：C∈[−−6,3]4131σ=−−(2C−)≥0513(2)将C1=2直接反映进单纯形表中：cj-2-1-500bCBXBx1x2x3x4x5-2x11-1/301/3-1/35-5x3011-1/52/53σj010/30-1/34/30x43-101-115-5x33/54/5101/56σj13051-30X=(0,0,6,15,0)maxz=30(3)因为原材料的市场价格0.8小于原材料的影子价格1，所以，可以买进原材料。假设买进⎛⎞11−⎛⎞85⎜⎟33⎛⎞45原材料100单位，则此公司拥有原材料的总额为130。b´＝⎜⎟⎜⎟=⎜⎟3⎜⎟12⎝⎠130⎜⎟⎜⎟⎜⎟⎝⎠111⎝⎠55将b´反映进单纯形表中：cj-3-1-500bCBXBx1x2x3x4x5-3x11-1/301/3-1/385/3-5x3011-1/52/5111σj03001w=-30最终的单纯形表 cj-3-1-500bCBXBx1x2x3x4x5-5x36/53/511/5090x5-310-1185σj32010w=-45⎛⎞11⎜⎟33−⎛⎞3(4)xxx++≤320为非基变量，σ=−−−−13(),5⎜⎟⎜⎟=≥101232⎜⎟12⎝⎠2⎜⎟−⎝⎠55所以，最优解不变。（5）将原问题的最优解X=（5，0，3，0，0）代入不等式xxx++≤320中，不等式123仍然成立，故最优解不变。（6）将原问题的最优解X=（5，0，3，0，0）代入不等式32xxx++≤20中，不等123式不成立，所以最优解将发生变化。将新的约束条件反映进单纯形表中：cj-3-1-5000bCBXBx1x2x3x4x5x6-3x11-1/301/3-1/305-5x3011-1/52/5030x631200120-3x11-1/301/3-1/305-5x3011-1/52/5030x6000-3/51/5120σj030010w=-30最终单纯形表为：cj-3-1-5000bCBXBx1x2x3x4x5x6-3x11-1/300-2/95/940/9-5x301101/3-1/38/30x40000-1/3-5/35/3σj030010w=-80/3X*=（40/9，0，8/3，5/3，0，0）Maxz=80/3 4运输问题1、运输问题表上作业法的基本步骤。答：表上作业法的基本步骤可参照单纯形法归纳如下：（1）找出初始基可行解：即要在m×n阶产销平衡表上给出“m+n−1”个数字格（基变量）；（2）求各非基变量（空格）的检验数，判断当前的基可行解是否是最优解，如已得到最优解，则停止计算，否则转到下一步；(3)确定入基变量，若min{σ↓σ<}0=σ，那么选取x为入基变量；ijijlklk(4)确定出基变量，找出入基变量的闭合回路，在闭合回路上最大限度地增加入基变量的值，那么闭合回路上首先减少为“0”的基变量即为出基变量；（5）在表上用闭合回路法调整运输方案；（6）重复2、3、4、5步骤，直到得到最优解。2、“最小元素法”和“伏格尔”法的基本思想及基本操作。答：最小元素法的基本思想是就近供应，即从单位运价表中最小的运价开始确定产销关系，依此类推，一直到给出基本方案为止。伏格尔法把费用增量定义为给定行或列次小元素与最小元素的差（如果存在两个或两个以上的最小元素费用增量定义为零）。最大差对应的行或列中的最小元素确定了产品的供应关系，即优先避免最大的费用增量发生。当产地或销地中的一方在数量上供应完毕或得到满足时，划去运价表中对应的行或列，再重复上述步骤，即可得到一个初始的基可行解。3、闭合回路的构成以及利用闭合回路法求检验数的基本操作。答：判断基可行解的最优性，需计算空格（非基变量）的检验数。闭合回路法即通过闭合回路求空格检验数的方法。从给定的初始方案的任一空格出发寻找闭合回路，闭合回路顶点所在格括号内的数字是相应的单位运价，单位运价前的“+”、“-”号表示运量的调整方向。空格处单位运量调整所引起的运费增量就是空格的检验数。仿照此步骤可以计算初始方案中所有空格的检验数。4、利用位势法求检验数以及利用闭合回路进行方案调整的基本操作。答：位势法求解非基变量检验数的基本步骤：第一步：把方案表中基变量格填入其相应的运价并令u=0；让每一个基变量x都有1ijc=u+v，可求得所有的位势；ijij第二步：利用σ=c−(u+v)计算各非基变量x的检验数ijijijij方案的优化基本步骤：在负检验数中找出最小的检验数，该检验数所对应的变量即为入基变量。在入基变量所处的闭合回路上，赋予入基变量最大的增量，即可完成方案的优化。在入基变量有最大增量 的同时，一定存在原来的某一基变量减少为“0”，该变量即为出基变量。切记出基变量的“0”运量要用“空格”来表示，而不能留有“0”。5、某玩具公司生产A、B、C三种玩具，每月的生产能力分别为1000、2000和2000件。玩具被运至甲、乙、丙三个百货商店销售。已知各家百货商店每月对三种型号玩具的总销量都是1500件，由于经营环境的原因，各商店销售不同型号玩具的盈利不同，具体数据见表1。又已知丙商店要求至少供应1000件C型玩具且拒绝A型玩具。求能够满足上述条件而又使总盈利最大的供销分配方案。表1甲乙丙A540B1689C121011解：此题属于产大于销问题，可以增加假想的需求部门丁，使供需平衡。由于部门丁不存在，故其盈利都为0。供需平衡表示如下所示：甲乙丙丁产量A54001000B168902000C12101102000销量150015001500500因为原问题为求最大值，故用类伏格尔法（求两最大元素之差，其他步骤相同）求解问题的初始可行基，得甲乙丙丁产量A5005001000B15005002000C50015002000销量150015001500500用位势法进行检验得：甲乙丙丁uiA（-7）4（-5）00B168（0）（-4）4C（-6）1011（-6）612450vj非基变量检验数全为非负，说明所得初始可行基已为最优解。表中将A调拨给丁500件，表明玩具A有500件销售不出去。6、已知某厂每月最多生产甲产品270吨，先运至A1、A2、A3三个仓库，然后再分别供应 B1、B2、B3、B4、B5五个用户。已知三个仓库的容量分别为50、100和150吨，各用户的需要量分别为25、105、60、30和70吨。已知从该厂经由各仓库然后供应各用户的储存和运输费用如表2所示。试确定一个使总费用最低的调运方案。表2B1B2B3B4B5A11015202040A22040153030A33035405525解：此题属于产销不平衡问题，仓库的总存储能力为300t，用户总需求量为290t，但该厂的最大生产能力为270t。故仓库有30t剩余，用户有20t得不到满足，故可假设存在仓库A4，它的存储量为20t，用户B6的需求量为30t。这样就转化为产销平衡问题。与因A4与B6都是假设的，不需要运输，故运价都为0，但是由A4运到B6的运输无法发生，因两者皆为假设的，运价为无穷大，设为M。得到产销平衡表如下所示：B1B2B3B4B5B6产量A11015202040050A220401530300100A330354055250150A400000M20销量2510560307030用伏格尔法求解初始基可行解得：B1B2B3B4B5B6产量A15050A2254530100A310605030150A42020销量2510560307030用位势法检验是否为最优解，得：B1B2B3B4B5B6uiA1（15）15(0)(15)(35)(20)0A22040(-30)30(0)(-5)25A3(15)3540(30)25020A4(10)(-10)(-15)(0)0(M+25)-5-5152055-20vj因检验数存在负数，故用闭合回路法调整得：B1B2B3B4B5B6产量A15050A2256015100A350607030150 A451520销量2510560307030用位势法检验得：B1B2B3B4B5B6uiA1（5）15(20)(5)(35)(20)0A220（10）1530(10)(5)15A3(5)35（20）(20)25020A4(10)0(15)0(10)(M+35)-155150155-20vj因检验数全为正，所以已得最优方案。即A3差30t没有得到满足，B2缺5t，B4缺15t。7、已知某运输问题的单位运价及最优调运方案如表3所示（括号中的数据代表运输数量），由于产地A2至销地B2的道路关闭，故最优调运方案将发生变化，试在原最优调运方案的基础上，寻找新的最优调运方案。表3B1B2B3B4B5aiA110205（4）9（5）109A2210（4）103064A31（3）20（1）710（1）4（3）8bj35463解：由于A2到B2道路关闭，则其运价为M，应令其出基，以实现最优调度。先将M反映进产销平衡表，然后用位势法作检验，有：B1B2B3B4B5uiA1（10）（1）59(7)0A2（21-M）M(24-M)（40-M）(22-M)M-19A3120（1）1041019593vj要令A2B2出基，即令其运输量为0，找出负检验数最小的来进行调整，得：B1B2B3B4B5产量A1459A2314A35128销量35463 用位势法作检验，有：B1B2B3B4B5uiA1（11）（1）59(7)0A22（M-22）(2)（18）63A3（1）20（1）1041-119593vj检验数已全为非负，故已得最优调度方案。8、已知某运输问题的单位运价及最优调运方案如表4所示，试回答下述问题：表4B1B2B3B4B5B6aiA12（20）1（30）333550A242（20）2（20）44440A33（10）542（39）41（11）60A44221（1）2（30）231bj305020403011（1）A1到B2、A3到B5、和A4到B1的单位运价，分别在什么范围内变化时上表中给出的最优方案不变；（2）若A1到B2的单位运价由1变为3，最优方案将发生怎样的变化；（3）若A3到B5的单位运价由4变为2，最优方案将发生怎样的变化；解：（1）设A1到B2的单位运价为x，因A1到B2是基变量，它的运价变化会引起非基变量检验系数的变化，此时，只需对其再进行位势法分析即可。B1B2B3B4B5B6uiA12x(3-x)(2)(1)(5)0A2（x）22（20）(1+x)(2+x)2-xA33（4-x）（3-x）2（1）11A4(x)(2-x)(1)12(2)02xx120vj要令最优方案不变，则非基变量的检验数非负；故有x>=0；3-x>=0；4-x>=0；2-x>=0；2+x>=0；1+x>=0解上述不等式得0<=x<=2。即A1到B2的单位运价在[0，2]内变化时，最有方案不变。A3到B5的单位运价属于非基变量，它的变化不会引起其它检验数变化，故只需保证其检验数非负即可。 先用位势法算出原方案的检验数：B1B2B3B4B5B6uiA121(2)(2)(1)(5)0A2（1）22（3）(1)(3)1A33（3）（2）2（1）11A4(2)(1)(1)12(2)0211120vj设A3到B5的单位运价为x，则其检验数满足x-（1+2）>=0，即x>=3。也就是说A3到B5的单位运价大于等于3时，最有方案不变。同理可以算出A4到B1的单位运价变化范围是[2，+∞)，此时最优方案不变。（2）把变化直接反映到表中可得下表：B1B2B3B4B5B6uiA123(0)(2)(1)(5)0A2（3）22（20）(4)(5)-1A33（1）（0）2（1）11A4(3)(-1)(1)12(2)0233120vj因存在检验数为负数，最优方案发生改变，用闭合回路法调整得：B1B2B3B4B5B6aiA1212950A2202040A39401160A413031bj305020403011重新计算检验数，得：B1B2B3B4B5B6uiA123(0)(2)(0)(5)0A2（3）22（4）(2)(5)-1A33（1）（0）2（0）11A4(3)2(0)（1）2(3)-1233130vj非基变量检验数均为非负，故为最优方案。（3）把A3到B5的单位运价改为2，然后求检验数得： B1B2B3B4B5B6uiA121(2)(2)(1)(5)0A2（1）22（3）(1)(3)1A33（3）（2）2（-1）11A4(2)(1)(1)12(2)0211120vj由于存在负检验数，故最优方案发生变化，此时用闭合回路法调整得：B1B2B3B4B5B6aiA1203050A2202040A3109301160A43131bj305020403011重新计算检验数，得：B1B2B3B4B5B6uiA121(0)(2)(0)(5)0A2（3）22（4）(2)(5)-1A33（1）（0）2411A4(1)(-1)(-1)1（-1）(2)0233130vj检验数有负数，用闭合回路法调整得：B1B2B3B4B5B6aiA1203050A2202040A310391160A413031bj305020403011重新计算检验数，得：B1B2B3B4B5B6uiA121(2)(2)(1)(5)0A2（1）22（2）(1)(3)1A33（3）（2）2（1）11A4(2)(1)(1)12(2)0211120vj检验数全为非负，故已得最优方案。 5整数规划1、用分枝定界法求解下述整数规划问题（1）maxz=+xx（2）maxz=+4xx3121214xx+≤951341xx+≤21212−+≤63xx142xx+≤91212xx,≥0且取整xx,≥0且取整1212解：（1）用单纯型法求得相应星星规划问题L,最终单纯型表：0cj1100bCBXBx1x2x3x41x1101/32-3/323/21x2011/1625/4810/3σj00-3/16-91/48Z=5/29(0)T(0)即：X=(3/2,10/3,0,0)，Z=29/5在L基础上分别增加约束条件x≤1和x≥8，分别形成两个子线性规划L和L01112L：maxz=+xxL：maxz=xx+11221214x+9x≤5114x+7x≤511212-6x+3x≤1-6x+20x≤11212x≤1x≥811x,x,x,x,x≥0x,x,x,x≥0123452345(1)T(1)求解L和L有：X=(1,7/3)Z=10/312(2)T(2)X=()3,1Z=4(1)(2)**TL有最优解，又Z＜Z，故整数规划有最优值Z=4，X=()3,12此题求解过程如下图： L0(0)T(0)X=(3/2,10/3,0,0)，Z=29/5x≤1x≥811LL12(1)T(1)(2)T(2)X=()1,7/3Z=10/3X=()3,1Z=4（2）定义相应线性规划L为：0maxz=+4xx312341xx+≤21242xx+≤912xx,0≥1234242xx+≤934xx+≤121212(0)T(0)解得：X=(6/5,21/10)，Z=111/10在L基础上分别增加约束条件x≤1和x≥2，分别形成两个子线性规划L和L01112 L：maxz=+4xx3L：maxz=+4xx31122123x+4x≤123x+4x≤1212124x+2x≤94x+2x≤91212x≤1x≥211x,x≥0x≥0122(1)T(1)求解得：X=(1,9/4)Z=43/4(2)T(2)X=(2,1/2)Z=19/2在L基础上分别增加约束条件x≤2和x≥3，分别形成两个子线性规划L和L12234(3)T(3)解得：X=()1,2Z=10L无解4*T*故：X=()1,2Z=10此题求解过程如L0(0)T(0)X=(6/5,21/10)，Z=111/10x≤1x≥211LL12(1)T(1)(2)T(2)X=()1,9/4Z=43/4X=()2,1/2Z=19/2x≤2x≥322LL34(3)T(3)X=()1,2Z=10无可行解 2、某航空公司为满足客运量日益增长的需要，正考虑购置一批新的远程、中程及短程的喷气式客机。每架远程客机价格670万元，中程客机500万元，短程客机350万元。该公司现有资金12000万元可用于购买飞机。据估计年净利润（扣除成本）每架远程客机82万元，中程客机60万元，短程客机40万元。设该公司现有熟练驾驶员可用来配备30架新购飞机。维修设备足以维修新增加40架新的短程客机，每架中程客机维修量相当于4／3架短程客机，每架远程客机维修量相当于5／3架短程客机。为获取最大利润，该公司应购买各类客机各多少架?解：设购买远程、中程及短程的喷气式客机数量分别为x，x，x，数学模型如下：123maxz=82x+60x+40x123670xxx++≤50035012000123xxx++≤30123x≤241x≤302x≤403xxx,,0≥且取整123解得：xxx==17，，1=0，有最大利润1454元。1233、某市为方便学生，拟在新建的7个居民小区增设若干所学校。已知各备选校址代号及其能覆盖的居民小区编号如表1所示，问要覆盖所有居民小区至少应建多少所学校？对应的校址代号是哪些？表1备选校址ABCDEF小区编号1，5，71，2，51，3，52，4，53，64，6解：对每一个学校定义一个变量xj1，当某居民小区可由第j个学校负责x＝j0，当某居民小区不可由第j个学校负责则对于第1个小区：xxx++≥1123对于第2个小区：xx+≥124对于第3个小区：xx+≥135 对于第4个小区：xx+≥146对于第5个小区：xxxx+++≥11234对于第6个小区：xx+≥156对于第7个小区：x=116Minz=∑Xjj=1*T*解得：X=(1,0,0,1,1,0)Z=34、求解下述0-1规划问题（1）maxz=−+−+2xxxxx5341234532754xxxxx−+−+≤612345xxxxx−+−+≤242012345x=⋅⋅01or(j=1,2,3,4,5)j（2）maxz=+++2xxxx5341234−+++≥40xxxx1234−+++≥2424xxxx41234xxxx+−+≥11234x=⋅⋅01or(1j=,2,3,4)j解：（1）将0－1规划问题换形为：minwxxxxx=++++−′′345′112145323547xxxxx++++≥′′′821453xxxxx++++≥′422′′521453x,,,,xxxx′′′取0或124153 显然零解不满足，分枝：W=-510x=14W=-8W=-4W=-141118x′=1x=0x′=1145W=-7W=-10W=-714W=-2x=125419x′=01x=04W=-6W=-626x′=15x=115227W=-5x′=05W=-11W=-21W=-6W=-9x′=15248x=14x=062x5′=0W=-1x′=11W=-9W=-5253x=094W=-4x′=0W=-81W=-8x′=1516127x4=1x′=05W=-317W=-722W=-2x=04W=-7x′=1313x′=1205x′=0233x′=0W=-75W=-621 (2)将0－1规划问题换形为：minwxxxx=+++−2′′′′34514134241xxxx′′′′−−−≥13422244xxxx′′′′−−−≥−41342−+−−≥−xxxx′′′′11342x′′′′,,,xxx=01or1234显然零解不满足，分枝：W=-122(可行解)W=-14x′=111W=-9x′=013**T故XZ==()0,1,1,1,125、求解例5-3所述的0-1规划问题。解：将0－1规划问题换形为：min2wxxxxxxx=++++++−53′′′′′′′0303535404524035276485xxxxxxx′′′′′′′++++++≥95901001051101202051352764−−−≥−xxx′′′2132xxx′′′++≥1132−−≥−xx′′154−−≥−xx′′176xo′j==01rj(1,2,3,4,5,6,7) 显然零解不可行，用隐枚举法分枝定界：**TXZ==()0,1,1,1,0,1,0,2106、有四项工作要甲、乙、丙、丁四个人去完成，每项工作只允许一个人去完成，每个人只完成其中一项工作。已知每个人完成各项工作的时间如表2所示，问应指派哪个人去完成哪项工作才能使总的消耗时间为最少？表2工作1工作2工作3工作4甲10131619乙14181713丙21121114丁14161812解：变换系数矩阵：02691440100032360找到独立零元素并在次变换：026100330100041250最后得到下表中的独立零元素：（0）0410011（0）120（0）61（0）30故最优方案为：甲—J，乙—J，丙—J，丁—J此时总消耗时间最少。14327、甲、乙、丙、丁四人要去完成五项工作，每项工作只由一个人来完成，其中有一人兼做一项工作。试指出每个人去完成哪项（或哪两项）工作才能使总的消耗时间为最少?已知每个人完成各项工作的时间如表3所示。JJJJJ12345甲1215101820乙812201411丙189161215丁2022151012 解：JJJJJ12345甲1215101820乙812201411丙189161215丁2022151012戊89101011变换系数矩阵：2508804126190734101250001221得最终表：35（0）88（0）3115010(0)73411127(0)00011(0)故最优方案为：甲—J，乙—J，丙—J，丁—J,而乙或丁兼任J312458、某电子系统由三种元件组成，为使系统正常运转，每个元件都必须工作良好。如一个或多个元件安装几个备用件将提高系统的可靠性。已知系统运转可靠性为各元件可靠性的乘积，而每一元件的可靠性则是备用件数量的函数，具体数值见表4。又三种元件的价格分别是20、30和40元，重量分别是2、4和6千克。已知全部备用件的费用预算限制为150元，重量限制为20千克，问每个元件各安装多少备件，才能使系统的可靠性最大。表4备用件数量元件1元件2元件300.50.60.710.60.70.920.70.91.030.81.01.040.91.01.051.01.01.0 解：设元件1的备用件数从0到5分别位x、xx...，元件2备用件数从0到3分别设为126x、xx...，因为在3时已达到最优，故不需再考虑备用件数位4、5的情况；同理设元件78103的备用件数从0到2为x、、xx。111213maxZxxxxx=+++++×+++(0.50.60.70.80.9xxxx)(0.60.70.9x)×12345678910(0.7xx++0.9x)111213643⎧⎪20∑∑∑(ix−+1)ii30(ix−+1)++6140(ix−1)i0≤150ii==11i=1⎪643⎪⎪2∑∑∑(ix−+−+−≤1)ii4(ix1)++616(ix1)i020⎨ii==11i=1⎪61013⎪∑∑∑xxxiii===1,1,1⎪iii===1711⎪⎩xi==01(或1,2...13)i求解得：xxx===1,1,1，即元件1、2、3的备用件数分别为2、2、1。3912 第7章动态规划1、某公司打算向它的三个营业区增设6个销售店，每个营业区至少增设1个。各营业区每年增加的利润与增设的销售店个数有关，具体关系如表1所示。试规划各营业区应增设销售店的个数，以使公司总利润增加额最大。表1增设销售店个数营业区A营业区B营业区C1100（万元）120（万元）150（万元）216015016531901701754200180190解：阶段：将每个营业区作为一个阶段，即k=1,2,3状态变量：S代表从第k各营业区到第3个营业区的店数k决策变量：x代表第k个营业区的销售店数K状态转移律：SSx=−KK+1K边界条件：S=6S=014决策允许集合DS()=≤{x0xS≤}KKKKK阶段标准函数f(S)=max{g(x)+f(S−x)}(k=)1,2,3kkkkk+1kk0≤xk≤Skf(S)=044当k=3时：f(S)=max{g(x)+}0=max{g(x)}3333330≤x3≤S30≤x3≤S3∗于是有下表2，表中x表示第三个阶段的最优决策。3表2（单位：万元）1234S3∗1234x3150165175190f(S)33当k=2时： f(S)=max{g(x)+f(S−x)}22223220≤x2≤S2于是有表3。表3（单位：万元）x2S21234∗f2(S2)x21120+015012120+150150+015013120+165150+150170+030024120+175150+165170+150180+032035120+190150+175170+165180+1503353当k=1时：f(S)=max{g(x)+f(S−x)}11112110≤x1≤S1于是有表4。表4x1g1（x1）+f2（s1–x1）∗f1(S1)x1S10123460+345100+375160+320190+300200+2704903故最优分配方案为：A区建3个销售店，B区建2个销售店，C区建1个销售店，总利润为490万元。2、某工厂有100台机器，拟分4个周期使用，在每一周期有两种生产任务，据经验把机器投入第一种生产任务，则在一个周期中将有六分之一的机器报废，投入第二种生产任务，则有十分之一的机器报废。如果投入第一种生产任务每台机器可收益1万元，投入第二种生产任务每台机器可收益0.5万元。问怎样分配机器在4个周期内的使用才能使总收益最大？解：阶段：将每个周期作为一个阶段，即k=1,2,3，4状态变量：第k阶段的状态变量S代表第k个周期初拥有的完好机器数k决策变量：决策变量x为第k周期分配与第一种任务的机器数量，于是S−x该周期分kkk配在第二种任务的机器数量。状态转移律：SSS=+−5/60.9(xS)0.9=−1/15xKK+1KKKK允许决策集合DS()=≤{x0xS≤}KKKKK令最优函数：fSkK()=+max{}0.5SK0.5xfKk++1(0.9SK−1/15xK)xDSKKK∈() 边界条件：fS()=055当k=4时：fS()m=+ax{0.50.5SxfS+()}4444550≤≤xS44=+max{0.5Sx0.5}440≤≤xS44∗因f(S)是关于x的单调递增函数，故取x=S，相应有fS()=S；依次类推，可求44444444得：∗当k=3时：x=S，fS()11/6=S33333∗当k=2时：x=S，fS()91/36=S22222∗当k=1时：x=S，fS(==100)671/216S=310.6511111计算表明，每一期都将全部机器投入第一种任务中，其中S=100，S=83，S=69，S=5812343、某公司生产一种产品，估计该产品在未来四个月的销售量分别为300、400、350和250件。生产该产品每批的固定费用为600元，每件的变动费用为5元，存储费用为每件每月2元。假定第一个月月初的库存为100件，第四个月月底的存货为50件。试求该公司在这四个月内的最优生产计划。解：阶段：将今后4个月中的每一个月作为一个阶段，即k=1,2,3,4；状态变量：第k阶段的状态变量S代表第个月初产品存储量；kk决策变量：决策变量x代表第k个月的生产量；k状态转移律：S=S+x−d（d是第k个月的销售量）；k+1kkkk边界条件：S=100，S=50，fS()0=；1555固定生产费用0,χ=0kC=600,χ>0κk和存贮费Z==+22SS(x−d)变动生产费用G5=χkk+1kkkκk最优指标函数：最优指标函数具有如下递推形式 fS()m=+in{CGZfS++()kkkκkk+11k+xkfSkk()m=+in{}Ck52xk+(Sxdkkk+−)++fSxdkkkk+1(−)xk当k=4时：表1S4050100150200250300X4300250200150100500F4（S4）22001950170014501200950100当K=3时：()minfS33=+{}C352x3+(Sxd333+−)+fS44()x3表2x3050100150200250300350400450∗x3f3(S3)S3045546547535045500005043044045046030043000000104054154254354452504050000000153803904004104204302003800000000020355365375385395405355150，35500000000045025330340350360370380330100，3300000000004003030531532533534535530550，3050000000003503522029030031032033028002200000000004020522528529530525520500000000 当K=2时：表3S3050100150200250300350400450∗x2f2(S2)0715072504007150506900700071003506900100665067506850695030066501506400650066006700680025064002006150625063506450655066502006150当K=1时:表4x1050100150200250300350400450∗x1f1(S1)S11008750885089509050915092502008750利用状态转移律，按上述计算的逆序可推算出最优策略为：第1个月生产200件，第2个月生产400件，第3个月生产350件，最后一个月生产300件。4、用动态规划求解下述规划问题52（1）maxz=∏mi（2）maxz=2x1−x1+x2i=1522∑mi=102x1+3x2≤6i=1m≥0(i=)5,4,3,2,1x,x≥0i12解：（1）解：阶段：将问题的变量数作为阶段，即k=3,2,1，4，5；决策变量：决策变量x；k状态变量：状态变量S代表第阶段的约束右端项，即从kx到x占有的份额；kk5状态转移律：S=S−x；k+1kk边界条件：S=10，fS()1=；166允许决策集合：0≤x≤Skk当k=5时：fS55()max{=×==00≤≤xSxfS566()}max{}≤≤xSxS55|x55∗=S5555 当k=4时：fS()m=×=ax{xfS()}max{(xSx−)}4445544400≤≤xS44≤≤xS44dh设hxSx=−()，于是令=−=Sx20444dx444可得xS=/2442又因dh=−2<0，所以：xS=/2是fS()的极大值点dx244444于是：12fS44()=4S4|x44∗=12S当k=3时：2fS()max{=×=xfS()}max{(xSx−)/4}3334433300≤≤xS33≤≤xS332=1/27S3|xS33∗=/3当k=2时：3fS()m=×=ax{xfS()}max{(xSx−)/27}2223322200≤≤xS22≤≤xS2214fS22()=256S2|x22∗=14S当k=1时：14fS()max{=×=×−xfS()}max{x(Sx)}1112212561100≤≤xS11≤≤xS11同理：4114⎛⎞(fS11==××10)S1⎜⎟S1=32|xS11∗=15=25256⎝⎠5∗∗1SSx=−=−=1028xS==2211224∗∗SSx=−=−=826xS=/32=322333∗*SSx=−=4xS=/22=4344**SSx=−=2xS==254455∗T∗故最优解为：X=(2,2,2,2,2)最优值为：z=32（2）解：阶段：将问题的变量数作为阶段，即k=1,2； 决策变量：决策变量x；k状态变量：状态变量S代表第阶段的约束右端项k;k2状态转移律：SSx=−2；211边界条件：S=6，fS()0=；1332阶段指标：VSx(,2)=−xxVSxx(,)=111112222基本方程：fS()ma=+x{VSx(,)fS()}(k=1,2,3)kkkkkk++11kSk0≤≤xkak其中：a=2a=312当k=2时：fS()m=+=ax{xfS()}max{}x222332SS2200≤≤xx22≤≤aa22S2*S2关于x的单调增函数，故fS()==x222233当k=1时：2fS()max{2=−xxfS+()}111122S10≤≤x2222=−max{2xxfSx+(−2)}11211S10≤≤x2222Sx11−2=max{2xx−+}110≤≤xS13225、某公司经销A、B、C三种产品，由于运输能力的限制，该公司每月只能把6吨的产品运回公司进行销售。产品A、B、C的单件重量分别为20、30和40公斤；进货的批量分别为50、40和20件；单位产品利润分别为80、130和150元。试确定该公司每月A、B、C三种产品的最佳进货量，以使总利润最大。 6、某公司需要在近四周内采购一批原料，估计在未来四周内的价格可能有60、80、90和100四种状态，各状态发生的概率分别为0.2、0.3、0.3和0.2，试求各周应以什么样的价格购入原料，才能使采购价格期望值最小。解：阶段：将每一周作为一个阶段，即k=4,3,2,1；决策变量：决策变量x代表第周是否决定采购，kx=1代表第k周决定采购，x=0kkk代表第周决定等待；k状态变量：状态变量S代表第周原材料的市场价格；kk中间变量：y代表第周决定等待，而在以后采取最佳子策略时的采购价格期望值；kk最优指标函数：是否采购决定于目前市场价格与等待价格期望值的相对大小，如果前者大于后者，应决定等待；如果前者小于后者，则应决定采购。于是：f(S)=min{S,y}kkkk边界条件：对于第4周，因为没有继续等待的余地，所以：f(S)=S444即：fS(==60)60、f(S=80)=80fS(=90)=90fS(==100)10044444444yEfS==+++{()}0.2f(60)0.3f(80)0.3f(90)0.2f(100)kk++11kk+1k+1k+1k+1⎧⎫1;fS()=Skkkx=⎨⎬k⎩⎭0;fS()=ykkk当k=4时：只有采购一种选择fS(6==0)60、f(S=80)=80fS(9=0)9=0fS(==100)10044444444当k=3时：y=×+×+×+×=0.2600.3800.3900.2100833⎧60;S=60⎫3⎪⎪⎪80;S=80⎪3于是：fS()===min{,Sy}min{,83}S⎨⎬3333383;S=90⎪3⎪⎪83;S=100⎪⎩⎭3⎧⎫1;S=60,803即第三周的最佳决策为：x=⎨⎬3⎩⎭0;S=90,1003当k=2时：y=×+×+×+×=0.2600.3800.3830.28377.52 ⎧60;S=60⎫2⎪⎪⎪77.5;S=80⎪2于是：fS()===min{,Sy}min{,77.5}S⎨⎬2222277.5;S=90⎪2⎪⎪77.5;S=100⎪⎩⎭2⎧⎫1;S=602即第二周的最佳决策为：x=⎨⎬2⎩⎭0;S=80,90,1002当k=1时：y=0.2600.377.50.377.50.277.5×+×+×+×=741⎧60;S=60⎫2⎪⎪⎪74;S=80⎪2于是：fS()===min{,}min{,74}SyS⎨⎬1111174;S=90⎪2⎪⎪74;S=100⎪⎩⎭2⎧⎫1;S=601即第一周的最佳决策为：x=⎨⎬1⎩⎭0;S=80,90,1001由以上计算可知，最佳的采购策略为：第一周,第二周只有价格是60时才采购，否则就等待；第三周只要价格不超过80就要采购，否则继续等待；如果已经等待到了第四周，那么无论什么价格都只有采购，别无选择。7、某工厂生产一种精密仪器，今后四个月的订单分别为2、3、4台。已知生产费用C（万元）同生产量x的关系为：⎧06当x>⎪12⎪⎪60xx−<当x≤4C=⎨2⎪92+当x6又若生产出来的产品当月销售不出去，其库存费用为每台每月0.2万元。设在第一个月月初及第四个月月末该产品无库存，试确定在满足需求的条件下，使该工厂生产与库存总费用最小的生产方案。解：阶段：将今后4个月中的每一个月作为一个阶段，即k=1,2,3,4； 状态变量：第k阶段的状态变量S代表第个月存储量；kk决策变量：决策变量x代表第k个月的生产量；k状态转移律：S=S+x−d（d是第k个月的销售量）；k+1kkkk边界条件：SS==0，fS()0=；1555生产费用C和存贮费ZkkZ=(2.0S+x−d)kkkk最优指标函数：最优指标函数具有如下递推形式fS()m=+in{CZfS+()kkkkk+11k+xkfSkk()m=++in{}Ck0.2(SxdfSxdkkkkkkk−)+++1(−)xk当k=4时：表1S401234X443210F4（S4）1613．5105．50当K=3时：表2x50123456∗x3f3(S3)S503534.7634.713231.731.4631.4229.529.729.427.1627.132627.226.425.121.8621.8421.523.723.922.119.822519.851619.220.419.616.820016613.715.916.114.3013.7710.411.610.8010.4当K=2时：表3x30123456∗x2f2(S2)S3048.247.646.543.4643.4 144.745.143.541.441.6541.4240.241.64138.439.638638334.737.137.535.936.63635.9034.7431.63332.434.13333.932.8031.6当K=1时:表4x1012345∗x1f1(S1)S1053.455.154.453.42,653.4利用状态转移律，按上述计算的逆序可推算出最优策略有两种：（1）第1个月生产2台，第2个月和第3个月生产6台，最后一个月不生产;(2)第1个月生产6，第2个月不生产，第3个月生产6台，最后一个月生产2台。总费用为53.4万元。8、某研发部（乙方）拟承担一种新产品的研发任务，甲方提供研发经费10万元。为适应市场竞争的需要，合同要求乙方应在三个月内向甲方交付一台合格样品，否则乙方将退还甲方10万元的研发费。据估计，研发时投产1台即合格的概率为0.35，投产一批的准备费用为0.25万元，每台的研发费用为1万元。若投产一批而未得到合格样品，可再投产一批，但每批的研发周期是一个月。试分析该研发部应否接受此研发任务，如果接受应该采用怎样的研发策略。解：阶段：将每个试制周期（1个月）作为一个阶段，即k=3,2,1；决策变量：决策变量x代表第k阶段投产试制的台数；k状态变量：状态变量S代表第k阶段初是否已获得合格样品，尚无合格样品时S=1，kk已获得合格样品时S=0；k⎧,3,2,1Λ;Sk=1⎫允许决策集合：Dk(Sk)=⎨⎬⎩;0Sk=0⎭状态转移律：PS(==1)(0.65)xk，PS(0==−)1(0.65)xk；k+1k+1边界条件：S=1，fS(1==)10，f(S=)0=0，；14444阶段指标函数：⎧0.2+xx;>0⎫kkCx()=⎨⎬kk⎩⎭0;x=0k最优指标函数：f(S=)0=0kk fS(==1)min{Cx()(0.65)+xxkkfS(=+−1)[1(0.65)]fS(=0)}kkkkk++11kk++11kxDSkkk∈()=+min{Cx()(0.65)x2fS(=1)}kkk++11kxDSkkk∈()当k=3时：f(S=)0=033fS(=1)=+min{Cx()(0.65)x3fS(=1)}333344xDS333∈()表1x3∗012345x3f3(S3)S30001107.756.4866.044.8836当k=2时：f(S=)0=022fS(==1)min{Cx()(0.65)+x2fS(=1)}222233xDS222∈()表2x2∗0123x2f2(S2)S2000165.154.784.924.78当k=1时：(fS=1)=+=min{()(0.65)Cxx1fS(1)}111122xDS111∈()表3x1∗0123x1f1(S1)S114.784.364.274.5624.27即该公司的最佳试制计划为：第一个月初投产试制2台；如果在第二个月初无合格样品出现，再投产试制2；如果在第三个月初仍然无合格样品出现，再投产试制3。按此最佳试制方案最小期望总费用是4.27元。 9图论1、判断下列说法是否正确（1）图论中的图不仅反映了研究对象之间的关系，而且是真实图形的写照，因而对图中点与点的相对位置、边的长短曲直等都要严格注意。（错）（2）当图的点集确定后，树图是所有图中边数最少的简单图。（正确）（3）在连通图G中，其权数最大的边必不包含在其最小部分树内。（正确）（4）若图中从v1至各点均有唯一的最短路，则连接v1至其他各点的最短路在去掉重复部分后，恰好构成改图的最小部分树。（正确）（5）求网络最大流问题可用线性规划数学模型加以描述（正确）2、试回答：2（1）具有N个顶点的完全图有多少条边；Cn⎧⎡⎤nn⎡⎤⎪−−(1),n≥2且为奇数⎢⎥⎢⎥⎪⎣⎦22⎣⎦（2）具有N个顶点的二分图最多有多少条边；⎨2⎪⎡⎤n，为偶数n⎪⎢⎥⎩⎣⎦22（3）具有N个顶点的简单图最多有多少条边。Cn3、在某海上油田的一个区块上有8口油井，它们相互之间的距离如表1所示。已知1号井距离海岸最近，这一最近距离为5海里。试问从海岸经1号井铺设输油管线将各油井同陆地连接起来，应如何铺设才能使输油管线的长度最短，最短输油管线的铺设长度是多少？表1（单位：海里）到2#井3#井4#井5#井6#井7#井8#井从1#井1.32.10.90.71.82.01.52#井0.91.81.22.62.31.13#井2.61.72.51.91.04#井0.71.61.50.95#井0.91.10.86#井0.61.07#井0.5解：此问题可转化为求最小部分数来求，用kruskal顺序生枝法求解，得到如下图的最小部分数，总长度为5.2+5＝10.2。 50.740.70.85海岸10.50.687610.9324、已知图1，试求：（1）最小部分树；（2）v点到其他各点的最短路；1（3）各点之间的最短路。解：（1）8v218vv68v1876v4v585vv73(2)lg7(3)n≤≤3即最多运算到D即可lg208126∞∞∞∞80∞∞∞912∞12∞∞010515∞69100810∞∞(0)D=∞∞58078∞∞∞1210701618∞∞15∞816020∞∞∞∞∞18200 ⎛⎞0812614162234⎜⎟8019917122530⎜⎟⎜⎟12190105121330⎜⎟691008101628(2)⎜⎟D=⎜⎟14175807825⎜⎟⎜⎟16121210701518⎜⎟22251316815020⎜⎟⎜⎟⎝⎠343030282518200(2)（３）则在矩阵D中即可以找到V1到各点的最短路以及各点之间的最短路。5、A、B、C、D、E、F、G代表七个村落，村落之间的道路连通情况如图2所示（边上的数据为距离，单位为公里）。这七个村落拟合建一所小学，已知A村有小学生50人、B村有小学生40人、C村有小学生60人、D村有小学生20人、E村有小学生70人、F村有小学生80人、G村有小学生100人，试问拟合建的小学应建在哪一个村落，才能使学生上学所走的总路程最短。B5.5F1.51.5A1.82.25.03.9G1.21.6D3.03.2CE图2(3)解：N≤lg6/lg23≤即最多运算到D即可⎛⎞01.51.21.8∞∞∞⎜⎟1.50∞2.25.05.5∞⎜⎟⎜⎟1.2∞01.6∞∞∞(0)⎜⎟D=⎜⎟1.82.21.603.0∞∞⎜⎟∞∞5.03.003.93.2⎜⎟⎜⎟∞∞5.5∞3.901.5⎜⎟⎝⎠∞∞∞∞3.21.50 ⎛⎞01.51.21.84.878⎜⎟1.502.72.25.05.57⎜⎟⎜⎟1.22.701.64.68.27.8(2)⎜⎟D=⎜⎟1.82.21.603.06.96.2⎜⎟4.85.04.63.003.93.2⎜⎟⎜⎟75.58.26.93.901.5⎜⎟⎝⎠877.86.23.21.50在D(2)中第一行乘以A地区的人数，同理，其他各行分别乘以B,C,D,E,F,G地区的学生人数。得到以下表:ABCDEFGA0756090240350900B60010888200220280C72162096276492468D364432060138124E3363503222100273224F5604406565523120120G8007007806203201500Σ1864177119581656140816231616由此表得出：E地区最为合适6、PERT网络问题表2作业作业代码作业时间（天）紧前作业产品设计与工艺设计a60------外购零、部件b45a下料与锻造c10a工艺装备制造1d20a模具与铸造e40a机械加工1f18c工艺装备制造2g30d机械加工2h15d、e机械加工3k25g装配调试l35b、f、k、h（1）某新产品研发工程的各项作业、作业时间以及它们之间的相互关系如表2所示，试绘制该工程的网络图并进行网络的结点和作业时间计算；（2）若该工程每天的间接费用为600元，各项作业的直接费用与时间数据如表3所示，试确定使总费用最小的最优方案。表3 作正常情况下采取措施的情况下直接费用率业作业时间直接费用极限时间直接费用（元/天）a6010,0006010,000------b454,500306,300120c102,80054,300300d207,0001011,000400e4010,0003512,500500f183,600105,440230g309,0002012,500350h153,750105,750400k256,250159,150290l3512,0003512,000------7、求如图3所示网络的最大流（弧旁数字为弧的容量）3vv148116610v315vtvs812189解：5vv25图3（3，0）vv14（8，0）（6，0）（11，0）（6，0）vsvt（10，0）（15，0）v3vt（8，0）（9，0）（12，0）（18，0）（5，0）v5v2 （3，3）vv14（8，7）（6，4）（11，11）（6，6）vsvt（10，10）（15，2）v3vt（8，0）（9，5）（12，0）（18，11）（5，5）v5v2最大流为226318．邮递员投递区域的街道分布如图4所示，222图中数字为街道长度（单位为公里）。3313“O”为邮局所在地，试为邮递员设计11.53一条最佳的投递路线，使其每天完成投483递任务并返回邮局所经历的路线最短。2.5361图4631222331311.534832.5361图4'