张清华_图论课后题答案 27页

'第1章图论预备知识1.1解：(1)p={,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}(2)p={,{a},{{b,c}},{a,{b,c}}}(3)p={,{}}(4)p={,{},{{}},{,{}}}(5)p={,{{a,b}},{{a,a,b}},{{a,b,a,b}},{{a,b},{a,a,b}},{{a,b},{a,b,a,b}},{{a,b},{a,a,b},{a,b,a,b}}}1.2解：(1)真(2)假(3)假(4)假1.3解：(1)不成立，A={1}B={1,2}C={2}(2)不成立，A={1}B={1,2}C={1,3}1.4证明：设(x,y)∈(A∩B)X(C∩D)说明x∈A∩B,y∈C∩D由于x∈A,y∈C所以(x,y)∈AXC由于x∈B,y∈D所以(x,y)∈BXD所以(x,y)∈（AXC）∩（BXD）反过来，如果（x,y）∈(AXC)∩（BXD）由于(x,y)∈（AXC）所以x∈A,y∈C由于(x,y)∈（BXD）所以x∈B,y∈D所以x∈(A∩B)y∈(C∩D)所以(x,y)∈(A∩B)X(C∩D)所以(A∩B)X(C∩D)=(AXC)∩（BXD）1.5解：Hasse图12249431025 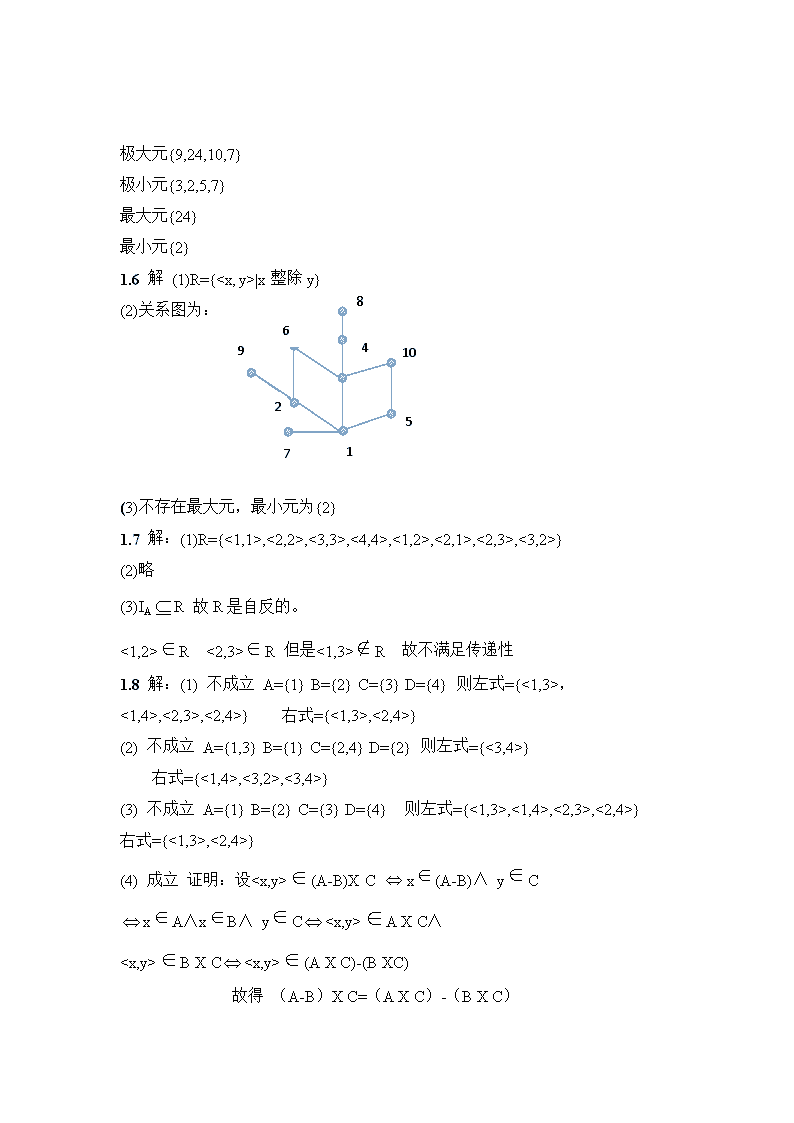极大元{9,24,10,7}极小元{3,2,5,7}最大元{24}最小元{2}1.6解(1)R={|x整除y}468(2)关系图为：9102571(3)不存在最大元，最小元为{2}1.7解：(1)R={<1,1>,<2,2>,<3,3>,<4,4>,<1,2>,<2,1>,<2,3>,<3,2>}(2)略(3)IAR故R是自反的。<1,2>R<2,3>R但是<1,3>R故不满足传递性1.8解：(1)不成立A={1}B={2}C={3}D={4}则左式={<1,3>，<1,4>,<2,3>,<2,4>}右式={<1,3>,<2,4>}(2)不成立A={1,3}B={1}C={2,4}D={2}则左式={<3,4>}右式={<1,4>,<3,2>,<3,4>}(3)不成立A={1}B={2}C={3}D={4}则左式={<1,3>,<1,4>,<2,3>,<2,4>}右式={<1,3>,<2,4>}(4)成立证明：设(A-B)XCx(A-B)∧yCxA∧xB∧yCAXC∧BXC(AXC)-(BXC)故得（A-B）XC=（AXC）-（BXC） 1.9略1.10略1.11解：A为n个元素的优先级和，A上有2n2个不同的二元关系，理由为：设A，B为集合，AXB的任何子集所定义的二元关系称作从A到B的二元关系，特别当A=B时，称作A上的二元关系，若|A|=n，则|AXA|=n2，那么A上共有2n2个不同的二元关系。1.12略1.13解：1)真.由于R1和R2和R2都是自反的,因而对任何,都有(x,x)∈R1,(x,x)∈R2.因此,对任何x∈A,都有(x,x)∈R1R2.所以R1R2是自反的。2)假.令A={a,b},R1={(a,b)},R2={b,a}.那么R1R2={(a,a)},它就不是A上的反自反关系.3)假.令A={a,b,c},R1={(a,b),(b,a)},R2={(b,c),(c,b)}.那末R1R2={(a,c)},就不是A的对称关系.4)假.令A={a,b,c,d},R1={(a,c),(b,c)},R2={(c,b),(d,a)}易证R1,R2都是反对称关系.但是R1R2={(a,b),(b,a)}就不是A上的反对称关系.5)假.令A={a,b,c},R1={(a,c),(b,a),(b,c)},R2={(c,b),(a,c),(a,b)},易证R1和R2都是传递关∈系,但R1R2={(a,b),(b,b),(b,c)}就不是A上的传递关系.1.14证明：由任意的a，存在一个b，使得∈R,由对称性所以∈R,由传递性∈R,所以R是等价关系。1.15证明：①x∈A，∈R,∈S→∈R∩S，所以R∩S有自反性；②x,y∈A,因为R,S是反对称的，∈R∩S∧∈R∩S(∈R∧∈S)∧(∈R∧∈S)(∈R∧∈R)∧(∈S∧∈S)x=y∧y=xx=y所以，R∩S有反对称性。③x,y,z∈A,因为R,S是传递的，∈R∩S∧∈R∩S∈R∧∈S∧∈R∧∈S∈R∧∈R∧∈S∧∈S∈R∧∈S∈R∩S所以，R∩S有传递性。 所以R∩S也是A上的偏序关系。1.16解：r(R)={<1,1>,<2,2>,<3,3>,<4,4>,<5,5>,<1,2>,<2,3>,<2,5>,<3,4>,<4,3>,<5,5>}s(R)={<1,2>,<2,1>,<2,3>,<3,2>,<2,5>,<5,2>,<3,4>,<4,3>,<5,5>}t(R)={<1,2>,<1,3>,<1,4>,<1,5>,<2,3>,<2,4>,<2,5>,<3,3>,<3,4>,<4,3>,<4,4>,<5,5>}1.17(1)证明：①对任意a,b,a+b=a+b,故得(a,b)R(a,b),关系R具有自反性;②如果(a,b)R(c,d),则a+d=b+c,c+b=d+a,故得(c,d)R(a,b),关系R具有对称性;③如果(a,b)R(c,d),(c,d)R(e,f),则a+d=b+c,c+f=d+e,故得a+f=b+e,(a,b)R(e,f),关系R具有传递性;于是关系R是等价关系.1.18略1.19略1.20解：(1)单射(2)满射(3)既不是单射，也不是满射(4)满射(5)双射1.21解：(1)O(n3)(2)O(n5)(3)O(n3n!)第2章图2.1解：(1) a:出度为3、入度为1b:出度为2、入度为2c:出度为2、入度为3d:出度为2、入度为3e:出度为2、入度为2abcde     (2)a:出度为3、入度为1b:出度为1、入度为2c:出度为3、入度为3d:出度为3、入度为2e:出度为0、入度为3abcde     2.2解：构成无向图的度序列：(1)、(2)、(3)、(4)、(6)构成无向简单图的度序列：(2)、(3)、(4)2.3解：补图为：     2.4 解：设图G中结点数为n,则有3x4+3x(n-3)=2x12.求得n=7,即图G有7个结点.2.5证明将习图2.2的两图顶点标号为如下的(a)与(b)图作映射f:f(vi)®ui(1£i£10)容易证明，对"vivjÎE((a)),有f(vivj)=uiujÎE((b))(1£i£10,1£j£10)由图的同构定义知，两个图是同构的。2.6解：同构对应关系：a—8、b—7、c—4、d—9、e—5、f—6、g—1、h—2、i—10、j—3.2.7证：设在一有向完全图G中，边数为n.则可知deg+vi=deg-vi=n.即所有结点的入度和等于所有节点的出度和，即所有结点的入度的平方和等于所有节点的出度的平方和。2.8 解：(1)            (2)                    2.9证明：用反证法。设无向图G只有两个奇点u,v，若u,v不连通，即它们之间没任何通路，则G至少有两个连通分支G1,G2，且u,v分别属于G1和G2，于是G1和G2中各有一个奇度结点，与握手定理矛盾，因此u,v必连通。2.10解：点割集为：{v1，v3}、{v4}、{v6}割点为：v4、v62.11解：强连通图：(a）单相连通图：（b）（c）（d）弱连通图：（a）（b）（c）（d）2.12 证明:设v0v1…vk为G中一条最长路，则v0的邻接顶点一定在该路上，否则，与假设矛盾。现取与v0相邻的脚标最大者，记为l，则l³d,于是得圈v0v1v2…vlv0,该圈长为l+1，显然不小于δ+1。2.13证明：证其逆否命题：e不是割边当且仅当e含在G的某个圈中。 必要性：设e=xy不是割边。假定e位于G的某个连通分支G1中，则G1-e仍连通。故在G1_e中有(x,y)路P，P+e便构成G1中一个含有e的圈。 充分性：设e含在G的某个圈C中，而C含于某连通分支G1中，则G1-e仍连通。故W(G-e)=W(G)，这说明e不是割边,证毕。2.14证明：用数学归纳法证明： （1）n=1时，G为平凡图，显然G连通。（2）n=2时，m≥12n-1n-2+1=1此时G为K2，当然连通。（3）假设当n=k（k≥2）时，m≥12n-1n-2+1结论成立。 当n=k+1时，若此时每个结点度数为k，则结论显然成立，否则必存在一个结点v度数至多只有k-1度，即这个结点最多只有k-1条边和它相连。因为此时总的边数m≥12kk-1,则其它k个结点之间的边数m"≥12kk-1-(k-1)=12k-1k-2。根据归纳假设，显然这k个结点之间是连通的，而根据上面我们知道，至少有一条边使v和其它结点相连，所以此时这个图是连通的,结论成立。2.15证明：（1）因为G连通，且G无割边，所以任意两个结点u,v，都存在简单道路p=u…wv.又因为G无割边，所以，删除边wv后，子图依然连通，即w,v存在简单道路p",以此类推，可以找到一条和p每条边都不相同的p’’=v…u,这样p和p’’就构成了一条回路。   （2）因为G中任意两个结点都位于同一回路中，所以任意结点u,和任意边e的两个端点v1,v2都分别在两个回路C1，C2中，如果C1=C2=u…v1…v2…u,那么将回路中v1…v2,用v1v2=e替换，就得到新的新的回路，并满足要求。如果C1≠C2，C1=u…v1…u,C2=u…v2…u,那么构成新的道路P=u…v1…u…v2…u,在其中将重复边剔出掉，得到新的回路C3，其中包含v1,v2结点，可以将回路中v1…v2用v1v2=e替换，就得到新的新的回路，并满足要求。  （3）对任意两条边e1,e2其端点分别为u1,u2,v1,v2。根据（2）存在回路C1 = u1…v1v2…u1,C2=u2…v1v2…u2。那么可以形成新的闭道路P=u1…v1v2…u2…v1v2…u1,在其中将重复边剔出到，得到新的回路C3，其中包含e2和u1,u2结点，可以将回路中u1…u2用u1u2=e1替换，就得到新的新的回路，包含e1,e2,满足要求。  (4)因为任意两条边都在同一回路中，所以不存在割边。假设边e是割边，那么删除此边，图不连通，分支中的任何一对不在同一分支中的边，不能构成回路，与条件矛盾。所以，G中无割边。2.16解：(1)deg(v1)=2、deg(v2)=3(2)否(3)4(4)略2.17解：(1)A=0101001101010100(2)A2=0111020101110011A3=0212012202120201A4=0323041303230322V1到V4长度为1、2、3、4的路各有1、1、2、3条。 2.18解：无向图G:    v1v2v3v4v5可达矩阵P=1111111111111111111111111有可达矩阵可知改图为强连通图。2.19解：(1)邻接矩阵A=1200000100011010(2)G中长度为3的通路有23条，其中有7条为回路。(3)图G为强连通图2.20解：邻接矩阵A=1201200000011010关联矩阵M(G)=211100110000001000112.21 解：(1)当r=1时，没有长度大于等于1的圈。　　当2≤r≤s时，有长度为4,6,…,2r的圈，它们都是偶圈，因而非同构的圈共有r-1种。　　(2)至多有r个顶点彼此不相邻。　　(3)至多有r条边彼此不相邻。(4)k=λ=r2.22证明：反证法。若存在某个具有奇数个面，且每个面均有奇数条棱的多面体V，不妨设V有r(r为奇数)个面，设为R1,R2,…,Rr，S1,S2,…,Sr分别为它们的棱数，均为奇数。作无向图G如下：在V的每个面中放一个顶点vi，i=1,2,…,r,且两个面Ri与Rj有公共面就连边。若存在这样的无向图G，则d(vi)均为奇数Si，由握手定理得i=1γdvi=i=1γSi=2m(m为边数)　　但因r,Si(i=1,2,…,n)均为奇数，上面等式不可能成立。故不存在这样的无向图G，从而也不存在满足要求的多面体。2.23解：设G是n阶m条边的自补图,即G为n阶m条边的简单图,且G≅G̅。于是，G̅的边数m’=m，且m+m"=2m=n(n-1)/2。于是n(n-1)=4m，因而n=4k，或n-1=4k，k为正整数。2.24证明：为偶数(n为奇数)。 于是，若为奇数，必有dG(v)也为奇数。故与G中奇度顶点个数相等。2.25解:都可以实现，如下图   (1)     (2)2.26解：(1)错误、(2)正确、(3)正确2.27略2.28解：无向完全图Kn当n≥3且n为奇数时才是欧拉图。当n>3且n为偶数时存在欧拉路而不存在欧拉回路。2.29略2.30略2.31略第3章树与最短路径3.1该树的结点个数n=5，故边数m=n-1=4,因为，所以5 个结点分配的度数为8，由于树是简单连通图，知，则该树的度数序列必是下列情况之一，(1)1，1，2，2，2(2)1，1，1，2，3(3)1，1，1，1，4这些度数序列对应的简单树为3.2该树的结点个数为，则边数，又因为，所以可知一棵树的结点个数之和为。3.3设有n个一度结点，则结点个数为=3+5+8+n，边数为=3+5+8+n-1,则.可得n=23.3.4设有n个一度结点，则：3.5反证法。假设没有结点度数大于等于3的结点，则只有度为1的结点3个和度为2的结点n个。边数：3+n-1，度数：3+2n.所以2（3+n-1）=3+2n。等式左边为偶数，右边为奇数，相互矛盾，假设不成立。所以至少有一个结点度数大于等于3.3.6 设度为的结点个数为则则由于，故全为0.当时，只有两个度为1的结点，所以T是一条直线。当时，有两个度为1的结点，其他结点度数都为2，T仍为一条直线。综上T是一条直线。3.7=>若为度数序列,则该树的结点个数为n，边数为n-1,所以<=若，则该树的结点为n，且结点度数依次为。即是一棵树的度数序列。3.8证明假设中没有树叶，则，是二部图结点分类，且中顶点的出度最少为2，则，可得与题中给的相矛盾。所以中至少有一片树叶。3.9T是一棵树，则T中任意两个结点之间有且仅有一条路，所以T中任意两点仅有唯一的简单通路，反之亦成立。3.10Kruskal算法可求得如下最小生成树:4 5345433323.11证明:因为G为连通图，所以结点v的关联便只有一条。又因为G的任何一棵生成树T必为G的生成子图且连通，即T包含G的所有结点且连通，而v的关联边只有e一条边，故e一定是任何一棵树的枝。3.12证明：如果简单连通图G无回路，则G本身就是生成树。即G的任何一条边都可以是某一生成树的枝。若G中有回路，则去掉任意一条边，则图仍连通，若图中仍有回路，重复上述过程知道图中无回路为止。去掉的边不一样，则得到的生成树不一样，又因为去边是在回路中任意去掉的一条边，所以G中任一条边都可以是某一生成树的枝。3.13正则二叉树为为完全二叉树且所有叶结点在同一层。因为完全二叉树的分支节点的出度都是2，则可知除根节点外，其他每层上的结点个数都为偶数，故一棵正则二叉树必有奇数个结点。3.14 385166219100119813649643025161495143.156727401314179823111235573.160次迭代1次迭代 2次迭代3次迭代4次迭代 5次迭代6次迭代7次迭代结束到各结点的最短路径为：3.17 3.183.19解：图中有两个奇点E,F。取一条连接EF的路EGF，添加重复边（E，G）和（G，F），经检验可得满足定理的条件，即为最优方案,其最优回路:DBACBEGEDFGFCD.3.20最邻近算法：acedba37bdecab37cedbac37dbeacd36最短哈密顿回路为：dbeacd最邻近插入法：aaacaaceaacdeaabcdeaacbdeaacdbeaacdeba其权值分别为：52，40，36，43最短哈密顿回路为：acdbea第五章独立集、支配集与匹配5.1证明：由G是二部图可知，其子图H也是二部图，显然二部图的顶点划分（X，Y）中的X，Y均是二部图的独立集，则有，其中是子图H的顶点数，是图H的最大独立集中具有的点的数目。 反证法：若G不是二部图，则G含有奇圈H，H是G的子图，但这与已知条件矛盾，故G是二部图。5.2证明：G是二部图，则其子图H也是二部图，因为，故对子图H有，则必有一个匹配关联G中所有结点，故G有一个完美匹配。G有一个完美匹配，则子图H也有完美匹配，故该匹配关联H的所有结点，所以。5.3(1)G中极小支配集为{v1,v3},{v2,v4,v5}，支配数2。 (2)G中极小点覆盖集为{v1,v3},{v2,v4,v5}，点覆盖数2。 (3)G中极大点独立集为{v1,v3},{v2,v4,v5}，点独立数3。 (4)G中极大匹配为{a,c},{a,f},{b,d},{b,f},{e,c},{e,d}， 匹配数2。 (5)G中极小边覆盖集为{a,b,f},{a,e,c},{b,e,d},{d,c,e}, {d,f,b},{c,f,a}，边覆盖数3。5.4证明：G是二分图，并且则，又，故。5.5（a）极小点覆盖{a,c,e,g},{b,c,d,e,g}{b,d,e,f}{b,c,d,f}极大独立集{b,d,f}{a,f}{a,c,g}{a,e,g}最小点覆盖{a,c,e,g}{b,d,e,f}{b,c,d,f}最大独立集{b,d,f}{a,c,g}{a,e,g}(b)极小点覆盖{b,c,e,f}{b,c,d,f}{b,c,d,e}{a,c,e,f}{a,c,d,e}{a,b,d,e}极大独立集{a,d}{a,e}{a,f}{b,d}{b,f}{c,f}最小点覆盖{b,c,e,f}{b,c,d,f}{b,c,d,e}{a,c,e,f}{a,c,d,e}{a,b,d,e}最大独立集{a,d}{a,e}{a,f}{b,d}{b,f}{c,f}5.6 5.7(1)(2)5.8证明：设M为树的一个完美匹配，则满足：（1）T的所有点均为M饱和点，且与所有叶子结点关联的边均在T的任意一个匹配里。（2）T的顶点数n=2|M|为偶数，而T的边数m=2n-1=2|M|-1为奇数。反证：设和都是树的完美匹配，并且他们是不同的，则，设导出子图为H。由于和都是T的完美匹配，则H中定点的度均为2,所以H中存在圈，这与T是树相矛盾。故树至多有一个完美匹配。5.9（1）归纳法n=1时完美匹配数是1n=2时完美匹配数是3，满足（2n-1）！！设当n=k时，完美匹配数是（2k-1）！！，当n=k+1时，即向中加入两点u，v，则多出4k+1条边，（1）取的一个完美匹配，则只加入边uv有为的一个完美匹配，无妨设为中的边（2）则去掉添加有另一个的完美匹配添加有另一个的完美匹配。（3）对同样的操作则共有2k种设法，算上共有2k+1种，（4）不同完美匹配有（2k-1）！！每一种均可增加为2k+1，所以不同完美匹配有（2k+1）（2k-1）！！=（2k+1）！！种，得证。（2）对于有n！种完美匹配。5.10利用匈牙利算法可求得最大匹配5.11略5.12 5.13由Kuhn-Munkres算法可得。第六章平面图与着色6.1略6.2略6.3由题意可得：n=6，m=（46）/2=12由欧拉公式n-m+r=2可得：r=8.6.4n-m+r=n-30+20=2所以n=12.6.5证明：反证法假设极大平面图G是非联通的，则它至少有两个连通分支，在这两个连通分支的外部边界上各取一顶点，则这两个顶点是不相邻的，在这两个顶点之间加一条边，则所得的图还是平面图，这与G是极大平面图相矛盾，所以极大平面图一定是连通图。6.6证明：用反证法，若分情况讨论。（1），G中存在顶点，设与相邻的顶点v，并设v除与相邻外还依次的与相邻。因不与相邻，加边{，}不破坏平面性，这与G为极大平面图相矛盾，所以。（2）。G中存在顶点，设与相邻的顶点v和，这时v与相邻，否则加边{，}不破坏平面性，这与G为极大平面图相矛盾，设v除与和相邻外，还依次的与相邻。在G中不能与相邻（因为），加边{}不破坏平面性，这又矛盾与G为极大平面图，所以。6.7解：因为G为极大平面图，所以G是连通的，由欧拉公式得：r=m-n+2（1）设G的平面图各面边界长度之和为l，G的平面图每个面的边界之长均为3，所 以3r=l=2m（2）将（1）代入（2）中可得m=3n-6.6.8证明：G为自对偶平面图，所以G为联通平面图，由欧拉公式：n-m+r=2（1）；自对偶图的性质可得：=r=n（2）；将（2）式代入（1）式可得m=2n-2.6.9证明：=>：为G的面，为的结点，G的对偶图为，可得又因为为欧拉图所以为偶数，为偶数，所以G的每一个面都有偶数条边围城。<=：G的面，为的结点，G的对偶图为，可得，又因为G的每一面均有偶数条边围城，所以为偶数，所以为偶数。故中所有结点的度是偶数，无奇度结点，所以为欧拉图。6.10证明：G有n个结点m条边，则。假设每一个面的度数大于等于5，则，整理得，这与题目给出的相矛盾，故假设不成立，即至少有一个面的度数小于5.6.11证明：假设G和都是平面图，则对图G可得（1）对图可得（2）；整理（1）式和（2）式得：，又因为，故，这与相矛盾，故假设不成立，即G和至少有一个是非平面图。6.12 证明（1）由于G无割点所以G肯定无割边，且每两个面之间最多有一条公共边，所以是简单图，因此中至少有两个度相同的顶点，即G中至少有两个面相同的的度数。（2）设G中有k个度为5的面，，又因为为简单平面图，所以G中至少有12个这样的面。6.13没做出来6.14证明：n=15，m=（32+36+8）/2=38，3n-6=45-6=39没做出来感觉题有问题6.15（1）收缩边（）（），所得图中存在与同胚的子图，故为非平面图。（2）收缩边，得到，故该图为非平面图。6.16 面的个数片B选取的片B选取的面加入的回路2（）3（）4（） 5（）6所以该图是非可平面图。面的个数片B选取的片B选取的面加入的回路2（）（）（）（）5（）（） （）7所以该图是非可平面图。6.17对偶图6.181432121212341121346.19结点太多，需加的边也多，此题计算太麻烦，感觉不好。'