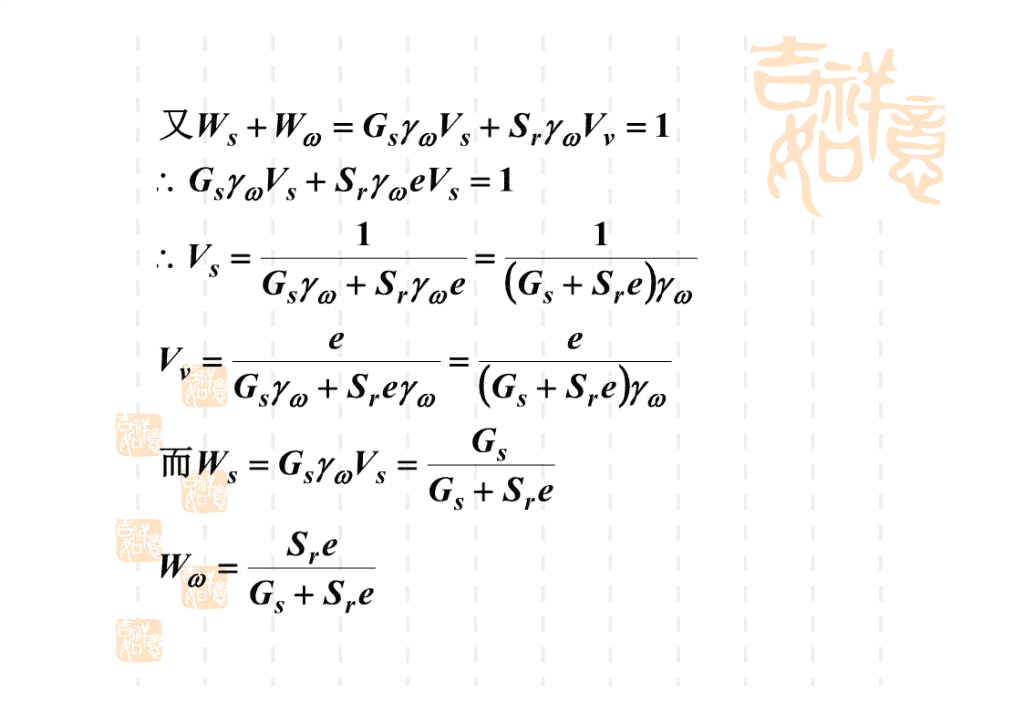《土力学》习题课(带解答).pdf 60页

'2010.12 【例1】已知某土样的孔隙比、比重和饱和度，用三相草图计算：γd、γsat、γ’。（分别假设Vs=1、V=1、W=1）解：1.设W=1，由WsGsWsGsVsVsVveVveVsVsVSrVSrVvWSrVvVv 又WsWGsVsSrVv1GsVsSreVs111VsGsSreGsSreeeVvGsSreGsSreGs而WsGsVsGsSreSreWGsSre GsWsGsSreGsdV1e1eGsSreWsVvsatVGseGseSrGseSrGse1e1eGseSrGs1sat1e 2.设V=1，由1VvVseVveVs1eVseVv又VvVs11eWs1GsWsGsVs1eVeSrSrVSrVvVv1eWsGsdV1eWsVvGseGsesatV1e1e1e 3.设Vs=1，则VveVve,V1VsWsGsWsGsVsWsGsdV1eWsVsGseGsesatV1e1eGs1sat1e 【例2】某完全饱和土样，厚2.0cm，环刀面积30cm2，在压缩仪上做压缩试验，试验结束后取出称重为105g，烘干后干土重为85g，设土粒比重为2.70，求：⑴压缩前土重？⑵压缩前后孔隙比变化？【例3】某一施工现场需要填土，基坑体积为2000m3，填土土方是从附近的土丘开挖而来。经勘察，填土的比重为2.70，含水量为15%，孔隙比为0.60，要求填筑结束时的含水量为17%，干密度为17.6kN/m3，问：⑴取土场土的重度、干重度、饱和度是多少？⑵应从取土场取多少方土？⑶碾压时应洒多少水？填土的孔隙比是多少？ 【例4】取A、B两试样，测定其指标如表，试计算：⑴哪一土样粘粒含量高？⑵哪一土样孔隙比大？⑶哪一土样饱和重度大？⑷确定A、B土样名称及状态？ωL(%)ωP(%)ω（%）dsSrA3012452.701B2916262.681 解：⑴IPA=30-12=18，IPB=29-16=13由于IPA＞IPB，所以A土样的粘粒含量高⑵由于Sr=1，所以eA=ωds=0.45×2.70=1.215A土样的孔隙eB=ωds=0.26×2.68=0.7比e比较大⑶dse2.71.215103satA17.67kN/m1e11.215dse2.680.7103satB19.88kN/m1e10.7 ⑷P4512ILA1.83＞1LP3012且IPA18＞17A土样是流塑状态的粘土P2626ILB0.77（0.75-1之间）LP2916且IPB13在（10-17之间）B土样为软塑状粉质粘土 【例5】通过变水头试验测定某粘土的渗透系数k，土样横断面面积A=30cm2，长度L=4cm，渗透仪水头管（细玻璃管）断面积a=0.1256cm2，水头差从△h1=130cm降低到△h2=110cm所需时间t=8min。试推导变水头试验法确定渗透系数的计算公式，并计算该粘土在试验温度时的渗透系数k。 【例6】某渗透试验装置如图所示。土样Ⅰ的渗透系数k1=2×10-1cm/s，土粒比重ds1=2.72，孔隙比e1=0.85。土样Ⅱ的30cm渗透系数k2=1×10-1cm/s，土粒比重20cmds2=2.72，孔隙比e2=0.80。土样横断面积30cmⅠA=200cm2。30cmⅡ求：⑴图示水位保持恒定时，渗透流量Q多大？⑵若右侧水位恒定，左侧水位逐渐升高，升高高度达到多少时会出现流土现象？ 【例7】某地基地表至4.5m深度范围内为砂土层；4.5m—9.0m为粘土层，其下为不透水页岩，地下水位距地表2.0m。已知水位以上砂土的平均孔隙比为0.52，平均饱和度为37%；粘土的含水量为42%；砂土和粘土的比重均为2.65。计算地表至粘土层范围内的竖向总应力、有效应力和孔隙水砂土压力。粘土不透水页岩 【例8】试计算图中所示地基土中的自重应力分布2ma319kN/m8m粗砂319.5kN/msatb3319.3kN/m，19.4kN/m4msat粘土20%，55%,24%cLP 解：⑴水下的粗砂层受到水的浮力作用，其有效重度为：3sat19.5109.5kN/m⑵粘土层因为ω＜ωP，所以IL＜0，故认为土层不受水的浮力作用，下层粘土层还要承受土层顶面以上静水压力的作用。故土中各点的自重应力如下：a点：z=0，σca=γ×z=0b点：z=8m，“b点上”位于粗砂层中，σcb上=γ’z=9.5×8=76kPa“b点下”位于粘土层中，σcb下=76+γwh=76+10×（8+2）=176kPac点：z=12m，σcc=176+19.3×4=253.2kPa 【例9】试以分层总和法求下图中基础甲的最终沉降量（考虑乙基础的影响）4m4m4m5m5m5m6mF=1940kNF=1940kNF=1940kN318kN/m1.5m填土乙甲乙粉质粘土2m3sat19.5kN/m2m粘土20.1kN/m3sat 土样e—p曲线e0.7710.7281粉质粘土：a0.43MPa120.20.11.0000.8960.8451粘土：a0.51MPa120.20.10.900粘土0.800粉质粘土0.70000.10.20.30.4压力p 【例10】图示天然地基，该地基由粉质粘土和中砂组成，粉质粘土透水，其在水面以上的重度γ=18kN/m3，在水面以下的重度γsat=20kN/m3。试求：⑴原地下水位时，A-A’面上有效自重应力分布图；⑵地下水位下降后，A-A’面上有效自重应力分布图；⑶计算由于地下水位下降，引起的粉质粘土层的沉降。粉质粘土层e--pp（kPa）e2m原地下水位500.671000.65粉质粘土6m下降后地下水位1500.6310m中砂A’A2000.618 解：⑴原地下水位时，2m、6m、10m深处的土自重有效应力分别为：cz2h1218236kPacz6cz2sat10h23362010476kPacz10cz6sat10h3476104116kPa⑵地下水位下降后，2m、6m、10m深处自重有效应力变为：cz2h1218236kPacz6h12h231824108kPacz10cz6sat10h34108104148kPa ⑶2m～6m处，土的有效自重应力在地下水位升降前后平均值分别为：1初始应力P1：cz367656kPa21终了应力P2：cz3610872kPa2利用已知条件，查得e1=0.668；e2=0.662则2m～6m深处的沉降量为：e1e20.6680.658S1h4001.6787cm1e110.668同理，可得6m～10m深处的地下水位升降前后有效自重应力平均值分别为： 76116cz96kPa2108148cz128kPa2并查得e1=0.652；e2=0.6390.6520.639S24003.1477cm10.652故，总沉降量为：S=S1+S2=1.6787+3.1477=4.8264cm 【例11】某场地地表以下为4m厚的均质粘性土，该土层下卧坚硬岩层。已知粘性土的重度γ=18kN/m3，天然孔隙比e0=0.85，回弹再压缩系数Ce=0.05，压缩指数Cc=0.3，前期固结压力Pc比自重应力大50kPa。在该场地大面积均匀堆载，荷载大小为p=100kPa。求因堆载引起的地面最终沉降量？ 【例12】已知原状土样高h=2cm，截面积A=30cm2，重度γ=19.1kN/m3，颗粒比重ds=2.72，含水量ω=23%，进行压缩试验，试验结果见下表，试绘制压缩曲线，并求土的压缩系数a1-2值。压力p（kPa）050100200400稳定时的压缩量△h（mm）00.4800.8081.2321.735【例13】某地基软土层厚10m，其下为不透水硬层，软土的固结系数为0.015cm2/s，渗透系数为5×10-7cm/s，拟用堆载预压法处理。如果荷载瞬时施加，并可视为大面积均布荷载，大小为70kPa。求：①地基平均超静孔隙水压力消散50%时需要多少天？②一年后地基的固结沉降是多少？③一年后10m深度处的有效应力是多少？ 解：⑴已知U=50%＞30%所以28TvU1e4228Tv即0.51e42得Tv0.1958Cvt0.015t即0.195822H1000从而得t151天 Cvt0.0151365243600(2)由Tv0.4730422H1000228Tv80.47304有U1e41e474.77%22kEsk1eCvCvEsak则最终沉降7k70510100SHH100023.33cmEsCv0.01510则一年后地基的固结沉降为S1U1S0.747723.3317.45cm ⑶设一年后10m深处土的有效应力为x，则平均有效应力为：70x70270从而有U101070xEsEs270x即74.77%702x34.608kPax 【例14】某地基软土层厚20m，其渗透系数为1×10-6cm/s，固结系数为0.03cm2/s，其表面透水，下卧层为砂层，地表作用有98.1kPa的均布荷载，设荷载是瞬时施加的，求：⑴固结沉降完成1/4时所用的时间（不计砂层沉降）？⑵一年后地基的固结沉降是多少？⑶若粘土层的侧限压缩模量增大一倍，渗透系数缩小一倍，地基的固结沉降有何变化？ 【例15】三轴固结不排水剪试验测得土的有效应力抗剪强度指标为c’、φ’，试证明不固结不排水剪强度cu（φ=0）与c’、φ’有如下关系：ccossin3cu1sin【例16】为测定某粘性土的抗剪强度指标，先取一土样做固结排水条件下的直剪试验，当σn=50kPa时，测得破坏时的剪应力τf=57.74kPa；另取一相同条件的土样，做固结排水三轴压缩试验，当围压σ3=50kPa时，破坏时作用在土样上的大主应力σ1=250kPa，试利用以上试验数据，求该粘性土的c、φ。 〔例16〕解1.由直剪试验，有fctg即57.74c50tg2otg451257.74c50o2tg4522ooo整理得：5050tg452ctg45115.48tg45〈a〉2222.由三轴压缩试验，可得：2oo13tg452ctg45222oo即25050tg452ctg45〈b〉22 3.将b式代入a式，得2o50250115.8tg452oo29.9930c57.7450tg28.87kPa 【例17】从饱和粘性土中一点取出一筒土样，切取多个试样，进行直剪固结快剪试验，测得正常固结部分ccq=0，φcq=20°；超固结部分ccq=30kPa，φcq=7°.问：⑴该土的先期固结压力是多少？⑵如该土样在地基中的自重应力为80kPa，问其天然状态不排水抗剪强度是多少？⑶如在地面施加大面积均布荷载p=120kPa，固结稳定后，该取土点的不排水强度是多少？ 【例18】某饱和粘土的有效内摩擦角为30°，有效粘聚力为12kPa，取该土样做固结不排水剪切试验，测得土样破坏时σ3=260kPa，σ1-σ3=135kPa，求该土样破坏时的孔隙水压力？【例19】饱和粘性土试样在三轴仪中进行固结不排水剪切试验，施加的围压σ3是196kPa，试样破坏时主应力差σ1-σ3=274kPa，孔压u=176kPa，如果破坏面与水平面成58°角，试求破坏面上的正应力、剪应力、有效正应力与最大剪应力。 〔例19〕解1274196470kPa3196kPa1—313则cos22211o470196470196cos258273kPa22131osin2470196sin258123kPa22u27317697kPao最大剪应力发生于45面上，则1o470196max13sin245137kPa22 【例20】某正常饱和粘性土试样，进行不固结不排水试验得φu=0，cu=15kPa；对同样的土进行固结不排水试验得有效应力抗剪强度指标c’=0,φ’=30°。求：⑴如果试样在不排水条件下剪切破坏，破坏时的有效大主应力和有效小主应力各是多少？⑵如果试样某一面上的法向应力突然增加到200kPa，法向应力刚增加时沿这个面的抗剪强度是多少？经很长时间后沿这个面的抗剪强度又是多少？ 【例21】某饱和粘性土由固结不排水试验测得的有效应力抗剪强度指标为c’=20kPa，φ’=20°。⑴如果该土样受到总应力σ1=200kPa和σ3=120kPa的作用，测得孔隙水压力u=100kPa，则该土样是否会破坏？⑵如果对该土样进行固结排水试验，围压σ3=120kPa，问：要试样破坏应施加多大的偏压？ q=20kPaγ=20kN/m3c=5kPa4mφ=30°粘土K0=0.55【例22】某挡土墙如图所示，已实测到挡土墙墙后的土压力合力值为64kN/m。试用朗肯土压力公式说明此时墙后土体是否已达极限平衡状态？为什么？ 解：⑴求挡土墙背上的主动土压力30oktg245o0.33a2B点：aBhqka2cka200.33250.330.89kPaC点：aChcqka2cka204200.33250.3327.56kPa1总主动土压力：Ea0.8927.56456.9kN/m2 ⑵挡土墙背上的静止土压力：B点：0qk0200.5511kPaC点：020420k055kPa1E011554132kN/m2⑶判断实测：E64kN/m＞Ea56.9kN/m，还未达极小值又E64kN/m＜E0132kN/m，未超出静止平衡状态所以，墙后土体尚未达极限平衡状态 【例23】如图所示的挡土墙，求墙背所受的侧压力（墙背垂直光滑，填土水平）γ=18kN/m31.5mc=10kPaφ=20°γ=18kN/m3sat3.5mc=0kPaφ=30° 【例24】图示挡土墙，墙背垂直光滑，填土水平。填土指标如图所示。已测得墙体移动，使墙后填土达朗肯极限平衡状态时，A点的水平压力为25kPa，求：⑴绘出墙背土压力分布并计算墙背总土压力；⑵画出土中过A点q=20kPa的剪切破坏面，并标明夹角；γ=18.5kN/m3⑶求土中过A点的2mc=10kPa剪破面上的法向力粘土φ=20°σf和剪切力τf。1mγ=18kN/m3A砂土c=0kPa3mφ=30° 解：1.主动土压力系数20oktg245o0.720.49a1230oktg245o0.33a22主动土压力强度：①a1qka12cka1200.492100.7＜0存在临界深度z01令azz01qka12c1ka1001z010.4633m ②a2上18.5220ka12cka118.52200.492100.4913.93kPaa2下18.5220ka22c2ka218.52200.3319kPa③a318.52201830.3337kPa主动土压力：1Ea113.9320.463310.703kN/m21y0120.463333.5122m3 1Ea21937384kN/m211931.53719312y021.3393m1193371932EaEa1Ea294.703kN/mEa1y01Ea2y02y1.5849mEa2.当挡土墙后土体达主动极限平衡时，在墙后土中形成两组破裂面，与大主应力作用面夹角45°+φ/2A点大主应力为竖向力，小主应力为水平力因此，过A点的剪切破坏面与水平面成45°+φ/2=60° 3.过A点的剪破面上aA18.5218120ka22c2ka2750.3325kPaoosincossin30cos30f1o18.52181201sin1sin3021.65kPafc21.65又fcftgfo37.5kPatgtg30 【例25】有一挡土墙，墙高8.6m，墙底宽度6m，埋置于地下1.5m处，墙后填土指标列于图中。在离墙P趾A点3.2m处作用着竖直线荷载=2400kN/m，该地基土及墙背填土的重度粘土γ=20kN/m3。3.2mγ=20kN/m3试求基础中点下8.6mc=10kPa深度为φ=20°7.2m处P的M点的1.5m附加应A6m力。7.2mM 【例26】某挡土墙墙背铅直光滑，墙高H=7m，填土面水平，填土表面作用有均布荷载，各土层层厚及相关指标、地下水的情况见下图，求土压力强度分布、土压力大小及总土压力大小？q=15kPaγ=20kN/m312mc1=12kPa，φ1=10°γ=18kN/m322mc2=25kPa，φ2=16°γ’3=12kN/m33mc3=8kPa，φ3=20° 解：1各层土的主动土压力系数10oktg245o0.83920.704a1216oktg245o0.75420.568a2220oktg245o0.720.49a322A、B、C、D各点主动土压力强度第一层土：aAqka12c1ka1150.7042120.839＜0存在临界深度z01,令0az01 即z01qka12c1ka10z010.68maB上q1h1ka12c1ka1152020.7042120.83918.6kPa第二层土：aB下q1h1ka22c2ka2152020.5682250.754＜0存在临界深度z02；令0az02即：1h12z02qka22c2ka20z020.63mac上q1h12h2ka22c2ka2152021820.5682250.75414kPa 第三层土：ac下q1h12h2ka32c3ka3152021820.49280.733.4kPaadq1h12h23h3ka32c3ka3152021821230.49280.751kPa3每层土的土压力Ea值11Ea1h1z01aB上2-0.6818.612.28kN/m2211Ea2h2z02ac上20.63149.59kN/m22 Ea3ac下h333.43100.2kN/m11Ea4h3adac下35133.426.4kN/m224总土压力EaEaEa1Ea2Ea3Ea4148.47kN/m方向：水平指向墙背作用点：zEaEa1z1Ea2z2Ea3z3Ea4z4h1z01h2z02h3h3Ea123Ea23Ea3Ea43323z1.86mEa 5总水压力：1212Eh10345kN/m22总推力：EEaE193.47kN/m 【例27】图示条形基础，基础底面宽b=2.0m，作用于基础底面处的轴向荷载N沿基础长度方向每米200kN，地基土有关指标见图，地基为均质粘土。试判别地基中A点是否在塑性变形区的边界线上。（K0=1.0）N=200kN/m31.2mγ=19kN/m3c=30kPa2.0mφ=20°1.0mA1.0m 由公式：p01sin00p030sin0N200又p0p0d0d191.277.2kPab2.0A点的大小主应力为：77.210.4636sin265622.3877.230.4636sin26560.4046 若A点在塑性区边界上，则应满足极限平衡条件，即2oo1计算3tg452ctg452220o20o42.20tg245o230tg45o22171.77kPa＞164.18kPa又由于侧压力系数k01,各方向自重应力相等，即110dz22.38191.2191.064.18kPa330dz0.4046191.2191.042.20kPa所以A点不在塑性区边界上 【例28】某柱下条形基础，由于条件所限，基础宽度不得大于2m。地基土的γ=18.8kN/m3，c=110kPa，φ=4°，求至少需多大埋深才能安全承受800kN/m的竖向中心荷载？B解：假设建筑允许塑性区最大开展范围是zmax4P14cNc0dNqbNr由4，查表得Nc3.51,Nq1.25,Nr0.06,P141103.5118.8d1.2518.820.06388.35623.5d 建筑要求：pf80018.8d388.35623.5d2d2.48m 【例29】若假定地基破坏的滑动面形状如右图，当不计土体本身的重力时，试推导地基的极限承载力公式。〔证明〕地基滑动时假设破裂面为ACD，将其分为Ⅰ区和Ⅱ区，分别进行分析：Puq⑴对Ⅰ区，在Pu作用下土体在水平向伸展，近似于墙后AE45D土体的主动状态，因此，2Ⅰ区为主动区：ⅠⅡC 对于主动区，1竖向力，3水平力1a2oo2oo31tg452ctg45atg452ctg45-2222⑵对Ⅱ区，在Ⅰ区作用下Ⅱ区中的土体在水平向压缩，近似于墙后土体的被动状态，因此，Ⅱ区为被动区：对于被动区：1水平力；3竖向力3竖向力q2oo13tg452ctg45222ooqtg452ctg4522 ⑶取EC竖直面，在达极限平衡时应保持静止不动Ⅰ区水平力=Ⅱ区水平力2oo2ooPutg45--2ctg45-qtg452ctg4522222oooqtg452ctg452ctg45-222Pu2otg45-2cNcqNq 【例30】一幢16层的建筑物底板尺寸为20m×30m，底板放置在均匀的饱和粘性土层上，埋深3m。粘性土的ρ=2.0g/cm3，地下水位较深，现场原位十字板测定土的τf=60kPa，室内重塑土做无侧限抗压强度试验qu=40kPa，设计的基底压力为200kPa，问地基的安全系数有多大？如要求的安全系数如下表，问设计是否合理？灵敏度StKs永久结构临时结构≥43.02.52--42.72.01--22.51.8≤12.21.6'