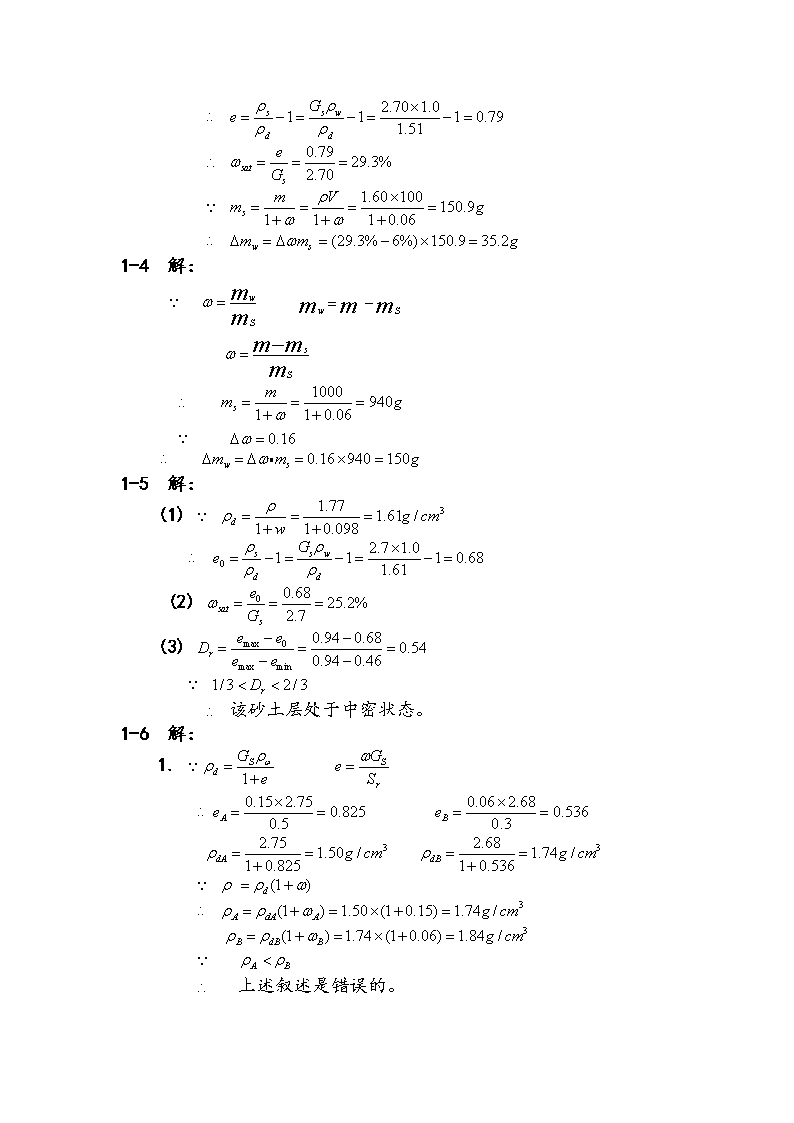《土力学》课后习题答案.doc 48页

'土力学1-1解：(1)A试样(1)B试样1-2解：已知：=15.3g=10.6g=2.70饱和=1又知：15.3-10.6=4.7g(1)含水量==0.443=44.3%(2)孔隙比(3)孔隙率(4)饱和密度及其重度(5)浮密度及其重度(6)干密度及其重度1-3解： 1-4解：1-5解：(1)(2)(3)该砂土层处于中密状态。1-6解：1.上述叙述是错误的。 2.上述叙述是错误的。3.上述叙述是正确的。1-7证明：(1)(2)(3)1-8解：(1)对A土进行分类①由粒径分布曲线图，查得粒径大于0.075㎜的粗粒含量大于50%，所以A土属于粗粒土；②粒径大于2㎜的砾粒含量小于50%，所以A土属于砂类，但小于0.075㎜的细粒含量为27%，在15%～50%之间，因而A土属于细粒土质砂；③由于A土的液限为16.0%，塑性指数，在17㎜塑性图上落在ML区，故A土最后定名为粉土质砂(SM)。(2)对B土进行分类①由粒径分布曲线图，查得粒径大于0.075㎜的粗粒含量大于50%，所以B土属于粗粒土；②粒径大于2㎜的砾粒含量小于50%，所以B土属于砂类，但小于0.075㎜的细粒含量为28%，在15%～50%之间，因而B土属于细粒土质砂； ③由于B土的液限为24.0%，塑性指数，在17㎜塑性图上落在ML区，故B土最后定名为粉土质砂(SC)。(3)对C土进行分类①由粒径分布曲线图，查得粒径大于0.075㎜的粗粒含量大于50%，所以C土属于粗粒土；②粒径大于2㎜的砾粒含量大于50%，所以C土属于砾类土；③细粒含量为2%，少于5%，该土属砾；④从图中曲线查得，和分别为0.2㎜，0.45㎜和5.6㎜因此，土的不均匀系数土的曲率系数⑤由于，所以C土属于级配不良砾(GP)。1-9解：(1)即(2)t(3)[2-1]如图所示为某地基剖面图，各土层的重度及地下水位如图，求土的自重应力和静孔隙水应力。 2m2m3m1m1m地下水位γ=18.5kN/m3γ=18kN/m3γsat=20kN/m3γsat=19kN/m3γsat=19.5kN/m3OABCDE解：各层面点自重应力计算如下：O点：A点：B点：C点：D点：E点：各层面点的静孔隙水应力如下：O、A、B点为0；E点：绘图如下： [2-2]某矩形基础，埋深1m,上部结构传至设计地面标高处的荷载为P=2106kN，荷载为单偏心，偏心距e=0.3。求基底中心点、边点A和B下4m深处的竖向附加应力解：已知：P=2106kN,γ0=17kN/m3,d=1m,e0=0.3,l=6m,b=3m,z=4m.36OAB(1)基底压力：∵G=γdlb=20×1×6×3=360kN,Fv=P+G=2106+360=2466kN∴(2)基底附加应力：O、BA(3)O、B点竖向附加应力：可认为仅由矩形均布荷载 引起，附加应力系数及附加应力值见下表。A点竖向附加应力：可认为有矩形均布荷载pn和三角形荷载pt两部分引起，即：附加应力系数及附加应力值见下表。附加应力计算表O点B点A点荷载型式矩形均布矩形均布矩形均布三角形分布l(m)3361.5b(m)1.531.56z(m)4444l/b2140.25z/b2.66671.3332.66670.6667Ks(查表2-2)0.08600.13770.10480.0735(查表2-3)σz计算式4Kspn2Kspn2Kspn2Kt2pt 17.6910.47σz(kPa)41.2833.0528.16[2-3]甲乙两个基础，它们的尺寸和相对位置及每个基底下的基底净压力如图所示，求甲基础O点下2m处的竖向附加应力。解：甲基础O点下2m处的竖向附加应力由基础甲、乙共同引起，计算中先分别计算甲、乙基础在该点引起的竖向附加应力，然后叠加。（1）甲基础在O点下2m处引起的竖向附加应力：由于O点位于基础中心，荷载为梯形荷载，在O点的竖向附加应力和梯形荷载平均得的均布荷载相等，即可取pn=(100+200)/2=150kPa由图可知：l=1m，b=1m,z=2m故：l/b=1.0,z/b=2.0Oabcdefgh查表2-2的附加应力系数为：Ks=0.0840所以，基础甲在O点以下2m处引起的竖向附加应力为：（2）乙基础在O点下2m处引起的竖向附加应力：pn=200kPa附加应力计算如下表：计算区域lbzl/bz/bKs=Kspn obdf44210.50.231546.3obcg422210.199939.98oaef422210.199939.98oahg222110.175235.041.38(3)O点下2m处引起的竖向附加应力：[2-4]解：（1）（2）求偏心距：所以，偏心距 求基底压力：求基底净压力：求附加应力：；附加应力系数及附加应力计算表：M点N点条形均布荷载三角形荷载条形均布荷载三角形荷载x0606b6666z3366x/b0101z/b0.50.511Ksz(查表2-6)0.479--0.409--Ktz(查表2-7)--0.353--0.25030.08--25.69-- (kPa)(kPa)--46.49--32.93(kPa)76.5758.62[2-5]题略解：（1）自重应力：（2）竖向附加应力：偏心距：基底压力：O3m2m基底净压力：附加应力：可按均布荷载考虑，附加应力计算如下表： M点N点l1.51.5b11z1.53.5l/b1.51.5z/b1.53.5Ks(查表2-2)0.14610.0479(kPa)70.0722.97(3)静孔隙水应力：[3-1]已知：A＝120cm2，ΔH＝50cm，L=30cm，t＝10S，Q=150cm3，求k。解：[3-2]已知：n＝38%，Gs＝2.65。 解：（1）由图1-28查得：;;可得：查图1-28得小于粒径1.25mm的土粒百分含量为：P＝26%。则P<0.9Pop=51.3%所以，该土为管涌型。（2）查图1-28得：；则 [3-3]已知：：n＝36%，Gs＝2.65。解：（1）查图1-29可得，；则：由图1-29可知，土样C为级配不连续土。从图中查得小于粒组频率曲线谷点对应粒径的土粒百分含量为：P=43%>35%所以，土样C为流土型。（2）[3-4]已知：Gs=2.68，n=38.0%，相邻等势线间的水头损失为Δh=0.8m，h2=2m，，发生流土的临界水力梯度icr=1.04。 解：（1）b点在倒数第三根等势线上，故该点的测压管水位应比下游静水位高。从图中量测得b点到下游静水位的高差为则，b点测压管中的水位高度为所以，b点的孔隙水应力为：其中，由下游静水位引起的静孔隙水应力为：而由渗流引起的超静孔隙水应力为： b点的总应力为：所以，b点的有效应力为：（2）从图中查得网格5,6,7,8的平均渗流路径长度为，而任一网格的水头损失为Δh=0.8m，则该网格的平均水力梯度为所以，地表面5-6处不会发生流土。[3-5]已知：,,,地下水位以上砂土层厚h1=1.5m，地下水位以下砂土层厚h2=1.5m，粘土层厚h3=3.0m。解：由图可知，粘土层顶面测压管水位为（以粘土层底面作为高程计算零点）；粘土层底面测压管水位为（1）粘土层应力计算：粘土层顶面应力：总应力：孔隙水应力：有效应力：粘土层底面应力：总应力： 孔隙水应力：有效应力：（1）要使粘土层发生流土，则粘土层底面的有效应力应为零，即所以，粘土层底面的测压管水头高度应为，则，粘土层底面的承压水头应高出地面为11.76-6.0=5.76m。[4-1]解：(1)由l/b=18/6=3.0<10可知，属于空间问题，且为中心荷载，所以基底压力为基底净压力为(2)因为是均质粘土，且地下水位在基底下1.5m处，取第1分层厚度为H1=1.5m，其他分层厚度Hi=3.0m（i>1）。(3)求各分层点的自重应力（详见表1）(4)求各分层点的竖向附加应力（详见表1）表1各分层点的自重应力和附加应力计算表（l=9m,b=3m） 点自重应力附加应力号Hizizi/bl/bKs(查表2-2)01.528.650030.250071.3513.045.151.50.5030.239168.2426.078.154.51.5030.164046.8139.0111.157.52.5030.106430.36412.0144.1510.53.5030.072120.58(5)确定压缩层厚度。由表1可知，在第4计算点处，所以，取压缩层厚度为10.5m。(6)计算各分层的平均自重应力和平均附加应力（详见表2）。(7)由图4-29根据和分别查取初始孔隙比e1i和压缩稳定后的孔隙比e2i（结果见表2）。表2各分层的平均应力及其孔隙比 层号层厚(m)平均自重应力(kPa)平均附加应力(kPa)加荷后的总应力(kPa)初始孔隙比e1i压缩稳定后的孔隙比e2i0-11.536.9069.80106.700.9280.8001-23.061.6557.53119.180.8710.7852-33.094.6538.59133.240.8140.7613-43.0127.6525.47153.120.7710.729(8)计算地基的沉降量。[4-2]解：(1)属于平面问题，且为偏心荷载作用，偏心距e=1.0