《机械原理》第七版西北工业大学习题答案(特别全答案详解).pdf 67页

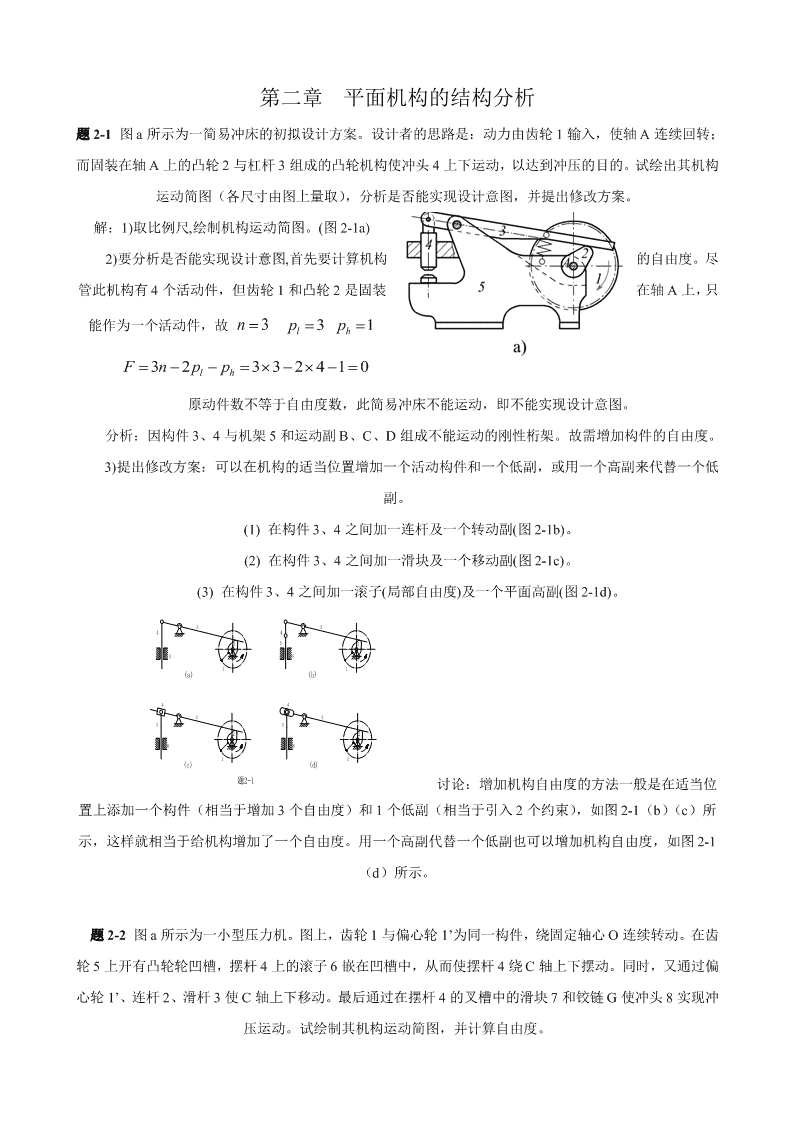
'第二章平面机构的结构分析题2-1图a所示为一简易冲床的初拟设计方案。设计者的思路是：动力由齿轮1输入，使轴A连续回转；而固装在轴A上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。试绘出其机构运动简图（各尺寸由图上量取），分析是否能实现设计意图，并提出修改方案。解：1)取比例尺,绘制机构运动简图。(图2-1a)2)要分析是否能实现设计意图,首先要计算机构的自由度。尽管此机构有4个活动件，但齿轮1和凸轮2是固装在轴A上，只能作为一个活动件，故n3p3p1lhF3n2pp332410lh原动件数不等于自由度数，此简易冲床不能运动，即不能实现设计意图。分析：因构件3、4与机架5和运动副B、C、D组成不能运动的刚性桁架。故需增加构件的自由度。3)提出修改方案：可以在机构的适当位置增加一个活动构件和一个低副，或用一个高副来代替一个低副。(1)在构件3、4之间加一连杆及一个转动副(图2-1b)。(2)在构件3、4之间加一滑块及一个移动副(图2-1c)。(3)在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-1d)。33442525611(a)(b)443355226611(c)(d)题2-1讨论：增加机构自由度的方法一般是在适当位置上添加一个构件（相当于增加3个自由度）和1个低副（相当于引入2个约束），如图2-1（b）（c）所示，这样就相当于给机构增加了一个自由度。用一个高副代替一个低副也可以增加机构自由度，如图2-1（d）所示。题2-2图a所示为一小型压力机。图上，齿轮1与偏心轮1’为同一构件，绕固定轴心O连续转动。在齿轮5上开有凸轮轮凹槽，摆杆4上的滚子6嵌在凹槽中，从而使摆杆4绕C轴上下摆动。同时，又通过偏心轮1’、连杆2、滑杆3使C轴上下移动。最后通过在摆杆4的叉槽中的滑块7和铰链G使冲头8实现冲压运动。试绘制其机构运动简图，并计算自由度。 解：分析机构的组成：此机构由偏心轮1’（与齿轮1固结）、连杆2、滑杆3、摆杆4、齿轮5、滚子6、滑块7、冲头8和机架9组成。偏心轮1’与机架9、连杆2与滑杆3、滑杆3与摆杆4、摆杆4与滚子6、齿轮5与机架9、滑块7与冲头8均组成转动副，滑杆3与机架9、摆杆4与滑块7、冲头8与机架9均组成移动副，齿轮1与齿轮5、凸轮(槽)5与滚子6组成高副。故解法一：n7p9p2lhF3n2pp372921lh解法二：n8p10p2局部自由度F1lhF3n(2ppp)F38210211lh题2-3如图a所示为一新型偏心轮滑阀式真空泵。其偏心轮1绕固定轴A转动，与外环2固连在一起的滑阀3在可绕固定轴心C转动的圆柱4中滑动。当偏心轮1按图示方向连续转动时，可将设备中的空气按图示空气流动方向从阀5中排出，从而形成真空。由于外环2与泵腔6有一小间隙，故可抽含有微小尘埃的气体。试绘制其机构的运动简图，并计算其自由度。题2-4解：1)取比例尺,绘制机构运动简图。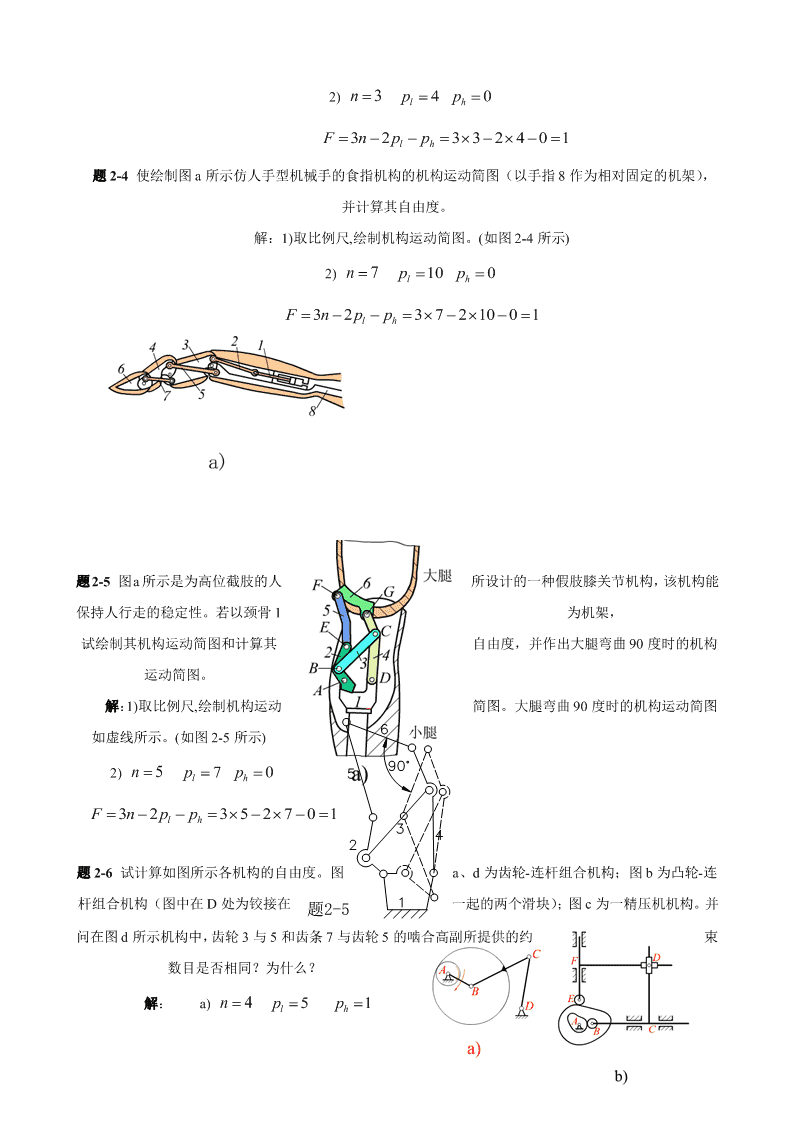(如图题2-3所示)４Ｃ２３Ａ１Ｂ题2-3 2)n3p4p0lhF3n2pp332401lh题2-4使绘制图a所示仿人手型机械手的食指机构的机构运动简图（以手指8作为相对固定的机架），并计算其自由度。解：1)取比例尺,绘制机构运动简图。(如图2-4所示)2)n7p10p0lhF3n2pp3721001lh题2-5图a所示是为高位截肢的人所设计的一种假肢膝关节机构，该机构能保持人行走的稳定性。若以颈骨1为机架，试绘制其机构运动简图和计算其自由度，并作出大腿弯曲90度时的机构运动简图。解：1)取比例尺,绘制机构运动简图。大腿弯曲90度时的机构运动简图如虚线所示。(如图2-5所示)2)n5p7p0lhF3n2pp352701lh题2-6试计算如图所示各机构的自由度。图a、d为齿轮-连杆组合机构；图b为凸轮-连杆组合机构（图中在D处为铰接在题2-5一起的两个滑块）；图c为一精压机机构。并问在图d所示机构中，齿轮3与5和齿条7与齿轮5的啮合高副所提供的约束数目是否相同？为什么？解：a)n4p5p1lh F3n2pp342511lhb)解法一：n5p6p2lhF3n2pp352621lh解法二：n7p8p2虚约束p0局部自由度F2lhF3n(2ppp)F37(2820)21lhc)解法一：n5p7p01A3ElhO2F3n2pp352701lh(b)解法二：n11p17p0lh虚约束p2pp3n2100362局部自由度F0lhF3n(2ppp)F311(21702)01lhd)n6p7p3lhF3n2pp362731lh齿轮3与齿轮5的啮合为高副（因两齿轮中心距己被约束，故应为单侧接触）将提供1个约束。齿条7与齿轮5的啮合为高副（因中心距未被约束，故应为双侧接触）将提供2个约束。题2-7试绘制图a所示凸轮驱动式四缸活塞空气压缩机的机构运动简图。并计算其机构的自由度（图中凸轮1原动件，当其转动时，分别推动装于四个活塞上A、B、C、D处的滚子，使活塞在相应得气缸内往复运动。图上AB=BC=CD=AD）。解：1)取比例尺,绘制机构运动简图。(如图2-7(b)所示)2)此机构由1个凸轮、4个滚子、4个连杆、4个活塞和机架组成。凸轮与4个滚子组成高副，4个连杆、4个滚子和4个活塞分别在A、B、C、D处组成三副复合铰链。4个活塞与4个缸（机架）均组成移动副。解法一：n13p17p4lh虚约束： 因为ABBCCDAD，4和5，6和7、8和9为不影响机构传递运动的重复部分，与连杆10、11、12、13所带入的约束为虚约束。机构可简化为图2-7（b）重复部分中的构件数n10低副数p17高副数p3局部自由度F3lhp2pp3n217331034lh局部自由度F4F3n(2ppp)F313(21744)41lh解法二：如图2-7（b）局部自由度F1F3n(2ppp)F33(2310)11lh题2-8图示为一刹车机构。刹车时，操作杆1向右拉，通过构件2、3、4、5、6使两闸瓦刹住车轮。试计算机构的自由度，并就刹车过程说明此机构自由度的变化情况。（注：车轮不属于刹车机构中的构件。）解：1)未刹车时，刹车机构的自由度n6p8p0lhF3n2pp362802lh2)闸瓦G、J之一刹紧车轮时，刹车机构的自由度n5p7p0lhF3n2pp352701lh3)闸瓦G、J同时刹紧车轮时，刹车机构的自由度n4p6p0lhF3n2pp342600lh题2-9试确定图示各机构的公共约束m和族别虚约束p″，并人说明如何来消除或减少共族别虚约束。解：(a)楔形滑块机构的楔形块1、2相对机架只能在该平面的x、y方向移动，而其余方向的相对独立运动都被约束，故公共约束数m4,为4族平面机构。pp3i55F6mnimp6425431iim1F6nip62533将移动副改为圆柱下刨，可减少虚约束。0i Ａ题(b)由于齿轮1、2只能在平行平面内运动，故为公共约束数m3,为3族平面机构。p2p1545F6mnimp3n2pp322211ilhim1F6nip6225142将直齿轮改为鼓形齿轮，可消除虚约束。0i(c)由于凸轮机构中各构件只能在平行平面内运动，故为m3的3族平面机构。p3p1F1545F6mnimpF63353p43pF1i54im1F6nipF63534112将平面高副改为空间高副，可消除虚约束。0i题2-10图示为以内燃机的机构运动简图，试计算自由度，并分析组成此机构的基本杆组。如在该机构中改选EG为原动件，试问组成此机构的基本杆组是否与前者不同。解：1)计算此机构的自由度n7p10p0lhF3n2pp3721001lh2)取构件AB为原动件时机构的基本杆组图2-10（b）所示。此机构为二级机构。3)取构件GE为原动件时机构的基本杆组图2-10（c）所示。此机构为三级机构。 3D3322C24B174H771E6A5F466155G(a)(b)(c)图2-10题2-11图a所示为一收放式折叠支架机构。该支架中的件1和5分别用木螺钉联接于固定台板1`和活动台板5`上，两者在D处铰接，使活动台板能相对于固定台板转动。又通过件1、2、3、4组成的铰链四杆机构及连杆3上E点处销子与件5上的连杆曲线槽组成的销槽联接使活动台板实现收放动作。在图示位置时，虽在活动台板上放有较重的重物，活动台板也不会自动收起，必须沿箭头方向推动件2，使铰链B、D重合时，活动台板才可收起（如图中双点划线所示）。现已知机构尺寸lAB=lAD=90mm,lBC=lCD=25mm，试绘制机构的运动简图，并计算其自由度。AED解：1)取比例尺,绘制机构运动简图。(如图2-11所示)2)E处为销槽副，销槽两接触点公法线重合，只能算作一个高副。Cn4p5p1图2-11lhBF3n2pp342511lh第三章平面机构的运动分析题3-1试求图示各机构在图示位置时全部瞬心的位置(用符号Pij直接标注在图上)解： ∞P13P23(P13)P23(P24)3P13(P34)B34B2P2C34C4∞AP14(P24)P14P12P12AD11(b)(a)P34∞P23PP23P13P3412P13A2BB33∞2P344∞4ACP14P12P24P14C(c)11(d)P13C34CP143B2BP23M∞OP24P34∞P13P12AvMP2321P121(f)(e)题3-2在图示在齿轮-连杆机构中,试用瞬心法求齿轮1与齿轮3的传动比w1/w3.解：1）计算此机构所有瞬心的数目N(N1)K1522）为求传动比需求出如下三个瞬心P、P、P如图3-2所示。13163613PP136133）传动比计算公式为：133P16P13 2CP12P234B5P131P36P16AD36图3-1题3-3在图a所示的四杆机构中，lAB=60mm，lCD=90mm，lAD=lBC=120mm，ω2=10rad/s，试用瞬心法求：1）当φ=165°时，点C的速度Vc；2）当φ=165°时，构件3的BC线上速度最小的一点E的位置及速度的大小；3）当Vc=0时，φ角之值（有两个解）解：1)以选定比例尺,绘制机构运动简图。(图3-3)2）求VC，定出瞬心P13的位置。如图3-3（a）ECP3434Bω2P232ADP14P121(a)P13C1P34P133P13C2P344B14ω2P2332ADADP14P14P12P1211ω2(b)2(c)B2P23图3-3vlB2AB32.56radsvClCP1330.4mslABlBP133）定出构件3的BC线上速度最小的点E的位置。因为BC线上速度最小的点必与P13点的距离最近，所以过P13点引BC线延长线的垂线交于E点。如图3-3（a） vEP0.375msEl1334）当v0时，P13与C点重合，即AB与BC共线有两个位置。作出v0的两个位置。CC量得26.4226.612题3-4在图示的各机构中，设已知各构件的尺寸、原动件1以等角速度ω1顺时针方向转动。试用图解法求机构在图示位置时构件3上C点的速度及加速度。解：a)速度方程：vC3vBvC3BvC2vC2C3ntntkr加速度方程：aC3aC3aBaC3BaC3BaC2aC3C2aC3C2p′(c2′,k′,c3′,a′)Bp(c2、c4、a)13ω1C2Ab(c3)b′(n3′)(a)4b)速度方程：vB3vB2vB3B2ntKr加速度方程：aB3aB3aB2aB3B2aB3B2p′(n3′,d′,a′)C3D24Bp(b3,d,c3,a)1b2′b3′ω1b2(b1)A(b1′,k′,c3′,)(b)b)速度方程：vB3vB2vB3B2ntKr加速度方程：aB3aB3aB2aB3B2aB3B2 p(a,d)Cb3′3c31A2Db′(b1′,b2′,k′)ω14p′n3′,c3′(c)b2(b1,b3)题3-5在图示机构中，已知各构件的尺寸及原动件1的角速度ω1（为常数），试以图解法求φ1=90°时，构件3的角速度ω3及角加速度α3（比例尺如图）。（应先写出有关的速度、加速度矢量方程，再作图求解。）解：1)速度分析：图3-5（b）lAB0.015m0.001vl100.0150.15mslAB15mmB11ABvB0.15ms速度方程：vB3vB2vB3B2v0.0042mmpb35速度多边形如图3-5(b)vbb0.004237.570.158mB3B2V23svB3vpb30.004227.782.2351转向逆时针3ll0.00152.2sBDBDCp′b3n3′23Bb3′1ω1Dk′A4(a)b1p(b)b1′,b2′(c)2aB21.5ms2)加速度分析：图3-5（c）a0.0428mmpb35ntKraaaaaB3B3B2B3B2B3B2n222222al2.260.0520.265msal100.0151.5msB313BdB211ABk2a2v22.2350.1580.71msB3B23B3B2taB3anb30.0428129.84132转向顺时针。lBD0.00152.2sBDl题3-6在图示的摇块机构中，已知lAB=30mm，lAC=100mm，lBD=50mm，lDE=40mm。曲柄以等角速度ω1=10rad/s 回转，试用图解法求机构在φ1=45°位置时，点D和点E的速度和加速度，以及构件2的角速度和角加速度。lAB0.03m解：1)选定比例尺,l0.002mm绘制机构运动简图。(图3-6(a))AB152）速度分析：图3-6（b）vl100.030.3msB1ABvB0.3ms速度方程vC2vBvC2BvC3vC2C3v0.005mmpb60由速度影像法求出VE速度多边形如图3-6(b)vpd0.00544.830.224mvpe0.00534.180.171mDVsEVsvCBvbc20.00549.521（顺时针）3ll0.00261.53sBCBccp′c3′2c3pBD2Cc2′k′A3ω1d4ee′(a)Ed′(b)b(c)b′c2″图3-62aB23ms3）加速度分析：图3-6（c）a0.04mmpb75ntkraaaaaaaC2BC2BC2BC3C2C3C2C3由加速度影像法求出aE加速度多边形如图3-6(c)222al100.033msB11AB222al20.1220.5msC2B12CBk2a2v22.0.1750.7msC2C323C2C3aDapd0.04652.6m2stape0.04712.8maC2Bac2c20.0425.68.391Ea222slBC0.00261.53sBCl（顺时针）题3-7在图示的机构中，已知lAE=70mm，lAB=40mm，lEF=60mm，lDE=35mm，lCD=75mm，lBC=50mm，原 动件1以等角速度ω1=10rad/s回转，试以图解法求点C在φ1=50°时的速度Vc和加速度ac。解：1)速度分析：以F为重合点(F1、F5、、F4)有速度方程：vF4vF5vF1vF5F1ms以比例尺0.03速度多边形如图3-7(b)，由速度影像法求出VB、VDvmmvvvvvCBCBDCD2ms2)加速度分析：以比例尺a0.6mmntkr有加速度方程：aF4aF4aF4aF1aF5F1aF5F1由加速度影像法求出aB、aDntntaaaaaaaCBCBCBDCDCDvpc0.69mCVsd′n3′(F1,F5,F4)F5f1d4b′1n2′ω1p′pc′bAECcf4,(f5)23(b)B(a)Dk′图3-7(c)n4′aCapc3m2f4′(f5′)s题3-8在图示的凸轮机构中，已知凸抡1以等角速度10rads转动，凸轮为一偏心圆，其半径1R25mm,l15mm,l50mm,90，试用图解法求构件2的角速度与角加速度。ABAD122解：1)高副低代，以选定比例尺,绘制机构运动简图。(图3-8)2)速度分析：图3-6（b）vvl100.0150.15ms取B4、、B2B4B11AB为重合点。速度方程：vB2vB4vB2B4速度多边形如图3-8(b)vpb0.00523.50.1175mvbb0.005320.16mB2V2sB2B4V42svB2vpb20.11752.291转向逆时针2ll0.001254sBDBD p′b2Cb2"α24b2′2Bk′ω2ω1A1b4pD(b)b4′3图3-8(c)3）加速度分析：图3-8（c）ntKraaaaaB2B2B4B2B4B2B4nn222n222aal100.0151.5msal2.290.00125410.269msB4B111ABB212Bdk2a2v22.290.160.732msB2B42B2B4taB2ab2b20.04129.361转向顺时针。22lBD0.0012541sBDl题3-9在图a所示的牛头刨床机构中，h=800mm，h1=360mm，h2=120mm，lAB=200mm，lCD=960mm，lDE=160mm，设曲柄以等角速度ω1=5rad/s逆时针方向回转，试用图解法求机构在φ1=135°位置时，刨头上点C的速度Vc。lAB0.12m解：选定比例尺,l0.001mm绘制机构运动简图。(图3-9(a))AB12解法一：速度分析：先确定构件3的绝对瞬心P36，利用瞬心多边形，如图3-9（b）由构件3、5、6组成的三角形中，瞬心P36、P35、P56必在一条直线上，由构件3、4、6组成的三角形中，瞬心P36、P34、P46也必在一条直线上，二直线的交点即为绝对瞬心P36。vB1ms速度方程vB3vB2vB3B2v0.05mmpb20vvl50.21ms方向垂直AB。B2B11ABVB3的方向垂直BG（BP36），VB3B2的方向平行BD。速度多边形如图3-9(c)速度方程vCvB3vCB3vpc1.24mCVs ∞P56FC511P35∞66262P23P15P13B535312(B1,B2,B3)ω144P12A(b)(d)P16b1,b213P6246Ec4D∞b3p53P56P34(c)4(e)(a)GP36图3-9解法二：确定构件3的绝对瞬心P36后，再确定有关瞬心P16、P12、P23、P13、P15，利用瞬心多边形，如图3-9（d）由构件1、2、3组成的三角形中，瞬心P12、P23、P13必在一条直线上，由构件1、3、6组成的三角形中，瞬心P36、P16、P13也必在一条直线上，二直线的交点即为瞬心P13。利用瞬心多边形，如图3-9（e）由构件1、3、5组成的三角形中，瞬心P15、P13、P35必在一条直线上，由构件1、5、6组成的三角形中，瞬心P56、P16、P15也必在一条直线上，二直线的交点即为瞬心P15。如图3-9(a)P15为构件1、5的瞬时等速重合点vvAP1.24mCP15115ls题3-10在图示的齿轮-连杆组合机构中，MM为固定齿条，齿轮3的齿数为齿轮4的2倍，设已知原动件1以等角速度ω1顺时针方向回转，试以图解法求机构在图示位置时，E点的速度VE以及齿轮3、4的速度影像。解：1)选定比例尺绘制机构运动简图。(图3-10(a))l2）速度分析：此齿轮-连杆机构可看成ABCD及DCEF两个机构串联而成。则速度方程：vCvBvCBvEvCvEC以比例尺v作速度多边形，如图3-10(b)vEVpe取齿轮3与齿轮4的啮合点为K，根据速度影像原理，在速度图(b)中作dck∽DCK，求出k点，以c为圆心，以ck为半径作圆g3即为齿轮3的速度影像。同理fek∽FEK，以e为圆心，以ek为半径作圆g4即为齿轮4的速度影像。5FkBE4(d,f)pc21K3eCbAωg316DMMg4(a)(b) 题3-11如图a所示的摆动式飞剪机用于剪切连续运动中的钢带。设机构的尺寸为lAB=130mm，lBC=340mm，lCD=800mm。试确定剪床相对钢带的安装高度H（两切刀E及E`应同时开始剪切钢带5）；若钢带5以速度V5=0.5m/s送进时，求曲柄1的角速度ω1应为多少才能同步剪切？解：1)选定比例尺,l0.01m绘制机构运动简图。(图3-11)mm两切刀E和E’同时剪切钢带时,E和E’重合,由机构运动简图可得H708.9mm2)速度分析：速度方程：vCvBvCB由速度影像pec∽DCEvEVpe3）VE必须与V5同步才能剪切钢带。vpbpbvpbvBVE51lABlABpelABpelAB加速度方程：ntkraaaaaaB3B3B3B2B3B2B3B2CB2ω1E1E′A34cb70.89peD图3-11题3-12图a所示为一汽车雨刷机构。其构件1绕固定轴心A转动，齿条2与构件1在B点处铰接，并与绕固定轴心D转动的齿轮3啮合（滚子5用来保证两者始终啮合），固联于轮3的雨刷3作往复摆动。设机构的尺寸为lAB=18mm，；轮3的分度圆半径r3=lCD=12mm，原动件1以等角速度ω1=1rad/s顺时针回转，试以图解法确定雨刷的摆程角和图示位置时雨刷的角速度。解：1)选定比例尺,l0.001m绘制机构运动简图。(图3-12)mm在图中作出齿条2和齿轮3啮合摆动时占据的两个极限位置C′和C″，可得摆程角39.53max2）速度分析：图3-12（b）vB21lAB0.018ms速度方程：vB3vB2vB3B2以比例尺v作速度多边形，如图3-12(b) vpbB3v30.059rads转向逆时针vbb0.01845m23lB3B2V23sBDlBDp′″b3BB′130.0°39.5°21ω1AC′CC″4b2′B″b3b2b3D3pk′(a)(b)(c)图3-12n223）加速度分析：aB211lAB0.018msn22al0.00018msB313BDk2a2v0.00217ms以比例尺作加速度多边形如图3-12(c)B3B23B3B2atabbB3a331.711转向顺时针。32lBDsBdl题3-13图a所示为一可倾斜卸料的升降台机构。此升降机有两个液压缸1、4，设已知机构的尺寸为lllll750mm，l2000mm，m500mm。若两活塞的相对移动速度分别BCCDCGFHEFIJEI为v0.05ms常数和v0.03ms常数，试求当两活塞的相对移动位移分别为2154s350mm和s260mm时（以升降台位于水平且DE与CF重合时为起始位置），工件重心S处的2154速度及加速度和工件的角速度及角加速度。 解：1）选定比例尺,l0.05m绘制机构运动简图。(图3-13)此时mml0.5s0.85mlls20.261.74mAB21GHIJ54ms2）速度分析：取v0.002vB2vB1vB2B1mm作速度多边形，如图3-13（b）由速度影像法vvv，求得d、g，再根据GDB2vvvvvvvvH4GH4GH5H4H5EH5H4vIvDvIDvEvIE继续作图求得vI，再由速度影像法求得：vvps0.041m80.015rad（逆时针）SvslsIDdsSeig81IAD7bph4C2Eh56F3B4G5(a)H(b)图3-13b22)加速度分析（解题思路）ntntkr根据aaaaaaa作图求得a，再由加速度影像法根据B2B2B2B1B1B2B1B2B1BntntkraaaaaaaaH4GH4GH4GH5H5H4H5H4H5taID作图求得aH5，再由加速度影像法求得：aS，8lID第四章平面机构的力分析 题4-1在图示的曲柄滑块机构中，设已知lAB=0.1m，lBC=0.33m，n1=1500r/min（为常数），活塞及其附件的重量G3=21N，连杆质量G2=25N，JS2=0.0425kg·m2，连杆质心S2至曲柄销B的距离lBS2=lBC/3。试确定在图示位置时活塞的惯性力以及连杆的总惯性力。解：1)选定比例尺,l0.005m绘制机构运动简图。(图4-1(a))mm2）运动分析：以比例尺作速度多边形，如图4-1(b)v以比例尺作加速度多边形如图4-1(c)aaCapc23.44m2aS2aps22100m2ssatncC2Ba5150122lBCsBCl3)确定惯性力G活塞3：FI3m3aS33aC3767(N)方向与pc相反。gG连杆2：FI32m2aS22aS25357(N)方向与ps相反。g2MJ218.8(Nm)（顺时针）I2S22M总惯性力：FF5357(N)lI20.04(m)(图4-1(a))I2I2h2FI2′FI2b′pcB0.04s′12C2S2An13n′b′cp4(a)(b)(c)图4-1题4-2机械效益Δ是衡量机构力放大程度的一个重要指标，其定义为在不考虑摩擦的条件下机构的输出力（力矩）与输入力（力矩）之比值，即Δ=M/MF/F。试求图示各机构在图示位置时的机械效益。图a所示为一铆钉机，图b为一小型rdrd压力机，图c为一剪刀。计算所需各尺寸从图中量取。（a）(b)(c) 解：(a)作铆钉机的机构运动简图及受力图见4-2（a）由构件3的力平衡条件有：FrFR43FR230由构件1的力平衡条件有：FR21FR41Fd0按上面两式作力的多边形见图4-2（b）得FFcotrd（b）作压力机的机构运动简图及受力图见4-2（c）由滑块5的力平衡条件有：GFR65FR450由构件2的力平衡条件有：FR42FR32FR120其中FR42FR54按上面两式作力的多边形见图4-2（d）得GFtFR41DFR36F653Ft1AFdBFR43FR322GθFR21θCA1FR322FFR12FR42R21FR16FFR45R42BFR2343Frθ6FR45FtFR43FR414F65EFrFR235FR12FdG(a)Fr(b)(c)(d)图4-2(c)对A点取矩时有FaFbrdba其中a、b为Fr、Fd两力距离A点的力臂。GFt题4-3图a所示导轨副为由拖板1与导轨2组成的复合移动副，拖板的运动方向垂直于纸面；图b所示为由转动轴1与轴承2组成的复合转动副，轴1绕其轴线转动。现已知各运动副的尺寸如图所示，并设G为外加总载荷，各接触面间的摩擦系数均为f。试分别求导轨副的当量摩擦系数fv和转动副的摩擦圆半径ρ。解：1）求图a所示导轨副的当量摩擦系数f，把重量G分解为G左，G右Vfl2lllsin121GG，GG，fGFFG左右vf左f右llllll121212fl2lsin1fvll12 2）求图b所示转动副的摩擦圆半径ll21支反力FG，FGR左R右llll1212假设支撑的左右两端均只在下半周上近似均匀接触。对于左端其当量摩擦系数2fVf，摩擦力FfG左2f左v右左摩擦力矩MFercos45f左v左对于右端其当量摩擦系数ff，摩擦力FfGV右2f右v右右摩擦力矩MFrf右v右MMf左f右摩擦圆半径G题4-4图示为一锥面径向推力轴承。已知其几何尺寸如图所示，设轴1上受铅直总载荷G，轴承中的滑动摩擦系数为f。试求轴1上所受的摩擦力矩M（分别一新轴端f和跑合轴端来加以分析）。f解：此处为槽面接触，槽面半角为。当量摩擦系数f代入平vsin轴端轴承的摩擦力矩公式得33Rr若为新轴端轴承，则M3fGfv22RrRr若为跑合轴端轴承，则MfGfv2题4-5图示为一曲柄滑块机构的三个位置，F为作用在活塞上的力，转动副A及B上所画的虚线小圆为摩擦圆，试决定在三个位置时，作用在连杆AB上的作用力的真实方向（各构件的重量及惯性力略去不计）解：图a和图b连杆为受压，图c连杆为受拉.，各相对角速度和运动副总反力方向如下图 FR12Aω2112ω23BFR32Mω1PO34(a)AFR12ω21ω232BM1ωPO3FR324(b)BMω1ω23PO3ω211FR3224FR12A(c)图4-5题4-6图示为一摆动推杆盘形凸轮机构，凸轮1沿逆时针方向回转，F为作用在推杆2上的外载荷，试确定在各运动副中总反力（FR31，FR12及FR32）的方位（不考虑构件的重量及惯性力，图中虚线小圆为摩擦圆，运动副B处摩擦角为φ=10°）。解:1)取构件2为受力体，如图4-6。由构件2的力平衡条件有：PFR12FR320三力汇交可得F和FR32R122)取构件1为受力体，FR21FR12FR31ωFR3223FR21B2CFR12ω1FR12ω1MFR32M11AA3P310°FR31图4-6P题4-9在图a所示的正切机构中，已知h=500mm，l=100mm，ω1=10rad/s（为常数），构件3的重量G3=10N，质心在其轴线上，生产阻力Fr=100N，其余构件的重力、惯性力及所有构件的摩擦力均略去不计。试求当φ1=60°时，需加在构件1上的平衡力矩Mb。提示：构件3受力倾斜后，构件3、4将在C1、C2两点接触。解:1)选定比例尺绘制机构运动简图。l2）运动分析：以比例尺，作速度多边形和加速度多边形如图4-1(c)，如图4-9（a）(b)va 22BBb60°1ω1FI3Fr33G3′AC1C1FR43hL′FI34FR43C2C2(c)FrFrb′3cpBF′′G3R43-FR43k′1FR21edFR41FR12b1pAa′b3,b2b′(e)(d)1(a)(b)图4-93)确定构件3上的惯性力GFma3a66.77(N)I333g34)动态静力分析：以构件组2,3为分离体，如图4-9(c),由F0有FR12FrFI3G3FR43FR430以2Nmm作力多边形如图4-9(d)P得FFea38NR21R12P以构件1为分离体，如图4-9(e)，有FlM0FFR21ABbR41R21MFl22.04Nm顺时针方向。bR21AB题4-10在图a所示的双缸V形发动机中，已知各构件的尺寸如图（该图系按比例尺μ1=0.005m/mm准确作出的）及各作用力如下：F3=200N，F5=300N，F＇I2=50N，F＇I4=80N，方向如图所示；又知曲柄以等角速度ω1转动，试以图解法求在图示位置时需加于曲柄1上的平衡力偶矩Mb。解:应用虚位移原理求解，即利用当机构处于平衡状态时，其上作用的所有外力（包括惯性力）瞬时功率应等于零的原理来求解，可以不需要解出各运动副中的反力，使求解简化。1)以比例尺作速度多边形如图4-10vvpc55mvpe57mvpt52mCVvsEVvsT2V2vspbvpt53mvradT4V4vs1lslAB 5′EFI4′36FI4pF5T4C2T2S4F3S24′bBFI2′FI21Dt2cAω1et4d图4-102）求平衡力偶矩：由Pivicosi0，MFvFvFvcosFvcos0b13c55I2T2T2I4T4T4ABlMbF3pcF5peFI2vT2cosT2FI4vT4cosT446.8Nmpb顺时针方向。第五章机械的效率和自锁(1)题5-1解:（1）根据己知条件，摩擦圆半径fr0.20.010.002marctanf8.53v计算可得图5-1所示位置45.6714.33（2）考虑摩擦时，运动副中的反力如图5-1所示。（3）构件1的平衡条件为：MFlsin21R21ABFR21FR23Mlsin2AB构件3的平衡条件为：FR23FR43F30按上式作力多边形如图5-1所示，有FFR233sin90sin90Fsin90McosMcosR2311（4）FF330coslsin2coslsinABAB（5）机械效率：F3lABsincos0.071530.92140.91F30lABsin2coscos0.075530.96880.9889 FR12Bω21F3βα2ω23FR2390°+φM11ωβF3AC3FR43FR3290°-φ-β4BαFR211FR43FR41M1FR23图5-1F3A3题5-2df2v解:（1）根据己知条件，摩擦圆半径1arctanf12arctanf22作出各运动副中的总反力的方位如图5-2所示。（2）以推杆为研究对象的平衡方程式如下：Fx0FR12sin1FR32cos1FR32cos20Fy0FR12cos1GFR32sin1FR32sin20dMC0FR12blsin1G2FR32cos2lFR32sin2d2FR12cos1ecos0（3）以凸轮为研究对象的平衡方程式如下：MFhR12ecosresintan1hcos1（4）联立以上方程解得Gecosresintan1MMGecos012ecostanl2ecos12eccostanM0l2Mecosresintan1 Mlb2′′R32φωrFR12θh22F11dφBeA3R31′R32FF2φ图5-2讨论：由于效率计算公式可知，φ1，φ2减小，L增大，则效率增大，由于θ是变化的，瞬时效率也是变化的。题5-322解:该系统的总效率为0.950.970.920.822123P55001.2103电动机所需的功率为Nv8.0290.822题5-4解：此传动属混联。第一种情况：PA=5kW,PB=1kWPP输入功率PA27.27kWPB22.31kWAB21A21APr传动总效率0.63电动机所需的功率PPP9.53kWP电ABd第二种情况：PA=1kW,PB=5kWPP输入功率PA21.44kWPB211.55kWAB21A21APr传动总效率0.462电动机所需的功率PPP12.99kWP电ABd题5-5解：此题是判断机构的自锁条件，因为该机构简单，故可选用多种方法进行求解。解法一：根据反行程时0的条件来确定。反行程时（楔块3退出）取楔块3为分离体，其受工件1、1′和夹具2作用的总反力FR13和FR23以及支持力F′。各力方向如图5-5（a）、(b)所示，根据楔块3的平衡条件，作力矢量三角形如图5-5（c）所示。由正弦定理可得FFcos当0时，FFR23sin2R230sin φFR23φFR13FR23vα-2φ2313F"F"ααFR23190°+φFR13FR13φφF"(a)(b)(c)图5-5于是此机构反行程的效率为FR320sin2FsinR32令0，可得自锁条件为：2。解法二：根据反行程时生产阻力小于或等于零的条件来确定。根据楔块3的力矢量三角形如图5-5（c），由正弦定理可得Fsin2FR23若楔块不自动松脱，则应使F0即得自锁条件为：2cos解法三：根据运动副的自锁条件来确定。由于工件被夹紧后F′力就被撤消，故楔块3的受力如图5-5(b)所示，楔块3就如同受到FR23（此时为驱动力）作用而沿水平面移动的滑块。故只要FR23作用在摩擦角φ之内，楔块3即发生自锁。即，由此可得自锁条件为：2。讨论：本题的关键是要弄清反行程时FR23为驱动力。用三种方法来解，可以了解求解这类问题的不同途径。第六章机械的平衡题6-1图示为一钢制圆盘，盘厚b=50mm，位置Ⅰ处有一直径φ=50mm的通孔，位置Ⅱ处是一质量m2=0.5kg的重块。为了使圆盘平衡，你在圆盘上r=200mm处制一通孔。试求此孔德直径与位置。（钢的密度=7.8g/cm3）解：解法一：先确定圆盘的各偏心质量大小225mb57.80.7648kgm0.5kg12442d设平衡孔质量mb根据静平衡条件b4mrmrmr01122bbmrcosmrcos135mrcos21032.52kgmmbbb1122 mrsinmrsin135mrsin210104.08kgmmbbb112222mr(mrsin)(mrcos)109.04kgmmbbbbbbbb4mb由r200mmm0.54kgd42.2mmbbb在位置相反方向挖一通孔b1mbrbsinb180tg18072.66180282.66bmrcosbbb解法二：kgmm由质径积矢量方程式，取2作质径积矢量多边形如图6-1（b）WmmW平衡孔质量mb0.54kg量得72.6bWrbbθbm1WⅠ题6-2在图示的转子中，已知各偏心质量r1ⅠWbm2r2m1=10kg，m2=15kg，m3=20kg，m4=10kg，它ⅡWⅡ们的回转半径分别为r1=40cm，r2=r4=30cm，(a)(b)图6-1r3=20cm，又知各偏心质量所在的回转平面的距离为l12=l23=l34=30cm，各偏心质量的方位角如图。若置于平衡基面Ⅰ及Ⅱ中的平衡质量mbⅠ及mbⅡ的回转半径均为50cm，试求mbⅠ及mbⅡ的大小和方位。解：解法一：先确定圆盘的各偏心质量在两平衡基面上大小60m230m260m32060m340m10kgm5kgmkgmkg2Ⅰ2Ⅱ3Ⅰ3Ⅱ9090903903根据动平衡条件(mbⅠrb)xmiricosim1r1cos120m2Ⅰr2cos240m3Ⅰr3cos300283.3kgcm (mbⅠrb)ymirisinim1r1sin120m2Ⅰr2sin240m3Ⅰr3sin30028.8kgcm2222mr(mr)(mr)（283.8）（28.8）284.8kgcmbbⅠbⅠbxbⅠby(mbrb)Ⅰ284.81(mbⅠrb)ymbⅠ5.6kgbⅠtg548rb50(mbⅠrb)x同理(mbⅡrb)xmiricosim4r4cos30m2Ⅱr2cos240m3Ⅱr3cos300359.2kgcm(mbⅡrb)ymirisinim4r4sin30m2Ⅱr2sin240m3Ⅱr3sin300210.8kgcm2222mr(mr)(mr)359.2210.8416.5kgcmbbⅡbⅡbxbⅡby(mbrb)Ⅱ416.5tg1(mbⅡrb)y145mbⅡ7.4kgbⅡrb50(mbⅡrb)x解法二：根据动平衡条件21mrmrmrmr0112233bⅠb3312mrmrmrmr0442233bⅡb33kgmm由质径积矢量方程式，取10作质径积矢量多边形如图6-2（b）Wmmm1W2ⅡWbⅡm4r1θbⅡr4W2ⅠW3ⅡW1ⅠW4Ⅱr3m3W3ⅠθbⅠm2r2WbⅠ(a)(b)图6-2WmbⅠ5.6kg6bⅠWrbⅠbWmbⅡ7.4kg145bⅡWrbⅡb题6-3图示为一滚筒，在轴上装有带轮。现已测知带轮有一偏心质量m1=1kg；另外，根据该滚筒的结构，知其具有两个偏心质量m2=3kg，m3=4kg，各偏心质量的位置如图所示（长度单位为mm）。若将平衡基面选在滚筒的端面，两平衡基面中平衡质量的回转半径均取为400mm，试求两平衡质量的大小及方位。若将 平衡基面Ⅱ改选为带轮中截面，其他条件不变，；两平衡质量的大小及方位作何改变？解：(1)以滚筒两端面为平衡基面时，其动平衡条件为3.51.59.5mrmrmrmr0bⅠbⅠ11223311111114.59.51.5mrmrmrmr0bⅡbⅡ112233111111以2kgcmmm，作质径积矢量多边形，如图6-3（a），(b)，则WWmbⅠ1.65kg，138bⅠWrbⅠbWmbⅡ0.95kg，102bⅡWrbⅡbW2ⅠW3ⅠW2ⅠW3ⅠW2ⅠW2ⅠW1Ⅰ102°102°WbⅠ138°WbWbⅠⅠW3Ⅰ159°WbⅠW3ⅠW1Ⅰ(a)(b)(d)(c)W1Ⅰ图6-3（2）以滚轮中截面为平衡基面Ⅱ时，其动平衡条件为513mrmrmr0bⅠbⅠ223314.514.59.51.5mrmrmrmr0bⅡbⅡ11223314.514.5以2kgcmmm，作质径积矢量多边形，如图6-3（c），(d)，则WWmbⅠ2271.35kg159bⅠWr40bⅠbWmbⅡ2140.7kg，102bⅡWr40bⅡb题6-4如图所示为一个一般机器转子，已知转子的重量为15kg。其质心至两平衡基面Ⅰ及Ⅱ的距离分别l1=100mm，l2=200mm，转子的转速n=3000r/min，试确定在两个平衡基面Ⅰ及Ⅱ内的需用不平衡质径积。当转子转速提高到6000r/min时，许用不平衡质径积又各为多少？ 解：（1）根据一般机器的要求，可取转子的平衡精度等级为G6.3，对应平衡精度A=6.3mm/s(2)n3000rmin2n314.16rads604e1000A20.05mmrme1520.05100.03kgcm可求得两平衡基面Ⅰ及Ⅱ中的许用不平衡质径积为l2002mrmr3020gcmⅠⅠll20010012l1001mrmr3010gcmⅡⅡll20010012(3)n6000rmin2n628.32rads604e1000A10.025mmrme1510.0251015kgcm可求得两平衡基面Ⅰ及Ⅱ中的许用不平衡质径积为l2002mrmr1510gcmⅠⅠll20010012l1001mrmr155gcmⅡⅡll20010012题6-5在图示的曲柄滑块机构中，已知各构件的尺寸为lAB=100mm，lBC=400mm；连杆2的质量m2=12kg，质心在S2处，lBS2=lBC/3；滑块3的质量m3=20kg，质心在C点处；曲柄1的质心与A点重合。今欲利用平衡质量法对该机构进行平衡，试问若对机构进行完全平衡和只平衡掉滑块3处往复惯性力的50%的部分平衡，各需加多大的平衡质量（取lBC=lAC=50mm），及平衡质量各应加在什么地方？解：（1）完全平衡需两个平衡质量，各加在连杆上C′点和曲柄上C″点处。平衡质量的大小为mCm2lBS2m3lBClBC1240320405192kgmCmm2m3lABlAC1921220105448kg（2）部分平衡需一个平衡质量，应加曲柄延长线上C″点处。平衡质量的大小为mmll12238kgmmll1644kgB22S2CBCC22BS2BCmm8kgmmm24kgBB2CC23 故平衡质量为mCmB1mClABlAC8241040kg225第七章机械的运转及其速度波动的调节题7-1如图所示为一机床工作台的传动系统，设已知各齿轮的齿数，齿轮3的分度圆半径r3，各齿轮的转动惯量J1、J2、J2`、J3，因为齿轮1直接装在电动机轴上，故J1中包含了电动机转子的转动惯量，工作台和被加工零件的重量之和为G。当取齿轮1为等效构件时，试求该机械系统的等效转动惯量Je。解：根据等效转动惯量的等效原则，有22nvSiiJemiJSii12222223GvJeJ1J2J2J3g11112222Z1Z1Z1Z2G2Z1Z2JeJ1J2J2J3r3ZZZZgZZ222323题7-2已知某机械稳定运转时其主轴的角速度ωs=100rad/s，机械的等效转动惯量Je=0.5Kg·m2，制动器的最大制动力矩Mr=20N·m（该制动器与机械主轴直接相联，并取主轴为等效构件）。设要求制动时间不超过3s，试检验该制动器是否能满足工作要求。解：因此机械系统的等效转动惯量Je及等效力矩Me均为常数，故可利用力矩形式的机械运动方程式d2MJ其中：MM20Nm0.5kgmeeerdtJe0.5dtdd0.025dM20rt0.0250.0252.5sSS由于t2.5s3s所以该制动器满足工作要求。题7-3图a所示为一导杆机构，设已知lAB=150mm，lAC=300mm，lCD=550mm，质量为m1=5kg（质心S1在A点），m2=3kg（质心S2在B点），m3=10kg（质心S3在lCD/2处），绕质心的转动惯量为JS1=0.05kg·m2，JS2=0.002kg·m2，JS3=0.2kg·m2，力矩M1=1000N·m，F3=5000N。若取构件3为等效构件，试求φ1=45°时，机构的等效转动惯量Je3及等效力 矩Me3。解：由机构运动简图和速度多边形如图可得1vB2lABpb2lBC3010423.24vlpbl261503B3BC3ABvS2vB2pb2300.420.485vlpb/l263B3BC3BCvS3ll20.275CS3CD3故以构件3为等效构件时，该机构的等效转动惯量为222JJ1JJmvS2mvS3e3S1S2S3233332222J0.053.2310.0020.230.485100.2752.186kgme3等效力矩为MMFve33113S3s3b3MM1FvS3de3133310003.23150000.775(b)b2,s21856Nm题7-4在图a所示的刨床机构中，已知空程和工作行程中消耗于克服阻抗力的恒功率分别为P1=367.7W和P2=3677W，曲柄的平均转速n=100r/min，空程中曲柄的转角φ1=120°。当机构的运转不均匀系数δ=0.05时，试确定电动机所需的平均功率，并分别计算在以下两种情况中的飞轮转动惯量JF（略去各构件的重量和转动惯量）：1）飞轮装在曲柄轴上；2）飞轮装在电动机轴上，电动机的额定转速nn=1440r/min。电动机通过减速器驱动曲柄。为简化计算减速器的转动惯量忽略不计。解：（1）根据在一个运动循环内，驱动功与阻抗功应相等。可得 PTPtPt1122PtPtppP11221122T1212367.73677332573.9W（2）最大盈亏功为601WPPtPPmax1112n112573.9367.7603100441.24Nm（3）求飞轮转动惯量当飞轮装在曲柄轴上时，飞轮的转动惯量为900Wmax900441.242J80.473kgmF2222n1000.05当飞轮装在电机轴上时，飞轮的转动惯量为22n1002JFJF80.4730.388kgmnn1440讨论：由此可见，飞轮安装在高速轴（即电机轴）上的转动惯量要比安装在低速轴（即曲柄轴）上的转动惯量小得多。题7-5某内燃机的曲柄输出力矩Md随曲柄转角的变化曲线如图a所示，其运动周期，曲柄的T平均转速n620rmin，当用该内燃机驱动一阻力为常数的机械时如果要求运转不均匀系数0.01，m试求： 1)曲轴最大转速nmax和相应的曲柄转角位置max；2)装在曲轴上的飞轮转动惯量J（不计其余构件的转F动惯量）。解:1)确定阻抗力矩因一个运动循环内驱动功应等于阻抗功，有1MTTAOABC20026200解得M6116.67Nmr22)求nmax和max作其系统的能量指示图（图b），由图b知，在c处机构出现能量最大值，即C时，nnmax故maxC200116.67max2030130104.16200这时n1n10.01620623.1rminmax2m23)求装在曲轴上的飞轮转动惯量JFWA200116.6720200116.67130200116.671maxaABc61802006180200289.08Nm900Wmax90089.082故J2.113kgmF2222n6200.01题7-6图a所示为某机械系统的等效驱动力矩M及等效阻抗力矩M对转角的变化曲线，为其变ederT2222化的周期转角。设己知各下尺面积为A200mm，A260mm，A100mm，A190mm，abbccdde2222Aef320mm，Afg220mm，Aga500mm，而单位面积所代表的功为A10Nmmm，试求系统的最大盈亏功Wmax。又如设己知其等效构件的平均转速为nm1000rmin。等效转动惯量为2J5kgm。e 试求该系统的最大转速n及最小转速n，并指出最大转maxmin束及最小转速出现的位置。解：1）求Wmax作此系统的能量指示图（图b），由图b知：此机械系统的动能最小及最大值分别出现在b及e的位置，即系统在及处，be分别有n及n。maxminWAAAmaxAbccdde102601001902500Nm2)求运转不均匀系数900Wmax900Wmax9002500JJ设J00.0456Fe22F2222nnJ10005mme3)求n和nmaxminn1n10.045610001022.8rminmax2m2maxen1n10.04561000977.2rminmin2m2minb第8章课后习题参考答案8-l铰链四杆机构中，转动副成为周转副的条件是什么?在下图所示四杆机构ABCD中哪些运动副为周转副?当其杆AB与AD重合时，该机构在运动上有何特点?并用作图法求出杆3上E点的连杆曲线。答：转动副成为周转副的条件是：（1）最短杆与最长杆的长度之和小于或等于其他两杆长度之和；（2）机构中最短杆上的两个转动副均为周转副。图示ABCD四杆机构中C、D为周转副。当其杆AB与AD重合时，杆BE与CD也重合因此机构处于死点位置。8-2曲柄摇杆机构中，当以曲柄为原动件时，机构是否一定存在急回运动，且一定无死点?为什么?答：机构不一定存在急回运动，但一定无死点，因为：（1）当极位夹角等于零时，就不存在急回运动如图所示， （2）原动件能做连续回转运动，所以一定无死点。8-3四杆机构中的极位和死点有何异同?8-4图a为偏心轮式容积泵；图b为由四个四杆机构组成的转动翼板式容积泵。试绘出两种泵的机构运动简图，并说明它们为何种四杆机构，为什么?解机构运动简图如右图所示，ABCD是双曲柄机构。因为主动圆盘AB绕固定轴A作整周转动，而各翼板CD绕固定轴D转动，所以A、D为周转副，杆AB、CD都是曲柄。8-5试画出图示两种机构的机构运动简图，并说明它们各为何种机构。图a曲柄摇杆机构图b为导杆机构。8-6如图所示，设己知四杆机构各构件的长度为amm240，b600mm,cmmd400mm,500。试问:1)当取杆4为机架时，是否有曲柄存在?2)若各杆长度不变，能否以选不同杆为机架的办法获得双曲柄机构和双摇杆机构?如何获得?3)若a、b﹑c三杆的长度不变，取杆4为机架，要获得曲柄摇杆机构,d的取值范围为何值?:解(1)因a+b=240+600=840≤900=400+500=c+d且最短杆1为连架轩．故当取杆4为机架时，有曲柄存在。(2)、能。要使此此机构成为双曲柄机构，则应取1杆为机架；两使此机构成为双摇杆机构，则应取杆3为机架。(3)要获得曲柄摇杆机构,d的取值范围应为440~760mm。8-7图示为一偏置曲柄滑块机构，试求杆AB为曲柄的条件。若偏距e=0，则杆AB为曲柄的条件是什么?解(1)如果杆AB能通过其垂直于滑块导路的两位置时，则转动副A为周转副，故杆AB为曲柄的条件是AB+e≤BC。(2)若偏距e=0,则杆AB为曲柄的条件是AB≤BCl28mml52mml50mml72mm8-8在图所示的铰链四杆机构中，各杆的长度为1，2，3，4，试求: 1)当取杆4为机架时，该机构的极位夹角、杆3的最大摆角、最小传动角min和行程速比系数K;2)当取杆1为机架时，将演化成何种类型的机构?为什么?并说明这时C、D两个转动副是周转副还是摆转副;3)当取杆3为机架时，又将演化成何种机构?这时A、B两个转动副是否仍为周转副?解(1)怍出机构的两个极位，如图,并由图中量得：θ=18.6º,φ=70.6º,γmin=22.7º18018018.6k12.318018018.6(2)①由l1+l4≤l2+l3可知图示铰链四杆机构各杆长度符合杆长条件；小②最短杆l为机架时，该机构将演化成双曲柄机构；③最短杆1参与构成的转动副A、B都是周转副而C、D为摆转副；（3）当取杆3为机架时，最短杆变为连杆，又将演化成双摇杆机构，此时A、B仍为周转副。l160mm,l260mm,8-9在图示的连杆机构中，已知各构件的尺寸为ABBClmm200,lmm80,CDAD构件AB为原动件，沿顺时针方向匀速回转，试确定:1)四杆机构ABCD的类型;2)该四杆机构的最小传动角min；3)滑块F的行程速比系数K。 解（1)由lAD+lBC40º8-25图示为一牛头刨床的主传动机构，已知lAB=75mm，lDE=100mm，行程速度变化系数K=2，刨头5的行程H=300mm。要求在整个行程中，推动刨头5有较小的压力角，试设计此机构。k12118018060解先算导杆的摆角k121取相应比例尺μl作图，由图可得导杆机构导杆和机架的长度为：LCD=μl.CD=300mm,lAC=μl.AC=150mm;导杆端点D的行程D1D2=E1E2=H/μl为了使推动刨头5在整行程中有较小压力角，刨头导路的位置h成为H=lCD(1+cos(φ/2))/2=300[(1+cos(60/2))/2=279.9mm 点津本题属于按行程速比系数K设计四杆机构问题，需要注意的是：①导杆CD的最大摆角与机构极位夹角相等：②因H=300mm，且要求在整个行中刨头运动压力角较小。所以取CD1=CD2=300mm,则D1D2=H=300mm。8-26某装配线需设计一输送工件的四杆机构，要求将工件从传递带C1经图示中间位置输送到传送带C2上。给定工件的三个方位为：M1(204，-30)，θ21=0º；M2(144，80)，θ22=22º；M3(34，100)，θ23=68º。初步预选两个固定铰链的位置为A(0，0)、D(34，一83)。试用解析法设计此四杆机构。解由题可知,本题属于按预定的连杆位置用解析法设汁四杆机构问题，N=3，并已预选xA,yA和xD,yD坐标值，具体计算过程略。355080758-27如图所示，设要求四杆机构两连架杆的三组对应位置分别为:1，1，2，2，1251053，3。试以解析法设计此四杆机构。解：（1）将α,φ的三组对应值带入式（8-17）（初选α0=φ0=0）Cos(α+α0)=p0cos(φ+φ0)+p1cos[(φ+φ0)-(α+α0)]+p2cos35pcos50pcos(5035)p012cos80pcos75pcos(75p80)012cos125pcos105pcos(105p125)得012解之得（计算到小数点后四位）p0=1.5815,p1=-1.2637,p2=1.0233（2）如图所示，求各杆的相对长度，得n=c/a=p0=1.5815,l=-n/p=1.251522mln12lp1.58312（3）求各杆的长度：得d=80.00a=d/l=80/1.2515=63.923mm b=ma=1.5831ⅹ63.923=101.197mmc=na=1.5851ⅹ63.923=101.094mm8-28试用解析法设计一曲柄滑块机构，设已知滑块的行程速度变化系数K=1．5，滑块的冲程H=50mm，偏距e=20mm。并求其最大压力角αmax。k11.5118018036解：计算k11.51并取相应比例尺μl根据滑块的行程H作出极位及作θ圆，作偏距线，两者的交点即铰链所在的位置，由图可得：lAB=μl.(AC2-AC1)/2=17mm,lBC=μl.(AC2+AC1)/2=36mm8-29试用解析法设计一四杆机构，使其两连架杆的转角关系能实现期望函数y=^，l≤z≤10。8-30如图所示，已知四杆机构。ABCD的尺寸比例及其连杆上E点的轨迹曲线，试按下列两种情况设计一具有双停歇运动的多杆机构：1)从动件摇杆输出角为45º：2)从动件滑块输出行程为5倍曲柄长度。8-31请结合下列实际设计问题，选择自己感兴趣的题目，并通过需求背景调查进一步明确设计目标和技术要求，应用本章或后几章所学知识完成相应设计并编写设计报告。1)结合自己身边学习和生活的需要，设计一折叠式床头小桌或晾衣架，或一收藏式床头书架或脸盆架或电脑架等；2)设计一能帮助截瘫病人独自从轮椅转入床上或四肢瘫痪已失去活动能力的病人能自理用餐或自动翻书进行阅读的机械；3)设计适合老、中、青不同年龄段使用并针对不同职业活动性质(如坐办公室人员运动少的特点)的健身机械；4)设计帮助运动员网球或乒乓球训练的标准发球机或步兵步行耐力训练，或空军飞行员体验混战演习训练(即给可能的飞行员各方位加一个重力)，或宇航员失重训练(即能运载一人并提供一个重力加速度)的模拟训练机械； 5)设计放置在超市外投币式的具有安全、有趣或难以想像的运动的小孩“坐椅”或能使两位、四位游客产生毛骨悚然的颤动感觉的轻便“急动”坐车。 第9章课后参考答案9-1何谓凸轮机构传动中的刚性冲击和柔性冲击?试补全图示各段s一、v一、一曲线，并指出哪些地方有刚性冲击，哪些地方有柔性冲击？答凸轮机构传动中的刚性冲击是指理论上无穷大的惯性力瞬问作用到构件上，使构件产生强烈的冲击；而柔性冲击是指理论上有限大的惯性力瞬间作用到构件上，使构件产生的冲击。s-δ,v-δ,a-δ曲线见图。在图9-1中B，C处有刚性冲击，在0，A，D，E处有柔性冲击。9—2何谓凸轮工作廓线的变尖现象和推杆运动的失真现象?它对凸轮机构的工作有何影响?如何加以避免?答在用包络的方法确定凸轮的工作廓线时，凸轮的工作廓线出现尖点的现象称为变尖现象：凸轮的工作廓线使推杆不能实现预期的运动规律的现象件为失真现象。变尖的工作廓线极易磨损，使推杆运动失真．使推杆运动规律达不到设计要求，因此应设法避免。变尖和失真现象可通过增大凸轮的基圆半径．减小滚子半径以及修改推杆的运动规律等方法来避免。s9—3力封闭与0/32/34/35/32几何v封闭凸轮机构的许用压a力角的确定是题9-1图否一样?为什么?答力封闭与几何封闭凸轮机沟的许用压力角的确定是不一样的。因为在回程阶段-对于力封闭的凸轮饥构，由于这时使推杆运动的不是凸轮对推杆的作用力F，而是推杆所受的封闭力．其不存在自锁的同题，故允许采用较大的压力角。但为使推秆与凸轮之间的作用力不致过大。也需限定较大的许用压力角。而对于几何形状封闭的凸轮机构，则需要考虑自锁的问题。许用压力角相对就小一些。9—4一滚子推杆盘形凸轮机构，在使用中发现推杆滚子的直径偏小，欲改用较大的滚子？问是否可行?为什么?答不可行。因为滚子半径增大后。凸轮的理论廓线改变了．推杆的运动规律也势必发生变 化。9—5一对心直动推杆盘形凸轮机构，在使用中发现推程压力角稍偏大，拟采用推杆偏置的办法来改善，问是否可行?为什么?答不可行。因为推杆偏置的大小、方向的改变会直接影响推杆的运动规律．而原凸轮机构推杆的运动规律应该是不允许擅自改动的。9-6在图示机构中，哪个是正偏置?哪个是负偏置?根据式(9-24)说明偏置方向对凸轮机构压力角有何影响?答由凸轮的回转中心作推杆轴线的垂线．得垂足点，若凸轮在垂足点的速度沿推杆的推程方向．刚凸轮机构为正偏置．反之为负偏置。由此可知．在图示机沟中，两个均为正偏置。由dsd/etan22()res0可知．在其他条件不变的情况下。若为正偏置(e前取减号)．由于推程时(ds/dδ)为正．式中分子ds/dδ-eds／dδ。故压力角增大。负偏置时刚相反，即正偏置会使推程压力角减小，回程压力角增大；负偏置会使推程压力角增大，回程压力角减小。9—7试标出题9—6a图在图示位置时凸轮机构的压力角，凸轮从图示位置转过90º后推杆的位移；并标出题9—6b图推杆从图示位置升高位移s时，凸轮的转角和凸轮机构的压力角。解如图(a)所示，用直线连接圆盘凸轮圆心A和滚子中心B，则直线AB与推杆导路之间所夹的锐角为图示位置时凸轮机构的压力角。以A为圆心,AB为半径作圆,得凸轮的理论廓线圆。连接A与凸轮的转动中心O并延长，交于凸轮的理论廓线于C点。以O为圆心．以OC为半径作圆得凸轮的基圆。以O为圆心,以O点到推杆导路的距离OD为半径作圆得推杆的偏距圆；。延长推杆导路线交基圆于G-点，以直线连接OG。过O点作OG的垂线，交基圆于E点。过E点在偏距圆的下侧作切线．切点为H点．交理论廓线于F点，则线段EF的长即为凸轮从图示位置转过90后推杆的位移s。方法同前，在图(b)中分别作出凸轮的理论廓线、基圆、推杆的偏距圆。延长推杆导路线交基圆于G点，以直线连接OG。以O为圆心，以滚子中心升高s后滚子的转动中心K到O点的距离OK为半径作圆弧，交理论廓线于F点。过F点作偏距圆的切线，交基圆于E点，切点为H。则∠GOE为推杆从图示位置升高位移s时-凸轮的转角，∠AFH为此时凸轮机构的压力角。 (a)(b) 9—8在图示凸轮机构中，圆弧底摆动推杆与凸轮在B点接触。当凸轮从图示位置逆时针转过90。时，试用图解法标出：1)推杆在凸轮上的接触点；2)摆杆位移角的大小；3)凸轮机构的压力角。解如图所示，以O为圆心，以O点到推杆转动中心A的距离AO为半径作圆，得推杆转动中心反转位置圆。过O点怍OA的垂线，交推杆转动中心反转位置圆于D点。以O`为圆心．以O`点到推杆圆弧圆心C的距离CO’为半径作圆．得凸轮的理论廓线。以O为圆心，作圆内切于凸轮的理论廓线圆，得凸轮的基圆。以D为圆心，以AC为半径作圆弧，交凸轮的理论廓线于E点，交凸轮的圆于G点。用直线连接EO’，交凸轮的实际廓线于F点，此即为推杆在凸轮上的接触点；而∠GDE即为摆杆的位移角；过E点并垂直于DE的直线与直线EF间所夹的锐角即为此时凸轮机构的压力角。9—9已知凸轮角速度为1．5rad／s，凸轮转角0~150时，推杆等速上升16mm;150~180时推杆远休，180~300时推杆下降16mm;300~360时推杆近休。试选择合适的推杆推程运动规律，以实现其最大加速度值最小，并画出其运动线图。解推杆在推程及回程段运动规律的位移方程为：(1)推程：s=hδ／δ00º≤δ≤150º(2)回程：等加速段s=h一2hδ2／δ`200º≤δ≤60º等减速段s=2h(δ’一δ)2／δ20`60º≤δ≤120º计算各分点的位移值如表9．3： 根据表9-3可作所求图如下图：9—10设计一凸轮机构，凸轮转动一周时间为2s。凸轮的推程运动角为60º，回程运动角为150。，近休止运动角为150º。推杆的行程为15mm。试选择合适的推杆升程和回程的运动规律，使得其最大速度值最小，并画出运动线图。9一11试设计一对心直动滚子推杆盘形凸轮机构，滚子半径r，=10mm，凸轮以等角速度逆时针回转。凸轮转角δ=0º～120º时，推杆等速上升20mm；δ=120º～180º时，推杆远休止；δ=180º～270º时，推杆等加速等减速下降20mm；δ=270º～：360º时，推杆近休止。要求推程的最大压力角α。。≤30º，试选取合适的基圆半径，并绘制凸轮的廓线。问此凸轮机构是否有缺陷，应如何补救。9一12试设计一个对心平底直动推杆盘形凸轮机构凸轮的轮廓曲线。设已知凸轮基圆半径rn=30mm，推杆平底与导轨的中心线垂直，凸轮顺时针方向等速转动。当凸轮转过120~1~r推杆以余弦加速度运动上升20。。，再转过150º时，推杆又以余弦加速度运动回到原位，凸轮转过其余90º时，推杆静止不动。问这种凸轮机构压力角的变化规律如何?是否也存在自锁问题?若有，应如何避免?解推杆在推程及回程运动规律的位移方程为（1)推程S=h[1-cos(πδ/δ0)]/2：0º≤δ≤120º（2）回程．S=h[1+cos(πδ/δ0`)]/20º≤δ≤150º计算各分点的位移值如表9-4l：根据表9-4可作所求图如下图： 这种凸轮机构的压力角为一定值，它恒等于平底与导路所夹锐角的余角．与其他因素无关。这种凸轮机构也会是存在自锁问题，为了避免自锁．在设计时应该在结构许可的条件下，尽可能取较大的推杆导路导轨的长度。并尽可能减小推gan9的悬臂尺寸。9一13一摆动滚子推杆盘形凸轮机构(参看图9—23)，已知lOA=60mmr0=25mm，lAB=50mm，rr=8mm。凸轮顺时针方向等速转动，要求当凸轮转过180º时，推杆以余弦加速度运动向上摆动25º；转过一周中的其余角度时，推杆以正弦加速度运动摆回到原位置。试以作图法设计凸轮的工作廓线。解推扦在推程及回程段运动规律的位移方程为(1)推程：s=Φ[1-cos(πδ/δ0)/20º≤δ≤180º(2)回程：s=Φ[1-(δ/δ`0)十sin(2πδ/δ`0)]/(2π)oº≤δ≤180º计算各分点的位移值如表9．5：根据表9。5作图如图所示9—14试设计偏置直动滚子推杆盘形凸轮机构凸轮的理论轮廓曲线和工作廓线。已知凸轮轴置于推杆轴线右侧，偏距e=20mm，基圆半径r。=50mm，滚子半径r，=10mm。凸轮以等角速度沿顺时针方向回转，在凸轮转过角占，：120。的过程中，推杆按正弦加速度运动规 律上升矗=50mm；凸轮继续转过炙=30。时，推杆保持不动；其后，凸轮再回转角度如=60时，推杆又按余弦加速度运动规律下降至起始位置；凸轮转过一周的其余角度时，推杆又静止不动。解(1)汁算推杆的位移并对凸轮转角求导：当凸轮转角δ在o≤δ≤2π／3过程中，推杆按正弦加速度运动规律上升h=50rnm。则12sh[sin()]2001233sh[sin()]50[cos(3)]222可得000≤δ≤2π/3ds11233h[cos()]50[cos(3)]d221110≤δ≤2π/3当凸轮转角占在2π／3≤δ≤5π／6过程中，推杆远休。S=50，2π／3≤δ≤5π／6ds/dδ=0，2π/3≤δ≤5π／6当凸轮转角δ在5π/6≤δ≤7π／6过程中，推杆又按余弦加速度运动规律下降至起始位置。则hs[1cos(0]`20可得h()50512s{1cos[]}{1cos[3()]}22635π／6≤δ≤7π／6dsh()5512sin[]3sin[3()]d226335π／6≤δ≤7π／6当凸轮转角δ在7π/6≤δ≤2π过程中，推杆近休。S=07π／6≤δ≤2πds/dδ=07π≤δ≤2π(2)计算凸轮的理论廓线和实际廓线：i本题的计算简图如图（a)所示。选取坐标系如图(b)所示，由图（b)可知，凸轮理论廓线上B点(即滚子中心)的直角坐标为:x=(s0+s)cosδ-esinδy=(s0+s)sinδ+ecosδ式中：s221/2221/20=(r0-e)=(50-20)=45.826mm由图(b)可知凸轮实际廓线的方程即B’点的坐标方程式为ix`=x-rrcosθY`=y-rrsinθ因为dy/dδ=(ds/dδ-e)sinδ+(s0+s)cosδdx/dδ=(ds/dδ-e)cosδ-(s0-s)sinδdxds/sin22(dxd/)(dyd/)dyds/cos22(dxd/)(dyd/)所以 故x`=x-10cosθy`=y-10sinθ由上述公式可得理论轮廓曲线和工作廓线的直角坐标．计算结果如表9．6凸轮廓线如下图昕示。9—15图示为一旅行用轻便剃须刀，图a为工作位置，图b为正在收起的位置(整个刀夹可以收入外壳中)。在刀夹上有两个推杆A、B，各有一个销A’、B’，分别插入外壳里面的两个内凸轮槽中。按图a所示箭头方向旋转旋钮套时(在旋钮套中部有两个长槽，推杆上的销从中穿过，使两推杆只能在旋钮套中移动，而不能相对于旋钮套转动)，刀夹一方面跟着旋钮套旋转，并同时从外壳中逐渐伸出，再旋转至水平位置(工作位置)。按图b所示箭头方向旋转旋钮套时，刀夹也一方面跟着旋钮套旋转，并先沿逆时针方向转过900成垂直位置，再逐渐全部缩回外壳中。要求设计外壳中的两凸轮槽(展开图)，使该剃须刀能完成上述动作，设计中所需各尺寸可从图中量取，全部动作在旋钮套转过2π角的过程中完成。解由题意知。两推杆相差180º布置，所以它们各自对应的凸轮槽应为等距线。当两销予都到达推杆B的最高位置时．推杆B不再升高．而推轩A继续升高，此段推杆B对应的凸轮槽应为水平的，而推杆A对应的凸轮槽不变。为了安装方便．将推杆A．B所对应的凸轮槽与端部连通。为了保证能同时将A,B推杆以及旋钮套从外壳中取出．将凸轮槽适当向水平方向伸展。据此没计凸轮槽展开图如图所示。图中．第l位置为两推杆最下位置时情况：第4位置为推杆B不再上升而推杆A继续上升的情况；第5位置为题图中的工作位置。第6，7位置是装拆时的位置。 第11章课后参考答案11-1在给定轮系主动轮的转向后，可用什么方法来确定定轴轮系从动轮的转向？周转轮系中主、从动件的转向关系又用什么方法来确定?答：参考教材216~218页。11-2如何划分一个复合轮系的定轴轮系部分和各基本周转轮系部分?在图示的轮系中，既然构件5作为行星架被划归在周转轮系部分中，在计算周转轮系部分的传动比时，是否应把齿轮5的齿数,Z5计入?答：划分一个复合轮系的定轴轮系部分和各基本周转轮系部分关键是要把其中的周转轮系部分划出来，周转轮糸的特点是具有行星轮和行星架，所以要先找到轮系中的行星轮，然后找出行星架。每一行星架，连同行星架上的行星轮和与行星轮相啮合的太阳轮就组成一个基本周转轮糸。在一个复合轮系中可能包括有几个基本周转轮系（一般每一个行星架就对应一个基本周转轮系)，当将这些周转轮一一找出之后．剩下的便是定轴轮糸部分了。在图示的轮系中．虽然构件5作为行星架被划归在周转轮系部分中，但在计算周转轮系部分的传动比时．不应把齿轮5的齿数计入。 11-3在计算行星轮系的传动比时，式iHmH=1-imn只有在什么情况下才是正确的?答在行星轮系，设固定轮为n,即ωHn=0时,imH=1-imn公式才是正确的。11-4在计算周转轮系的传动比时，式iHHmn=(nm-nH)／(nn-nH)中的imn是什么传动比，如何确定其大小和“±”号?答:iHmn是在根据相对运动原理，设给原周转轮系加上一个公共角速度“-ωH”。使之绕行星架的固定轴线回转，这时各构件之间的相对运动仍将保持不变，而行星架的角速度为0，即行星架“静止不动”了．于是周转轮系转化成了定轴轮系，这个转化轮系的传动比，其大小可以用iHHmn=(nm-nH)／(nn-nH)中的imn公式计算；方向由“±”号确定，但注意，它由在转化轮系中m.n两轮的转向关系来确定。11-5用转化轮系法计算行星轮系效率的理论基础是什么?为什么说当行星轮系为高速时，用它来计算行星轮系的效率会带来较大的误差?答:用转化轮系法计算行星轮系效率的理论基础是行星轮系的转化轮系和原行星轮系的差别，仅在于给整个行星轮系附加了一个公共角速度“-ωH”。经过这样的转化之后，各构件之间的相对运动没有改变，而轮系各运动副中的作用力(当不考虑构件回转的离心惯性力时)以及摩擦因数也不会改变。因而行星轮系与其转化轮系中的摩擦损失功率PHf应相等。用转化轮系法计算行星轮系效率没有考虑由于加工、安装和使用情况等的不同，以及还有一些影响因素如搅油损失、行星轮在公转中的离心惯性力等，因此理论计算的结果并不能完全正确地反映传动装置的实际效率。11-6何谓正号机构、负号机构?各有何特点?各适用于什么场合?答:行星轮系的转化轮系中当传动比iHH1n>o，称为正号机构；当传动比i1nliⅢl时，出现封闭功率流。这种封闭的功率流将增大摩擦功率损失，使轮系的效率和强度降低，对于传动极为不刊。11-8在确定行星轮系各轮齿数时，必须满足哪些条件，为什么?答设计行星轮系时，各轮齿数的选择应满足四个条件；对于不同的轮系，这四个条件具体表达式不尽相同，下面以内齿轮3固定，各轮均为标准齿轮的2K—H型轮系为例加以说明。(1)保证实现给定的传动比：z3=(i1H-1)z1(2)满足同心条件(即保证两太阳轮和系杆的轴线重合):Z3=z1+2z2(3)满足k个行星轮均布安装(即满足装配条件)：N=(z3+z1)/k(n为整数)(4)满足邻接条件（即保证相邻行星轮不致相互碰撞)：(z1+z2)sin(180º/k)>z2+2ha*11-9在行星轮系中采用均载装置的目的何在?采用均载装置后会不会影响该轮系的传动比? 答在行星轮系中，常把某些构件作成可以浮动的．在轮系运转中，如各行星轮受力不均匀。这些构件能在一定的范围内自由浮动，以达到自动调节各行星轮载荷的目的。采用均载装置后不会影响该轮系的传动比。11-10何谓少齿差行星传动?摆线针轮传动的齿数差是多少?在谐波传动中柔轮与刚轮的齿数差如何确定?答少齿差行星传动是指在行星轮系中．当行星轮1与内齿轮2的齿数差△z=z2-z1=1～4时．就称为少齿差行星传动；摆线针轮传动的齿数差是1；在谐波传动中柔轮与刚轮的齿距相同．但齿数不等，刚轮与柔轮的齿数差通常等于波数n，即zr-zs=n011-11图示为一手摇提升装置，其中各轮齿数均为已知，试求传动比i15并指出当提升重物时手柄的转向。zzzz503040522345i577.7815zzzz2015118解：12"3"4"当提升重物时手柄的转向逆时针（从左向右看手柄）。11-12图示为一千分表的示意图，已知各轮齿数如图，模数m=0.11mm(为非标准模数)若要测量杆1每移动0.001mm时，指针尖端刚好移动一个刻度(s=1.5mm)。问指针的长度尺等于多少?(图中齿轮5和游丝的作用是使各工作齿轮始终保持单侧接触，以消除齿侧间隙对测量精度的影响。)解：由图可知，轮2（2`）、3、（3`）、4、5组成定轴轮系且n2=n2`,n3=n3`n`23zz3416121i(1)2`4nzz12016010042`3`n4=-100n`2杆1和齿轮2是一对齿条与齿轮的外啮合，设杆1每移动0.001时间为t 1vnmz12222v20.001/t0.21n2mzt0.1129319220nnn100`100422319t由图知，指针摆一个刻度的s=1.5mm则摆角θ有关系式θ=s/R即θ=n4t=s/Rs15Rmm23.925nt204t则319t11-13图示为绕线机的计数器。图中1为单头蜗杆，其一端装手把，另一端装绕制线圈。2、3为两个窄蜗轮，z2=99，．Z3=100。在计数器中有两个刻度盘，在固定刻度盘的一周上有100个刻度，在与蜗轮2固连的活动刻度盘的一周上有99个刻度，指针与蜗轮3固连。问指针在固定刻度盘上和活动刻度盘上的每一格读数各代表绕制线圈的匝数是多少?又在图示情况下，线圈已绕制了多少匝?解：因i13=nl/n3=z3／z1=100，故n3=n1／100，即蜗杆每转一转，蜗轮3转过1／100转，指针相对固定刻度盘转过一个格度，说明指针在固定刻度盘上的每一格读数代表被绕制线圈绕制了一匝。i12=nl／n2=z2／z1=99，故n2=n1／99，即蜗杆转一转，蜗轮2转过l／99转。由于蜗轮2、3转向相同，故蜗杆每转一转，指针相对活动刻度盘转过l／100-1／99=-1／9900转(即相对向后倒转，所以活动刻度盘刻度的增大方向与固定刻度盘者相反)，因活动刻度盘上有99个刻度，故指针在活动刻度盘上的每一格读数，代表被绕制线圈已绕制了9900／99=100匝。今指针在活动刻度盘上的读数为13.××，在固定刻度盘上的读数为5.×，所以线圈已绕制的匝数为活动刻度盘上的整数读数×100+固定刻度盘上的整数读数=13×100+5=1305匝11-14图示为一装配用电动螺丝刀的传动简图。已知各轮齿数为z1=z4=7，z3=z6=39。若n1=3000r／min，试求螺丝刀的转速。解：此轮系为一复合周转轮系。在1-2-3-H1行星轮系中 h1z339ii11111H13z17在4-5-6-H2行星轮系中H2Z639ii1114H246Z47392III（1+）43.1812HH11H427故nH2=n1/i1H2=3000/43.18=69.5r/min转向以n1相同11-16如图所示为两个不同结构的锥齿轮周转轮系，已知z1=20，z2=24，z2，=30，z3=40，n1=200r／min，n3=-100r／min。求nH等于多少?(a)Hnn1Hzz232440i1.613nnzz2030解：312H‘Hin31n13n[1.6（100）-200]/（1.6-1）=-600r/minhHi113(b)Hnn1Hzz232440i1.613nnzz2030解：3H12‘Hin31n13n[1.6（-100）-200]/（-1.6-1）=15.385r/minhHi11311-17在图示的电动三爪卡盘传动轮系中，设已知各轮齿数为z1=6，z2=z2，=25，z3=57，z4=56。试求传动比i14。 解:图示轮系为一周转轮系(整个轮系只有一个行星架，去掉周转轮系部分后，无定轴轮系部分，故整个轮系为一周转轮系)。该轮系共有三个中心轮，故称之为3K型行星传动。此轮系的右端由轮2’、4和件H组成一差动轮系，左端由轮1、2、3和件H组成一行星轮系，此行星轮系将差动轮系中的构件2’和H封闭起来(即使构件2和H之间有固定速比关系)，整个轮系类似于一个封闭式行星轮系。此轮系也可认为是由轮1、2、3和行星架H组成的行星轮系与由轮4、2’、2、3和行星架H组成的另一行星轮系组合而成。故为求解此轮系的传动比，必须列出两个方程。如下的解法，求解最简便。在轮1、2、3及行星架H组成的行星轮系中，轮3为固定轮，故11-18图示为手动起重葫芦，已知z1=Z2，=10，z2=20，z3=40。设各级齿轮的传动效率(包括轴承损失)η1=0.98，曳引链的传动效率η2=0.97。为提升重G=10kN的重物，求必须施加于链轮A上的圆周力F。4zz232040iww1i1()14141319zz解：12"=1010wm4Q40Qwm160P所以1pi144pQ/47I10/40.99308.64N1411-19图示为纺织机中的差动轮系，设z1=30，z2=25，z3=z4=24，z5=18，z6=121，n1=48～200r／rain，nH=316r／min，求n6等于多少? HNNH125241212ZZZ246I（-1）5.616NNH6302418ZZZ解：1351N6（N-N）+NH1HHI16当n1=48～200r/min时11n6(48316)316(200316)3165.65.6268.14295.29(/min)rN6与n1及nH的转向相同11-20图示为建筑用绞车的行星齿轮减速器。已知z1=z3=17，z2=z4=39，z5=18，z7=152，n1=l450r／min。当制动器B制动、A放松时，鼓轮H回转(当制动器B放松、A制动时，鼓轮H静止，齿轮7空转)，求nH等于多少?解：11-21在图示轮系中，设各轮的模数均相同，且为标准传动，若已知z1=z2，=z3，=z6，=20，z2=z4=z6=z7=40。试求：1)当把齿轮1作为原动件时，该机构是否具有确定的运动?2)齿轮3、5的齿数应如何确定?3)当n1=980r／min时，n1及n3各为多少? 故有确定的运动。11-22图示为隧道掘进机的齿轮传动，已知z1=30，z2=85，z3=32，z4=21，z5=38，z6=97，z7=147，模数均为10mm，且均为标准齿轮传动。现设已知n1=1000r／min，求在图示位置时，刀盘最外一点A的线速度。提示：在解题时，先给整个轮系以一ωH角速度绕oo轴线回转，注意观察此时的轮系变为何种轮系，从而即可找出解题的途径。 解：图示轮系为一装载式(一个行星轮系装载在另一个行星轮系的行星架上)的复杂行星轮系，为了求解这种行星轮系，可采用两次转化的方法。第一次转化时给整个轮系一个(-ωH)角速度绕OO轴旋转，所得的转化轮系如图b所示，这已是大家十分熟悉的复合轮系了。左边是一个以齿轮6为固定轮的行星轮系，右边为定轴轮系。通过第一次转化后，各构件的转速为nHi=ni-nH通过第二次转化可求得左边行星轮系的传动比为（a）由定轴轮系部分有nH=nl／(2.8333×26.1655)=13.489r／min由式(c)可得n2=n4=-334.696r／rain由式(e)可得n3=-48.477r／min最后可得刀盘A点的线速度为VA=[(rl+r2)nH+(r4+r5)n3+200n5]×2π／60000=1.612m／0式中：r1=150mm，r2=425mm，r4=105mm，r5=190mm。'