答案_北京理工大学出版社_修改.pdf 33页

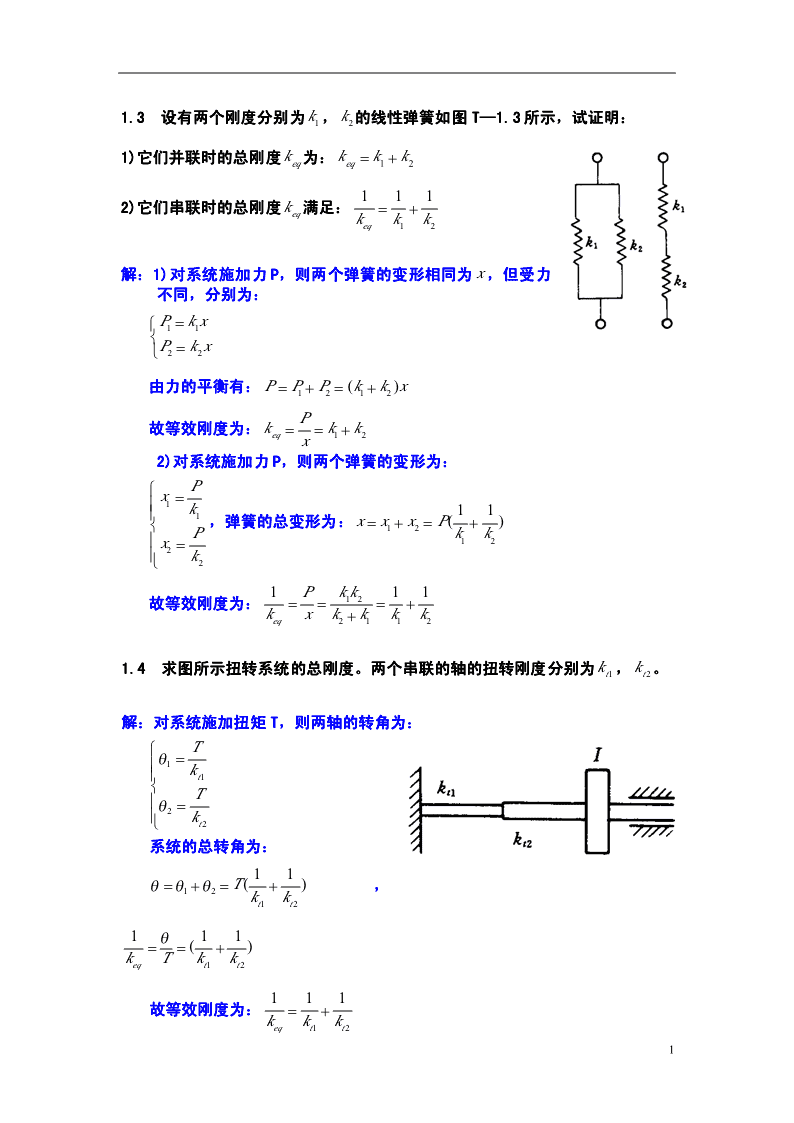
'1.3设有两个刚度分别为k，k的线性弹簧如图T—1.3所示，试证明：121)它们并联时的总刚度k为：k=k+keqeq121112)它们串联时的总刚度k满足：=+eqkkkeq12解：1)对系统施加力P，则两个弹簧的变形相同为x，但受力不同，分别为：⎧P=kx11⎨⎩P=kx22由力的平衡有：P=P+P=(k+kx)1212P故等效刚度为：k==k+keq12x2)对系统施加力P，则两个弹簧的变形为：⎧Px=⎪1⎪k111⎨，弹簧的总变形为：x=x1+x2=P(+)Pkk⎪x=122⎪k⎩21Pkk1112故等效刚度为：===+kxk+kkkeq21121.4求图所示扭转系统的总刚度。两个串联的轴的扭转刚度分别为k，k。t1t2解：对系统施加扭矩T，则两轴的转角为：⎧Tθ=⎪1⎪kt1⎨T⎪θ=2⎪k⎩t2系统的总转角为：11θ=θ+θ=T(+)，12kkt1t21θ11==(+)kTkkeqt1t2111故等效刚度为：=+kkkeqt1t21 1.5两只减振器的粘性阻尼系数分别为c1，c2，试计算总粘性阻尼系数ceq1)在两只减振器并联时，2)在两只减振器串联时。解：1)对系统施加力P，则两个减振器的速度同为ẋ，受力分别为：⎧P=cẋ11⎨⎩P=cẋ22由力的平衡有：P=P+P=(c+cx)̇1212P故等效刚度为：c==c+ceq12ẋ2)对系统施加力P，则两个减振器的速度为：⎧Pẋ=⎪1⎪c111⎨，系统的总速度为：ẋ=ẋ1+ẋ2=P(+)Pcc⎪ẋ=122⎪c⎩2P11故等效刚度为：c==+eqẋcc121.6一简谐运动，振幅为0.5cm，周期为0.15s，求最大速度和加速度。2π2π−3解：简谐运动的ω==(rads/)，振幅为510×m；nT0.15⎧−32πx=×510cos(tm)()⎪0.15⎪⎪−32π2π即：⎨ẋ=−×510×tsin(tms)(/)0.150.15⎪⎪−32π22π2⎪̇̇x=−×510×(t)cos(tms)(/)⎩0.150.15⎧−32πẋ=×510×(/)ms⎪⎪max0.15所以：⎨⎪ẋ̇=×510−3×(2π)(/2ms2)max⎪⎩0.151.1试举出振动设计、系统识别和环境预测的实例。1.2如果把双轴汽车的质量分别离散到前、后轴上去，在考虑悬架质量和非悬架质量两个离散质量的情况下，画出前轴或后轴垂直振动的振动模型简图，并指出在这种化简情况下，汽车振动有几个自由度?2 1.7一加速度计指示出结构振动频率为82Hz，并具有最大加速度50g，求振动的振幅。2解：由ẋ̇=A×ω可知：maxn2ẋ̇ẋ̇509.8/×ms9.8maxmaxA====m22222ω(2πf)(2π×25)1/s50πn1.8证明：两个同频率但不同相角的简谐运动的合成仍是同频率的简谐运动，即：Acosωt+Bcos(ωt−ϕ)=Ccos(ωt−θ)，并讨论ϕ=0,π/2，π三种特例。证明：Acosωt+Bcos(ωt−ϕ)=Acosωt+Bcosωtcosϕ+Bsinωtsinϕ=(AB+cos)cosϕωt+Bsinsinϕωt22=(AB+cos)ϕ+(sin)cos(Bϕωt−θ)22=A+2ABcosϕ+Bcos(ωt−θ)=Ccos(ωt−θ)⎧Bsinϕθ=arctg()⎪其中：⎨AB+cosϕ⎪22⎩C=A+2ABcosϕ+B1)当ϕ=0时：θ=0;C=AB+；2)当ϕ=π时：θ=arctgBAC(/);=A2+B2；23)当ϕ=π时：θ=0;C=AB−；1.9把复数4+5i表示为指数形式。iθ225解：4+5i=Ae，其中：A=4+5，θ=arctg()41.10证明：一个复向量用i相乘，等于把它旋转π/2。ππiiθ+iθiθ22证明：Ae×=iAe×e=Ae3 1.11证明：梯度算子∇是线性微分算子，即∇[af(x,y,z)+bg(x,y,z)]=a∇f(x,y,z)+b∇g(x,y,z)这里，a,b是与x、y、z无关的常数。1.12求函数g(t)=Acospωt+Bcosqωt的均方值。考虑p与q之间的如下三种关系：①q=np，这里n为正整数；②q/p为有理数；③q/p为无理数。1.13汽车悬架减振器机械式常规性能试验台，其结构形式之一如图T—1.13所示。其激振器为曲柄滑块机构，在导轨下面垂向连接被试减振器。试分析减振器试验力学的基本规律(位移、速度、加速度、阻尼力)。图T—1.131.14汽车悬架减振器机械式常规性能试验台的另一种结构形式如图T—1.14所示。其激振器采用曲柄滑块连杆机构，曲柄被驱动后，通过连杆垂向带动与滑块连接的被试减振器。试分析在这种试验台上的减振器试验力学的基本规律，并与前题比较。图T—1.144 2.1弹簧下悬挂一物体，弹簧静伸长为δ。设将物体向下拉，使弹簧有静伸长3δ，然后无初速度地释放，求此后的运动方程。解：设物体质量为m，弹簧刚度为k，则：mg=kδ，即：ω=km/=g/δn取系统静平衡位置为原点x=0，系统运动方程为：⎧mẋ̇+kx=0⎪⎨x=2δ（参考教材P14）0⎪ẋ=0⎩0解得：xt()=2cosδωtn2.2弹簧不受力时长度为65cm，下端挂上1kg物体后弹簧长85cm。设用手托住物体使弹簧回到原长后无初速度地释放，试求物体的运动方程、振幅、周期及弹簧力的最大值。解：由题可知：弹簧的静伸长△=0.850.650.2()−=mg9.8所以：ω===7(rads/)n△0.2取系统的平衡位置为原点，得到：2系统的运动微分方程为：ẋ̇+ωx=0n⎧x(0)=−0.2其中，初始条件：⎨（参考教材P14）⎩ẋ(0)=0所以系统的响应为：xt()=−0.2cosωtm()nmg弹簧力为：F=kxt()=xt()=−cosωtN()kn△2π因此：振幅为0.2m、周期为()s、弹簧力最大值为1N。75 2.3重物m悬挂在刚度为k的弹簧上并处于静平衡位置，另一重物m从高度为12h处自由落到m上而无弹跳，如图所示，求其后的运动。1解：取系统的上下运动x为坐标，向上为正，静平衡位置为原点x=0，则当m有x位移时，系统有：12E=(m+mx)̇T12212U=kx2由dE(+U)=0可知：(m+mx)̇̇+kx=0T12即：ω=k/(m+m)n12mg⎧x=2⎪0k系统的初始条件为：⎨ṁ2x=−2gh⎪0⎩m+m1212（能量守恒得：mgh=(m+mx)̇）21202因此系统的响应为：xt()=Acosωt+Asinωt0n1nmg⎧A=x=200⎪k其中:⎨ẋmg2ghk02⎪A==−1⎩ωkm+mn12mg2ghk即：=2ω−ωxt()(costsint)nnkm+m122.4一质量为m、转动惯量为I的圆柱体作自由纯滚动，圆心受到一弹簧k约束，如图所示，求系统的固有频率。解：取圆柱体的转角θ为坐标，逆时针为正，静平衡位置时θ=0，则当m有θ转角时，系统有：1212122E=Iθ̇+m(θ̇r)=(I+mr)θ̇T22212U=kr(θ)222由dE(+U)=0可知：(I+mr)θ̇̇+krθ=0T22即：ω=kr/(I+mr)（rad/s）n6 2.5均质杆长L、重G，用两根长h的铅垂线挂成水平位置，如图所示，试求此杆相对铅垂轴OO微幅振动的周期。2.6求如图所示系统的周期，三个弹簧都成铅垂，且k=2,kk=k。2131解：取m的上下运动x为坐标，向上为正，静平衡位置为原点x=0，则当m有x位移时，系统有：12E=mẋT2121252kk12U=kx+kx=kx（其中：k=）11226k+k125由dE(+U)=0可知：mẋ̇+kx=0T135k3m1即：ω=（rad/s），T=2π（s）n3m5k17 2.7如图所示，半径为r的均质圆柱可在半径为R的圆轨面内无滑动地、以圆轨面最低位置O为平衡位置左右微摆，试导出柱体的摆动方程，求其固有频率。解：设物体重量W，摆角坐标θ如图所示，逆时针为正，当系统有θ摆角时，则：2θU=WR(−r)(1−cos)θ≈WR(−r)2设ϕ̇为圆柱体转角速度，质心的瞬时速度：(Rr−)υ=(Rr−)θ̇=rϕ̇，即：ϕ̇=θ̇cr记圆柱体绕瞬时接触点A的转动惯量为I，则：AW21W2W2I=I+r=r+rACg2gg1213W2R−r23W22E=Iϕ̇=(r)(θ̇)=(R−r)θ̇TA222gr4g121W22（或者理解为：E=Iϕ̇+(R−r)θ̇，转动和平动的动能）Tc22g3W2由dE(T+U)=0可知：(R−r)θ̇̇+WR(−r)θ=02g2g即：ω=（rad/s）n3(R−r)2.8横截面面积为A，质量为m的圆柱形浮子静止在比重为γ的液体中。设从平衡位置压低距离x(见图)，然后无初速度地释放，若不计阻尼，求浮子其后的运动。解：建立如图所示坐标系，系统平衡时x=0，由牛顿第二定律得：γAgmẋ̇+γ(Axg)=0，即：ω=nmx=x0有初始条件为：{ẋ=00γAgπ所以浮子的响应为：xt()=xsin(t+)m28 2.9求如图所示系统微幅扭振的周期。图中两个摩擦轮可分别绕水平轴O1，O2转动，它们相互啮合，不能相对滑动，在图示位置(半径O1A与O2B在同一水平线上)，弹簧不受力。摩擦轮可以看做等厚均质圆盘，质量分别为m1，m2。解：两轮的质量分别为mm,，因此轮的半径比为：12rm11=rm22由于两轮无相对滑动，因此其转角比为：θrθ̇121==θrθ̇212取系统静平衡时θ=0，则有：111221122122E=(mr)θ̇+(mr)θ̇=(m+mr)θ̇T111222121122224121212U=kr(θ)+kr(θ)=(k+k)(rθ)11122212112221222由dE(+U)=0可知：(m+mr)θ̇̇+(k+kr)θ=0T1211121122(k+k)m+m1212即：ω=（rad/s），T=2π（s）nm+m2(k+k)12122.10如图所示，轮子可绕水平轴转动，对转轴的转动惯量为I，轮缘绕有软绳，下端挂有重量为P的物体，绳与轮缘之间无滑动。在图示位置，由水平弹簧维持平衡。半径R与a均已知，求微振动的周期。解：取轮的转角θ为坐标，顺时针为正，系统平衡时θ=0，则当轮子有θ转角时，系统有：121P21P22E=Iθ̇+(θ̇R)=(I+R)θ̇T22g2g12U=ka(θ)2P222由dE(+U)=0可知：(I+R)θ̇̇+kaθ=0TgP2I+R2ka2πg即：ω=（rad/s），故T==2π（s）nP22ωkaI+Rng9 2.11弹簧悬挂一质量为m的物体，自由振动的周期为T，如果在m上附加一个质量m1，则弹簧的静伸长增加△l，求当地的重力加速度。解：m∵T=2πk24πm∴=kT∵mg=kl△12kl△4πml△∴=g=mTm112.12用能量法求图所示三个摆的微振动的固有频率。摆锤重P，(b)与(c)中每个弹簧的弹性系数为k/2。(1)杆重不计；(2)若杆质量均匀，计入杆重。解：取系统的摆角θ为坐标，静平衡时θ=0（a）若不计杆重，系统作微振动，则有：1P22E=(L)θ̇T2g12U=PgL(1−cos)θ≈PgLθ2P2由dE(+U)=0可知：Lθ̇̇+PLθ=0Tgg即：ω=（rad/s）nL如果考虑杆重，系统作微振动，则有：1P2211221PmL22E=(L)θ̇+(mL)θ̇=(+)Lθ̇TL2g232g32LPmθLU=PgL(1−cos)θ+mg(1−cos)θ≈(+)gLL2g22由dE(+U)=0可知：P+mL2θ̇̇+P+mLθ=T()L()gL0g3g210 PmL(+)gg2即：ω=（rad/s）nPmL(+)Lg3（b）如果考虑杆重，系统作微振动，则有：1P2211221PmL22E=(L)θ̇+(mL)θ̇=(+)Lθ̇TL2g232g32PmLθ1kL2U≈(+)gL+()(θ)×2g22222PmkLL(+)g+g24即：ω=（rad/s）nPmL(+)Lg3（c）如果考虑杆重，系统作微振动，则有：1P2211221PmL22E=(L)θ̇+(mL)θ̇=(+)Lθ̇TL2g232g32PmLθ1kL2U≈−(+)gL+()(θ)×2g22222kLPmL−(+)g4g2即：ω=（rad/s）nPmL(+)Lg32.13求如图所示系统的等效刚度，并把它写成与x的关系式。22a+b答案：系统的运动微分方程mẋ̇+kx=02a11 2.14一台电机重470N，转速为1430r／min，固定在两根5号槽钢组成的简支梁的中点，如图所示。每根槽钢长1.2m，重65.28N，弯曲刚度EI＝1.66×105N·m2。(a)不考虑槽钢质量，求系统的固有频率；(b)设槽钢质量均布，考虑分布质量的影响，求系统的固有频率；(c)计算说明如何避开电机和系统的共振区。2.15一质量m固定于长L，弯曲刚度为EI，密度为r的弹性梁的一端，如图所示，试以有效质量的概念计算其固有频率。wL3/(3EI)2.16求等截面U形管内液体振动的周期，阻力不计，假定液柱总长度为L。解：假设U形管内液柱长l，截面积为A，密度为ρ，取系统静平衡时势能为0，左边液面下降x时，有：12E=ρAlẋT2U=ρAx××g×x由dE(+U)=0可知：ρAlẋ̇+2gAxρ=0T2g2l即：ω=（rad/s），T=π（s）nlg12 2．17水箱l与2的水平截面面积分别为A1、A2，底部用截面为A0的细管连接。求液面上下振动的固有频率。解：设液体密度为ρ，取系统静平衡时势能为0，当左边液面下降x时，右边液1面上升x，液体在水箱l与2和细管中的速度分别为xxẋ̇̇,,，则有：2123121212E=[ρAh(−xx)]̇+[ρALx]̇+[ρAh(+xx)]̇T11133222222ρA12A122≈[Ah+AL()+Ah()]ẋ13212AA32（由于：h−x≈h;h+x≈h;Aẋ=Aẋ=Aẋ;Ax=Ax）121122331122x+x12U=ρAxg12AAA111由dE(+U)=0可知：[(1h+)+L()]ẋ̇+g(1+)x=0T11AAA232A1g(1+)A2即：ω=（rad/s）nAA11h(1+)+L()AA232.18如图所示，一个重W、面积为A的薄板悬挂在弹簧上，使之在粘性液体中振动。设T1、T2分别为无阻尼的振动周期和在粘性液体中的阻尼周期。试证明：2πW22µ=T−T22gATT12并指出µ的意义(式中液体阻尼力Fd=m•2Av)。13 1x02.19试证明：对数衰减率也可用下式表示δ=ln，(式中xn是经过n个循nxn环后的振幅)。并给出在阻尼比ζ为0.0l、0.1、0.3时振幅减小到50%以下所需要的循环数。解：设系统阻尼自由振动的响应为xt()；t时刻的位移为x；t=t+nT时刻的位移为x；则：00n0n−ζωtxXen0cos(ωt−ϕ)0=d0=eζωnnTd−ζω(t+nT)xXen0dcos[ω(t+nT)−ϕ]nd0dxx1x000所以有：ln=ζωnT=nδ=nln，即：δ=lnndxxnxn1n211−ζ当振幅衰减到50%时，x=0.5x，即：n=ln2=ln2n0δ2πζ1)当ζ=0.01时，n=11；要11个循环；2)当ζ=0.1时，n=1.1；要2个循环；3)当ζ=0.3时，n=0.34；要1个循环；2.20某双轴汽车的前悬架质量为m1=1151kg，前悬架刚度为k1=1.02×105N／m，若假定前、后悬架的振动是独立的，试计算前悬架垂直振动的偏频。如果要求前悬架的阻尼比ζ=0.25，那么应给前悬架设计多大阻尼系数(c)的悬架减振器?14 2.21重量为P的物体，挂在弹簧的下端，产生静伸长δ，在上下运动时所遇到的阻力与速度v成正比。要保证物体不发生振动，求阻尼系数c的最低值。若物体在静平衡位置以初速度v0开始运动，求此后的运动规律。解：设系统上下运动为x坐标系，系统的静平衡位置为原点，得到系统的运动微分方程为：PPẋ̇+cẋ+x=0gδcc系统的阻尼比：ζ==2mkPP2gδ系统不振动条件为：ζ≥1，即：c≥2/Pgδ⎧x=00物体在平衡位置以初速度υ0开始运动，即初始条件为：⎨ẋ=υ⎩00此时系统的响应为：（可参考教材P22）−ζωtωtζ2−1−ωtζ2−11)当ζ>1时：xt()=en(Aen+Aen)12⎧1υ0A=±⎪⎪1,22ωζ2−1其中：⎨ng⎪ω=n⎪⎩δ⎧A=02)当ζ=1时：xt()=Ae−ωnt+Ate−ωnt，其中：112⎨A=υ⎩20即：xt()=υte−ωnt03)当ζ<1时：xt()=e−ζωnt(Ccosωt+Csinωt)1d2d⎧C=0⎪1υ其中：υω，即：xt()=e−ζωnt0sinωt⎨C2=0/ddω⎪2dω=ω1−ζ⎩dn2.22一个重5500N的炮管具有刚度为3.03×105N／m的驻退弹簧。如果发射时炮管后座1.2m，试求：①炮管初始后座速度；②减振器临界阻尼系数(它是在反冲结束时参加工作的)；③炮管返回到离初始位置0.05m时所需要的时间。2.23设系统阻尼比ζ=0.1，试按比例画出在ω＝0.5、1.0、2.0三种情况下ωn微分方程的向量关系图。15 2.24试指出在简谐激励下系统复频率响应、放大因子和品质因子之间的关系，并计算当ζ=0.2、ω=5rad/s时系统的品质因子和带宽。n2.25已知单自由度系统振动时其阻力为cv(其中c是常数，v是运动速度)，激励为F=F0sinωt，当ω=ωn即共振时，测得振动的振幅为X，求激励的幅值F0。若测得共振时加速度的幅值为A，求此时的F0。2.26某单自由度系统在液体中振动，它所受到的激励为F=50cosωt(N)，系统在周期T＝0.20s时共振，振幅为0.005cm，求阻尼系数。2π解：由T=0.20s时共振可知，系统固有频率为：ω==10πnTF当ω→ω时，已知响应振幅：0，（参教材P30）X=ncω5F100所以：c==(Nsmi/)Xωπ2.27一个具有结构阻尼的单自由度系统，在一周振动内耗散的能量为它的最大势能的1.2%，试计算其结构阻尼系数γ。2.28要使每一循环消耗的能量与频率比无关，需要多大的阻尼系数。2.29若振动物体受到的阻力与其运动速度平方成正比，即2⎧F=aẋẋ≤0d⎨2⎩Fd=−aẋẋ>0求其等效阻尼系数和共振时的振幅。解：实际上，这是一种低粘度流体阻尼。设系统的运动为：xt()=Xcos(ωt−ϕ)2ω=αxdẋc∫π/w2=∫αxdAHẇ(|()|wwt)(−ϕ)0π/w2=∫α[|aHw()|(wwt−ϕ)][|−Hw()|wAsin(wt−ϕ)]dx0π/waX3333=−3wAsin(ωt−ϕ)dt∫0Aπ/w333=∫−awXsin(ωt−ϕ)dt03223=−αXw[2(0)ϕ−(0)ϕ]316 ω=axωd38ax3ω2=CπωX238a3xω2C=e3π2.29x=Xcos(ωt−ϕ)•x=−ωXsin(ωt−ϕ)••πω/2/πω22W=αxdx+−αxdxc∫0∫πω/πω/2222=∫αωXsin(ωt−ϕ)(−ωXcos(ωt−ϕ))dt02/πω2222+∫−αωXsin(ωt−ϕ)(−ωXcos(ωt−ϕ))dtπω/832=αXω32W=W=CπωXPCω=4ax3ω2d38aXωC=3π832F03πF0X==cω8aXω2X=3πF0=13πF08axw22w22ann2.29•2•⎧αxx≤0Fd=⎨•2•⎩−αxx≥0•T/42ω=Fdx=4αxdxe∫d∫0•T/43=4∫αxdx0T/4333=4∫Zωcos(ωt−ϕ)dt0832=αZω32ω=ω=CπωZPCω=8αZωe3πZ=F0Z=3πF0C0ω8αZω217 2.30KGlⅡ电动机重P，装在弹性基础上，静下沉量为d。当转速为nr／min时，由于转子失衡，沿竖向有正弦激励，电机产生振幅为A的强迫振动。试求激励的幅值，不计阻尼。2.31电动机重P，装在弹性梁上，使梁有静挠度d。转子重Q，偏心距为e。试求当转速为w时，电动机上下强迫振动的振幅A，不计梁重。2.32一飞机升降舵的调整片铰接于升降舵的O轴上(图T—2.32)，并由一联动装置控制。该装置相当于一刚度为kT的扭转弹簧。调整片转动惯量为I，因而系统固有频率ω=K/I，nT但因kT不能精确计算，必须用试验测定ω。为此固定升降舵，利用弹n簧k2对调整片做简谐激励，并用弹簧k1来抑制。改变激励频率ω直至图T—2.32达到其共振频率ω。试以ω和试TT验装置的参数来表示调整片的固有频率ω。n解：设调整片的转角为θ，系统的微分方程为：2Iθ̇̇+[k+(k+kL)]θ=kLysinωtT12222kT+(k1+kL2)系统的共振频率为：ω=0I22因此：k=Iω−(k+kL)T0122调整片的固有频率为：2kT2(k1+kL2)ω==ω−n0II18 2.33如图所示由悬架支承的车辆沿高低不平的道路行进。试求W的振幅与行进速度的关系，并确定最不利的行进速度。解：由题目2.33T=Lw=2π=2πVVTLy=Ycos2πVtL••wX=−K(x−y)••wX=KYcos2πVtL••wX+Kx=KYcos2πVtL2πVwS2X(s)+KX(s)=KYL(2πV)2+s2LKY2πVX(s)=Lω2=K(s2+(2πV)2)(ws2+K)nwL2ω2Y2aYX=nsina+sinωtω2+a2ω2−a2nnnYYYKL2YX====22222222[1−(a/ω2)]+01−(a/ωn)1−4πVwKL−TπVwn2KLLV=k/w2π2.33ω=2πTω=2πvLTv=L••mX+KX=Ky••22X+ωX=ωynnYω2X=n22ωn−ωYω2Yω2X=n=n2222ωn−ωω2−4πvn2L2RL2V=4π2m19 2.34单摆悬点沿水平方向做简谐运动(图T—2.34)，x=asinwt。试求在微幅的强迫振动中偏角q的变化规律。已知摆长为L，摆锤质量为m。2.35一个重90N的飞机无线电要与发动机的频率1600～2200r/min范围的振动隔离，为了隔离85%，隔振器的静变形需要多少?2.36试从式(2.95)证明：1.无论阻尼比ζ取何值，在频率比ω/ωn=2时，恒有X＝A。2.在ω/ω<2，X/A随ζ增大而减小，而在ω/ω>2，X/A随ζnn增大而增大。2.37某位移传感器固有频率为4.75Hz，阻尼比z=0.65。试估计所能测量的最低频率，设要求误差≤1％，≤2％。2.38一位移传感器的固有频为率2Hz，无阻尼，用以测量频率为8Hz的简谐振动，测得振幅为0.132cm。问实际振幅是多少?误差为多少?2.39一振动记录仪的固有频率为fn＝3.0Hz，阻尼比z=0.50。用其测量某物体的振动，物体的运动方程已知为x=2.05sin4pt+1.0sin8pt(cm)证明：振动记录仪的振动z将为z＝1.03sin(4pt-500)+1.15sin(8pt-1200)(cm)20 2.40求单自由度无阻尼系统对图所示激励的响应，设初始条件为零。解：ah(t)=1e−ξωntsinωtmωdd1−ξω(t−τ)h(t−τ)=ensin[ω(t−τ)]mωddh(t)=1sinωtmωddh(t−2)=1sin[ω(t−τ)]mωddtF1X(t)=dcosω(t−τ)=(cosωt)∫nRn0t=F1sinω(t−τ)d(t−τ)1∫0mωnnttFFX(t)=F(t)h(t−τ)dτ+−F(t)h(t−τ)dτ=1[cosω(t−t)]−2[1−cosω(t−t)]∫1∫2Rn1Rn10t1ttt1X(t)=F(t)h(t−τ)dτ+−F(t)h(t−τ)dτ+0*h(τ−t)∫1∫2∫20t1t2FF=1[cosω(t−t)−cosωt]−2[cosω(t−t)−cosω(t−t)]Rn1nRn2n1bFFF(τ)=0tF(t−τ)=0(t−τ)tt11ttFX(t)=F(t)h(t−τ)=−1[0(t−τ)dcosωt∫0ωn∫0t1nFsinωt=0[t−n]Rtωt1n1t1tFsinω(t−t)−sinωtX(t)=F(τ)h(t−τ)dτ+0*h(t−τ)dτ=1[cosω(t−t)]−n1n]∫01∫tRn1ωnt1CF(τ)=F0tF(t−τ)=F0(t−τ)tt11tX(t)=F(t)h(t−τ)dτ=F1[1−cosω(t−t)+1sinωt]∫0Rnt1ωnt1ntt1F1sinωn(t−t1)−sinωntX(t)=F(τ)h(t−τ)dτ+0*h(t−τ)dτ=[−cosωt−]∫01∫tRnωnt121 2.41求图T—2.41所示系统的传递函数，这里激励是x3(t)。2.42一弹簧质量系统从一倾斜角为300的光滑斜面下滑，如图所示。求弹簧与墙壁开始接触到脱离接触的时间。解：弹簧接触墙壁时，m的速度为：υ=2gssin30°=gs0以接触时m的位置为原点，斜下方为正，则m的微分方程为：mẋ̇+kx=mgsin30°⎧x=00考虑到系统的初始条件：⎨ẋ=gs，采用卷积分计算系统的响应为：⎩0ẋmgsin30°k0其中：xt()=sinωt+(1−cosωt)ω=nnnωkmn当m与墙壁脱离时应有xt()=01gsmg故由：xt()=sinωt+(1−cosωt)=01n1n1ω2knk4sk可得到：t=2arctg(−)1mmg也就是弹簧与墙壁开始接触到脱离接触的时间。22 2.43一个高F0、宽t0的矩形脉冲力加到单自由度无阻尼系统上，把这个矩形脉冲力看做两个阶跃脉冲力之和，如图所示。用叠加原理求t>t0后的响应。2.44如图T—2.44所示，系统支承受凸轮作用，运动波形为图中所示的锯齿波，求系统的稳态响应。2.45证明式(2.136)，即卷积积分满足交换律h(t)∗F(t)=F(t)∗h(t)3.1如图所示扭转系统。设I=2;Ik=k12t1t21．写出系统的刚度矩阵和质量矩阵；2．写出系统的频率方程并求出固有频率和振型，画出振型图。解：1)以静平衡位置为原点，设II,的转角θθ,为广义坐标，画出II,隔离体，121212根据牛顿第二定律得到运动微分方程：⎧⎪Iθ̇̇+kθ+k(θ−θ)=0⎧⎪Iθ̇̇+(k+k)θ−kθ=011t11t21211t1t21t22⎨，即：⎨⎪⎩Iθ̇̇+k(θ−θ)=0⎪⎩Iθ̇̇−kθ+kθ=022t22122t21t22⎡I0⎤⎡k+k−k⎤1t1t2t2所以：[M]=⎢⎥,[K]=⎢⎥⎣0I⎦⎣−kk⎦2t2t2⎧⎫⎪⎪θ̇̇⎧⎫θ11系统运动微分方程可写为：[M]⎨⎬+[K]⎨⎬=0…………(a)θ̇̇θ⎪⎪⎩⎭2⎩⎭2或者采用能量法：系统的动能和势能分别为1212E=Iθ̇+Iθ̇T11222223 12121212U=kθ+k(θ−θ)=(k+k)θ+kθ−kθθt11t212t1t21t22t1122222求偏导也可以得到[M],[K]⎡20⎤⎡2−1⎤由于I=2;Ik=k，所以[M]=I⎢⎥,[K]=k⎢⎥12t1t22t1⎣01⎦⎣−11⎦⎧⎫θ1⎧⎫u12)设系统固有振动的解为：⎨⎬=⎨⎬cosωt，代入（a）可得：⎩⎭θ2⎩⎭u22⎧⎫u1([K]−ω[M])⎨⎬=0…………(b)u⎩⎭222k−2ωI−k2t12t1得到频率方程：△(ω)==02−kk−ωIt1t1222422即：△(ω)=2Iω−4kIω+k=02t12t12224kI±(4kI)−×42I×k(2±2)k2t12t122t1t1解得：ω==1,224I2I22(2−2)k(2+2)k所以：t1