《现代控制理论》课后习题答案5.pdf 12页

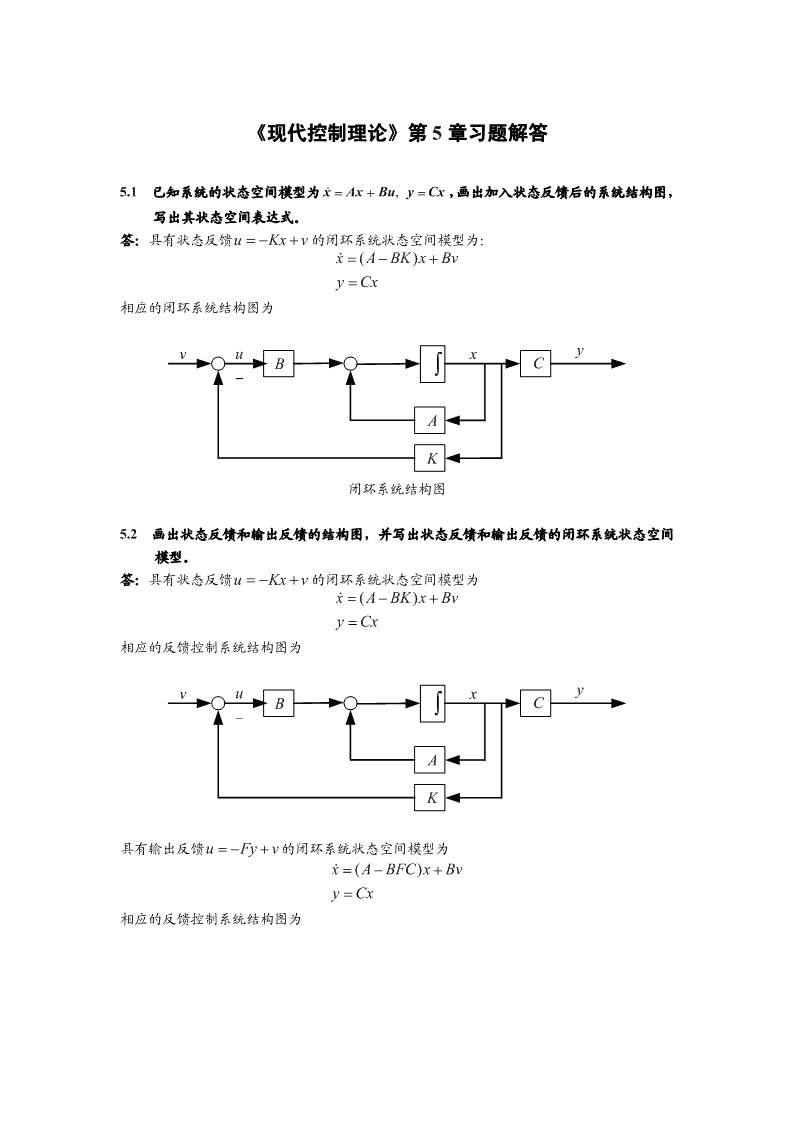
'《现代控制理论》第5章习题解答5.1已知系统的状态空间模型为x"=Ax+Bu,y=Cx，画出加入状态反馈后的系统结构图，写出其状态空间表达式。答：具有状态反馈uK=−x+v的闭环系统状态空间模型为：x"=()ABKxBv−+yC=x相应的闭环系统结构图为vuxyBCAK闭环系统结构图5.2画出状态反馈和输出反馈的结构图，并写出状态反馈和输出反馈的闭环系统状态空间模型。答：具有状态反馈uK=−x+v的闭环系统状态空间模型为x"=()ABKxBv−+yC=x相应的反馈控制系统结构图为vuxyBCAK具有输出反馈uF=−y+v的闭环系统状态空间模型为x"=()ABFCxBv−+yC=x相应的反馈控制系统结构图为 vuxyBCAF5.3状态反馈对系统的能控性和能观性有什么影响？输出反馈对系统能控性和能观性的影响如何？答：状态反馈不改变系统的能控性，但不一定能保持系统的能观性。输出反馈不改变系统的能控性和能观性。5.4通过检验能控性矩阵是否满秩的方法证明定理5.1.1。答：加入状态反馈后得到闭环系统S，其状态空间模型为Kx"=()ABKxBv−+yC=x开环系统S的能控性矩阵为0n−1Γ=[,][ABBAB?AB]c闭环系统S的能控性矩阵为Kn−1Γ−[(ABKBBABKB),][=(−)?(ABKB−)]cK由于()A−=BKBAB−BKB22()(ABK−=BA−−ABKBKA+BKBKB)2=−ABABK()(BBK−ABK−BKB)@mmm−1以此类推，()ABKB−总可以写成ABABABB,,,的线性组合。因此，存在一个适当非奇异的矩阵U，使得Γ−[(ABKB),]=Γ[,]ABUcKc由此可得：若rank(Γ[,])AB=n，即有n个线性无关的列向量，则Γ[(ABKB−),]也有ccKn个线性无关的列向量，故rank(Γ−[(ABKBn),])=cK5.5状态反馈和输出反馈各有什么优缺点。答：状态反馈的优点是，不改变系统的能控性，可以获得更好的系统性能。其缺点是，不能保证系统的能观性，状态x必须可测，成本高。输出反馈的优点是：保持系统的能控性和能观性不变，结构简单，只用到外部可测信号。其缺点是，由于用到的信号少，它所达到的系统性能往往有限，有时甚至都不能达到闭环系统的稳定性。5.6应用能控性检验矩阵的方法证明状态反馈不改变系统的能控性。然而，对以下系统 ⎡010⎤⎡⎤x"=+⎢⎥⎢xu⎥⎣−−231⎦⎣⎦yx=[]31可以通过选择适当的状态反馈增益矩阵来改变闭环系统的能观性。答：对于用能控性检验矩阵的方法证明状态反馈不改变系统的能控性，在题5.4中已经证明。开环系统的能观性矩阵为⎡C⎤⎡31⎤Γ==0[]AC,⎢⎥⎢⎥⎣CA⎦⎣−20⎦由于能观性矩阵满秩，故系统是能观的。设Kkk=[]，引入状态反馈uK=−+xv后，闭环系统的状态矩阵是12⎡01⎤AAB!=−=K⎢⎥⎣−−23kk−−⎦12闭环系统的能观性矩阵为⎡⎤C!⎡31⎤Γ=⎡⎤AC!!⎢⎥=0⎣⎦!!⎢⎥⎣⎦CA⎣−−2kk−⎦12取K=−[20]，则可得⎡31⎤Γ=⎡⎤AC!!0⎣⎦⎢⎥⎣00⎦该矩阵不是满秩的，故系统是不能观的。这个例子说明了状态反馈的引入使得原来能观的系统变得不能观了。5.7证明定理5.1.2。证明：先证能控性。对任一输出反馈系统都可对应地构造等价的一个状态反馈系统。由定理5.1.1知，状态反馈不改变系统的能控性，因而，输出反馈也不改变系统的能控性。设被控系统S的状态空间模型为：0x"=Ax+BuyC=x引入状态反馈后，闭环系统S的状态空间模型为：Fx"=()ABFCxBv−+yC=x系统S和S的能观矩阵分别为0F⎡⎤C⎡C⎤⎢⎥⎢⎥CACABFC()−Q=⎢⎥，Q=⎢⎥00F⎢⎥@⎢@⎥⎢⎥n−1⎢n−1⎥⎣⎦CA⎣CABFC()−⎦TTTT可以看出，CABFC(−)每个行均可表为⎡CAC,⎤各行的线性组合，同理有⎣⎦T2TTTTT2CABFC()−是⎡CACAC,,()⎤各行的线性组合，如此等等。据此可以导出：⎣⎦rankQ≤rankQoFo 由于S又可以看成为S的输出反馈系统，因而有oFrankQ≤rankQooF由以上两式可得rankQ=rankQooF因此，系统S完全能观测等价于S完全能观测。F05.8采用状态反馈实现闭环极点任意配置的条件是什么？答：采用状态反馈实现闭环极点任意配置的条件是，开环系统是能控的。5.9采用状态反馈实现闭环极点任意配置，其状态反馈增益矩阵K的行数和列数如何确定，计算方法有几种？答：状态反馈增益矩阵K的行数是输入变量的个数，列数是状态变量的个数。计算方法有：1.直接法；2.变换法；3.利用爱克曼公式求解。5.10为什么要进行极点配置？解决系统极点配置问题的思路和步骤是什么？答：对一个线性时不变系统，其稳定性和动态性能主要是由系统极点所决定，闭环极点在复平面的适当位置上就可以保证系统具有一定的性能。因此，为了得到期望的系统性能，可以通过改变闭环系统极点位置的方式来实现，这就是极点配置的思想。解决极点配置问题的思路如下：1、要改变系统的行为，自然想到所考虑的系统应该是能控的。因此，从能控系统入手来分析系统的求解问题；2、一般的能控系统也是很复杂的，为了求解问题，从最简单的能控系统开始，即从三阶的能控标准型模型出发分析极点配置问题的解，进而推广到阶能控标准型模型；n3、对一般的能控系统，设法将它化成等价的能控标准型模型，进而利用第2步的方法得到极点配置问题的解。解决极点配置问题的具体方法和步骤如下：（1）直接法：1、检验系统的能控性。如果系统是能控的，则继续第2步。2、利用给定的期望闭环极点，可得到期望的闭环特征多项式为nn−1()λλλλ−()−−??()λλλ=++bbλ+λ+b12nn−1103、系统矩阵A−BK的特征多项式nn−1det[λλI−−(ABK)]=+aλ+++?aaλn−1104、两个多项式相等即等号两边λ同次幂的系数相等，导出关于K的分量kk,?的一1n个线性方程组，求解该线性方程组，可得要求的增益矩阵K。（2）变换法：1、检验系统的能控性。如果系统是能控的，则继续第2步。2、利用系统矩阵A的特征多项式nn−1det(λλλI−=+Aa)+++?aλan−110确定aa,,,?a的值。01n−13、确定将系统状态方程变换为能控标准形的变换矩阵T。若给定的状态方程已经是能 控标准形，那么T=I。非奇异线性变换矩阵T可由下式决定：−1TAA=Γ[,!B!](Γ[,])Bcc4、利用给定的期望闭环极点，可得到期望的闭环特征多项式为nn−1()λλλλ−()−−??()λλλ=++bbλ+λ+b12nn−1105、确定极点配置状态反馈增益矩阵K：Kbaba=−[0011−?babaTnnnn−−−−2−21−1]5.11已知系统状态方程⎡11⎤⎡1⎤xx"=+⎢⎥⎢⎥u⎣01⎦⎣1⎦计算状态反馈增益矩阵，使得闭环极点为−2和−3，并画出反馈系统的结构图。⎡⎤11⎡⎤1答：由A=⎢⎥，B=⎢⎥，得能控性矩阵为⎣⎦01⎣⎦1⎡12⎤Γ=c(,)AB[]BAB=⎢⎥⎣11⎦det(Γ(,))AB=−≠10c所以系统是能控的。由于⎡⎤λ−−112det(λIA−=)⎢⎥=−+λλ21⎣⎦01λ−系统的能控标准形矩阵对是⎡01⎤⎡0⎤A!=⎢⎥，B!=⎢⎥⎣−12⎦⎣1⎦故状态变换矩阵为：⎡0112⎤⎡−⎤⎡11−⎤−1TA=Γ[,](!BA!Γ[,])B=−⎢⎥⎢⎥=⎢⎥cc⎣1211⎦⎣−⎦⎣10⎦根据给定的期望闭环极点，可得闭环特征多项式为：2()λλλλ−−=()(2λ++)(3λ)5=λλ++612因此，状态反馈增益矩阵是KT=[57]=[12−5]结构图为 x"xx"x22115.12给定系统⎡−21⎤⎡0⎤x"=+⎢⎥⎢xu⎥⎣01−⎦⎣1⎦（1）画出模拟结构图；（2）画出单位阶跃响应曲线。若动态性能不满足要求，可否任意配置闭环系统极点？（3）若指定闭环极点为－3和－3，求状态反馈增益矩阵，并画出单位阶跃响应曲线。答：（1）模拟结构图ux"xx"x2211∫-∫-2（2）其单位阶跃响应曲线如图所示StepResponse0.5System:g0.45SettlingTime(sec):4.6System:g0.4RiseTime(sec):2.970.350.30.25Amplitude0.20.150.10.05001234567Time(sec)系统的能控性矩阵为：⎡01⎤Γ=c(,)AB[]BAB=⎢⎥⎣11−⎦ 而det(Γ=(,))AB−10≠，故系统是能控的。因此，若系统性能不满足要求，可以通过配c置闭环系统极点来改善系统性能。（3）设状态反馈增益矩阵Kkk=[]，可得12⎡λ+−21⎤λI−−()ABK=⎢⎥⎣kkλ++1⎦122det(λλIAB−−(K))=+++++(3kkk)λ22212由指定的闭环极点−3和−3，可得期望的闭环特征多项式为：22(3λλ+)=++6λ9由此可得：kk==1,3，即K=[13]12极点配置后的闭环系统为：⎡−21⎤⎡0⎤x"=−()ABKxBv+=⎢⎥⎢x+⎥v⎣−−14⎦⎣1⎦它的单位阶跃响应曲线为：StepResponse0.12System:g0.1SettlingTime(sec):1.94System:gRiseTime(sec):1.30.080.06Amplitude0.040.02000.511.522.5Time(sec)对比两图可以发现，系统的动态性能大大改善。(1s+)5.13已知系统的传递函数为Gs()=，根据其能控标准形实现设计一个状态反馈2ss(3+)控制器，将闭环极点配置在－2，－2和－1处，并说明所得的闭环系统状态空间模型是否能观。(1s+)答：由系统的传递函数Gs()=，可以得到系统的能控标准形为：2ss(3+)⎡010⎤⎡0⎤⎢⎥⎢⎥x"=+001xu0⎢⎥⎢⎥⎢⎣003−⎥⎢⎦⎣1⎥⎦yx=[110]设状态反馈增益矩阵Kkkk=[]，则123 ⎡λ−10⎤⎢⎥λI−−()ABK=−01λ⎢⎥⎢⎣kkk+λ+3⎥⎦12332det(λλI−−(ABK))=++(3k)λ++kλk321由指定的闭环极点−2、−2和−1可得期望的闭环特征多项式：232(2λλλλλ++)(1)=++58+4由此可得：kkk===4,8,2，即K=[482]。因此，要设计的状态反馈控制器是123ux=−[482]极点配置后的闭环系统为：⎡010⎤⎡0⎤⎢⎥⎢⎥x"=+001xv0⎢⎥⎢⎥⎢⎣−−−4851⎥⎢⎦⎣⎥⎦yx=[110]该系统的能观性矩阵为：⎡C⎤⎡110⎤⎢⎥⎢⎥Γ==o[]AC⎢CA⎥⎢011⎥2⎢⎣CA⎥⎢⎦⎣−484−−⎥⎦det(Γo[AC])=0因此所得的闭环系统状态空间模型是不能观的。5.14已知系统的传递函数为(1ss−+)(2)Gs()=(1sss+)(2−+)(3)试问能否用状态反馈将闭环系统的传递函数变为s−1Gs()=c(2ss+)(3+)若有可能，试给出相应的状态反馈控制器，并画出控制系统结构图。s−1答：能够用状态反馈将闭环系统的传递函数变为Gs()=。c(2ss+)(3+)根据原系统的传递函数可以得到能控标准形。由定理5.1.3，对能控的单输入单输出系统，只要不发生零极点相消的现象，状态反馈就不能改变零点。因此我们只能用状态反馈把原系统变换为(1ss−)(2+)Gs()=c2(2ss+)(3+)即将闭环系统极点配置在−2、−2和−3的位置上。原系统的状态方程为：⎡010⎤⎡0⎤⎢⎥⎢⎥x"=+001xu0⎢⎥⎢⎥⎢⎣652−⎥⎢⎦⎣1⎥⎦ yx=−[211]设状态反馈增益矩阵Kkkk=[]，则123⎡λ−10⎤⎢⎥λI−−()ABK=−01λ⎢⎥⎢⎣kkk−65−+λ+2⎥⎦12332det(λλIAB−−(K))=++(2k)λ+−+−(k5)λk6321由指定的闭环极点−2、−2和−3可得期望的闭环特征多项式：232(2λλλλλ++)(3)=+++71612由此可得：kkk===18,21,5，即K=[18215]。因此，要设计的状态反馈控制器123是ux=−[18215]相应的闭环系统是：⎡⎤0100⎡⎤⎢⎥⎢⎥x"=+0010xv⎢⎥⎢⎥⎢⎥⎣⎦−−−12167⎢⎣1⎥⎦yx=−[211]结构图为ux"x"x"y3215.15已知系统的状态空间模型⎡⎤005⎡−20⎤⎢⎥⎢⎥x"=−101xu+−12⎢⎥⎢⎥⎢⎥⎣⎦013⎢⎣01⎥⎦yx=[001]（1）验证开环系统是不稳定的，系统是能控能观的；T（2）证明该系统可以采用输出反馈uhhy=[]使得闭环系统渐近稳定；12T（3）验证该系统不能采用输出反馈uhhy=[]任意配置闭环系统极点。12答：(1)由于系统的特征值为-0.1607，6.5676，14.4931，所以开环系统是不稳定的。系统的能控 性矩阵是⎡−200555⎤⎢⎥Γ[,]AB=122114−−−−c⎢⎥⎢⎣011112⎥⎦其秩rankΓ[,]AB＝3，所以系统是完全能控的。c系统的能观性矩阵是⎡001⎤⎢⎥Γ=0[]AC,⎢013⎥⎢⎣138⎥⎦由于rankΓ[A,C]＝3，故系统也是完全能观的。0T（2）在输出反馈uhhyH=[]=y作用下，闭环系统为12x"=()ABHCx+yC=x其闭环状态矩阵是：⎡005⎤⎡−−20⎤⎡0025h+⎤1⎢⎥⎢⎥⎡⎤h1⎢⎥ABHC+=101−+−12⎢⎥[]00110=hh12−−21⎢⎥⎢⎥h⎢⎥⎣⎦2⎢⎣013⎥⎢⎦⎣01⎥⎦⎢⎣01h+3⎥⎦2该系统的特征多项式为：32det(λλIAB−+(HC))=+−−+−+++−(h3)λλ(hh21)(2h5)2121设配置极点后的系统特征多项32⎧−−=3hb22式为λλλ+bb21++b0，则有⎪⎨21hh−+=b211⎪⎩25hb−=10即需满足115−2bb−−=b13222闭环系统渐近稳定，则须有三个负根，即b，b和b都必为正，这与上式矛盾，故原系统123T不可能用输出反馈uhh=[12]y来镇定原系统。原题有误。5.16极点配置可以改善系统的过渡过程性能，加快系统的响应速度。它对稳态性能有何影响？如何消除对稳态性能的负面影响？答：极点配置可以改善系统的过渡过程性能，加快系统的响应性能，但可能使闭环系统产生稳态误差。可以引进一个积分器来抑制或消除系统的稳态误差，这样一种跟踪控制器的设计问题可以通过建立增广系统，进而求解增广系统的极点配置问题来得到既保持所期望的动态性能，又无静差的比例－积分控制器。5.17考虑例5.4.2中的倒立摆系统，假定风以一个水平力wt()作用在摆杆上，以5(wt)作 用在小车上，此时系统的动态方程是⎡0100⎤⎡⎤⎡00⎤⎢⎥⎢⎥⎢⎥0010−14x"=++=AxBuEw⎢⎥⎢⎥⎢x+u+⎥w⎢0001⎥⎢⎥⎢00⎥⎢⎥⎢⎥⎢⎥⎣00110⎦⎣⎦⎣−16⎦yC==x[1000]xT其中：xyy=["θθ"]是系统的状态向量，θ是摆杆的偏移角，y是小车的位移，是作用在小车上的力。再按例u5.4.2的要求设计控制器，并画出闭环系统的状态响应曲线，解释摆杆偏移角的稳态值非零的原因。答：增广系统的状态空间模型是⎡⎤01000⎡0⎤⎡0⎤⎢⎥⎢⎥⎢⎥00100−14w⎡⎤xx"⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥=+⎢⎥00010⎢⎥⎢0⎥u+⎢0⎥⎣⎦qq"⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥001100⎢−1⎥⎢6w⎥⎣⎦⎢⎥10000⎣⎢0⎦⎥⎢⎣−yr⎥⎦⎡⎤xy=[]10000⎢⎥⎣⎦q采用极点配置方法，基于以上模型来设计增广系统的极点配置状态反馈控制器uK=−−xKq12根据给定的性能要求，选择闭环极点为λ=−+13j，λ=−−13j，λ=λλ==−512345执行以下M文件：a=[01000;00-100;00010;001100;10000];b=[0;1;0;-1;0];c=ctrb(a,b)rank(c)求得能控性矩阵：⎡01010⎤⎢⎥101011⎢⎥Γ=c[]AB⎢0101−−10⎥⎢⎥−−10110−121⎢⎥⎢⎣00101⎥⎦以及该矩阵的秩为5，所以增广系统是能控的。因此可以对增广系统进行任意极点配置。特别的，对以上给定的闭环极点，执行以下的M文件：A=[0100;00-10;0001;00110];B=[0;1;0;-1]; C=[1000];AA=[Azeros(4,1);C0];BB=[B;0];J=[-1+j*sqrt(3)-1-j*sqrt(3)-5-5-5];K=acker(AA,BB,J)得到系统的状态反馈增益矩阵K=-55.0000-38.5000-175.0000-55.5000-50.0000因此，要设计的控制器是tux=+[5538.517555.5]50∫[]y()1τ−dτ0执行以下M文件：A=[0100;00-10;0001;00110];B=[0;1;0;-1];C=[1000];K1=[-55-38.5-175-55.5];K2=-50;a=[A-B*K1-B*K2;C0]；b=[0;4;0;6;-1]；c=[C0]；d=0；sys=ss(a,b,c,d);ltiview({"step"},sys);可得闭环系统单位阶跃响应：'