《误差理论与数据处理》部分课后作业参考答案.docx 22页

'《误差理论与数据处理》部分课后作业参考答案1-18根据数据运算规则，分别计算下式结果：（1）3151.0+65.8+7.326+0.4162+152.28=？（2）28.13X0.037X1.473=？【解】（1）原式≈3151.0+65.8+7.33+0.42+152.28=3376.83≈3376.8(2)原式≈28.1X0.037X1.47=1.528359≈1.52-12某时某地由气压表得到的读数（单位为Pa）为102523.85，102391.30，102257.97，102124.65，101991.33，101858.01，101726.69，101591.36，其权各为1，3，5，7，8，6，4，2，试求加权算术平均值及其标准差。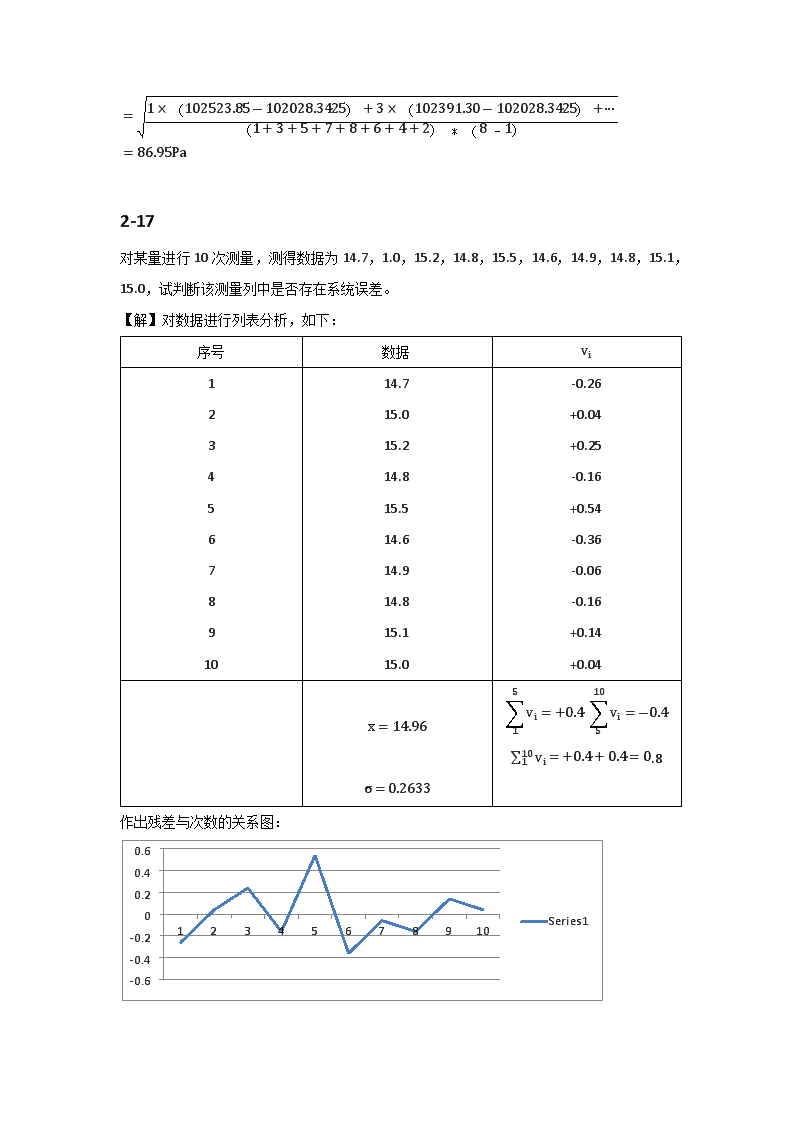【解】（1）加权算术平均值：=100000+1×2523.85+3×2391.30+5×2257.97+7×2124.65+8×1991.33+∙∙∙1+3+5+7+8+6+4+2=102028.3425Pa（2）标准差： =1×（102523.85-102028.3425）+3×（102391.30-102028.3425）+∙∙∙1+3+5+7+8+6+4+2*（8-1）=86.95Pa2-17对某量进行10次测量，测得数据为14.7，1.0，15.2，14.8，15.5，14.6，14.9，14.8，15.1，15.0，试判断该测量列中是否存在系统误差。【解】对数据进行列表分析，如下：序号数据vi1234567891014.715.015.214.815.514.614.914.815.115.0-0.26+0.04+0.25-0.16+0.54-0.36-0.06-0.16+0.14+0.04x=14.96σ=0.263315vi=+0.4510vi=-0.4110vi=+0.4+0.4=0.8作出残差与次数的关系图： （1）线性系统误差：根据关系图利用残余误差观察法可知，不存在线性系统误差。根据不同公式计算标准差比较法可得：按贝塞尔公式：按别捷尔斯公式：u=σ2σ1-1=0.26420.2633-1=0.0032<2n-1=23故不存在线性系统误差。（2）周期性系统误差：u=i=1n-1vivi+1=-0.26×0.04+0.04×0.24+0.24×-0.16+-0.16×0.54+0.54×(-0.36)+∙∙∙=0.1112T+=30，判断两组数据可能存在系统误差。2-19等精度测得某一电压10次，测得结果（单位为V）为25.94，25.97，25.98，26.01，26.04，26.02，26.04，25.98，25.96，26.07。测量完毕后，发现测量装置有接触松动现象，为判明是否因接触不良而引入系统误差，将接触改善后，又重新做了10次等精度测量，测得结果（单位为V）为25.93，25.94，25.98，26.02，26.01，25.90，25.93，26.04，25.94，26.02。试用t检验法（取α=0.05）判断两组测量值之间是否有系统误差。【解】计算两组测量结果的算术平均值：x=110x=26.001y=110y=25.971Sx2=110(xi-x)2=0.00155Sy2=110(yi-y)2=0.00215t=26.001-25.97110×1010+10-210+1010×0.00155+10×0.00215=1.48由v=10+10-2=18，取α=0.05，查t分布表，得ta=2.1。因|t|=1.480.097201即它含有粗大误差，故将此测得值剔除。再根据剩下的13个测得值重新计算，无粗大误差。2）格罗布斯准则由表1计算得x(平均值)=28.57067按测得值的大小，顺序排列得今有两测得值可怀疑，但由于故应先怀疑是否含有粗大误差计算查表2-13[课程用书]则故表1中第四个测得值含有粗大误差，应予以剔除。剩下14个数据，再重复上述步骤，判别是否含有粗大误差，计算查表2-13[课程用书] 故表1中第十四个测得值含有粗大误差，应予以剔除。余下测得值也不含粗大误差。3）狄克松准则顺序号顺序号顺序号顺序号28.41128.529928.492228.52101028.493328.53111128.494428.53121228.55528.53131328.56628.53141428.57729.521528.5188首先判断最大值。因，故按式（2-93）[课程用书]计算统计量查表2-14的则故第四个测得值含有粗大误差，应予以剔除。剩下14个数据，再重复上述步骤。对，计算不含有粗大误差。对，按式（2-94）计算查表2-14的则 故第十四个测得值含有粗大误差，应予以剔除。对剩下13个数据，再重复上述步骤，不含有粗大误差。2-26对某被测量进行间接测量得：，，，其权分别为5:1:1，试求的测量结果及其标准差？【解】3-7通过电流表的电流与指针偏转角服从下列关系：式中为决定于仪表结构的常数，，两次测得、。试求两种情况下的、及其极限误差，并分析最佳测量方案。【解】由于题中给出的是角度的极限误差，所以对计算函数要做如下变形，因,由三角函数随机误差（极限误差）计算公式（3-21），有：， (1)当时，把代入关系式，有：相应的极限误差为：当时，把代入关系式，有：相应的极限误差为：根据求得测量电流的误差传递式（1），欲使极限误差变小,必须满足最小，又因为为常数，这意味着只能使最大。又因为电流表指针偏转角在范围内变化，当时，单调递减，为使趋小，应该越小越好，则测得的电流误差小。与上诉计算结果验证一致。3-10通过电流表的电流I与指针偏转角度服从下列关系：若测得,试求电流I的标准差。【解】由已知，将分别对C和求导，得 所以有3-13假定从支点到重心的长度为L的单摆振动周期为T，重力加速度可由公式中给出，若要求测量g的相对标准差，试问按等作用原则分配误差时，测量L和T的相对标准差应该是多少？【解】由等作用分配原则，则有由相对标准差的定义，有 其中，测量g的相对标准差。3-14对某一质量进行4次重复测量，测得数据（单位：g）为428.6，429.2，426.5，430.8。已知测量的已定系统误差，测量的各极限误差分量及其相应的传递系数如下表所列。若各误差均服从正态分布，试求该质量的最可信赖值及其极限误差。序号极限误差/g误差传递系数随机误差未定系统误差12.1-12-1.513-1.014-0.5154.5-16-2.21.471.0-2.28-1.81【解】4-6某数字电压表说明书指出，该表在校准后的两年内，其2V量程的测量误差不超过±（14× 读数+量程）V，相对标准差为20%，若按均匀分布，求1V测量时电压表的标准不确定度。设该表校准一年后，对标称值为1V的电压进行16次重复测量，得观测值的平均值为0.92857V，若以平均值作为测量估计值，试分析影响测量不确定度的主要来源，分别求出不确定度分量，说明评定方法的类别，求测量结果的合成标准不确定度及其自由度。【解】（1）∵电压表测量误差不超过±（14×读数+量程）V，且电压服从均匀分布∴标准不确定度为自由度为（2）A类不确定度：自由度：B类不确定度：自由度：由于两种不确定度的传递系数为1，且两者互不相关合成不确定度为自由度为根据置信概率，自由度，查t分布表得即包含因子，于是电压测量的展伸不确定度为依据“三分之一准则”对展伸不确定度进行修约，得展伸不确定度最后不确定度的报告电压测量结果 说明：以上测量结果中符号以后的数值是展伸不确定度，是由合成标准不确定度以及包含因子确定的。对应的置信概率，自由度。4-8在测长仪上对同一圆柱截面的直径进行了9次重复测量，其单次测量标准差为；已知测长仪的示值误差为；仪器的分辨力为，按均匀分布，相对标准差都为10%；测量时温度控制在，对测量影响不超过（按计算得到），其相对标准差为20%。若用平均值作为直径测量结果的估计值，求直径测量合成标准不确定度及其自由度。【解】重复测量引起的标准不确定度为自由度示值误差引起的标准不确定度（按均匀分布）自由度仪器分辨力引起的标准不确定度（按均匀分布）自由度温度变化引起的标准不确定度自由度由于四种不确定度的传递系数为1，且互不相关合成不确定度为 自由度为4-9用漏电测量仪直接测量正常使用中微波炉的漏电电流，5次重复测量的平均值为0.320mA，平均值的标准差为0.001mA；已知漏点测量仪的示值误差范围为5%，按均匀分布，取相对标准差为10%；测量时环境温度和湿度的影响范围为2%，按三角分布，其相对标准差为25%；试给出漏电电流测量的不确定度报告（置信概率为99%）。【解】A类：B类：根据“三分之一”准则对展伸不确定度进行修约，则故漏电电流为。其展伸不确定度是由合成标准不确定度及包含因子确定的，对应的置信概率，自由度。5-5 测力计示值与测量时的温度t的对应值独立测得如下表所示：t/℃151821242730F/N43.6143.6343.6843.7143.7443.78设t无误差，F值随t的变化呈现性关系F=k0+kt，试给出线性方程中系数k0和k的最小二乘估计及其相应精度。【解】，，，列表如下：111543.6112251543.61654.15211843.6313241843.63785.34312143.6814412143.68917.28412443.7115762443.711049.04512743.7417292743.741180.98613043.7819003043.781313.406135262.1563195135262.155900.19又 又6-7在4种不同温度下观测某化学反应生成物含量的百分数，每种在同一温度下重复观测3次，数据如下:温度x/℃150200250300生成物含量的百分数y77.476.778.284.184.583.788.989.289.794.894.795.9【解】序号x/℃y/%x2/℃2y2/%2xy/℃%115077.43225005995.4011614.5220084.10400007072.8116820325089.27625007969.1322317.5430095.13900009049.7228539∑900345.9321500030087.0679291 t=1Nxt=900℃x=225℃t=1Nxt2=215000℃2(t=1Nxt)2/N=202500℃2lxx=t=1Nxt2-(t=1Nxt)2/N=12500℃2t=1Nyt=345.93%y=86.48%t=1Nyt2=30087.06%2(t=1Nyt)2/N=29916.89%2lyy=t=1Nyt2-(t=1Nyt)2/N=170.17%2b=lxylxx=0.1165b0=y-bx=60.27y=60.27+0.1165xN=4t=1Nxtyt=79291℃%(t=1Nxt)(t=1Nyt)/N=77834.25℃%lxy=t=1Nxtyt-(t=1Nxt)(t=1Nyt)/N=1456.75℃%现在进行方差分析。U=mblxy=509.13QL=mlyy-U=1.38QE=t=1Ni=1m(yti-yt)2=2.7492来源平方和自由度方差F显著性回归失拟误差509.131.382.75128509.130.690.34381481.102.007F(1,8)0.01=11.26F(2,8)0.01=8.65总计512.2611———F=UvUQEvQE=1481.10F>F(1,8)0.01=11.26 F1=QLvQ1QEvQE=2.007F1Fα=0.01，则回归是高度显著地（或者称为在0.01水平上显著）。矩阵解法：（原题见上）6-7【解】1）通过矩阵求回归方程：输入：x=[1111;150200250300];ytbar=[77.484.189.395.1];b=(x")(ytbar")输出结果b=[60.240.12]所以求出回归方程：Y=60.24+0.12*X 1）方差分析和显著性分析Lxx=12500；Lyy=170.37；Lxy=1457.50;Xbar=225(x的平均值)Ybar=86.47(y的平均值)平方和自由度U509.831QE2.398QL1.272对结果进行F检验：F=(U/γU)/(QE/γQE)=1706.56>F0.01(1，8)=11.26F1=(QL/γQL)/(QE/γQE)=2.12F0.01(1，10)=10.04分析：1）F和F2检验结果都很显著，说明回归是高度显著的。其中F显著说明回归平方和相对于实验误差是高度显著的；而F2显著说明回归平方和相对于残余平方和高度显著。2）另外F1的检验结果不显著，说明失拟误差相对于实验误差是可以忽略不计的。3）所以通过上述显著性检测说明，说明方程拟合的效果很好！具体计算过程（matlab计算过程）：m=3;n=4;ytbar=[77.484.189.395.1];x=[150200250300]; y=[77.476.778.2;84.184.583.7;88.989.289.7;94.894.795.7];lxx=sum(x.^2)-sum(x)^2/nlyy=sum(ytbar.^2)-sum(ytbar)^2/nlxy=sum(x.*ytbar)-sum(x)*sum(ytbar)/nxbar=sum(x)/nybar=sum(ytbar)/nb=lxy/lxxb0=ybar-b*xbarU=m*b*lxyQL=m*lyy-UQE=0;fori=1:nforj=1:mQE=QE+(y(i,j)-ytbar(i))^2;endendQEvu=1vQE=n*(m-1)vQL=n-2F=(U/vu)/(QE/vQE)F1=(QL/vQL)/(QE/vQE)F2=(U/vu)/((QE+QL)/(vQE+vQL))6-9【解】首先等式两边同时取对数：lny=lna+b*lnx取b1=lna,b2=bZ1=logyZ2=logx确定回归方程x1=[111111;1.5852.5123.9796.3109.98815.85]; y=[0.031620.022910.020890.019500.018620.01512];x1=log(x1);fori=1:6x1(1,i)=1;endb=x1"(log(y))"求出b=-3.4305b2=-0.2718直线拟合（x,y坐标为log（x），log（y））：通过画图结果显示曲线拟合结果很好！'