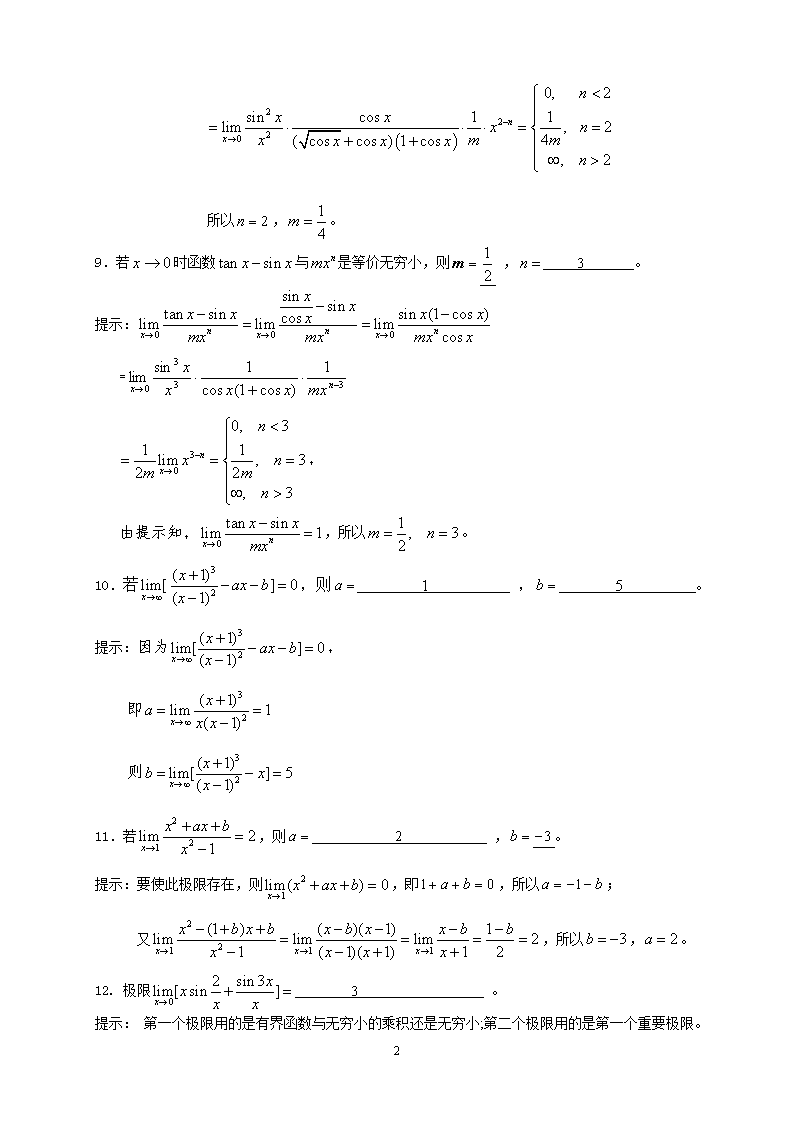《高等数学练习题》全部答案.doc 31页

'《高等数学》第一章综合练习题（一）参考答案一、填空题1．函数的定义域为。提示：即解不等式组，可得2．设函数的定义域为，则的定义域为。提示：即解不等式：。3．若函数的定义域为，则函数的定义域为。提示：即解不等式。4．若函数的定义域为，则函数的定义域为。提示：即解不等式5．若函数的定义域为，则函数的定义域为。提示：即解不等式，可得6．函数的定义域为。提示：即解不等式组，可得7．若极限，则2，。提示：要使此极限存在，则，即，所以；又，所以。8．若时函数与是等价无穷小，则，2。提示：由于31 所以，。9．若时函数与是等价无穷小，则，3。提示：=，由提示知，，所以。10．若，则1，5。提示：因为，即则11．若，则2，。提示：要使此极限存在，则，即，所以；又，所以，。12.极限3。提示：第一个极限用的是有界函数与无穷小的乘积还是无穷小;第二个极限用的是第一个重要极限。31 13.极限3。提示：注意与第六题的不同之处。14．若时，是比高阶的无穷小，则的取值范围是。提示：由题意是比高阶的无穷小知，，所以。15．若，则的取值范围是。提示：16．函数的反函数是。17.函数的反函数是。18．如果，则。提示：所以：。19．如果，则=。提示：设，则所以。20．设，则。31 提示：提示：令可得，在把带入即可。《高等数学》第一章综合练习题（二）参考答案一、单项选择题1．下列结论不正确的是（C）。A．基本初等函数在其定义域内是连续的B．基本初等函数在其定义区间内是连续的C．初等函数在其定义域内是连续的D．初等函数在其定义区间内是连续的2.下列说法正确的是（D）A．无穷小的和仍为无穷小B．无穷大的和仍为无穷大C．有界函数与无穷大的乘积仍为无穷大D.收敛数列必有界3．若无穷小量与是等价的无穷小，则是（D）无穷小A．与同阶不等价的B．与等价的C．比低阶的D．比高阶的4．设函数在闭区间上连续，则下列说法正确的是（C）A．必存在B．必存在C．必存在D.必存在5.下列说法不正确的是（B）。A．两个无穷小的积仍为无穷小B．两个无穷小的商仍为无穷小C．有界函数与无穷小的乘积仍为无穷小D.在同一变化过程中，无穷大的倒数为无穷小6．偶函数的定义域一定是（B）A.包含原点的区间B.关于原点对称C.D.以上三种说法都不对7．若是奇函数，是偶函数，且有意义，则是（A）。偶函数奇函数非奇非偶函数奇函数或偶函数8．下列函数中,(B)是奇函数.A．B．C．D．9．若在内单调增加,是单调减少,则在内(B)A.单调增加B.单调减少C.不是单调函数D.无法判定单调性10．函数的图形对称于直线（C）A.B.C.D.11．若是奇函数,且对任意实数,有,则必有(B)。A.B.0C.1D.231 12．下列各式中正确的是（A）13．若，则（C）A．B．C．D．提示：14．设，则等于（D）。提示：设，则（因为，所以）所以15．设，则（C）。提示：，令，则故16．极限（B）不存在17．当时，的极限是（D）。A．0B．C．D．不存在31 提示：，，所以当时，的极限不存在18．当时，的极限是（D）不存在提示：；；当时，的极限不存在。19．设，则（D）。A．1B．不存在C．D．提示：??20．若时，，则（）提示：《高等数学》第二章综合练习题参考答案一、填空题1．若在处可导，且，则。提示：根据导数的定义所以可得：2．设在处可导，且，，则。31 提示：3．若，则。提示：由题意知：且4．设函数在处二阶可导，且，则。提示：5．若曲线与曲线相切，则。提示：两条曲线相切，说明有一个交点，所以还说明他们具有共同的切线，所以切线的斜率相同，即所以可以得到：，即。所以可得6．若极限，则。提示：7．设函数在处可导，且，则1。提示：8．若，则。提示：9．设，则提示：由知：10．设，则微分。31 提示：用对数求导法求的导数为：所以二、单项选择题1．若。则（D）。提示：2．已知为可导的偶函数，且，则曲线在处的切线方程为（A）。提示：3．设曲线在处的切线是水平的，则当时，较之为（D）无穷小。A．同阶不等价B．等价C．低阶D．高阶提示：因为曲线在处的切线是水平的，所以即，所以较之为高阶无穷小。4．设，则（B）提示：令，则，则，所以5．设可导，则（C）提示：6．函数在处是（C）。31 A．连续且可导B．不连续不可导C．连续不可导D．不连续但可导提示：，所以所以该函数在不可导。但是从图形上看该函数在点连续。7．下列函数中在点处连续但不可导的是（C）。解：根据连续与可导的关系，可导一定连续，知，不连续一定不可导。所以下面的函数中，在处没有定义，所以一定不连续，所以一定不可导在处没有定义，所以一定不连续，所以一定不可导处即可导也连续，所以，，所以不可导。8．设函数在处可导，且，则（C）。提示：9．函数在点处可导，下列极限等于是（C）。提示：10．设在处可导，当由增至时，极限（A）.A．0B．1C．D．不存在提示：根据在处可导知在处可微，由可微的性质知：是31 的高阶无穷小，所以（计算）10.设，求导数解：当时，当或时，又所以及均不存在所以《高等数学》第三章综合练习题（一）参考答案一、填空题1．曲线的垂直渐近线方程为。提示：垂直渐近线是：若，则称直线为曲线的垂直渐近线。所以对本题有：当时，即为其垂直渐近线。2．曲线的渐近线方程为。提示：显然根据垂直渐近线的定义知道，该曲线没有垂直渐近线斜渐近线是指：若，则直线为曲线的斜渐近线。31 其中中的参数和是由极限和确定。所以对本题所以有渐近线为直线又，所以时无渐近线。所以该曲线仅有一条渐近线为3．曲线的斜渐近线方程为。提示：所以斜渐近线为与4．曲线的斜渐近线方程为。提示：所以斜渐近线为5．曲线的斜渐近线方程为。提示：31 所以斜渐近线为6．曲线的斜渐近线方程为。提示：所以斜渐近线为与7．曲线的垂直渐近线方程为。提示：所以垂直渐近线为8．函数在区间上的最小值为，最大值为10。提示：令，得，计算9．若点为曲线的一个拐点，则，。提示：因为点为曲线的一个拐点，所以有：，且在该点处即：，所以解之得：10．设有连续导数，，且，则。31 提示：倒数第二个等号用到了条件有连续导数，所以且。二、单项选择题1．设在上可导，且，则在内至少有一点，使得（B）。不存在提示：因为在上可导，所以由拉格朗日中值定理知：在内至少有一点，，使得又，所以2．设，且当时，有，则当时，有（B）以上都不对提示：令，所以，且所以当时，，即3．若二次可微，且是它的一个拐点，则处必有（A）成立。取得极值切线不存在取得极值以上都不对提示：因为二次可微，则存在，又是它的一个拐点，所以可知，所以在该点取得极值。4．设函数可微，则当时，较之为（D）无穷小A．同阶不等价B．等价C．低阶D．高阶提示：因函数可微，所以由定义知：，且，所以。5．若，则点一定是函数的（B）。A．极大值点B．极小值点C．最大值点D．最小值点提示：由知，，31 根据极值的第二判别定理知，函数在该点一定取得极小值。6．下列各函数在上满足罗尔定理条件的是（A）提示：在点没有定义在点不可导时，，7．设在上连续，在内可导，且，则在内曲线上至少有一条切线平行于直线（D）。提示：设在上连续，在内可导，且，由拉格朗日中值定理知：在内至少存在一点，使得即该点的斜率为。8.下列各函数在上满足拉格朗日中值定理条件的是（B）提示：的定义域为的定义域为的定义域为9．若，，且，则上（D）成立。单调递增单调递增10．曲线（C）。仅有垂直渐近线有斜渐近线有斜渐近线没有渐近线提示：见第一题第四小题。11．设点是曲线的拐点，则（A）。为任意实数，31 提示：点是曲线的拐点，说明：（1）（2）,即（3）若，则曲线为直线，无拐点。12.是偶函数，且在内有，，则在内有（C）。A．，，，，提示：利用偶函数图像关于轴对称可得13.是奇函数，且在内有，，则在内有（D）。A．，，，，提示：利用奇函数图像关于原点对称可得14．提示：《高等数学》第四章课外综合练习题参考答案一、填空题1．若不定积分，则。解：记则所以2．已知的一个原函数为，则。解：=31 3．若不定积分，则。解：4．若不定积分，则。解：5．不定积分=。解：6．不定积分=。解：=7．不定积分。解：8．已知的一个原函数为，则。解：=9．若，则不定积分。解：记则10．不定积分=。解：=（）二、单项选择题1．设，且，则=（B）。31 ....注意：不定积分的定义2．设，则的结果是（C）。A．B．C．D．注意：（）3．若，则下列等式中一定成立的是（B）。A．B．（C为某常数）C．D．注意：原函数的有关性质4．等于（A）A．B．C．D．注意：性质有5．下列等式中不成立的是（C）。A.B.C.D.注意：不定积分的性质6．（C）。A．B．C．D．注意：分部积分公式7．设，则（D）。A.B.C.D.注意：三、计算题1．求不定积分：解：设，则31 原式==2．求不定积分：解：=（）3．求不定积分：解：令，则原式====4．求不定积分：解：令，原式5．求不定积分：解：6．求不定积分：解：===7．求不定积分：解：令，则31 8．求不定积分：解：令，则：原式==+=+-所以：原式=9．求不定积分：解：设原式====10．求不定积分：解：令，则《高等数学》第五章课外综合练习题（一）参考答案一、填空题1．设为连续函数，且，记，则。提示：因为所以2．设为连续函数，则=0。提示：3．设为连续的偶函数，且，则________。提示：因为为连续的偶函数，所以4．设为连续的奇函数，且，则______。31 提示：因为为连续的奇函数，所以05．设是的一个原函数，则定积分。提示：因为为的原函数，所以所以==16．由曲线与直线所围成的平面图形的面积为。提示：（草图略）以为积分变量，则所围成的平面图形的面积7．由曲线与直线所围成的平面图形的面积为。提示：（草图略）以为积分变量，则所围成的平面图形的面积8．由曲线与直线及直线所围成的平面图形的面积为。提示：（草图略）以为积分变量，则所围成的平面图形的面积9．由曲线与直线所围成的平面图形的面积为。提示：（草图略）以为积分变量，则所围成的平面图形的面积10．由曲线与直线所围成的平面图形的面积为。提示：（草图略）以为积分变量，则所围成的平面图形的面积11．定积分=。提示：令，则31 所以12．定积分。提示：13．定积分______。提示：14．极限=。提示：原式===15．设可积，且有，则。提示：=所以二、单项选择题1．极限（C）。A．B．0C．1D．2提示：2．设，其中是连续函数，则（C）。.0...不存在提示：31 3．设是可导的连续函数，则等于（D）A.B.C.D.提示：4．设，，则下列不等式成立的是（D）。A．B．C．D．提示：利用奇函数在关于原点对称的区间上的定积分为零，可以得到，所以：5．下列定积分中，其值为零的是（D）A．B．C．D．提示：因为是奇函数6．设，其中是连续函数，则（D）。.0...提示：7．提示：因为定积分是一个确定的数，所以其导数为零。8．设为连续的偶函数，且，则等于（B）。A.B.C.0D.231 提示：9．设为上的连续函数，则曲线，，及轴所围成的曲边梯形面积为（　C　）A．　B．C．D．提示：利用定积分的几何意义。10．设为连续函数，记，其中，，则的值（C）A．依赖于和B．依赖于、和C．依赖于和，不依赖于D．依赖于，不依赖于提示：定积分只与被积函数及积分区间有关，而与积分变量的记法无关。《高等数学》第五章课外综合练习题（二）参考答案一、计算下列极限1．解：2．解：原式=3．31 解：原式===24．解：二、计算下列积分1．解：令，则原式====所以：原式=2．解：所以3．解：原式====4．解：令，则：31 原式==—=—所以：原式=5．解：所以6．解：令，则7．原式====8．解：令，则9．解：31 10．解：原式====—==高等数学》第五章课外综合练习题（三）参考答案一、设，，，试求积分：解：=二、设，，，试求定积分：解：三、已知及，求定积分解：31 四、设具有二阶连续导数，证明证明：因为）所以：五、设函数在区间[，]上连续，且，记，证明方程在区间（，）内有且仅有一个实根。证：因为所以从而在上可导，且在上是单调增的又，所以，，即方程在区间内有且仅有一个根六、设函数在区间[0，1]上连续，证明证：令，则时，时，==所以七、设二阶可导，证明：31 证明：左式=====右式八、设，其中为正整数，证明：证明：九、设函数在区间[，]上连续，证明：，并计算。证明：因为所以：因此十、设在上可导，且满足条件，证明：在区间内至少存在一点，使得等式=0成立。证明：设则其中且在上可导所以由罗尔定理得：在内至少存在一点，使得又，故结论成立。《高等数学》第六章课外综合练习题参考答案一、求下列方程的通解31 1．解：原方程可改写为分离变量得：上式两边同积分，得：即：，此即为所求。2．解：所给方程的通解为====3.解：所给方程可改写为两边同积分得此即为所求4.解：所给方程可改写为两边同积分得：化简得即为所求5.解：所给方程的通解为二、求下列方程满足条件的特解31 1.解：原方程可改写为两边积分得又得所以即为所求2．解：原方程可改写为两边积分得又，所以所以即为所求3.，解：分离变量得两边同时积分得；化简得：，即为所求微分方程的通解。又，所以则，即为所求微分方程的特解。4.解：所给方程的通解为31 ===又，代入通解得：所以即为所求解5.解：所给方程的通解为又，得所以，即为所求31'