- 2.81 MB
- 2022-04-22 11:46:55 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
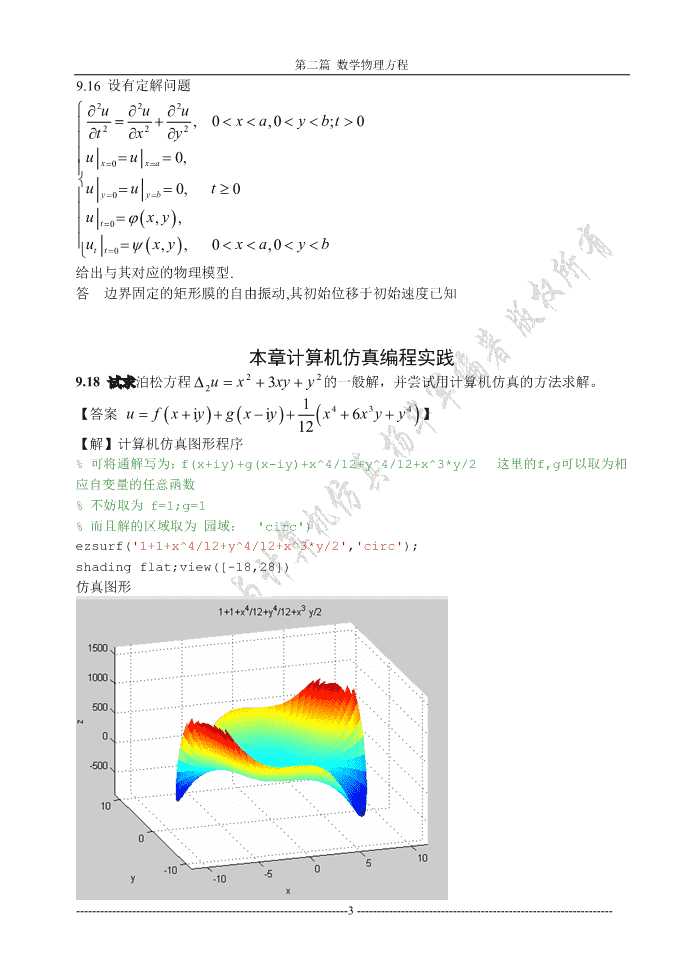
'第二篇数学物理方程第二篇数学物理方程部分第九章数学建模——数学物理定解问题习题及解答9.1长为l的均匀细弦,两端固定于x=0,xl=,弦中的张力为T.在x=h点处,以横向0力F拉弦,达到稳定后放手任其自由振动,写出初始条件.0⎧Flhx()−0,x∈[0,]h⎪⎪Tl0【答案u|=⎨】t=0Fhlx()−⎪0,x∈[,]hl⎪Tl⎩09.2长为l的均匀杆两端受拉力F作用而作纵振动,写出边界条件.0【答案YSu|==F,YSu|F】xx==00xxl09.3长为L的均匀杆,两端有恒定热流进入,其强度为q,写出这个热传导问题的边界条0件.【答案−=ku|,qku|=q】xx==00xxL09.4一根长为L的均匀细弦,两端固定于x=0,xL=,用手将弦于x=l处朝横向拉开距离h,然后放手任其振动,试写出其定解问题.2uau−=0;(0,)0(,);(,0)0,ut==Ltux=ttxxt⎧hxx(0≤≤l)【答案⎪⎪l】ux(,0)=⎨⎪H(Lx−≤)(lxL≤)⎪⎩Ll−9.5有一均匀细杆,一端固定,另一端受到纵向力Ft()=Fsinωt作用,试写出其纵振动0方程与定解条件.2sinωt【答案uau−=0;(0,)utultF=0,(,)=;(,0)ux=0,(,0)ux=0】ttxxx0tYs9.6有一均匀细杆,一端固定,另一端沿杆的轴线方向被拉长ε而静止(设拉长在弹性限度内).突然放手任其振动,试推导其其纵振动方程与定解条件.2ε【答案uau−=0;(0,)0ut==ultux(,);(,0)=xux,(,0)0=】ttxxxtl9.7长为l的理想传输线,一端x=0接于交流电源,其电动势为Etsinω,另一端x=l开0路。试写出线上的稳恒电振荡方程和定解条件.221iωt【答案vv−==aa0,(),|v=Ee,|i=0】ttxxx==00xlLC9.8研究细杆导热问题,初始时刻杆的一端温度为零度,另一端温度为T,杆上温度梯度0均匀,零度的一端保持温度不变,另一端与外界绝热,试写出细杆上温度的变化所满足的方程,及其定解条件.--------------------------------------------------------------------1----------------------------------------------------------------
第二篇数学物理方程22【答案uau−==0,(akcut/ρ);(0,)=0,ult(,)=0;(,0)ux=Txlx/,∈(0,)l】txxx09.9试推导均匀弦的微小横振动方程.2【答案具有类型:uauf−=,详细自行讨论】ttxx9.10试推导出一维和三维热传导方程.22【答案具有类型:uaufuauuu−=−++=;()f,详细自行讨论】txxtxxyyzz9.11试推导静电场的电势方程.【答案具有类型:uuf+=,详细自行讨论】xxyy9.12推导水槽中的重力波方程.水槽长为l,截面为矩形,两端由刚性平面封闭.槽中的水在平衡时深度为h.【提示:取x沿槽的长度方向,取u为水的质点的x方向位移】【答案取x沿槽的长度方向,u为水的质点的x方向位移,则ug=hu】ttxx9.11.有一长为l的均匀细弦,一端固定,另一端为弹性支撑,设弦上各点受有垂直于平衡位置1的外力,外力线密度已知,开始时.弦处受到冲量I作用,试写出其定解问题.222⎧∂∂uu2⎪=+af()x,0tx∈>(),l,t022∂∂tx⎪⎪∂ult(),⎪ut()0.=+=hult(),0t≥0答⎨∂x⎪ux(),0=0⎪⎪Il⎛⎞⎪uxt(),0=−δ⎜⎟xx∈[]0,l⎩ρ⎝⎠29.14由一长为l的均匀细杆,侧面与外界无热交换,杆内有强度随时间连续变化的热源,设在同一截面上具有同一热源强度及初始温度,且杆的一端保持零度,另一端绝热,试推导定解问题.2⎧∂∂uu2⎪=+af()x,,tx∈>()0,,0lt2∂t∂x⎪⎪∂ult(),(答⎨ut()0,==≥0,t0)⎪∂x⎪ux()(),0=∈ϕx,x[]0,l⎪⎩9.15设有高为h半径为R的圆柱体,圆柱体内有稳恒热源,且上下底面温度已知,圆柱侧面绝热,写出描述稳恒热场分布的定解问题.222⎧∂∂∂∂uuuu11⎪+++=f()rzrR,,θθ∈[0,,)∈[0,2,π)()zh∈0,2222∂∂∂∂rrrrθz⎪⎪答⎨uA==,uBzz==0h⎪∂u⎪=0rR=⎪⎩∂r--------------------------------------------------------------------2----------------------------------------------------------------
第二篇数学物理方程9.16设有定解问题222⎧∂∂∂uuu⎪=+,0<<<<>xayb,0;0t222∂∂∂txy⎪⎪uu==0,xx==0a⎪⎨uu==≥0,t0⎪yy==0b⎪⎪uxt=0=ϕ(),,y⎪⎩uxtt=0=<ψ(),,0yx),()】aaa11.3求解细圆锥形均质杆的纵振动.【提示作变换ux=v/】f()()xatfxat−++12【答案u=】x11.4半无限长杆的端点受到纵向力Ft()=Asinωt作用,求解杆的纵振动.tuxϕ()()1xat++−ϕatxxat+>=a,(+a∫ψξξ)d220【答案】1atx−aAxaA++∫ψξξ()dcos(ωt−)−2aY0SωaYSωC11.5已知初始电压分布为Acoskx,初始电流分布为Akcosx,求解无线长理想传输L线上电压和电流的传播情况,【答案v=Akcos(xa−=tiCL),/Akcos(xa−t)】11.6在GL=CR条件下求无限长传输线上的电报方程的通解.R−t11xat+【答案exL{[(ϕ++−+at)(ϕψxat)]∫()dξξ】22axat−11.7已知端点通过电阻R而相接,初始电压分布为Acoskx,初始电流分布为CLAkx/cos.求解半无限长理想传输线上电报方程的解;在什么条件下端点没有反射(遮住情况叫作匹配)?LL【答案匹配的条件是R=,因此叫作特征阻抗】0CC本章计算机仿真11.8试用计算机仿真的方法,将11.2的弦振动规律以图形的分式表示出来.【解】计算机仿真程序w=pi;a=2;A=1.2;x=0:0.01:10;fort=1:0.5:25u=A*sin(pi*(t-x/a));plot(x,u);title("弦振动")xlabel("x")ylabel("u")--------------------------------------------------------------------6----------------------------------------------------------------
第二篇数学物理方程pause(0.0000001);end;11.9试用计算机仿真的方法,将11.5中的电压分布和电流分布用图形表示出来.【解】计算机仿真程序w=pi;a=2;A=1.2;k=2*pi;C=0.006;L=0.003;x=0:0.001:10;fort=1:0.5:25subplot(2,1,1);v=A*cos(k*(t-x/a));plot(x,v);title("电压动态分布")xlabel("x")ylabel("v")pause(0.0000001);--------------------------------------------------------------------7----------------------------------------------------------------
第二篇数学物理方程subplot(2,1,2);i=sqrt(C/L)*A*cos(k*(t-x/a));plot(x,i);title("电流动态分布")xlabel("x")ylabel("i")pause(0.0000001);end;第12章习题解答12.1求解下列本征值问题的本征值和本征函数(1)Xx′′()+===λXx()0;(0)x0,()xl′0(2)Xx′′()+===λXx()0;(0)x′0,()xl′01(3)()Xx′′+===λXx()0;()0xa,()0xb--------------------------------------------------------------------8----------------------------------------------------------------
第二篇数学物理方程21nn++221(1)λ==(π),nX0,1,2,L;()xx=sinπnn22llnn2【答案(2)λ==(π),nX0,1,2,L;()xx=cosπ】nnllnn2π(3)λ===−(π),nX1,2,;()sinLx(xa)nnba−ba−12.2长为l的杆,一端固定;另一端受力F而伸长,求解放手杆的振动.011∞()na++πtnx()π8Fl0n122【答案∑(1)−cossin】22YSπn=0(2n+1)ll12.3长为l的的弦,两端固定,弦中张力为T.在距一端为x的一点以力F把弦拉开,然00后突然撤除此力,求弦的振动.【答案初始位移=FlxxlT()−0(1)∂∂tx⎪⎪⎨utult(0,)==>x(,)0t0(2)⎪ux(,0)=ϕ(),x(3)⎪⎪⎩uxt(,0)=∈ψ(),xx(0,)(4)l--------------------------------------------------------------------9----------------------------------------------------------------
第二篇数学物理方程解:用分离变量法解,令uxtTtXx(,)=()()(5)并将(5)代入(1),(2),得固有值问题⎧Xx""()+=λXx()0(6)⎨⎩XX(0)=="()l0(7)2及TtaTt&&()+λ()(8)21n+2解(6)—(7)得λπ()xn==(),0,1,2,Ln2l21n+Xx()==sinπxn,0,1,2,Ln2l将λ代入(8)解得n21nn+21+TC=+cosππatDsinatn,(=0,1,2,L)nnn22ll∴uxtTtXx(,)==()()(n0,1,2,L)nnn叠加得∞⎛⎞21nn++2121n+uxt(,)=+∑⎜⎟CnncosππatDsinatsinπx(9)n=0⎝⎠22ll2l令(9)满足(3),(4)得∞21n+ux(,0)==ϕπ()x∑Cnsinx(10)n=02l∞21nn++21uxtn(,0)==ψπ()x∑Dasinπx(11)n=022ll21n+由Fourier展式的唯一性知,C与Daπ分别为ϕ()x与ψ()x关于nn2l∞⎧⎫21n+⎨⎬sinπx的展开式系数.⎩⎭2ln=0l22n+1∴Cxx=ϕπ()sind(12)xn∫ll20--------------------------------------------------------------------10----------------------------------------------------------------
第二篇数学物理方程l22ln2+1Dx=⋅ψπ()sinxdxn∫(2na+1)πl2l0l42n+1==∫ψπ()sinxxd(xn0,1,2,L)(13)(2na+1)π2l0所以,带有系数(12)~(13)的(9)即为定解问题(1)~(4)的形式解。12.8解定解问题22⎧∂∂∂uuu11⎪++=0,0l,t022∂∂tx⎪⎪⎨ut(0,)=0⎪ult(,)=≥sinωtt0⎪⎪⎩ux(,0)=≤00xl≤tx解:令uxtvxtwxt(,)(,)=+(,),其中wt=sinω.则vxt(,)满足定解问题l--------------------------------------------------------------------18----------------------------------------------------------------
第二篇数学物理方程222⎧∂∂vv2ωx⎪=atx+sinω0<<>l,t022∂∂txl⎪⎪vtvlt(0,)==(,)0t≥0⎨⎪vx(,0)=0⎪ω⎪vx(,0)=−x0≤≤xlt⎩l由7-9题知,vxt(,)=vxtvxt(,)+(,).其中vxtvxt(,)与(,)分别满足定解问题121222⎧∂∂vv112222⎪22=a⎧∂∂vv222ωx∂∂tx⎪22=at+sinω⎪∂∂txl⎪vtvl(0,)==(,)t0⎪⎪11⎨与⎨vtvl22(0,)==(,)t0⎪vx(,0)=01⎪vx(,0)==vx(,0)0⎪⎪22tω⎪vx(,0)=−x⎪⎩1t⎩l解之得∞n2ωππlnnvxt1(,)=−∑(1)2sinat⋅sinxn=1an()πll∞⎧⎫−n+12ωπlnsint+sinωωωωnntsintsintvxt2(,)=−∑(1)2⎨⎬−sinxn=1an()πω⎩⎭+ωnnω−ωlanπ其中ω==(n1,2,L)nl所以,原问题的解xuxtvxtvxt(,)=++(,)(,)sinωt12l12.14解定解问题2⎧∂∂uu2⎪=+02∂∂tx⎪⎪uA=⎨x=0⎪uB=≥t0,,AB为常数⎪xl=⎪ux=≤ϕ()0x≤l⎩t=0解:注意泛定方程非齐次项与t无关。故可设uxtvxtwx(,)(,)=+(),且取wx()满足--------------------------------------------------------------------19----------------------------------------------------------------
第二篇数学物理方程⎧wA(0)=(1)⎨⎩wl()=B(2)BA−可取wx()=−Ax(3)l于是vxt(,)满足齐次边界问题2⎧va=+vxtxx⎪⎨vtvlt(0,)==(,)0⎪vx(,0)=−=ϕϕ()xwx()()x⎩1令l2nπfxx=sind(4)xn∫ll0l2nπϕϕ=−[()xwx()]sinxxd(n=1,2,L)(5)n∫ll0则由固有函数法可得222222∞⎛⎞−−anππtttan()−τnπ22vxt(,)=+∑⎜⎟ϕτellfe∫dsinx(6)1nn⎜⎟ln=1⎝⎠0其中ϕ,f由(4),(5)给出。1nn12.15解定解问题2⎧∂∂uu2αx⎪=+abe002∂∂tx⎪⎪⎨uu==0t≥0xx==0l⎪⎪uxt=0=≤ϕ()0x≤l⎪⎩解:注意泛定方程非齐次项与t无关。故可设uxtvxtwx(,)(,)=+()。令wx()满足条件2−αx⎧awxbe""()+=0(4)⎨⎩ww(0)=()l(5)解得--------------------------------------------------------------------20----------------------------------------------------------------
第二篇数学物理方程⎧b−αxwx()=−+eAxB+⎪22aα⎪⎨w(0)=0⎪wl()0=⎪⎩bb−αx得AeB=−(1−),=2222laαaαbb−−ααxlb可取wx()=−e−(e−1)x+222222alαaααa则vxt(,)满足2⎧∂∂vv2⎪=a2∂∂tx⎪⎪⎨vv==0xx==0l⎪vx=−=ϕϕ()()wxx()⎪t=01⎪⎩解得222∞−anπ2tnπvxt(,)=∑Celsinx(7)nn=1l其中l2nπCx=−[()ϕw()]sinxxd(8)xn∫ll0原定解问题(1)~(3)的解为222∞−anπ2tnπuxt(,)=+∑Celsinxwx()(9)nn=1l其中wxt(,)由(6)给出,C由(8)给出。n12.16.解定解问题--------------------------------------------------------------------21----------------------------------------------------------------
第二篇数学物理方程2⎧ua=0ttxx⎪⎪utult(0,)==(,)0t≥0x⎨⎪ux(,0)0=⎪ux(,0)=≤v0xl≤⎩t0∞21nn++218lv0(答:uxt(,)==∑BnnsinatππsinxB,22)n=122llaπ(2n+1)12.17长为l的理想传输线,远端开路.先把传输线充电到电位差v,然后把近端短路。求0解线上电压v(,)xt.dvv|==0,|−(RLj+)|0,|==vv,xx==00lx==lt0dt[答案定解条件1v||=−j=0tt==00xtC4v∞1(2na++1)πtnx(21)π0解v(,)xt=n∑cossin】πn=021nll+2212.18在矩形区域0,0ttxxt⎪⎪⎨u=0,u=0,t≥0x=0xx=l⎪G⎪u=u,u=−u,0≤x≤l⎪⎩t=00tt=0C021LG+RCRG其中a=,b=,c=,R,L分别是每一回路单位长度的串联电阻与电感,LCLCLCC,G分别为单位长度的分路电容和电导(线间漏电).【解】由于这个问题也是线性齐次方程和齐次边界条件,所以也可用分离变量法,设u()()()x,t=XxTt,代入方程和边界条件可得""()"()()(2)Tt+bTt+cTt+aλTt=0(12.2.42)""⎧⎪X()x+λX()x=0⎨(12.2.43)()"()⎪⎩X0=Xl=0经讨论,本征值问题(12.2.43)的本征值与特征函数为2⎧⎛2n+1⎞⎪λn=⎜⎟,⎪⎝2l⎠⎨n=0,1,2,L⎪()2n+1Xx=sinπx⎪n⎩2l把λ的值代入方程(12.2.42),解得nb−tT()t=e2()Ccosωt+Dsinωtnnnnn222⎛2n+1⎞⎛b⎞2其中ωn=c+⎜πa⎟−⎜⎟,并已假定ωn>0.⎝2l⎠⎝2⎠这样我们得到解的形式为+∞b−t2n+1u()x,t=∑e2()Ccosωt+Dsinωtsinπx(12.2.44)nnnnn=02l代入初值条件,有+∞2n+1∑Cnsinπx=u0n=0l+∞⎛b⎞2n+1G∑⎜−Cn+ωnDn⎟sinπx=−u0n=0⎝2⎠2lC由Fourier级数理论,得2l2n+14u0C=usinπxdx=(12.2.45)n∫0l02l()2n+1πb2l⎛G⎞2n+14Gu0−Cn+ωnDn=∫⎜−⎟u0sinπxdx=−2l0⎝C⎠2lC()2n+1π--------------------------------------------------------------------23----------------------------------------------------------------
第二篇数学物理方程2u0⎛RG⎞解得Dn=⎜−⎟(12.2.46)()2n+1πωn⎝LC⎠把(12.2.45),(12.2.46)式代入(12.2.44)式,得解为b+∞2u−t1⎡CR−LG⎤2n+1u()x,t=0e2∑2cosωt+sinωtsinπx⎢nn⎥πn=02n+1⎣LCωn⎦2lb−t由于解的表达式中有衰减项e2,所以即使导线的电阻和线间漏电都很小,传输线上的电压仍将随时间的推移而指数地衰减到零.nπa12.22设弦的一端(x=0)固定,另一端(x=L)以sinωt(ω≠,n=1,2,L)作周期L振动,且初值为零.试研究弦的自由振动.解:依题意,得定解问题22⎧∂u2∂u⎪2=a2,()00(19)∂t∂x⎪⎪⎛nπa⎞⎨u(0,t)=0,u(L,t)=sinωt,⎜ω≠⎟(20)⎝L⎠⎪⎪⎪u(x,0)=0,u(x,0)=0⎩t由于边界条件是非齐次的,首先应把边界条件齐次化.令W=Ax+B,由边界条件(20)sinωt式,得:0=W(0,t)=B,sinωt=W(L,t)=AL,,所以A=,B=0,从而LxW(x,t)=sinωt.Lx再令u(x,t)=V(x,t)+sinωt,则得:L2⎧2ωxV=aV+sinωt⎪ttxxL⎪⎨V(t,0)=0,V(t,L)=0⎪ωx⎪V(0,x)=0,V(0,x)=−t⎩L虽然我们已经知道这个定解问题的解法,但毕竟比较复杂.由于原定解问题中的非齐次边界条件比较特殊,如果我们一开始选取W(x,t)时,就使这个函数既满足泛定方程(19),又满足边界条件(20),这样,令u=V+W后,得到的关于V(x,t)的泛定方程也是齐次的,而且显然比按照上述一般方法得到的非齐次方程的求解要简单.为此,令W(x,t)=X(x)sinωt,由边界条件(20)式,可知X(0)=0,X(L)=1.把2ωW(x,t)代入泛定方程(19),且消去sinω.t,得:X′′+X=02a--------------------------------------------------------------------24----------------------------------------------------------------
第二篇数学物理方程ωxωx所以X(x)=Ccos+Csin12aa1由X(0)=0,得C=0;再由X(L)=1,得:C=12ωLsinaωxsin1ωxa于是X(x)=sin,从而W(x,t)=sinωtωLaωLsinsinaa再令u=W(x,t)+V(x,t),代入原定解问题,就得到关于V的定解问题:22⎧∂V2∂V⎪2=a2∂t∂x⎪⎪⎪V(t,0)=V(t,L)=0⎨⎪ωxsin⎪a⎪V(0,x)=0,Vt(0,x)=−ωωL⎪sin⎩a即得:∞n+1(−1)nπatnπxV(t,x)=2ωaL∑sinsin22n=1(ωL)−(nπa)LL最后,把V(x,t)和W(x,t)加起来,就得到原定解问题的12.23求下例定解问题22⎧∂u2∂u⎪2=a2+A,(00)(10)∂t∂x⎪⎪⎨ux=0=0,ux=L=B(11)⎪∂u⎪u==0(12)t=0t=0⎪⎩∂t的形式解,其中A,B均为常数.【解】:这个定解问题的特点是:方程及边界条件都是非齐次的.根据上述原则,首先应将边界条件化成齐次的.由于方程(10)的自由项及边界条件都与t无关,所以我们有可能通过一次代换将方程与边界条件都变成齐次的.具体做法如下:令u(x,t)=V(x,t)+W(x),代入方程(10),得:22∂V2⎡∂V⎤2=a⎢2+W′′(x)⎥+A∂t⎣∂x⎦为了使这个方程及边界条件同时化成齐次的,选W(x)满足2⎧⎪aW′′(x)+A=0⎨(13)⎪⎩Wx=0=0,Wx=L=B--------------------------------------------------------------------25----------------------------------------------------------------
第二篇数学物理方程(13)式是一个二阶常系数线性非齐次方程的边值问题,它的解可以通过两次积分求得A2⎛ALB⎞W(x)=−x+⎜+⎟x222a⎝2aL⎠求出函数W(x)之后,再由(12)式可知函数V(x,t)为下列定解问题22⎧∂V2∂V⎪2=a2,(00)(14)∂t∂x⎪⎪⎨Vx=0=Vx=L=0(15)⎪∂V⎪V=−W(x),=0(16)t=0t=0⎪⎩∂t的解.采用分离变量法,可得(14)式满足齐次边界条件(15)式的解为:∞⎛nπanπa⎞nπV(x,t)=∑⎜Cncost+Dnsint⎟sinx(17)n=1⎝LL⎠L利用(16)式中第二个条件可得:D=0.n于是定解问题式(14)、(15)、(16)的解可表示为:∞nπanπV(x,t)=∑Cncostsinxn=1LL代入(16)式中第一个条件得:∞nπ−W(x)=∑Cnsinxn=1L∞A2⎛ALB⎞nπ即2x−⎜2+⎟x=∑Cnsinx2a⎝2aL⎠n=1L由傅氏级数的系数公式可得:2.L⎡A2⎛ALB⎞⎤nπCn=∫.0⎢2x−⎜2+⎟x⎥sinxdxL⎣2a⎝2aL⎠⎦LA.LL2nπ⎛A2B⎞.nπ=xsinxdx−⎜+⎟xsinxdxa2L∫∫.0L⎝a2L2⎠.0L222AL2⎛AL⎞=−+⎜+B⎟cosnπ233⎜222⎟anπnπ⎝anπ⎠(18)因此,原定解问题的解为:∞A2⎛ALB⎞nπanπu(x,t)=−2x+⎜2+⎟x+∑Cncostsinx2a⎝2aL⎠n=1LL其中C由(18)式确定.n12.24一个半径为ρ的薄圆盘,上下两面绝热,圆周边缘温度分布为已知,求达到稳恒状0--------------------------------------------------------------------26----------------------------------------------------------------
第二篇数学物理方程态时圆盘内的温度分布.在第一章讲过,热传导问题达到稳恒状态时温度分布与时间无关,应满足拉普拉斯方2程∇u=0.因为边界形状是个圆周,它在极坐标下的方程为ρ=ρ,所以在极坐标系下0边界条件可表为u=f(θ),既然边界条件用极坐标系形式表示出来很简单,所以我们ρ=ρ0就在极坐标系下求解这个定解问题.为此,先将它表示成2(1)⎧21∂∂u1∂u⎪∇u=(ρ)+22=0,(ρ<ρ0)⎨ρ∂ρ∂ρρ∂θ⎪u(ρ,θ)=f(θ)(2)⎩0此外,因为自变量ρ,θ的取值范围分别是[0,ρ]与[0,2π],而圆盘内部的温度值绝不可能0是无限的,特别是圆盘中心点的温度值应该是有限的,并且(ρ,θ)与(ρ,θ+2π)实际上表示同一点,温度应该相同,即应该有u(0,θ)<+∞(3)u(ρ,θ)=u(ρ,θ+2π)(4)现在来求满足方程(1)及(2)、(3)、(4)的解.先令u(ρ,θ)=R(ρ)Φ(θ),代入方程(1)得:211ρR′′+ρR′Φ′′R′′Φ+R′Φ+RΦ′′=0,即=−2ρρRΦ令比值为常数λ,即得两个常微分方程Φ′′+λΦ=02ρR′′+ρR′−λR=0再由条件(3)及(4)可得R(0)<+∞Φ(θ+2π)=φ(θ)(5)这样一来,我们得到了两个常微分方程的定解问题:⎧Φ′′+λΦ=0⎨(6)⎩Φ()(θ+2π=Φθ)2⎧⎪ρR′′+ρR′−λR=0与⎨(7)⎪⎩R(0)<+∞先解哪一个呢?要看哪一个可以定出本征值.由于条件(5)满足可加性(即所有满足(5)的函数叠加起来仍旧满足(5)),所以只能先解问题(6).采用与§2.1中同样的方法可以得到:当时λ<0,问题(6)无非零解;当λ=0时,它的解为:Φ(θ)=a′(常数);002当λ﹥0时,取λ=β,这时(6)的解为:Φ(θ)=a′cosβθ+b′sinβθβββ且为使Φ(θ)以2π为周期,β必须是整数n,取n=1,2,3,L(只取正整数的理由与§2.1相同),则可将上面得到的解表示成:Φ(θ)=a′cosnθ+b′sinnθnnn--------------------------------------------------------------------27----------------------------------------------------------------
第二篇数学物理方程22至此,我们已经定出了本征值问题(6)的本征值β=n,本征函数Φ(θ).然后是解问nn题(7).其中的方程是欧拉(Euler)方程,它的通解为:R=c+dlnρ,当λ=0;(n=0)000n−n2R=cρ+dρ,当λ=n(n=1,2,3,⋯)nnnn为了保证R(0)<+∞|,只有d=0(n=0,1,2,⋯),即R=cρ(n=0,1,2,L).nnn因此利用叠加原理,方程(1)满足条件(3)、(4)的解可以表示为级数∞a0nu(ρ,θ)=+∑ρ()ancosnθ+bnsinnθ(8)2n=1a0此式中的就是a′c;a,b分别是a′c与b′c.最后为了确定系数ab,我们利用00nnnnnnnn2边界条件(2)得:∞a0∑n()f(θ)=+ρccosnθ+bsinnθ(9)0nn2n=1nn因此,a,ρa,ρb就是f()θ展开为傅氏级数时的系数,即有00n0n⎧1.2π⎪a0=∫f(θ)dθ⎪π.0⎪1.2π⎨an=n∫f(θ)cosnθdθ(10)ρπ.0⎪0⎪1.2π⎪b=f()θsinnθdθnρnπ∫.0⎩0将这些系数代入(8)式即得所求的解.为了以后应用方便,还可以将解(8)写成另一种形式.为此,将(10)式所确定的系数代入(8)式经过简化后n1.2π⎡1∞⎛ρ⎞⎤u()ρ,θ=∫.0f(t)⎢+∑⎜⎜⎟⎟cos()θ−t⎥dt(11)π⎢⎣2n=1⎝ρ0⎠⎥⎦∞21n11−k*)利用下面已知的恒等式+∑kcosn()θ−t=()2,()k<1可将2n=121−2kcosθ−t+k(11)中的解u()ρ,θ表达为:221.2πρ−ρ()0uρ,θ=f(t)dt(12)2π∫.0ρ2+ρ2−2ρρcos()θ−t00公式(12)称为圆域内的泊松公式.它的作用在于把解写成了积分形式,这样便于作理论上的研究.注:*)这个恒等式的证明:∞∞1∑∑n()11n[in()θ−t−in()θ−t]+kcosnθ−t=+ke+e2nn=112=2--------------------------------------------------------------------28----------------------------------------------------------------
第二篇数学物理方程∞∞11∑[]i()θ−tn1∑[−i()θ−t]n=+ke+ke22n=12n=1i()θ−t−i(θ−t)11ke1ke=++(因|k|<1)i()θ−t−i()θ−t221−ke21−ke1kcos(θ−t)+iksin(θ−t)=[1++21−kcos(θ−t)−iksin(θ−t)kcos(θ−t)−iksin(θ−t)+]1−kcos(θ−t)+iksin(θ−t)21⎡2kcos(θ−t)−2k⎤=⎢1+2⎥2⎣1−2kcos(θ−t)+k⎦211−k=221−2kcos(θ−t)+k计算机仿真编程实践12.25试计算机仿真求解例12.9.1,并用计算机仿真方法将结果以图形表示出来.【解】计算机仿真程序%下面给出计算机仿真编程实践中的12.25其余习题类似进行分析和仿真g="squareg";%定义单位方形区域b="squareb3";%左右零边界条件,顶底零导数边界条件c=1;a=0;f=0;d=1;l=10;A=2;[p,e,t]=initmesh("squareg");x=p(1,:)";%注意坐标向量都是列向量y=p(2,:)";u0=A*sin(5*pi/l*x);ut0=0;n=31;tlist=linspace(0,5,n);%在0~5之间产生n个均匀的时间点u1=hyperbolic(u0,ut0,tlist,b,p,e,t,c,a,f,d);delta=-1:0.1:1;[uxy,tn,a2,a3]=tri2grid(p,t,u1(:,1),delta,delta);gp=[tn;a2;a3];newplot;%建立新的坐标系newplot;M=moviein(n);umax=max(max(u1));umin=min(min(u1));--------------------------------------------------------------------29----------------------------------------------------------------
第二篇数学物理方程fori=1:n,...%注意"⋯"符号不可省略ifrem(i,10)==0,...%当n是10的整数倍时,在命令窗口打印出相应的数字fprintf("%d",i);...end,...pdeplot(p,e,t,"xydata",u1(:,i),"zdata",u1(:,i),"zstyle","continuous","mesh","on","xygrid","on","gridparam",gp,"colorbar","off");...axis([-1,1,-1,1uminumax]);caxis([uminumax]);...M(:,i)=getframe;...ifi==n,...fprintf("donen");...end,...endnfps=2;movie(M,10,nfps);12.26试计算机仿真求解习题12.6,并用计算机仿真方法将结果以图形表示出来.【解】计算机仿真程序--------------------------------------------------------------------30----------------------------------------------------------------
第二篇数学物理方程g="squareg";%定义单位方形区域b="squareb3";%左右零边界条件,顶底零导数边界条件c=1;a=0;f=0;d=1;l=10;h=2;[p,e,t]=initmesh("squareg");x=p(1,:)";%注意坐标向量都是列向量y=p(2,:)";u0=4.*h./l^2.*x.*(l-x);ut0=0;n=31;tlist=linspace(0,5,n);%在0~5之间产生n个均匀的时间点u1=hyperbolic(u0,ut0,tlist,b,p,e,t,c,a,f,d);delta=-1:0.1:1;[uxy,tn,a2,a3]=tri2grid(p,t,u1(:,1),delta,delta);gp=[tn;a2;a3];newplot;%建立新的坐标系newplot;M=moviein(n);umax=max(max(u1));umin=min(min(u1));fori=1:n,...%注意"⋯"符号不可省略ifrem(i,10)==0,...%当n是10的整数倍时,在命令窗口打印出相应的数字fprintf("%d",i);...end,...pdeplot(p,e,t,"xydata",u1(:,i),"zdata",u1(:,i),"zstyle","continuous","mesh","on","xygrid","on","gridparam",gp,"colorbar","off");...axis([-1,1,-1,1uminumax]);caxis([uminumax]);...M(:,i)=getframe;...ifi==n,...fprintf("donen");...end,...endnfps=2;movie(M,10,nfps);%读者也可以直接利用本题的答案,编出仿真图形结果∞32hn(2+1)πat(2n+1)πx【答案uxt(,)=∑cossin】33n=0(2nl+1)πl12.27试计算机仿真求解习题12.17,并用计算机仿真方法将结果以图形表示出来.--------------------------------------------------------------------31----------------------------------------------------------------
第二篇数学物理方程【解】计算机仿真程序g="squareg";%定义单位方形区域b="squareb3";%左右零边界条件,顶底零导数边界条件c=1;a=0;f=0;d=1;l=10;v0=12;[p,e,t]=initmesh("squareg");x=p(1,:)";%注意坐标向量都是列向量y=p(2,:)";u0=v0;ut0=0;n=31;tlist=linspace(0,5,n);%在0~5之间产生n个均匀的时间点u1=hyperbolic(u0,ut0,tlist,b,p,e,t,c,a,f,d);delta=-1:0.1:1;[uxy,tn,a2,a3]=tri2grid(p,t,u1(:,1),delta,delta);gp=[tn;a2;a3];newplot;%建立新的坐标系newplot;M=moviein(n);umax=max(max(u1));umin=min(min(u1));fori=1:n,...%注意"⋯"符号不可省略ifrem(i,10)==0,...%当n是10的整数倍时,在命令窗口打印出相应的数字fprintf("%d",i);...end,...pdeplot(p,e,t,"xydata",u1(:,i),"zdata",u1(:,i),"zstyle","continuous","mesh","on","xygrid","on","gridparam",gp,"colorbar","off");...axis([-1,1,-1,1uminumax]);caxis([uminumax]);...M(:,i)=getframe;...ifi==n,...fprintf("donen");...end,...endnfps=2;movie(M,10,nfps);--------------------------------------------------------------------32----------------------------------------------------------------
第二篇数学物理方程12.28试计算机仿真求解习题12.18,并用计算机仿真方法将结果以图形表示出来.【解】计算机仿真程序a=1.4;b=2;A=1.8;B=0.6;[X,Y]=meshgrid(0:0.1:10);v0=0;forn=0:500;v=sinh((2.*n+1).*pi.*(a-X)./b).*1./((2.*n+1)^3.*sinh((2.*n+1).*pi.*a./b)).*sin((2.*n+1).*pi.*Y./b);v0=v0+v;end;u=B.*sinh(pi.*(b-Y)./a)./sinh(pi.*b./a).*sin(pi.*X/a)+8.*A.*b^2./pi^3.*v0;meshz(X,Y,u);title("u的分布");xlabel("x");ylabel("y");--------------------------------------------------------------------33----------------------------------------------------------------
第二篇数学物理方程zlabel("u")______________________________________________________________________________第13章幂级数解法――本征值问题习题及解答__________________________________________________________13.1将下列二阶线性常微分方程化成施-刘型方程的形式(1)超几何级数微分方程(高斯方程)xx(1−+++−+=)[y′′(1αβγα)]xy′βy0(2)汇合超几何级数微分方程xy′′+−−=()γxy′αy0ddγ11++−αβγyγ−αβγ+−(1)[(1xx−)]+−=αβxx(1)y0dxdx【答案】ddγγ−−xxy1−(2)[xe]−=αxey0dxdx--------------------------------------------------------------------34----------------------------------------------------------------
第二篇数学物理方程13.2求解下列本征值问题,并证明各题中不同的本征函数相互正交,并求出模的平方.⎧⎧Xx′′()+=λλXx()0Xx′′()+=Xx()0(1)⎨⎨;(2)⎩⎩Xa()0()==XbXa()0=,()XlhXl+′()0=nπ2【答案(1)本征函数Xx()=−sin(xan),(=1,2,L);模Nba=−()/2nnba-xxn(21)本征函数X()xnx==sin,(1,2,L);为方程xc−ηtgx=0的根,η=lh/.模nnl2l1Nx=+[1sin2]】nn22xn计算机仿真实践13.3利用计算机仿真验证习题13.2的本征函数的正交性,并求出其模.【解】计算机仿真程序%主要讨论和验证(1),对于(2)方法是类似的%验证正交性质symsnkxa=0;b=12;forn=1:100fork=1:100ifn~=ky=sin(n*pi/(b-a)*(x-a))*sin(k*pi/(b-a)*(x-a));w=int(y,x,-12,12)end;end;end;%求模symsnkxa=0;b=12;forn=1:100y=sin(n.*pi.*(x-a)./(b-a));m0=sqrt(int(y.^2,x,-12,12))end;――――――――――――――――――――――――――――――――――――――第14章格林函数法习题及解答————————————————————————14.1在圆ρ=R内求解拉普拉斯方程的第一边值问题--------------------------------------------------------------------35----------------------------------------------------------------
第二篇数学物理方程∆=+=uuu0(ρ0内求解拉普拉斯方程的第一边值问题∆=+=uuu0,(y>0),|u=fx()20xxyyy=y+∞fx()0【答案uxy(,)=dx】∫220π−∞()xx−+y014.3在圆形域ρ≤a上,分别求解方程∆=u0使满足边界条件uA|c=osϕ.2ρ=aA【答案u(,)ρϕρϕ=cos】a14.4在圆形域ρ≤a上,分别求解方程∆=u0使满足边界条件2uA|s=+Binϕρ=aB【答案uA(,)ρϕρ=+sinϕ】a计算机仿真编程实践14.5在圆ρ=a内,利用计算机仿真的方法求解拉普拉斯方程的第一边值问题∆=+=uuu0,(ρ0内,利用计算机仿真的方法求解拉普拉斯方程的第一边值问题∆=+=uuu0,(y>0),|u=10.20xxyyy=用图形把结果表示出来.y+∞10【答案uxy(,)=dx】∫220π−∞()xx−+y0【解】计算机仿真程序clf,x=-4:0.5:4;y=x;symsx0;Z=int(10*y./(pi*((x-x0).^2+y.^2)),x0,-inf,+inf)第15章综合习题--------------------------------------------------------------------36----------------------------------------------------------------
第二篇数学物理方程用傅氏变换法求解下列15.1;15.2;15.3题;用拉氏变换法求解下列15.4;15.5;15.6题15.1二维波动,初始速度为零,初始位移在圆ρ=1以内为1,在圆外为零,试求u|.ρ=0⎧1,(ta<1/)⎪【答案u|=⎨at】ρ=01−>,(ta1/)⎪22⎩at−115.2半无界杆,杆端x=0有谐变热流Bsinωt进入,求长时间以后的杆上温度分布uxt(,).aB−xaω/(22)ωπ[答案etsin(ω−−x)]2kω24a−λx15.3研究半无限长细杆导热问题.杆端x=0温度保持为零.初始温度分布为Be(1−)22Bat22λλ−x22atxλλ−+λxatxx【答案e[()()eerfc−−eerfc]()Berf222atat2at215.4求解一维无界空间中的扩散问题即uau−==0,|uϕ()xtxxt=02()x−ξ+∞1−2【答案uxt(,)=∫ϕ()[ξξe4at]d】−∞2atπ215.5求解一维无界空间的有源输运问题uaufxtu−==(,),|0txxt=02()x−ξ+∞t1−24()at−τ【答案uxt(,)=∫∫d[ξef(,)]dξττ】−∞τ2()at−τπ215.6求解无界弦的受迫振动ua−=ufx(,),|tu=ϕψ(),xu|=()xttxxt==00tt11xat++1txat()−τ【答案[(ϕxat++−+)(ϕψxat)]∫∫()dξξ+dτ∫f(,)dξτξ】22aaxat−−20(xat−τ)计算机仿真编程实践15.7利用计算机仿真方法(Matlab中的傅里叶变换法)对习题15.1进行求解.【解】计算机仿真图形显示%Assumea=2%仿真求解由读者思考,下面仅仅给出仿真显示a=12.0t=0.1:0.01:2ift>1.0/au=1-a*t./sqrt((a*t).^2-1);endplot(t,u)图形:--------------------------------------------------------------------37----------------------------------------------------------------
第二篇数学物理方程15.8利用计算机仿真(Matlab等):拉普拉氏变换法对习题15.6进行求解.【解】计算机仿真程序%任意假设f(x,t)=A=2.56;fai(x)=x;pusi(x)=B=6.7%仿真求解由读者思考,下面仅仅给出仿真显示%可以推出此情况下的解为u(x,t)=x+B*t+A/2*t^2,仿真显示为A=2.56;B=6.7;[x,t]=meshgrid([0:0.1:12]);u=x+B*t+A/2*t.^2;mesh(u)--------------------------------------------------------------------38----------------------------------------------------------------
第二篇数学物理方程第16章综合习题16.1求解一半径维a的无限长导体圆柱壳内的电场分布。设柱面上的电势为⎧u,(0<ϕ<π)1u=⎨.⎩ux,(π<<2)π2uuuu1212+−−12ay【答案u(,)ρϕ=+tan】2222πaxy−−16.2试求垂直于z平面,并与z平面交于圆||1z=及|1z−|5=/2的两个圆柱之间的静电场。设两柱面之间的电势差为1.z+114【答案u=ln||】ln2z+4计算机仿真实践16.3计算机仿真方法求解例16.2.1【解】计算机仿真程序u0=50;a=100.0;[X,Y]=meshgrid([-2.5:0.1:2.5]);u=u0/pi*atan(2*a*Y./(X.^2+Y.^2-a^2));mesh(u)--------------------------------------------------------------------39----------------------------------------------------------------
第二篇数学物理方程16.4计算机仿真方法求解例16.2.3【解】计算机仿真程序v1=5;v2=13;a=56.0;[X,Y]=meshgrid([0:0.1:5]);u=(v1+v2)/2+(v1-v2)/pi*atan(2*a*X.*sin(X)./(X.^2-Y.^2));mesh(u)16.5计算机仿真求方法解习题16.1【解】计算机仿真程序v1=8;v2=6;a=26.0;--------------------------------------------------------------------40----------------------------------------------------------------
第二篇数学物理方程[X,Y]=meshgrid([0:0.1:12]);u=(v1+v2)/2+(v1-v2)/pi*atan(2*a*Y./(a^2-X.^2-Y.^2));mesh(u)16.6计算机仿真方法求解习题16.2【解】参考计算机仿真程序[X,Y]=meshgrid([1:0.2:3]);u=1.0/(2.0*log(2))*log(((X+1/4.0).^2+Y.^2)/((X+4.0).^2+Y.^2));mesh(u);第17章综合习题17.1在什么样的曲线上,以下泛函取得极值2⎪⎧J[()]yx=−(y′22)dxyx⎨∫1⎪⎩yy(1)==0,(2)−1x2【答案yx()=−(1x)】617.2求下列泛函满足边界条件的极值曲线3⎧J[()]yx=−∫(3xyyx)d⎪1⎨9⎪yy(1)==1,(3)⎩2【答案解出:yx=3/2,但不满足边界条件,故所求变分问题无解】17.3求下列泛函的极值曲线:--------------------------------------------------------------------41----------------------------------------------------------------
第二篇数学物理方程2π22(1)[()]Jyx=−∫(y′yxy)d;(0)=1,(2yπ)=1;0222(2)[()]Jyx=++∫(y′′2yyyxy)d;(1)1,(2)=0;=y0123(3)[()]Jyx==∫xyxy′d;(0)1,(1)=4.y0sinh(2−x)3322【答案:(1)cosxCx+=sin;(2);(3)y(x+1),yy==(3x−1)】sinh117.4求连接一平面上两定点间的曲线段中最短的曲线.【答案ycxc=+即为直线】12计算机仿真实践17.5计算机仿真求解例17.2.1,并把结果用图形表示出来.【解】计算机仿真程序%取值c1,c2如下,严格的值应该根据初始条件得出c1=1.2;c2=15.78;t=0:2*pi/99:pi;x=c1/2.0*(t-sin(t))+c2;y=c1/2.0*(1-cos(t))plot(x,-y)17.6计算机仿真求解例17.2.2,并把结果用图形表示出来.【解】计算机仿真程序%由例题17.2.2容易得到极值函数为forn=1:5x=0:0.1:10yn=sqrt(2)*sin(n.*pi*x)plot(x,yn)end--------------------------------------------------------------------42----------------------------------------------------------------
第二篇数学物理方程%由例题17.2.2容易得到所求泛函的极值为(n*pi)^217.7计算机仿真求解例17.3.1,并把结果用图形表示出来.【解】计算机仿真程序x=0:0.1:10y=x.*(1-x.^2)/6plot(x,y)17.8计算机仿真求解习题17.1,并把结果用图形表示出来.【解】计算机仿真程序和图形--------------------------------------------------------------------43----------------------------------------------------------------
第二篇数学物理方程x=0:0.1:10y=x.*(1-x.^2)/6plot(x,y)17.9计算机仿真求解习题17.3,并把结果用图形表示出来.【解】计算机仿真程序%ex19.9(1)c=23.98;x=0:0.1:10y=cos(x)+c*sin(x);subplot(2,2,1),plot(x,y)%ex19.9(2)x=0:0.1:10y=sinh(2-x)/sinh(1)subplot(2,2,2),plot(x,y)%ex19.9(3)x=0:0.1:10y=(x+1).^(2/3)subplot(2,2,3),plot(x,y)--------------------------------------------------------------------44----------------------------------------------------------------
第二篇数学物理方程17.10计算机仿真验证习题17.4,并把结果用图形表示出来.【解】计算机仿真程序c1=19.78;c2=56.98;x=0:0.5:10y=c1*x+c2plot(x,y)第二篇数学物理方程综合测试题--------------------------------------------------------------------45----------------------------------------------------------------
第二篇数学物理方程一填空(20分)2⎧uau−=−0,(∞0)ttxx1.定解问题⎨的解为uxt(,)=_________________.⎩ux(,0)==0,(,0)1uxt⎧Xx′′()+=λXx()02.确定下列本征值问题⎨⎩XX(0)=0,′()l=0的本征值λ=,本征函数X()x=223.已知J[()]yx=−∫[()y′2xyx]d,则δJ=_____________________.1⎧uu−=1xxyy⎪4.定解问题⎨ux(,0)=x的解为uxy(,)=_____________________.⎪ux(,0)0=⎩y二.试用行波法求解右行波的初值问题(20分)⎧ua+=−u0,(∞<,0)tx⎨⎩ux(,0)=ϕ()x三.试求定解问题(20分)⎧22π2aπua=+usin(x)sin(t),(0,t0)⎪ttxxll⎪⎨ut(0,)==≥0,(,)ult0(t0)⎪uxt(,)==≤0,(,)uxt0(0xl≤)⎪t⎩π3π四.设沿x,,yz方向边长分别为abc,,的长方形,除上顶zc=的面上电势为sin(x)sin(y)外,所以ab其它几个面的电势均为零,求盒内各处的电位分布函数uxyz(,,).(20分)五.试用傅氏变换法求解定解问题2⎧uaub=++ucutxxx⎨⎩ux|=ϕ()t=0第二篇综合测试题答案22(2k+1)π(2k+1)π一1【答案】.uxt(,)=t;2【答案】.λ==,0k,1,2,L;Xx()==sinxk,0,1,2,L。24l2l22y3【答案】δδJ=−2(∫yxyx′′+)d;4【答案】.x−0212laπ2πata2π二【答案】.uxt(,)=−ϕ(xat);三【答案】.uxt(,)=−(sinttcos)sin2πaal2πll19sinh(+πz)ct()xb−+ξt2πxy2πab22e∞−24at四【答案】.uxyz(,,)sinsin=;五.uxt(,)=∫ϕ()ξξedab192aπt−∞sinh(+πc)22ab--------------------------------------------------------------------46----------------------------------------------------------------'
您可能关注的文档
- 习题答案《控制系统计算机辅助设计》薛定宇.pdf
- 习题答案《量子力学教程》周世勋PDF.pdf
- 习题解答(79年版《量子力学教程》周世勋教授编).pdf
- 书后练习题及答案.doc
- 案_Visual_Basic_程序设计基础_浙江科技出版社_陈庆章_主编.doc
- 书法鉴赏 新 -刘琳-课后习题.docx
- 书法鉴赏习题答案.pdf
- 书法鉴赏课后题答案.doc
- 事业单位公开招聘工作人员考试《综合基础知识》真题及答案.doc
- 二建《建筑工程》精品试题及标准答案(2009版)第1套.pdf
- 二建《建设工程施工管理》历年真题及答案解析.pdf
- 二建《建设工程法规及相关知识》精品试题及标准答案(2009版)第2套.pdf
- 二建法规习题讲义.doc
- 二建考试试题答案及解析.doc
- 二级人力资源1-6章课后习题答案.doc
- 二级劳动关系课后习题答案.pdf
- 二级建造师《市政公用工程》精品试题及标准答案(2009版-4).pdf
- 二级建造师《市政公用工程》精品试题及标准答案(2012版-3).pdf
相关文档
- 施工规范CECS140-2002给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程
- 施工规范CECS141-2002给水排水工程埋地钢管管道结构设计规程
- 施工规范CECS142-2002给水排水工程埋地铸铁管管道结构设计规程
- 施工规范CECS143-2002给水排水工程埋地预制混凝土圆形管管道结构设计规程
- 施工规范CECS145-2002给水排水工程埋地矩形管管道结构设计规程
- 施工规范CECS190-2005给水排水工程埋地玻璃纤维增强塑料夹砂管管道结构设计规程
- cecs 140:2002 给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程(含条文说明)
- cecs 141:2002 给水排水工程埋地钢管管道结构设计规程 条文说明
- cecs 140:2002 给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程 条文说明
- cecs 142:2002 给水排水工程埋地铸铁管管道结构设计规程 条文说明