任彦硕《自动控制原理》全部答案.pdf 97页

'习题解答第1章题1-1：试列举几个日常生活中见到的控制系统的例子，它们是开环控制还是闭环控制？它们如何工作？比如家里孵化小鸡，人们观察温度计，当温度高时，人们将温度调低；温度低时人们将温度调高。这是开环控制。又比如养鸡厂里面孵化小鸡，他们有孵化器，当外界温度高的，孵化器自动的进行调节，将温度降下来；当外界温度低的，孵化器自动的进行调节，将温度升起来。这是闭环控制。题1-2：自动控制系统通常由那些基本环节组成？各环节起什么作用？给定环节：给定输入量，通过此环节作用于系统。比较环节：完成将给定量与反馈量进行比较的功能。放大环节：将偏差信号放大以便驱动控制信号。执行机构：由它的动作使被控量得到控制，是控制系统的末端环节。被控对象：受系统控制的物理量，被控量常选为输出量。反馈环节：将检测到的被控量反馈传输到输入端与给定量进行比较以实现闭环控制。题1-3：如何理解自动控制技术已发展到了计算机控制时代经典控制理论仍然起着重要作用？经典控制理论是当今自动控制技术的基础，当今自动控制技术是由经典理论慢慢发展完善起来的，到当今的计算机控制时代，核心控制思想还是经典控制理论，而且实际应用中系统以单入单出多见。这使得经典理论有广泛的应用空间，经典理论仍起到重要的作用。题1-4：对自动控制系统有那些基本要求？为什么这样要求？本课程要完成的主要任务是什么？**（1）当给定电压u降低时，由于u并没有下降，故I不变。而u降低时nn2nI减小，故I≠0，此时电容C放电，u↓，u↓，电机转速n↓。测速发电13ctd*机发出的电压u下降，使得u与u相等，达到新的平衡。nnn（2）电网电压降低时，由于u不变，故使u↓，电机转速↓，发电机发出的ctd电压u↓，I↓，I≠0，电容C充电，u↑，使得u↑，达到新的平衡。n23ctd（3）如果将图中的测速发电机的极性反接，系统就不能正常工作。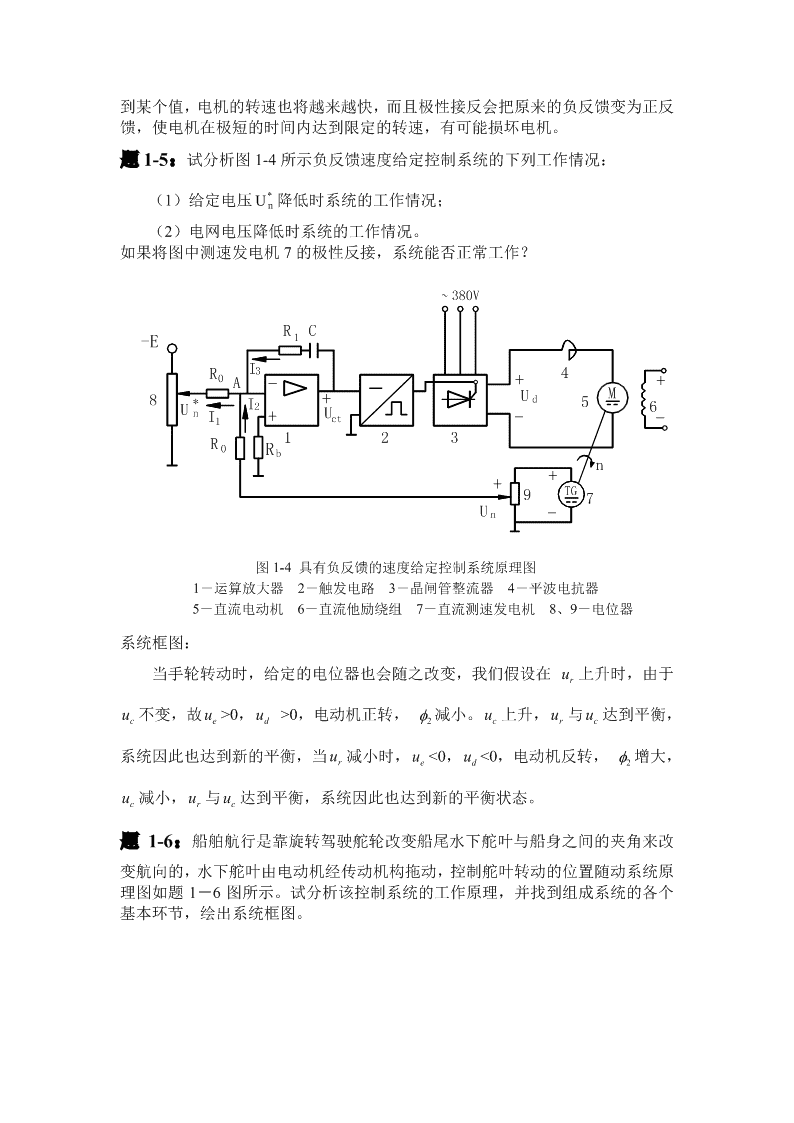因为那样电容C始终处于充电状态，u会一直上升达到电容的额定电压，u也会一直上升ctd 到某个值，电机的转速也将越来越快，而且极性接反会把原来的负反馈变为正反馈，使电机在极短的时间内达到限定的转速，有可能损坏电机。题1-5：试分析图1-4所示负反馈速度给定控制系统的下列工作情况：*（1）给定电压Un降低时系统的工作情况；（2）电网电压降低时系统的工作情况。如果将图中测速发电机7的极性反接，系统能否正常工作？380V~RC-E1RI340A-++8*+Ud5MI26UnI+Uct--1123R0Rbn++9TG7Un-图1-4具有负反馈的速度给定控制系统原理图1－运算放大器2－触发电路3－晶闸管整流器4－平波电抗器5－直流电动机6－直流他励绕组7－直流测速发电机8、9－电位器系统框图：当手轮转动时，给定的电位器也会随之改变，我们假设在u上升时，由于ru不变，故u>0，u>0，电动机正转，φ减小。u上升，u与u达到平衡，ced2crc系统因此也达到新的平衡，当u减小时，u<0，u<0，电动机反转，φ增大，red2u减小，u与u达到平衡，系统因此也达到新的平衡状态。crc题1-6：船舶航行是靠旋转驾驶舵轮改变船尾水下舵叶与船身之间的夹角来改变航向的，水下舵叶由电动机经传动机构拖动，控制舵叶转动的位置随动系统原理图如题1－6图所示。试分析该控制系统的工作原理，并找到组成系统的各个基本环节，绘出系统框图。 18φ713+2+ue+-+ud5EE-nuurc2--4+6-题1－6图船舶舵叶位置随动控制系统原理图1－手轮2－给定电位器3－检测电位器4－放大器5－伺服电动机6－他励绕组7－传动机构8－舵叶系统中，“开门”和“关门”两个开关是互锁的，即在任意时刻，只有开门（或关门）一个状态，这一状态对应的电压和与大门连接的滑动端对应的电压接成反极性（即形成偏差信号）送入放大器。放大器的输入电压送给伺服电机，伺服电机与卷筒同轴相连，大门的开启和关闭是通过伺服电机的正反转来控制的。与大门连接的滑动端对应的电压与“开门”滑动端对应的电压相等时，大门停止开启；与大门连接的滑动端对应的电压与“关门”滑动端对应电压相等时，大门停止关闭。设“开门”滑动端对应的电压为u，“关门”滑动端对应的电压为u，与大gkgg门连接的滑动端对应的电压为u。f开门时，将“开门”开关闭合，“关门”开关断开，此时u0，fggggf此偏差信号经过放大器放大后带动可逆直流伺服电机转动，并带动可调电位器滑动端上移，直至∆u=0时，伺服电机停止，大门开启。关门时，将“开门”开关断开，“关门”开关闭合，此时u>u，∆u=u-u<0，fgkgkf此偏差信号经过放大器放大后带动可逆直流伺服电机向相反方向转动，可调电位器滑动端下移，直至∆u=0时，伺服电机停止，大门关闭。从工作原理上分子，系统稳定运行（大门“全开”或“全关”）时，系统的输出量完全等于系统的输入量（大门“全开”时，u=u；大门“全关”时，u=u）。fgkfgg故该系统属于恒值、无差系统。题1-7：吊起式安装的油库大门控制系统如题1－7图所示。试叙述该系统的工作原理，并绘出系统框图。 K伺服放大器减速机构•电动机E题1－7图油库大门位置随动控制系统原理图当由于某种原因使得原动机的转速上升时，发电电动机的端电压U上升，从而R1使u下降（u为负），又u=-（u+u），所以u+u<0且u>0，这使得uff1rfrf12R0上升，励磁电流增大，发电机两端电压下降，从而达到新的平衡。当由于某种原因使得原动机的转速下降时，u上升，此时u+u>0，u<0，ufrf12下降，励磁电流减小，发电机两端电压上升，从而达到新的平衡。 习题解答第2章题2-1：题2-1图中a、b所示电路为RC无源网络，图c和图d为RC有源网络。试求以u(t)为输入量，u(t)为输出量的各电网络的传递函数。rc+++C+RC111R2R2u(rt)u(ct)u(rt)u(ct)R1C2C−−−2−a)b)C3R3C2R2R2C2R1R1−−u(rt)−u(ct)u(rt)−u(ct)++RbRbc)d)题2-1图电网络1R+2Us()sCRCCs+Cc22121(a)Ts()===Us()11(R++R)CCsC+CrRR+++12121212sCsC121R+22Us()sCRRCCs++()RCRCs+1c212121122(b)Ts()===()112()1UsRRCCs+RC++RCRCs+r//RR++121211221212sCsC12Us()Us()Us()RCs+1rcc22(c)=⇒=Ts()=R1Us()RCs1R+r122sC2(d)Usr()=Usc()Usc()R21⇒=Ts()=R1(/R/1)Usr()R12RC2s+12sC2题2-2：试用运算法建立题2-2图所示LC、RLC电网络的动态结构图，并求解自u(t)至u(t)信号传输的传递函数。io +L1L2++L+R1+++u(it)u(ct)C1C2u(ot)u(it)u(ct)CR2u(ot)−−−−−−−a)b)题2－2图a)LC网络b)RLC网络Us()=+sLI()sU()s⎫iL11c⎪UscL()=+sL22I()sUo()s⎪Us0()1(a)⎬⇒Ts()==42sU=−I()sI()sUs()LLCCs+(LC++LCLC)s+1cL12L⎪i1212112212sU=I()s⎪oL2⎭Us()=+RI()sU()s⎫iR11c⎪UscR()=+sLI2()sUo()s⎪Us0()R2(b)⎬⇒Ts()==2sCU=−I()sI()sUs()LCRs+(RRC++L)sR+RcR12R⎪i11212UR=I()s⎪oR22⎭题2-3：−0.2T热敏电阻随温度变化的特性为R=10000e，其中T为温度，R为阻aa值。试用小信号线性化方法提取温度分别为20C、60C时的线性化近似关系式。R=−10000ee−0.2TT002000−0.2(T−T)0aT=20时，RT=−36.6+9300aT=60时，RT=−0.0122+0.7930题2-4：题2-4图a为机器人手臂双质量块缓解运动冲击的物理模型；图b为由两级减震环节构成的运动系统，它可以是汽车减震系统的物理模型。试分别建立它们以F(t)为输入量，x(t)为输出量的传递函数模型。1F(t)x(t)x(2t)m1fx(1t)fk11F(t)Mmk2x(2t)k题2-4图弹簧－质量－阻尼器平移运动模型(a) 2⎧dx()td[x(t)−x(t)]112⎪Mk++f[(xt)−x(t)]=F(t)212⎪dtdt⎨222⎪d[x(t)−x(t)]dxt()dx()tdxt()12212kf+−[(xt)x(t)]=m或F(t)−M=m⎪⎩12222dtdtdtdt2⎧⎪MsX(s)+−ks[(Xs)X(s)]+f[(Xs)−X(s)]=F(s)11212⇒⎨222⎪⎩ks[(Xs)−+X(s)]f[(Xs)−X(s)]=msX(s)或F(s)−MsX(s)=msX12122122Xs()ms++ksf1⇒=22F()ss[Mms++(Mm)ks++(Mm)f](b)2⎧dx()td[x(t)−x(t)]112⎪mf++k[(xt)−x(t)]=F(t)21112⎪dtdt⎨2⎪dx[(t)−x(t)]dx(t)121f+−k[x(t)x(t)]=kxt()或F()t−m=kxt()⎪⎩111222222dtdt2⎧⎪msXs()+−fs[(Xs)X(s)]+k[(Xs)−X(s)]=F(s)1112112⇒⎨2⎪⎩fsX[(s)−+X(s)]k[(Xs)−X(s)]=kX(s)或F(s)−msX(s)=kX(s)1211222122Xs()fs++kk1112⇒=32Fs()mfs++m(kk)s+kfs+kk1122112题2-5：题2-5图所示系统中，他励直流电动机拖动经减速器减速的负载运转，作用其上的大小可变的直流电压由晶闸管整流装置提供。设电网电压u的幅值、2频率、初相均不变，整流装置输出的电压u(t)与形成触发移相脉冲的电压u(t)满di足ut()=2.34Ucos[Ku(t)]其中K为常数。试完成：d21i，1°(1)Ku(t)=35时整流装置非线性特性的线性化；1i(2)绘制系统动态结构图；(3)求出分别以u(it)、M(ct)为输入量，ω1(t)为输出量的传递函数。 u2LR+ia+M(t)r+mf11u(t)iu(t)dEaJ1ωf2M(t)c-1J--r22ω2+if-题2-5图电枢控制直流电动机拖动开环系统a(1)u(t)=−2.34U{0.820.57[Kut()−35]}=2.34U{1.168−0.57Kut()}di2121i(2)参照教材式(2-5)、(2-6)、(2-17)⎧2.73U2⎪Usdi()=−1.34K12UU(s)本题第(1)问⎧Mcc′()sM=()s/is⎪⎪⎪ir=/r⎪21⎨LsIaa()s++RI()sCeΩ1()s=Ud()s教材式(2−5)其中，⎨2JJ=+J/i⎪Ms()=−CI()s教材式(26)⎪12ma⎪⎪fff=+/i2⎪⎩JsΩΩ()s+=f()sM()s−M′()s教材式(2−17)⎩1211c由上面的关系式可得系统动态结构图为：M′()scU2M()s+Js+fLs+R2.73CmsUs()—Ω()si1—11.34KU12Ce(3)将动态结构图化简可得：①()Ms=0⇒Ms′()=0ccΩ()s11⇒=322.73CU−+1.34KCUsU(s)JLs(JR+fL)s+(fR+CC)smm212ime②()Us=0iΩ()s11⇒=322.73CU−+(LsR)M′(s)JLs+(JR+fL)s+(fR+CC)smc2me Ω()s11⇒=322.73iCU−+(LsR)M(s)iJLs+(iJR+ifL)s+(ifR+iCC)smc2me题2-6：运算放大器电路如题2-6图所示，其中各参数为：CC==1µF，12R1=Ω60k，R=220kΩ，R1=kΩ，R1=00kΩ。试计算传递函数U(s)/U(s)。1234crC1R2C2R4R3−−Ru(t)1++u(t)rc题2-6图运算放大器电路Us()U()sU(S)US()r11c=−,=−11RR//RR+3412sCsC122Us()Us()U()sRRRCCs+RCs++RCs1cc1412121122⇒=Ts()=⋅=(−)(−)Us()U()sUs()RRCsrr131222RRRCCs++RRCsRRCs+R22ss++237.5625124121412424==RRCss132题2-7：题2-7图为单容水箱控制水位的闭环控制系统，两个调节阀的开度分别为µ和µ。其中µ的开度由直流伺服电动机控制，旋转角度与开度成正比，比121例系数为K。试绘制动态结构图，并求解以给定电压u(t)为输入量，水位高度µ1rh(t)为输出量的传递函数。 R1RaLaR0+−+uta()−+R0ω(t)θ(t)µ1Q+−rUSutr()-US−+ht()µ2Qc题2-7图单容水箱水位闭环控制系统参照教材式(2-8b)、(2-58)设水箱横截面积为F，反馈电压为u(t)，水面高度与反馈电压比例为K；ff⎧Us()Us()−U()sdrf⎪=由题图得出RR⎧La⎪10⎪Tl=R⎪2Us()⎪ad⎪(1TTs++Ts)Ω(s)=教材式(2−8b)lmm⎪JRCa⎪e⎪T=m⎪⎪Ω()s⎪CCem⎨=⋅Ksµ11µ()由题图得出其中，⎨⎪s⎪K=2k10H1⎪Hs()=−K1教材式(258)⎪k2⎪⎪µ()sTs+1⎪11⎪2FH0⎪T=⎪Hs()=KU()s由题图得出1ffk⎪⎩2⎪⎩由上面的关系式可得系统动态结构图为：Us()Hs()rR11K112R0CTel(1Tms+Tms+)Ksµ1Ts1+1—Us()f1Kf将动态结构图化简可得：Hs()KKf=2U()ss(Ts++1)(TTsTs+1)+Krl1mm KR11其中，K=KKRCµ10fe题2-8：试用动态结构图简化方法求解题2-8图所示两系统的传递函数。HH11+C(s)R(s)−C(s)GGGGGGGG12341234−R(s)−+−H2H2H3题2-8图系统动态结构图GG()GG+H34121(a)Ts()=，简化步骤如下：1+−GGGGGGH1234232⇓⇓⇓⇓ ⇓GGGG1234(b)Ts()=，简化步骤如下：1++GGHGGH+GGGGH23134212343方法一：⇓⇓ ⇓⇓⇓方法二：方法三： 方法四：题2-9：试应用梅逊增益公式计算题2-9图所示信号流图的如下传输：C(s)C(s)(1)T=；(2)T(s)=。12R(s)N(s)—eN(s)fR(s)bcdC(s)a—g—h题2-9图信号流图(1)Ta=bcd，∆=111Le=−，Lb=−g，Lc=−h123∆=11−LL−−L+LL=+e+bg+ch+ech12313C()sabcdTs()==1R()s1++ebg+ch+ech(2)T=fcd，∆=1+e11Le=−，L=−bg，Lc=−h123∆=11−LL−−L+LL=+e+bg+ch+ech12313Cs()fcd(1+e)Ts()==2Ns()1++ebg+ch+ech题2-10：试应用梅逊增益公式计算题2-10图所示信号流图的传递函数。 1GG31R(s)C(s)−1111−1G4G2−1题2-10图信号流图TG=G，∆=11131TG=G，∆=12242TG=−GG，∆=131241TG=−GG，∆=142131L=−GG，L=−GG，LG=GG，LG=GG，LG=G11322431244213512∆=1(+GG+GG−GG1+G+G)13241234Cs()GG+−GGGGG−GGG1324123124Ts()==R()sG1++GGG−GG(1+G+G)13241234题2-11：试绘出题2-11图所示系统的信号流图，并应用梅逊增益公式计算它们的传递函数。a) b)题2-11图系统动态结构图(a)系统的信号流图为：TG=GGG，∆=1112341L=−GG，LG=−GH，LG=−GGH，LG=−GGGH134223231231412343∆=1+GG+GGGH+GGH+GGGGH34123123212343Cs()GGGG1234Ts()==R()sG1++GGGGH+GGH+GGGGH34123123212343(b)系统的信号流图为：TG=GGG，∆=1112341TG=GGG，∆=1+GH25234211L=−GH，L=−GH，LG=−GH，1112223233LG=−GGGH，LG=−GGGH412344552344 ∆=1−LL−−L−L−L+LL+LL+LL12345121315=+1GH+GH+GGH+GGGGH+GGGGH11222331234423454++GGHHGGGHH+GGGGGHH1212123131234514Cs()GGG()G++GGGH23415151Ts()==Rs()∆题2-12：题2-12图为双输入双输出控制系统信号流图。由图可见，R(s)对C(s)21没有信息传输（传递函数为0）。如果R(s)对C(s)的传输也为0，则系统实现了12解耦控制（等效于C(s)由R(s)单独控制，C(s)由R(s)单独控制）。试求传递1122函数C(s)/R(s)；G(s)所在支路是人为设置的，希望通过配置其传递函数来实215现解耦，试找出G(s)由其它支路传递函数表达的解耦条件。5−H(s)1R(1s)G(1s)G(2s)C(1s)11G(s)5G(s)6R(s)C(s)221G(3s)G(4s)1−H(s)2题2-12图双输入双输出系统信号流图T=G()sG()sG()sG()sG(s)，∆=11126341T=G()sG()sG(s)，∆=121542LG=−()sG()sH(s)，LG=−()sG()sH(s)11212342∆=1+G(s)(Gs)H(s)+G(s)(Gs)H(s)+G(s)(Gs)G(s)(Gs)H(s)H(s)121342123412Cs()G()sGs()G()sGs()Gs()+G()sGs()G()s212346145Ts()==R(s)1++G(sG)(s)H(s)G(sG)(s)H(s)+G(sG)(sG)(sG)(s)H(s)H(s)1121342123412解耦条件：Gs()=−G()sG()sG(s)5236 习题解答第3章5题3-1：某单位负反馈闭环控制系统的开环传递函数为G(s)=，试求闭环系统s在单位阶跃输入函数作用下的响应特性，并计算调节时间。Cs()G()s5Ts()===Rs()1++G(s)s55111⇒=Cs()T()sR()s=⋅=−ss++55sst−T−5t⇒ct()=−1e=−1e⇒=T0.2⇒tT==30.6(∆=0.05)或tT=4=∆0.8(=0.02)ss5题3-2：某单位负反馈控制系统的开环传递函数为G(s)=，试计算该系s(0.2s+1)统单位阶跃响应的最大超调量、上升时间、峰值时间和调节时间。Cs()G()s25Ts()===2Rs()1++G(s)s5s+252⇒ω=25，2ξω=5nn⇒ω=5，ξ=0.5nξπ−32−π1−ξ3⇒σ%=×ee100%=×100%=16.3%；ππ−343t==π=0.48；rωξ1−245nπ23t==π=0.73；pωξ1−215n34t==1.2(∆=0.05)或t==1.6(∆=0.02)ssξωξωnn题3-3：题3-3图所示为一位置随动控制系统的动态结构图，输出量为电动机拖动对象的旋转角度。将速度量反馈回输入端比较环节后构成负反馈内环，速度反 馈系数为τ。试计算：(1)无速度负反馈时系统的阻尼比ζ和自然振荡角频率ωn，输入量为单位斜坡函数时的稳态误差；(2)若满足二阶系统最佳参数，τ应取何值？R(s)E(s)4C(s)−−s(0.5s+1)τs题3-3图二阶系统动态结构图Cs()G()s8Ts()===2R()sG1++(s)s(8τ+2)s+82(1)τ=0⇒ω==82.83；ξ==0.35；n42ss+21es==limE(s)lims[1−T(s)]R(s)l=ims=0.25ss22ss→→00s→0ss++28s(2)二阶系统最佳参数：ξ=0.707，又2ζωτ=8+2，ω=2.83⇒τ=0.25nn题3-4：某单位负反馈二阶控制系统的单位阶跃响应特性曲线如题3－4图所示，图中显示发生在最大超调量时刻的峰值时间和响应峰值，试根据这两条信息确定K该系统开环传递函数为G(s)=的参数K和a。s(s+a)c(t)1.6System:g1.4Time(sec):2.36Amplitude:1.351.210.80.60.40.2t00246810 题3-4图二阶系统单位负反馈阶跃响应特性曲线ξπ−Cs()G()sk1−ξ2Ts()===；σ%=×e100%=35%2R()sG1++(s)sas+kπ⇒ξ=0.32，又t==2.36⇒=ω1.4；pn2ωξ1−n2⇒K==ω1.96；a==2ξω0.896nn题3-5：某速度给定控制系统的动态结构图如题3-5图所示。在给定输入量为r(t)=10v直流电压时要求期望的转速输出量为c(t)=1000r/min。试问：稳态反馈系数α应为多少？在确定的α值下要求系统具有最佳阻尼比，K值应为多少？R(s)KC(s)s(0.1s+1)−α题3-5图二阶系统动态结构图Cs()G()sK10KTs()====22R()sG1++(s)H(ss)0.1s+αKs+10s+10αK10K1010cs′(∞=)limC(s)=limsT(s)R(s)=lims==10002ss→→00s→0ss++1010ααKs⇒α=0.01；b()∞10或c′(∞=)==1000⇒α=0.01；αα系统具有最佳阻尼比，即ξ=0.707⇒2ξωω=1.414=10nn2ω=10αK⇒K=500n题3-6：已知三个单位负反馈控制系统的开环传递函数分别为30(0.3s+1)(1)G(s)=2s(0.1s++1)(0.5s1) 20(0.3s+1)(2)G(s)=s(s−1)(0.5s+1)10(s−1)(3)G(s)=3s(s++2)(s3)试分别应用劳斯稳定判据、胡尔维茨稳定判据判别上述系统的稳定性，对不稳定的系统还应指出不稳定的闭环极点数。432(1)特征方程：0.05ss++0.6s+9s+30=04s0.051303s0.692劳斯表：s0.25301s−630s30第一列符号变换2次，系统不稳定；不稳定的闭环极点数为2个．0.6900D1=0.60.051300D=0.152胡尔维茨行列式D=00.690D=−9.45300.05130D=−283.54胡尔维茨行列式非正定，所以系统不稳定．32(2)特征方程：0.5ss++0.55s+20=03s0.552s0.520劳斯表：1s−150s20第一列符号变换2次，系统不稳定；不稳定的闭环极点数为2个．0.5200D1=0.5胡尔维茨行列式D=0.550D=−7.5200.520D=−1503胡尔维茨行列式非正定，系统不稳定．543(3)特征方程：ss+++56s10s−10=0 5s16104s50−103s612劳斯表：2s−10−101s60s−10首列元素符号改变3次，系统不稳定，不稳定的极点有3个．50−1000D1=5161000D2=30胡尔维茨行列式D=050−100D=−3003016100D=−180040050−10D=180005胡尔维茨行列式非正定，系统不稳定．题3-7：已知三个控制系统的特征方程式如下，试应用劳斯稳定判据判定系统的稳定性；对不稳定的系统要求指出不稳定的极点数；对存在不稳定虚根的要求计算出具体值。32(1)s2++2s5s+30=065432(2)s++2s8s1+2s+20s1+6s+16=06542(3)s2++s32s+20s+s+6=032(1)特征方程：ss++225s+30=03s152s2230劳斯表：180s220s30第一列全为正，系统稳定．65432(2)特征方程：ss++28s+12s+20s+16s+16=0 6s1820165s212164s212163劳斯表：s002s6161s0.330s1642由于出现全零行：Fs()=21s++21s6=0解得系统不稳定的闭环极点：sj=±2；sj=±21,23,46542(3)特征方程：ss++232s+20s+s+6=06s1322065s2014s3219.563劳斯表：s−1.220.6252s35.8961s0.830s6首列元素符号改变2次，系统不稳定，不稳定的极点有2个．题3-8：已知某单位负反馈控制系统的开环传递函数为5G(s)=s(0.1s+1)(0.2s+1)试判断该系统是否稳定？若将S平面虚轴向左平移一个单位，系统是否稳定？32特征方程：0.02ss++0.3s+5=032即ss++1550s+250=03s1502s15250劳斯表：1100s30s250第一列全为正，系统稳定．32设s=r−1，特征方程：0.02(r−1)+0.3(r−1)+(r−1)+5=0 32即r+12r+23r+214=03r1232r12214劳斯表：1r5.160r214系统仍然稳定．题3-9：已知某单位负反馈控制系统的开环传递函数为K(0.3s+1)(0.4s+1)G(s)=s(0.1s+1)(0.8s+−1)(0.5s1)试确定闭环系统稳定时K的取值范围。432特征方程：4ss++37(12Ks−40)+(70K−100)s+100K=04sK412−40100K3sK3770−1002164K−1080sK100劳斯表：372111480KK−+228900108000s164K−10800sK100若系统稳定则：⎧164K−1080>0⎪37⎪2⎪11480KK−+228900108000⎨>0⎪164K−1080⎪100K>0⎪⎩⇒>k19.46题3-10：已知单位负反馈控制系统的开环传递函数为K(s+1)G(s)=s(Ts+1)(2s+1)试确定闭环系统稳定时K和T的取值范围，并作出稳定区域图。32特征方程：2(Ts++2T)s+(1+K)s+K=0 3sT21+K2sT2+K劳斯表：1(1++KT)(2)−2KTs2+T0sK若系统稳定则：⎧2T>0⎪⎪2+T>0T+2⎨(1+K)(2+T)−2KT即：0<0⎪>0T−22+T⎪⎩K>0K6T+24K1，此时τ>0.457)，此时系统有两个不相等的负实数闭环极点，其中一个负实数闭环极点沿着负实轴向左趋向于−∞，另一个负实数闭环极点沿着负实轴向右趋向于原点(系统开环零点).当τ足够大时，原二阶系统可近似为一个由第二个闭环极点(即沿着负实轴向右趋向于原点的负实数闭环极点)所描述的一阶系统，此时原系统的性能主要由这个近似的一阶系统决定.根轨迹如下图(以原点为圆心的圆弧)：题4-4：某负反馈控制系统的开环传递函数具有如下的形式K(s+2)gG(s)H(s)=2s(s++3s4.5)试判断点(-1,j2)、(-1,j3)是否在根轨迹上？如果有不在根轨迹上的点，试计算该点满足相角条件尚需的差额。s+21根轨迹方程：=−2ss(3++s4.5)Kg 零点与极点：z=−2，p=−1.5±1.5j，p=011,23利用辐角条件：点(-1，j2)在根轨迹上：DDDαβ−−β−β=arctan2−45−arctan7−(180−arctan2)=−180123符合幅角条件．点(-1，j3)不在根轨迹上：DDαβ−−β−β=arctan3−arctan3−arctan9−(180−arctan3)=−192.1123不符合幅角条件．D补偿方法：添加一对开环零极点，所偿角为12.1．根轨迹如下图：8642isxA0gaIm-2-4-6-8-3-2.5-2-1.5-1-0.500.511.52RealAxis题4-5：已知负反馈控制系统的开环传递函数分别为KKgg(1)G(s)H(s)=(2)G(s)H(s)=22s(s++2s10)(s−+1)(s3s+10)试绘制它们的根轨迹并确定使系统稳定的K值范围。g11(1)根轨迹方程：=−2ss(++2s10)Kg 零点与极点：p=−1±3j，p=01,23根轨迹趋向：nm−≥2，见图DD⎧⎪ϕ=±60,±180k渐近线：⎨⎪⎩−=σ−0.67kD出射角：β=∓18.4sc与虚轴交点：32特征方程：ss++210s+K=0g3s1102sK2g1sK10−0.5g0sKg2当K=20时，22s+=00⇒=sj±3.16g1,2所以0210，即103．1233Re(s)−0.5761这说明所确定的点能充当闭环主导极点．实际系统根轨如下： (2)根据闭环主导极点：22ω==|s|0.576+0.576=0.81nξπ0.707π−−1−ξ21−0.7072σ%=e×100%=e×100%=4.33%3t==5.24sξωn(3)该点对应的根轨迹放大倍数和开环放大倍数：||ss⋅+|1|⋅+|s3|K==0.943(计算这个值，可代入该阻尼比的根轨迹上任g|2s+|2意一个根，为了计算方便代s=−2.848)；KK==0.633g3(4)稳态速度误差系数：Ks(2+)2gKs==limG(s)H(s)lims=K=0.63vgss→→00ss(1++)(s3)3(5)系统实际指标比该点的二阶指标：超调量小；如果要求系统有该点二阶指标的超调量，则能够通过改变阻尼线而获得；由于系统自身受非主导极点的影响，在根轨迹放大倍数不变的情况下，主导极点的根轨迹超调量比实际系统的超调量稍大一些.因此，为了使系统有该点二阶指标的超调量，可适当减小阻尼比，增大超调量.由根轨迹可以看出，增大阻尼比(减小阻尼角)同时会使ω减n小，闭环主导极点与虚轴距离变小，系统的响应变慢了，调节时间增大了.所以，对系统的某一项性能的改变，其他的性能会做反方向变化.此外，还可以通过减 小根轨迹放大倍数或开环放大倍数来实现上述目的.题4-7：某负反馈控制系统的开环传递函数为K(1−s)gG(s)=s(s+1)(s+3)试绘制以K为参变量的根轨迹，并确定系统稳定的K取值范围。ggs−11零度根轨迹方程：=ss(1++)(s3)Kg零点与极点：z=1，p=0，p=−1，p=−31123根轨迹趋向：nm−≥2，见图，且正实轴上存在根轨的区间∂Kg分离点与会合点：=0⇒=s−0.37(分离点)；s=1.95(会合点)12∂s与虚轴交点：32特征方程：s+4s+(3−K)s+K=0gg3sK13−g2sK4g1sK31−.25g0sKg2当K=2.4时，42s+=.40⇒=sj±0.77g1,202.7根轨迹如下图： 题4-11：已知负反馈控制系统的动态结构图题4-11图所示。试在闭环根轨迹上确定合适的K值使超调量σ≤%25%，调节时间ts≤3.8s，并且位置稳态误差应尽可能的小。R(s)2(s+5)C(s)K2−(s++3)(s2s+2)s+511根轨迹方程为：=−=−2(3ss++)(2s+2)2KKg零点与极点：z=−5；p=−3；pj=−±1112,3根轨迹趋向：nm−≥2，见图⎧±+180(12n)D⎪ϕ==±90k渐近线：⎨2⎪−=σ0⎩kD出射角：β=±77sc6U由es=⋅limE(s)=⋅lims[1−T(s)]⋅R(s)=ssss→→0010K+6⇒e↓则K↑ssξπ−21−ξDσ%=×e100%≤25%⇒ξ≥0.4037，取ξ=0.404⇒θ=66.17D用一个二阶系统近似原系统：做阻尼比为ξ=0.404(阻尼角为θ=66.17)的阻尼线交根轨迹于s=−0.789±j1.8591,2Re(s)−3.4223由于ss++s=−5，则s=−3.422，µ==>3．1233Re(s)−0.7891这说明所确定的点s=−0.789±j1.859能充当闭环主导极点．1,222ss++3|2s+2|0.422|(−3.422)−2×3.422+2|K===1.836g|s+−5||53.422|1⇒=KK=0.918．g2 22验证：由闭环主导极点s得ω==|s|0.789+1.859=2.021n133t===3.676<3.8，满足要求．sξω0.404×2.02n根轨迹如下图： 习题解答第5章题5-1：试绘制下列开环传递函数的幅相频率特性曲线。10(1)G(s)H(s)=(s++1)(0.2s1)5(s+1)(2)G(s)H(s)=2(s++3)(s2s+2)100(3)G(s)H(s)=(s++1)(s3)(s+4)题5-6：试绘制题5-1各开环传递函数的对数幅频特性渐近线和半对数相频特性曲线。21010−−12jωω2(1)Gj()ωωH()j==22(jjω++1)(0.2ωω1)(1+)(1+0.04ω)210−2ω实频特性：P(ω)=22(1+ω)(1+0.04ω)−12ω虚频特性：Q(ω)=22(1+ω)(1+0.04ω)相频特性：ϕ(ωω)=−arctan−arctan0.2ωNyqist曲线：a起点：ω=0⇒P(0)=10，Q(0)=0，ϕ(0)=0a终点：ω=∞⇒∞P()=0，Q()∞=0，ϕ()∞=−180与虚轴交点：P()ω=0⇒=ω2.236⇒=Q(ω)−3.73Nyqist曲线如下： 11转折频率1：ω==1；转折频率2：ω==5TT1222对数幅频特性：LA(ωω)==20lg()20lg10−20lgω+1−20lg(0.2ω)+1半对数相频特性：ϕ(ωω)=−arctan−arctan0.2ωBode图如下： 5(1+jω)(2)Gj()ωωH()j=2(3+−jjω)(2ωω+2)22225(3+−ω)(2ωω)+20−2(1+2ω)jω=2222(9+−ωω)[(2)+4ω]2225(3+ω)(2−ω)+20ω实频特性：P(ω)=2222(9+ω)[(2−ω)+4ω]2−10(1+2ω)ω虚频特性：Q(ω)=2222(9+ω)[(2−ω)+4ω]ωω相频特性：ϕω()=−arctanωarctan−arctan231−0.5ωNyqist曲线：5a起点：ω=0⇒=P(0)，Q(0)=0，ϕ(0)=06a终点：ω=∞⇒∞P()=0，Q()∞=0，ϕ()∞=−180与虚轴交点：P()ω=0⇒=ω2.09⇒=Q(ω)−0.66Nyqist曲线如下： 5(1+jjω)0.83(ω+1)Gj()ωωH()j==22(3+−jjωω)(2+2ω)(j0.33ω+1)[(j0.7ω)+jω+1]11转折频率1：ω==1.414；转折频率2：ω==3TT12对数幅频特性：522ω222LA(ω)==20lg(ωω)20lg+20lg+1−20lg()+1−20lg(1−0.5ω)+ω63ωω半对数相频特性：ϕω()=−arctanωarctan−arctan231−0.5ωBode图如下：23100100[12−+8ωω(−19ω)j](3)Gj()ωωH()j==222(1++jjωω)(3)(4+jω)(1+ω)(3+ωω)(4+)2100(12−8ω)实频特性：P(ω)=222(1+ω)(3+ω)(4+ω)3100(ω−19ω)虚频特性：Q(ω)=222(1+ω)(3+ω)(4+ω)相频特性：ϕ(ωω)=−arctan−arctan0.33ω−arctan0.25ω Nyqist曲线：a起点：ω=0⇒P(0)=8.33，Q(0)=0，ϕ(0)=0a终点：ω=∞⇒∞P()=0，Q()∞=0，ϕ()∞=−270与虚轴交点：P()ω=0⇒=ω1.22⇒=Q(ω)−4.77与实轴交点：Q()ω=0⇒=ω4.36⇒=P()ω−0.71Nyqist曲线如下：8.33Gj()ωωH()j=(jjωω++1)(0.331)(j0.25ω+1)111转折频率1：ω==1；转折频率2：ω==3；转折频率3：ω==4TTT123对数幅频特性：222LA(ωω)==20lg()18.4−20lgω+1−20lg(0.33ω)+1−20lg(0.25ω)+1半对数相频特性：ϕ(ωω)=−−arctanarctan0.33ω−arctan0.25ωBode图如下： 题5-2：已知某一控制系统的单位阶跃响应为c(t)=−11.8e−4t+0.8e−9t试求该系统的开环频率特性。11.80.836Cs()=−+=ss+49s++s(s4)(s+9)Cs()3636⇒Ts()==⋅s=Rs()ss(4++)(s9)(4s++)(s9)Ts()36⇒Gs()==21(−+Ts)s13s3613即Gj()ω=ωjjω(1+)13题5-3：已知两个最小相位系统开环频率特性分别对应满足如下的两组信息：(1)ϕω()=−90a−arctanω+arctan2ω−arctan3ω；A(1)=3aω(2)ϕω()=−180−arctan+arctan2ω−arctan8ω；A(2)=102试确定它们的开环传递函数。 111(1)含有一个，一个，一个2s+1，一个ss+13s+1Ks(2+1)⇒=GsH()()sss(1++)(3s1)22K⋅+()21ωK⋅+()21A()ω=，A(1)==32212⋅⋅10ωω⋅+1(⋅3ω)+16(2s+1)⇒=K6⇒=GsH()()sss(1+)(3s+1)111(2)含有一个，一个，一个2s+1，一个2s0.5s+18s+1Ks(2+1)⇒=GsH()()s2ss(0.5+1)(8s+1)2K⋅+()21ωK⋅17A()ω=，A(2)==1022222⋅⋅5257ωω⋅+(0.5)1⋅(8ω)1+220(2s+1)⇒=K220⇒=GsH()()s2ss(0.5+1)(8s+1)题5-4：如下10个控制系统的开环传递函数分别为K(1)G(s)H(s)=；(T12s1++)(Ts1)(T3s1+)K(2)G(s)H(s)=s(T12s++1)(Ts1)K(3)G(s)H(s)=2s(Ts+1)K(T2s+1)(4)G(s)H(s)=2(T21>T)s(T1s+1)K(5)G(s)H(s)=3sK(T12s++1)(Ts1)(6)G(s)H(s)=3s K(T56s+1)(Ts+1)(7)G(s)H(s)=s(T1s++1)(T234s1)(Ts+1)(Ts+1)K(8)G(s)H(s)=(K>1)Ts−1K(9)G(s)H(s)=(K<1)Ts−1K(10)G(s)H(s)=s(Ts−1)适当选择各题正值参数有题5-4图中顺序对应题号的开环幅相频率特性，试判断它们的稳定性。jQ(ω)jQ(ω)jQ(ω)jQ(ω)jQ(ω)图1图2图3图4图5P(ω)−1P(ω)P(ω)−1P(ω)−1P(ω)−1−1jQ(ω)jQ(ω)jQ(ω)jQ(ω)图10jQ(ω)图6图7图8图9P(ω)−1P(ω)P(ω)−1P(ω)−1P(ω)−1−1题5-4图控制系统的开环幅相频率特性(1)P=0，N=2，Z=2；不稳定(2)P=0，N=0，Z=0；稳定(3)P=0，N=2，Z=2；不稳定(4)P=0，N=0，Z=0；稳定(5)P=0，N=2，Z=2；不稳定 jjϕϕK−j3ϕlimG(eεε)H(e)=lim=∞e3j3ϕε→00ε→εe(6)P=0，N=0，Z=0；稳定(7)P=0，N=0，Z=0；稳定(8)P=1，N=-1，Z=0；稳定(9)P=1，N=0，Z=1；不稳定(10)P=1，N=1，Z=2；不稳定jjϕϕKj(−180a−ϕ)limG(eεε)H(e)=lim=∞ejjϕϕε→00ε→εεe(Te−1)题5-5：某控制系统的动态结构图如题5-5图所示，试绘制该系统的开环幅相频率特性，并判别系统的稳定性。如果系统不稳定，有几个不稳定的闭环极点？R(s)10C(s)−s(s−1)0.01s+1题5-5图负反馈控制系统10(0.01s+1)开环传递函数：G(s)H(s)=s(s−1)2210(0.01jjω+−1)10.1ωω+(10−0.1)ω开环频率特性：Gj()ωωH()j==22jjωω(1−+)ω(1ω)210.1ω实频特性：P()ω=−22ω(1+ω)2(10−0.1ω)ω虚频特性：Q(ω)=22ω(1+ω)aa相频特性：ϕ(ωω)=−arctan(0.01)90−(180−arctanω)Nyqist曲线：a起点：ω=0⇒=P(0)−10.1，Q(0)=∞，ϕ(0)=−270a终点：ω=∞⇒∞P()=0，Q()∞=0，ϕ()∞=−90与实轴交点：Q()ω=0⇒=ω10⇒P()ω=−0.1 Nyqist曲线如下：将上图局部放大：由Nyqist曲线可以看出，P=1，N=1，Z=2；不稳定；不稳定的极点为2个． 题5-7：某负反馈控制系统的开环传递函数为10(s+1)G(s)H(s)=2s(0.2s+1)(s+5)试绘制该系统的开环对数幅频特性渐近线和半对数相频特性曲线，并求出幅值裕度和相位裕度。2(jω+1)开环频率特性：Gj()ωωH()j=−22ωω(0j.2+1)11转折频率1：ω==1；转折频率2：ω==5TT1222对数幅频特性：L(ωω)=+620lg+1−40lgω−20lg(0.2ω)+1低频渐近线：L′()ω=−20lg240lgω⇒=L′(1)20lg2−40lg1=6dBdda半对数相频特性：ϕ(ωω)=−arctan180−2arctan0.2ω221⋅ω+幅频特性：A()ω=22ωω⋅+[(0.2)1]幅值裕度：aaϕω()=−arctanω180−2arctan0.2ω=−180ggg⇒ω=3.87g22221ωω⋅+[(0.2)1]3.87××[(0.23.87)+1]gg⇒h====3；A()ω21⋅+ω222×3.87+1gghh′==20lg20lg3=9.54dB相位裕度：2221⋅+ωω21⋅+ccA()ω=≈=1⇒ω=2.197c222cωω⋅+[(0.2)1]ωcccaaaa⇒γϕ=+180(ω)=+180arctan2.197−180−2arctan0.2×2.197=18.085cBode图如下： BodeDiagramsFrom:U(1)100806040200-20-40)B(d-60deu-80itagn-100M);deg-140(eash-160P-180)-2001(:YTo-220-240-260-280-2-10121010101010Frequency(rad/sec)题5-8：试根据题图所示最小相位系统的开环对数幅频特性渐近线写出相应的开环传递函数。L(ω)L(ω)L(ω)036040−2−1−1+1ω−1ω2−23ω1ω21ω1ωω1ω2ω−2题5-8图最小相位系统开环对数幅频特性渐近线K(1)Gs()H()s=，又20lgK=40⇒=K100ss(1++)(1)ωω12100⇒=Gs()H()sss(1++)(1)ωω12sK(1+)ω12(2)Gs()H()s=，低频渐近线20lgK−20lgω，L(1)=362ss(1+)ω2即20lgK=36⇒=K63 s63(+1)ω1⇒=GsH()()s2ss(1+)ω2Ks(3)Gs()H()s=，低频渐近线20lgK+20lgω，L(3)=0ss(1++)(1)ωω12111即20lgK==20lg20lg⇒K=ω331s3⇒=Gs()H()sss(1++)(1)ωω12题5-9：某单位负反馈控制系统的开环传递函数为1.5(s+1)G(s)=s(5s+1)(0.02s+1)试根据获得的频域指标（1）γ和ωc；（2）Mr和ωb。估算时域指标σ%和ts。21.5⋅+ω1(1)开环幅频特性：A()ω=22ωω⋅(5)++1(0.02ω)1对数幅频特性：222L(ω)=20lgA(ω)=20lg1.5+20lgω+1−20lgω−20lg(5ω)+1−20lg(0.02ω)+1π半对数相频特性：ϕ(ωω)=−arctan−arctan5ω−arctan0.02ω222220lgA(ω)=20lg1.5+20lgω+1−20lgω−20lg(5ω)+1−20lg(0.02ω)+1ccccc21.5×+ω11.5c=≈20lg20lg=0222ωω(5)++1(0.02ω)1ω(5ω)+1ccccc⇒=ω0.57c 1.5或A()ω==1⇒ω=0.57cc2ωω(5)+1ccπaϕω()=−arctan0.57−arctan5×0.57−arctan0.02×0.57=−131.6c2aa⇒=γϕ180+(ω)=48.4c1σ%≈+0.160.4(−1)⇒σ%=29.49%；sinγKπ⎫t≈s⎪ωc⎪⎬⇒K=2.789，ts=15.38K=+21.5(11−1)+2.5(−1)2⎪sinγγsin⎪⎭(2)1.5(ss+1)1.5+1.5闭环传递函数：Ts()==32ss(5++1)(0.02s1)+1.5(s+1)0.1s+5.02s+2.5s+1.51.5+j1.5ω闭环频率特性：Tj()ω=23(1.5−+5.02ω)j(2.5ωω−0.1)21.5ω+1M(ω)=2232(1.5−5.02ω)+(2.5ω−0.1ω)21.5ω+1d()2232dM()ω(1.5−+5.02ωω)(2.5−0.1ω)||==0ddωωωω==rr()ωω⇒ω=0.45r21.5ω+1r⇒MM==(ω)=1.35(精确值)rr2232(1.5−+5.02ωω)(2.5−0.1ω)rrr11或M===1.337(近似值)rasinγsin48.4221.5ωω++11.51bbMM(ω)=≈=0.707(0)=0.707b2232222(1.5−+5.02ωω)(2.5−0.1ω)(1.5−5ω)+(2.5ω)bbbbb⇒ω=0.8156bσ%≈+0.160.4(M−1)⇒σ%2=9.48%；r Kπ⎫t≈⎪sωb⎬⇒K=2.789，ts=10.742⎪KM=+21.5(−1)+2.5(M−1)⎭rrNyqist曲线如下：局部放大： Bode图:闭环频率特性: 题5-10：某单位负反馈控制系统的开环传递函数为10−0.5sG(s)=es1+试用奈氏稳定判据判定闭环系统的稳定性。10j(0−.5ω)开环频率特性：Gj()ω=ejω+110幅频特性：A()ω=2ω+1a相频特性：ϕ(ωω)=−arctan−0.5ω=−arctanω−0.5×57.3ω()a令ϕω()=−90⇒ω=1.3⇒与虚轴交点：QA()ω=()ω=−61111a分别令ϕω()=−arctanω−0.5×57.3ω=−180，gg11g1aaaϕω()=−arctanω−0.5×57.3ω=−180−360=−540gg22g2⇒ω=3.7，ω=15.8g1g2⇒首次交负实轴为PA()ω=()ω=−2.6，gg11第二次交负实轴为PA()ω=()ω=−0.63gg22 包围(1−,j0)点2圈，闭环系统不稳定．补充一题：s+2某系统的开环传递函数为Gs()H()s=，试绘制其幅相频率特性曲线，并判2s+1别其稳定性．解：奈氏路径如图(a)所示jω+2jϕ(ω)Gj()ωωH()j==A(ω)e21−ω224+ωω/(1−ω)其中，A()ω=，ϕω()=arctan221−ω2/(1−ω)ω=0：A()ω=2，ϕ()ω=0aω→1：A()ω→∞，ϕω()→26.6−aω→1：A()ω→∞，ϕω()→−153.4+aω→∞：A()ω→0，ϕω()→−90对应虚轴上(0,j1)点右边的小半圆，Gj()ωH(jω)轨迹由下式计算：jϕje++ε21−2j−−jjϕϕ5(+63.4a)liεε→→m00Gs()H(s)|sj=+εejϕ==limjϕ2lεi→m0e=liε→m0e()je++εε122εaaa当ε→0，ϕ从−90变化到90时，可得到一个半径为∞，相角从26.6减小到 a−153.4的半圆．幅相频率特性曲线如图(b)所示．由图(b)可见，奈氏曲线不包围(1−,j0)点，又系统在右半s平面的开环极点数为0，所以该闭环系统是稳定的． 习题解答第6章题6-1：设图1-7导弹发射架方位随动控制系统的开环传递函数为KG(s)H(s)=s(0.2s+1)(0.03s+1)a在给定位移输入信号以最大转速30/s旋转时输出位移允许有3密位(1密位a=0.06)的稳态误差，试确定开环放大系数K，绘出系统的伯德图，并讨论串联超前校正对系统动态响应性能改善的效果。1limsE⋅=(s)lims⋅⋅R(s)ss→→001(+Gs)H(s)ss(0.2++1)(0.03s1)3030=⋅lims⋅==0.18s→0ss(0.2++1)(0.03s1)+KsK⇒=K166.7；系统伯德图略；串联超前校正可提高系统的截止频率和相位裕度，从而使系统的超调量减小、调节时间变短，动态性能得到改善。题6-2：设某单位负反馈控制系统的开环传递函数为KG(s)H(s)=s(0.5s+1)在给定输入信号为单位斜坡函数时满足稳态误差e≤0.02，试确定开环放大系数ssK，并计算确定K值下的相位裕度。若要求系统有50°的相位裕度，如何进行串联超前校正？1=0.02，K=50；K50A()ω≈=1⇒ω=10ccωω⋅0.5ccaaaa⇒γϕ=+180(ω)=−18090−arctan5=11.3；c校正过程参考例6-1题6-3：题6-3图所示三个控制系统的开环对数幅频特性渐近线L和串联校正0环节的对数幅频特性渐近线L均已知。试写出它们校正后的开环传递函数表达c 式，并计算图a、图b所示两系统校正后的相位裕度和幅频裕度，时域指标的超调量和调节时间。L(ω)L(ω)L(ω)40Lc40−140L0−1Lc−1L2020+1070ωω10ω3ω4ω0.1110−211060100ω1ω2ω5ω6−20−20L0−2−20−2Lca)b)c)题6-3图系统开环对数幅频渐近线和串连校正装置对数幅频渐近线70s+170(s+1)(1)L=，L=，L=；0css(0.1+1)10s+1ss(10+1)(0.1s+1)70ωcA()ω≈=1⇒ω=7ccωω⋅10ccaaaa⇒γϕ=+180(ω)=+180arctan7−90−arctan70−arctan0.7=47.7；caϕω()=−180⇒ω=∞⇒h=∞；gg1σ≈+0.160.4(−1)⇒σ%3=0%；sinγKπ⎫t≈s⎪ωc⎪⎬⇒ts=1.27K=+21.5(11−1)+2.5(−1)2⎪sinγγsin⎪⎭L(ω)L(ω)L(ω)40Lc40−140L0−1Lc−1L2020+1070ωω10ω3ω4ω0.1110−211060100ω1ω2ω5ω6−20−20L0−2−20−2Lc600.1s+160(2)L=，L=，L=；0css(0.1+1)0.01s+1ss(0.01+1)60aaaaA()ω≈=1⇒ω=⇒60γϕ=+180(ω)=−18090−arctan0.6=59；cccωc aϕω()=−180⇒ω=∞⇒h=∞；ggK60⎫ω===77.46⎪nT0.01⎪⎬⇒σ%7=%，ts=0.06；1111⎪ξ===0.64522KT0.6⎪⎭或者2ξ⎫γ=arctan⎪4214+−ξ2ξ⎪⎬⇒ξ=0.5956，σ%9=.7%，ts=0.066⎪tω≈sc⎪tanγ⎭可以看出，第一种方法算得的结果更准一些，因为第二种方法用到相位裕度γ，而计算γ所用到的ω是近似计算的结果。cL(ω)L(ω)L(ω)40Lc40−140L0−1Lc−1L2020+1070ωω10ω3ω4ω0.1110−211060100ω1ω2ω5ω6−20−20L0−2−20−2Lcss3.16(++1)(1)ωω10034(3)L=，L=，0cssss(1++)(1)(1+)(+1)ωωωω1625ss316(++1)(1)ωω34L=ssss(++1)(1)(+1)(+1)ωωωω1256题6-4～题6-10：(略)题6-11：图6-29中的各传递函数若为G(s)=15110G(s)=2s(0.25s+1)(0.05s+1) R(s)C(s)G(1s)G(2s)−−G(cs)图6-29局部负反馈校正要求校正后系统的开环传递函数为150(1.25s+1)G(s)=s(16.67s++1)(0.03s1)2试确定反馈校正装置的传递函数。Gs()G()sGs()G()s−G()sGs()112121Gs()=⇒Gs()==−c1(+Gs)G(s)G()sGs()G()sGs()2c22432−+0.0006ss0.6136+15.18s⇒Gs()=c10(1.25s+1)题6-12：某复合控制系统的动态结构图如题6-12图所示。(1)试设计前馈控制器传递函数G(cs)，使斜坡输入时的稳态误差为零；(2)选择K值使响应呈过阻尼性质。G(cs)+R(s)K5C(s)0.2s+1s(0.6s+1)−E(s)题6-12图按给定量补偿的复合控制系统动态结构图5K(1)令Gs()=ss(0.2++1)(0.6s1)(1+−G()s)Gs()1G()sGs()ccΦ()sT=−1(s)=−1=1(++Gs)1Gs()ss(0.2+1)(0.6s+−1)5KG(s)Uc⇒Es()==Φ()sR()s⋅2ss(0.2++1)(0.6s1)+5Ks 5(KGs)cU[1−]ss(0.2++1)(0.6s1)−5KG(s)Usces==limE(s)lims⋅⋅==0ss2ss→→00ss(0.2++1)(0.6s1)+5Ks5Ks⇒Gs()=c5K(2)系统特征方程：ss(0.2+1)(0.6s++1)5K=011⇒根轨迹方程：=−ss(++1.67)(s5)41.67K⇒分离点：σ=−0.75，此时K=0.070125，d响应呈过阻尼性质，则K<0.070125，可取K=0.07，满足要求．题6-13：按扰动量补偿的复合控制系统的动态结构图如题6-13图所示。试确定扰动补偿传递函数G(Ns)使响应不受阶跃扰动量的影响。N(s)G(Ns)KNK2+R(s)1+KC(s)2KTs1+1s(T2s+1)−E(s)题6-13图按扰动量补偿的复合控制系统动态结构图1K2令Gs()=，Gs()=12Ts+1sT(1s+)12KN[(+⋅Gs)KG(s)]G(s)N12KKTs++KKKG()sU2NN12NCs()==N()s⋅1(++KGs)G(s)s(Ts1)(Ts+1)+KKs12122⇒KTs++KKKG()s=0NN12NKT(1s+)N1⇒Gs()=−NKK2或者按扰动量补偿的完全补偿条件(参照教材95页“2.按扰动量补偿的复合控制”)： KNKG()sG()s=−1NK2KT(1s+)N1⇒Gs()=−NKK2 习题解答第7章题7-1：试计算题7-1图所示非线性特性的描述函数。yykbkxxcbca)b)题7-1图非线性特性(a)⎧KAsinω+tb0≤≤ωtψ⎪cy(t)=⎨πψ=arcsinKc+ψb≤ωt≤A⎪⎩2A01=12πBy1=ω∫(t)sint⋅dωtπ0π44ψ=ω∫∫(KAsin2t+bsinωt)⋅dωt+2(Kc+b)sinωt⋅dωtππ0ψ⎡⎤24b2KAcc⎛⎞c=+⎢⎥arcsin+1−⎜⎟ππ⎢⎥AA⎝⎠A⎣⎦⎡⎤2B1=+4b2K⎢⎥c+c−⎛⎞cN(A)=arcsin1⎜⎟(A≥c)AππAA⎢⎥A⎝⎠A⎣⎦(b)⎧⎧b⎪00≤≤ωtψ1⎪⎪ψ=1arcsin⎪Ay(t)=ω⎨K(Asint−b)ψ1≤≤ωtψ2⎨c⎪π⎪ψ=2arcsin⎪K(c−ψb)2≤≤ωt⎪⎩A⎩2A01=12πBy1=ω∫(t)sint⋅dωtπ0π44ψ2=ω∫∫(KAsin2t−Kbsinωt)⋅dωt+2K(c−b)sinωt⋅dωtππψψ12 ⎡⎤222KAcbc⎛⎞cb⎛⎞b=−⎢⎥arcsinarcsin+1−⎜⎟−1−⎜⎟π⎢⎥AAAA⎝⎠AA⎝⎠⎣⎦⎡⎤22B1=−2K⎢⎥cb+c−⎛⎞c−b−⎛⎞bN(A)=arcsinarcsin1⎜⎟1⎜⎟(A≥c)Aπ⎢⎥AAA⎝⎠AA⎝⎠A⎣⎦题7-2：试计算题7-2图所示非线性结构图的描述函数。xkMycd题7-2图非线性串联环节死区+继电的非线性特性的串联等效特性：⎧00≤≤ωψt⎪cd+/ky(t)=⎨πψ=arcsinMψω≤t≤A⎪⎩2A01=12πBy1=ω∫(t)sint⋅dωtπ0π4=ω∫2Msint⋅dωtπψ24M⎛⎞cdd=−1(⎜⎟+A≥c+)π⎝⎠AkAk2B14M⎛⎞cddN(A)==1(−+⎜⎟A≥c+)AπAA⎝⎠kAk题7-3：试计算题7-3图所示非线性系统的自振振幅和频率。e5−1k1=cs(s+0.5)1−题7-3图非线性系统结构图12π211241N(A)=+[arcsin(1−)+2(1−)−()]−j(1−)(A≥1)ππ2AAAAAA 11−=−(A≥1)N(A)12π211241[+−arcsin(1)+2(1)−−()]−j(1)−ππ2AAAAAA10G(j)ωωH(j)=j(ωωj2+1)1令G(jωω)H(j)=−N(A)解得自振点的振幅和频率：A4=.907；ω=2.066rad/sxx题7-4：非线性系统如题7-4图所示，试用描述函数法分析系统的稳定性。reye=3y2cs(s++1)(s2)−题7-4图非线性系统结构y(t)==e3(Asinωt)3A01=12πBy1=ω∫(t)sint⋅dωtπ0π4=ω∫2A(34sint)⋅dωtπ03A3=4B3A2N(A)=1=A414−=−为负实轴：−∞→02NA(A)3A2G(j)ωωH(j)=j(ωωj+1)(jω+2)1令G(jωω)H(j)==−N(A) 解得临界点的振幅和频率：A2=；ω=1.414rad/sxx所以A<2，ω<1.414rad/s时，系统稳定．题7-5：非线性系统如题7-5图所示，试用描述函数法确定自振的振幅和频率。re1y11y210c1−1s(s++1)(s2)−题7-5图非线性系统结构图饱和+继电的非线性特性的串联等效特性：⎧10e>⎪y=⎨0e=0即y(t)=1(ω>t0)⎪⎩−<10eA01=12πBy1=ω∫(t)sint⋅dωtπ0π4=ω∫2sint⋅dωtπ04=πB14N(A)==AπA1Aπ−=−N(A)410G(j)ωωH(j)=j(ωωj+1)(jω+2)1令G(jωω)H(j)=−N(A)解得自振点的振幅和频率：A2=.122；ω=1.414rad/sxx题7-6：确定下列二阶微分方程在相平面上奇点的位置，指明奇点的性质，并 绘出相变量的方向场。(1)""ee++"3e=0(2)""c2++c"6c=0(3)""c1++.5c"6c+5=0(1)令e""=0，e"=0，解得奇点为(,ee")=(0,0)2⎧ωn=3ω=3⎫⎪⎪n⎬⎨⇒1，所以奇点为稳定焦点21ξω=⎪⎭⎪ξ=<1n⎩232−ω−3n等倾线斜率：β==21ξω++aan相变量的方向场如图e"e(2)令c""=0，c"=0，解得奇点为(,cc")=(0,0)2⎧ωn=6ω=6⎫⎪⎪n⎬⎨⇒1，所以奇点为稳定焦点22ξω=⎪⎭⎪ξ=<1n⎩62−ω−6n等倾线斜率：β==22ξω++aan相变量的方向场如图c" c5(3)令c""=0，c"=0，解得奇点为(,cc")=−(,0)6⎧ω=62nω=6⎫⎪⎪n⎬⎨⇒，所以奇点为稳定焦点1321ξω=.5⎪⎭⎪ξ=<1n⎩422−−ωc5−−65"n等倾线方程：cc==+21ξω++aa.51.5+an相变量的方向场如图c"c5−6题7-7：确定下列二阶微分方程在相平面上奇点的位置，指明奇点的性质，并绘出相变量的方向场。(1)""ee++"e=0(2)""c++signc"6c=0 (3)""c6++c5=0(1)系统方程：⎧ee""++"e=0(e≥0)⎨⎩ee""+−"e=0(e<0)令e""=0，e"=0，解得奇点为(,ee")=(0,0)2ω=1⎫=⎪⎧ω1nne≥0时，⎬⎨⇒，所以奇点为稳定焦点21ξω=⎪⎭⎩ξ=0.5<1n2−ω−1n等倾线斜率：β==21ξω++aan2e<0时，系统特征方程ss+−=10⇒s=−1.618,+0.618，所以奇点为鞍1,2点2ω1n等倾线斜率：β==21ξω++aan相变量的方向场如图e"e(2)系统方程：⎧cc""++61=0(c">0)⎪⎨cc""+=60(c"=0)⎪⎩cc""+−61=0(c"<0)⎧1(,cc"")=−(,0)(c>0)⎪6⎪令c""=0，c"=0，解得奇点：⎨(,cc"")=(0,0)(c=0)⎪1⎪(,cc"")=<(,0)(c0)⎩6 ⎧⎪ω=6n⎨，所以奇点为中心点⎪⎩ξ=02−−ωc1−−61""nc>)等倾线方程：cc==+(02ξω+aaan2−ω6n"=)等倾线斜率：β==−(0c2ξω+aan2−−ωc1−61""nc<)等倾线方程：cc==+(02ξω+aaan相变量的方向场如图c"1c61−6(3)系统方程：⎧cc""++65=0(c≥0)⎨⎩cc""−+65=0(c<0)⎧5(,cc")=−(,0)(c≥0)⎪⎪6令c""=0，c"=0，解得奇点为⎨⎪(,cc")=<(5,0)(c0)⎪⎩6⎧⎪ω=6nc≥0时，⎨，所以奇点为中心点⎪⎩ξ=02−−ωc5−65−"n等倾线方程：cc==+2ξω+aaan2c<0时，系统特征方程s−60=⇒s=±6，所以奇点为鞍点1,2 2ω6n等倾线斜率：β==2ξω+aan相变量的方向场如图c"c题7-8：试用相平面法绘制题7-8图所示系统的相轨迹图。已知r(t)=⋅51(t)，输入量作用前系统处于静止状态。r(t)e(t)1c(t)−s题7-8图线性系统结构图1闭环传函：Ts()=；s+1微分方程：ct"()+ct()=5；奇点为：(,cc")=(5,0)；由特征方程得c"=−c，即等倾线方程β=−1；对系统的微分方程求一阶导数得dc""−cct""()+=c"()t0⇒相轨迹方程==−1=a⇒=βa=−1dcc"起始点：cc(0)==0,"(0)5系统的相轨迹如图 5c"c05 习题解答第8章题8-1：试计算下列函数的Z变换。(1)f(t)=δ(t−kT)(2)f(t)=t−at(3)f(t)=+(1t)e(4)f(t)=ωcostk(5)f(t)=a∞−nk−−k(1)F()zZ==[f(t)]∑f(nT−kT)z=δ(0)z=zn=0(2)∞−−k12−−3Fz()==Z[f(t)]∑kTz=T(z+2z+3z+??)k=0T−−11−2−3=−(1zz)(+2z+3z+??)−11−zT−−12−3=+(zz+z+??)−11−z−1Tz=⋅−−1111−−zz−1TzTz=()或−122(1−−zz)(1)−−aT2aT−−atatzzTez+−(1T)ze(3)Fz()==Z[f(t)]Z[e]+Z[te]=+=−−aTaT22−aTze−−()ze()ze−jtωω−jtee+−1(zzzzcosωT)(4)Fz()==Z[f(t)]Z[]=(+)=jTωω−jT222ze−ze−−z2zcosωT+1∞kk−−12−21z(5)Fz()==Z[f(t)]∑az=1+az+az+??=−1=k=01−azz−a题8-2：试计算下列拉氏变换象函数离散化后的Z变换表达式。1(1)F(s)=3(s+a) 1(2)F(s)=s(s+a)a(3)F(s)=2s(s+a)ω(4)F(s)=22(s+a)+ωs(5)F(s)=22(s+a)+ω112−at(1)Fs()=⇒f(t)=te3()sa+221−−121−−aT−aT−11(2Tz1+z)1(2−atTez1+ez)Zt[]=⇒Fz()==Z[te]−13−−aT1322(1−z)22(1−ez)11−at(2)Fs()=⇒f(t)=[1(t)−e]ss()+aa−aT1(zzz1−e)Fz()==Z[f(t)](−)=−−aT2aT−aTaz−−1[zeaz−(1+e)z+e]a1111111−at(3)Fs()==−⋅++⋅⇒f(t)=−1(t)+t+e22ss()++aassasaaa2−−aTaT11zzTzz(e+T−+1)(T+1)ze+zFz()==Z[f(t)]−⋅++⋅=22−−aTaTaz−−1(z1)aze−a(z−1)(ze−)ω−at(4)Fs()=⇒f(t)=esinωt22()sa++ω−1zTsinωωzsinTZt[sinω]==21−−2zz−+2cosωωT11−2zcosT+z−−aT1−atezsinωT⇒Fz()==Z[esinωt]−−aT11−−aT212−+ezcosωT(ez)s−at(5)Fs()=⇒f(t)=ecosωt22()sa++ω−1zz(c−−osωωT)1zcosTZt[cosω]==21−−2zz−+2cosωωT11−2zcosT+z −−aT1−at1c−ezosωT⇒Fz()==Z[ecosωt]−−aT11−−aT212−+ezcosωT(ez)题8-3：试用长除法计算如下Z变换象函数的时域脉冲序列。10z(1)C(z)=2z2+z+520.3z+0.25z(2)C(z)=32z−+2z1.6z−0.6520.792z(3)C(z)=2(0.208−+4.16zz)(z−1)10z−1−2−−−345−6(1)Cz()==10z−20z−10z+120z−190z−220z+??2z++25z*⇒=c(t)10δδ(t−T)−20(tT−2)−10δ(t−3T)+120δ(tT−4)−−190δδ(tT5)+220(t−6T)+??20.3zz+0.25−−12−3−4(2)Cz()==0.3z+0.85z+1.22z−0.87z+??32zz−+21.6z−0.65*⇒c(t)=0.3δδ(t−T)+0.85(tT−+2)1.22δ(t−3T)−0.87δ(tT−+4)??(3)20.792z−−12−3Cz()==0.792z+4.08672z+17.63z+??32zz−+5.164.368z−0.208*⇒=ct()0.792δδ(t−T)+4.08672(t−2T)+17.63δ(t−3T)+??题8-4：试用部分分式法计算下列Z变换象函数的反变换。210z10z(1)C(z)=；(2)C(z)=(z－2)(z−1)(z−0.5)2(z−1)z(1−e−aT)−22z(3)C(z)=；(4)C(z)=−aT−13(z−−1)(ze)(1−z)Cz()101010z10z(1)=−⇒Cz()=−zzz−21−−zz21−k⇒=ck()10⋅(2−1) k+1k−110z(2)Cz()z=⇒2(zz−−0.5)(1)k+1k−110zRes[(Cz)z]zz→1=−lim(z1)2=40z→1(0zz−−.5)(1)k+1k−1211⎧⎫dz010k10Res[(Cz)z]=−⎨⎬[(z0.5)]=−−zz→221kk−−2(2−−1)!⎩⎭dz(z0.5)(z−1)22z→0.555k⇒=ck()40−−kk−23−22Cz()11zz−ak(3)=−⇒Cz()=−⇒c(k)=1−e−−aTaTzzz−−11ez−−ze22zz(z++1)z2z(z1)T1zT(4)Cz()==−=−332232(1zz−−)(1)(1z−)T2(1z−)T(z−1)2121⇒=c()k(kT)−kT=k(k−1)2TT2题8-5：已知Z变换象函数为20.8zC(z)=2(0.21−0.4z+−z)(z1)试计算该象函数对应的离散时间脉冲序列前5步的脉冲值，并计算该脉冲序列的终值。20.8z−−12−3−4−5Cz()==0.8z+1.12z+1.08z+0.9968z+0.97192z+??32zz−+1.40.61z−0.21*⇒=ct()0.8δδ(t−T)+1.12(t−2T)+1.08δ(t−3T)+0.9968(t−4T)+0.97192(t−5T)??2*0.8z0.8cz(∞=)lim(−1)C(z)=lim==0.9876543212zz→→11zz−+0.40.210.81题8-6：试用迭代法确定下式差分方程c(k)+0.6c(k−+1)2c(k−2)=r(k)当输入序列为r(k)=δ(k)，初始条件为c(0)=0，c(1)=1时的直到k=6的解序列。c(0)=0c(1)=1 cc(2)=−0.6(1)−2c(0)+r(2)=−0.6+1=0.4cc(3)=−0.6(2)−2c(1)+r(3)=−0.6×0.4−2+1=−1.24cc(4)=−0.6(3)−2c(2)+r(4)=0.6×0.76−2×0.4+1=0.944cc(5)=−0.6(4)−2c(3)+r(5)=−0.6×0.656+2×0.76+1=2.9136cc(6)=−0.6(5)−2c(4)+r(6)=−0.6×2.1264−2×0.656+1=−2.63616题8-7：试用Z变换法求解下式离散函数差分方程的解****c(t++2T)2c(t+T)+3c(t)=r(t)*⎧1t=0**已知输入函数为r(t)=⎨，c(0)=0，c(T)=1。⎩0t≠0ck(++2)2ck(+1)+3ck()=r(k)22⇒[zC(z)−−zc(0)zc(1)]+[2zCz()−2zc(0)]+3Cz()=12⇒zC()z−+z2zC(z)+3C()z=1zz+11z⇒Cz()=⇒zC()z=(+)2zz++232zj+−12z++1j21kk⇒+ck(1)=[(−1+j2)+(−1−j2)]21kk−−11⇒=ck()[(−1+j2)+(−1−j2)]2题8-8：试用Z变换法求解如下离散函数差分方程的解。(1)c(k++2)1.5c(k+1)+c(k)=r(k)；c(0)=0，c(1)=0；r(k)=k。(2)c(k+−2)3c(k)=coskπ；c(0)=1，c(1)=0。k(3)c(k++2)5c(k+1)+3c(k)=cosπ；c(0)=0，c(1)=1。2(1)ck(2++)1.5ck(+1)+ck()=r(k);c(0)=0,c(1)=0;r(k)=k2z⇒zC()z++1.5zCz()Cz()=2(1z−) z⇒Cz()=22(1zz−)(++1.5z1)用留数法计算结果：37kk37()−+jj(−−)2(k−1)4444ck()=++7777777jj()−+(−j)(−−j)244244(2)ck(2+−)3ck()=coskπ;c(0)=1,c(1)=022z(czz−osπ)⇒zC()z−−z3C(z)==2z−2czzosπ++112zz(1++z)3z+2⇒Cz()==1+22(3zz−)(+−1)(3zz)(+1)用留数法计算结果：kk−−21k−17122kk−−22(−1)ck()=+δ()k⋅3[1−(−1)]−⋅3[1−(−1)]+442k(3)ck(++2)5ck(+1)3+ck()=cosπ;c(0)=0,c(1)=12πzz(c−os)222z⇒zC()z−+z5zC(z)+3C()z==π22z+1zz−+2cos122zz(1++z)⇒Cz()=22(1zz+)(++5z3)用留数法计算结果：kkkk22jj()−aa(1+a++)a(aa+1)111222ck()=+++222(2+−jj5)2(25)(a+1)(a−a)(a+1)(a−a)112221−+513−−513其中，a=，a=1222题8-9：试计算下列拉氏变换象函数对应的脉冲传递函数。1(1)G(s)=(s+1)(s+2)K(2)G(s)=s(s+a) 2ω(3)nG(s)=22s2+ζω+ωnn−−TT211zzz()e−e(1)Gs()=−⇒=Gz()−=−−TT22−T−Tss+12+ze−−ze()ze−(ze−)−aTK11KzzKz(1−e)(2)Gs()=−()⇒=Gz()(−)=−−aTaTass+aaz−−1(zeaz−1)(ze−)22ωωωξ1−nnn(3)Gs()==()s++ξω22(1−ξ)ω21(−+ξξ22sω)+(ω1−ξ2)2nnnnωze−ξωnTsinωξT1−2nn⇒=Gz()1(−−ξω22ze−−ξωnnTT)2zeξωcosT1−ξ2+1n2题8-10：试计算题图系统的开环和闭环脉冲传递函数。其中，G(s)=；s(s+1)H(s)=0.01。设采样周期为T0=.1s，虚设采样开关T与采样开关T同期动作。21TC(*s)2T1*R(s)E(s)G(s)−C(s)B(s)H(s)题8-10图采样系统动态结构图222Gs()==−ss(1++)ss122zz2z2z0.2z⇒=Gz()−=−=−Tzz−−11ez−−z0.9(z−1)(z−0.9)0.020.020.02GsH()()s==−ss(1++)ss1zzzz0.002z⇒=GH(z)0.02(−)=0.02(−)=−Tzz−−11ez−−z0.9(z−1)(z−0.9) 0.2zGz()(zz−−1)(0.9)0.2zTz()===1(Gz)H(z)0.002zz21.898z0.+−+91+(zz−−1)(0.9)5(s+1)题8-11：试计算题图系统的闭环脉冲传递函数。其中，G(s)=，cs−Ts1e−2G(s)=，H(s)=0.01；设采样周期为T0=.1s，虚设采样开关T与采oss+22样开关T、T同期动作。13TC(*s)2T*T3*R(s)1E(s)E(s)E(1s)1G(cs)G(os)−C(s)B(s)H(s)题8-11图数字系统动态结构图zz5(2−1)Gz()=+5(1)=cz−−11zzz−−121zz0.18Gz()==Z[][−]=0−2Tzs(2s+−)zz1z−ez−0.82zz−−121zz0.0018GH(z)=⋅0.01Z[]=⋅0.01[−]=0−2Tzs(s+−2)zz1z−ez−0.825(2z−1)0.18Gz()G()zzz−−10.821.8z−0.9c0Tz()===1+−Gz()GH(z)5(2z−1)0.0018z21.8z0.81+c01+zz−−10.82题8-12：试判别具有如下特征方程的离散系统的稳定性。32(1)z+1.73z++=2.5z0.650432(2)z−+1.368z0.42z+0.09z+0.02=0w+1(1)令z=，则离散系统在w域下的特征方程：w−1325.88ww++0.280.72w+1.12=0 由劳斯稳定判据可知，系统不稳定．w+1(2)令z=，则离散系统在w域下的特征方程：w−14320.162ww++1.0045.28w+8.204w+2.718=0由劳斯稳定判据可知，系统稳定．题8-13：试分别判定题8-10、题8-11系统的稳定性。(1)题8-10的系统特征方程：2zz−+1.8980.9=0w+1令z=，则离散系统在w域下的特征方程：w−120.002ww++0.23.798=0由劳斯稳定判据可知，系统稳定．(2)题8-11的系统特征方程：2zz−+1.80.81=0w+1令z=，则离散系统在w域下的特征方程：w−120.01ww++0.383.61=0由劳斯稳定判据可知，系统稳定．题8-14：已知离散控制系统的动态结构图如题图所示，试分别求T=1s和T0=.5s时系统临界稳定的K值，并讨论采样周期T对稳定性的影响。TC(*s)2TR(s)1−TsK1e−ss(s+1)−C(s)题8-14图采样系统动态结构图系统开环脉冲传递函数：zK−−11z++Tz−1Gz()==Z[]K[+]2−Tzs(1s+−)z1z−e−+zz2−1K(0.368z+0.264)T=1s时，Gz()=+K[]=zz−−10.368(z−1)(z−0.368) 系统特征方程：2zK+−(0.3681.368)z+0.264K+0.368=0w+1令z=，则离散系统在w域下的特征方程：w−120.632Kw+−(1.2640.528K)w+2.736−0.104K=01.264由于K不能为0，所以当K==2.39时系统临界稳定．0.528−+zz1.5−1K(0.107z+0.09)T=0.5s时，Gz()=+K[]=zz−−10.607(z−1)(z−0.607)系统特征方程：2zK+−(0.1071.607)z+0.09K+0.607=0w+1令z=，则离散系统在w域下的特征方程：w−120.116Kw+−(0.7860.18K)w+3.214−0.017K=00.786由于K不能为0，所以当K==4.367时系统临界稳定．0.18可见，采样周期越小，系统稳定性越好．题8-15：试计算题8-14T0=.1s、K=1，输入量为r(t)=(1+t)1(t)时系统的稳态误差。Ts=0.1、K=1时，系统开环脉冲传递函数：−+zz1.1−10.0048z+0.0048Gz()=+=zz−−10.9048(z−1)(z−0.9048)系统特征方程：2zz−+1.90.9096=0特征根：azj=±0.950.0843=0.953∠±5.07在单位圆内，系统稳定．1,2由于系统是Ⅰ型系统，单位阶跃输入时稳态误差为0；单位斜坡输入时速度误差系数：10.0048z+0.0048kz=−lim(1)G(z)=−lim10(z1)=1.01vzz→→11Tz(−−1)(z0.9048) 1稳态误差为e()∞==0.99．kv'