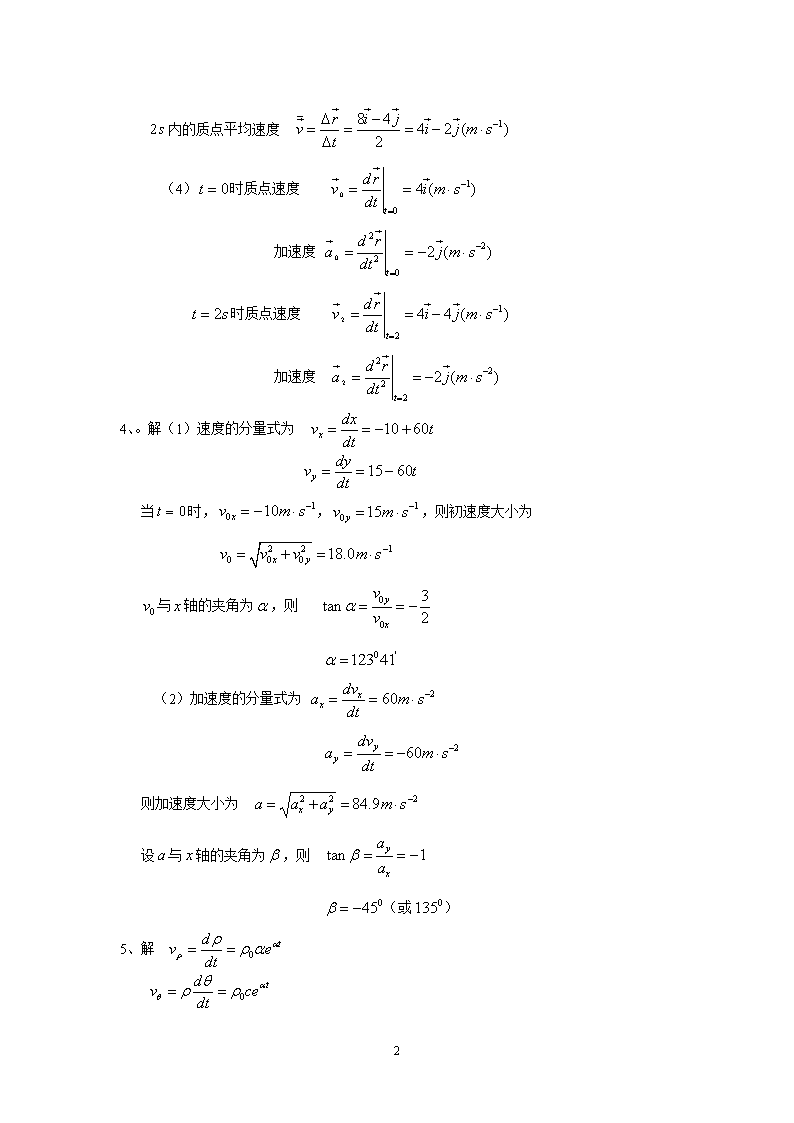- 3.36 MB
- 2022-04-22 11:35:16 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'大学物理题库参考答案力学部分1、。解(1)质点在4.0s内位移的大小(2)由得知质点的换向时刻为则所以,质点在4.0s时间间隔内的路程为(3)时2、。解(1)当时,则得质点运动方程为(2)当时3、。解(1)根据质点的运动方程可知:得质点的轨迹方程为:质点运动的轨迹是以(0,4)为顶点、开口向下的抛物线。(2)时质点位矢(m)时质点位矢(m)(3)内的质点位移(m)36
内的质点平均速度(4)时质点速度加速度时质点速度加速度4、。解(1)速度的分量式为当时,,,则初速度大小为与轴的夹角为,则(2)加速度的分量式为则加速度大小为设与轴的夹角为,则(或)5、解36
6、解7、解直角坐标系的原点与极坐标的极点相重合,且为质点运动所沿的圆周的圆心。则直角坐标与极坐标有如下关系其中,相反的关系可表示为设时,质点处于圆周与轴的交点上。由题已知,所以则,质点的位置矢量可以表示为质点的运动速度可以表示为8、解根据牛顿第二定律,质点的加速度因36
所以解得当时则得因所以解得当时则得9、解(1)建立直角坐标系,取沿斜面向下为x轴,垂直斜面向上为y轴根据牛顿第二定律列出方程:解方程得当斜面倾角变为时,让物体从斜面顶端自由下滑,这时解得:物体从斜面顶端自由滑下时得:(2)为使下滑时间最短,令则有解得:36
此时,10、解物体A、B的受力情况如图所示;(1)假设物体B向下滑,物体A向上滑,加速度为。对物体B:(1)对物体A:(2)解以上两方程得所以,系统中的物体A沿斜面向上滑动,物体B沿斜面向下滑动。(2)物体运动的加速度大小为(3)由方程(2)解得11、解:因,在直线运动中,根据牛顿运动定律有依据质点运动的初始条件,积分得又因,并由质点运动的初始条件,积分得12、解子弹射入木块作完全非弹性碰撞,根据动量守恒定律有(1)子弹处于木块内一起滑行,根据功能原理有(2)解(1)、(2)两式得36
13、解⑴根据动能定理有:(3分)解方程得:(1分)⑵因(2分)所以得:(2分)⑶由上式得:(2分)根据牛顿第二定律有:代入得:(4)列车所经过的路程,对于直线运动14、解若把小球、弹簧和地球看作为一个系统,则小球只受弹性力和重力,所以在小球的运动过程中机械能守恒。把小球处于点B时的位置取作系统的重力势能零点,系统的弹力势能零点应取在弹簧未发生形变时的状态,即O点。设由于小球受重力的作用,弹簧伸长了,而到达了A点。则应有(1)因为小球处于点A时所受的重力和弹性力相平衡,故有(2)(2)代入(1)解得15、解(1)根据已知可得得对上式积分得(2)在从到的时间内,黏性阻力所作的功A36
16、解取Q点的势能为零,则有即求得小球到达Q点时的速率为设小球到达Q点时绳子的张力为T,则沿轨道法向可以列出方程解得在小球从P到Q的过程中的任意一点上,沿轨道切向作位移元,重力所作元功为重力所作的总功17、解(1)设发动机的牵引力为,路面的摩擦力为。因为汽车在水平路面上行驶,则有解得发动机的功率为(2)设汽车沿斜面向上行驶时发动机的牵引力为,则36
解得发动机的功率为18、解从点O到点A的过程中任意一点P的坐标为,在点P发生时所作的功从点O到点A的过程中所作的总功19、解将物体、弹簧和地球作为一个系统,这个系统没有外力的作用,也没有非保守内力的作用,故系统机械能守恒。则所以20、解设物体离开球面时速度为,对于由物体、球体和地球所组成的系统,没有外力和非保守内力的作用,机械能守恒。故有(1)在物体离开球体之前,物体在球面上的运动过程中,应满足下面的关系(2)在物体离开球体的瞬间,且这时,则代入(2)式有代入(1)式解得21、解(1)重物、36
和地球作为一个系统,这个系统不受外力作用,所以机械能守恒。开始时的重力势能=最后的重力势能+和的动能,所以解得:(2)开始时和都具有动能解得:22、解:设小球受到的平均冲力为,根据题意,它是沿方向。根据动量定理有解得小球在轴方向上不受力的作用,动量守恒,故有小球受到撞击后的运动速率小球所受的平均冲力23、解:(1)因子弹受到均匀阻力,所以子弹在木块内作匀减速运动,故有(2)根据动量定理,冲量(3)根据动量定理有解得36
24、解:(1)设x沿初始运动的方向y沿最终的运动方向,初始动量最终动量:所需冲量:大小:方向与的夹角:(2)因为,当//时所需时间最短,25、解:均匀扇形薄片,取对称轴为轴,由对称性可知质心一定在轴上。有质心公式设均匀扇形薄片密度为,任意取一小面元,又因为所以对于半圆片的质心,即代入,有 26、解:在质点运动的平面内取如图所示坐标。按的分量式有36
其中,,代入后得则27、解:(1)He原子量为4,所以。弹性碰撞动量守恒、机械能守恒,故有把代入得解得(2)能量的比例28、解:(1)取的方向为轴的正方向。根据动量守恒有根据题意,代入上式解得(2)动量的改变29、解:设中子的质量为,与碳核碰撞前、后的速度分别为、;碳核的质量为36
,碰撞前、后的速度分别为0和V,因为是正碰,根据动量守恒有(1)总动能守恒,有(2)解方程(1)(2)得算得中子动能的减少因所以30、解:设,根据已知当x=0时,;当x=L时,=0可得在x=0到x=L过程中F所作的功由动能定理有得x=L处的质点速率为31、解:以向下为正方向。设球碰撞前后的速度分别为和。根据小球在落下后到碰撞前这段时间机械能守恒有:解得:从小球弹起时刻到最高点:解得:设是传给地板的动量,根据动量守恒定律有:解得:32、解:当系统的质量增加时只有内力起作用,所以瞬时动量守恒。(1)m物体在绳子拉紧前的速率为36
其动量也就是系统的动量为,绳子拉紧后的瞬间,系统的速率(两物体共同的速率)为,根据动量守恒有即而且,系统的加速度为即其中以动量的方向为正方向。运用匀加速运动公式,得出系统回到原处所花的时间满足即(2)动能减少的比例为33、解:由于动量守恒,摩擦力为。根据动能定理,,得解得碰撞中所以消耗的部分占34、解:根据机械能守恒可求得碰撞前A的速度即36
两球一起的速度V,根据动量守恒有两球上升的高度为,根据机械能守恒有解得35、解:设轴向东,轴向北。根据动量守恒定律有得在轴上有,在轴上有,其中是与正向所成的角。解得,并求得36、解:以小车前进方向为正方向,人跳上小车是完全非弹性碰撞。故有其中是人与车一起运动的速度,是人原有速度,是小车原有速度。则(1)从后面跳上车,与同方向。故(2)从迎面跳上车,与方向相反,故36
37、解:小球与物体相碰撞的速度可由下式求得(1)小球与物体相碰撞,在水平方向上满足动量守恒,碰撞后小球的速度变为,物体的速度为V,在水平方向上有(2)完全弹性碰撞,动能不变,即,(3)碰撞后,小球在到达张角的位置的过程中机械能守恒,应用(4)由以上四式可解得所以38、解:由题意,质点的质量为,质点受力产生的加速度为因为,积分得质点的速度t时刻质点的位置矢量为(1)当时质点在时所受的相对坐标原点O的力矩为36
(2)当时角动量39、解:在子弹与物块的撞击过程中,在沿斜面的方向上,根据动量守恒有(1)在物块上滑的过程中,若令物块刚滑出斜面顶端的速度为,并取A点的重力势能为零,由系统的功能原理可得(2)由式(1)(2)可得40、解:N、G合力矩为零,T为有心力,故物体角动量守恒(1)拉力提供向心力所以绳子刚被拉断时物体的线速度为代入(1)式解得41、解:(1)取小球作匀速圆周的水平面为平面,取轴竖直向上,如图所示。小球相对于O点的角动量沿轴方向,故有36
(2)小球在运动中所受到的细绳的张力和重力的合力处于平面内并指向O点,所以小球所受相对于O点的力矩等于零,故小球的角动量守恒,即由上式得可得与之间的关系,为42、解:根据题意,重物的质量为,以托盘、弹簧、重物和滑轮为质点系。以滑轮中心为参考点,系统所受合外力矩为零,故角动量守恒,有解得托盘向下的速度为根据能量守恒有解得弹簧弹起的最大高度为H,所以有则43、解:地球绕太阳运动过程中受到有心力的作用,所以角动量守恒,有即(1)根据机械能守恒有(2)解式(1)(2)得近日点速度大小为远日点的速度大小为36
44、解:(1)当角速度一定时,切向速度也是一定的,所以切向加速度此时法向加速度可见是恒定的。(2)当角加速度一定时,即恒定,于是得到由此可得切向加速度为是恒定的。法向加速度是时间的函数。45、解:飞轮作匀变速转动,所以角加速度制动后的角速度变为,所以有解得46、解:(1)细圆环:相对于通过其中心并垂直于环面的轴的转动惯量为转动动能(2)薄圆盘相对于通过其中心并垂直于盘面的轴的转动惯量转动动能为47、解:(1)均匀细直杆的转动惯量:36
四个质点相对于同一转轴的转动惯量:系统相对转轴总转动惯量为48、解:对于物体选择竖直向上为轴正方向,对于物体选择竖直向下为轴正方向,对于顺时针方向为正方向。根据牛顿第二定律和转动定理有:; , 解得: 49、解:(1)根据题意知解得轮子的角加速度(2)根据转动定理有所以(3)因所以50、解:设上段绳子的拉力为,下段绳子的拉力为,则36
代入数值解方程求得根据已知解得51、解:由定义得施加的力矩52、解:在匀变速转动中,角加速度由转动定律,可得飞轮所经历的时间53、解:根据质点的牛顿定律和刚体的转动定律,有(1)(2)(3)由角加速度和线加速度之间的关系,有(4)(5)解上述方程组,得36
54、解:整个圆盘对OO轴转动惯量为挖去的小圆盘对OO轴转动惯量剩余部分对OO轴的转动惯量(2)由平行轴定理,剩余部分对的转动惯量55、解:(1)碎块抛出时的初速度为由于碎块竖直上抛运动,它所能到达的高度为(2)圆盘在裂开的过程中,其角动量守恒,故有圆盘未碎时的角动量碎块对轴的角动量破裂后盘的角动量56、解:球壳的面密度为,如图所示,圆环的半径为,周长为,环的宽度为,所以面积质量36
设该圆环关于轴的转动惯量为。该轴到环上各点的距离为,所以整个球壳的转动惯量57、解:均匀薄板的面密度,宽为的转动惯量为总的转动惯量58、解:根据题意可知物体,,由得:由可得:由转动定律有解得轮子的角速度轮子的转动动能59、解:(1)将两个圆盘看为一个系统,这个系统不受外力矩作用,总角动量守恒,即合成一体后的角速度(2)上盘落下后两盘总动能和改变量为60、解:(1)闸瓦作用于飞轮的摩擦力矩的大小为(2)从开始制动到停止,飞轮的角加速度可由转动定理求得36
根据得飞轮转过的角度为飞轮转过的转数为因飞轮从开始制动到停止所经历的时间(3)摩擦力所作的功61、解:取定滑轮的转轴为z轴,正方向垂直于纸面向外。(1)根据牛顿定律和转动定理有其中解得物体下落的加速度为圆盘的角加速度(2)绳子的张力62、解:(1)直杆顶端触及地面时的角加速度此时直杆处于水平位置,所受重力矩的大小为直杆倒地的过程中,以过点B垂直于杆的直线为轴,杆相对于些轴的转动惯量为由转动定理得36
(2)直杆顶端触及地面时的线速度根据机械能守恒,有得此时顶端的线速度63、解:将木棒和子弹看作一个系统,该系统不受外力矩作用,所以角动量守恒,即其中,解得64、解:水对水库底面的压力为侧面取窄条为面积元,所受的压力为整个侧面所受的压力为对于的侧面:对于的侧面:侧面总压力为65、解:可以认为水从龙头流出后各处都是大气压,根据伯努力方程有可为(1)根据连续性方程有(2)根据题意,代入(1)解得36
(3)将式(3)代入(2)得由题知,就是在水龙头出口以下处的直径66、解:取图中虚线AB所示的流线,并运用伯努利方程可以认为,解得67、解:(1)对D、C两点运用伯努利方程将,,,代入上式,得可求得管内的流速,为(2)对B、C两点运用伯努利方程得解得因最小值为零,当时,由上式可求得36
这表示当C点的位置低到使时,。68、解:(1)利用伯努利方程有根据题意知,代入上式,解得(2)水不流动时,,所以69、解:由伯努利方程有由题意知,,代入上式,解得70、解:利用伯努利方程有(1)因为空气是水平流动的,则由题中图可知代入(1)式得(2)根据连续性方程得则代入(2)式解得71、解:36
选取一流线AB,因,所以,根据伯努利方程,有又因所以,得水从小孔时速度水流内的每一个质点都沿着平抛运动的轨迹运动。下落时间满足方程解得:因此在下落过程中的水平位移72、解:由伯努利方程:解得:根据连续性方程,得单位时间内水流出的体积时间内水的流量73、解:水流自由下落h后,速度为若水流骒稳定流动的,则满足:水又是不可压缩的,即所以74解:(1);;36
振幅:初相位:(2)时:75、解:物体作简谐振动:故:第76题图76、解:如图:物体在任一位置受到的弹力为:即得:其中第77题图77、解:是轴弹簧;两弹簧受到的弹力相同,均为F又两弹簧伸长量为设:两弹簧串联后的劲度系数为k则:又:即得:由牛顿第二定律:36
78、解:设物体的质量为m,以平衡位置O为原点建立如图所示的坐标系。物体所受的力有向下的重力mg和向上的支持力,则物体的运动方程(1)由简谐振动可以求得加速度当振动达到目的最高点时,木板的加速度的大小不一也达到最大值,为:(2)第78题图负号表示加速度的方向向下。如果这时物体仍不脱离木板,物体就能够跟随木板一起上下振动。将式(2)代入式(1),得(3)物体不脱离木板的条件是取其最小值代入式(3),得求得物体和木板一起振动的最大振幅,为79、解:据题意物体的振动方程为:(1)(2)36
80、解:根据波源的振动方程可知:波幅,角频率,初相位,波速求得波的周期波长波函数则有(m)81、解:(1)合振动的振幅为0.1m。初相位为。(2)当36
82、解:无阻尼有阻尼时83、已知:求:解:84、已知:平面简谐波:;;求:;并写出波函数解:波函数为:(其中为波源的初相角)85、已知:平面简谐波沿轴负方向行进:;;求:;并写出波函数解:36
因为波沿轴负方向行进,所以,波函数为:86、已知:求:(1),,,;(2)解:(1)(2)87、已知:求:解:③88、已知:驻波相邻波节的距离为130cm,求:传播速率和波长解:36
89、解:⑴简谐运动系统中振子运动的速度,故氢原子振动的最大速度为⑵氢原子的振动能量90、解:⑴由振动方程可得:角频率,振幅,初相,则周期⑵简谐运动的能量⑶简谐运动的动能和势能分别为则在一个周期中,动能与势能对时间的平均值分别为91、解:⑴根据振动曲线可知振动的周期,振幅,⑵振动方程为92、解:根据波动曲线可知:振幅,所以波长频率36
初相位波动方程(m)93、解:,,,根据波动方程得:94、解:(1)绳上行波的横向速度为(2)横向加速度(3)时95、解:(1)根据图像可知:振幅,已知根据振动方程可以得到原点处的振动方程:m当时,,由图像可知时,,所以初相位m(2)已知,根据波动方程得:96、解:设火车行驶的速度的大小为V,火车汽笛的频率为,声音速度36
当火车迎面驶来时,观察者观测到的频率:①当火车远离时,观察者观测到的频率:②式①、②联立方程组解得97、解:当超声波从探测器传向车辆时,车辆是观察者,车辆接收到的超声波的频率为;式中是空气中的声速,V是车辆的行驶速度,是探测器发出的超声波的频率。在超声波被车辆反射回探测器的过程中,车辆变为波源,而探测器成为观察者。这时探测器所接收到的反射波频率为:所以得:由上式解出车辆的行驶速度为:而:所以该车没有违章。大学物理习题集——相对论部分98、解:由洛仑兹逆变换:得:36
99、解:①②③④⑤100、解:101、解:36'
您可能关注的文档
- 大学物理知识总结习题答案(第四章)静电场.doc
- 大学物理答案(上).doc
- 大学物理答案第十六章.doc
- 大学物理简明教程答案.pdf
- 大学物理简明教程课后习题加答案《完整版》.doc
- 大学物理课后习题答案(上).docx
- 大学物理课后习题答案(下).docx
- 大学物理课后习题答案.doc
- 大学物理课后答案9-10.doc
- 大学生_必备资料下载.doc
- 大学生信息检索习题以及答案 (2).doc
- 大学生信息检索习题以及答案.doc
- 大学生健康教育习题答案.doc
- 大学生创业基础章节检测习题.docx
- 大学生必备资料库.doc
- 大学英语B考试题库答案2.doc
- 大学英语五(含答案).doc
- 大学英语六级试卷和答案-《大学英语(高起本)3》练习题.doc
相关文档
- 施工规范CECS140-2002给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程
- 施工规范CECS141-2002给水排水工程埋地钢管管道结构设计规程
- 施工规范CECS142-2002给水排水工程埋地铸铁管管道结构设计规程
- 施工规范CECS143-2002给水排水工程埋地预制混凝土圆形管管道结构设计规程
- 施工规范CECS145-2002给水排水工程埋地矩形管管道结构设计规程
- 施工规范CECS190-2005给水排水工程埋地玻璃纤维增强塑料夹砂管管道结构设计规程
- cecs 140:2002 给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程(含条文说明)
- cecs 141:2002 给水排水工程埋地钢管管道结构设计规程 条文说明
- cecs 140:2002 给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程 条文说明
- cecs 142:2002 给水排水工程埋地铸铁管管道结构设计规程 条文说明