工程力学课后答案(第二版少学时).doc 79页

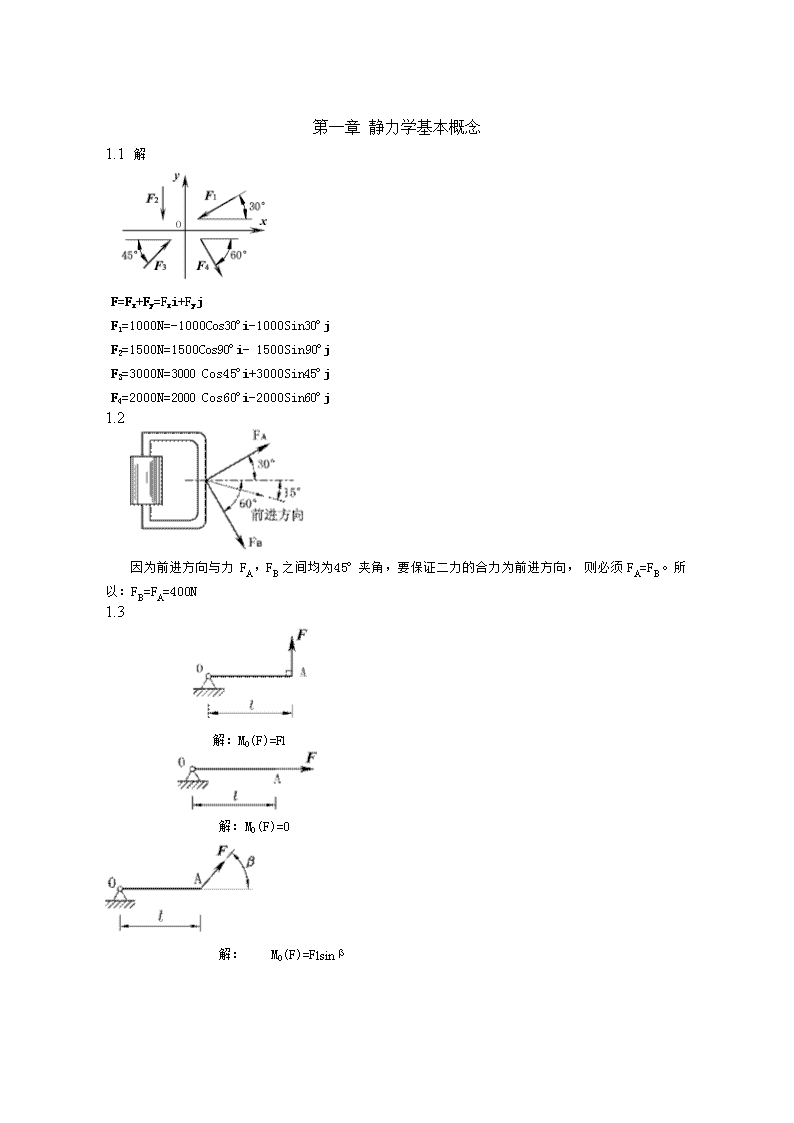
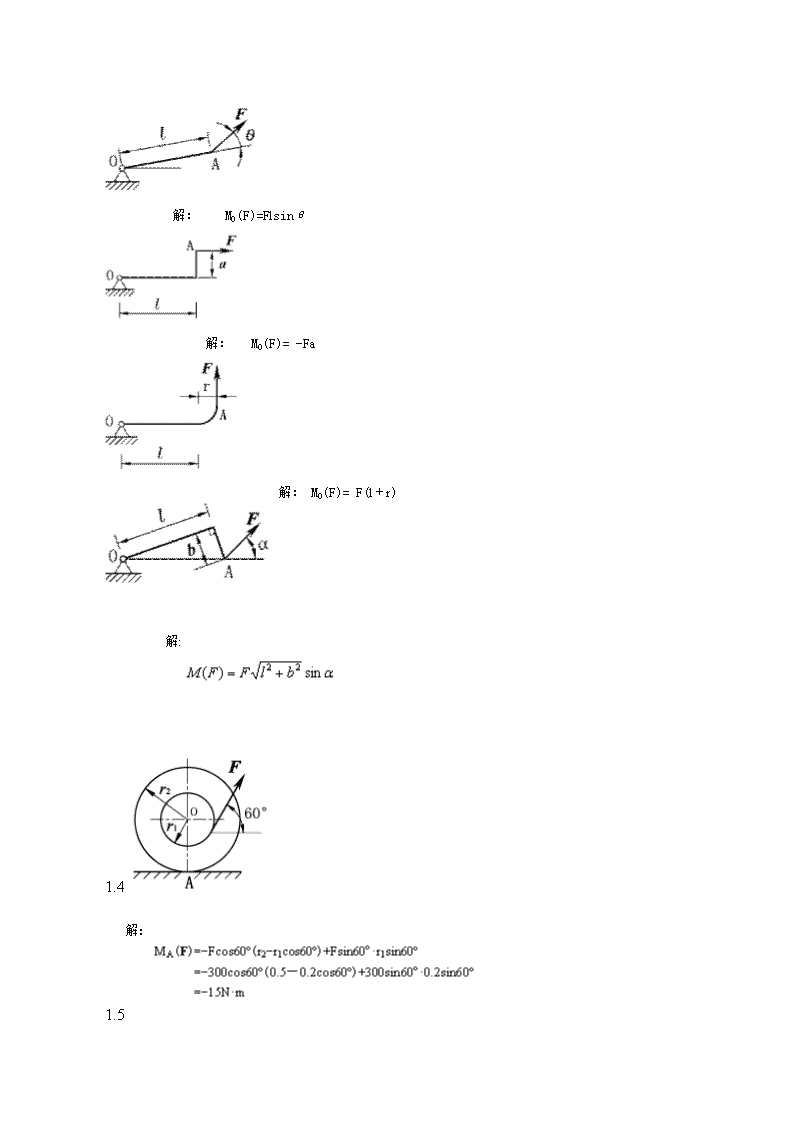
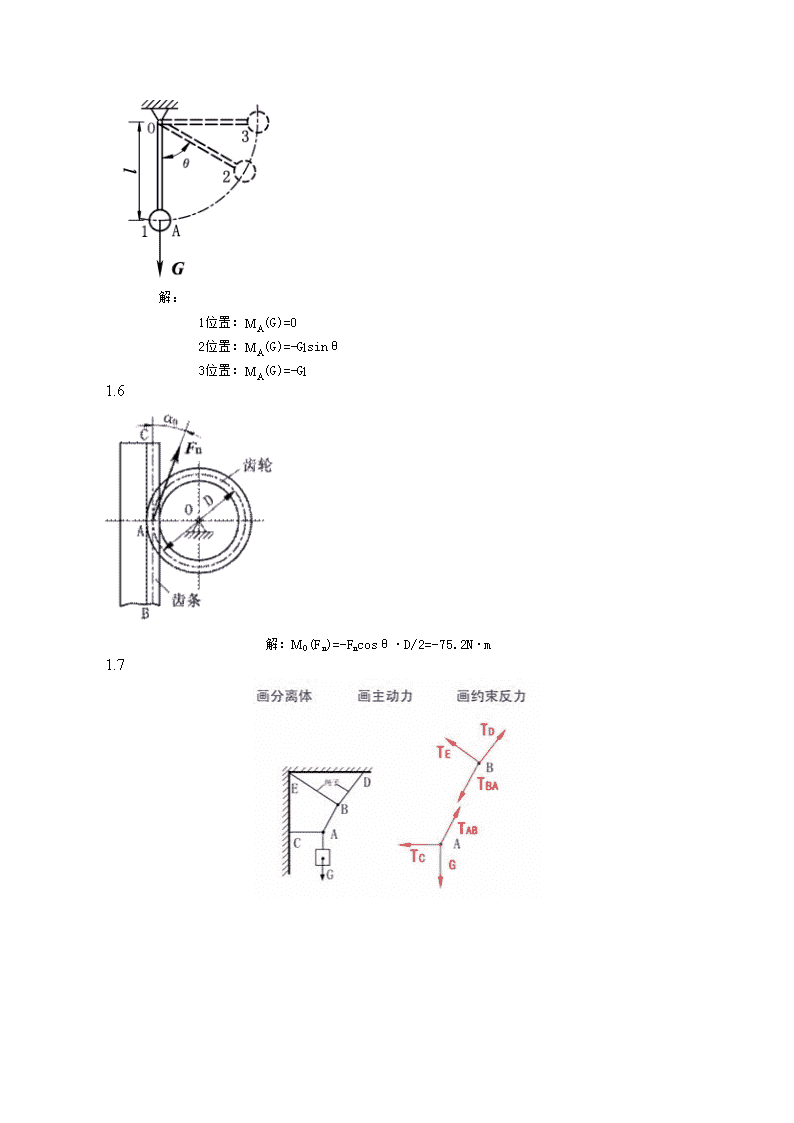
'第一章静力学基本概念1.1解F=Fx+Fy=Fxi+FyjF1=1000N=-1000Cos30ºi-1000Sin30ºjF2=1500N=1500Cos90ºi-1500Sin90ºjF3=3000N=3000Cos45ºi+3000Sin45ºjF4=2000N=2000Cos60ºi-2000Sin60ºj1.2因为前进方向与力FA，FB之间均为45º夹角，要保证二力的合力为前进方向，则必须FA=FB。所以：FB=FA=400N1.3解：MO(F)=Fl解：MO(F)=0解：MO(F)=Flsinβ 解：MO(F)=Flsinθ解：MO(F)=-Fa解：MO(F)=F(l＋r)解:1.4解:1.5 解：1位置：MA(G)=02位置：MA(G)=-Glsinθ3位置：MA(G)=-Gl1.6解：MO(Fn)=-Fncosθ·D/2=-75.2N·m1.7 1.8 第二章平面力系2.1力系简化解：（1）主矢大小与方位：F/Rx＝∑Fx＝F1cos45º+F3+F4cos60º＝100Ncos45º+200N+250cos60º＝395.7NF/Ry＝∑Fy＝F1sin45º-F2-F4sin60º＝100Nsin45º-150N-250sin60º＝-295.8N （2）主矩大小和转向：MO＝∑MO(F)＝MO(F1)+MO(F2)+MO(F3)+MO(F4)+m＝0-F2×0.3m+F3×0.2m+F4sin60×0.1m+F×0.1m＝0-150N×0.3m+200N×0.2m+250Nsin60×0.1m+50N×0.1m＝21.65N·m(Q)向O点的简化结果如图所示。2.2起吊重量解：根据O点所能承受的最大力偶矩确定最大起吊重量G×0.15m＝5kN·mG＝33.33kN2.3求支架的力A图：解:（1）取销钉A画受力图如图所示。AB、AC杆均为二力杆。（2）建直角坐标系，列平衡方程：∑Fx＝0，-FAB+FACcos60°＝0∑Fy＝0，FACsin60°-G＝0（3）求解未知量。FAB＝0.577G（拉）FAC＝1.155G（压） B图：解（1）取销钉A画受力图如图所示。AB、AC杆均为二力杆。（2）建直角坐标系，列平衡方程：∑Fx＝0，FAB-FACcos60°＝0∑Fy＝0，FACsin60°-G＝0（3）求解未知量。FAB＝0.577G（压）FAC＝1.155G（拉）C图：解（1）取销钉A画受力图如图所示。AB、AC杆均为二力杆。（2）建直角坐标系，列平衡方程：∑Fx＝0，-FAB+Gsin30°＝0∑Fy＝0，FAC-Gcos30°＝0（3）求解未知量。FAB＝0.5G（拉）FAC＝0.866G（压）D图：解（1）取销钉A画受力图如图所示。AB、AC杆均为二力杆。（2）建直角坐标系，列平衡方程：∑Fx＝0，-FABsin30°+FACsin30°＝0∑Fy＝0，FABcos30°+FACcos30°-G＝0（3）求解未知量。FAB＝FAC＝0.577G（拉） 2.4约束力解（1）取圆柱A画受力图如图所示。AB、AC绳子拉力大小分别等于G1，G2。（2）建直角坐标系，列平衡方程：∑Fx＝0，-G1+G2cosα＝0∑Fy＝0，FN＋G2sinα-G＝0（3）求解未知量。2.5求滚轮A，B所受到的压力解（1）取翻罐笼画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fx＝0，FNAsinα-FNBsinβ＝0∑Fy＝0，FNAcosα+FNBcosβ-G＝0（3）求解未知量与讨论。将已知条件G=3kN，α=30°，β=45°分别代入平衡方程，解得：FNA＝2.2kNFNA＝1.55kN有人认为FNA=Gcosα，FNB=Gcosβ是不正确的，只有在α=β=45°的情况下才正确。 2.6求AB和AC所受的力A图：解（1）取滑轮画受力图如图所示。AB、AC杆均为二力杆。（2）建直角坐标系如图，列平衡方程：∑Fx＝0，-FAB-Fsin45°+Fcos60°＝0∑Fy＝0，-FAC-Fsin60°-Fcos45°＝0（3）求解未知量。将已知条件F=G=2kN代入平衡方程，解得：FAB＝-0.414kN（压）FAC＝-3.15kN（压）B图：解：（1）取滑轮画受力图如图所示。AB、AC杆均为二力杆。（2）建直角坐标系如图，列平衡方程：∑Fx＝0，-FAB-FACcos45°-Fsin30°＝0∑Fy＝0，-FACsin45°-Fcos30°-F＝0（3）求解未知量。将已知条件F=G=2kN代入平衡方程，解得：FAB＝2.73kN（拉）FAC＝-5.28kN（压）2.7求挡板所受的压力解（1）取两圆管画受力图如图所示。 （2）建直角坐标系如图，列平衡方程：∑Fx＝0，FNcos30°－Gsin30°－Gsin30°＝0（3）求解未知量。将已知条件G=4kN代入平衡方程，解得：FN＝4.61kN若改用垂直于斜面上的挡板，这时的受力上图右建直角坐标系如图，列平衡方程：∑Fx＝0，FN－Gsin30°－Gsin30°＝0解得：FN＝4kN2.8求支座A，B处的约束力A图：解（1）取AB杆画受力图如图所示。支座A，B约束反力构成一力偶。（2）列平衡方程：∑Mi＝015kN·m-24kN·m+FA×6m＝0（3）求解未知量。FA＝1.5kN（↓）FB＝1.5kN（↑）B图：解（1）取AB杆画受力图如图所示。支座A，B约束反力构成一力偶。（2）列平衡方程：∑Mi＝0，FA×lsin45°-F×a＝0（3）求解未知量。C图：解（1）取AB杆画受力图如图所示。支座A，B约束反力构成一力偶。 （2）列平衡方程：∑Mi＝0，20kN×5m－50kN×3m＋FA×2m＝0（3）求解未知量。FA＝25kN（↓）FB＝25kN（↑）2.9求螺栓A，B，C，D所受的力解螺栓A，B受力大小（1）取电动机画受力图如图所示。螺栓A，B反力构成一力偶。（2）列平衡方程：∑Mi＝0，－M＋FA×a＝0（3）求解未知量。将已知条件M=20kN·m，a=0.3m代入平衡方程，解得：FA＝FB＝66.7kN螺栓C，D受力大小（1）取电动机和角架画受力图如图所示。螺栓C，D反力构成一力偶。（2）列平衡方程：∑Mi＝0，－M＋FC×b＝0（3）求解未知量。将已知条件M=20kN·m，b=0.6m代入平衡方程，解得：FC＝FD＝33.3kN2.10求连杆AB所受的力解 求连杆AB受力（1）取曲柄OA画受力图如图所示。连杆AB为二力杆。（2）列平衡方程：∑Mi＝0，－M1＋FAB×OAsin30º＝0（3）求解未知量。将已知条件M1=1N·m，OA=0.4m，代入平衡方程，解得：FAB＝5N；AB杆受拉。求力偶矩M2的大小（1）取铰链四连杆机构OABO1画受力图如图所示。FO和FO1构成力偶。（2）列平衡方程：∑Mi＝0，－M1＋M2－FO×（O1B－OAsin30º）＝0（3）求解未知量。将已知条件M1=1N·m，OA=0.4m，O1B=0.6m代入平衡方程，解得：M2＝3N·m2.11求钢绳拉力F和A，B的反力解（1）取上料小车画受力图如图所示。（2）建直角坐标系如图，列平衡方程：∑Fx＝0，F-Gsinα＝0∑Fy＝0，FNA+FNB-Gcosα＝0∑MC(F)＝0，-F×（d－e）-FNA×a+FNB×b＝0（3）求解未知量。将已知条件G=240kN，a=1m，b=1.4m，e=1m，d=1.4m，α=55°代入平衡方程，解得：FNA＝47.53kN；FNB＝90.12kN；F＝196.6kN2.12求立柱A端的约束反力 解（1）取厂房立柱画受力图如图所示。A端为固定端支座。（2）建直角坐标系如图，列平衡方程：∑Fx＝0，q×h－FAx＝0∑Fy＝0，FAy－G－F＝0∑MA(F)＝0，－q×h×h/2－F×a＋MA＝0（3）求解未知量。将已知条件F=60kN，q=2kN/m，G=40kN，a=0.5m，h=10m代入平衡方程，解得：FAx＝20kN（←）；FAy＝100kN（↑）；MA＝130kN·m（Q）2.13求图示梁的支座反力A图：解（1）取梁AB画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fx＝0，FAx-Fcos45º＝0∑Fy＝0，FAy-Fsin45º+FNB＝0∑MA(F)＝0，-Fsin45º×2m+FNB×6m＝0（3）求解未知量。将已知条件F=6kN代入平衡方程。解得：FAx＝4.24kN（→）；FAy＝2.83kN（↑）；FNB＝1.41kN（↑）。B图：解（1）取梁AB画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fx＝0，FAx-Fcos30º＝0∑Fy＝0，FAy-q×1m-Fsin30º＝0 ∑MA(F)＝0，-q×1m×1.5m-Fsin30º×1m+MA＝0（3）求解未知量。将已知条件F=6kN，q=2kN/m代入平衡方程，解得：FAx＝5.2kN（→）；FAy＝5kN（↑）；MA＝6kN·m（Q）。C图：解（1）取梁AB画受力图如图所示。因无水平主动力存在，A铰无水平反力。（2）建直角坐标系，列平衡方程：∑Fy＝0，FA-q×2m+FB＝0∑MA(F)＝0，-q×2m×2m+FB×3m+M＝0（3）求解未知量。将已知条件q=2kN/m，M=2kN·m代入平衡方程，解得：FA＝2kN（↑）；FB＝2kN（↑）。D图：解（1）取梁AB画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fx＝0，FAx-q×a＝0∑Fy＝0，FAy＝0∑MA(F)＝0，-q×a×0.5a+MA＝0（3）求解未知量。将已知条件q=2kN/m，M=2kN·m，a=1m代入平衡方程，解得：FAx＝2kN（→）；FAy＝0；MA＝1kN·m（Q）。E图：解（1）取梁AB画受力图如图所示。因无水平主动力存在，A铰无水平反力。（2）建直角坐标系，列平衡方程： ∑Fy＝0，FA-q×a＋FB-F＝0∑MA(F)＝0，q×a×0.5a+FB×2a-M-F×3a＝0（3）求解未知量。将已知条件F=6kN，q=2kN/m，M=2kN·m，a=1m代入平衡方程，解得：FA＝-1.5kN（↓）；FB＝9.5kN（↑）。F图：解（1）取梁AB画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fx＝0，FA－FBx＝0∑Fy＝0，FBy－F＝0∑MB(F)＝0，-FA×a+F×a+M＝0（3）求解未知量。将已知条件F=6kN，M=2kN·m，a=1m代入平衡方程，解得：FA＝8kN（→）；FBx＝8kN（←）；FBy＝6kN（↑）。G图：解（1）取梁AB画受力图如图所示。（2）建直角坐标系如图，列平衡方程：∑Fx＝0，FAx-FBsin30º＝0∑Fy＝0，FAy-F+FBcos30º＝0∑MA(F)＝0，-F×a-FBsin30º×a+FBcos30º×2a+M＝0（3）求解未知量。将已知条件F=6kN，M=2kN·m，a=1m代入平衡方程，解得：FB＝3.25kN（↖）；FAx＝1.63kN（→）；FAy＝3.19kN（↑）。H图：解：求解顺序：先解CD部分再解AC部分。解CD部分（1）取梁CD画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fy＝0，FC-F+FD＝0∑MC(F)＝0，-F×a＋FD×2a＝0 （3）求解未知量。将已知条件F=6kN代入平衡方程，解得：FC＝3kN；FD＝3kN（↑）解AC部分（1）取梁AC画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fy＝0，-F/C-FA＋FB＝0∑MA(F)＝0，-F/C×2a＋FB×a＝0（3）求解未知量。将已知条件F/C=FC=3kN代入平衡方程，解得：FB＝6kN（↑）；FA＝3kN（↓）。梁支座A，B，D的反力为：FA＝3kN（↓）；FB＝6kN（↑）；FD＝3kN（↑）。I图：解：求解顺序：先解CD部分再解ABC部分。解CD部分（1）取梁CD画受力图如上左图所示。（2）建直角坐标系，列平衡方程：∑Fy＝0，FC-q×a+FD＝0∑MC(F)＝0，-q×a×0.5a+FD×a＝0（3）求解未知量。将已知条件q=2kN/m，a=1m代入平衡方程。解得：FC＝1kN；FD＝1kN（↑）解ABC部分（1）取梁ABC画受力图如上右图所示。（2）建直角坐标系，列平衡方程：∑Fy＝0，-F/C+FA+FB-F＝0∑MA(F)＝0，-F/C×2a+FB×a-F×a-M＝0（3）求解未知量。将已知条件F=6kN，M=2kN·m，a=1m，F/C=FC=1kN代入平衡方程。解得：FB＝10kN（↑）；FA＝-3kN（↓）梁支座A，B，D的反力为：FA＝-3kN（↓）；FB＝10kN（↑）；FD＝1kN（↑）。J图：解：求解顺序：先解IJ部分，再解CD部分，最后解ABC部分。 解IJ部分（1）取IJ部分画受力图如右图所示。（2）建直角坐标系，列平衡方程：∑Fy＝0，FI-50kN-10kN+FJ＝0∑MI(F)＝0，-50kN×1m-10kN×5m+FJ×2m＝0（3）求解未知量。解得：FI＝10kN；FJ＝50kN解CD部分（1）取梁CD画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fy＝0，FC-F/J+FD＝0∑MC(F)＝0，-F/J×1m+FD×8m＝0（3）求解未知量。将已知条件F/J=FJ=50kN代入平衡方程。解得：FC＝43.75kN；FD＝6.25kN（↑）解ABC部分（1）取梁ABC画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fy＝0，-F/C-F/I-FA+FB＝0∑MA(F)＝0，-F/C×8m+FB×4m-F/I×7m＝0（3）求解未知量。将已知条件F/I=FI=10kN，F/C=FC=43.75kN代入平衡方程。解得：FB＝105kN（↑）；FA＝51.25kN（↓）梁支座A,B,D的反力为：FA＝51.25kN（↓）；FB＝105kN（↑）；FD＝6.25kN（↑）。K图：解：求解顺序：先解BC段，再解AB段。解BC段解AB段 （1）取梁BC画受力图如上左图所示。（2）建直角坐标系，列平衡方程：∑Fy=0，FC-q×a+FB=0∑MB(F)=0，-q×a×0.5a+FC×2a=0（3）求解未知量。将已知条件q=2kN/m，a=1m代入平衡方程。解得：FC=0.5kN（↑）；FB=1.5kN（1）取梁AB画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fy=0，FA-q×a-F/B=0∑MA(F)=0，-q×a×1.5a＋MA-F/B×2a=0（3）求解未知量。将已知条件q=2kN/m，M=2kN·m，a=1m，F/B=FB=1.5kN代入平衡方程，解得：FA=3.5kN（↑）；MA=6kN·m（Q）。梁支座A,C的反力为：FA=3.5kN（↑）；MA=6kN·m（Q）；FC=0.5kN（↑）L图：解：求解顺序：先解AB部分，再解BC部分。解AB部分（1）取梁AB画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fy=0，FA-F+FB=0∑MA(F)=0，-F×a+FB×a=0（3）求解未知量。将已知条件F=6kN，a=1m代入平衡方程。解得：FA=0；FB=6kN解BC部分（1）取梁BC画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fy=0，FC-F/B=0∑MC(F)=0，F/B×2a＋M－MC=0（3）求解未知量。将已知条件M=2kN·m，a=1m，F/B=FB=6kN代入平衡方程。解得：FC=6kN（↑）；MC=14kN·m（P）。梁支座A,C的反力为：FA=0；MC=14kN·m（P）；FC=6kN（↑）2.14试求A，B间的最小距离解（1）取水塔和支架画受力图如图所示。当AB间为最小距离时，处于临界平衡，FA=0。 （2）建直角坐标系，列平衡方程：∑MB(F)＝0，-q×6m×21m+G×0.5lmin＝0（3）求解未知量。将已知条件G=160kN，q=16kN/m代入平衡方程，解得：lmin＝2.52m2.15试求汽车的最大起重量G解:（1）取汽车起重机画受力图如图所示。当汽车起吊最大重量G时，处于临界平衡，FNA=0。（2）建直角坐标系，列平衡方程：∑MB(F)=0，-G2×2.5m+Gmax×5.5m+G1×2m=0（3）求解未知量。将已知条件G1=26kN，G2=4.5kN代入平衡方程，解得：Gmax=7.41kN2.16试求汽车自重G2解:（1）分别取BCE和AOB画受力图如图所示。 （2）建直角坐标系，列平衡方程：对BCE列∑Fy＝0，FBy－G2＝0对AOB列∑MO(F)＝0，－F/By×a＋F×l＝0（3）求解未知量。将已知条件FBy=F/By，F=G1代入平衡方程，解得：G2＝lG1/a2.17求驱动力偶矩解：求解顺序：先解锯弓，再解锯床转盘。解锯弓（1）取梁锯弓画受力图如图所示。（2）建直角坐标系，列平衡方程：∑FX=0，F-FBAcos15º=0∑Fy=0，FD+FBAsin15º-FC=0∑MB(F)=0，-FC×0.1m+FD×0.25m+F×0.1m=0（3）求解未知量。将已知条件F=5kN代入平衡方程。解得：FBA=5.18kNFD=-2.44kN(↓)FC=-1.18kN(↑)解锯床转盘（1）取锯床转盘画受力图如图所示。　（2）建直角坐标系，列平衡方程：∑FX=0，FABcos15º-FOX=0∑Fy=0，FOy-FABsin15º=0∑MO(F)=0，-FABcos15º×0.1m+M=0（3）求解未知量。将已知条件FAB=FBA=5.18kN代入平衡方程，解得：FOX=5kN（→）FOy=1.34kN(↑)M=500N·m(Q)2.18求作用于曲柄OA上之力偶矩M解： （1）分别取电机O，连杆AB，推料板O1C画受力图如图所示。（2）取连杆AB为研究对象∑MA(F)＝0，-F/By×2m-G2×1m＝0∑MB(F)＝0，-FAy×2m+G2×1m＝0∑Fx＝0，FAx-F/Bx＝0将已知条件G2=300N代入平衡方程，解得：FAy=150N；F/By=150N；FAx＝F/Bx（3）取推料板O1C为研究对象∑MO1(F)＝0，-FBx×0.4m×sinα+G×0.4m×cosα-FBy×0.4m×cosα+F×0.4m＝0将已知条件G=600N，α=45°，F=1000N，F/By＝FBy＝-150N代入平衡方程，解得：FBx=2164NFAx＝F/Bx＝2164N（4）取电机O为研究对象∑MO(F)＝0，-F/Ax×0.2m×cosα+F/Ay×0.2m×sinα+M＝0将已知条件FAx＝F/Ax＝2164N，FAy＝F/Ay＝150N，α=45°代入平衡方程，解得：M＝285N·m。2.19求人能够达到的最大高度　解：设能够达到的最大高度为h，此时梯子与地面间的摩擦力为最大静摩擦力。（1）取梯子画受力图如图所示。（2）建直角坐标系，列平衡方程：∑Fy＝0，FNB－G－G人＝0∑MA(F)＝0， -G×0.5l×cosα-G人×(l-h/sinα)×cosα-Ffm×l×sinα+FNB×l×cosα＝0Ffm＝fSFNB（3）求解未知量。将已知条件G=200N，l=3m，fS＝0.25，G人＝650N，α=60°代入平衡方程。解得：h=1.07mm2.20尺寸b应为多大解：由砖的受力图与平衡要求可知：Ffm＝0.5G＝0.5F；FNA＝FNB至少要等于Ffm/fs＝F＝G再取AHB讨论，受力图如图所示：要保证砖夹住不滑掉，图中各力对B点逆时针的矩必须大于各力对B点顺时针的矩。即：F×0.04m＋F/fm×0.1m≥F/NA×b代入Ffm＝F/fm＝0.5G＝0.5F；FNA＝F/NA＝F＝G可以解得：b≤0.09m＝9cm2.21求制动所需的最小力F1的大小A图：解：（1）取圆轮、制动装置画受力图如图所示。（2）建直角坐标系，列平衡方程：取圆轮列平衡方程：∑MO(F)＝0，-Ffm×r+M＝0Ffm＝fSFN解得Ffm＝M/r；FN＝M/rfS取制动装置列平衡方程：∑MA(F)＝0，-F1×b-F/fm×c+F/N×a＝0 解得：B图：解：（1）取圆轮、制动装置画受力图如图所示。（2）建直角坐标系，列平衡方程：取圆轮列平衡方程：∑MO(F)＝0，-Ffm×r+M＝0Ffm＝fSFN解得Ffm＝M/r；FN＝M/rfS取制动装置列平衡方程：∑MA(F)＝0，-F2×b+F/N×a＝0解得：C图：解：（1）取圆轮、制动装置画受力图如图所示。（2）建直角坐标系，列平衡方程：取圆轮列平衡方程：∑MO(F)＝0，-Ffm×r+M＝0Ffm＝fSFN解得Ffm＝M/r；FN＝M/rfS取制动装置列平衡方程：∑MA(F)＝0，-F3×b＋F/fm×c＋F/N×a＝0解得： 第四章轴向拉伸与压缩4.1求轴力画轴力图A图：解：（1）分段计算轴力杆件分为2段。用截面法取图示研究对象画受力图如图，列平衡方程分别求得：FN1=F（拉）；FN2=-F（压）（2）画轴力图。根据所求轴力画出轴力图如图所示。B图：解：（1）分段计算轴力杆件分为3段。用截面法取图示研究对象画受力图如图，列平衡方程分别求得：FN1=F（拉）；FN2=0；FN3=2F（拉）（2）画轴力图。根据所求轴力画出轴力图如图所示。 C图：解：（1）计算A端支座反力。由整体受力图建立平衡方程：∑Fx＝0，2kN-4kN+6kN-FA＝0FA＝4kN(←)（2）分段计算轴力杆件分为3段。用截面法取图示研究对象画受力图如图，列平衡方程分别求得：FN1=-2kN（压）；FN2=2kN（拉）；FN3=-4kN（压）（3）画轴力图。根据所求轴力画出轴力图如图所示。D图：解：（1）分段计算轴力杆件分为3段。用截面法取图示研究对象画受力图如图，列平衡方程分别求得：FN1=-5kN（压）；FN2=10kN（拉）；FN3=-10kN（压）（2）画轴力图。根据所求轴力画出轴力图如图所示。 4.2求应力和应变解：4.3求杆件变形解:由截面法可以计算出AC，CB段轴力FNAC=-50kN（压），FNCB=30kN（拉）。4.4求应力和变形 4.5校核强度4.6校核强度 4.7设计直径4.8求所吊重物重量 　　4.9求许用荷载　　4.10求弹性模量和泊松比 4.11求许用荷载4.12求支座反力第五章剪切与挤压的实用计算5.1计算切断力 5.2求螺栓直径与螺栓头高度的比例5.3计算焊接板的许用荷载 5.4求接头处所需的尺寸5.5求拉杆的许用荷载 第六章圆轴扭转6.1扭矩图A图：解：（1）计算扭矩。将轴分为2段，逐段计算扭矩。对AB段：∑MX＝0，T1－3kN·m＝0可得：T1＝3kN·m对BC段：∑MX＝0，T2－1kN·m＝0可得：T2＝1kN·m（2）画扭矩图。根据计算结果，按比例画出扭矩图如图。B图： 解：（1）计算扭矩。将轴分为3段，逐段计算扭矩。对AB段：∑Mx＝0，T1＋4.5kN·m－1.5kN·m－2kN·m＝0可得：T1＝-1kN·m对BC段：∑Mx＝0，T2－1.5kN·m－2kN·m＝0可得：T2＝3.5kN·m对BC段：∑Mx＝0，T3－2kN·m＝0可得：T3＝2kN·m（2）画扭矩图。根据计算结果，按比例画出扭矩图如图。6.2是否有利解：（1）计算外力偶矩。MA=9549×60/200=2864.7N·m同理可得：MB=954.9N·m，MC=716.2N·m，MD=1193.6N·m（2）计算扭矩。将将轴分为3段，逐段计算扭矩。对AB段：∑Mx＝0，T1＋MB＝0可得：T1＝-954.9N·m对BC段：∑Mx＝0，T2＋MB－MA＝0可得：T2＝1909.8N·m对BC段：∑Mx＝0，T3－M＝0可得：T3＝1193.6N·m（3）画扭矩图。根据计算结果，按比例画出扭矩图如右图。（4）将轮A和轮C位置对调后，由扭矩图可知最大绝对值扭矩较之原来有所降低，对轴的受力有利。 6.3求圆轴传递功率解：WP=πd3/16=24543.7mm3由τmax=T/WP可得：T=1472.6N·m由M=T=9549×P/n可得：P=T×n/9549=18.5kW6.4空心与实心轴比较6.5校核轴强度和刚度 6.6设计轴直径 6.7求钢材的E和G第七章平面弯曲内力7.1指定截面上的剪力和弯矩A图　B图 C图D图 7.2画剪力图和弯矩图A图B图 C图 D图 E图 F图 7.3梁的剪力图和弯矩图解：（1）由静力平衡方程得：FA=F，MA=Fa，方向如图所示。（2）利用M，FS，q之间的关系分段作剪力图和弯矩图。（3）梁最大绝对值剪力在AB段内截面，大小为2F。梁最大绝对值弯矩在C截面，大小为2Fa。B图 解：（1）由静力平衡方程得：FA=3ql/8（↑），FB=ql/8（↑）。（2）利用M，FS，q之间的关系分段作剪力图和弯矩图。（3）梁的最大绝对值剪力在A右截面，大小为3ql/8。梁的最大弯矩绝对值在距A端3l/8处截面，大小为9ql2/128。C图解：（1）由静力平衡方程得：FB=2qa，MB=qa2，方向如图所示。（2）利用M，FS，q之间的关系分段作剪力图和弯矩图。（3）梁的最大绝对值剪力在B左截面，大小为2qa。梁的最大绝对值弯矩在距AC段内和B左截面，大小为qa2。D图 解：（1）由静力平衡方程得：FA=qa/2（↓），FB=qa/2（↓）。（2）利用M，FS，q之间的关系分段作剪力图和弯矩图。（3）梁的最大绝对值剪力在AC和DB段内，大小为qa/2。梁的最大弯矩绝对值在AB跨中间截面，大小为5qa2/8。E图 解：（1）由静力平衡方程得：FA=9qa/4（↑），FB=3qa/4（↑）。（2）利用M，FS，q之间的关系分段作剪力图和弯矩图。（3）梁最大绝对值剪力在A右截面，大小为5qa/4。梁最大弯矩绝对值在A截面，大小为qa2/2。F图解：（1）由静力平衡方程得：FA=F（↑），FB=3F（↑）。（2）利用M，FS，q之间的关系分段作剪力图和弯矩图。（3）梁最大绝对值剪力在DB段内截面，大小为3F。梁最大弯矩绝对值在D截面，大小为3Fa。 G图解：（1）由静力平衡方程得：FA=4.5qa（↑），FB=0.5qa（↑）。（2）利用M，FS，q之间的关系分段作剪力图和弯矩图。（3）梁最大绝对值剪力在A右截面，大小为3.5qa。梁最大弯矩绝对值在A右截面，大小为3qa2。　H图解：（1）由静力平衡方程得：FA=1.25qa（↑），FB=0.75qa（↑）。（2）利用M，FS，q之间的关系分段作剪力图和弯矩图。（3）梁最大绝对值剪力在CA段内截面，大小为qa。梁最大弯矩绝对值在A右截面，大小为qa2。 7.4试画梁的荷载图和弯矩图解：利用M，FS，q之间的关系推出荷载图和弯矩图如下。7.5判断图中的FS，M图是否有错A图解：有错，改正如下图。 B图解：有错，改正如下图。C图解：有错，改正如下图。 D图解：有错，改正如下图。第八章平面弯曲梁的强度与刚度计算 8.1立放和平放时产生的最大正应力8.2求梁内最大拉应力和最大压应力 8.3截面二次矩A图：B图：8.4截面二次矩 8.5选择此梁的工字钢型号 8.6求内经d的最大值8.7试校核此梁的强度 8.8设计正方形截面和矩形截面 8.9求最大许可荷载[F]8.10试校核压板的强度 8.11点和b点的正应力和切应力 8.12求梁内最大正应力和切应力8.13试校核梁的强度 8.14试选择合适的工字钢型号 第九章应力状态与强度理论9.1求试样拉力F9.2求最大正应力和最大切应力9.3绘出A点处的原始单元体A图解： B图解：9.4求图示单元体指定斜面上的应力A图：B图： C图：9.5求主应力的大小和主平面的方位A图： B图：C图： 9.6求主应力的大小和主平面的方位A图：B图 9.7试对钢制零件进行强度校核1）2） 9.8试对铸铁零件进行强度校核1）2）9.9按第三强度理论设计壁厚δ9.10第三和四强度理论校核轴的强度 第十章组合变形时杆件的强度计算10.1试求切口的允许深度10.2试校核梁的强度 10.3最大压应力之比10.4确定许用荷载[F] 10.5选择圆柱的内径d 10.6按第三强度理论校核轴的强度 10.7按第三强度理论校核轴的强度 '