- 1.82 MB
- 2022-04-22 11:42:05 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
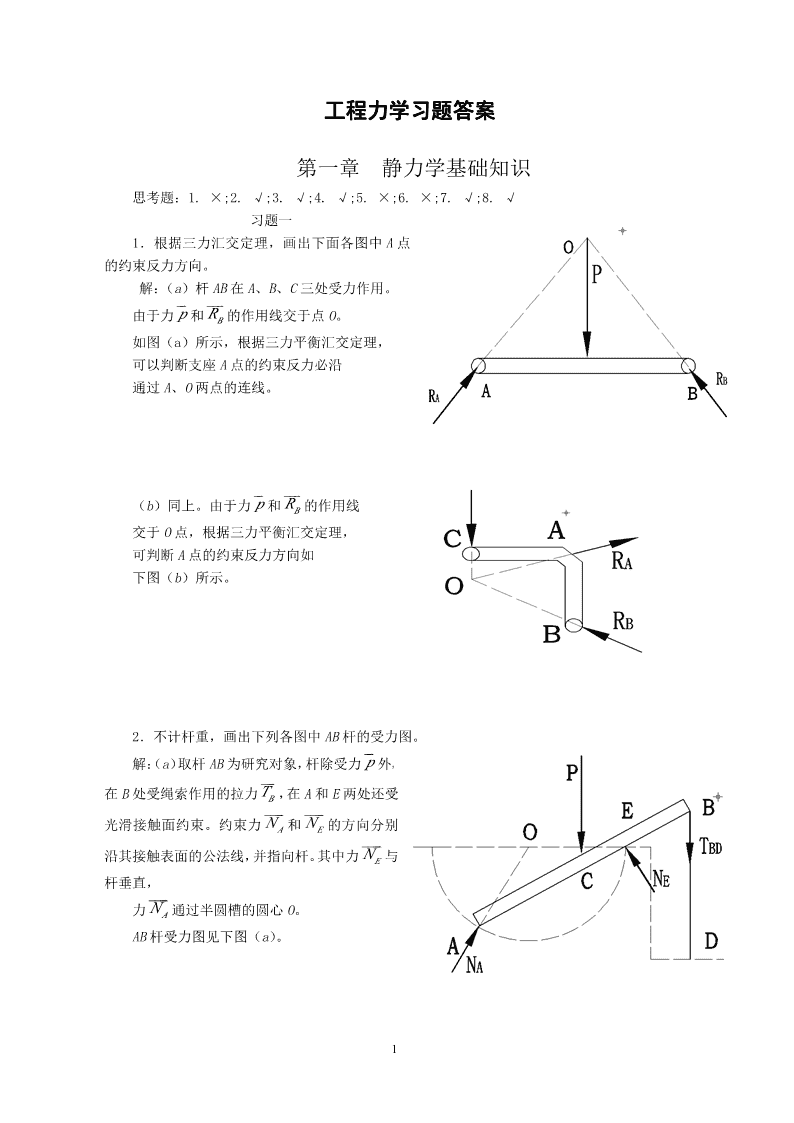
'工程力学习题答案第一章静力学基础知识思考题:1.×;2.√;3.√;4.√;5.×;6.×;7.√;8.√习题一1.根据三力汇交定理,画出下面各图中A点的约束反力方向。解:(a)杆AB在A、B、C三处受力作用。�����由于力p和R的作用线交于点O。B如图(a)所示,根据三力平衡汇交定理,可以判断支座A点的约束反力必沿通过A、O两点的连线。�����(b)同上。由于力p和R的作用线B交于O点,根据三力平衡汇交定理,可判断A点的约束反力方向如下图(b)所示。2.不计杆重,画出下列各图中AB杆的受力图。��解:(a)取杆AB为研究对象,杆除受力p外,���在B处受绳索作用的拉力T,在A和E两处还受B��������光滑接触面约束。约束力N和N的方向分别AE����沿其接触表面的公法线,并指向杆。其中力N与E杆垂直,����力N通过半圆槽的圆心O。AAB杆受力图见下图(a)。1
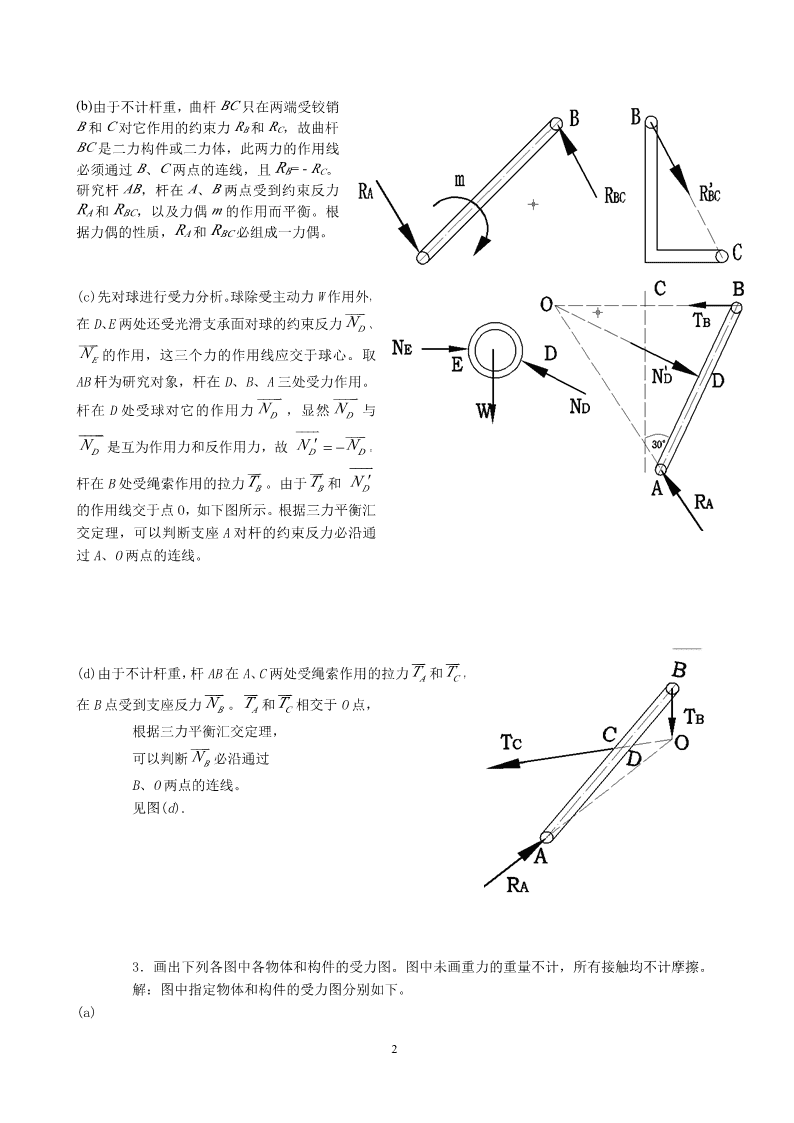
(b)由于不计杆重,曲杆BC只在两端受铰销B和C对它作用的约束力RB和RC,故曲杆BC是二力构件或二力体,此两力的作用线必须通过B、C两点的连线,且RB=-RC。研究杆AB,杆在A、B两点受到约束反力RA和RBC,以及力偶m的作用而平衡。根据力偶的性质,RA和RBC必组成一力偶。(c)先对球进行受力分析。球除受主动力W作用外,����在D、E两处还受光滑支承面对球的约束反力N、D����N的作用,这三个力的作用线应交于球心。取EAB杆为研究对象,杆在D、B、A三处受力作用。����������杆在D处受球对它的作用力N,显然N与DD�������������N是互为作用力和反作用力,故N′=−N。DDD����������杆在B处受绳索作用的拉力T。由于T和N′BBD的作用线交于点O,如下图所示。根据三力平衡汇交定理,可以判断支座A对杆的约束反力必沿通过A、O两点的连线。������(d)由于不计杆重,杆AB在A、C两处受绳索作用的拉力T和T,AC����������在B点受到支座反力N。T和T相交于O点,BAC根据三力平衡汇交定理,����可以判断N必沿通过BB、O两点的连线。见图(d).3.画出下列各图中各物体和构件的受力图。图中未画重力的重量不计,所有接触均不计摩擦。解:图中指定物体和构件的受力图分别如下。(a)2
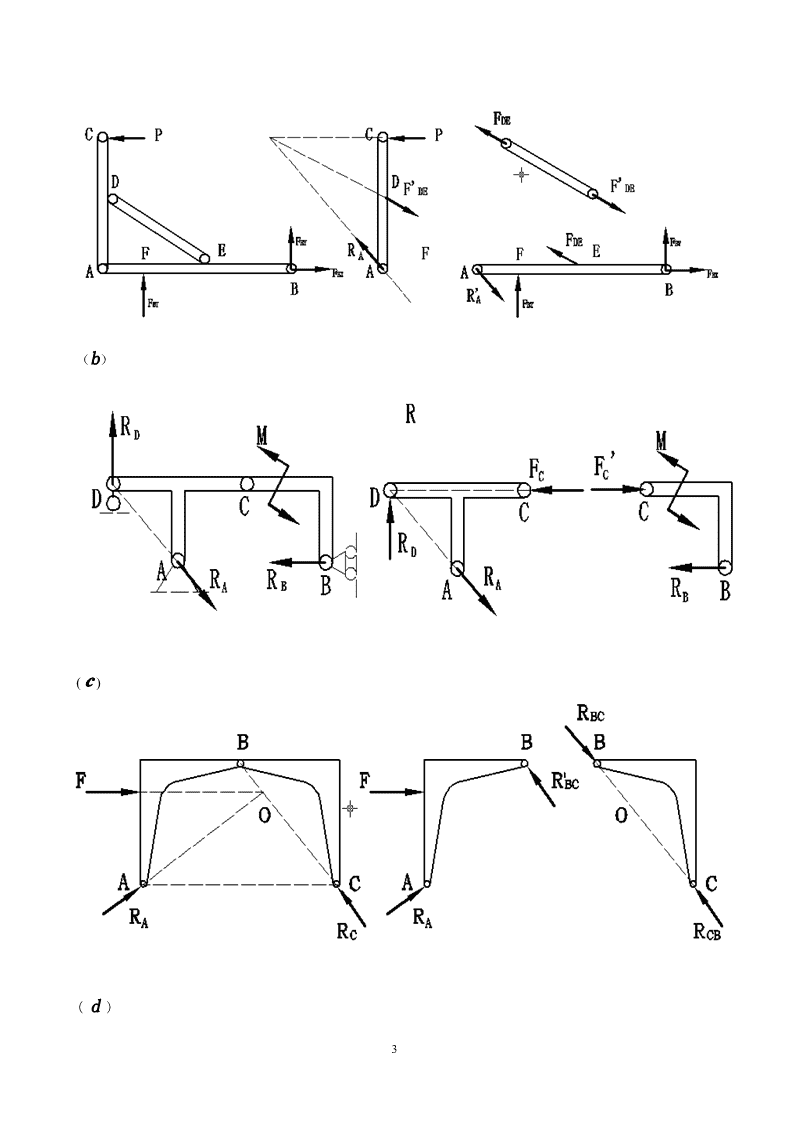
(b)(c)(d)3
(e)(f)4
(g)(h)5
(i)6
7
工程力学习题答案第二章力系的简化与平衡思考题:1.√;2.×;3.×;4.×;5.√;6.×;7.×;8.×;9.√.习题二1.平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm,求此力系向O点简化的结果,并确定其合力位置。���解:设该力系主矢为R′,其在两坐标轴上的投影分别为R、R。由合力投影定理有:xy角Rx=∑xi=1.53−=-1.5kNRy=∑yi=−2kN22R′=(∑xi)+(∑yi)=2.5kNsinα=∑yRi/′=−0.8;cosα=∑xRi/′=−0.6α≈53°(合力或主矢与x轴所夹锐角)由合力矩定理可求出主矩:���3M0=∑MF0()i=×30.310×−15000.21008020000.5×−−−×=−580N.m合力大小为:R=R"=2.5kN,方向α≈53°如图所示。580位置:d=M′/R==0.232m=23.2cm,位于O点的右侧。02500�2.火箭沿与水平面成β=25角的方向作匀速直线运动,如图所示。火箭的推力F=100kN与运动1�方向成θ=5角。如火箭重P=200kN,求空气动力F和它与飞行2方向的交角γ。解:火箭在空中飞行时,若只研究它的运行轨道问题,可将火箭作为质点处理。这时画出其受力和坐标轴x、y如下图所示,可列出平衡方程。1
∑y=0;F2−Gcos(θ+β)=0(G应为P)�故空气动力F=Gcos30=173kN2��由图示关系可得空气动力F与飞行方向的交角为γ=90+α=95。(α应为Υ)23.如图所示,移动式起重机不计平衡锤的重为P=500kN,其重心在离右轨1.5m处。起重机的起重量为P=250kN,突臂伸出离右轨10m。跑车1本身重量略去不计,欲使跑车满载或空载时起重机均不致翻倒,求平衡锤的最小重量P以及平衡锤到2左轨的最大距离x。解:起重机整体受力如图。满载时要使起重机��不发翻倒,需同时满足FNA≥0和∑MB()F=0,Px(+3)3−F−1.5P−10P=02NA1解得:Px(+3)≥3250(1)2��空载时,要使起重机不翻倒,需同时满足∑MA()F=0,Px−3F−4.5P=0和F≥02NBNB解得:Px≤2250(2)2由(1)、(2)两式得:P≥333.3kN,x≤6.75m2即:P=333.3kN,x=6.75m2minmax4.梁AB的支承和荷载如图,CB⊥AB,梁的自重不计。则其支座B的反力R大小为多少?B解:梁受力如图所示:��由∑MA()F=0得:22�(−××+4211040−××−140××+4Rsin30×=40(40应为4)B22=-8+10-2√2–8√2+2RBRB=5√2–1=6.07kN(-4×2×1+10-40.sin45°×1-40.cos45°×4+RBsin30°×4=0)解得;(RB=502169.7−=kN)RB=5√2–1=6.07kN5.起重机构架如图示,尺寸单位为cm,滑轮直径为d=20cm,钢丝绳的倾斜部分平行于BE杆,吊起的荷载Q=10kN,其它重量不计。求固定铰链支座A、B的反力。解:先研究杆AD如图(a)2
(下面第一种解法是弯路,请看第二种解法)(a)(b)yAECyDyAAxAD600yBxAxDACDxBBQ3310(解法1)由几何关系可知:tanα=,sinα=,CD=45sinα��由∑MA()F=0,YDi800+Qsin(800α−CD)=0∑Y=0,YA+Qsinα+YD=0解得:Y=−5.875kN,Y=−0.125kNDA再研究整体,受力如图(b),由∑Y=0,YA+YB−Q=0∑X=0,XA+XB=0��∑MA()F=0,XBi600−Q(80030010++)=0解得:Y=10.125kN,X=−18.5kN,X=18.5kNBAB(解法2)解:(1)取整体为研究对象,画受力图,列平衡方程∑Yi=0,YA+YB–Q=0YA+YB=Q=10kN(1)∑Xi=0,XA+XB=0(2)∑MD=0,XB.6-YA.8-YB.8–Q.3.1=0XB=111/6=18.5kN代入(2)式,得XA=-18.5kN取ACD杆为研究对象,画受力图∑MD=0,-YA×8–Q×0.1=0YA=-10×0.1/8=-0.125kN代入(1),得Y=-Y+10=10.125kN3
6.平面桁架的支座和荷载如图所示,求杆1,2和3的内力。解:用截面法,取CDF部分,受力如图(b),D1CD1CF1Ca/2FCF32FADF2EFFF2F3a/2FFBFAa/3a/3a/3由∑X=0,−F3=0��2∑MD()F=0,−aF−aF2=032解得:F=0,F=−F(压)323再研究接点C,受力如图(c)��aa有∑MF()F=0,F1i−F2i=0(g为×号F1.a/2–F2.a/3=0)234解得:F=−F(压)197.梁的支座及荷载如图所示,求支座的约束力。解:(a)AB梁受力如图(a)所示。QFFAxMFAyFNBbbbb(a)由∑X=0,FAX=0∑Y=0,FAY−qbF−+FNB=0��b∑MA()F=0,FNBi2bM−−Fbqb+i=0(注意:式中的“g”是“×”号,以下同)24
FM5解得:F=0,F=−+qb,AXAY22b4FM1F=+−qbNBF22b4q(b)AB梁受力如图(b)所示。由∑X=0,FAX=0Y=0,−+FF−1qbFi3+=0AB∑AYNBFAx2��1FAyFNB∑MA()F=0,Fb−qbbFi3i+NBi2b=0b2bb23313解得:F=F+qb,F=−F+qbAYNB2424(c)先研究BC梁,如图(c)所示。1���由∑MB()F=0,FNCi6cos30−2063××=0(应为sin30°)�∑X=0,FBX−FNCsin60=0�∑Y=0,FBY−206×−FNCcos60=0解得:F=120kN,F=603kN,F=60kNNCBXBY再研究AB梁.受力如图(c2)所示。FAy40kNm由∑X=0,FAX−FBX′=0FAxBFBx"A∑Y=0,FAY−FBY′=0��MAFBy"∑MA()F=0,MA−3FBY′−40=0解得:F=104kN,F=60kN,M=220kΝimAXAYA(d)先研究CD梁,受力如图(d)。12.5kN/m5kN.m由∑X=0,FCX=0FCx∑Y=0,FND+FCY−2.52×=0C��∑MD()F=0,−4FCY−+52.523××=0FCyFND5
解得:F=2.5kN,F=0,CYCX2.5kN/mF=2.5kN5kNNDFAx再研究ABC梁,受力如图(d)所示。2A由∑X=0,FAX−FCX′=0��FAyFNB∑MB()F=0,−2FAY+×−512.5212××−FCY′=0∑Y=0,FAY+FNB−2.525×−−FCY′=0解得:F=0,F=−2.5kN,F=15kNAXAYNB�8.图示夹钳夹住钢管,已知钳口张角为20,F=F。问钢管与夹钳间的静摩擦因数至少应为多少1才夹得住而不至滑落?(应为F=F’)解:取钢管为研究对象,设管、钳摩擦力为F1、F1’,受力如图.列出平衡方程:�"��"�∑X=0,F1cos10+F1cos10−N1cos80−N1cos80=0①"""根据结构的对称性及F=F知:F=F,N=N②1111""钢管处于临界状态时:F≤fN,F≤fN③1111�cos80联立可解得:f≥=0.176�cos10既钢管与夹钳的静摩擦因数至少应为0.176才夹得住而不至滑落。(解法2):由考虑摩擦时物体平衡条件与主动力大小无关,而与其方向有关(见课本P61:(4)自锁现象),且当物体处于将要滑动的临界状态时Fmax=fN=tanfmN,fm=10°即f=tanfm=tan10°=0.1769.尖劈起重装置如图所示。尖劈A的顶角为α,B块受力F作用。A块与B块之间的静摩擦因数为1f(有滚珠处摩擦力忽略不计)。如不计A块与B块的重量,求能保持平衡的力F范围。2(a)6
解:当F较小时,B块有沿尖劈向下滑动趋势,此时B块及尖劈A受力如图(a)。2对滑块B有:∑Y=0,−F1+N1cosα+Fmaxsinα=0①处于临界状态时Fmax=fN1②F1将②代入①可得:N=③1cosα+fsinα""对于尖劈A:∑X=0,−F2+N1cosα+Fmaxcosα=0既:−F+Nsinα−fNcosα=0④211sinα−fcosαtanα−f联立③④可解得:F=F=F2min11cosα+fsinα1+ftanα再求F的最大值,此时B块有沿尖劈向上滑动趋势,受力如图(b)。用上述同样的办法可求得:2tanα+fF=F2max11−ftanα因此,使系统保持平衡的力F范围为:2tanα−ftanα+fF≤F≤F1211+ftanα1−ftanα10.杆子的一端A用球铰链固定在地面上,杆子受到30kN的水平力的作用,用两根钢索拉住,使杆保持在铅直位置,求钢索的拉力F、F和A点的约束力。T1T27
解:研究竖直杆子,受力如图示。���由∑MX()Fi=0,3049×−FT2cossinαβ=0①���∑MY()Fi=0,−6FT1+FT2coscosαβ=0②∑X=0,FT2coscosαβ+XA−FT1=0③∑Y=0,YA+FT2cossinαβ−30=0④∑Z=0,−FT2sinα+ZA=0⑤59由三角关系知:cosα==0.486,sinα==0.874106106sinβ=0.6,cosβ=0.8⑥将⑥代入①得:F=45.8kNT2将F=45.8kN代入②可得:F=26.7kNT2T1将F,F分别代入③、④、⑤可得:T1T2X=8.90kN,Y=16.67kN,Z=40.00kNAAA���既F=8.90i+16.67j+40.00k(kN)NA11.图示长方形均质薄板重P=200Ν,用球铰链A和蝶铰链B固定在墙上,并用绳子CE维持在水平位置。求绳子拉力及支承约束力。(提示:由于间隙,蝶铰链约束相当于轴心为y轴的轴承,只有两个约束力分量。)解:研究板,受力如图。设CD=a,BC=b���b�由∑MY(F)=0,pi−bFTsin30=02���∑MX(F)=0,�aaFsin30−pi+Fa=0TBZ2���∑MZ(F)=0,−aFBX=0∑X=0,��F+F−Fcoa30sin30=0AXBXT��∑Y=0,FAY−FcoaT30cos30=0�∑Z=0,FAZ−PF+Tsin30+FBZ=0解得:F=200Ν,F=F=0,TBZBXF=86.6Ν,F=150Ν,F=100Ν。AXAYAZ12.作用于齿轮上的齿合力F推动胶带轮绕水平轴AB作匀速转动。已知胶带紧边的拉力为200N,松边的拉力为100N,尺寸如图所示。求力F的大小和轴承A、B的约束力。8
解:整体受力如图所示,由����∑MZ()Fi=0,−Fcos20×1202008010080+×−×=0可得:F=70.9Ν����∑MY()Fi=0−Fsin20×100+FBX×350100250200250+×+×=0可得:F=−207ΝBX����∑MX()Fi=0,−Fcos20×100−FBY×350=0可得:F=−19.1ΝBY�∑X=0,FAX+FBX+100200+−Fsin20=0可得:F=−68.4ΝAX�∑Y=0,FAY+FBY+Fcos20=0可得:F=−47.6ΝAY13.匀质杆AB长L,杆重P,A端用球铰固连于水平面上,B端靠在铅直墙壁上,如图所示。已知A点到墙的距离OA=a,杆的B端与墙面间的静滑动摩擦因数为f,试用最简单的方法求杆将要滑下时的临角角度a。解:设AB杆处于临界状态,受力如图,由∑X=0,FAX−FScosα=0���∑MZ()Fi=0,22−aF+Fl−asinα=0AXNB式中,F=fFSsNBafs解得:tanα=22l−a14.已知木材与钢的静滑动摩擦因数为f=0.6,动滑轮摩擦因数为f=0.4,求自卸货车车厢sd提升多大角度时,才能使重的木箱开始发生滑动?解:取木材为研究对象,受力如图所示由∑X=0,FS−psinθ=0(1)∑Y=0,N−pcosθ=0(2)9
式中FS=ƒSN(3)联立(1)、(2)、(3)可得:�tanθ=f=0.6,θ=arctan0.6=31S15.在图示匀质板中,已知:L=5cm,R=5cm。试求图示平面图形的形心。(提示:半圆形的形心到圆心的距离h=4/3Rπ)cy4L3L2LⅡLRⅠⅢ-2L-LL2Lx解:如图,匀质板可以看作是由三角形板,矩形板和半圆形板拼接而成122Ⅰ:∆A=×2L×3L=3L,x=−L,y=L111232Ⅱ.∆A=2L×4L=8L,x=L,y=2L222π24RⅢ.∆A=R,x=2L+,y=L33323π22π2A=∆A+∆A+∆A=3L+8L+R1232由形心公式(2-33)得:2222π24L3(L−L)8+LLi+Li(2L+)∑∆Axii323πx===3.9cm(L=R)(g应为×号)cA22π23L+8L+R222π24L3LLi+8Li2L+Li(2L+)∑∆Ayii23πy===8.18cmcA22π23L+8L+R216.房屋建筑中,为隔壁而采用的空心三角形楼梯踏步如图所示,求其横截面的形心位置。解:用负面积法122三角形:∆A=×2820×=280,x=×28,y=×20111233圆形:∆A=−16π,x=20,y=14222yA=A1+A2=280-16p28cm1020cmr=4cm20cm14cmx
2280××2816−π×203形心:x==18.4cmc28016−π2280××2016−π×143y==13.2cmc28016−π11
工程力学习题答案第七章思考题1.内力是由于构件受到外力后,其内部各部分之间相对位置发生改变而产生的。(对)2.若杆件截面性状及尺寸一定,则载荷越大,横截面上的应力越大。(对)3.在相同载荷作用下,杆件材料越软,则横截面上的应力越低。(错)4.对于各向同性材料,同一点在不同方向上的应力相等。(错)5.若杆件的总变形为零,则杆内的应力必须等于零。(错)6.若杆件在某个方向的应力等于零,则该方向的应变也必定为零。(错)7.在轴向拉伸杆中,若一横截面的位移大于另一横截面的位移,则其应力也必是前者大于后者。(错)8.对于静不定结构,各杆内力的大小与材料的弹性模量E杆的横截面面积A有关,而静定结构,各杆内力的大小与EA无关。(对)习题七1.图示阶梯杆,P=2kN、P=3kN,d=12mm、d=8mm,l=500mm。试求:(1)绘轴力1212图;(2)最大正应力。解:(1)取1-1截面右段:N=P+P=5kN112取2-2截面右段:N=P=3kN22NNi411(2)σ==12Aπd113510××4==44.2MPa2π×123NNi4310××422σ====59.7MPa222Aπdπ×822∴σ=59.7MPamax2.钢杆受力P=400kN,已知拉杆材料的许用应力[]s=100MPa,横截面为矩形,如b=2a,试确定a、b的尺寸。解:根据强度条件,应有PPσ==≤[]σAabi将b=2a代入上式,解得3P40010×a≥=m=44.72mm62i[]σ210010××由b=2a,得b≥89.44mm1
所以,截面尺寸为b≥89.44mm,a≥44.72mm。3.图示为钢制阶梯形直杆,材料比例极限s=200MPa,许用应力[]s=160MPa,各段截面面积分别为:p222A=A=400mm,A=200mm,E=200GNm/。(1)求直杆的总变形;(2)校核该杆的强度。132解:首先根据已知条件,求各段内力N=803050+−=60kN3N=3050−=−20kN2N=30kN1根据内力求各段应力3N6010×3σ==Pa=150MPa3−6A40010×33N−2010×2σ==Pa=−100MPa2−6A20010×23N3010×1σ==Pa=75MPa1−6A40010×1(1)因为σ,σ,σ均小于材料比利极限σ,所以用虎克定律求总变形123P3σL1ii△L=∑=[σ11L+σ2L2+σ3L3]i=1EE1666=⎡7510××−110010××−215010××1⎤m=0.125mm9⎣⎦20010×(2)因为σ<[]σ,σ<[]σ,σ<[]σ所以杆件满足强度要求。12324.图示AB杆在B、C两点分别受集中力作用,已知杆长2l=20cm,横截面积A=2cm,材料的比例极限s=210MPa,屈服极限s=260MPa,弹性模量E=200GPa,受力后AB杆的总伸长为0.9mm,求AC、ppBC段的应变。解:首先求各段内力N=60kNN=−40kNBCAC根据内力求各段应力3N6010×BCσ===300MPa>σBC−4PA210×3N−4010×ACσAC==−4=−200MPa<σP(这里σAC应取绝对值,去掉–号)A210×因为AC段在弹性变形范围内,可用虎克定律求应变2
6σ−20010×ACε===−0.001AC9E20010×因为BC段超过弹性范围,应该用定义求应变△L△L−εiLBCACACεBC==(eAC=DLAC/LAC)LLBCBC−3−20.910×+0.0011010××==0.01−21010×25.图示为二杆所组成的杆系,AB为钢杆,其截面面积为A=600mm,钢的许用应力s=140MPa;1p32BC为木杆,截面面积A=3010?mm,其许用拉应力[]s=8MPa,许用压应力[]s=3.5MPa。求最2tc大许可载荷P。解:B铰链的受力如图所示∑X=0-NAB+NBCcosθ=0∑Y=0-P+NBCsinθ=0解上式得N=PctgiθN=P/sinθABBC根据强度条件,求许用荷载NPctgiθAB杆:AB≤[]σ1≤[]σAA11得−662.2P1≤A1i[]σitgθ=60010××14010××=132kN1.4BC杆受压,用[σ校核强度]CNPBC2=≤[σC]AsinθiA2263−62.2得P≤[σi]Aisinθ=3.510××3010××10×2C2222.2+1.4=88.6kN3所以系统最大许可载荷P=88.6kN6.图示结构中,梁AB的变形及重量可忽略不计。杆①、②的22横截面积均为400mm,材料的弹性模量均为200GNm/。已知:L=2m,l=1.5m,l=1m,为使梁AB在加载后仍保持水平,12载荷P的作用点C与点A的距离x应为多少?解:对AB杆进行受力分析∑MB=0−NLPLx1i+i(−)=0∑MA=0−Px+NL2i=0PLx(−)Px解上二式得:N=N=12LL3
欲使加载后AB保持水平,应有△l=△l12NlNl1122△l==△l=12EAEAPLxl(−)iP(2−x)1.5iPxii11得:==L22解得:x=1.2m7.试校核图示联接销钉的剪切强度。已知P=100kN,销钉直径d=30mm,材料的许用剪应力[]t=60MPa。若强度不够,应改用多大直径的销钉?P解:(1)剪切面上的剪力。Q=2校核销钉剪切强度3QPi410010××4τ====70.7MPa>[]τ22−6A2πd2××π30×10所以销钉强度不合格。QPi4(2)根据强度条件τ==≤[]τ2A2πd34iP410010××所以d≥==32.57mm62πτi[]2××π6010×8.木榫接头如图所示,a=b=12cm,h=35cm,h=4.5cm。p=40kN。试求接头的剪应力和挤压应力。解:作用在接头上的剪力Q=P,剪切面积为bh3P4010×接头的剪切应力为τ==Pa=0.952MPa−4bh123510××作用在接头上的挤压力和挤压面积分别为P和bc,−3P4010×接头的挤压应力为σ==Pa==7.41MPaj−4bc124.510××29.由五根钢杆组成的杆系如图所示。各杆横截面积均为500mm,E=200GPa。设沿对角线AC方向作用一对20kN的力,试求A、C两点的距离改变。解:A铰链受力如图所示,4
由平衡条件°∑X=0N1−Pcos45=0°∑Y=0Psin45−N2=022解上式得N=P,N=P=10√2kN由于1222结构对称,故有N=N=10√2kN342=N=P=10√2kN12B铰链受力如图,由平衡条件∑X=0N5cos45°−N1=0解得N=P=20kN533DL1=N1.a/EA=10√2×10.a/200×10×-4500=√2×10.a33⊿L5=20×10×√2.a/200×10×500-4=2√2.×10.a22-4⊿LAC=2√(a+⊿L1)-(√2.a/2-⊿L5/2)-√2a=6.83×10.a-42-42=2√(a+√2×10a)-(√2a/2-√2×10a)-√2.a-4-8-4-8=(2√1+2√2×10+2×10-1/2+2×10-2×10-√2)a-4=(2√0.5+2×(√2+1)×10-√2)a=(2√0.5+0.0004828-√2)a=(2×0.70744809–1.414213562).a=(1.41489618-1.414213562).a=0.0006826.a-4=6.83×10a22NiaN2a15杆系的总变形能为U=×4+2EA2EA2Pa(2+2)=2EA应用卡氏定理,A、C两点的距离改变为3∂UPa2010×aδ==(2+2)=(2+2)iA9−6∂PEA20010××50010×−3=0.68310×a5
10.厚度为10mm的两块钢板,用四个直径为12mm的铆钉搭接,若在上、下各作用拉力P=20kN,如图示,试求:(1)铆钉的剪应力;(2)钢板的挤压应力;(3)绘出上板的轴力图。解:(1)铆钉的剪应力P由题分析可得,每个铆钉剪切面上的剪力为43QPi42010×所以τ====44.23MPa22−6A4iπdπ×12×10(2)钢板的挤压应力PjPσ==jA4itdj32010×==41.67MPa−64101210×××(3)上板的轴力图11.求图示结构中杆1、2的轴力。已知EA、P、h,且两杆的EA相同。解:物块A受力如图∑X=0PN−−Nicos30°=0①12由图可知系统变形协调关系为⊿L2=⊿L1cos30°NLiNLi2211即=cos30°EAEA将L=2h,L=3h代入上式213得:N=N②214将②式代入①式,解得N=0.606PN=0.455P126
工程力学习题答案第八章轴的扭转判断题:1.传动轴的转速越高,则轴横截面上的扭矩也越大。(错)2.扭矩是指杆件受扭时横截面上的内力偶矩,扭矩仅与杆件所收的外力偶矩有关,而与杆件的材料和横截面的形状大小无关。(对)3圆截面杆扭转时的平面假设,仅在线弹性范围内成立。(错)4.一钢轴和一橡皮轴,两轴直径相同,受力相同,若两轴均处于弹性范围,则其横截面上的剪应力也相同。(对)5.铸铁圆杆在扭转和轴向拉伸时,都将在最大拉应力作用面发生断裂。(错)6.木纹平行于杆轴的木质圆杆,扭转时沿横截面与沿纵截面剪断的可能性是相同的。(错)7.受扭圆轴横截面之间绕杆轴转动的相对位移,其值等于圆轴表面各点的剪应变。(错)习题八1.直杆受扭转力偶作用如图所示,作扭矩图并写出|T|max2.直径D=50mm的圆轴,受到扭矩T=2.15kN.m的作用。试求在距离轴心10mm处的剪应力,并求轴横截面上的最大剪应力。3−3TiρTiiρ322.1510××1010××32解:τ====35MPa(单位:ρ44−12IπiDπ×50×10P4Nm.m/m)3T2.1510××163截面上的最大剪应力为:τ===87.6MPa(单位:Nm/m)max3Wπ×0.05P1
3.功率为150kw,转速为15.4r/s的电动机轴如图所示,轴外伸端装有带轮,试对轴进行强度校核。已知:[τ]=30MPa,d=135mm,d=90mm,d=75mm,d=70mm,d=65mm。12345N150解:外力偶矩m=9550=9550=1550N.mn15.460×由题可知,d为危险截面。4T155016i155016×所以τ====23MPa<[]τmax33−9Wπidπ×70×10P4所以满足强度要求。4.传动轴的转速n=8.3r/s,主动轮1的输入功率N=368kw,从动轮2、3分别输出功率N=147kw、12�2N=221kw。已知[]t=70MPa,[]q=1/m,G=80GN/m。(1)试按强度条件与刚度条件求AB段的直3径d,(2)如AB段与BC段选用同一直径d,试确定d的大小。(3)按经济观点,各轮应如何安排更为1合理?解:首先计算外力偶矩N3681m=9550=9550=7057N.m1n8.360×N1472m=9550=9550=2819N.m2n8.360×m=4238N.m3所以AB段扭矩T=m=7057N.mAB1BC段扭矩TBC=m3=4238N.mT16iTABAB(1)根据强度条件τAB==3≤[]τWπdP116T167057×可确定轴AB段的直径d≥3AB=3=80mm16πτ[]π×7010×由刚度条件θAB=TAB×18032TAB180≤[]θ=×4GIπGπdπP可确定轴AB的直径:2
180TABi32180705732××2d≥4=4=84.7mm(单位:°Nm/NmNm/Nm/(/((N/mN/N/mm°)1292Giπθ[]8010××π×1(2)因为T>T,所以若AB和BC选用同一直径,轴的直径取d=85mmABBC(3)主动轮放在两从动轮之间,可减小最大扭矩值、减小轴的横截面积,经济合理。5.实心轴与空心轴通过牙嵌式离合器连在一起,已知轴的转速n=1.67r/s,传递功率N=7.4kW,材料的[]t=40MPa,试选择实心轴的直径d1和内外径比值为1/2的空心轴的外径D2。解:轴所传递的扭矩为N7.4T=9550=9550×=705N.mn1.6760×由实心轴强度条件:T16Tτmax==3≤[]τWπidρ1可得实心圆轴的直径为16T16705×d≥3=3=44.8mm16πτ[]π×4010×空心圆轴的外径为:16T16×705=45.7mm(参考例8-2,用W=πD3(1-α4)/16)D≥3=3p2464πτ[](1−α)π×4010××(1−0.5)6.机床变速箱第Ⅱ轴如图所示,轴所传递的功率为N=5.5kW,转速n=200r/min,材料为45钢,[]t=40MPa,试按强度条件设计轴的直径。解:轴所传递的扭矩为T=9549N=95495.5=263N.mn200由圆轴扭转的强度条件T16iTτ==≤[]τmax3Wπidρ可得轴的直径为16T16263×d≥3=3=32.2mm6πτ[]4010××π取轴径为d=33mm27.某机床主轴箱的一传动轴,传递外力偶矩T=5.4N.m,若材料的许用剪应力[]t=30MPa,G=80GN/m,3
�[]q=0.5/m,试计算轴的直径。解:由圆轴扭转的强度条件T16iTτmax==3≤[]τWπidρ1可得轴的直径为16T165.4×d≥3=3=9.7mm16πτ[]π×3010×由圆轴刚度条件32T180T180=i≤[]θθ=Q=i≤[θ]4GdππGIπ2P可确定圆轴直径180×Ti321805.432××d≥4=4=16.7mm2292Giπi[]θ8010××π×0.5所以取直径d≥16.7mm8.驾驶盘的直径Ø=520mm,加在盘上的力P=300N,盘下面竖轴的材料许用应力[]t=60MPa。(1)当d竖轴为实心轴时,试设计轴的直径;(2)如采用空心轴,且a==0.8,试设计轴的内外直径;(3)比D较实心轴和竖心轴的重量。解:方向盘传递的力偶矩−3m=PØ=30052010××=156N.m(1)由实心轴强度条件T16Tτ==≤[]τmax3Wπdρ得轴的直径:16T16156×d≥3=3=23.6mm6πτ[]π×6010×(2)空心轴的外径为:34(公式:τmax=T/WP≤[τ],Wp=πD(1-α)/16)16T16156×D≥3=3=28.2mm464πτ[](1−α)π×6010××(10.8)−d=Diα=28.20.8×=22.6mm2WAd实实实(3)===1.9622WAD−d空空空空9.图示圆杆两端固定,试求AB、BC段的扭矩与杆内最大切应力。4
解:由外力偶的作用,A、C两点对圆杆作用的外力偶分别为m,m。AC所以T=−mT=mABABCC由平衡条件有:m+m=m①AC由变形协调关系,ϕAB=ϕBC根据θ=ϕ/L,ϕ=TL/GIp−mLimi2LAC得+=0得到m=2m②(由ACGIρGIρ22将②代入①得:T=m=m=×30=20kN.mABA33m1T==×30=10kN.mBC33杆内最大切应力位于AB段取3T2010××1640ABτ====12.73MPamax3Wπ×0.2πP5
工程力学习题答案第九章梁的弯曲判断题:1.梁发生平面弯曲时,梁的轴线必为载荷作用面内的平面曲线。(对)2.最大弯矩必定发生在剪力为零的横截面上。(错)3梁上某一横截面上的剪力值等于截面一侧横向力的代数和。而与外力偶无关;其弯矩值等于截面一侧外力对截面形心力矩的代数和。(对)4.两梁的跨度、承受载荷及支承相同,但材料和横截面面积不同,因而两梁的剪力图和弯矩图也不一定相同。(错)5.纯弯曲时,梁变形后横截面保持为平面,且其形状、大小均保持不变。(错,P201图9-15)6.平面弯曲时,中性轴垂至于载荷作用面。(对)7.若梁上某一横截面上弯矩为零,则该截面的转角和挠度必也为零。(错)8.若梁上某一段内各截面上的弯矩均等于零,则该段梁的挠曲线必定是一直线段。(对)9.两梁的横截面、支承条件以及承受载荷均相同,而材料不同,则两梁的挠曲线方程相同。(错E不同)10.不论载荷怎样变化,简支梁的最大挠度可以用梁的中点挠度来代表。(错)习题九1.设P、q、M、l、a均为已知,如图所示试列0出各题的剪力方程和弯矩方程式,绘出Q、M图并出Q值和M值。maxmax(a)解:AB段:Qx()=−P(0≤x≤L)Mx()=−Px(0≤x≤L)BC段:Qx()=−P(L≤x≤2)LMx()=2PLPx−(L≤x≤2)LQ=PM=PLmaxmax(b)解:AB段Qx()=−qxL(0≤x≤)212Mx()=−qx2L(0≤x≤)29BC段Qx()=−qx+qL8L3L(≤x≤)221
12992Mx()=−qx+qLx−qL2816L3L(≤x≤)225qL12Q=M=qLmaxmax882.绘出图示各梁的剪力图和弯矩图,求出Q和M,maxmax并用微分关系对图形进行校核。(a)解:根据平衡方程求支反力16R=kN,A326R=kNB3做剪力图,弯矩图20Q=kN,max364M=kN.mmax9(b)解:根据平衡条件球求支反力2pR=A3pR=B3做剪力图、弯矩图2pQmax=3Mmax=pa2
3.(a)∑MB=0,-R2A.4a-qa+q.2a.a=0,RA=qa/4(b)∑MB=0,qa×5a/2–RA.2a+qa.a+qa.a/2=0RB=7qa/4RA=2qa,RB=qaQA=qa/4,QB=QC–q.2a=qa/4-2qa=-7qa/4(a)M22A=0,MD=0+qa/4×a=qa/4(b)MA=0,MB=MA+0.5(0-qa).a=-qa/2,M22222E=MD+qa=5qa/4MC=MB+qa.a=-qa/2+qa=qa/2M222C=ME+qa/4×a=3qa/2MD=MC+0.5.(0–qa).a=qa/2–qa/2=0顶点M2F=MC+0.5(qa/4+0)×(2a×1/8)=49qa/324.已知图示各梁的载荷P、q,M和尺寸。(1)作剪力图和弯矩图;(2)确定Q值和|M值。maxmax解(a)(a)(b)RA=4Pa/3RB=5Pa/3QQ4qa/33+qa/3xx--qa5qa/3
M5pa/3M4pa/3x+x-qa/223qa/22(d)∑MB=0,-RA.a+qa/2×3a/4=0,RA=3qa/8,RB=qa/8,QA=3qa/8,Q2C=3qa/8-q.a/2=-qa/8,MA=0,MF=0+0.5.(3qa/8+0).3a/8=9qa/128M2C=MF–0.5.q.a/8.a/8=qa/16MB=MC–qa/8×a/2=0QQ3qa/83m/2ax++-xqa/8M3m/2a9qa/1282m/2Mx+-+-xm3m/275()eQmax=pMmax=pa22Q7p/2+x--p5p/2M5pa/2+x-pa4
(f)Qmax=30knMmax=15knm?(g)|Q|2max=qa|M|max=qa/2QQ30kN10kN+1x2x(g)Qmax=+qaMmax=qa-2-10kN-30kNqaMM2qa/2xx-+5kNm.-15kNm.15kNm.-qa12(h)Qmax=Mmax=qaqa/22228qa/2QA=RA=qa/2,QB=qa/2,QC=QA–q.a=-qa/2;MA=0,MC=MA+0.5(qa/2-qa/2)=0M2F=MA+0.5×(qa/2+0)×a/2=qa/8;Qqa/2qa/2x++-qa/2Mqa/82+x-2qa/85.设梁的剪力图如图所示,试作弯矩图及载荷图。已知梁上设有作用集中力偶。(a)q=1kN/m4kN3kN2kN3kNQ3kN1kNDx5BCA1kN3kN2m2m4m
M6kNm.4kNm.4.5kNm.+xMA=0,MB=0+3×2=6,MC=6-1×2=4,MF=4+0.5×(1+0)=4.5,MD=4.5+0.5×(0-3)×3=0(b)20kN/m10kN20kN/m10kNQ10kNxABECD10kN10kN1m1mM2.5kNm.+x-2.5kNm.MB=0+0.5×(-10+0)=-2.5MC=0+0.5×(10+0)=2.5b26.矩形截面悬臂梁如图所示,已知l=4m,=,q=10kN/m,[σ]=10MPa,试确定此梁横截面尺寸。h3解:梁的最大弯矩发生在固定端截面上,1212Mmax=ql=(104)=80knm223梁的强度条件m8010´[]s==?sw12bh66
632680103368010?3将b=h代入上式得£[s],h³()m263221010hh×32所以h=416mm,b=h=277mm3d327.简支梁承受布载荷如图所示。若分别采用截面面积相等的实心和空心圆截面,且D=40mm,=,1D52试分别计算它们的最大正压力。并问空心圆截面比实心截面的最大正应力减小了百分之几?解:因空心圆与实心圆面积相等,所以π2π22D=(D−d)1224422223242D=D−d=D−(D)=(D)12222255将D=40mm代入上式,得:1D=50mm,d=30mm22均布荷载作用下的简支梁,最大弯矩产生在梁跨度中间截面上232ql210××2M===1kN.mmax88实心圆截面梁的最大应力3M32M3210×maxmaxσ====159MPamax33wπDπ(0.04)11空心圆截面最大应力3MM3210×maxmaxσ′====93.6MPamax33w2πD2⎡d24⎤π(0.05)1()3⎡−4⎤⎢1(−)⎥⎢⎥32D⎣5⎦⎣2⎦空心圆截面梁比实心圆截面梁的最大正应力减少了σ−σ′15993.6−maxmax==41.1%σ159max8.T字形截面梁的截面尺寸如图所示,若梁危险截面承受在铅垂对称平面的正弯矩M=30kNm,试求:(1)截面上的最大拉应力和压应力;(2)证明截面上拉应力和等于压应力之和,而其组成的合力矩等于截面的弯矩。解:(1)计算T字形截面对形心轴的惯性矩7
33I=50150×+50150××502+150×50+50150××502Z121244=5312.510×mm最大拉应力发生在截面最下边缘3−3Myi3010××7510×1σ===42.35MPatmax4−12I5312.510××10z最大压应力发生在截面最上边缘3−3Myi3010××12510×2σ===70.59MPacmax4−12I5312.510××10zy1(2)证明:①中性轴上侧压力之和为(拉、压力公式:Fc=∫0My/Iz×b1dy)0.125MyiMi0.050.125M−4F=i0.05idy=ydy=i3.9062510×C∫0∫0IIIZZZ2-4=M/IZ[(1/2)×0.125-0]=M/IZ0.05×0.5×0.015625=M/Iz×3.91×10Nm中性轴下侧拉力之和为0.025Myi0.075MyiF=i0.05dy+i0.15idyt∫0I∫0.025IZZM⎡0.0250.075⎤=0.05ydy+0.15ydyI⎢⎣∫0∫0.025⎥⎦ZM−4=i3.9062510iIZ∴F=F所以截面上拉力之和等于压力之和。ct②截面上合力矩为2220.125My0.125My0.075My∫0i0.05idy+∫00.05dy+∫0.0250.15dyIIIzzzM−9=i0.0510ii1062500Iz−90.0510ii1062500=Mi=M4−125312.51010ii所以合力矩等于截面上的弯矩。9.T形截面的铸铁悬臂梁及其承载情况如图示,材料的许用拉应力[σ]=40MPa,许用压应力t[σc]=80MPa,试求梁的许可载荷[p]解:梁的弯矩图如图,弯矩的两个极值分别为µ1=0.8P,MA=2P×1.4-P×2=0.8Pµ2=0.6P,MC=-0.6P截面对形心轴的惯性矩为8
32(Iz=bh/12+Ah1,h1腹=153.6–100=53.6mm,h1翼=200-153.6+25=71.4mm)33⎡50200×215050×2⎤4I=⎢+5020053.6××++5015071.4××⎥mmz⎣1212⎦M4=10180cm0.8p根据弯曲正应力强度条件+Mσ=y≤[σ],M≤[σ].Iz/ymax_XmaxmaxIz0.6p由A截面的强度要求确定许可荷载。由抗拉强度要求得(A截面下缘拉应力最大)6−81[σt]Iz14010××1018010×P≤×=×N=52.8KN(y1=200-153.6+50=96.4mm−20.8y0.89.6410×1–2=9.64×10m)由抗压强度要求得(A截面上缘压应力最大)6−81[σc]Iz18010××1018010×-1P≤×=×N=66KN(y2=153.6mm=1.536×10.)−20.8y0.815.3610×2由C截面的强度要求确定许可载荷:由抗拉强度得:(C截面上缘拉应力最大)6−81[σt]Iz14010××1018010×P≤×=×N=44.1KN−20.6y0.615.3610×2显然C截面的压应力大于拉应力,不必进行计算。许用载荷为P≤44.1KN10.矩形截面的变截面梁AB如图示,梁的宽度为b,高度为2h(CD段)和h(AC、DB段许用应力为[σ],为使截面C、E、D上的最大应力均等于[σ],加强部分的长度2a应取多少?解:由题意可得C,D,E截面的弯矩值RA=RB=P/2PLM=M=i(−a)CD22PLM=iE22M截面上最大应力值为σ=maxWZMMCE欲使截面C,D,E上最大应力相等,则有=WWZ1Z2PLPL(−a)i2222即=12b2bh(2)h669
3L解得2a=411.直径d=7.5cm圆截面钢梁承受载荷如图示,钢的弹性摸量E=200GPa,试求梁内最大正应力,AB段变形后的曲率半径和跨度中点C的挠度。解:梁弯矩图如图所示MRA=RB=P,Mmax=10×0.4=4kNm梁内最大正应力3M410××32maxσ==max3−6Wπ×7.5×10z_X=96.58MPaAB段为线弯曲,变形后曲率半径4kN.m94−8EI20010×××π7.5×10zρ===77.4m(由P203公式9-8)3M410××64跨度中点C的挠度。2222y=ρ−ρ−L=77.4−77.4−0.75=3.6mmCAC212.筒化后的电动机轴受载及尺寸如图所示,E=200GN/m,定子与转子间的间隙δ=0.35mm,试校核刚度。解:电动机轴惯性矩44−12πdπ×130×1074I===1.410×mmZ6464C点的挠度34pl5gly=yp()+yq()=−−ccc48EI384EI(查表9-11⑤、⑦中ymax)3334−n⎡3.510××151.03510×××1⎤=⎢−⎥97−1220010××1.410××10⎣48384⎦=−0.0308mm因为y=0.0308<0.35c所以电动机轴满足刚度要求。13.用叠加法求图示各梁截面A的挠度和截面B的转角。EI为已知常数。10
解:(a)查表9-1②、④32查表9-1②挠度方程,将x=c=ι/2代入y=-Px(3c–x)/6EI,得:yA1=-Pι/24EI,23查表9-1④将x=ι/2代入挠度方程;得:yA2=-m(ι/2)/2EI=-Pι/8EI22/将c=ι/2代入②,得θB=-P(ι/2)/2EI=-Pι8EI22plmlplQ=Q=−,Q=−=−B1AB28EIEIEI333pl由叠加原理有yA=yA1+yA2=-Pι/24EI-Pι/8EI=−6EI29plQ=Q+Q=−BB1B28EI(b)由图查表9-1⑦,将x=ι/2代入挠度方程和转角方程,得:当q满布整梁时x=ι/2处的挠度(当q不满布时,应乘以长度比值)。45qlyA1=fA1=384EI45ql所以,yA=1/2•yA1=()↓768EI由表9-1⑦,用ι/2代换转角公式中的ι,得当q满布时ι/2处的转角,332ql1qlQ=,所以Q=Q=(↗)(Q应为θ)B1BB1384EI2384EI11
工程力学习题答案第十章组合变形1.已知单元体应力状态如图示(应力单位为ΜΡα),试求:(1)指定斜截面上的正应力和剪应力;(2)主应力的大小、主平面位置;(3)在单元体上画出平面位置和主应力方向;(4)最大剪应力.°解:(1)α=30斜截面上的应力:3050+3050−σ=+cos(230)(20)sin(230)×°−−×°50α22=52.3ΜΡα2030°3050−30τ=sin(230)20cos(230)×°−×°α2=18.7−ΜΡα(2)主应力和主平面30+5030+5022σ1σ=+()+20max22σ2=62.36ΜΡα31.72°30+5030-5022σ=−()+20min22=17.64ΜΡα2(20)×−tg2α=−=−2°3050−σα=−31.72°2°σ1(3)图σ=62.36ΜΡα1σ=17.64ΜΡα23050−22(4)τ=()+20=22.36Mpamax22.图示起重机的最大起重吊重量为P=40kN,横梁AC由两根18号槽钢组成,材料为Q235,许用应力[σ]=120Mpa,试校核横梁的强度。解:(1)外力分析:取AC为研究对象,受力如图,小车位于AC中点(此时梁的弯矩最大),平衡条件∑M()F=0:CNsin30°×3.5−×P1.75=0ABN=P=40kNAB∑F=0:Y°NABY+Nsin30−P=0YcCAB30°PXcY==20kNC2p1.75m1.75m∑F=0:X1
X=Ncos30°=34.64kNCAB(2)内力分析:见轴力图,弯矩图。AC梁为压,弯组合变形,危险截面位于AC中点。Mmax=201.75×(=YC×3.5/2)N=35kN.mX(-)34.64kNM35KN.M(3)应力分析18号槽钢(P388)3XW=×2152.2cmZ2A=29.292cm×363σ=σ′+σ′′=34.6410/(29.292100)3510/(2152.210)×××+×××=121ΜΡαmaxmax(σ拉+α弯max=N/A+Mmax/wz,二应力均为拉应力)(4)强度分析:∆σ121120−−3==8.310×=0.83%<5%满足要求(分母应为[σ])[]∆120为什么小车位于AC的中点时AC杆的弯矩最大:NABYc(1)由截面法可知:小车左侧剪力为YC>0,右侧为YC-P<0,30°故小车P的作用点为弯矩图直线升、降区间的转折点,该截面Xcp弯矩最大。求小车位于距C端为x截面上的弯矩:1.75m1.75m由∑MA=0,P×(L-x)-YC.L=0,得YC=(L-x)P/L2由YC对小车作用点之矩:M=YC•x=(L-x)P/L•x=-Px/L+Px,当M’=-2Px/L+P=0时,即x=L/2时,弯矩M值最大.3.手摇式提升机如图示,已知轴的直径d=30mm,材料为Q235钢,[]σ=80Mpa,试按第三强度理论求最大起重载荷Q。解:(1)轴的外力Q向轴简化为Q—弯曲力偶M=200Q=T—扭转n(2)内力—见图危险截面位中点:M=200Q(T=200Q)nQLM=max4MnQ600×==150Q(Nmm)200Q42X
轴发生弯曲与扭转组合变形(3)强度计算:22M+Mnmax应为T)σxd3=(MnWMZ22(200+150)×Q150Q=≤[]σ30.130×30.130××80Q≤X22150+200=860N∴最大起重载为860N.4.图示的钢制圆轴上有两个齿轮,齿轮C直径为d=300mm,其上作用着铅直切向力P=5kN,齿c1轮D的直径为d=150mm,其上作用着水平切向力P=10kN。若[σ]=100Mpa,试用第四强度理论求轴D2的直径。解:(1)外力分析,将P,P向AB轴简化,如图12CABd300Dcm=P•=×5122=750KN.mm(2)内力分析:P1P2150300150在m作用下轴发生扭转,在P、P作用下轴发生弯曲变形,所以AB轴为弯曲组合变形。123M:M=P×150ZC114P2P1=562.5KN.mmmm1MnM=×562.5D23=187.5KN.mmX3M:M=P×150MzyD124562.5N.m750N.m=1125KN.mm1XM=×1125C23=375KN.mmMY1125N.m22M:M=562.5+375C=676.1KN.mmX22M=1125+187.5D=1140.5KN.mm1140.5N.mM676.1N.m3X
(3)强度运算:22M+MDnσ=≤[]σxd4WZ223(1140.5+750×10)32×d≥3=51.8mmπ×1005.已知应力状态如图所示(应力单位为:MPa)。(1)分别用图解法和解析法求(a)、(b)中指定斜截面上的应力;(2)用图解法求(c)、(d)、(e)、(f)上主应力的大小与方向,在单元体上画出主平面的位置,求最大剪应力。3020(1)(a)解析法解:5030+5030−°20σ=+cos60α50502230°5045°=45MPa5030−°τ=sin60=8.66MPaα(b)2解析法求解:(a)5050σ=+cos90°−20sin90°45°2250D1=5MPa(0,50)50τ=sin90°+20cos90°2a45°250BA(50,0)=25MPa0(2)图解法:����⎧⎪σ=OA=50ΜΡa(c)1D2(0,-50)⎨����⎪⎩σ=OB=−50ΜΡa3σσ13τ=OD=50MPa40max120主平面位置(d)解:作应力图45°����40σ1=OA=55MPaσ3σ����1σ=OB=−35MPa3�����(d)ττ=CD=45MPamax13555�2α=270D1(-30,20)a(e)解:作应力图x����40σ1=OA=45MPa5520B0C2a0A����σ=OB=−45MPaD2(50,-20)335����40τ=OD=45MPaτmaxDD1(40,20)4(e)2aB0AD2(-40,20)
�2α=270����(f)σ1=OA=5MPaσ3����σ3=OB=−85MPaσ1����τmax=CD1=45MPa�2α=27τ0a0σσ3120σσ3σ31(0,20)2a80B8040AC0a020(f)σ401σ3�−46.图示一钢质圆杆,直径D=200mm,已知A点在与水平线60方向上的正应变ε�=4.110×,试602求载荷P。已知E=210GNm/,µ=0.28。解:(1)绕A点取一单元体,应力状态如图:σσ�360°σ�=−cos120=σ60224Aσσ�1llσ�=−cos(60)−=σ−30224(2)由广义虎克定律得:1ε�=⎡σ�−µσ�⎤60⎣60−30⎦Epσ2.72σ=[3−µ=]σσ�604E4E3−460°421010×××4.110×σ�σ=−302.72=126.6ΜΡα(3)载荷P:2σ�2σ�πD126.6××π200605−30P=σiA=126.6×==39.7810×Ν44σ327.扭矩M=2.510×Ν⋅m作用在直径D=60mm的钢轴上,若E=210GNm/,µ=0.28,试n�求圆轴表面上任一点在与母线成α=30方向上的正应变。解:(1)绕A点取一单元体,Mn应力状态如图:DaA5
332.510××10σ�τ=−603π×60=−58.9ΜΡα�(2)σ�=−τsin230×σ3030��=58.9sin60=51ΜΡα30°�σ−60�=−τsin2(60)⎡⎣×−⎤⎦=−51ΜΡασ�−601(3)ε30�=[σ30−µσ−60]E510.28(51)−×−−3==0.31110×321010×8.薄壁圆筒扭转一拉伸试验的示意图如图所示。若P=20kN,m=600N.m,且d=50mm,δ=2mm,试求:(1)A点在指定斜截面上的应力;(2)A点的主应力的大小及方向(用单元体表示)。τσmmp30°pσdσA解:(1)绕A点取单元体,应力为:33σP2010×2010×3σσ====63.66ΜΡασ11Aπδdπ×502×a03Mn60010×τ===70.63ΜΡα222πγδ2××π26×2σσ��(2)σ−60�=+cos(120)−+τsin(120)−σ122σ31�=×63.6670.63sin(120)+−4=−45.5ΜΡασ��τ�=sin(120)70.63cos(120)−−−−602=8.1ΜΡα(3)σσ2263.6663.6622σ=+()+τ=+()+70.63=109.3ΜΡαmax2222σσ2263.6663.6622σ=−()+τ=−()+70.63=−45.6ΜΡαmin2222σ=109.3ΜΡασ=-45.6ΜΡα136
2τ2(70.63)×−tg2α=−=−=2.220σ63.66��2α=65.74α=32.87007
Zy-第十章组合变形补充习题解答图10-1210-1若在正方形横截面短柱的中间开一槽,使横截面面积减少为原横截面面积的一半,如图10-13所示。试问开槽后的最大正应力为不开槽时最大正应力的几倍?图10-13−N−PP解:(1)开槽前为单向压缩状态则σ===max122A2(a)4a(2)开槽后中间段受力与轴线平行为压缩与弯曲的组合变形则aP−NM−P28Pσ=|−||=−|=max222AW(2)a124aZ2aa62(=-P/2a.a–p.0.5a/2a.a/6=2p/a)8Pσ4a2max2(3)最大应力比值为==8倍。σPmax124a10-2小型铆钉机座如图10-14所示,材料为铸铁,许用拉应力[σt]=30MPa,许4用压应力[σc]=80MPa。I—I截面的惯性矩I=3789cm,在冲打铆钉时,受力P=20kN作用。试校核I—I截面的强度。图10-141
解:(1)分析铆钉机座受力,由于外力与立柱轴线平行,故其发生拉弯组合变形(2)由于材料抗拉压性能不同,需校核拉压强度33NMy2010×2010××(40087.5)+tσ=+=+=22.52.67+=25.2MPa<[]30σ=MPat4AI(100200)25+×378910×Z(第2个分子应×87.5)33MyN20010××(40087.5)(22587.5)+×−2010×cσ=−=−c4IA378910×(100200)25+×Z=22.52.67+=32.7MPa<[σ]80=MPac3(第一个分子应为20×10,结果|-35.38+2.67|=32.7MPa)所以强度足够。10-3如图10-15所示电动机带动皮带轮转动。已知电动机功率P=12kW,转速n=900r/min,带轮直径D=200mm,重量G=600N,皮带紧边拉力与松边拉力之比为T:t=2,AB轴为直径d=45mm,材料为45号钢,许用应力[σ]=120MPa。试按第四强度理论校核该轴的强度。图10-15解:(1)计算拉力T,t,由轴的平衡条件知pD9549×=(T−t)n212D9549×=t9002t=1273NT=2t=2546N(2)计算轴危险截面的扭矩和弯矩DT=(T−t)=127Nm211M=FL=(T++tG)0.8×441=(12732546600)0.8++×4=884Nm(3)由第四强度理论2
2222M+0.75T884+0.75127×σ==xd3W0.145×Z=100MPa<[]120σ=MPa所以该轴强度足够。10-4如图10-16所示圆截面杆受载荷P和m的作用。已知:P=0.5kN,m=1.2kN·m,圆杆材料为45号钢,[σ]=120MPa。力P的剪切作用略去不计,试按第三强度理论确定圆杆直径d。图10-16解:(1)计算危险截面的扭矩和弯矩T=m=1.2KNm3M=pl=0.510××0.9=450Nmmax(2)由第三强度理论22223M+T450+1200×10W≥=Z[]σ1202331440000202500+×10d≥1π×12032d≥47.5mm取d=48mm10-5如图10-17所示拐轴在C处受铅垂力P作用。已知,P=3.2kN。轴的材料为45号钢,许用应力[σ]=160MPa。试用第三强度理论校核AB轴的强度。图10-17(1)计算危险截面的扭矩和弯矩3M=p×140=3.214010××3
3T=p×150=3.215010××(2)由第三强度理论22223M+T(3.2140)×+(3.2150)××10σ==xd33W0.150×Z=52.5MPa<[]120σ=MPa轴的强度足够10-6如图10-18所示,在AB轴上装有两个轮子,轮上分别作用力P和Q而处于平衡状态。已知:Q=12kN,D1=200mm,D2=100mm,轴的材料为碳钢,许用应力[σ]=120MPa。试按第四强度理论确定AB轴的直径。(1)计算外力P,由轮的平衡条件知DD12P=Q22QD12100×2P===6KND2001(2)计算扭矩D12005T=P=×6=×610Nmm22(3)计算AB支座反力∑mF()=0AN×500150=P=350QB(应为=150P+350Q)N=10.2KNBN=7.8KNA(4)画弯矩图,经分析知D截面为危险截面4
(5)由第四强度理论确定AB轴的直径22M+T0.75σ=≤[]σxdWZ22150+6000.7522≤120(根号内应为1530+600×0.7530.1d3261090010×d≥3=51.3mm1200.1×3(根号内10应在2次根号外面)取d=22mm10-7两端装有传动轮的钢轴如图10-20所示,轮C输入功率NP=14.7kW,转速n=120r/min,D轮上的皮带拉力F1=2F2,材料的许用应力[σ]=160MPa。按第四强度理论设计轴的直径。NN(F+F)AB12Mx4.2KNm(1)计算扭矩和皮带拉力FF,12p14.7m=9549×=9549×=1170NMn120D(F−F)×=m122(T=m)1170F=N=4679N20.25F=2F=9358N12(2)画轴的受力图,计算A、B支座约束力。5
∑mF()=0BN×350=(F+F)300,×N=12KNA12A(3)画弯矩图,经分析知B截面为危险截面(4)由第四强度理论设计轴的直径22M+0.75TDσ=≤[]σxd4WZ224210+0.751170×W≥Z[]σ3433110×0.1d≥,d≥64.6mm1603(0.1d)取d=65mm6'
您可能关注的文档
- 单辉祖_谢传锋_著)_高等教育出版社_课后答案.doc
- 工程力学答案.doc
- 工程力学答案.pdf
- 工程力学课后习题答案.doc
- 工程力学课后习题答案.pdf
- 工程力学课后答案 高等教育出版社出版.doc
- 工程力学课后答案(第二版少学时).doc
- 工程力学课后答案-高等教育出版社出版.doc
- 工程力学课后答案.doc
- 工程力学课后答案合_单祖辉主编.doc
- 工程化学(魏云鹤)习题解答.pdf
- 工程数学《复变函数》西安交通大学第四版高等教育出版社课后习题答案.doc
- 工程数学习题答案.doc
- 工程数学习题集(含部分湖大版《大学数学5》课后答案).doc
- 工程材料与成型工艺基础习题汇编答案--老师版.doc
- 工程材料习题解答.doc
- 工程材料力学性能-第2版习题答案.doc
- 工程材料及成型技术基础(吕广庶 张元明 著) 课后习题答案.doc
相关文档
- 施工规范CECS140-2002给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程
- 施工规范CECS141-2002给水排水工程埋地钢管管道结构设计规程
- 施工规范CECS142-2002给水排水工程埋地铸铁管管道结构设计规程
- 施工规范CECS143-2002给水排水工程埋地预制混凝土圆形管管道结构设计规程
- 施工规范CECS145-2002给水排水工程埋地矩形管管道结构设计规程
- 施工规范CECS190-2005给水排水工程埋地玻璃纤维增强塑料夹砂管管道结构设计规程
- cecs 140:2002 给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程(含条文说明)
- cecs 141:2002 给水排水工程埋地钢管管道结构设计规程 条文说明
- cecs 140:2002 给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程 条文说明
- cecs 142:2002 给水排水工程埋地铸铁管管道结构设计规程 条文说明