- 119.12 MB
- 2022-04-22 11:21:21 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
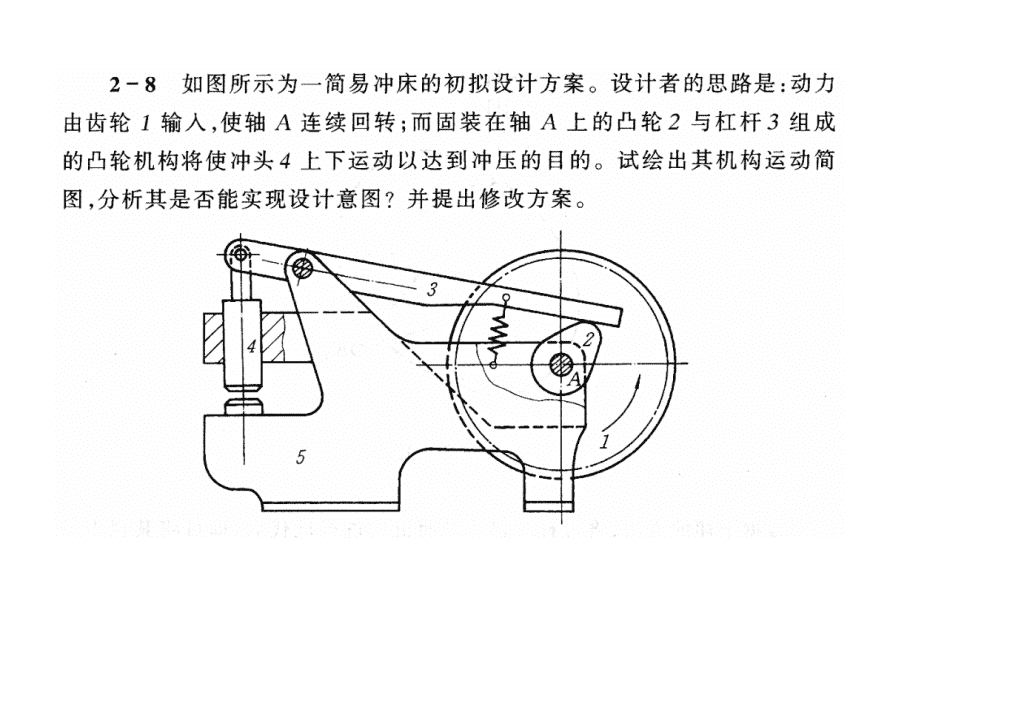
'《机械原理》作业题解第二章机构的结构分析
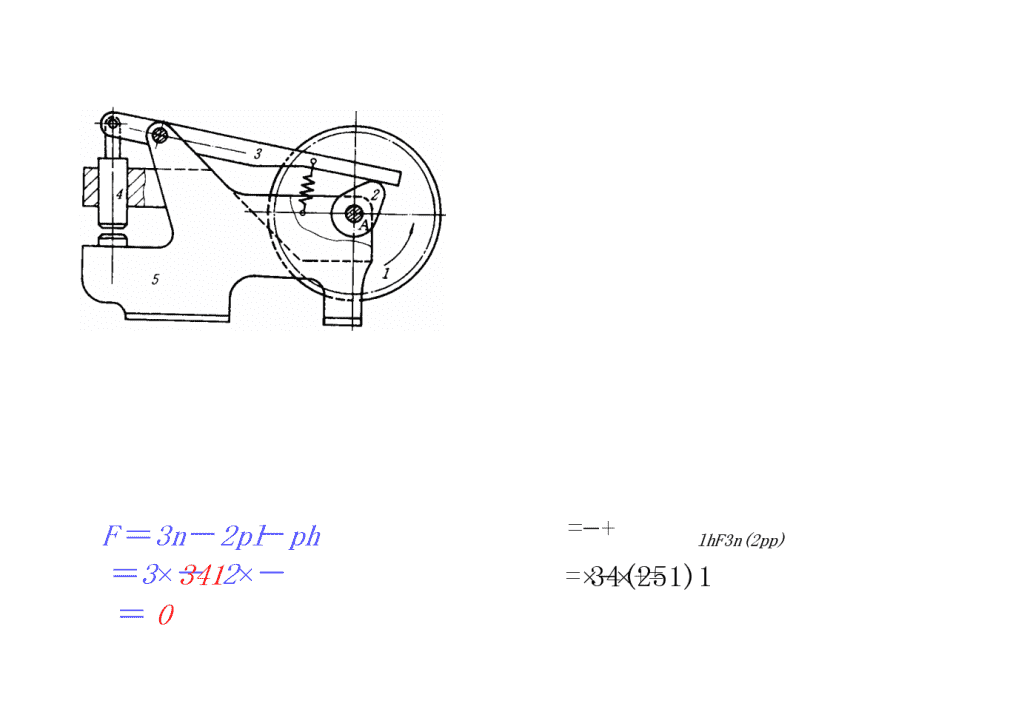
F=3n-2pl-ph=3×-2×-341=034(251)1lhF3n(2pp)=−+=×−×+=
1-1"2345789F"p")p(2p3nFhl−−+−=138(21020)1=×−×+−−=
46(2-3)133(240)1lhF3n(2pp)=−+=×−×+=
F"p")p(2p3nFhl−−+−=120)28(273=−−+×−×=F"p")p(2p3nFhl−−+−=134(250)01=×−×+−−=023032=×−+×=−+=3n"p2pp""h"l
102)017(2113=−−+×−×=F"p")p(2p3nFhl−−+−=2630102=×−+×=−+=3n"p2pp""h"l
(1)未刹车时n=6,pl=8,ph=0,F=2(2)刹紧一边时n=5,pl=7,ph=0,F=1(3)刹紧两边时n=4,pl=6,ph=0,F=0
《机械原理》作业题解第三章平面机构的运动分析
题3-1试求图示各机构在图示位置时全部瞬心。a)ACB4132P12P23P34P24P14→∞P14→∞P13→∞
题3-1试求图示各机构在图示位置时全部瞬心。b)ACB4132P12P34P24P14→∞P13P23→∞
题3-1试求图示各机构在图示位置时全部瞬心。ACB4132MvMc)P12P23P24P34→∞P13P14
解:1.绘机构运动简图2.求瞬心P133.求ω1/ω3题3-2在图示的齿轮-连杆组合机构中,试用瞬心法求齿轮1和3的传动比ω1/ω3。C2DBA13546P12P23P131361331613PPPPωω=P16P36
题3-4•在图示的四杆机构中,lAB=60mm,lCD=90mm,lAD=lBC=120mm,ω2=10rad/s,试用瞬心法求:•1)当φ=165时,点C的速度vC;•2)当φ=165时,构件3的BC线上(或其延长线上)速度最小的一点E的位置及其速度的大小;•3)当vC=0时,φ角之值(有两个解)。
题3-4解取μι作机构运动简图;并求出各瞬心如图所示。2lmmmmμ=P24ACB4132DP14P12P34P231)当φ=165时,点C的速度vC=?242122441424122442142448.5104.47(/)108.5PllvPPPPPPradsPPωμωμωω=⋅=⋅==×=⇒44.470.090.40(/)CCDvlmsω=⋅=×=解法2:利用瞬心P24利用瞬心P13瞬心P13为构件3的绝对瞬心P1331313BCllvvPBPCωμμ==⋅⋅13132131378.2100.060.40(/)118.5CBABPCPCvvlmsPBPBω===××=
题3-4解P24ACB4132DP14P12P34P232)当φ=165时,构件3的BC线上(或其延长线上)速度最小的一点E的位置及其速度的大小瞬心P13为构件3的绝对瞬心,构件3上各点在该位置的运动是绕P13的转动,则距P13越近的点,速度越小,过作BC线的垂线P13E⊥BC,垂足E点即为所求的点。E点距C点距离为P1331313BlElvPBPvEωμμ==⋅⋅13132131370.3100.060.36(/)118.5EBABPEPEvvlmsPBPBω===××=E234.368.6()lCEmmμ⋅=×=
题3-4解P24ACB4132DP14P12P34P233)当vC=0时,φ角之值(有两个解)?P13E4CCDvlω=⋅当ω4=0时,vC=0,而1224421424PPPPωω=当P24与P24重合时12244000CPPvω=⇒=⇒=则必然是杆2和杆3共线的位置,有两共线位置:①重叠共线位置②拉直共线位置2122726ϕϕ==쐠쐠1ϕ2ϕ
题3-5•在图示的各机构中,设已知各构件的尺寸及点B的速度,试作出其在图示位置时的速度多边形。ACBDEFvBvBACDFEGBb)a)
题3-5解a)解:顺序ACBDEFvBBCDEvvvv→→、CBCBvvv=+(1)求vC和vD(2)求vEECECDEDvvvvv=+=+p(a,f)ecdbDBDBvvv=+
题3-5解b)解:顺序BCEFvvvv→→→CBCBvvv=+(1)求vC(2)求vE:用速度影像法FEFEvvv=+vBACDFEGB(3)求vFp(a,d,g)(c)b(e)(f)
题3-8b)解b)1ACDB在图示各机构中,设已知各构件的尺寸,原动件以等角速度ω1顺时针方向转动;试以图解法求机构在图示位置时构件3上C点的速度及加速度。2341ω[解](1)取μι作机构运动简图;(2)速度分析取B为重合点:B(B1,B2,B3)1)求vB2ABllmmmABμ⎛⎞=⎜⎟⎝⎠2133()BBBCvvvv→=→211BBABvvlω==2)求vB33232BBBBvvv=+B(B1,B2,B3)方向:⊥BD⊥BA∥CD大小:?√?11/Bvvmsmmpbμ⎛⎞=⎜⎟⎝⎠取作速度图p(d)b2(b1)(b3)(c3)3)求vC3:用速度影像法30Cv=330CCDvlω==同时可求得
题3-8b)解(续)b)1ACDB2341ω[解](1)取μι作机构运动简图;(2)速度分析(3)加速度分析1)求aB2方向:B→A22111nBBBAABaaalω===2)求aB3B(B1,B2,B3)方向:B→D⊥BDB→A0∥CD大小:√?√0?211/""Baamsmmpbμ⎛⎞=⎜⎟⎝⎠取作加速度图p(d)b2(b1)(b3)(c3)3)求aC3:用加速度影像法23231""aBABCapcalμω===2133()BBBCaaaa→=→33323232ntkrBBDBDBBBBBaaaaaa=+=++其中k2B3B2B3B2a=2v=0ωp"(d")b"2(b"1)k"b"3c"3(n"3)
题3-8c)解在图示各机构中,设已知各构件的尺寸,原动件以等角速度ω1顺时针方向转动;试以图解法求机构在图示位置时构件3上C点的速度及加速度。[解](1)取μι作机构运动简图;(2)速度分析取B为重合点:B(B1,B2,B3)1)求vB2ABllmmmABμ⎛⎞=⎜⎟⎝⎠2133()BBBCvvvv→=→211BBABvvlω==2)求vB33232BBBBvvv=+方向:⊥BD⊥BA∥CB大小:?√?11/Bvvmsmmpbμ⎛⎞=⎜⎟⎝⎠取作速度图p(d)b2(b1)(b3)(c3)3)求vC3:用速度影像法33Cvvpcμ=ABCD12341ω3333pcpbDCpcpbDCDBDB=⇒=∵31CDCDCBABBCBCllvvlllω∴==⋅
题3-8c)解(续1)[解](3)加速度分析1)求aB212211nBBBAABaaalω===2)求aB3ABCD12341ωp(d)b2(b1)(b3)(c3)方向:B→A方向:B→D⊥BDB→A0∥CD大小:√?√0?其中0)0(k2B3B2B3B23B2Bva=2v=ω=∵211/""Baamsmmpbμ⎛⎞=⎜⎟⎝⎠取作加速度图2133()BBBCaaaa→=→33323232ntkrBBDBDBBBBBaaaaaa=+=++
题3-8c)解(续2)[解](3)加速度分析1)求aB22)求aB3ABCD12341ωp(d)b2(b1)(b3)(c3)方向:B→D⊥BDB→A0∥CD大小:√?√0?211/""Baamsmmpbμ⎛⎞=⎜⎟⎝⎠取作加速度图p"(d")b"2(b"1)k"b"3c"33)求aC3:用加速度影像法33"""~bcdBCDΔΔ作33""aCapcμ=2133()BBBCaaaa→=→33323232ntkrBBDBDBBBBBaaaaaa=+=++
题3-10解在图示的摇块机构中,已知lAB=30mm,lAC=100mm,lBD=50mm,lDE=40mm,ω1=10rad/s,试用图解法求机构在φ1=45°位置时,点D和E的速度和加速度;以及构件2的角速度和角加速度。BACD2341ω1E1ϕ[解](1)取μι作机构运动简图;(2)速度分析取C为重合点:C(C2,C3)0.002lmmmμ=2222cos1353010030100cos135123()BCABACABABlllllmm=+−⋅⋅=+−××=籰籰2,BCDE2vvvvω→→→
题3-10解(续)BACD2341ω1E1ϕ[解](1)取μι作机构运动简图;(2)速度分析取C为重合点:C(C2,C3)1)求vB1100.030.3(/)BABvlmsω==×=2)求vC222323CBCBCCCvvvvv=+=+方向:⊥AB⊥BC0∥BC大小:√?0?/0.005vmsmmμ=取作速度图p(c3)bc22,BCDE2vvvvω→→→
题3-10解(续2)BACD2341ω1E1ϕ[解](2)速度分析1)求vB2)求vC23)求vD和求vE用速度影像法p(c3)bc2250123BDBCbdBDlbcBCl===作得d点d0.00544.60.223(/)Dvvpdmsμ==×=4050DEBDdeDElbdBDl===并使得e点2debc⊥作e0.00532.00.16(/)Evvpemsμ==×=3)求ω22220.00549.02.0(/)0.123CBvBCBCvbcradsllμω×====顺时针2ω2,BCDE2vvvvω→→→
题3-10解(续3)BACD2341ω1E1ϕp(c3)bc2de2ω[解](3)加速度分析1)求aB2)求aC222232323ntkrCBCBCBCCCCCaaaaaaa=++=++方向:B→AC→B⊥CB0⊥CB向下∥BC大小:√√?0√?2/0.05amsmmμ⎛⎞=⎜⎟⎝⎠取作加速度图其中:p"(c"3)k"n"2b"22,BCDEaaaaα→→→1222100.033(/)nBBAABaalmsω===×=方向:B→A222222.00.1230.492(/)nCBBCalmsω==×=23323232222()22.0(0.00539.0)0.78(/)kCCCCvavccmsωωμ=⋅=⋅=×××=c"2
题3-10解(续4)BACD2341ω1E1ϕp(c3)bc2de2ω[解](3)加速度分析1)求aB2)求aC23)求aD和求aE用加速度影像法k"p"(c"3)b"n"2c"22""50123""BDBCbdBDlbcBCl===作得d"点2""0.0552.52.63(/)Daapdmsμ==×=d"""4050""DEBDdeDElbdBDl===并使得e"点2""""debc⊥作e"2""0.0556.22.81(/)Eaapemsμ==×=4)求α222222""0.0518.07.32(/)0.123tCBaBCBCancradsllμα×====顺时针2α22,BCDEaaaaα→→→
题3-11解在图示的机构中,已知lAE=70mm,lAB=40mm,lEF=60mm,lDE=35mm,lCD=75mm,lBC=50mm,原动件以等角速度ω1=10rad/s回转。试以图解法求在φ1=50°时点C的速度vC和加速度aC。[解](1)取μι作机构运动简图;0.001lmmmμ=sin50sinEFAEllAFE=∠륨BACD2341ω1E1ϕF651170sinsin50sinsin5063.360AEEFlAFEl−−⎛⎞⎛⎞∠===⎜⎟⎜⎟⎝⎠⎝⎠륨륨륨1805063.366.7AEF∠=−−=ÜÜÜÜsin66.7sin66.76071.9()sin66.7sin50sin50sin50AFEFAFEFllllmm=⇒==×=륨륨륨륨ÜÜ
题3-11解(续)[解](1)取μι作机构运动简图;(2)速度分析BACD2341ω1E1ϕF6515,BFFDCvvvvv→→→1)求vB和vF11100.040.4(/)BABvlmsω==×=2)求vF5(=vF4)45151FFFFFvvvv==+方向:⊥FE⊥AF∥AF大小:?√?/0.04vmsmmμ=取作速度图11100.0720.72(/)FAFvlmsω==×=pbf1f5(f4)
题3-11解(续2)[解](2)速度分析BACD2341ω1E1ϕF651)求vB和vF12)求vF5(=vF4)3)求vD用速度影像法或按以下方法求出:pbf1f5(f4)4440.0440.226.8(/)0.06FvEFEFvpfllradsμω==×==逆时针4ω426.80.0350.94(/)DDEvlmsω==×=3)求vCCBCBDDBvvvvv=+=+方向:√⊥CB√⊥CD大小:√?√?dc0.0417.50.70(/)Cvvpcmsμ==×=15,BFFDCvvvvv→→→
题3-11解(续3)pbf1f5(f4)dcBACD2341E1ϕF654ω1ω[解](3)加速度分析1)求aB和aF1515151444krntFFFFFFFEFEFaaaaaaa=++=+=方向:F→A⊥AF向下∥AFF→E⊥FE大小:√√?√?154,()BFFFDCaaaaaa=→→→1222100.044(/)nBBAABaalmsω===×=121122100.0727.2(/)nFFAAFaalmsω===×=2)求aF5方向:B→A方向:F→A其中:2224426.80.0643.1(/)nFEEFalmsω==×=25115111522()210(0.0435.7)18.56(/)kFFFFvavffmsωωμ=⋅=⋅=×××=
题3-11解(续4)pbf1f5(f4)dcBACD2341E1ϕF654ω1ω[解](3)加速度分析1)求aB和aF12/1amsmmμ⎛⎞=⎜⎟⎝⎠取作加速度图2)求aF5p"方向:F→A⊥AF向下∥AFF→E⊥FE大小:√√?√?b"k"f"1f"5(f"4)515151444krntFFFFFFFEFEFaaaaaaa=++=+=
题3-11解(续5)pbf1f5(f4)dcBACD2341E1ϕF654ω1ω[解](3)加速度分析1)求aB和aF12)求aF53)求aD加速度影像法ntntCBCBCBDCDCDaaaaaaa=++=++方向:√C→B⊥CB√C→D⊥CD大小:√√?√√?d"k"p"b"f"1f"5(f"4)4""50123""DEFEpdlpfl==作得d"点2""128.228.2(/)Daapdmsμ==×=4)求aC
k"p"b"f"1f"5(f"4)题3-11解(续6)pbf1f5(f4)dcBACD2341E1ϕF654ω1ω[解](3)加速度分析1)求aB和aF12)求aF53)求aD方向:√C→B⊥CB√C→D⊥CD大小:√√?√√?d"4)求aC其中:2222()(0.047.5)1.8(/)0.05nCBvCBBCBCvbcamsllμ×====2222()(0.0424.0)12.3(/)0.075nCDvCDCDCDvdcamsllμ×====2""12.82.8(/)Caapcmsμ==×=n"3c"n"2ntntCBCBCBDCDCDaaaaaaa=++=++
题3-14解在图示的齿轮—连杆组合机构中,MM为固定齿条,齿轮3的直径为齿轮4的2倍,设已知原动件以等角速度ω1顺时针方向回转。试以图解法求机构在图示位置时,E点的速度vE以及齿轮3、4的速度影像。[解](1)取μι作机构运动简图;(2)速度分析BACDEFMM234165BCEvv?v→→→1)求vBKvK1BABvlω=方向:⊥BA,指向ω1方向
题3-14解(续)[解](1)取μι作机构运动简图;(2)速度分析BACDEFMM234165BCKEvvvv→→→1)求vB2)求vCKCBCBvvv=+方向:∥AC⊥BA⊥CB大小:?√?/Bvvmsmmpbμ⎛⎞=⎜⎟⎝⎠取作速度图pbc3)求vKK点为两齿轮节圆的切点,是齿轮3和齿轮4的相对瞬心;而D点为齿轮3和齿条的相对瞬心,因齿条固定成为机架,故D点为齿轮3的绝对瞬心。∴vK⊥DKvK
题3-14解(续2)[解](1)取μι作机构运动简图;(2)速度分析BACDEFMM2341651)求vB2)求vC3)求vKKcpbvKKCKCvvv=+方向:⊥KD沿AC⊥KC大小:?√?或利用速度影像法~bcdBCDΔΔ作(d)k4)求vEEKEKvvv=+方向:⊥EF√⊥EK大小:?√?eEvvpeμ=g3g4BCKEvvvv→→→
1《机械原理》作业题解第五章机械的效率和自锁
2解:该系统的总效率为:221230.950.970.90.804ηηηη=⋅⋅=××=电动机所需的功率为:55001.28204()8,204()0.804PvNWkWη×====
3解:此传动属混联系统输入功率:""56.25()0.812()0.5AAABBBPPkWPPkWηη======系统的总效率:2212""510.920.970.636.252ABABPPPPηηη++=⋅⋅=××=++电动机所需的功率为:519.53()0.63ABdPPPkWη++====
4解法2:此传动属混联系统输入功率:"221"2217.22()2.31()AAABBAPPkWPPkWηηηηηη==⋅⋅==⋅⋅系统的总效率:""510.637.222.31ABABPPPPη++===++电动机所需的功率为:""7.222.319.53()dAAPPPkW=+=+=
5α补充例题1物体重为G,放在倾斜角为α的斜面上,物体与斜面的摩擦系数为f。求物体平衡时,水平力F的大小。[解]F若太大,物体上滑;F若太小,物体下滑;(1)求FmaxFGxyFNFfmaxmax0:cossin00:sincos0fNXFGFYFFGαααα=−−==−−=∑∑fNFfF=补充maxtan1tanfFGfαα+=−机械原理——机械的效率和自锁tanfϕ=令maxtan()FGαϕ=+
6αF"GxyFN[解]F若太大,物体上滑;F若太小,物体下滑;(1)求Fmax(2)求Fmin补充例题1解(续)αFGxyFNFfminmin0:cossin00:sincos0fNXFGFYFFGαααα=−+==−−=∑∑fNFfF=补充maxtan()FGαϕ=+Ffmintan1tanfFGfαα−=+maxtanfφ=令()()tantanGFGαϕαϕ−≤≤+mintan()FGαϕ=−机械原理——机械的效率和自锁
7补充例题2物体重为G,放在倾斜角为α的斜面上,物体与斜面的摩擦系数为f。1.求物体平衡时,水平力F的大小;2.求物体上升和下滑时的效率。[解](1)上升时,F为驱动力,G为阻力机械原理——机械的效率和自锁αF"GxyFNαFGxyFNFftan()FGαϕ=+理想驱动力:0tanFGα=0tantantan()tan()FGFGααηαϕαϕ===++(2)下降时,G为驱动力,F为阻力tan()tan()FFGGαϕαϕ=−→=−理想驱动力:0tanFGα=0/tantan()/tan()tanGFGFααϕηαϕα−===−
1《机械原理》作业题解第十一章机械的运转及其速度波动的调节
2[解]利用力矩形式的机械运动方程式:22eeeeeeeddJdJJMJMdtddtddtMωωωωϕ⇒⇒⋅+⋅=⋅==认为制动时是匀减速制动,则eeJtMωΔ=Δ02020()0100100(/)edrMMMNmradsω=−=−=−⋅⎧⇐⎨Δ=−=−⎩0.5(100)2.5()3()20ss=×−=<−所以该制动器满足工作要求
3[解](1)确定电动机的平均功率根据一个运动循环周期内的驱动功与阻力功相等1122dPTPtPt→=+121122233dTTPPPtPtPTT⋅+⋅+==122367.7236772573.9()3333PPW×=+=+=rdWW=tPt1t2TP1PdP2
4时间周期T:snT6.01006060===1220.2,0.433TTtsts====(2)求最大赢亏功max11()(2573.9367.7)0.2441.24()dWPPtJΔ=−=−×=tPt1t2TP1PdP2aba"aba"
5[]][90022max2maxδπδωnWWJmFΔΔ=≥05.010014.324.44190022×××=280.473()kgm=⋅05.0144014.324.44190022×××=20.388()kgm=⋅飞轮装在电动机轴上时:[](3)求飞轮转动惯量飞轮装在曲柄轴上时:][90022max2maxδπδωnWWJmFΔΔ=≥
6
7rdWW=作能量指示图πππϕϕ2/200)6/(×+==rddrMM700116.67()6Nm==⋅0ΕFG显然,在E处出现能量最小值,在F处出现能量最大值,即ϕ=ϕF时,n=nmax"1010420067.1162001303020°=−×°+°+°=Fϕmax(1/2)623.1()mnnr/minδ=+=(2)求nmax和φmax[解](1)确定阻抗力矩根据一个运动循环内的驱动功与阻力功相等,即:"401120067.11620°=×°=EϕrMΕFG
8)6)(67.116200(21maxEFWϕϕπ−+−=Δ89.084()J=max22900[]FWJnπδΔ≥2290089.0843.146200.01×=××22.113()kgm=⋅)10872161256)(67.116200(21πππ−+−=(3)求最大赢亏功(4)求飞轮转动惯量0ΕFGrMΕFG
9maxmaxminWEEΔ=Δ−Δ(3)求最大赢亏功方法二rMΕFG求从一周期开始至各处的赢亏功累积值f1f2f3()()1110011.667116.66711.878()22180ErfMJπϕ=−+⋅=−+××=−()()()()()212002130104.16711.667200116.66789.084()2180BAFErfMJϕϕϕϕπ=−+−⋅−⎡⎤⎣⎦=+−××−=⎡⎤⎣⎦()()311180180116.667116.66777.206()22180FrfMJπϕ=−−⋅=−−××=−
10maxmaxminWEEΔ=Δ−Δ(3)求最大赢亏功方法二rMΕFG求从一周期开始至各处的赢亏功累积值111.(:878)EOEEfJϕϕΔ==−→f1f2f321211.87889.08477.206():OFFEEEfffJϕϕΔ=Δ+=+=−+=→312311.87889.08477.20:60OGGFEEffffϕϕΔ=Δ+=++=−+−=→maxmin77.206()11.878()FEEEJEEJΔ=Δ=Δ=Δ=−maxmaxmin89.084()WEEJΔ=Δ−Δ=
《机械原理》作业题解第八章连杆机构及其设计
8-5画出机构运动简图,并说明各为何种机构?在图(a)中偏心盘1绕固定轴O转动.迫使滑块2在圆盘3的槽中来回滑动,而3又相对于机架转动。图(b)中偏心盘1绕固定轴O转动.通过构件2,使滑块3相对于机架往复移动解:(a)曲柄摇块机构(b)曲柄滑块机构
8-6如图,已知a=240mm,b=600mm,c=400mm,d=500mm,问:1)取杆4作机架时,是否有曲柄存在?2)能否选不同杆为机架得到双曲柄机构、双摇杆机构?3)若a、b、c三杆的长度不变,取杆4为机架,要获得曲柄摇杆机构,d的取值范围应为何值?解:∵minmax840LLabmm+=+=∴ABDabcdC1234mmdc900=+<且Lmin=a为连架杆有曲柄,1为曲柄1)2)1为机架,得到双曲柄机构3为机架,得到双摇杆机构3)若4为最短杆,则不可能成为曲柄摇杆机构,故不可能短杆,即d>240,还须满足杆长条件240600400440abcddabc+≤+⇒>+−=+−=600400240760adbcdbca+≤+⇒≤+−=+−=结论:mmd760440≤≤若4为最长杆,则d>240
8-8已知l1=28mm,l2=52mm,l3=50mm,l4=72mm,求:1)杆4为机架时,极位夹角θ、摆角、最小传动角τmin、行程速比系数K2)取杆1为机架,将演变为何种机构?说明C,D是转动副还是摆动副?3)取3为机架,又将演变为何种机构?A,B是否仍是转动副?解:该题宜采用图解法,直接作图求得相关参数ABCD1234C1C242123242211)(2)(arccoslllllll+−++=δ解析法:1)41223242122)(2)(arccoslllllll−−+−=δ°=−=6.1812δδθ°=−−+−+−+=5.702)(arccos2)(arccos432122423432212324llllllllllllϕ°=+−+=06.512)(arccos3224123221llllllγ°=+−+=73.222)(arccos3221423222llllllγ比较γ1,γ2,故γmin=γ2=22.73°23.1180180=−+=θθKmmllLL10014minmax2)=+=+mmll10232=+<且Lmin=l1为机架双曲柄机构,C,D均为摆动副3)Lmin=l1为连杆双摇杆机构,A,B均为周转副
θ2/)(12ACACllAB−=μ2/)(12ACACllBC+=μ或者另一解:C’2D解:1)计算极位夹角θ°8-23如图所示,现欲设计一铰链四杆机构,已知摇杆CD的长lCD=75mm,行程速比系数K=1.5,机架AD的长度为lAD=100mm,摇杆的一个极限位置与机架间的夹角为ψ=45°,试求曲柄的长度lAB和连杆的长度lBC。=362)按照急回机构作图CAC22/)("21ACACllAB−=μ2/)("21ACACllBC+=μ11180+−⋅°=KKθ
8-28试设计一曲柄滑块机构。已知滑块的行程速比系数K=1.5,滑块的行程H=50mm.偏距e=20mm。并求其最大压力角αmax。解:1)计算极位夹角θ2/)(12ACACllAB−=μ2)按照急回机构作图°=3611180+−⋅°=KKθC1C2H2θADBCe2/)(12ACACllBC+=μC’αmax?max=α
1《《机械原理机械原理》》作业题解作业题解第九章第九章凸轮机构及其设计凸轮机构及其设计
2课堂练习
3α2sα1s
4取μl=1(mm/mm)逆偏置情况如题9-6图a)所示
1《机械原理》作业题解第十章齿轮机构及其设计
2解:1)根据渐开线方程式/cos()tankbkkkkkrrinvαθααα=⎧⎨==−⎩1150coscos0.6931599()39.7151465tantan0.69315990.69315990.1375025()7.87831bkkkkkrradrradαθαα−−=====−=−==ẨẨ
3解:2)50.0872665()kradθ==⠨0.08722350.08726650.087925kθ<==<⠨3445"3450",?kkαα<<=⠨⠨用线形插值法3450"3445"3445"(0.08726650.087223)0.0879250.0872233445.31"kα−=+×−−=⠨⠨⠨⠨50/cos60.857cos3445.31"kbkrrα===⠨
4解:sin39sin2013.339rρα===ヨ111*111**coscos/2coscoscos/2coscos26cos20coscoscos29.24114222621baaaaaarrmzrrmzhmzzzhzhααααα−−−−−−===+====+++×ヨヨsin42sin29.2411420.516aarρα===ヨ或222242(39cos20)20.516aabrrρ=−=−=ヨ
51112121221212235025(1)10(19/5)()(1)22925455azmmzmiazziziz×⎧===⎪+×+⎪=+=+⇒⎨⎪==×=⎪⎩11*1111102525022502110270cos250cos20234.92aabdmzddhmddα==×=⎧⎪=+=+××=⎨⎪==°=⎩22*2222104545024502110470cos450cos20422.86aabdmzddhmddα==×=⎧⎪=+=+××=⎨⎪==°=⎩101015.7122mseππ×====
6**coscos2(22)bffaddmzddhmzhcαα===−=−−fbdd≥由有****(22)cos22cosaamzhcmzzhczαα−−≥⇒−−≥**2()2(10.25)41.451cos1cos20ahczα°++≥==−−42z≥若时,fbdd>41z>或时,fbdd>
7解:()()[]"tantan"tantan212211ααααπεα−+−=aazz1111111*111111*1coscoscoscoscos(2)cos19cos20coscos31.76678(2)1921baaaaaddmzddmzhzzhαααα−−−°−−°===+===++×1122*2cos42cos20coscos26.23619(2)4221aazzhαα°−−°===++×
8()()()()121122122tantan"tantan"costantan"tantan"224.109babaabaBBrrmrααααααααα=−+−=−+−⎡⎤⎣⎦=()()[]"tantan"tantan212211ααααπεα−+−=aazz()()2119tan31.76678tan20tan26.23619tan2021.644zπ°°°°⎡⎤=×−+−⎣⎦=cos5cos2014.761bpmπαπ°==××=1224.1091.64414.761bBBpαε===
9在P点啮合时,()()11111111tantan"costantan"11.3932baaBPBNPNrmzααααα=−=−=−=()()22222222tantan"costantan"13.5322baaBPBNPNrmzααααα=−=−=−=12,bbBPpBPp<<∵∴只有一对齿啮合在B1点啮合时,12bBBp>∵∴有两对齿啮合
1011"cos"coscos700cos20"coscos24.866582452"00""725aaaaαααα°−−°°=⇒====解:求标准中心距a12()20(3040)70022mzza+×+===coscos20"700711.981cos"cos24.86658aaαα°°==×=
11解:(1)求中心距a,同时修正β12()8(2040)248.4662cos2cos15mzzaβ°+×+===取a=248,则112()8(2040)cos14.5925522248mzzaβ−°+×+===×(2)求εγ取a=250,则112()8(2040)cos16.260222250mzzaβ−°+×+===×()()""11221tantantantan2sinattattβnzzBmαγαβεααααπεεεβεπ⎧⎡⎤=−+−⎪⎣⎦⎪=+⎨⎪=⎪⎩
12(2)求εγ()()""11221tantantantan2sinattattβnzzBmαγαβεααααπεεεβεπ⎧⎡⎤=−+−⎪⎣⎦⎪=+⎨⎪=⎪⎩()()()()()()11111111111222221tantan/costantan20/cos16.260220.76350()cos/coscos/(2co20.6114131.4163426s)31.44412()cos/coscos/(2cos)26.84583()1ta.774n205tnatbatatbataddzzddzzzαααβααβααβεαπ−−°°°−−°−°−°°°=====+===+==()()""122tantantan1.548()sin0.334()1.1.5650.3011882().856ttattβnzBmγαβαααβεπεεε⎡⎤−+−=⎣⎦===+=
13(2)求zv1和zv213222.06744.122.606()45.212()co4s3vvvzzzzβ=⎧=⇒⎨=⎩
1《机械原理》作业题解第十一章齿轮系及其设计
21234515512"3"4"5030405220151185200577.89nzzzzinzzzz==⋅⋅⋅=×××==
3z4解:轮系划分:复合轮系行星轮系部分:1-2-3-H1行星轮系部分:4-5-6-H221241H1HHiii=⋅在行星轮系部分1-2-3-H1中:112333()H1H1121zzzi1i11zzz=−=−−=+22566446454()HHzzzi1i11zzz=−=−−=+21241H1HHiii=⋅在行星轮系部分4-5-6-H2中:3643939211643.18477491zz11zz11⎛⎞⎛⎞=+⋅+⎜⎟⎜⎟⎝⎠⎝⎠⎛⎞⎛⎞=+⋅+==⎜⎟⎜⎟⎝⎠⎝⎠221300069.471(/min)43.184H1Hnnri===
4解:轮系划分:复合轮系定轴轮系部分:1-2-3-4行星轮系部分:4"-5-6-7行星轮系部分:7-8-9-H71H144H144"7Hiiiiii=⋅=⋅⋅241413zzizz=75664"74"64"54"()zzzi1i11zzz=−=−−=+在定轴轮系1-2-3-4中:在行星轮系4"-5-6-7中:899779787()HHzzzi1i11zzz=−=−−=+在行星轮系7-8-9-H中:
571H144"7Hiiii=⋅⋅2469134"7zzzz11zzzz⎛⎞⎛⎞=++⎜⎟⎜⎟⎝⎠⎝⎠问题:z4"=?根据基本构件的同心条件有:4"564"564"6522213123169rrrzzzzzz+=⇒+=⇓=−=−×=24691134"7604913116728.5836236994Hzzzzi1111zzzz⎛⎞⎛⎞×⎛⎞⎛⎞=++=×+×+=⎜⎟⎜⎟⎜⎟⎜⎟×⎝⎠⎝⎠⎝⎠⎝⎠113549124(/min)28.68HHnnri===转向与4相同
6解:轮系分析:差动轮系1123133312"2440()1.62030HHHHHnnnzzinnnzz−×===−=−=−−×()()()11331312001.610015.385(/min)11.6HHHninnir−=−−−×−==−−
7课堂例题如图所示。已知:z1=48,z2=48,z2"=18,z3=24,n1=250r/min,n3=100r/min,转向如图,试求nH的大小和方向解:122’3Hn1Hn2Hn3Hn1n3HHHnnnni−−=3113"2312zzzz⋅−=3418482448−=××−=转向同n1HHHininn1331311−−=()min)/(5034110034250r=⎟⎠⎞⎜⎝⎛−−−×⎟⎠⎞⎜⎝⎛−−=若n3转向如图,nH=?HHHininn1331311−−=min)/(3.16434110034250r=⎟⎠⎞⎜⎝⎛−−×⎟⎠⎞⎜⎝⎛−−=
8解:444/11HH1HHiiiii=⋅=(1)利用1-2-3-H组成的行星轮系,有:33311()1H21H1121zzziizzz=−=−−=+(2)利用4-(2"-2)-3-H组成的行星轮系,有:"3"34434411()1H22H22zzzziizzzz=−=−+=−344"3457116/5882557115625111HH22zziiizzzz++====−×−−×
9解:轮系分析:1-(2-3-4-5)-6-H为差动轮系112461666135()25241216055.602302418108HHHHHnnnzzzinnnzzz−===+⋅⋅−=××==1616()3163165.602()(/mi4n8~200268.2~5)29.3HHHnnnnir−−=+=+=
10解一:轮系划分:复合轮系差动轮系部分:1-(2-3)-4-H行星轮系部分:5-6-7-H6在差动轮系部分:1-(2-3)-4-H中12414413()HHHnnzzinnzz−==+⋅−在行星轮系部分:5-6-7-H中567755756511()1HHHnzzziinzzz==−=−−⋅=+-—①-—②由式②得545HHninn==⋅代入式①得
1112414413()HHHnnzzinnzz−==+⋅−545HHninn==⋅1145HHHHHnniinn−=⋅−111247247145135135(1)1(11)11145031.908(/min)39391521171718HHHnnnnzzzzzziizzzzzzr===−+⋅+−+⋅⋅+==××+
12解二:用反转法给整个机构加上-nH611177124713501()HHHHHHnnnninnnnzzznzzz−−==−−=−=−⋅⋅12471351145031.908(/min)39391521171718Hnnzzzzzzr=⋅⋅+==××+'
您可能关注的文档
- 机械制图习题集(第6版)参考答案.doc
- 机械制图试题库及答案.doc
- 机械制图课后习题第6版藏考答案.doc
- 机械制造技术习题答案.doc
- 机械制造装备设计第五章习题答案(关慧贞).doc
- 机械加工工艺及装备习题参考答案.doc
- 机械原理 朱龙英主编 习题解答(全).doc
- 龙英主编_习题解答(全).doc
- 机械原理_课后习题答案第七版.doc
- 机械原理习题卡答案.doc
- 机械原理习题及解答.doc
- 机械原理习题解答(高教2版).doc
- 机械原理课后答案.doc
- 机械员教材后的备考练习题及答案.doc
- 机械基础课后题答案.doc
- 机械工程控制基础(第六版)课后题目答案.doc
- 机械工程控制基础作业解答(1).doc
- 机械工程测试技术-课后习题及答案01.doc
相关文档
- 施工规范CECS140-2002给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程
- 施工规范CECS141-2002给水排水工程埋地钢管管道结构设计规程
- 施工规范CECS142-2002给水排水工程埋地铸铁管管道结构设计规程
- 施工规范CECS143-2002给水排水工程埋地预制混凝土圆形管管道结构设计规程
- 施工规范CECS145-2002给水排水工程埋地矩形管管道结构设计规程
- 施工规范CECS190-2005给水排水工程埋地玻璃纤维增强塑料夹砂管管道结构设计规程
- cecs 140:2002 给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程(含条文说明)
- cecs 141:2002 给水排水工程埋地钢管管道结构设计规程 条文说明
- cecs 140:2002 给水排水工程埋地管芯缠丝预应力混凝土管和预应力钢筒混凝土管管道结构设计规程 条文说明
- cecs 142:2002 给水排水工程埋地铸铁管管道结构设计规程 条文说明