电磁场与电磁波 第三章答案.pdf 34页

'第三章静电场重点和难点介绍电位满足的泊松方程和拉普拉斯方程，对于方程的定解条件，以及解的存在、稳定和惟一性问题应予说明，至于求解方法及惟一性证明可以从简。镜像法应重点讲解。强调镜像法的依据是惟一性定理，镜像法的理念是以镜像电荷代替边界的影响，从而把一个非均匀空间变为均匀空间。此外，还应说明仅在待求的场区等效。三种坐标系中求解拉普拉斯方程的方法，可以根据学时多少，适当取舍。若学时允许，建议介绍圆柱坐标系或球坐标系中的分离变量法。因为第九章中求解矩形波导中电磁波时还要使用直角坐标系中分离变量法。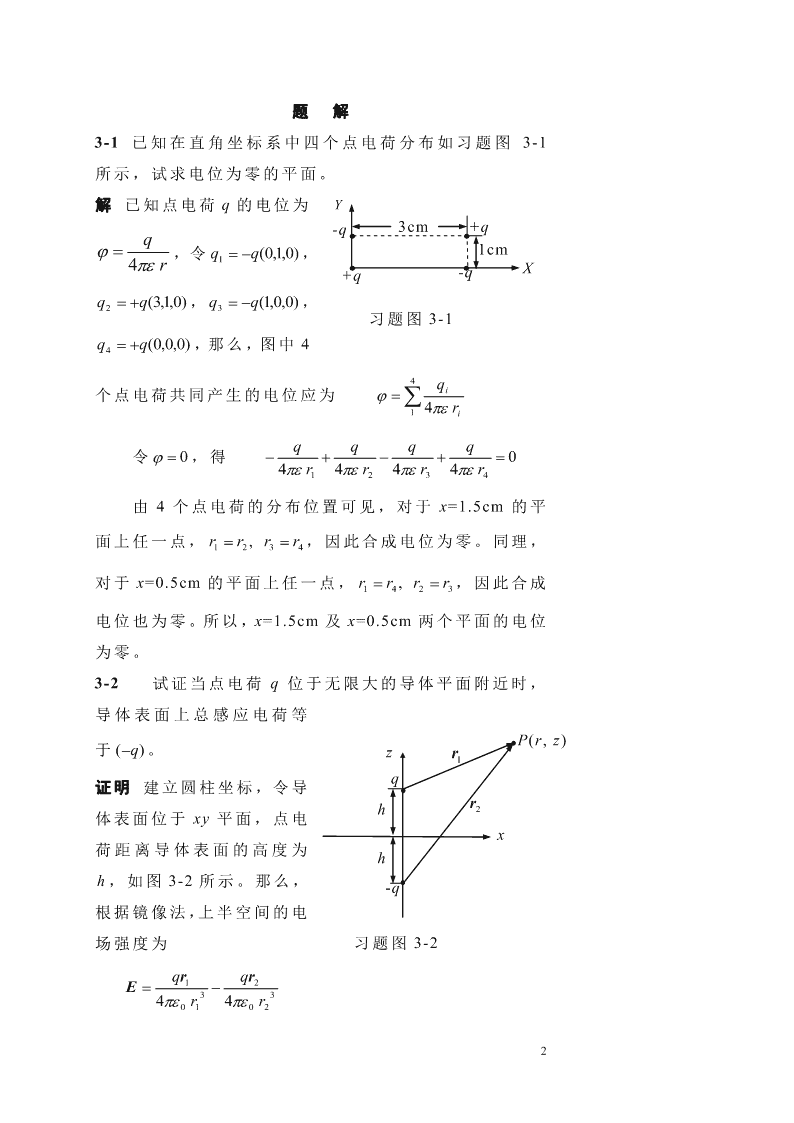重要公式电位方程：2有源区中电位满足泊松方程：2无源区中电位满足拉普拉斯方程：0泊松方程的积分解：(r)(r)G(r,r)dV0V[G(r,r)(r)(r)G(r,r)]dS00S1自由空间格林函数：G(r,r)04|rr|泊松方程的自由空间解：1(r)(r)G(r,r)dVV01 题解3-1已知在直角坐标系中四个点电荷分布如习题图3-1所示，试求电位为零的平面。解已知点电荷q的电位为Y-q3cm+qq，令qq(0,1,0)，1cm14r+q-qXqq(3,1,0)，qq(1,0,0)，23习题图3-1qq(0,0,0)，那么，图中444qi个点电荷共同产生的电位应为14riqqqq令0，得04r4r4r4r1234由4个点电荷的分布位置可见，对于x=1.5cm的平面上任一点，rr,rr，因此合成电位为零。同理，1234对于x=0.5cm的平面上任一点，rr,rr，因此合成1423电位也为零。所以，x=1.5cm及x=0.5cm两个平面的电位为零。3-2试证当点电荷q位于无限大的导体平面附近时，导体表面上总感应电荷等P(r,z)于(q)。zr1q证明建立圆柱坐标，令导rh2体表面位于xy平面，点电x荷距离导体表面的高度为hh，如图3-2所示。那么，-q根据镜像法，上半空间的电场强度为习题图3-2qrqr12E334r4r01022 qr1r2电通密度为DE()0334rr1233式中r3[r2(zh)2]2；r3[r2(zh)2]212那么，qrer(zh)ezrer(zh)ezD334[r2(zh)2]2[r2(zh)2]2qrr33er4[r2(zh)2]2[r2(zh)2]2zhzh33ez[r2(zh)2]2[r2(zh)2]2已知导体表面上电荷的面密度D，所以导体表面的sn感应电荷为qhhqhsDzz03334[r2h2]2[r2h2]22(r2h2)2则总的感应电荷为rdrq"dS2rdrqhqss0s03(r2h2)23-3根据镜像法，说明为什么只有当劈形导体的夹角为的整数分之一时，镜像法才是有效的？当点电荷位于两块无限大平行导体板之间时，是否也可采用镜像法求解。答根据镜像法，如果劈形导体的夹角不为的整数分之一时，则镜像电荷不能最终和原电荷重合，这样将会产生无限多个镜像电荷，每个镜像电荷都会产生一定的电位，导致合成电位无限大，因而无解。当点电荷位于两块无限大导体板之间时，可采用镜像法求解。此时虽然也会产生无限多个镜像电荷，但是远处的镜像电荷对于两板之间的场点贡献越来越小，因3 此可以获得一个有限的解。3-4一根无限长的线电荷平行放置在一块无限大的导体平面附近，如习题图3-4所示。已知线电荷密度10(C/m)，离开平面的高度h5m，空间媒质的相对介l电常数4。试求：①空ry间任一点场强及能量密度；l②导体表面的电荷密度；③rh当线电荷的高度增加一倍x时，外力对单位长度内的线导体电荷应作的功。习题图3-4解①建立圆柱坐标，令导体表面位于xz平面，导体上方场强应与变量z无关。根据镜像法，上半空间中任一点P(x,y)的场强为lr1lr2lxex(yh)eyxex(yh)eyE2222222rr12rr22rx(yh)x(yh)lxx2222ex2rx(yh)x(yh)(yh)(yh)2222eyx(yh)x(yh)电场能量密度为2244422222212lh(xyh2xh2xy2yh)wEr22222222r[x(yh)][x(yh)]已知导体表面的电荷面密度D，那么sny0lh2DE(C/m)sny0ryy0(x2h2)单位长度内线电荷受到的电场力可等效为其镜像线电荷对它的作用力，即4 2lFe2y2(2h)r可见，线电荷受到的是吸引力。所以，当线电荷的高度h增加一倍时，外力必须做的功为222h2hll11W(F)dldy2.8110（J）。hh2(2y)216hrr3-5在无限大的导体平面上空平行放置一根半径为a的圆柱导线。已知圆柱导线的轴线离开平面的距离为h，试求单位长度圆柱导线与导体平面之间的电容。解根据镜像法可知，无限大的导体平面与无限长圆柱导线之间的场分布与两根无限长平行圆柱导线之间的一半空间的场分布完全相同。因此，圆柱导线与导体平面之间的单位长度内的电容是两根平行圆柱导线的单位长度内的电容一倍。由教材3-3节获知两根平行圆柱导线的单位长度内的电容为C1DD2Darccoshln12a2a2a式中D为两根圆柱导线轴线之间的距离，a为圆柱导线的半径。因此，对于本题的圆柱导线与导体平面之间的单位长度内的电容为22C1hh2harccoshln1aaa若高度h>>a，上式还可进一步简化为2C12hlna5 3-6一根无限长线电荷平行放置h在夹角60的导电劈的中央部位，l离开两壁的距离为h，如习题图3-6(a)60h所示。若线电荷的线密度为l，试习题图3-6(a)求其电位分布函数。yPr5-lrr0l4r1rl60oxr3r-l2-ll习题图3-6(b)解根据镜像法，正如原书3-3节所述，需要引入5个镜像电荷，，，，和，1l2l3l4l5l它们离场点P的距离分别为r，r，r，r，和r，其位12345置如习题图3-6(b)所示。已知，无限长的线电荷产生的电场强度为lE2rr可见，空间某点r对于任一参考点r的电位为0rr1rll0(E)drdrlnrrr02r0r2rr对于本题，若取坐标原点作为电位参考点，因为原线电荷离坐标原点的距离为2h，离场点P的距离为r，l0那么该线电荷在P点产生的电位为6 2hllnp2rr0因为全部镜像电荷离坐标原点的距离均为2h，那么，劈间任一点P以坐标原点作为电位参考点的电位为2h2h2h2h2h2hl(lnlnlnlnlnln)2rrrrrr0012345rrrl135即ln2rrr00243-7已知点电荷q位于两块d无限大的接地的平行导体板之qd/3间，如习题图3-7所示。两板d习题图3-7间距为d，点电荷位于处，3试求两板间的电位分布。解选用圆柱坐标系，令下底板位于z=0平面，点电荷q位于z轴，则导体板之间任一点电位与角度无关。根据镜像法，必须在z轴上引入无限多个镜像电荷，它们的位置分别为：z5d7d正z轴上：q(0,)，q(0,)，33q11dq(0,)，．．．3-qd5d负z轴上：q(0,)，q(0,)，33r7dPr,zq(0,)，．．．3q-qxq则两板之间任一点Pr,z的电位为：7 11q1221222222rz(2nd)rz(2nd)40n13311q12212222rz[2(n1)]drz[2(n1)]d40n1333-8试证位于无限大导体平面上半球形导体上空的点电荷q受到的力的大小为235q16adF12442160d(da)式中a为球半径，d为电荷与球心的间距，0为真空介电常数，如习题图3-8(a)所示。qq0ddq′a0d′q″d″d0-q习题图3-8(a)习题图3-8(b)证明应用镜像法，将半球变为一个整球。那么，为了保证无限大导体平面和球面形成的边界电位为零，必须引入三个镜像电荷：q，q，q，其中q和q，以及q和q保证无限大平面边界的电位为零，q和q，以及q和q保证球面边界的电位为零。那么，根据镜像法，求得镜像电荷q和q分别为aaqq，qqdd8 22aa其位置分别位于d及d处。因此，点电荷q所dd受到的力应为三个镜像电荷产生的电场力的矢量和。由于三种电场力的方向均位于一条垂线上，矢量和变为标量和，即aaqqqqq(q)ddFFqFqFq22240(2d)a2a24(d)4(d)00dd235q16ad将上式整理后，即得F(1)244216d(da)03-9当孤立的不带电的导体球位于均匀电场E中，使用0镜像法求出导体球表面的电荷分布。（提示：利用点电荷与导体球之间的镜像关系。）解当导体球和点电荷之间的距离远远大于其半径时，可以认为该导体球附近的电场是均匀的，设E由点电荷q产生，q到球心的距离为f，球半径02a为a。根据镜像法，必须在球内距球心d处引入的镜fa像电荷qq。由于球未接地，为了保持总电荷量为零，f还必须引入另一个镜像电荷q，且应位于球心，以保持球面为等电位。那么球外任一点的电位为qqq4r4r4r01020式中r，r，r分别为该点到球心，电荷q以及电荷q的距12离，即9 q1aa4r2f22rfcosfr2d22rdcosfr0式中为线段r和f之间的夹角。已知导体表面的电荷密度DE，将电位函数代入得snra0rra0rra2aacos1qfcosaff1s34334(a2f22afcos)2(a2a2acos)2fa2ffq2因为E，即q4Ef，代入上式，考虑到fa，02004f0a即当0时，取上式极限，求得f3Ecoss003-10试证位于半径为a的导体球外的点电荷q受到的电场力大小为2322qa(2fa)F32224f(fa)0式中f为点电荷至球心的距离。若将该球接地后，再计算点电荷q的受力。2a证明根据镜像法，必须在球内距球心d处引入的镜fa像电荷qq。由于球未接地，为了保持总电荷量为零，f还必须引入另一个镜像电荷q，且应位于球心，以保持球面为等电位。那么，点电荷q受到的力可等效两个镜像电荷对它的作用力，即，2qqafqFee（N）12r222r4(fd)4(fa)0010 2qqaqFee（N）22r3r4f4f002322qa(2fa)合力为FFFe（N）123222r4f(fa)0当导体球接地时，则仅需一个镜像电荷q，故q所受到的电场力为F1。3-11在半径为a的接地导体球附近，沿径向放置一根长度为l的线电荷，如习题图3-11(a)所示。已知线电荷密度为l，近端离球心的距离为D，试求镜像电荷及其位置。alDl习题图3-11(a)xdxdxxolxxminxmax习题图3-11(b)解采用镜像法，应在球内径向位置引入一个镜像线电荷，离球心最近的一端对应原先的线电荷离球心的最ll远端，而的最远端对应的最近端。设上任一点距lll离球心为x，(DxDl)，上任一点距离球心为x，l则根据点电荷与导体球面的镜像规律，获知镜像线电荷的长度范围为11 22aaxDlD222aaa位置x与x的关系为x。因此，x，dxdx。2xxxa再根据电量关系dxdx，即可求得镜像电荷llxa的分布函数为llx3-12在半径为a的接地导体球附近，横向放置一根长度为l的线电荷，如习题图3-12(a)所示。已知线电荷密度为l，线电荷中心离球心的距离为D，试求镜像电荷及其位置。allD习题图3-12(a)dqmaxdfddqldlrθfdllDfdl习题图3-12(b)解求解方法与上题类似。对应于点电荷dqdl的镜像l线电荷为dqdl，如图3-12(b)所士示。设点电荷dq距lD离球心为f，则其镜像电荷dq离球心的距离为cos22aacosrfD由图可知12 1122D2Dsin22dl(fd)(df)2(d)(d)2coscos112sin22D()()Ddd22coscoscos114222222acosasin2adl(rd)(dr)2()dd2DDDaa因此，dqdqdldl，即镜像电荷分布函数llDD为adlDll2lDdlacos3-13已知一个不接地的半径为a的导体球携带的电荷为Q，若电荷为Q的点电荷移向该带电球，试问当点电荷受力为零时离球心的距离。(当点电荷所带电荷与导体球所带电荷相反时，点电荷肯定受到引力，即其受力不可能为零)。fQd-qqQ′′习题图3-10解如习题题3-10所示，如前所述，根据镜像法，若导体球原先不带电，对于点电荷Q，必须在球内距离球心2ad处引入一个镜像电荷q，而在球心处再放置另一个f电量为q的点电荷，以保持电荷守恒及导体球为等位13 体。本题中导体球已带有电量为Q的电荷，因此在球心处放置的另一个镜像电荷的电量应为(Qq)。那么，点电荷q将受到的镜像电荷的作用力为a2a2qQqqFFFffeQqq22r40fa24(f)0f要使点电荷受力为零，则f应满足下列方程a2a2qqqQff022240f40fa24(f)0f求解此高次方程可用作图法。为此，先将上式化简为1aa0232ffa2f(f)ff再化为关于的方程即afa1af032f2f1aaf若x，则上面的方程又可写为ax1x0x322x1x1x令y，y，分别作图求得y1和y2的交点，1x3222x1f即是所要求的解。根据题意可知x1，由下图可见ayy0的解位于x=1.5~2之间。其值近似为x1.62，即12f1.62a时，点电荷q受力为零。14 3-14试证位于内半径为a的导体球形空腔中的点电荷q受到的电场力大小为2qadF2224(ad)0式中d为点电荷离球心的距离。再计算腔中电位分布以及腔壁上的电荷分布。证明根据点电荷与导体球的镜像关系，可知点电荷q在a腔外的镜像电荷为qq，Zdq′2a距球心f；如下习题图dfqP(r,,3-14所示。则q所受到的力可θ)Ya等效为镜像电荷q对它的电X场力，其大小为习题图3-142qqqadF22224(fd)4(ad)00显然，腔内任一点P(r,)电位与无关，它可表示为1qaq()4r2d22rdcosdr2f22rfcos015 已知导体表面的电荷密度DEsnra0rra0(r)ra22q(da)求得s34a(a2d22adcos)23-15半径为a的不接地的a导体球中含有半径为b的球q’qdd2形空腔，如习题图3-15(a)所示。f1若在导体球外，离球心f处放置一个电量为q的点电荷，习题图3-15(a)在空腔中离腔心d1处放置另一个电量为q的点电荷，腔心与球心间距为d2，且腔心、球心、点电荷q及q均在一条直线上。试求腔中、导体球内外任一点场强。解由于导体球的屏蔽作用，球外点电荷q以及球面上的感应电荷对于腔中的场强没有贡献。因此，计算腔中场强仅需考虑腔内的点电荷q以及空腔内壁上感应电荷的作用。为了考虑腔壁上感应电荷的影响，可以应用镜像法，以一个腔外镜像电荷等效腔壁上感应电荷的影响。此时可以直接利用点电荷与导体球的镜像关系，导出腔外镜像电荷的位置与电量。如图3-15(b)所示，球外镜像电荷q的位置及电量分别为2bDD；qqdb1计算腔外场强也可应用镜像法，此时导体球的半径为a，如习题图3-15(b)所示。但是腔中必须引入两个镜像电荷q和q，其中q位于球心，q的位置和电量，以及0016 q的电量分别为02aaad；qq；qqq30fffd2aqqbq0qqd3d1fD习题图3-15(b)综上所述，腔内场强由两个点电荷q和q共同产生，腔外场强由三个点电荷q，q和q共同产生，而导体内的场强为零。3-16已知点电荷q位于半径为a的导体球附近，离球心的距离为f，试求：①当导体球的电位为时的镜像电荷；②当导体球的电荷为Q时的镜像电荷。解①如前所述，此时需要两个镜像电荷等效带电导体球2aa的影响。一个是离球心处，电量为qq的镜像电ff荷。另一个镜像电荷q位于球心，其电量取决于导体球的电位。已知导体球的电位为，而镜像电荷及球外点电荷对于球面边界的电位没有贡献，因此，球心镜像电荷q的电量应满足q4a0即q4a02a②当导体球携带的电荷为Q时，在离球心处的镜像f17 aa电荷仍然为qq，而球心处的镜像电荷qQq，ff以保持电荷守恒，即qqQ。3-17设点电荷q位于导体球壳附近，已知球壳的内半径为a，外半径为b，点电荷离球心的距离为f，壳内为真空，当球壳的电位为(0)时，试求：①球壳内外电场强度；②球壳外表面上最大电荷密度；③当距离f增加一倍时，系统能量改变多少？解①由于球壳的屏蔽作用，壳内场强为零。若建立的球坐标系如习题图3-17所示，那么壳外场强与坐标变量无关。P(r,,)rr1br2qZqqaf习题图3-17当球壳的电位为时，由上题获知位于球心的镜像电荷q应为q4b0壳外的场强将由点电荷q及其镜像电荷q和q共同产生，壳外的合成电位为1qqq()o4rrr0122bb式中镜像电荷qq，离球心的距离为，则壳外的ff电场强度为18 1qqqE()oo4rrr012qrfcosbf(rfb2cos)b332er4222242rrf2rfcos2rfbrfb202cosqfsinb3133er2242224rfb2rfbcos2rfrf202cos②球壳表面的电荷密度为22q(bf)0DEsnrb0rrb3b224bfb2fbcos2其最大值为q(bf)0smaxscos1b24bfb③系统能量的改变来自外力作的功。已知点电荷q受到的电场力为qqqqqqqbFeeee2r2r2r2r24f2fb0b4f4f0f0f由此可见，若q>0q<0，又因<0，故电场力的实际方向为(-er)。在外力作用下，当点电荷q离开球心的距离增加一倍时，外力F作的功为2f2fqbbrq2WFdrdrffr22224rb02qbbq1122222f804fbfb此功将全部转变为系统增加的能量。3-18证明无源区中电位分布函数不可能具有最大值或最小值。证明以直角坐标系为例。已知无源区中电位满足拉普拉斯方程19 2220222xyz该方程的通解为(x,y,z)X(x)Y(y)Z(z)。若此解在(x,y,z)000点取得极值，那么在该点应有0xyz2若是一维空间，因0，0，可见为常数，2xx即电位函数没有极值。222若是二维空间，0，0，显然222xyxyx2和不可能同时大于零或同时小于零，因此不可能有极2y大值或极小值。222同样对于三维空间，，和不可能同时大222xyz于零或同时小于零，因此不可能有极大值或极小值。综上所述，无源区中的电位分布函数不可能具有极大值或极小值。因此，无源区中电位分布函数不可能具有最大值或最小值。x3-19已知无限大的平板电容器Vd2(x)中的电荷密度kx，k为常数，oy填充介质的介电常数为，上板习题图3-19电位为V，下板接地，板间距为d，如习题图3-19所示。试求电位分布函数。解由习题图3-19可见，电位分布仅与坐标变量x有关，与坐标变量y，z无关。因此，电位方程简化为一维泊松2方程。设电位分布函数(x)，则由，得20 22dkx2dx4kx积分后，求得(x)AxB12其中A，B为待求常数。x0,03Vkd根据边界条件，求得B0，A，xd,Vd12因此，电位分布函数为43kxVkd(x)()x12d1233-20试证直角坐标系中的电位函数Cz/(x2y2z2)21C及圆球坐标系中电位函数均满足拉普拉斯方程，2r式中C为常数。证明已知直角坐标系中的拉普拉斯方程为2220222xyzCz将代入，则12223(xyz)25713z(x2y2z2)215x2z(x2y2z2)22x2571222222223z(xyz)15yz(xyz)22y25719z(x2y2z2)215z3(x2y2z2)2z2222111可见，0，即满足拉普拉斯方程。2221xyz球坐标系中的拉普拉斯方程为21211(r)(sin)022222rrrrsinrsin21 C由于，与及无关，代入上述方程，求得2r12212C(r)(r)0222rrrrrrC可见，电位函数也满足拉普拉斯方程。2r3-21已知长方体金属腔z的内部尺寸为abc，如习题图3-21所示。若侧壁及x底板均接地，上盖电位为cyb，试求腔内的电位分布函ao数。习题图3-21解已知直角坐标系中电位函数满足的拉普拉斯方程为2220222xyz应用分离变量法，令(x,y,z)X(x)Y(y)Z(z)222X2Y2Z2求得kX0；kY0；kZ02x2y2zxyz222式中kkk0。xyz为了满足0和0的边界条件，X(x)必须为x0xb正弦函数，即X(x)Asinkxxm式中k,m1,2,3。xb为了满足0和0的边界条件，Y(x)也必须y0ya为正弦函数，即Y(y)Bsinkyyn式中k,n1,2,3。ya22 n2m2由此求得kj()()zab为了满足0和的边界条件，Z(z)只能是z0zc双曲正弦函数，故n2m2(x,y,z)(Asinkx)(Bsinky)(Csinh()()z)xyab其级数解为nmnm22(x,y,z)AnBmsinxsinysinh()()zn1m1abab因，得zcnmCnmsinxsinyn1m1abn2m2式中CABsinh()()cnmnmab利用正弦函数的正交性，absxtysinsindxdy00ababnxmysxty00Cnmsinsinsinsindxdyn1m1abab当n=s，m=t时，上式右边积分才不为零。另由上式左边可知，只有当s和t都为奇数时，C才不为零，因此令sts(2n1)，t(2m1)，则16Cnm2(2n1)(2m1)最后求得23 2n12m1sin(x)sin(y)16ab(x,y,z)2n1m1(2n1)(2m1)12n122m122sinh[()()]zab12n122m122sinh[()()]cab3-22一根半径为a的介质圆柱Y放在均匀电场E中，如习题图0a3-22所示。若介质圆柱的介电X常数为，试求柱内外的电场0强度。EExˆ0习题图3-22解在圆柱坐标中电位所满足的拉普拉斯方程为2211(r)0222rrrrz由于电位函数(r,,z)与z无关，可令(r,,z)R(r)()其通解为m(r,)A0lnrr(AmsinmBmcosm)m1mr(CmsinmDmcosm)m1设圆柱内部的电位为，圆柱外部的电位为，电io位函数应满足下列边界条件：1，当r0时，应为有限值，因此柱内电位为imir(AmsinmBmcosm)m124 2，当r时，圆柱对电场的影响可以忽略，若取坐标原点(0,0)作为电位参考点(注意，电位参考点的选择对于电场强度的计算没有影响)，则柱外无限远处电位为(r)ExErcoso00可见，仅与r和cos有关，因此柱外电位的通解为o1ErcosDcoso01r3，在圆柱表面上（ra），电位应该连续，即，求oi得柱内电位的通解为rBcosi14，在圆柱表面上，电通密度应该连续，即io0rrarra0220由此求得，DaE，BE，所以10100020当ra时，(r,)Ercosi00102当ra时，(r,)ErcosaEcoso00r01已知E(ee)，求得rrr2E2000当ra时，E(r,)(ecosesin)eEirx000当ra时，220a0aEo(r,)erE0cos1eE0sin10r0r25 3-23若无限长的导体圆柱腔的内半径为a，腔壁被10a纵向地分裂成两部分，各X部分的电位如习题图3-23所示，试求腔内外的电位20分布。习题图3-23解与上题同理，由于电位与z无关，此时通解为m(r,)A0lnrr(AmsinmBmcosm)m1mr(CmsinmDmcosm)m1设圆柱内部的电位为，圆柱外部的电位为，电io位应该满足下列边界条件：1，当r=0时，应为有限值，则柱内电位为imir(AmsinmBmcosm)m12，当r时，为零，则柱外电位为omor(CmsinmDmcosm)m10(0)3，当ra时，。ra(2)0为了满足边界条件3，必须将展开成傅立叶级ra数，即令a0acosmbsinmramm2m1式中12112add()d000ra00026 12mam0racosd1m12mcosd()cosd000012mbm0rasind401m12m,m为奇数00sind(0)sindm0,m为偶数40求得sinm(m为奇数)ram1m再进行比较各自系数，即知m44a00BD0；A；C1m2m1mm2mmamm40r所以，柱内电位为isinm（m为奇数）m1mam40a柱外电位为osinm（m为奇数）。m1mrY3-24若无限长的导体圆柱010腔的内半径为a，腔壁被2a纵向地分裂成四部分，各X部分的电位如习题图3-243040所示，试求腔内外的电位分布。习题图3-24解与上题同理，由于电位与z无关，此时通解为m(r,)A0lnrr(AmsinmBmcosm)m1mr(CmsinmDmcosm)m1设圆柱内部的电位为，圆柱外部的电位为，电io位应该满足下列边界条件：27 1，当r=0时，应为有限值，则柱内电位为imir(AmsinmBmcosm)m12，当r时，为零，则柱外电位为omor(CmsinmDmcosm)m1(0)020()23，当ra时，ra3()0230(2)2为了满足边界条件3，必须将展开成傅立叶级数，即ra令a0acosmbsinmramm2m1式中31211ad2d2()d000ra00012mam0racosd0(m4k)20(m4k1)31m1mm2cosd2()cosd0000(m4k2)20(m4k3)m式中k0,1,2,3。28 12mbm0rasind0(m4k)203(m4k1)1m1mm2sind2()sind0000(m4k2)20(m4k3)m式中k0,1,2,3。0m4k20cosm20sinmm4k1m1mm求得ra0m4k22200cosmsinmm4k3m1mm式中k0,1,2,3。再比较各自的系数，即可确定和中的系数。io最后求得，柱内电位为0(m4k)m20rsinmcosm（m4k1）m1mai0(m4k2)m20rsinmcosm（m4k3）m1ma式中k0,1,2,3。柱外电位为0(m4k)m20asinmcosm（m4k1）m1mro0(m4k2)2m0asinmcosm（m4k3）m1mr式中k0,1,2,3。29 3-25当半径为a的导体球位于均匀电场E0中，如习aZ题图3-25所示。利用分离变量法求解球外场强及球0面上的电荷分布。EEzˆ00习题图3-25解已知在球坐标系中，电位所满足的拉普拉斯方程为21211(r)(sin)022222rrrrsinrsin应用分离变量法，令(r,,)R(r)()()考虑到场量与无关，此时通解可表示为n(n1)(r,)(CnrDnr)Pn(cos)，n0式中P(cos)为勒让德函数。n设球内电位为，球外电位为，电位应该满足下io列边界条件：1，已知电位参考点的选择不会影响电场强度的计算，若取球心为电位参考点，由于导体球为等位体，因此，当ra时，0。i2，当r时，若取球面作为为电位参考点，则Ercos。o02那么，由条件2可得，(ErDr)cos。再利用2013条件1，可得DaE。即球外电位为1030 32(EraEr)coso001因E(ee)，那么球外电场强度为rrr332aaE(r,)eE(1)coseE(1)sinr0303rr再由DE，求得导体球表面snra0rra0rra的电荷密度为3Ecoss003-26若在内半径为r1，外半Z径为r2，介电常数为的介质球壳中，同心地放置一个半径r2为a的导体球(ar），如习题a1r100X图3-26所示。若导体球的电荷为q，根据电位微分方程求习题图3-26出电位分布函数。解由于结构为球对称，电位与和都无关，故电位12微分方程为(r)02rrr直接积分求得ABr式中A和B为待定常数。将整个空间分成三个区域：A11）在arr区域中，令其电位为B；111rA22）在rrr区域中，令其电位为B；1222rA33）在rr区域中，令其电位为B。233r再根据边界条件，求解各个待定常数。①当r时，0，得B0。331 AA23②当rr时，，即B，且,满足下列关223223rr22系320rrrr2rr2AA12③当rr时，，即BB，且,满足下1121212rr11列关系120rrrr1rr1q1④当ra时，。0s2r4ara最后求得qqAA；A132440q()11q()00B；B124rr4r02102qq()11qq()00因此；；124r4rr4r4r002102q。34r03-27一个无限长的导体圆锥，夹角为2a，垂直地放在无限大的导体平面上。若导体圆锥电位为0，导1=1=00体平面电位为零，如习题习题图3-27图3-27所示，试求空间电位分布。解由题意知，圆锥与平面之间的电位仅是坐标变量32 的函数，因此本题可用直接积分法求解。设()，将其代入球坐标系中的拉普拉斯方程，得1dd(sin)02rsindd在不包括r0，0与的情况下，上面的方程可写成dd(sin)0，ddd积分求得sinAdAd即BAln(tan)Bsin2式中A，B为待定常数。,0由边界条件：，求得,020A，B0ln(tan)2将其代入的表达式中，求得电位函数为ln(tan)0()2。ln(tan)23-28若在厚度为d的无限大导体板上方h处，放置一个点电荷q，如习题图3-28所示。试求导体板上下方的电场强度。yyqqP(x,y)r1hhoodxxr2h习题图3-28(a)q′习题图3-28(b)33 解建立直角坐标，令导体板上表面位于y=0平面，如图3-28(b)所示。那么，导体板上方的电场将由点电荷q和其镜像电荷q共同产生的，该镜像电荷qq，距上表面为h，则上半空间的电场强度为qrqr12E(r)Eq(r)Eq(r)334r4r0102其中r与r分别为q和q到上半空间中任一点P(x,y)的位12置矢量，即rxe(yh)e；rxe(yh)e1xy2xy由于导体板下方无其它电荷，如果下表面上有电荷，应为均匀分布。但是因为导体板是无限大的，因此电荷密度为零，导体板下方不可能存在电场。实际上，无限大的导体可以认为是闭合的。因此，由于导体板的屏蔽作用，上方电荷不可能在下方产生电场。34'