电磁场与电磁波习题解答.pdf 64页

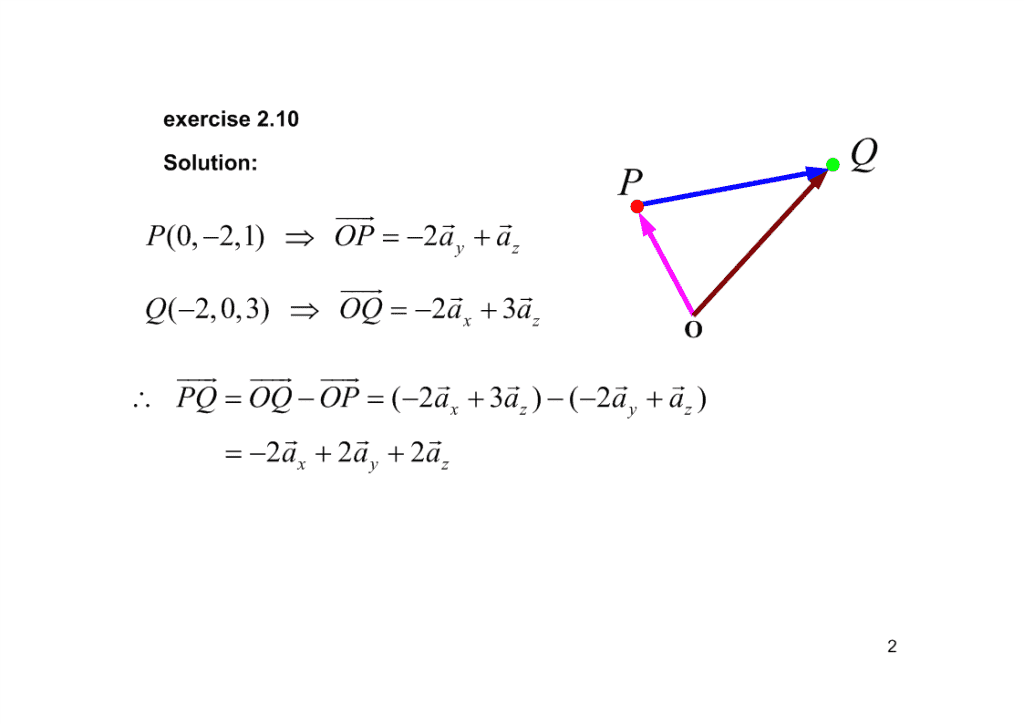
'exercise2.4Pythagoreantheorem(毕达哥拉斯定理，即勾股定理)Solution:GGGGGGGGGGGG2||A+=+•+=•+•+•BA()BA()BAABBA2BGG22=++•ABAB2GGGG∵AB⊥⇔•=AB0GGGA+BGGGGB222∴A⊥⇔+=+BA||BABGA1 exercise2.10Solution:QPJJJGGGPO(0,2,1)−⇒=P−+2aayzJJJGGGQO(2,0,3)−⇒=Q−2a+3axzOJJJGJJJGJJJGGGGG∴=−=PQOQOP(2−+−a3)(2a−+aa)xzyzGGG=−222aaa++xyz2 exercise2.11Solution:GGGGGGGGGGGG∵A=+−32aaaBaaaCaaa,484,765=−−=−−xyzxyzxyzGGG∴+=ABCGCGGGGB(组成一个三角形)A,,BCGGGGGA又∵AB•=0A⊥BGGG∴A,,BC组成一个直角三角形(right-angletriangle)GGCBGA3 GGGGGGGGAaaaBaAB=−+32,=2,?×=xyzySolution:GGGGGGGGAB×=(3aa−+×=−2)2aa6a4axyzyzxGGG=−46aa+xzazGayGax4 exercise2.28zSolution:GG∵ρρ=a,ρb沿xy平面上半径为b的闭合圆路径，yJJGGdl==bdaφ,02φπ→JJGφdlGGJJGJJGx∴ρρ⊥•dl,0dl=GJJG∴v∫ρ•=dl05 zexercise2.29Solution:(1)method1∵在以坐标原点为球心、半径为bby的球面上，GGGJJG2rb==ad,ssbin,θθφddarrxθπ=→0,0φπ=→2GGJJGGππ22∴•=v∫∫rds00∫()(sbabrr•inθθφdda)33ππ2==bd∫∫sinθθdbφπ4006 z(2)method2应用(Gauss)DivergenceTheorem：GG∫∫∇•Fdv=F•dsbvsyGGJJG∴•=∇v∫∫rds•rdvv(v是以坐标原点为球心、半径为b的x球的体积)GGGGGrx=ay++aza∇•=r3xyzGJJG433∴•==v∫∫rds33dv⋅=πb4πbv37 exercise2.33Solution:第一问：求标量函数f=12x2+yz2在点P(-1,0,1)对距离的最大变化率即是求||∇fP22∵fxy=+12z∂∂∂fffGGGGGG2∴∇=fa+a+a=24xa+za+2yzaxyzxyz∂∂∂xyzGG在P点：xyz=−1,=0,=1∴∇=fa|2Px−+4ay2∴在P点，标量函数f的梯度的大小为||∇=f24+=1577P8 第二问：求标量函数f=12x2+yz2在x,y和z方向的变化率即是求f在x,y和z三个方向的方向导数。2∂∂=fxxfyzfzy/24,/∂∂=,/2∂∂=z9 第三问：求f沿从点P(-1,0,1)到点Q(1,1,1)方向的变化率即是求在P点，f沿PQ方向的方向导数。QJJJGGGPPO(1,0,1)−⇒=P−a+axzJJJGGGGQO(1,1,1)⇒=+Qaa+axyzJJJGJJJGJJJGGG∴PQO=−=+QOPaa2xyOJJJGGGGPQ2aaxy+21GG∴沿PQ方向的单位矢量为aa==JJJG=+alxy||PQ21255+GG∵∇fa|2=−4+aPxy∴在P点，f沿PQ方向的方向导数为：∂fGGG21GG47=∇fa|(•=−24)aa+•(a+a)=−Plxyxy∂lP55510 exercise2.34Solution:(1)圆柱坐标系中G11∂∂F∂F∇•=()+φ+z∵FFρ∂ρ∂∂zρρρφGGGraz=+ρρazrrrρφ=ρ,0==,zzG1∂2∂z∴∇•=r()ρ+=+=213ρρ∂∂zG11∂∂1∂F(2)球坐标系中Fr2FFφ∵∇•=()+(sin)θ+2rθrr∂rsinθ∂∂θθrsinφGGrr=arrrrr=,0θφ==,0rG1∂3∴∇•=rr()3=2rr∂11 exercise2.35Solution:GGGG矩坐标系中：FFaFaFa=++xxyyzzG∂F∂F∂Fxyz∇•F=++∂xyz∂∂GGGG23Fx=−yax+3yzaz+xaxyzG∂∂∂2322∇•Fx=()(−yx+3)()yzz+x=−+y33xz+zx∂∂∂xyz将P点坐标(x=1,y=－1,z=2)代入上式即可12 exercise2.47Solution:22211∂∂∂ff∂f圆柱坐标系中∇=f()ρ++222ρρ∂∂∂ρρφ∂zΦ=Kbln(/)ρΦ与坐标变量φ和z无关∂ΦK=−∂ρρ211∂KK∂−()∴∇Φ=[()ρ⋅−]==0ρρ∂∂ρρρ∴同轴线内外导体之间的电介质中的电位分布函数满足拉普拉斯方程13 exercise3.7Solution:bG第一问：求空间各点的Ea∵体电荷密度为ρv=kr/，即电荷是球对称分布。GG∴空间中的电场强度可表示为E=Era()r在以坐标原点为球心的球面上的各点处电场强度大小相同。空间被分为三个区域：raarbrb<,,≤≤>在以坐标原点为球心、半径为r的球面（如图中虚线所示）上可利用高斯定律的积分形式，求空间各点的电场强度。14 GJJGDdsQ•=v∫sfbGJJG∴自由空间中EdsQ•=/εv∫sf0aGGE=Era()rErdsQ()/2=fε0ErQ⋅=4/πεv∫sf0Q是半径为r的球面所包围的自由电荷的总量。fG(1)rb时，bbkππ22∵Qd==ρvrdrddsinθθφfv∫∫∫∫a00arb22==42ππkr∫drkba(−)aGQGkba()22−Gf∴E()ra==a22rr42πεrrε200ErQ⋅=4/πεf0总结：空间中各点的电场强度为⎧0rar016 第二问：求穿过r=b的球面的电通量bGJJG22Ψ=DdsQ•==2(πkba−)v∫sfa（单位是库仑）Q是半径为b的球面所包围的自由电荷f的总量，即空间中总的自由电荷。17 exercise3.11Solution:假设无限长均匀带电导线位于坐标系的z轴，P导线上电荷的线密度为ρ。lGG空间中的电场强度可表示为E=Ea()ρρ在以z轴为中轴、半径为ρ、高度为1的圆柱面上可利用高斯定律的积分形式，求自由空间中的电场强度。GJJGGJJGDds•=ρEds•=ρ/εv∫slv∫sl0JJGJGGJG∵在圆柱面的上顶面、下底面，ds=±•dsa,0Eds=zGJJG21πGGEds•=ρ/ε()Ea•=(ρddzaφρ)/εv∫sl0∫∫00ρρl018 21πGGρ()()/lEa•=ρddzaφρlε0E=∫∫00ρρ2περ0GGρl∴Ea=2ρπερ0选取点A作为电位参考点(点A和点P的φPA和z坐标相同)，点A的ρ=a。自由空间中任意点P的电位为aaGJJGGGρρ⎛⎞allV=•Edl=()()la•=daρn⎜⎟P∫∫ρρρρ22περπε⎝⎠ρ00∴等电位面为ρ=constant即无限长均匀带电导线的等电位面为与该导线同轴的圆柱面。19 exercise3.23Solution:ε假设无限长的线电荷位于坐标系的z轴，电荷密度为ρ。l第一问：求电介质中的电场强度GG电介质中的电通量密度可表示为DDa=()ρρ在以z轴为中轴、半径为ρ、高度为1的圆柱面上利用高斯定律的积分形式，求电介质中的电通量密度。GJJG21πGGDds•=ρ()Da•(ρddzaφρ)=v∫sl∫∫00ρρlGGρρllD=Da=2ρπρ2πρGGGDρl∴电介质中的电场强度为E==a2ρεπερ20 第二问：将线电荷视为半径为α的圆柱体(α→0)，求电介质中的束缚电荷密度将电介质视为媒质1；半径为α的圆柱体所围区域是自由空间，视其为媒质2。εGGGGGρlDEPD=+ε,=a10111ρ2πρ21GGGGGGGDεε−−11ρ1rrl∴P=−=−=DEDεD=a1101112ρεεεπρrrrG11∂∂F∂F∵∇•FF=()+φ+zρ∂ρ∂∂zρρρφG∴ρ=−∇•=P0即电介质中束缚体电荷密度为0vb121 GGGGGε−1ρaPP()|rlρsbn=•−21sP=a1ρε2πρεrG∵媒质2是自由空间∴P=0221GG在圆柱面ρ=α上：aa=nρ∴在圆柱面ρ=α上，束缚面电荷密度为GGε−11ρε−ρrrllρ=•−aa(0)|=−C/m2sbρρρ=αε22πρεπαrr注意：在无限长的线电荷表面，单位长度内的束缚电荷为ε−11−εrrlim(2παρ⋅=)−ρ=ρsbllα→0εεrr1−ερrl单位长度内的总电荷：ρρtotal=+llρ=εεrr22 example3.18自由空间和电介质的分界面是平面y=0Solution:zplaney=0令y<0的区域为电介质，即媒质1；y>0的区域是自由空间，即媒质2。已知GGGG40ε=εε=ε20Ea|=++1340a50a102y=0xyzyGO求E|1y=0∵自由空间和电介质的分界面上无自由x面电荷，GGG∴边界条件aDDns•−=()12|ρsfDD1020ny||==ny=GGGaEEns×()12−=|0EE1020ty||==ty=23 GGGGGGA矢量A的法向分量为：A=•()AaannnGGGGG矢量A的切向分量为：A=•()AaatttGGGA=AA−tn在分界面y=0上：GGaa=nyGGGGaaaa==,tztx12GGGGEa|1=++3405a0a2y=0xyz法向分量24 GGGGEa|1=++3405a0a2y=0xyz法向分量GGG∴Ea|=+1350a20ty=xzGGEa|4=020ny=yGGGDE||==ε40εa202ny==20ny0yGGGGEE1020ty||===tyE1020ty|====+Eaty|13x50azGGGDD1020ny||===nyDD||==40εa1020ny==ny0yGGD10ny|=40ε0GGEa|===a10ny=yyεε401025 GGGE|1=+35aa010ty=xzGGEa|=10ny=y∴分界面上电介质一侧的电场强度为GGGEEE|||=+10y=010ty=1ny=GGG=++13aaxy50azV/m法向分量26 exercise3.38Solution:第一问：thepotentialfunctionineachmedium∵电介质1和电介质2中均无自由电荷∴两种电介质中的电位函数分别为Vd=+clnρac≤ρ≤111Vd=+clnρcb≤ρ≤222c,d,c,d是待求系数，由边界条件解出。1122∵求电位的最终目的是求电场强度，∴只需求出c和c。1227 Vd=+clnρac≤ρ≤111Vd=+clnρcb≤ρ≤222⎧V2|0ρ=b=cbd22ln+=0⎪⎪⎪VV10|ρ=a=cadV11ln+=0边界条件⎨VV12||cc=ccdccdln+=+ln⎪ρρ==1122⎪∂∂VVcc21||021εερ21cc−==sfεε||=⎪∂∂ρρ==21cc⎩nnρρ==ρρε2cc=12εGG∂VV∂1aa=−⇒=−nρ∂n∂ρ28 ⎧cbdln+=0⎧V022c=−⎪⎪1cbεcadVln+=⎪ln+1ln⎪110⎪⎪acε⎨ccdccdln+=ln+21122⎨⎪⎪c=−V0⎪=ε22cc⎪ε2cb⎪12ln+ln⎩ε1⎪⎩εac1两种电介质中的电位函数分别为Vd=+clnρac≤≤ρ111Vd=+clnρcb≤≤ρ22229 GG第二问：theandfieldsineachmediumEDVd=+clnρac≤ρ≤Vd=+clnρcb≤ρ≤111222GG∂VcGGVaEV=−∇=−11aa=−=0⋅ρ11ρρ∂ρρρcbε1ln+lnGGGVaacε20ρDE==ε⋅11111cbln+lnρεεac12GG∂VcGGVaEV=−∇=−22aa=−=0⋅ρ22ρρ∂ρρρε2cbln+lnεacG1GGVa0ρGGDE==ε⋅22211cb思考：为什么DD=ln+lnρ12εεac1230 第三问：thechargedistributionontheinnerconductorGGG根据边界条件aDD•−=()|ρns12sfG在圆柱面ρ=a两侧：GV0aρD=⋅111cbln+lnρ媒质2是导体，媒质1是电介质1，εεac12GGKGGVa∴aaD===,0,|D0⋅ρnaρρ21=11cbaln+lnεεac12∴在内导体的表面上(ρ=a)，自由面电荷密度为GGV10ρsf=•aDρρ1|=a=11cb⋅aC/m2ln+lnεεac1231 ∴对于单位长度的同轴电缆，内导体上的自由电荷总量为2πV0Qa=⋅=ρπ2fsf11cbln+lncoaxialcableεεac12第四问：thecapacitanceperunitlength此同轴电缆的单位长度电容为Qf21π1CC12Cl=====(F/m)VC111cbc11b1+C0ln++lnlnln+12εεπac22επaεcCC12121222πεπε12式中CC==,12⎛⎞cb⎛⎞ln⎜⎟ln⎜⎟⎝⎠ac⎝⎠32 第二章电子教案中计算电容部分有一例题：同轴线的内导体半径为a，外导体的内半径为b，内外导体之间填充介电常数为ε的电介质。此同轴线单位长度内的电容为2πεC=(F/m)⎛⎞bln⎜⎟⎝⎠a33 填充两层电介质的同轴电缆的单位长度电容为11CC12C===l(F/m)111cb1CC+ln++ln1222πεacπεCC121222πεπε12式中CC==,12⎛⎞cb⎛⎞ln⎜⎟ln⎜⎟⎝⎠ac⎝⎠即总电容等于两个电容器串联后的电容。34 zexercise5.10Solution:xI∵通有恒定电流I的无限长直导P线在自由空间中产生的磁场，磁通I密度为GIGµ双导线0B=ab2φπρyρ是场点到导线的垂直距离采用矩坐标系，场点P是平面x=0上的一点，其坐标为(0,y,z)，y的取值范围是a≤y≤−ba。GµIG∴左边导线在场点P产生的磁通密度为B=−0a1x2πyGµIG0右边导线在场点P产生的磁通密度为B=a2x2(πby−)35 ∴场点P处的磁通密度为GGGµI⎛⎞11G0B=+=BB−⎜⎟−a12x2π⎝⎠yby−平面x=0上，两导线之间区域的面积元为JJGGds=−dydzaxL∵支撑两条平行导线的两支架的间距为L，∴通过由两条平行导线和两个支架所形成的区间的磁通为GJJGba−L⎡⎤µI⎛⎞11GG0Φ=Bds•=⎢⎥−⎜⎟−a•−()dydza∫∫sa∫0xx⎣⎦2π⎝⎠yby−µµIIba−⎛⎞11LLba−⎛⎞1100=−∫∫⎜⎟dydz=−∫⎜⎟dy22ππaa⎝⎠yby−−0⎝⎠ybyµµILIL=+00⎡⎤ba−−−ba=⋅=ln|yyln(b)|ln10⎣⎦y==aya22ππ36 exercise5.12Solution:G∵∇•=B0GGGGB=++12xax25yacyzza1225++=c0c=−3737 yexercise5.24µ=µ10Solution:AOGGGGx已知Baaa=+−235T2xyzGGz求B(thefieldinfreespace)BBC1∵介质1是自由空间，介质2是电导µ=10µ20率有限的介质，：GGGGGG∴BHHBH==µµ,1==µ0µH1110122202G分界面(平面2y-x+4=0)上：J=0sfGGGGGGaHHJ×()−==|0HH||=ns12sf12tstsGGGGGaBB•()−=|0BB||=ns1212nsns38 GAGGGGG矢量A的法向分量为：A=•()AaannnGGGG矢量A的切向分量为：Atn=AA−∴关键是求出分界面上由介质2G指向介质1的法向单位矢量a。nGGJJJGa注意a是矢量CO的单位矢量。nn39 G(1)求an∵A点的坐标是(4,0,0)，B点的坐标是(0,-2,0)，JJJGJGJJGG∴OA==4,aOB−2axyJJJGJJJGJJJGGGBAOAOB=−=+42aaxyG∴分界面上的一个切向单位矢量a为：t1JJJGGGGGGBA422aaaa++JJJGxyxya===t1||BA255GGG分界面上的另一个切向单位矢量a为：aa=t2tz240 JJJGJJJGJJJG||OA⋅×||424OB||CO==JJJG=||BA255JJJGJJJGJJJG8222||||||41CA=−=OACO−6/5=5GGGGJJJGJJJGG821aa+6aa+8xyxy∴CA==||CAa⋅=t1555JJJGJJJGJJJGGGGGJJJGJJJGJJJG16aa+8G−+4aa8OACACO=−xyxyCO=−=CAOA−=4axJJJG55G注意an是矢量CO的单位矢量，JJJGGGGGGCO−+48aa5−+aa2JGJJxyxy∴a==⋅=n||CO54541 GGGG已知Baaa=+−235T2xyzGGG−+aa2xya=n5∴在分界面(平面2y-x+4=0)上：GGGGGGGGGGG−aaaa+−22+xyxyBBa=•=+−•()[aaaa(235)()]()22nnnxyz55GGGG4−+aaaaxy248−+xyGG=⋅==−+0.8aa1.6xy555GGGGGGGGB=−=+−−−+BB(2aaa35)(0.8a1.6)a222tnxyzxyGGG=+−2.8aaa1.45xyz42 GGGB=−0.8aa+1.62nxyGGGGB=+−2.8aaa1.452txyzGGGGGB2.8aaa+1.4−52txyzH==2tµµ1020GGGGGG2.8aaa+1.4−5xyzHH||=H=12tsts1t10µ0GGGGG2.8aaa+1.4−5GGGxyzB==µµHa=+−0.280.14a0.5a11tt10xyz10µ0GGGGGBB||=B=−0.8aa+1.612nsns1nxy43 GGGG∵B=+−0.28aaa0.140.51txyzGGGB=−0.8aa+1.61nxyG∴thefieldinfreespaceisBGGGGGGGGBBB=+=(0.8−+a1.6a)(0.28+a+0.14a−0.5)a111ntxyxyzGGG=−0.52aaa+1.74−0.5Txyz44 exercise5.28Solution:abcoaxialcable同轴线的内、外导体上分别通有大小相等、方向相反的直流I。采用圆柱坐标系，内导体的中轴线在z轴上。假设内导体上的电流沿+z方向。GG根据安培环路定律的积分形式：∫H•dl=∫Jvf•ds=Ifcs可求出内导体和内、外导体之间媒质中的磁场强度。(1)内导体中(0≤ρ≤a)GIGGJJGρπ2IGGIρ2Javf=2zIJfv=•∫∫fds=∫22adz•()ρρφdaz=πas00πaa45 (2)内、外导体之间的媒质中()ab≤ρ≤II=f(3)外导体之外的媒质中()ρ>bI=0fGG∵H=Ha()ρφGJJG2πGG∴H•=⇒dlIH()ρρa•daφ=⇒I2πHρ=Iv∫∫fφφffc0GIGf∴H=a2φπρ⎧IρG2aa0≤ρ≤⎧Iρ⎪2φ⎪0≤ρ≤a2πa2⎪⎪⎪aG⎪IGH=≤⎨aabρ≤If=≤⎨Iabρ≤φ⎪2πρ⎪0ρ>b⎪>⎪0ρb⎪⎩⎪⎩46 内导体和内、外导体之间媒质中的磁场强度分别为：GIρGGIGH=aa(0≤≤ρ)H=≤aa()ρ≤bi2φeφ2πa2πρ(1)内导体中的磁场能量密度为GGGGI2211µρ0wB=•=HHµ•=Hmi,ii0ii24228πa∴单位长度的同轴线，内导体中的磁场能量为22µµIIa21π003Ww==dvρρddφdz=mi,,∫∫vmi8124a00∫∫06ππ47 (2)内、外导体之间媒质中的磁场能量密度为GGGGI211µ0wB=•=HHµ•=Hme,ee0ee22228πρ∴单位长度的同轴线，内、外导体之间媒质中的磁场能量为22µµIIb121π⎛⎞b00W==wdvdρφddz=ln⎜⎟me,,∫∫vame2∫00∫84πρπ⎝⎠a(3)单位长度的同轴线中，储存的总磁场能量为22µµII⎛⎞b00WWWm=+=+mi,,meln⎜⎟(J/m)16ππ4⎝⎠a48 yexercise7.6baSolution:采用矩坐标系，N匝矩形线圈放置于PLIsinωtIsinωt平面z=0上，位于平行双线传输线mm的中间。Wd场点P是平面z=0上平行双线传输线x中间的一点，其坐标为(x,y,0)，x的取值范围是[0,d]。z∴左边导线在场点P产生的磁场强度为GItsinωGmH=−aleftz2πxGItsinωG右边导线在场点P产生的磁场强度为mH=arightz2(πdx−)49 y∴场点P处的磁场强度为GGGbaHHH=+leftrightPLImmsinωωtItGsinGImsinωtImsinωt=−aa+zz22ππxd(−x)WItsinω11Gd=−m()azx2πdxx−z场点P处的磁通密度为GGGµItsinω110m()B==µHa−0z2πdxx−以矩形线圈为边界的开曲面（图中蓝色阴影区域）的面元为：JJGGdW−+dWds=dxdya(:x→→yL:0)z2250 ∴与矩形线圈交链的磁通为GJJG⎡⎤µωItsin11GG0mΦ=Bds•=()−a•()dxdya∫∫ss⎢⎥zz⎣⎦2πdxx−dW+µωItsin⎛⎞11L0m2=−⎜⎟dxdy∫∫dW−2π⎝⎠dxx−02dW+µωLIsint⎛⎞110m2=−⎜⎟dx∫dW−2π⎝⎠dxx−2dW++dWµωLIsint⎡⎤0m22=−⎢⎥ln(xd−)|−ln|xdW−−dW2π⎣⎦xx==22µωLIsint0m=⋅ln1=02πdΦ∴矩形线圈中的感应电动势为eN=−=0dt51 exercise7.7Solution:(1)计算正方形截面环形螺线管的自感λNΦ假设螺线管通有恒定电流I，则L==II首先需计算穿过整个螺线管的全磁通（磁链）λ。计算穿过整个螺线管的磁链λ时，注意本题是教材example5.13的特例。52 example5.13所示的矩形截面环形螺线管，共有N匝。环的内半径为a，外半径为b，高度为h。若线圈中通有电流I，求穿过整个螺线管的全磁通。zaxiszaxisahb53 ExampleAtoroidalwindingwithNturnsiswoundintheformofaring.Theinnerandtheouterradiioftheringareaandb,andtheheightoftheringish.IfthewindingcarriesacurrentofI,findthemagneticfluxenclosedbythering.Solution:∵线圈是密绕的，∴磁场集中在螺线管内。∵电流分布的对称性，∴磁力线是以环形螺线管的中轴为GG圆心的同心园族。。H=Ha()ρφ在环内()ab≤≤ρ取半径为ρ的园作为积分路径，应用安培环路定律GJJGv∫HdlNI•=cGJJG2πGGHdl•=Ha()ρ•(ρφdaH)=⋅2πρv∫∫c0φφ54 H⋅2πρzaxisGJJGav∫HdlNI•=hcGNIGGµNIGbH=aφB=a2φπρ2πρGJJGJJGG通过单匝线圈的磁通量为Φ=B•ds,ds=ddzaρ∫sφµNIbhdρµNIh∴Φ=∫∫dz=ln(/)baa022πρπ2µNIh穿过整个螺线管的全磁通为：λ=Φ=Nbln(/)a2π韦伯匝数(Weber-turn)55 穿过整个螺线管的磁链为：zaxis2µNIhλ=Φ=Nbln(/)a2πah∴自感为2λNΦµµ0rNhbLb===ln(/)aII2π对于正方形截面环形螺线管，即hba=−已知条件为：a=20cm，b=25cm，N=200，µ=500r∴将以上各量代入自感计算公式，即可算出自感。56 (2)当线圈中通有的电流为i=2sin314tA时，求线圈中的感应电动势利用如下公式计算：dieL=dt公式中的自感L在第一问已求出。57 exercise7.9Solution:设载流长导线为回路1，正方形环为回路2。假设载流长导线沿z轴放置，其上的电流为I，在垂直于载流长导线的平面内，任选半径为ρ的园作为积分路径，应用安培环路定律：GJJGv∫H•dl=IcGGJJGG∵HHad==(),ρφφldaρφ,φ的变化范围是02,→π22ππGGH()ρρad•(φaH)==()ρρφπdH2()ρρ=I∴∫∫00φφGIG∴载流长导线在自由空间中产生的磁场强度为H=a1φGGµIG2πρ0磁通密度为B==µHa101φ2πρ58 长导线上通有电流I时，所产生的通过回路2的磁链为GJJJGλ=Φ=B•ds(∵正方形环的匝数为1)2121∫12s2JJJGG∵ds=ddzaρ,ρ的变化范围是bab→+,2φz的变化范围是0,→aaba+µµIIGGa⎛⎞ab+00∴λρ=•add()lza=n⎜⎟21∫∫φφb022πρπ⎝⎠b载流长导线与正方形环之间的互感为λµa⎛⎞ab+210ML===ln⎜⎟亨21Ib2π⎝⎠59 G⎧GG∂D⎪∇×HJ=+vfG∂t⎪G⎧⎪∇•=B0⎪G∂BG根据⎨∇×=−E推导出⎨⎪G∂t⎪⎩∇•Jvf=−∂ρvf/∂t⎪∇•D=ρvf⎪⎩Solution:(1)GGGG∂∂BG∇×=−EBt∂∂/⇒∇•∇×=−∇•()()()EB=−∇•=0∂tt∂（∵时间变量与空间变量是相互独立的，可以交换对时间变量和空间变量的微分次序）G∴∇•=Bconstant60 G∵在远离源的无穷远处，B=0G∴constant=0,即。∇•=B0(2)GGG∇×H=JDt+∂/∂vfGGGG∂∂DG⇒∇•∇×()(HJ=∇•+)=∇•J+()∇•D=0vfvf∂∂ttGG∂ρvf将∇•D=ρvf代入上式，可得∇•+=Jvf0，即∂tG∂ρvf∇•J=−vf∂t61 已知电场强度的瞬时值形式为GGGEt=−3cos(ωβx−45)°at+−4sin(ωβx+45)°aV/myz求电场强度的相量形式。Solution:GGsinxxcos(/2x)cos(/2),GGjωt∵=−π=−πErt(,)Re[()]=EreGGG∴E=3cos(ωβtx−−°+45)a4sin(ωβtx−+°45)ayzGG=3cos(ωβtx−−°+45)a4cos(ωβtx−−°45)ayzGG=+(3aa4)cos(ωβtx−−°45)yzGGjtx(4ωβ−−°5)=+Re[(3aa4)e]yzGG−+jx(4βω5°)jt=+Re[(3aa4)ee]yzGGG−jx(4β+°5)∴相量表示式为Eaa=+(34)eyz62 GGG−−0.2zjz0.5已知电场强度的相量形式为Eaj=+(34)aeeV/m，xy求电场强度的瞬时值形式。jπ/2Solution:推导中应用了je=+,cos(xπ/2)=−sinxGGEE==+Re[ejtωω]Re[(3aGj4aG)e−−0.2zeejzjt0.5]xy−−0.20zjzj.5ωωtGGjπ/2−−0.20zjzj.5t=+Re(3eeea)Re(4eeeea)xy−−0.2zjtz(ωω0.5)GG−−0.2zjtz(0.5+π/2)=+Re[3eea]Re[4eea]xy−−0.2zzG0.2G=−3cetos(0ωω.5z)4cae+−os(0t.5z+π/2)axy−−0.2zzGG0.2=−3ecos(ωωt0.5)za−−4esin(t0.5)zaxy63 exercise8.1Solution:GGGGGG在无源的线性、均匀、各向同性媒质中：ρ====0,σµε,,vfJvfEBHDE微分形式的Maxwell方程组为GGG∂HGG∂E∇×=−Eµ(1)∇×HE=σε+(2)∂t∂tGGGG∇•=BH00⇒∇•=(3)∇•=⇒∇•=DE00(4)GGGG∂∂EG将(2)式两边取旋度得：∇×∇×()(H=∇×σεEE+)=∇×+σε()∇×E∂∂ttGGG2利用矢量恒等式∇×∇×()()H=∇∇•HH−∇和(1)、(3)式，由上式可得：GGGGGG∂∂H2H2∂∂∂HH2−∇H=σµ()()−+ε−µ∇=Hµσ+µε2∂∂∂ttt∂tt∂64'