量子力学习题答案.pdf 9页

'同理可得两个方程2.1+=如图所示−=−()解−=左()右()+0x2=设粒子的能量为，下面就>和<两种情况来讨论+（一）E>的情形ℏ=||此时，粒子的波函数ψ(x)所满足的定态薛定谔方程为ℏℏ+=0=||,=||反射系数+=0−==其中+22透射系数=ℏ,=ℏ(−)2==其解分别为+()=+（二）E<的情形()=+令=(−),不变ℏ（1）粒子从左向右运动此时，粒子的波函数()所满足的定态薛定谔方程为右边只有透射波无反射波，所以为零+=0由波函数的连续性()|=()|得+=−=0其解分别为|=|()=+得−=()=+解得由在右边波函数的有界性得为零−（1）粒子从左向右运动=+()|=()|得+=2=+|=|由概率流密度公式ℏ得−=−=(∗−∗)2解得入射+=ℏ−=||2=ℏkℏk−J=|A|,J=|B|mm入射反射系数ℏ=||−===+ℏ=||,=0透射系数2反射系数===+===1（2）粒子从右向左运动左边只有透射波无反射波，所以为零透射系数 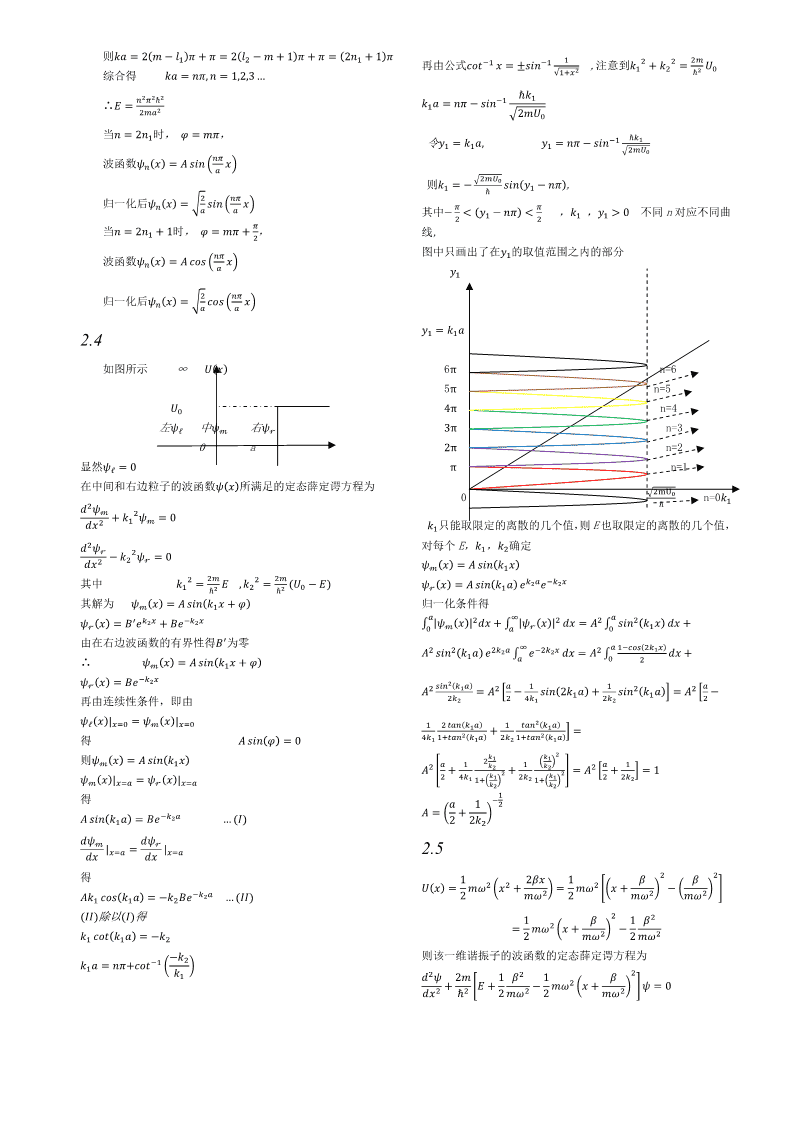其解是()=(+)==0由波函数连续性条件得(2)粒子从右向左运动()=0左边只有透射波无反射波，所以为零(+)=0同理可得方程∴=,+===(−)==0=1,2,3,4…ℏℏ=||∴=2J=0相应的=由于全部透射过去，所以()=+=±J=0反射系数=0因为正负号不影响其幅度特性可直接写成透射系数=1()=2.2由波函数归一化条件得()如图所示1−2|()|==2==12E=0x所以波函数()=在0∼有隧穿效应，粒子穿过垒厚为dx的方势垒的透射系数为（2）∞()∞[()]16(−)=ℏ,=左ℓ中右−0x总透射系数显然ℓ==0>0时只有中间有值∫[()]=ℏ在中间区域所满足的定态薛定谔方程为∫[]+=0=ℏ√2()==ℏℏ其解是()=(+)2.3由波函数连续性条件得以势阱底为零势能参考点，如图所示−+=0（1）2∞()∞+=0左ℓ中右20ax−∴+=,+=显然ℓ==022>0时只有中间有值2=(+)=在中间区域所满足的定态薛定谔方程为=2+=0当=2，为任意整数，=2则=2(−)=2(−)=2,=1,2,3…=ℏ当=2+1，为任意整数，=+ 则=2(−)+=2(−+1)+=(2+1)再由公式=±,注意到+=√ℏ综合得=,=1,2,3…ℏ=−ℏ∴=2当=2时，=，令=,=−ℏ波函数()=则=−(−),ℏ归一化后()=其中−<(−)<，，>0不同n对应不同曲当=2+1时，=+，线,图中只画出了在的取值范围之内的部分波函数()=归一化后()==2.4如图所示∞()6πn=65πn=54πn=4左ℓ中右3πn=30a2πn=2显然ℓ=0πn=1在中间和右边粒子的波函数()所满足的定态薛定谔方程为0n=0ℏ+=0只能取限定的离散的几个值，则E也取限定的离散的几个值，对每个E，，确定−=0()=()其中=,=(−)()=()ℏℏ其解为()=(+)归一化条件得()=+∫|()|+∫|()|=∫()+由在右边波函数的有界性得为零()∫=∫()+∴()=(+)()=()=−(2)+()=−再由连续性条件，即由ℓ()|=()|()()+=得()=0()()()=(则)++=+=1()|=()|得1()=…()=2+2|=|2.5得121()=+=+−()=−…()22()除以()得11=+−()=−22−则该一维谐振子的波函数的定态薛定谔方程为=+211++−+=0ℏ22 1令=+=+ℏ=0,1,2,3…2()=+同理=()则上式可化成1=+ℏ=0,1,2,3…212+−=0ℏ2令=+则=+=++1ℏ=(+1)ℏ令===ℏℏ则=0,1,2,3()()=()()+(−)=0=0,1,2…只有当−1=2有解式中()=()11==+=+ℏ2!√22()()=()能级简并度为+1=+ℏ−=0,1,2,3…3.2角动量算符=̂×̂=(+)×+()=+在极坐标系下=−ℏ=则2!√=22.6由能量本征值方程=2由()=()和已知条件可得+=0!√ℏ第三章令=ℏ3.1其解为能量本征值方程为=()=即由周期性(0)=(2)得=ℏ1归一化条件∫|()|=2=1−+=−(+)22则分离变量法，令==+1则有=221+−=0ℏ2121()=+−=02ℏ2ℏ令==ℏ=ℏ=2则3.4+−=0̂ℏ=+()=−+()−1=222由能量本征值方程=()=() ℏ−=[−()]2令(,,)=()(,)=当ℓ=0时(,,)=()(,)=()()6πn=6令()=此时()满足的方程为5πn=524πn=4+[−()]=0ℏ3πn=30<<时2πn=22πn=1+ℏ[+]=00n=0k>时ℏ2k只能取限定的离散的几个值，则E也取限定的离散的几个值，+ℏ=0对每个E，k，k确定只考虑−<<0时令()=()=[+]=−()=()ℏℏ其解分别为归一化条件得∫()4+∫()4=1可求()=(+)()=+得由波函数有界性1=+,具体求法见2.4()|/<∞88得()=()3.5()=由波函数连续性记(,)=|>()|=()|−=ℏ得1()=….()=ℏ−’()|‘()|=1=<≥<>−<>()−()ℏ=−−…..()1∗=<>−|>>=0()除以()得ℏ()−1=−−1同理=0()=−方差算符−1=+∆=−==−=ℏ再由公式=±,注意到+=11√ℏℏ−ℏℏ11=−=−+−2ℏℏ令=,=−ℏ,则=11=ℏℏ+−ℏ11−(−),=+−ℏℏℏ其中−<(−)<，，>0不同n对应不同曲(∆)=<∆>线,图中只画出了在y的取值范围之内的部分11=<+−>ℏℏ=<>=∆ 则(∆)=∆=(∆)+∆2+++(2++)−4(+)(+)+4=112=<+≥<−>222+++(−)+4=112=−=(+−)ℏ222++−(−)+4==ℏ2由测不准关系(∆)∆≥()当=代入，验证该式是成立的−−−+(−)+4==第四章2再由||+||=14.1得在动量表象中=ℏ，̂==则当=，同样ℏ第六章=−226.3代入=得解：在Sˆ表象，Sˆ的矩阵元为2zn+−=0ℏ2010i10Sˆcoscoscosn2102i0201令=,=,=ℏℏcoscosicosSn得2cosicoscos其相应的久期方程为+(−)=0cos(cosicos)−1=2220()=()(cosicos)cos则22221即22(cos2cos2)0=+ℏ=0,1,2,3…cos244归一化后的2()20(利用cos2cos2cos21)()=()4=2!√24.5所以Sˆ的本征值为。n2本征方程的矩阵形式+0==a+0设对应于S的本征函数的矩阵表示为(S)，n1n22b+−0=+−0则上式存在非零解的条件是coscosicosaa+−=0+−2cosicoscosb2b即−(2++)+(+)(+)−=0a(cosicos)bcosb解得 √cosicosb有=1cos√a√**22由归一化条件，得111(a,b)ab同理=√22b−2由δ在δ的表象下的矩阵得2cosicos2aa10−1cos0=−−22=a1−1cos−−方程有非零解的条件为det=0，−1cos即=1,=−1，的本征值、本征函数有两个11(Sn)cosicos当=1时，代入得=2由波函数归一化条件得||+||=12(1cos)√有=√1cos1cosicos012(Sn)01√22(1cos)同理=√1coscosicos−11222(1cos)26.3节的证明题同理可求得对应于S的本征函数为n2在中心场问题中（即氢原子中电子的状态）（1）当无自旋动量距与轨道动量矩的耦合（即存在L算符与S算符的相乘项）1cos电子的哈密顿量为21(Sn)cosicos2=+(⃗)−∙−∙22(1cos)求其本征值时转化为球坐标系下的方程(,,)=则方程左边可分解为|r＞|θ＞|φ＞|s＞三维表象下的三个方程，6.1三个表象下各自的波函数相乘即是H的本征函数。|r＞表象下是n+l阶连带拉盖尔多项式R(r)，记作F算符的本征设在的表象下的本征函数为=，值|θ＞|φ＞表象下的方程显示的对ψ的作用关系即是L算符本征值为，在的表象下的本征函数为=，本征值是球谐函数，，是与的共同本征函数为|̂＞表象下是()由在的表象下的矩阵得其本征函数为()，()01主量子数=1,2,3,4，…=10角量子数=0,1,2，…−1−10轨道量子数=0，±1，±2，…±=1−0自旋量子数=±−1（2）当存在自旋动量距与轨道动量矩的耦合方程有非零解的条件为det=0，1−电子的哈密顿量为即=1,=−1，的本征值、本征函数有两个=+(⃗)+(⃗)∙当=1时，代入得=2由波函数归一化条件得||+||=1同样求其本征值时转化为球坐标系下的方程(,,)=|r＞表象下也是+阶连带拉盖尔多项式() |＞|＞|̂＞表象下的方程显示的对ψ的作用关系即是总动量矩()算符主量子数=1,2,3,4，…=+，，是属于不同自由度的，，，分别为其角量子数=0,1,2，…−1分量磁量子数=−−,−+1−,……,+类似于在轨道角动量矩的性质内量子数=±，具有共同本征函数下面先求J的本征函数○1=+量子力学全书重点的本征函数为球谐函数，，本征值为ℏ，=0，±1.量子力学三大作用：奠基作用、渗透作用、设计作用1，±2，…±2.量子力学中粒子的特点的本征函数为()，本征值为ℏ，=±单一粒子具有波粒二象性则J的本征函数为，()，本征值为(+)ℏ=多粒子体系具有全同性ℏ3.量子力学的三大原理：显然的简并度为2态叠加原理：若波函数ψ，ψ，…，ψ，是描述粒子的一属于本征值的本征函数可表示为些可能态，则这些波函数线性叠加得到的ψ=∑Cψ也是描述粒子的可能态=，()+，(),测不准原理：对于任意两个不可对易的力学量算符F与G，设通过=，确定，可得|θ＞|φ＞|s＞表象下的本征函数其满足F，G=FG−GF=iK，则有(K)○2=++这是定义类似于，不能直接+(ΔF)(ΔG)≥4=+++++ℏ对于时间与能量∆E∙∆t≥=++++++2∙+∙+∙全同性原理：全同系的状态不因交换两个粒子而改变，其运=++2++动状态只能用对称或反对称的波函数来描述在|s＞表象下4.量子力学的三大概率，分布概率=跃迁概率，散射概率3ℏ01ℏ0−ℏ105.量子力学的三大景象=+ℏ+2++42102020−1薛定谔景象ℏ=随时间变化，不变−3=+ℏ+ℏ4+−海森伯景象取t时刻，含时由=求得（以下只要记住就行）互作用景象（狄拉克景象）116.量子力学的三大方程=±±+1ℏ=j(j+1)ℏ22薛定谔方程：j=+时含时形式：ℏ⎡++1⎤ℏ=−+(⃗)22⎢⎥2+1=⎢⎥定态形式：⎢1⎥⎢−+2⎥ℏ−+(⃗)=⎣2+1⎦2j=−时(,)=(,)ℏ1⎡−+⎤2海森伯方程⎢⎥2+1=⎢⎥泡利方程⎢1⎥⎢++2⎥7.波函数⎣2+1⎦物理含义：描述微观物体的运动状态，|Ψ|dτ是Ψ描述的粒至此该情况下的本征函数为子在体积元dτ内出现的概率 性质：连续性，有界性，单值性，归一性厄米算符线性条件：(+)=+∗厄米条件：∫∗=∫本征函数:正交归一性、完备性具有完备的共同本征函数：两算符必须对易力学量的完备集合1.力学量的数目至少等于系统的自由度2.这一组力学量必须两两对易3.这一组力学量必须相互独立8.常见力学量算符9.力学量的表象与矩阵力学P12210.自旋电子自旋的两个假设1.每个电子都有自旋动量距，在空间任意方向上只能取ℏ两个值±2.自旋磁距=−ℏ泡利矩阵=δ10δ=0−101δ=100−iδ=i0自旋波函数P1766.30式11.双粒子系下波函数的形式P205，P20612.散射截面'