陕师大《大学物理学》(上册_)习题解答.doc 67页

'大学物理学(上册)习题解答陕西师范大学物理学与信息技术学院基础物理教学组2006-6-2667 第2章运动学2－1一质点作直线运动，其运动方程为,x以m计，t以s计。试求：（1）质点从t=0到t=3s时间内的位移；（2）质点在t=0到t=3s时间内所通过的路程解（1）t=0时，x0=2；t=3时，x3=－1；所以，（2）本题需注意在题设时间内运动方向发生了变化。对x求极值，并令可得t=1s,即质点在t=0到t=1s内沿x正向运动，然后反向运动。分段计算，路程为2－2已知质点沿x轴作直线运动，其运动方程为。试求：（1）质点在最初4s内位移；（2）质点在最初4s时间内所通过的路程解（1）t=0时，x0=2；t=4时，x4=－30所以，质点在最初4s内位移的大小（2）由可求得在运动中质点改变运动方向的时刻为t1=2s,t2=0(舍去)则，所以，质点在最初4s时间间隔内的路程为2－3在星际空间飞行的一枚火箭，当它以恒定速率燃烧它的燃料时，其运动方程可表示为，其中是喷出气流相对于火箭体的喷射速度，是与燃烧速率成正比的一个常量。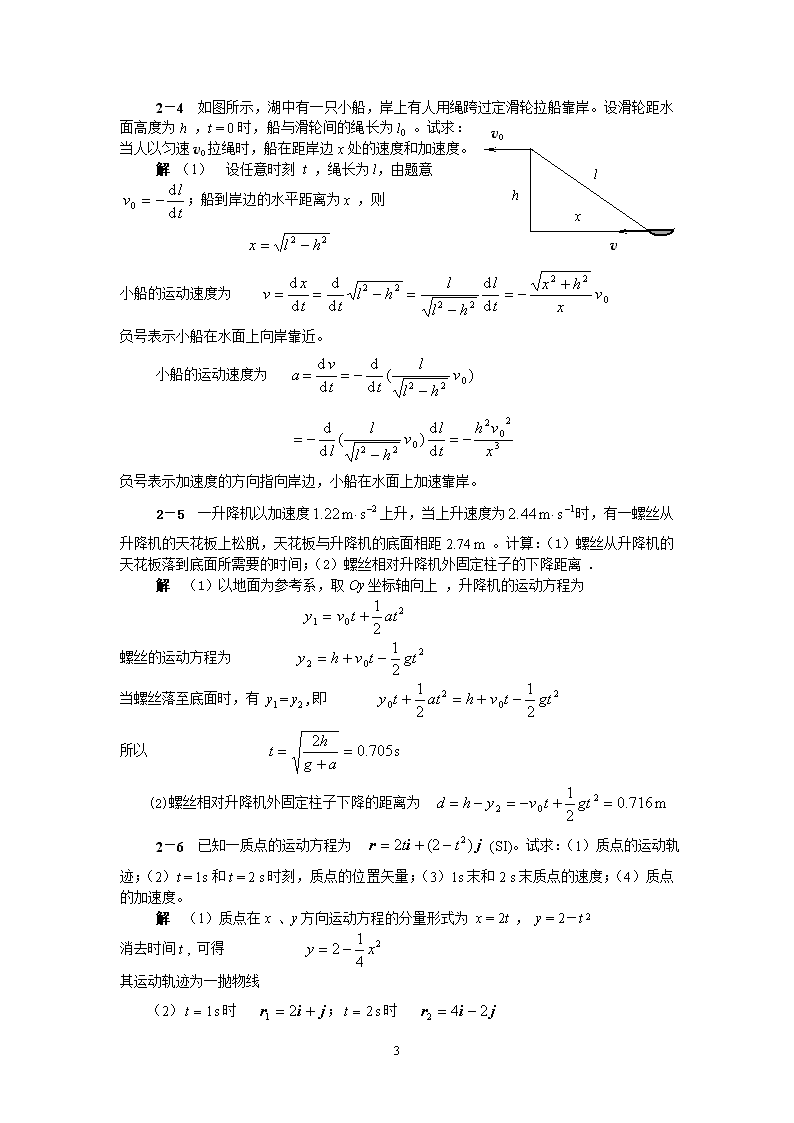试求：（1）t=0时刻，此火箭的速度和加速度；（2）t=120s时，此火箭的速度和加速度解；（1）t=0时，v=0，（2）t=120s时，67 vxlv0h2－4如图所示，湖中有一只小船，岸上有人用绳跨过定滑轮拉船靠岸。设滑轮距水面高度为h，t=0时，船与滑轮间的绳长为l0。试求：当人以匀速v0拉绳时，船在距岸边x处的速度和加速度。解（1）设任意时刻t，绳长为l，由题意；船到岸边的水平距离为x，则小船的运动速度为负号表示小船在水面上向岸靠近。小船的运动速度为负号表示加速度的方向指向岸边，小船在水面上加速靠岸。2－5一升降机以加速度上升，当上升速度为时，有一螺丝从升降机的天花板上松脱，天花板与升降机的底面相距2.74m。计算：（1）螺丝从升降机的天花板落到底面所需要的时间；（2）螺丝相对升降机外固定柱子的下降距离.解（1）以地面为参考系，取Oy坐标轴向上，升降机的运动方程为螺丝的运动方程为当螺丝落至底面时，有y1=y2,即所以(2)螺丝相对升降机外固定柱子下降的距离为2－6已知一质点的运动方程为(SI)。试求：（1）质点的运动轨迹；（2）t=1s和t=2s时刻，质点的位置矢量；（3）1s末和2s末质点的速度；（4）质点的加速度。解（1）质点在x、y方向运动方程的分量形式为x=2t，y=2－t2消去时间t,可得其运动轨迹为一抛物线（2）时；时67 （3）质点运动的速度v时v1即，（q1为v1与x轴的夹角）时v2即，（q2为v2与x轴的夹角）（4）质点运动的加速度2－7一质点在Oxy平面上运动，其运动方程为试求：（1）质点的轨迹方程；（2）质点的速度、加速度。解（1）质点运动方程的分量式为，消去时间参数t，可得运动的轨迹方程（2）速度v加速度2－8一质点在Oxy平面上运动，其运动方程为试求质点在5s时的速度和加速度。解速度v加速度t=5s时的速度为加速度2－9一质点从坐标原点开始沿抛物线y=0.5x2运动，它在Ox轴上分速度为一恒量，试求：（1）质点的运动方程；（2）质点位于x=2m处的速度和加速度。解（1）因为常数，故ax=0。当t=0时，x=0，可得质点在x方向的运动方程为又由质点的抛物线方程，有67 所以（2）任意时刻；由和x=2，可得t=0.5s所以，当质点位于x=2.0m时，其速度，加速度2－10一汽艇以速率沿直线行驶。发动机关闭后，汽艇因受到阻力而具有与速度v成正比且方向相反的加速度，其中k为常数。试求发动机关闭后，（1）任意时刻t汽艇的速度；（2）汽艇能滑行的距离。解本题注意根据已知条件在计算过程中进行适当的变量变换。（1）由，得（2）因为，所以发动机关闭后汽艇能滑行的距离为2－11一物体沿x轴作直线运动，其加速度为，k是常数。在t=0时，，。试求（1）速率随坐标变化的规律；（2）坐标和速率随时间变化的规律。解本题注意变量变换。（1）因为；所以（2）因为，可得又因为，所以2－12一质点沿x轴作直线运动，其速度大小，（SI制）。质点的初始位置在x轴正方向10m处，试求：（1）时，质点的加速度；（2）质点的运动方程；67 （3）第二秒内的平均速度。解根据题意可知，时，，（1）质点的加速度时，（2）由两边积分因此，质点的运动方程为（3）第二秒内的平均速度为2－13质点作圆周运动，轨道半径r=0.2m，以角量表示的运动方程为（SI）。试求：（1）第3s末的角速度和角加速度；（2）第3s末的切向加速度和法向加速度的大小。解（1）因为故，以t=3s代入，，（2），2－14一质点在半径为r=0.10m的圆周上运动，其角位置为。（1）在t=2.0s时，质点的法向加速度和切向加速度各为多少？（2）t为多少时，法向加速度和切向加速度的量值相等？解(1)由于，则，法向加速度切向加速度t=2.0s时，，（2）要使,则有所以t=0.55s2－15一汽车发动机曲轴的转速，在12s内由20r/s均匀地增加到45r/s。试求：67 （1）发动机曲轴转动的角加速度；（2）在这段时间内，曲轴转过的圈数。解（1）由于角速度（n为单位时间内的转数），根据角加速度的定义，在匀速转动中角加速度为（2）发动机曲轴转过的角度为在12s内曲轴转过的圈数为圈2－16某种电机启动后转速随时间变化的关系为，式中。求：（1)t=6s时的转速；(2)角加速度随时间变化的规律；(3)启动后6s内转过的圈数。解(1)根据题意，将t=6s代入，即得（2）角加速度随时间变化的规律为（3）t=6s时转过的角度为则t=6s时电动机转过的圈数圈2－17半径为r=0.50m的飞轮在启动时的短时间内，其角速度与时间的平方成正比，在t=2s时，测得轮缘上一点的速度值为。求：（1）该轮在t′=0.5s的角速度，轮缘上一点的切向加速度和总加速度；（2）该点在2s内所转过的角度。解由题意，因ωR=v,可得比例系数所以(1)则t′=0.5s时，角速度为角加速度切向加速度总加速度67 (2)在2s内该点所转过的角度2－18一质点在水平面内以顺时针方向沿半径为2m的圆形轨道运动。已知质点的角速度与时间的平方成正比，即（SI制）。式中k为常数。已知质点在第2s末的速度为32m/s。试求t=0.5s时质点的速度和加速度。解首先确定常数k。已知t=2s时，v=32m/s,则有故，，当t＝0.5s，，，2－19由山顶上以初速度v0水平抛出一小球，若取山顶为坐标原点，沿v0方向为x轴正方向，竖直向下为y轴正方向，从小球抛出瞬间开始计时。试求：（1）小球的轨迹方程；（2）在t时刻，小球的切向加速度和法向加速度。解（1）小球在x轴作匀速直线运动，y轴上作自由落体上述两方程联立消t，可得小球的轨迹方程（2），t时刻，小球的速率t时刻，小球的切向加速度因为，所以，法向加速度2－20已知声音在空气中传播的速率为344m/s。当正西方向的风速为30m/s时，声音相对于地面向东、向西和向北传播的速率各是多大？解，向东传播的声音的速率向西传播的声音的速率向北传播的声音的速率67 2－21一架飞机从A处向东飞到B处，然后又向西飞回到A处。已知A、B间的距离为l，空气相对地面的速率为u，飞机相对空气的速率v’保持不变。试证：（1）假定空气是静止的（即u＝0），飞机往返飞行时间为；（2）假定空气的速度方向向东，飞机往返飞行时间为；（3）假定空气的速度方向向北，飞机往返飞行的时间为。试证：由速度关系v=u+v¢（1）u＝0时，飞机往返飞行时间为（2）空气相对地面的速度为u向东，从A®B所需时间为从B®A所需时间为所以，飞机往返飞行时间为（3）空气相对地面的速度为u向北，如图2－21所示，vv¢u(a)Avv¢u(b)B习题2－21从A®B，飞机相对地面的速度为；从B®A飞机相对地面的速度的大小与从A®B等值，但方向相反。所以，飞机往返飞行的时间为67 第3章牛顿定律及其内在随机性3-1一木块能在与水平面成q角的斜面上匀速下滑。若使它以速率v0沿此斜面向上滑动，试证明它能沿该斜面向上滑动的距离为v02/（4gsinθ）。上滑fmgN下滑fmgN解选定木块为研究对象，取沿斜面向上为x轴正向，下滑（1）上滑（2）由式（2）知，加速度为一常量，有（3）解上述方程组，可得木块能上滑的距离3-2在一水平直路上，一辆车速的汽车的刹车距离为s=35m。如果路面相同，只是有1:10的下降斜度，这辆汽车的刹车距离将变为多少？解：在水平路上为定值，则，而所以设斜面夹角为a，刹车距离为，加速度为，则所以代入已知数值，注意sina=0.1,可得3-3如图所示，质量m=0.50kg的小球挂在倾角的光滑斜面上。mgNT（1）当斜面以加速度a=2.0m/s2水平向右运动时，绳中的张力及小球对斜面的正压力各是多大？（2）当斜面的加速度至少为多大时，小球将脱离斜面？解：(1)对小球x向：y向：可得67 小球对斜面的压力（2）小球刚要脱离斜面时N=0，则，由此二式可解得3-4在水平面上一辆汽车以速率v行驶，当汽车与前面一堵墙相距为d时，司机才发现自己必须制动或拐弯。设车辆与地面之间的静摩擦系数为ms.问若司机制动停车（不拐弯），他需要的最小距离d1为多大？若他不制动而作90o拐弯（作圆弧形行驶），他需要的最小距离d2又有多大？哪种办法最安全？解：汽车制动时，受到摩擦力作用，作匀减速直线运动，在拐弯情况下，汽车作圆周运动，摩擦力提供向心力。通过求出两种情况下汽车制动的距离，比较可以知道第一种方法更安全。设汽车质量为m加速度为a，则在制动时有，所以若不制动而拐弯，则有所以由于d1v>0,k为常量）(v>V)(1)画出分布函数图；（2）用N和V定出常数K；（3）用V表示出平均速率和方均根速率。解：（2）由,则（3）8-20一飞机在地面时机舱中的压力计指示为,到高空后压强降为．设大气的温度均为27．0℃．问此时飞机距地面的高度为多少?(设空气的摩尔质量为)解由,则有8-21在压强为下，氮气分子的平均自由程为，当温度不变时，在多大压强下，其平均自由程为1.0mm．解由及p=nkT8-22目前实验室获得的极限真空约为，这与距地球表面km处的压强大致相等．试求在27℃时单位体积中的分子数及分子的平均自由程．(设气体分子的有效直径(cm．)解由p=nkT67 8-23容器内储有1mol的某种气体，今从外界输入的热量，测得温度升高10K，求该气体分子的自由度。解由1mol气体，外界输入的热量即i=58-24若氖气分子有有效直径为，问在温度为600K，压强为时氖分子1s内的平均碰撞次数为多少？解8-25如果理想气体的温度保持不变，当压强降为原值的一半时，分子的碰撞频率和平均自由程如何变化?解由则则8-26对于气体有范德瓦斯常,当0℃时其摩尔体积为,试求其压强．如果将其当作理想气体处理，结果又如何?解由范氏方程，其压强为视为理想气体8-27的临界温度为31℃，临界压强为，求1mol的的临界体积。解（1）范德瓦耳斯方程即（1）为V的三次方程，但临界点只有一个，该点三根相等，即或（2）67 临界点，应有代入（1）式，并对比（1）（2）式系数，则有解之得即临界点p,V,T关系式）（2）由上式第9章热力学第一定律及其应用9-1一打足气的自行车内胎，若在7.0℃时轮胎中空气压强为Pa，则在温度变为37.0℃时，轮胎内空气压强为多少?(设内胎容积不变．)解则9-2在湖面下50.0m深处(温度为4.℃)，有一个体积为m的空气泡升到湖面上来，若湖面的温度为17.0℃，求气泡到达湖面的体积．(取大气压强为Pa)解9-3氧气瓶的容积为，其中氧气的压强为Pa，氧气厂规定压强降到Pa时，就应重新充气，以免经常洗瓶．某小型吹玻璃车间平均每天用去在Pa压强下的氧气，问一瓶氧气能用多少天?(设使用过程中温度不变)解方法1则67 （2）方法2设瓶内氧气等温膨胀到压强为市的体积为每天用去则9-4位于委内瑞拉的安赫尔瀑布是世界上落差最大的瀑布，它高979m．如果在水下落过程中，重力对它所作的功中有50％转换为热量使水温升高，求水由瀑布顶部落到底部而产生的温差．(水的比热容为．)解由则9-5在1g氦气中加进1J的热量，若氦气压强并无变化，它的初始温度为200K,求它的温度升高多少？解等压过程温度升高9-6如图所示，一定量的空气，开始在状态a，其压强为Pa，体积为，沿直线ab变化到状态b后，压强变为Pa，体积变为。求此过程中气体所作的功bpV2,VV1p1p2习题9－6图Oa解9-7气缸内贮有2.0mol的空气，温度为27℃，若维持压强,而使空气的体积膨不变胀到原体积的3倍，求空气膨胀时所作的功．解9-8压强为,体积为得氮气，从初始温度300K加热到400K，如加热时（1）体积不变，（2）压强不变，问各需热量多少？那一个过程热量大？为什么？解（1）等体过程：A=0，吸热等体过程吸热只用于增加内能，不对外做功，需热量较少。（2）等压过程：吸热67 等压过程吸热一部分用于增加内能，一部分用于对外做功，需热量较大。9-9一定量的空气，吸收了J的热量，并保持在Pa下膨胀，体积从增加到，问空气对外作了多少功?它的内能改变了多少?解等压膨胀，对外做功内能变化9-101.0mol的空气从热源吸收了热量J，其内能增加了J，在这过程中气体作了多少功?是它对外界作功，还是外界对它作功?解负号表外界对系统做功。9-110.1kg的水蒸气自120℃加热升温至140℃．问：(1)在等体过程中，(2)在等压过程中，各吸收了多少热量?解（1）等体过程吸热（2）等压过程吸热9-12一压强为Pa，体积为的氧气自0℃加热到100℃，问：(1)当压强不变时，需要多少热量?当体积不变时，需要多少热量?(2)在等压或等体过程中各作了多少功?解由题意，（1）等压过程系统吸热等体过程系统吸热(2)方法1等压过程等体过程方法2氧气内能变化67 9-13在300K的温度下，2mol理想气体的体积从等温压缩到，求在此过程中气体作的功和吸收的热量．解等温过程气体做功系统吸热9-14空气由压强为Pa、体积为等温膨胀到压强为Pa然后再经等压压缩到原来体积．试计算空气所作的功。解等温膨胀做功等压压缩做功，由等温过程，则总功9-15温度为27℃、压强为Pa的一定量氮气，经绝热压缩，使其体积变为原来的1／5，求压缩后氮气的压强和温度．解绝热压缩9-16将体积为、压强为Pa的氢气经绝热压缩，使其体积变为，求压缩过程中气体所作的功，(氢气的摩尔热容比)解由氢气绝热压缩做功习题9－17图VV1V2,T1=300KpObadcT2=200K9-170.32kg的氧气作图中所示循环abcda，设，=300K，=200K，求循环效率．(已知氧气的定体摩尔热容的实验值=21.1)解：系统作的净功为67 9-18一卡诺热机的低温热源温度为7℃，效率为40％，若要将其效率提高到50％求高温热源的温度需提高多少度?Op1p2习题9－19图VV1V2,pbac解由则9-19有一以理想气体为工作物质的热机，循环如图所示，其中a®b为绝热线。试证明热机效率为解该热机的循环效率为，其中而，则等压过程BC：；等体过程CA：；则有（证毕）9-20一热机在1000K和300K的两热源之间工作。如果（1）高温热源提高到1100K,(2)低温热源降到200K，求理论上的热机效率各增加多少？为了提高热机效率那一种方案好？解由卡诺循环效率（1）效率提高（2）效率提高理论上方案2效率提高得多，但实际上通常将大气作为低温热源，以降低造价。如必须降低低温热源温度则需用致冷机，将使总造价大幅度提高，就不合算了。故方案1更为合理。9-21在夏季，假定室外温度恒定为37.0℃，启动空调使室内温度始终保持在17.067 ℃．如果每天有J的热量通过热传导等方式自室外流入室内，则空调一天耗电多少?(设该空调致冷机的致冷系数为同条件下的卡诺致冷机致冷系数的60％．)解空调制冷系数为室内温度恒定时，有，则空调一天所好电功第10章不可逆过程与熵10-1质量为m=1kg、温度为的冰，在时完全熔化成水。已知冰的熔解热，试求：冰经过熔化过程的熵变。解的冰熔成的水是一个不可逆过程。可以设想冰与一个温度为的恒温热源接触，不断从热源吸取热量使冰逐渐熔解，过程是可逆的。其熵变为10-2把质量为m=1kg、温度为的水，放在的恒温炉子上加热，最后达到。水的比热容，分别求水和炉子的熵变。解水的熵变为炉子的熵变10-3在1.013×105Pa压强下，1mol铜的温度由300K升高到1200K，试计算其熵变。已知在此温度范围内铜的定压摩尔热容为，其中，。67 解10-4在冬季的某一日，设室内温度为，室外温度为，一座房子散热的速率为2×108J/h。在1s内这一散热过程的熵变为多少?解此传热过程是不可逆过程。传热过程中，室内和室外的温度基本未变，可假设一个可逆过程求其熵变，即10-5一个人一天大约向周围环境散发8×106J热量，试估算一个人一天产生多少熵？忽略人进食时带进体内的熵，设人体温度为，环境的温度按计算。解设人体温度为，环境温度为T2＝17oC＝290K。一天产生的熵（即人和环境熵的增量之和）为10-6一辆汽车匀速开行时，消耗在各种摩擦上的功率是P=20kW。求由于这个原因在10秒内产生熵是多少？设气温为12oC.解10秒内产生熵为10-7在一个大气压下，质量为m=0.03kg、温度为的冰与温度为的恒温热源接触，变为的蒸汽。试求：（1）各个过程的熵变；（2）整个过程的总熵变。（已知冰的比热容，水的比热容，在气压为1atm=1.013×105Pa下，冰的熔解热，水的汽化热）。解（1）的冰升温至时的熵变：的冰等压等温地熔成的水时的熵变：的水等压升温至时的熵变：67 的水等压等温汽化为的水蒸汽时的熵变:（2）在一个大气压下，的冰变为的水蒸汽时的总熵变为10-8一个金属筒内放有2.5kg水和0.7kg冰，温度为而处于平衡态。（1）今将金属筒置于比稍有不同的房间内使筒内达到水和冰质量相等的平衡态。求在此过程中冰水混合物的熵变以及它和房间的整个熵变各是多少。（2）现将筒放到温度为的恒温箱内使筒内的冰水混合物状态复原。求此过程中冰水混合物的熵变以及它和恒温箱的整个熵变各是多少。解（1）要达到水和冰的质量相等，需有0.9kg的水变为冰。这是在保持温度为的情况下发生的。这一过程的熵变为与此同时，环境（）吸热引起的熵变为水和房间的总熵变为（2）冰水混合物的熵变为恒温箱放热的熵变为总熵变为10-9在一绝热容器中，使温度为T1的理想气体，体积由V1自由膨胀到V2,然后再用活塞压回到V1。分别求在以下两种情况下，整个过程的熵变：（1）无限缓慢压缩到V1；（2）很快压缩到V1，。解（1）由于自由膨胀过程，Q=0,A=0,所以，T1=T2，因此设计一等温可逆过程计算其熵变无限缓慢压缩到V1的过程是可逆绝热过程，熵变。67 整个过程的熵变习题10-10用图146023pO20（2）初态（V1，T1），末态（），设计一可逆等容过程连接始末二态，其熵变为10-101mol理想气体的状态变化如图10-10所示，其中1－3为等温线，1－4为绝热线。试分别由下列三种过程（1）1®2®3；（2）1®3；（3）1®4®3。计算气体的熵变。解（1）1®2®3而，所以（2）1®3（3）1®4®3由于，，所以三次计算的相等，都等于习题10-11图1VV2=2V123pOV1p2p10-11理想气体的状态变化如图9.15所示，其中1－2为等温线。试分别由下列两种过程（1）1®3®2；（2）1®2；67 计算理想气体的熵的变化。解（1）1®3®2由于，，所以可得（2）1®210-12在绝热容器中，有两部分同种液体在等压下混合，这两部分液体的质量相等，都等于m，但初始温度不同，分别为T1和T2，且T1T2。一热机工作于这两个不同温度的物体之间，热机从高温物体吸取热量使其温度下降，热机放出热量给低温物体使其温度升高，最终使两物体温度都变为，热机停止工作。假设两物体吸热、放热都是在等压下进行的，且定压摩尔热容量为常数。（1）试求热机对外所做的总功；（2）利用熵增加原理证明热机对外所做的功A满足：解（1）在整个过程中热机从高温物体吸收的总热量为，向低温物体放出的总热量为根据热力学第一定律，热机对外所做的总功为（2）利用熵增加原理证明：高温物体的熵变化为低温物体的熵变为系统总的熵变为因为总系统是孤立系统，,因而，即，故热机所作的功A满足10-15掷一个骰子后，分别给出下列信息：（1）是奇数，但不是3；（2）不是4；（3）就是5；其信息量各为多少？解（1）一个骰子有6个面，每种数字出现的概率，收到该信息“结果是奇数”概率为，则该信息的信息量为若第二个信息：“结果不是3”，的可能结果，每个可能结果的概率，则第二个信息的信息量为67 两条信息的总信息量为（2）一个骰子有6个数字（6个面），N1=6，所给信息是“数字不是4”，收到这一信息后，可能结果，那么这条信息的信息量为（3）所给信息是“出现的数字为5”,则事情变成完全确定，，这条信息具有最大的信息量，即10-16计算机处理1.40Mb信息，折合为热力学熵的单位（J/K）为多少？解因为J.K所以，1.40Mb信息的信息量为67'