化工热力学 (第三版) 上册 (陈钟秀 著) 化学化工出版社 课后答案_NoRestriction 23页

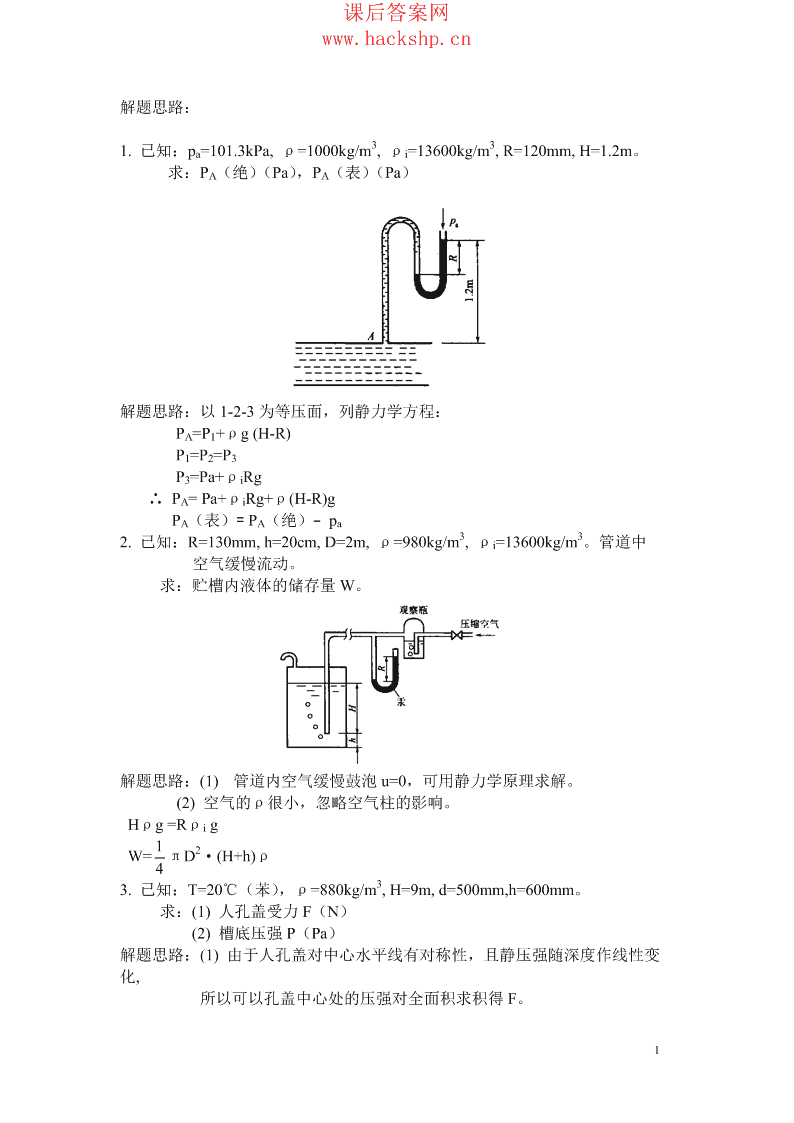
'课后答案网www.hackshp.cn解题思路：331.已知：pa=101.3kPa,ρ=1000kg/m,ρi=13600kg/m,R=120mm,H=1.2m。求：PA（绝）（Pa），PA（表）（Pa）解题思路：以1-2-3为等压面，列静力学方程：PA=P1+ρg(H-R)P1=P2=P3P3=Pa+ρiRg∴PA=Pa+ρiRg+ρ(H-R)gPA（表）=PA（绝）-pa332.已知：R=130mm,h=20cm,D=2m,ρ=980kg/m,ρi=13600kg/m。管道中空气缓慢流动。求：贮槽内液体的储存量W。解题思路：(1)管道内空气缓慢鼓泡u=0，可用静力学原理求解。(2)空气的ρ很小，忽略空气柱的影响。Hρg=Rρig12W=πD·(H+h)ρ433.已知：T=20℃（苯），ρ=880kg/m,H=9m,d=500mm,h=600mm。求：(1)人孔盖受力F（N）(2)槽底压强P（Pa）解题思路：(1)由于人孔盖对中心水平线有对称性，且静压强随深度作线性变化,所以可以孔盖中心处的压强对全面积求积得F。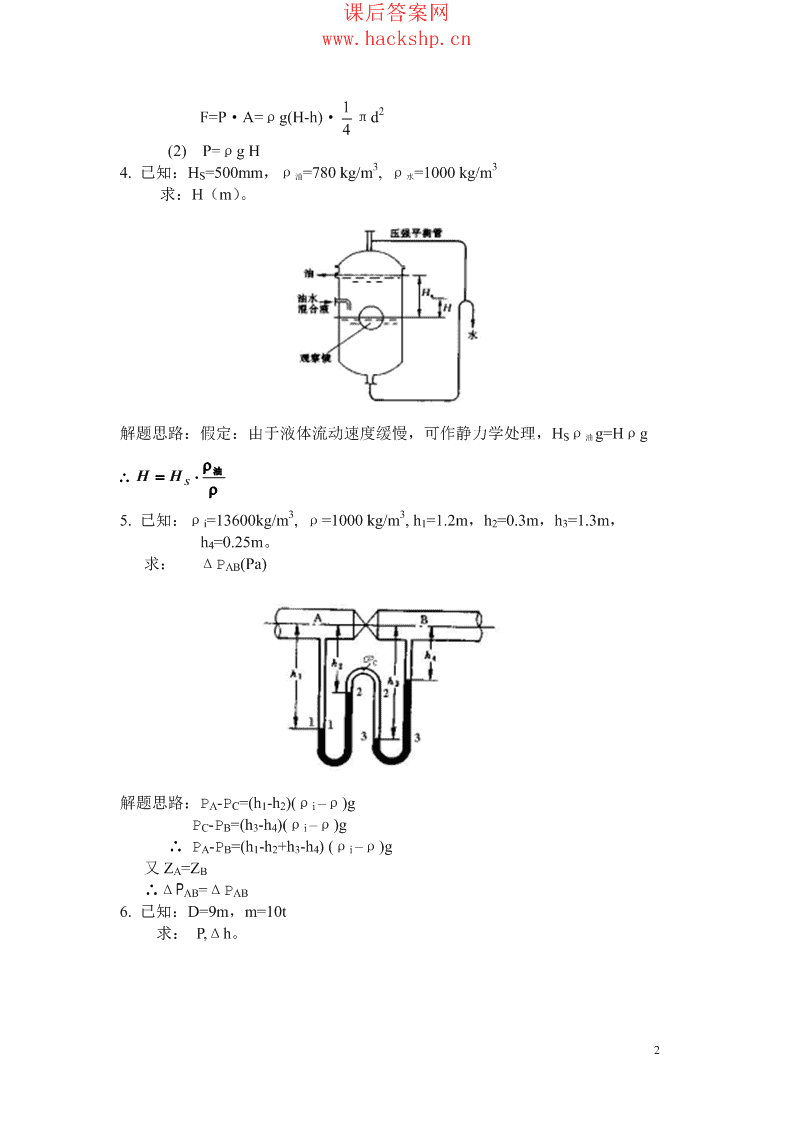1 课后答案网www.hackshp.cn12F=P·A=ρg(H-h)·πd4(2)P=ρgH334.已知：HS=500mm，ρ油=780kg/m,ρ水=1000kg/m求：H（m）。解题思路：假定：由于液体流动速度缓慢，可作静力学处理，HSρ油g=Hρgρ油∴H=H⋅Sρ335.已知：ρi=13600kg/m,ρ=1000kg/m,h1=1.2m，h2=0.3m，h3=1.3m，h4=0.25m。求：ΔPAB(Pa)解题思路：PA-PC=(h1-h2)(ρi–ρ)gPC-PB=(h3-h4)(ρi–ρ)g∴PA-PB=(h1-h2+h3-h4)(ρi–ρ)g又ZA=ZB∴ΔPAB=ΔPAB6.已知：D=9m，m=10t求：P,Δh。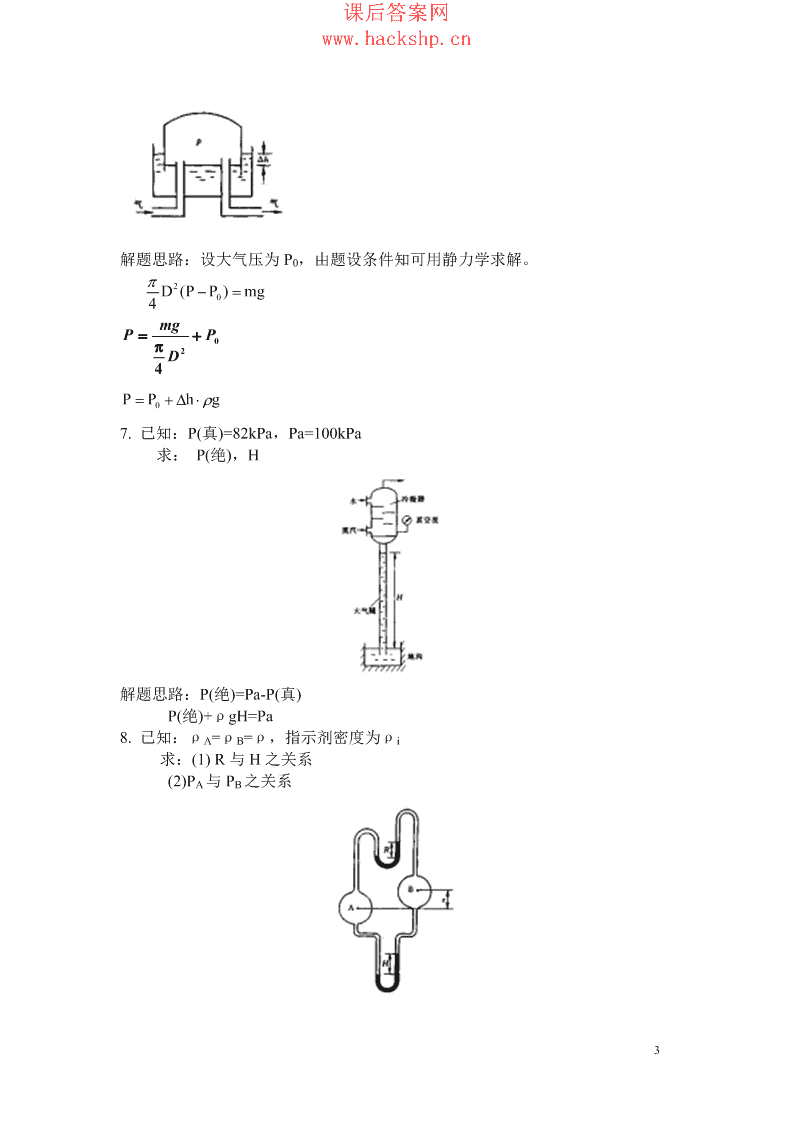2 课后答案网www.hackshp.cn解题思路：设大气压为P0，由题设条件知可用静力学求解。π2DP(−P)=mg04mgP=+P0π2D4P=P+∆h⋅ρg07.已知：P(真)=82kPa，Pa=100kPa求：P(绝)，H解题思路：P(绝)=Pa-P(真)P(绝)+ρgH=Pa8.已知：ρA=ρB=ρ，指示剂密度为ρi求：(1)R与H之关系(2)PA与PB之关系3 课后答案网www.hackshp.cn解题思路：(1)由静力学可知：PA-PB=R(ρi–ρ)g=H(ρi–ρ)g(2)∵ρi>ρ∴PA-PB=H(ρi–ρ)g>0即PA>PBPA+ZAρg>PB+ZBρgPA>PB+(ZB-ZA)ρg>PB9.已知：如图所示：2d求证：P=P−hg(ρ−ρ)−hgρBa2112D解题思路：作1-1等压面，由静力学方程得P+hρg=P+∆hρg+hρg（1）a1B12π2π2∵∆h⋅D=h⋅d442d∴∆h=h⋅代入（1）式2D2d得P+hρg=P+h⋅ρg+hρga1B212D10．已知：dp=ρ(Xdx+Ydy+Zdz),Ph=0=Pa,T=const,大气为理想气体。求：大气压与海拔高度h之间的关系。解：大气层仅考虑重力，所以X=0，Y=0，Z=-g，dz=dh∴dp=-ρgdhpM又理想气体ρ=RT其中M为气体平均分子量，R为气体通用常数。4 课后答案网www.hackshp.cn311．已知：钢管φ114×4.5mmP=2MPa(绝)，T=20℃，空气流量qV0=6300m/h(标准状态)，求：u、qm、G解题思路：（1）Pqv=nRTTP10∴q=q××V1V0TP01qV1∴u=12πd4pM(2)ρ=RT∴G=uρ⋅29(3)ρ=0224.q=ρ⋅qm0V03312．已知：qV=60m/h，dA=100mm,dB=200mm,hAB=0.2m,ρi=1630kg/m,3ρ=1000kg/m,求：(1)指示剂哪侧高，R=？(2)扩大管道改为水平放置，压差计的读数有何变化？解题思路：(1)取A、B两个管截面列柏努利方程22PuPuAABB得+=+ρ2ρ2ρ22∴P=P−P=(u−u)ABABBA2ΔPBA=Rg(ρi-ρ)(2)若改为水平放置后，由于uA、uB不变，则ΔPBA也不变，由ΔPBA=Rg(ρi-ρ)R值也不变，即压差计指示的是总势能差。3313．已知：d=200mm,R=25mm,ρi=1000kg/m，ρ=1.2kg/m。5 课后答案网www.hackshp.cn3求：qV(m/h)解题思路：列1-2两截面伯努利方程22PuPu1122+gz+=+gz+12ρ2ρ2P1=Pa，z1=z2，u1=0ρ2∴P−P=ua222由U形压差计，Pa-P2=Rg(ρi-ρ)(忽略空气柱)12∴q=u⋅πdV22414．已知：H=0.8m，h=0.6m，D=0.6m，d=10mm，CO=0.62，求：液面下降0.5m所需的时间。解题思路：列1-2截面伯努利方程，小孔中心处为基准面22PuPu1122+gz+=+gz+12ρ2ρ2P1=P2=Pa，z2=0,z1=H-h=0.8-0.6=0.2m,u1=0∴u=2g(H−h)2小孔实际流速u0=C0u2∵液面下降0.5m1d29．已知：T=20℃（苯），H=5m,P1=P2=Pa，Ф32×3mm，ε=0.05mm,l=100m求：qV解题思路：列两槽液面间柏努利方程222PuPulu1122+gz+=+gz++λ⋅12ρ2ρ2d2P1=P2=Pa，u1=u2=0，z1=H,z2=02lu∴gH=λ⋅d2.005εd/==.000226假设流动已进入阻力平方区，查莫迪图λ=0.02316 课后答案网www.hackshp.cn2gHd∴u=λl3T=20℃，苯ρ=880kg/m,μ=0.67mPa·SρudRe=µ查莫迪图λ2gHd与假设λ有差距，重新计算u=λl3330．已知：d=2m,ε/d=0.0004,ρ烟气=0.67kg/m，μ=0.026mPa·S,qv=80000m/h,3ρair=1.15kg/m，P1（真）=0.2kPa求：H解题思路：列烟囱底部（1截面）与顶部（2截面）柏努利方程22PuPu1122+gz+=+gz++Σh121f−2ρ2ρ2烟烟烟囱d1=d2,∴u1=u2z1=0,z2=HP1=Pa-P1（真）P2=Pa-ρairgH2HuΣh=⋅λ⋅1f−2d2qvu=12πd4ρudRe=µε/d=0.0004,查表得λ17 课后答案网www.hackshp.cn∴1-2截面间柏努利方程为2−P1(真）−ρairgHHu=+gH+λ⋅ρρd2烟烟烟囱得以排气的必要条件是ρ烟<ρ外，若ρ烟≮ρ外时，P1≮0，即无法起到抽吸作用。H增加,P1降低（即真空度增加）,抽吸量增加。231．已知：A=3m,h=2m,H0=4m,l=10m,λ=0.022,φ32×3mm求：τΔH=1m=?解题思路：列1-1和2-2截面间柏努利方程22PuPu1122+gz+=+gz++Σh121f−2ρ2ρ2P1=P2,z1=0,z2=-H，u1=02luΣh=λ⋅fd22luH=1(+λ)d2g对水槽作质量衡算：12−dH⋅A=u⋅πd⋅dτ4-33332．已知：qv=2.5×10m/s,P(表)=0.2MPa，H=6m,ρ=1100kg/m,Ф40×3mm,L=50m,λ=0.024求：He(J/N)18 课后答案网www.hackshp.cn解题思路：列两槽面间柏努利方程222PuPulu1122+z++He=+z++λ⋅12ρg2gρg2gd2gP1=Pa,P2-Pa=0.2MPa,Z2-Z1=6m,u1=u2=033．已知：ZAA’=6m，dBC=600mm,lBC=3000m,dCD=dCE=250mm,lCD=lCE=2500mm,λ=0.04,忽略局部阻力求：qV解题思路：由连续性方程qV=qVBC=qVCD+qVCE222u1d1=u2d2+u3d3∵hf2=hf322lulu2233∴λ⋅=λ⋅d2d223l=l,d=d2323u=u23u1d12因而u=()22d2由A、A’两截面列柏努利方程22lulu1122Z=λ⋅+λ⋅AA"d2gd2g12λl121d14l22=[u+()u]112gd4dd12212q=πd⋅uv11434．已知：lAB=6m,d1=41mm,lBC=15m,lBD=24m,d2=d3=25m,λ=0.03求：(1)qV1、qV2、qV3(2)D阀关闭，qV3’19 课后答案网www.hackshp.cn解题思路：(1)从B点至两管口列柏努利方程22uu23h+=h+f2f32222lulu2233即：(λ+)1=(λ+)1d2d223由连续性方程：qV1=qV2+qV3222u1d1=u2d2+u3d3由槽内液面至C阀出口处截面列柏努利方程：222luluu11333Hg=λ⋅+λ⋅+d2d2213（2）D阀关闭时：连续性方程：qV1’=qV3’22u"⋅d=u"⋅d,1133由槽内液面至C阀出口处截面列柏努利方程：222luluu11333Hg=λ⋅+λ⋅+d2d221335．已知：dB=dC=20mm,lB=2m,lC=4m,λ=0.028求：(1)ζB=ζC=0.17时，qVB/qVC(2)H增加，ζB=ζC=24时，q’VB/q’VC(3)均布条件20 课后答案网www.hackshp.cn解题思路：(1)由汇点0至两管口截面列柏努利方程：22uuBCh+=h+fBfC2222luluBBCC∴(λ+ζ+)1=(λ+ζ+)1BCd2d2BClCλ+ζ+1CudBC∴=uClBλ+ζ+1BdBd=dBClCλ+ζ+1CqudVBBC∴==qVCuClBλ+ζ+1BdB（2）ζ=24时qVB∴qVCqVB与qVC的比值与H的变化无关。（3）计算说明流体均布是以能量损失为条件的。36．已知：qm=5000kg/h，L=100km,d=300mm,P2=0.15MPa(绝压)，T=20℃，3λ=0.016,ρ=0.85kg/m(标准状态)。求：P1解题思路：对等温流动222P1P2−P1l2Gln++λG=0P2Pνd2211511TP01293.1013×10ν==⋅⋅=××1ρρTP.085273P100115.128×10=P1qmG=A.试差求得P(绝）1237．已知：d=300mm,M=60,T=40℃,P=101.3kN/m,μ=0.02mPa·S,用毕托管测流速，Rmax=30mmH2O，21 课后答案网www.hackshp.cn求：uMPT0解题思路：ρ=××224.PT0由毕托管流速计算式2gR(ρ−ρ)iu=ρ2gR(ρ−ρ)maxi∴u=maxρρudmaxRe=maxµuu查~R图,得emaxuumaxmax338．已知：孔板流量计测流量d=5cm,d0=25mm,R=220mmHg,ρ=1050kg/m,μ=0.6mpa·s求：qVd02252解题思路：面积比m=()=()=.025d504设Red>Red极限=8×10由图1-54，查得C0=0.6252gR(ρ−ρ)i∴u=C00ρu=mu0ρud验证：Re=dµ339．已知：转子流量计qvair=400~4000l/h，ρf=2670kg/m，求：q上限vco2解：由转子流量计qρ(ρ−ρ)vco2airfco2=qρ(ρ−ρ)vairco2fair∵ρ气<<ρf∴ρf-ρ=ρf，ρf-ρair=ρfco222 课后答案网www.hackshp.cnqvco2ρairMair∴==qρMvairco2CO223'