工程热力学课后答案--华自强张忠进(第三版)pdf下载H05 40页

'第五章热力学第二定律5-1蒸汽机中所用新蒸汽的温度为227℃，排出乏汽的温度为100℃，如按卡诺循环计算，试求其热效率。T2373解η=1−=1−=.0254tT50015-2海水表面温度为10℃，而深处的温度为4℃。若设计一热机利用海水的表面和深处作为高温热源及低温热源并按卡诺循环工作，试求该热机的热效率。T2277解η=1−=1−=.00212tT28315-3一卡诺热机的热效率为课后答案网40%，若它从高温热源吸热4000kJ/h，而向25℃的低温热源放热，试求高温热源的温度及热机的功率。Twww.hackshp.cn298解T=2==497K11−η1−4.0tP=Q&1ηt=4000×4.0=1600kJ/h=0.44kW5-4某内燃机每作出1kWñh的功需消耗汽油514.8g。已知每千克汽油燃烧时可放出41868kJ的热量，试求该内燃机的实际热效率。 热力学第二定律·63·解W0W01×3600.0167167.η=====%tQGQ.05148×418681p5-5有报告宣称某热机自160℃的热源吸热，向5℃的低温环境放热，而在吸热1000kJ/h时可发出功率0.12kW。试分析该报告的正确性。解在给定温度范围内的卡诺效率为：T2278η=1−=1−=.0358=358.%T4331而报告所提到的热机的热效率为：W0.012×3600η===.0432=432.%tQ10001该热机的热效率大于卡诺效率，这是不可能。5-6有A、B两个卡诺热机，A从温度为700℃的热源吸热，向温度为t的热源放热。课后答案网B则从温度为t的热源取得A排出的热量并向温度为100℃的热源放热。试求：当两热机的循环净功相同，或者两热机的热效率相的时，温度www.hackshp.cnt的数值。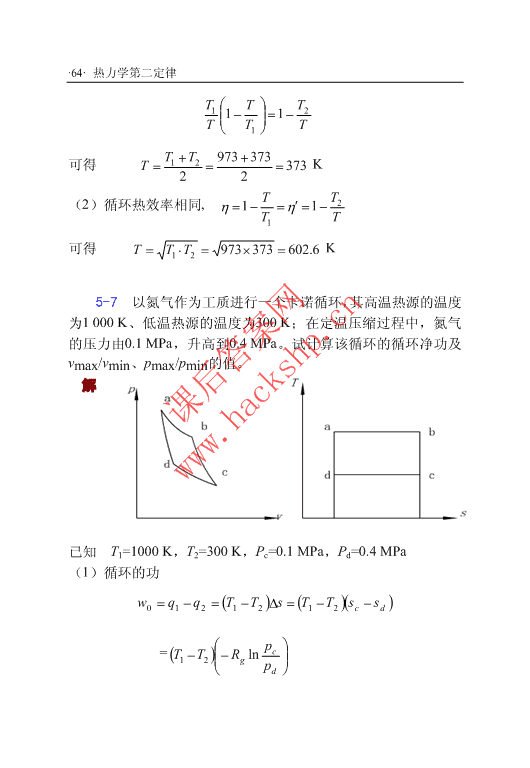解（1）循环净功相同W=W′00⎛T⎞⎛T2⎞Q1⎜⎜1−⎟⎟=Q1′⎜1−⎟⎝T1⎠⎝T⎠Q⎛T⎞T1⎜1−⎟=1−2⎜⎟Q2⎝T1⎠T ·64·热力学第二定律T⎛T⎞T1⎜1−⎟=1−2⎜⎟T⎝T1⎠T可得T1+T2973+373373T===K22TT2（2）循环热效率相同,η=1−=η′=1−TT1可得T=T⋅T=973×373=6026.K125-7以氮气作为工质进行一个卡诺循环，其高温热源的温度为1000K、低温热源的温度为300K；在定温压缩过程中，氮气的压力由0.1MPa，升高到0.4MPa。试计算该循环的循环净功及vmax/vmin、pmax/pmin的值。解课后答案网www.hackshp.cn已知T1=1000K，T2=300K，Pc=0.1MPa，Pd=0.4MPa（1）循环的功w0=q1−q2=(T1−T2)∆s=(T1−T2)(sc−sd)⎛p⎞=()T−T⎜−Rlnc⎟12⎜gp⎟⎝d⎠ 热力学第二定律·65·()⎛1.0⎞=1000−300⎜−.02968ln⎟=700×.04115=288kJ/kg⎝4.0⎠（2）最大容积与最小容积之比：1Vmaxvcvcvdpd⎛pa⎞k==⋅=⎜⎟Vvvvp⎜p⎟minadac⎝d⎠114.0⎛Ta⎞k−1⎛1000⎞4.0=⎜⎟=4⎜⎟=811.1.0⎜⎝Td⎟⎠⎝300⎠（3）最高压力与最低压力之比：k4.1pmaxpapapd⎛Ta⎞k−1pd⎛1000⎞4.04.0==⋅=⎜⎟=⎜⎟=270pppp⎜T⎟p⎝300⎠1.0mincdc⎝d⎠c5-8有一台可逆热机，工质为理想气体，其工作循环由三个过程，即定容加热过程1-2、绝热膨胀过程2-3及定压放热过程3-1组成。试证明该循环的热效率为课后答案网⎛v⎞⎜3⎟k−1kwww.hackshp.cn[]Tvv−T⎝⎜v1⎠⎟η=1−1311=1−tTpp−Tpp−1121121 ·66·热力学第二定律证明由循环热效率公式有q2cp(T3−T1)η=1−=1−t()qcT−T1v21p21-2为等容过程，因此有:T=T21p1v33-1为等压过程，因此有：T=T31v1将其代入循环热效率公式，即有：⎛v⎞⎜3⎟k−1⎜⎟k[]T1v3v1−T1⎝v1⎠η=1−=1−tTpp−Tpp−11211215-9按上题所述循环，设工质为空气，p＝0.35MPa，t＝课后答案网11307℃，p＝0.7MPa。试把该循环表示在p-v图以及T-s图上，并求2吸热量、放热量、循环净功及循环热效率。解按5-8所述的循环，并已知：www.hackshp.cnT1=580K；p1=0.35MPa；p2=0.7MPa；Rg=0.2871kJ/kg·K；cp0=1.004kJ/kg·K，则有：RgT1.02871×5803v1===.0476m/kg=v2p3501pv700×.0476T=22==11604.K2Rg.02871p3=p1=.035MPa 热力学第二定律·67·k−14.0⎛p⎞k⎛.035⎞4.1⎜3⎟T3=T2⎜⎟=11604.⎜⎟=9519.K⎝p2⎠⎝7.0⎠q1=cv0()T2−T1=.0716(11604.−580)=4154.kJ/kgq=c(T−T)=.1004(9519.−580)=3732.kJ/kg2p031q0=q1−q2=4154.−3732.=422.Kw0422.η===.0102=102.%tq4154.15-10一个热机循环由定容加热过程1-2，定温膨胀过程2-3及定压放热过程3-1三个过程组成。设T及T固定不变，而p取两121个不同的值，从而得到两个循环。试把该两循环表示在p-v图及T-s图上，并分析两者的热效率及循环净功间的关系。课后答案网www.hackshp.cn解已知T1=T1′;T2=T3=T2′=T3′p3=p1p3′=p1′v1=v2v1′=v2′ ·68·热力学第二定律p1v1RgT1RgT1′p1v1′′p1p1′p3p3′=======pvRTRT′p′v′pp′pp′22g2g2222222q=c(T−T)=c(T′−T′)=q′2p31p312⎛p⎞q=c()T−T+T⎜−Rln3⎟1v212⎜gp⎟⎝2⎠⎛p′⎞=c()T′−T′+T′⎜−Rln3⎟v212⎜gp′⎟⎝2⎠=cv(T2′−T1′)+T2′(s3′−s′2)=q1′因此有：w=q−q=q′−q′=w′012120ww′η=0课后答案网=0=η′ttqq′11www.hackshp.cn5-11有质量相同的两个物体，温度各为T及T。现以这两AB个物体作为低温热源及高温热源，用一可逆卡诺热机在它们之间工作并产生功。因这两个物体的热力学能是有限的，故与热机发生热交换后其温度会发生变化。设物体的比热容为定值，试证明两物体的终了温度及热机输出的功的总量各为T＝TT；W＝mc(T＋T－2TT)AB0pABAB证明物体A初终两态的温度为TA及T;物体B初终两态的温度为TB及T,它们的熵变分别为： 热力学第二定律·69·TT∆s=mcln，∆s=mclnApBpTTAB可逆条件下的熵方程可表示为：isol∆s=∆s+∆s+∆s=0ABknj热机经过一个循环，因此有∆s=0knjTT即B∆s=−∆s;ln=lnABTTA可以得出：T=TTAB根据能量方程，有：W0=Q1−Q2课后答案网=mc(T−T)−mc(T−T)pApB=mcp(TAwww.hackshp.cn+TB−2T)=mcp(TA+TB−2TA⋅TB)5-12卡诺热机按逆向循环工作时称为逆向卡诺循环，如图5-16所示。现利用它来制冷，消耗循环净功w，由低温热源吸热q20向高温热源放热q1，试证明其制冷T系数的公式为ε＝r2。T−T图5-16逆向卡诺循环的T-s图r1r2 ·70·热力学第二定律证明制冷装置的制冷系数为ε：q2q2ε==WWq−q012T()s−s=r2cdT()()s−s−Ts−sr1bar2cdTr2=Tr1−Tr25-13若利用逆向卡诺循环作热泵，其循环如图5-16所示。冬天由室外低温环境吸热q而向室内供热q，其所消耗循环净功21为w。一般采用供热系数ξ＝q/w作为评价热泵循环能量转010换完善程度的指标。试证明逆向卡诺循环的供热系数的公式为Tξ＝r1T−T课后答案网r1r2证明热泵的供热系数可表示为ζ：q1q1Tr1(sb−sa)Tr1ζ==www.hackshp.cn==Wq−qT()s−s−T()s−sT−T012r1bar2cdr1r25-14某热泵按逆向卡诺循环工作，由室外0℃的环境吸热向室内供热，使室内气温由10℃升高到20℃，设房间的散热损失可忽略不计，试求对应于1kg空气热泵所消耗的功，并和利用电热器直接供热时所消耗的功进行分析比较。解参考等效卡诺循环m=1kg;c=.1004kJ/kg·Kp0 热力学第二定律·71·Q=mc∆T=1×1.004×（20-10）=10.04kJ/kg1p0283+293Trm1==288K2T=T=273Krm2r2热泵的供热系数ζQ1Trm1288ζ====192.WT−T288−2730rm1rm2加热一公斤空气热泵所消耗的功为W0Q110.04W===.0522kJ/kg0ξ192.若采用电加热器取暖时：W0′=Q1=课后答案网10.04kJ/kg5-15有报告宣称设计了一种热工设备，它可以在环境温度www.hackshp.cn为15℃时，把65℃的热水中35%的水变为100℃的沸水，而把其余部分冷却为15℃的水。试用热力学第二定律分析该报告的正确性。解（1）65%的热水冷却到环境温度T0的过程是通过一个可逆机进行的,Q=.065mc(65−15)=26mc1pp()65+273+(15+273)Trm1==313K2 ·72·热力学第二定律T1−T0312−288η===.008tT3131W=Qη=26mc×.008=.208mc01tpp（2）35%65℃的热水加热到100℃的过程是通过一个热泵来实现的，()65+273+(100+273)Trm′1==3557.K2热泵的供热系数ζT′3557.ξ＝rm1==.527T′−T3557.−288rm10Q1′12.25mcp而W′===.233mc0pξ.527放热过程中所能做出的最大可用功比热泵所需的最小功还’小，W0﹤W0,所以这个过程是不可能实现的。课后答案网5-16有报告宣称设计了一种热工设备，它可以在环境温度为30℃时，把50℃的热水中www.hackshp.cn90%的水变为10℃的冷饮水，而把其余部分变为30℃的水。试用热力学第二定律分析该报告的正确性。解（1）假定50℃的热水冷却到环境温度T0的过程是通过一个可逆机进行的Q=mc()50−30=20mc1pp()50+273+(30+273)T==313Krm12Trm1−T0313−303η===.0032tT313rm1 热力学第二定律·73·W=Qη=20mc×.0032=.06386mc01tpp（2）假定0.9m30℃的水进一步冷却到10℃的过程是通过一个可逆制冷机来实现的，Q=9.0mc(30−10)=18mc1pp303+283Trm2==293K2热泵的供热系数ζξ＝Trm229329.32==T−T303−2930rm2Q2′18mcpW′===.0614mc0pξ29.32’可逆热机所作的功大于制冷机所需要的功，W0﹥W0,所以这个过程是可能实现的。课后答案网5-17气缸中工质的温度为850K，定温地从热源吸热1000kJ，且过程中没有功的耗散。若热源温度为www.hackshp.cn(1)1000K；(2)1200K。试求工质和热源两者熵的变化，并用热力学第二定律说明之。图5-17解按题意过程中无功的耗散，因此系统内部的气体经历 ·74·热力学第二定律了一个可逆的等温过程，(∆s)=0irrsystem系统的熵方程可表示为：Q1000∆s===.1176kJ/KT8502第一种情况：A1000T1=K，因热库中经历的都是可逆过程，其中由于可逆引起的熵变(∆s)热库=0，所以热库的熵变就等于热熵irrHRA−Q−1000流：∆s===−1kJ/KAT10002孤立系统A的熵变：isolAHRAkJ/K﹥0∆s=∆s+∆s=−1+.1176=.0176孤立系统A的熵变大于零，这是由于热库与系统之间的温差传热课后答案网所引起的。第二种情况：B1200T1=Kwww.hackshp.cnHRB−Q−1000热库的熵变为：∆s===−.0833kJ/KBT12002孤立系统B的熵变：isolBHRB∆s=∆s+∆s=−.0833+.1176=.0343kJ/K﹥0计算结果表明，孤立系统B的熵变大于孤立系统A的熵变,isolBisolA,这是由于第二种情况的温差大，∆s﹥∆s相应的不可逆性大的结果。5-18有一台热机，从温度为1100K的高温热源吸热1000kJ，并向温度为300K的低温热源可逆地放热，从而进行一个双热 热力学第二定律·75·源的循环，并作出循环净功690kJ。设定温吸热时无功的耗散，试求吸热过程中工质的温度及工质和热源两者熵变化的总和。解根据热力学第一定律：Q=Q−W=1000−690=310kJ21按题意，放热过程是可逆的，因此有：T=300K2又知系统吸热时无功的耗散，因此系统经历了一个内部的可逆的循环其热效率可表示为：课后答案网WT2690η==1−==.069tQT1000www.hackshp.cn11T2300T===9677.K11−η1−.069t假想在高温热源与热机之间存在一个温度为T的热源，高温热源1与热机之间的传热是通过它来实现的。整个孤立系统的熵变在数值上就等于高温热源与热源T之间温差传热所引起的熵产。对上1右图的孤立系统可写出熵方程如下：isol−100010001000310∆s=+−++∆ssystem11009677.9677.300 ·76·热力学第二定律其中∆s=0system1000310−+=06977.300isol−10001000即有∆s=+=.0124kJ/K11009677.对左图的孤立系统所写出的熵方程也可得到相同的结果：isol−1000310∆s=++∆ssystem=.0124kJ/K11003005-19一台可逆热机，从高温热源吸热，并分别向温度为370℃、270℃的两低温热源放热。设吸热及放热过程均为可逆定温过程，热机循环的热效率为28%，循环净功为1400kJ，向370℃的热源放出的热量为2000kJ。试求高温热源的温度，并把该循环表示在T-s图上。解课后答案网www.hackshp.cn已知W0=1400kJ；ηt=.028，则Q1为：W01400Q===5000kJ1η.028t根据热力学第一定律： 热力学第二定律·77·Q2′=Q1−W1−Q2=5000−1400−2000=1600kJ对孤立系统写出熵方程（可逆的条件下）：isolQ1Q2Q2′∆s=−++=0TTT′122Q500050001T====8255.K1′Q2Q220001600.311+.295++TT′643543225-20一可逆热机，从227℃的热源吸热，并向127℃和77℃的两热源分别放热。已知其热效率为26%及向77℃的热源放热的热量为420kJ，试求该热机的循环净功。解WQ−Q−Q′0122η===.026tQQt1Q2Q2′=7.04−课后答案网(1)QQ11可逆条件下孤立系统的熵方程为：isolQ1Q2Q2′∆s=−+www.hackshp.cn+=0TTT′12211Q21Q2′T1Q2T1Q2′1=++=TTQT′QTQT′Q121212121500Q500Q′QQ′2+2=.1252+.14292=1()2400Q350QQQ1111将(1)式代入（2）式有：⎛Q′⎞Q′.125⎜.074−2⎟+.14292=1⎜⎟QQ⎝1⎠1 ·78·热力学第二定律Q′().1429−.1252=1−().125×.074=.0075Q1Q′.00752==.0419Q.1429−.1251Q′4202Q1===10024.kJ.0419.0149W0=Q1ηt=10024.×0.26=2606.kJ5-21设有两个可逆循环1-2-3-1及1-3-4-1。如图5-17所示，1-2及3-4为定熵过程，2-3及4-1为定温过程，1-3则为T与s成线性关系的过程。试求两循环循环净功的关系以及循环热效率间的关系。解设W0,η及W0′,η′分别为可逆循环1231及1341的循环功及效率。课后答案网s1W0=Q1+Q2=TA()s3−s1+∫Tds=◊1231s2s1W0′=Q1′+Q2′=∫www.hackshp.cnTds+TB()s1−s3=◊1341s2s1W0−W0′=()TA+TB()s3+s1−2∫Tdss2=◊abs3s1a−2◊13s3s11=0W0=W0′s1ηWQQ′∫sTds◊13ss1=01=1=2=31﹤1即η<η′η′W′Q′QT()s−s◊23ss2011A3131 热力学第二定律·79·5-22设有质量相同的某种物质两块，两者的温度分别为TA、及TB。现使两者相接触而温度变为相同，试求两者熵的总和的变化。解能量平衡方程：mc(T−T)=mc(T−T)pApB2T=TA+TB接触前的总熵：s2=2msA+B=m(sA+B+sA+B)接触前后熵的变化：∆s=s2−s1=m(sA+B−sA)(+sA+B−sB)⎡TT⎤=mcp⎢ln+ln⎥TT⎣AB⎦课后答案网⎡T+TT+T⎤=mclnAB+lnAB⎥p⎢2T2T⎣AB⎦www.hackshp.cn5-23有两个容器。容器A的容积为33m，其中有压力为0.8MPa、温度为17℃的空气。容器B的容积为13m，内为真空。设把两容器连通，让A内空气流入B。当两容器内压力相同时，又把两者分开。若整个过程中各容器均为绝热，试计算该过程中空气熵的变化。解BA ·80·热力学第二定律33已知：VA=3m；VB=1m；pA1=8.0MPa；TA1=290K；pB1=0MPa；cp0=.1004kJ/kg·K；Rg=.02871kJ/kg·K连通前容器A内的质量:3pV8.0×10×3m=A1A==28.826kgRT.02871×290gA1能量方程中，Q=;0W=;0∆U=0U1=U2mcvTA1=mAcvTA2+mBcvTB2mTA1=mATA2+mBTB2联通后容器A与B中的压力相等：mRTmRTAgA2BgB2p=p=p==A2课后答案网B22VVABmATA2VA==3mTVBB2www.hackshp.cnB因此有：mT=4mTA1BB211mBTB2=mTA1=×28.826×290=208.98944mATA2=3mBTB2=6269.655容器A中的剩余气体（m)经历了一个可逆的绝热过程，因此有：A 热力学第二定律·81·k−14.0⎛p⎞k⎛6.0⎞.14⎜A2⎟TA2=T1⎜⎟=290⎜⎟=2671.K⎝p1⎠⎝8.0⎠6269.6556269.655m===23.473kgAT2671.A2mB=m−mA=28.826−23.473=.5353kg2089.89TB2==390.44K.5353过程中的总熵变等于m及m这两部分质量熵变的总和，而m的ABA熵变为零（剩余质量经历了一个等熵过程），因此等于流出部分质量m的熵变。B⎡Tp⎤⎡Tp⎤A2A2B2B2∆s=mA⎢cpln−Rln⎥+mB⎢cpln−Rln⎥TpTp⎣课后答案网11⎦⎣11⎦⎡Tp⎤=0+mclnB2−RlnB2⎥B⎢p⎣www.hackshp.cnT1p1⎦⎡3906.0⎤=.5353.1004ln−.02871ln⎢⎥⎣2908.0⎦=2.0343kJ/K5-24气缸中有0.1kg空气，其压力为0.5MPa、温度为1100K，设进行一个绝热膨胀过程，压力变化到0.1MPa，而过程效率为90%。试求空气所作的功、膨胀终了空气的温度及过程中空气熵的变化，并把该过程表示在p-v图及T-s图上。 ·82·热力学第二定律解初态参数：p=5.0MPa；T=1100K；11RgT1.02871×11003v===.0632m/kg1p5001从初态1等熵膨胀到2s时所作的功为W：sW=mc(T−T)课后答案网sv12sk−14.0⎛p⎞k⎛1.0⎞4.1其中T=T⎜2⎟=1100⎜⎟=6945.K2s1⎜pwww.hackshp.cn⎟5.0⎝1⎠⎝⎠则W=1.0×.0716(1100−6945.)=29.03kJs已知绝热效率为90%，可算出实际的功量W12W12=Ws⋅η=29.03×9.0=26.13kJ根据绝热过程的能量方程，可算出T：2 热力学第二定律·83·mcv()T1−T2=W12=26.1326.13T2=T1−=1100−365=735K.01×.0716RgT2.02871×7353v===.211m/kg2p1002RgT2s.02871×6945.3v===.199m/kg2sp1002不可逆过程1-2的熵变：⎡Tp⎤22∆s12=m⎢cpln−Rgln⎥Tp⎣11⎦⎡7351.0⎤=1.0.1004ln−.02871ln=0.00562kJ/K⎢⎥⎣11005.0⎦5-25气缸中有0.1kg空气，压力为0.1MPa、温度为300K，设经历一个绝热压缩过程，压力变化到课后答案网0.3MPa，而过程效率为90%。试求压缩过程中消耗的功、压缩终了空气的温度及过程中空气熵的变化，并把该过程表示在www.hackshp.cnp-v图及T-s图上。解初态参数：p=1.0MPa;T=300K;11 ·84·热力学第二定律RgT1.02871×3003v===.086m/kg1p1001等熵压缩过程1-2s的终态参数：k−14.0⎛p⎞k⎛3.0⎞4.1⎜2⎟T2s=T1⎜⎟=300⎜⎟=4106.K⎝p1⎠⎝1.0⎠W2s=mcv(T1−T2s)=1.0×.0716(300−4106.)=−.792kJ实际压缩过程12的终态参数：W2s−.792W===−8.8kJ12η9.0W128.8T=T−=300+=423K21mc1.0×.0716v绝热压缩过程1-2的熵变：⎡Tp⎤∆s=mcln课后答案网2−Rln2⎢pg⎥⎣T1p1⎦⎡4233.0⎤=1.0⎢.1004www.hackshp.cnln−.02871ln⎥=0.003kJ/K⎣3001.0⎦5-26有一台涡轮机，其进口的燃气温度为1100K，压力为0.5MPa。设进行一个绝热膨胀过程，其压力降低到0.1MPa，而过程效率为90%。试求燃气所作的轴功、膨胀终了的温度及过程中燃气的熵的变化。设燃气的气体常数R＝0.2871kJ/(kg·K)，g比定压热容c＝1.004kJ/(kg·K)。p0k−14.0⎛p⎞k⎛1.0⎞4.1解等熵过程：T=T⎜2⎟=1100⎜⎟=6945.K2s1⎜p⎟5.0⎝1⎠⎝⎠ 热力学第二定律·85·W=h−h=c(T−T)=.1004(1100−6945.)=4071.kJ/kgs12sp012s实际过程1-2：W12=Ws⋅η=4071.×9.0=3664.kJ/kgq=∆h+W12=0W12=h1−h2W3664.12T=T−=1100−=735K21cp.1004T2p2∆s=cln−RlnpgTp117351.0=.1004lln−.02871ln=0.0573kJ/kg·K11005.05-27有一台内燃机用涡轮增压器，在涡轮机进口处工质的压力为0.2MPa，温度为课后答案网650℃，出口处工质的压力为0.1MPa，且涡轮机中工质绝热膨胀的效率为90%。涡轮机产生的功率全部用于驱动增压器，增压器入口处工质的压力为www.hackshp.cn0.1MPa、温度为27℃，增压器中对工质进行绝热压缩时过程的效率为90%。假设工质的性质和空气相同，试求当输气量为0.1kg/s时，涡轮机的功率，排气的温度以及增压器出口处空气的温度及压力。解 ·86·热力学第二定律k−14.0⎛p⎞k⎛.01⎞4.1（1）对于涡轮机：T=T⎜2⎟=923⎜⎟=7572.K2s1⎜p⎟2.0⎝1⎠⎝⎠W=h−h=c(T−T)(=.1004923−7572.)=1665.kJ/kg12s12sp12sW12=W12s⋅η=1665.×9.0=150kJ/kgW=c(T−T)12p012W15012T=T−=923−=7737.K21cp0.1004（2）增压器:按题意有：W34=−W12=−150kJ/kgW34s=ηW34=9.0×(−150)=−135kJ/kg=cp0(T3−T4s)课后答案网W1353T=T−=300+=4343.K4s3cp0.1004www.hackshp.cnk−14.0⎛T⎞k⎛4343.⎞4.1⎜4s⎟p4s=p3⎜⎟=1.0⎜⎟=.0365MPa⎝T3⎠⎝300⎠W=c(T−T)34p034W15034T=T−=300+=4493.K43cp0.1004NT=m&W12=1.0×150=15kW 热力学第二定律·87·5-28一封闭的绝热气缸，用无摩擦的绝热活塞把气缸分为A、B两部分，且各充以压缩空气。开始时用销钉固定活塞，使VA＝0.33＝0.63＝4bar，t＝127℃；p＝2bar，m，Vm，这时pBAABt＝27℃。然后拔去销钉，让活塞自由移动，而B内气体受压缩。B设B部分气体压缩过程的效率为95%，试求当A、B两部分气体达到压力相同的过程中，两部分气体各自熵的变化以及总的熵变化，并分析过程的不可逆因素何在。解根据已知数据可以求出A与B中的质量：pV400×3.0m=A1A1==1.045kgARgTA1.02871×400课后答案网pV200×6.0B1B1m===.1393kgBRT.02871×300gB1www.hackshp.cn整个气缸与外界无功量及热量交换，因此总的热力学能不变：∆U=∆UA+∆UB=;0∆UA=−∆UB即有：mAcv(TA2−TA1)=mBcv(TB1−TB2)mBmBT=T+T−T（1）A2A1B1B2mmAA活塞在p=p=p时达到平衡，这时有：A2B22 ·88·热力学第二定律mRTmRTAgA2BgB2p==（2）2VVA2B23又知：V+V=9.0m（3）A2B2由（2）及（3）可得出：mVm9.0−VBA2BB2TA2=TB2=TB2（4）mVmVAB2AB2由（1）及（4）可得出：mA⎛⎜mA⎞⎟TA1+TB1⎜TA1+TB1⎟VB2mB⎝mB⎠TB2==0.9-VB29.01+VB2⎛.1045⎞⎜400+300⎟VB2⎝.1393⎠=课后答案网=666.75VB29.0根据式（5）的关系，利用状态方程即可求出p：2www.hackshp.cnmRTmR666.75VBgB2BgB2p=p==2B2VVB2B2=666.75mR=666.75×.02871×.1393=266.65kPaBg已知B中绝热过程效率为η=.095，则有：BWmc(T−T)BsBvB1B2sη==（6）B()WmcT−TBBvB1B2T−T式（6）可表示为：T=T−B1B2s（7）B2B1ηB 热力学第二定律·89·式（7）中的T可根据等熵过程的参数关系求得：B2sk−14.0⎛p⎞k⎛266.65⎞4.1⎜2⎟TB2s=TB1⎜⎟=300⎜⎟=3257.K⎝pB1⎠⎝200⎠代入式（7）后可求得T：B2TB1−TB2s300−325.7KT=T−=300−=327.05B2B1η.095BTB2327.053VB2===.0491m666.7566.6753VA2=9.0−VB2=9.0−.0491=.0409mpV266.52×.0409T=2A2==363.77KA2mARg.1045×.02871A及B中空气熵的变化分别为课后答案网：⎡Tp⎤A2A2∆sA=mA⎢cpln−Rgln⎥⎣www.hackshp.cnTA1pA1⎦⎡363.77266.65⎤=.1045.1004ln−.02871ln⎢⎥⎣400400⎦=0.022kJ/K⎡Tp⎤∆s=mclnB2−RlnB2BB⎢pg⎥⎣TB1pB1⎦⎡327.05266.65⎤=.1393.1004ln−.02871ln⎢⎥⎣300200⎦=0.0057kJ/K ·90·热力学第二定律∆s=∆sA+∆sB=.0022+.00057=.00277kJ/Kk−14.0⎛p⎞k⎛266.65⎞4.1⎜2⎟TA2s=TA1⎜⎟=400⎜⎟=356.24K⎝pA1⎠⎝400⎠TA1−TA2400−363.77η===.0828〈ηABT−T400−356.24A1A2sA与Ｂ中都是不可逆绝热过程，Ａ中的不可逆性较大。5-29有一热机循环由以下四个过程组成：1-2为绝热压缩过程，过程中熵不变，温度由80℃升高到140℃；2-3为定压加热过程，温度升高到440℃；3-4为不可逆绝热膨胀过程，温度降至80℃，而熵增为0.01kJ/K；4-1为定温放热过程，温度为80℃。设工质为空气，试把该循环表示在T-s图上并计算：(1)除过程3-4外其δq余各过程均为可逆过程时的克劳修斯积分值∫，以及该循环中T课后答案网r系统熵的变化∫ds；(2)假设热源仅为440℃及80℃的两个恒温热源时，系统和热源两者总的熵变。www.hackshp.cn解已知T1=353Ｋ；T2=413Ｋ；s1=s2；p1=p2；T3=713Ｋ；T=T=353K；41∆s34=s4−s3=.001kJ/K2341dqdqdqdqdq（１）∫=∫+∫+∫+∫TTTTT1234 热力学第二定律·91·T3()=0+cln+0+s−sp14T2T3()()=cln+s−s+s−sp2334T2T3T2()=cln+cln+s−spp34TT23=－0.01kJ/K∫ds=0wholeHR1HR2−Q23Q41（2）∆s=∆s+∆s=+TT34c(T−T)p23()=+s−s41T3c(T−T)p23()()=+s−s+s−s4332T3cp(T2−T3)()T3=+s−s+cln课后答案网T43pT32.1004(413−713)713=+.001+.1004lnwww.hackshp.cn713413=−.0422+.001+.0548=.0136kJ/K5-30一绝热容器内有某种流体5kg，为使流体处于均匀状态，采用搅拌器不断搅动流体。设搅拌过程中流体的温度由15℃升高至20℃，已知环境温度为15℃，流体的比热容为6kJ/(kg·K)。试求：(1)搅拌过程中消耗的功及作功能力的损失；(2)假设用100℃的热水循环来加热流体而使流体温度由15℃升高到20℃时作功能力的损失。并说明消耗的功和作功能力损失不同的原因。 ·92·热力学第二定律解WsT=3735kg5kg已知m=5kg；c=6kJ/kg·K；T0=T1=288K；T2=293K；常数；HR373KV1=V2=V=T=流体在过程中所获得的能量：∆U=mc()T2−T1=5×6(293−288)=150kJ过程中流体火用的变化为：课后答案网∆A12=()U2−U1+p0(V2−V1)−T0(s2−s1)⎛293⎞=150+0www.hackshp.cn−288⎜5×6ln⎟=150－148.7=1.287kJ⎝288⎠（1）用输入轴功的办法：Ws=−∆U12=−150kJ功量的火用流：AW=−[Ws−p0(V2−V1)]=−Ws=150kJ过程的不可逆性（即火用损）为：I=AW−∆A12=150−.1287=1487.kJ 热力学第二定律·93·（2）利用热库（THR）供热的办法：=373K系统从热库吸入的热量为：HR(150)150Q=−Q=−−=K热库输出热量的火用值为：HRT0288Q−1=−150−1=34.18kJHRT373温差传热所引起的火用损为：I=34.18−.1287=32.89kJ可见，第二种办法比第一种办法的火用损失小。5-31气缸中有0.1kg的空气，温度为17℃、压力为0.1MPa，经绝热压缩后其温度为207℃、压力为0.4MPa。若室温为17℃，大气压力为0.1MPa，试求该过程的压缩功及作功能力的不可逆性损失。0.1kg课后答案网Wwww.hackshp.cn解初态参数：T1=T0=290K；p1=p0=100kPa；mRgT11.0×.02871×2903V===.0083m1p1001终态参数：T=480K；p=400kPa；22mRgT21.0×.02871×4803V===00.34m2p4002系统熵的变化： ·94·热力学第二定律⎡Tp⎤∆s=mcln2−Rln212⎢pg⎥Tp⎣11⎦⎛4804.0⎞=1.0⎜1.004ln−.02871ln⎟=.00108kJ/K⎝2901.0⎠能量方程：Q=∆U+W=012W=−∆U=mc(T−T)12v12=1.0×.0716(290−480)=−136.kJ功量的火用流A：WAW=−[]W−p0(V2−V1)=136.+100(.0034−.0083)=7.8kJ系统火用的变化：课后答案网∆A12=()U2−U1+p0(V2−V1)−T0(s2−s1)=136.−www.hackshp.cn.490−290(.00108)=5.57kJ不可逆损失（火用损）为：I=AW−∆A12=7.8−.557=.313kJ利用熵方程也可得到相同的结果：isol(HRWRo)I=T0∆s=T0∆s+∆s+∆s=T0∆s12=200×.00108=3.13kJ 热力学第二定律·95·5-32汽车用蓄电池中储存的电能为1440W·h。现采用压缩空气来代替它。设空气压力为6.5MPa、温度为25℃，而环境的压力为0.1MPa，温度为25℃，试求当压缩空气通过容积变化而作出有用功时，为输出1440W·h的最大有用功所需压缩空气的体积。解已知蓄电池存储的电能为1440W·h，因此代用的储气筒内存储的压缩空气的最大存用功也是1440W·h。初态参数：T1=T0=298K；p1=5.6MPa1kg压缩空气的火用值：课后答案网∆A1−0=(u1−u0)()+p0v1−v0−T0(s1−s0)其中：u1−u0=0(T1=T0)www.hackshp.cnRgT1RgT0p0p0()v1−v0=p0(−)=RgT0(−)1p1p0p1()p1T0s1−s0=T0(−Rgln)p0p1p0因此有：∆A1−0=RgT0(ln+−)1p0p1 ·96·热力学第二定律5.61.0=.02871×298(ln+−)1=272.9kJ/kg1.05.6为使储气筒的压缩空气具有1440W·h的做功能力，储气量应不小于:Wu.144×3600m===19kg∆A2729.1−0在初态下，19kg压缩空气所占的体积为:mRgT119×02.871×2983V1===.025mp5.61031×5-33有一个刚性容器，其中压缩空气的压力为3.0MPa，温度和环境温度相同为25℃，环境压力为0.1MPa。打开放气阀放出一部分空气使容器内压力降低到1.0MPa。假设容器内剩余气体在放气时按可逆绝热过程变化，试求：(1)放气前后容器内空气比火用ex,H的值；(2)空气由环境吸热而恢复到25℃时，空气的比火用ex,H的值；(3)整个过程中课后答案网1kg空气的作功能力的损失，并分析各部分损失的原因。解www.hackshp.cnp1=3MPa,p2=0.1MPa,p3=?，p0=1.0MPaT1=298K，T2=?K,T3=298K,T0=298K。刚性容器中剩余气体经历了一个等熵过程: 热力学第二定律·97·k−14.0⎛p⎞k⎛0.1⎞4.1⎜2⎟T2=T1⎜⎟=298⎜⎟=2177.K⎝p1⎠⎝0.3⎠初态时的火用值A：1∆A1=()u1−u0+p0(v1−v0)−T0(s1−s0)⎛⎜RgT0⎞⎟p1⎛⎜p1p0⎞⎟=p0⎜p−v0⎟+RgT0lnp=RgT0⎜ln+−1⎟⎝1⎠0⎝p0p1⎠⎛31.0⎞=03.2871×298⎜ln+−1⎟=208.kJ/kg⎝1.03⎠状态2时的火用值A2：∆A2=(u2−u0)+p0(v2−v0)−T0(s2−s0)其中：u2−u0=cv(T2−T0)=.0716(2177.−298)=−575.课后答案网⎛pT⎞p()V−V=R⎜02−T⎟020g⎜p0⎟⎝2⎠www.hackshp.cn⎛1.0×2177.⎞=.02871⎜−298⎟=−793.⎝0.1⎠⎛Tp⎞T()s−s=T⎜cln2−Rln2⎟0200⎜pTgp⎟⎝00⎠⎛2177.0.1⎞=298⎜.1004ln−.02871ln⎟=−2909.⎝2981.0⎠A2=−575.−793.+2909.=154.14kJ/kg2-3为等容吸热过程： ·98·热力学第二定律T3=T0=298Kp20.1p=T=298=.1369MPa33T2177.2状态3时的火用值A：3∆A3=()u3−u0+p0(v3−v0)(−T0s3−s0)⎜⎛RgT3⎞⎟p3⎛⎜p0p3⎞⎟=p0⎜−v0⎟+RgT0ln=RgT0⎜−1+ln⎟⎝p3⎠p0⎝p3p0⎠⎛1.0.1369⎞=05.2871×298⎜−1+ln⎟=144.6kJ/kg⎝.03691.0⎠每公斤剩余气体作功能力的下降：I=Wrev1−0−课后答案网Wrev3−0=A1−A3+p0(V3−V1)⎛TT⎞=2083.−144.56+Rp⎜3−1⎟www.hackshp.cng0⎜pp⎟⎝31⎠⎛298298⎞=2083.−1444.56+.02871×1.0⎜−⎟=671.kJ/kg⎝.13693⎠或者：I=T0()s3−s1⎛Tp⎞p⎜33⎟3=T0⎜cpln−Rgln⎟=−RgT0lnTpp⎝11⎠1.1369=−.02871×298×ln=671.kJ/kg3 热力学第二定律·99·5-34有一台燃气轮机，其涡轮机进口处燃气的温度为850℃，压力为0.55MPa。经绝热膨胀后排气压力为0.1MPa。若环境温度为25℃，燃气的气体常数R＝2874J/(kg·K)，比热容c＝1.10gp0kJ/(kg·K)，涡轮机效率为90%，试求1kg燃气所作的轴功、燃气及废气的比火用、由初态变化到终态时的作功能力及该涡轮机中膨胀过程的作功能力的损失。解已知：T1=1123K；p1=.055MPa；T0=298K；p0=p2=1.0MPa；R=.02874kJ/kg·K；k=.1353gcp0=.110kJ/kg·K；cv0=.08126kJ/kg·K；k−1.0353⎛p⎞k⎛0.1⎞.1353⎜2⎟T2s=T1⎜⎟=1123⎜⎟=7198.K⎝p1⎠课后答案网⎝0.55⎠w=h−h=c(T−T)=.110(1123−7198.)=4435.kJ/kg2s12sp012swww.hackshp.cnw12=w2sη=4435.×9.0=399.15kJ/kgc()T−Tp012η=c()T−Tp012sT2=T1−η(T1−T2s)=1123−9.0(1123−7198.)=7601.K初态时的火用值A：1 ·100·热力学第二定律⎛Tp⎞A=c()T−T−T⎜cln1−Rln1⎟1p0100⎜p0Tgp⎟⎝00⎠⎛1123.055⎞=.110()1123−298−298⎜.110ln−.0287ln⎟⎝298.010⎠=618.6kJ/kg状态2时的火用值A：2⎛Tp⎞A=c()T−T−T⎜cln2−Rln2⎟2p0200⎜p0Tgp⎟⎝00⎠()⎛7601.⎞=.110×760.1−298−298×⎜.110×ln⎟⎝298⎠=2014.kJ/kgWrev12=()h1−h2−T0(s1−s2)=A1−A2=618.61−2014.=412.7kJ/kgI=Wrev12−W12=417.22−399.15=181.kJ/kg课后答案网5-35按习题5-31中压气机的压缩过程及环境条件，试求该www.hackshp.cn压气机的轴功，进、出口处空气的比火用ex,H，由初态变化到终态时的作功能力及该过程作功能力的损失。解由5-31可知：T1=T0=290K；p1=p0=100kPa；T2=480K；p2=400kPa；33V1=.0083m；V2=.0034m；1m=0.kg；S2−S1=.00108kJ/K； 热力学第二定律·101·W=m(h−h)=mc(T−T)1212p12=1.0×.1004(290−480)=−19.08kJA1=0kJ；A2=m[]()h2−h1−T0(s2−s0)⎡()⎛4804.0⎞⎤=1.0×⎢.1004×480−290−290×⎜.1004×ln−.02871×ln⎟⎥⎣⎝2901.0⎠⎦=15.95kJWrev12=m[]()h1−h2−T0(s1−s2)=9A1−A2=−A2=−15.5kJI=Wrev12−W12=课后答案网(−15.95)−(−19.08)=.313kJwww.hackshp.cn'