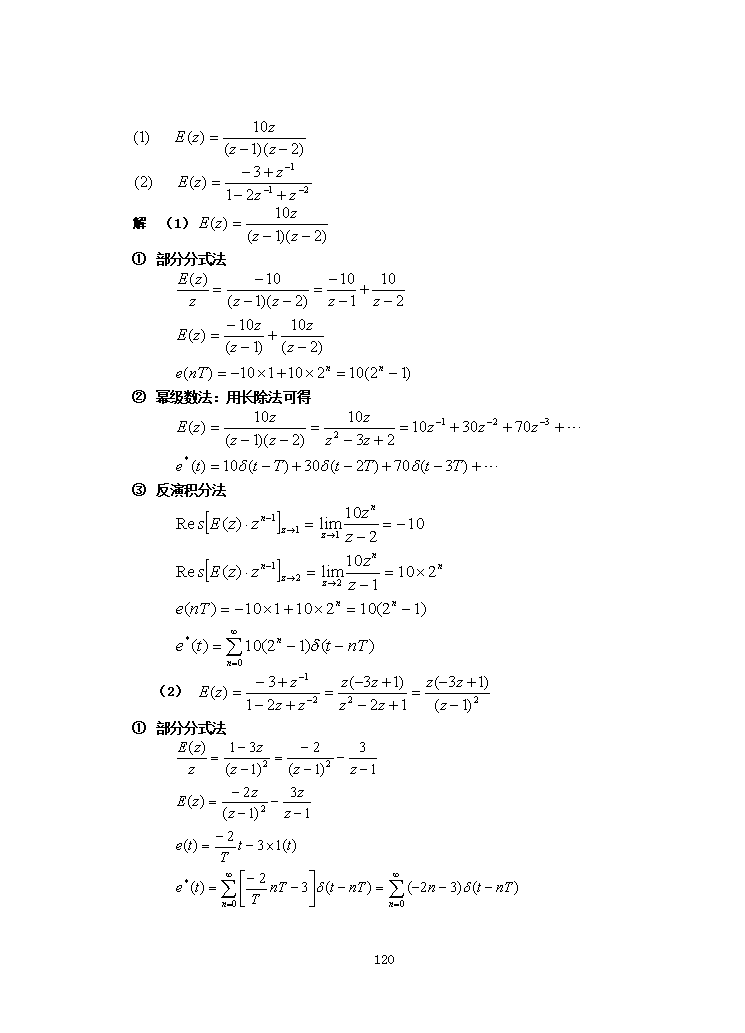《自动控制原理》习题及解答.doc 19页

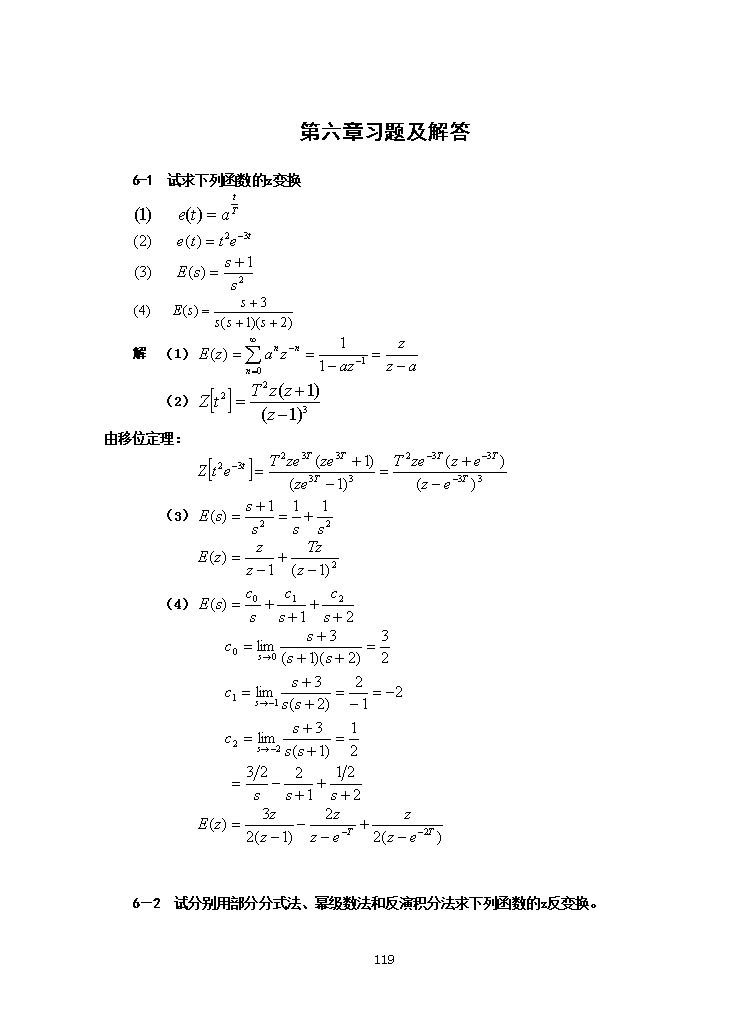
'第六章习题及解答6-1试求下列函数的z变换解（1）（2）由移位定理：（3）（4）6－2试分别用部分分式法、幂级数法和反演积分法求下列函数的z反变换。137 解（1）①部分分式法②幂级数法：用长除法可得③反演积分法（2）①部分分式法137 ②幂级数法：用长除法可得③反演积分法6-3试确定下列函数的终值解（1）（2）6-4已知差分方程为初始条件：c(0)=0,c(1)=1。试用迭代法求输出序列c(k),k=0，1，2，3，4。解依题有6-5试用z变换法求解下列差分方程：137 解（1）令，代入原方程可得：。对差分方程两端取变换，整理得（2）对差分方程两端取变换，整理得137 (3)对差分方程两端取变换得代入初条件整理得（4）由原方程可得6-6试由以下差分方程确定脉冲传递函数。解对上式实行变换，并设所有初始条件为得根据定义有137 6-7设开环离散系统如题6-7图所示，试求开环脉冲传递函数。解（）（）（）137 6－8试求下列闭环离散系统的脉冲传递函数或输出变换。题6-8图离散系统结构图解（）将原系统结构图等效变换为图解6-8(a)所示图解6-8(a)137 （）由系统结构图（）由系统结构图6－9设有单位反馈误差采样的离散系统，连续部分传递函数输入，采样周期。试求：（1）输出变换；图解6-9（2）采样瞬时的输出响应；（3）输出响应的终值。解（1）依据题意画出系统结构图如图解6-9所示137 （2）（3）判断系统稳定性列朱利表1-0.168426.2966-46.174725225-14.174726.2966-0.16843-624.971149.94-649.64闭环系统不稳定，求终值无意义。6-10试判断下列系统的稳定性（1）已知离散系统的特征方程为（2）已知闭环离散系统的特征方程为（注：要求用朱利判据）（3）已知误差采样的单位反馈离散系统，采样周期T=1(s)，开环传递函数解（1）系统特征根幅值有特征根落在单位圆之外，系统不稳定。（2）用朱利稳定判据（）137 10.80.3610.21210.210.360.83-0.360.088-0.2-0.24-0.2-0.20.088-0.3650.0896-0.071680.0896所以，系统不稳定。（3）用朱利稳定判据（）1-0.3687.95.91215.97.9-0.3683-0.8658.8110.076-11设离散系统如题6-11图所示，采样周期T=1(s)，Gh(s)为零阶保持器，而要求：137 （1）当K=5时，分别在w域和z域中分析系统的稳定性；（2）确定使系统稳定的K值范围。解（1）当时解根得以代入并整理得中有系数小于零，不满足系统稳定的必要条件。（2）当为变量时以代入并整理得由劳斯判据可得系统稳定的值范围为：6-12利用劳思判据分析题6-12图所示二阶离散系统在改变和采样周期的影响。解根据已知的可以求出开环脉冲传递函数闭环特征方程为：题6-12图137 即令，进行变换，得化简整理后得可得如下劳思表：得系统稳定的条件解得6-13题6-13图所示采样系统周期试确定系统稳定时的值范围。解由于则广义对象脉冲传递函数137 开环脉冲传递函数为闭环特征方程进行变换，令，化简后得列出劳斯表如下若系统稳定，必须满足即6-14如题6-12图所示的采样控制系统，要求在作用下的稳态误差，试确定放大系数及系统稳定时的取值范围。解因为所以由上式求得。该系统的特征方程为即令代入上式得列出劳斯表如下137 系统若要稳定，则劳斯表得第一列系数必须全部为正值，即有由此得出时，该系统是稳定的。6-15设离散系统如题6-15图所示，其中采样周期试用终值定理计算系统的稳态误差。解系统开环脉冲传递函数为将代入并整理得137 6-16设离散系统如题6-16图所示，其中，试求静态误差系数，并求系统在作用下的稳态误差。解系统开环脉冲传递函数为将代入并整理得6-17已知离散系统如题6-17图所示，其中ZOH为零阶保持器，.当时，欲使稳态误差小于，试求值。解首先验证系统的稳定性137 Jurry：①②0-111-10-1-1③解出④综合①②③④，稳定的范围为使稳态误差为0.1时的值：系统是Ⅰ型系统，阶跃输入下的稳态误差为零，斜坡输入下的稳态误差为常值时不稳定，不能使6-18试分别求出题6-15图和题6-16图所示系统的单位阶跃响应。解（a）137 将代入得(b)6-19已知离散系统如题6-19图所示其中采样周期，连续部分传递函数137 试求当时，系统无稳态误差，过渡过程在最少拍内结束的数字控制器。解查教材中表6-4有：6-20设离散系统如题6-20图所示其中采样周期，试求当时，系统无稳态误差、过渡过程在最少拍内结束的。解系统开环脉冲传递函数为令可取得则137 6-21已知采样系统如题6-21图所示，其中采样周期，要求设计一个数字控制器，使系统在斜坡输入下，调节时间为最短，并且在采样时刻没有稳态误差。题6-21图具有数字控制器的采样系统题6-21表最少拍无静差系统设计结果输入信号要求的要求的消除偏差所需时间解根据题6-21表，对于斜坡输入信号，最少拍系统闭环脉冲传递函数应该为广义对象的脉冲传递函数为根据可实现性对及的约束条件，中的极点应包含在的零点之中，这一点已满足，不必改变，中包含的延迟因子，也已包含在之中，且，所以按题6-21表设计的是可以实现的。即137'