固体物理课后习题答案.pdf 28页

'第一章晶体的结构第一章晶体的结构1.1试证明体心立方格子和面心立方格子互为正倒格子。解：我们知体心立方格子的基矢为：⎧GaGGG⎪ai1=()−++jk2⎪⎪GaGGG⎨ai2=−()j+k⎪2⎪GaGGG⎪ai3=+()j−k⎩2根据倒格子基矢的定义，我们很容易可求出体心立方格子的倒格子基矢为：⎧G2πGG⎪ba12=×()a3Ω⎪⎪G2πGG⎨ba23=×()a1⎪Ω⎪G2πGG⎪ba31=×()a2⎩ΩGGG13Ω=⋅×=aaa123()a2GGGijkaaaaaa−−GGaaaG22G2222Gaa23×=−=i+j+k222aaaaaa−−aaa222222−222aa22GG=+jk22GG2πG2πa2GGG2πGba1=×()23a=3()j+kj=+()kΩa2a2同理GG2πGGG2πGbi23=+=+(k),bi(j)aa⎧GG2πG⎪bj1=+()ka⎪⎪GG2πG⎨bi2=+()k⎪a⎪GG2πG⎪bi3=+()j⎩a由此可知，体心立方格子的倒格子为一面心立方格子。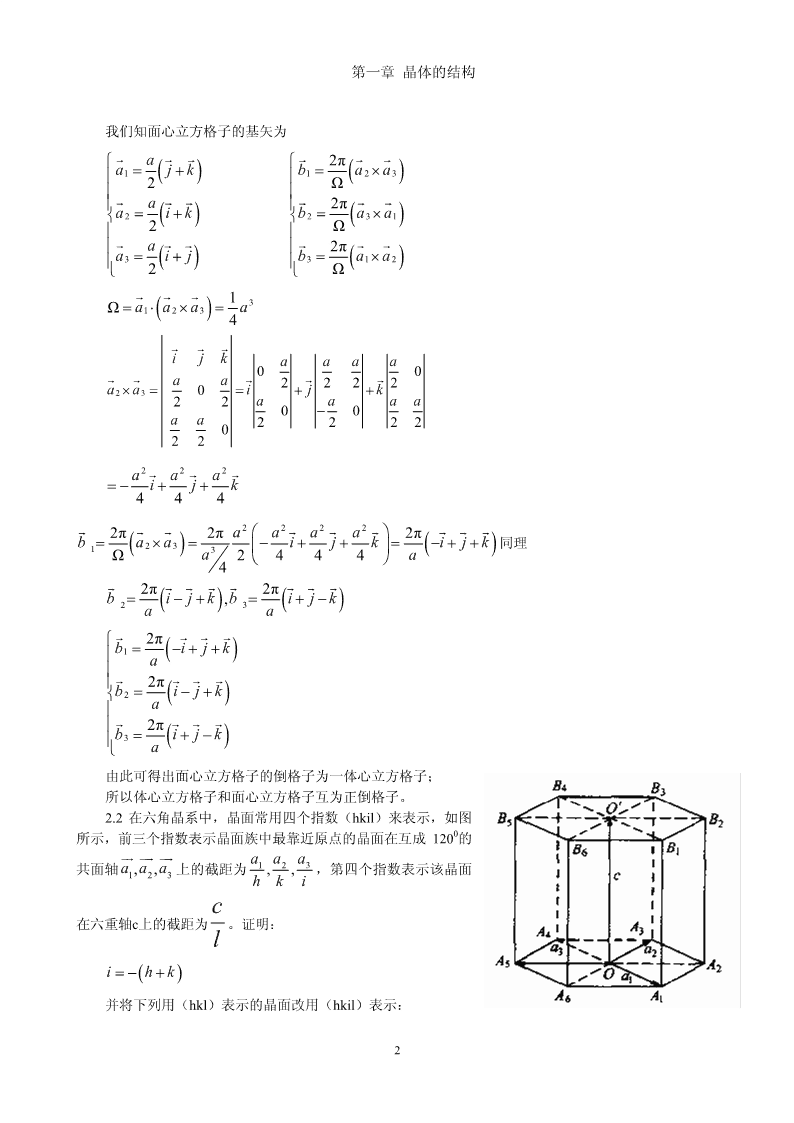1 第一章晶体的结构我们知面心立方格子的基矢为⎧GGaG⎧GG2πG⎪aj1=+()k⎪ba12=×()a32Ω⎪⎪⎪GGaG⎪GG2πG⎨ai2=+()k⎨ba23=×()a1⎪2⎪Ω⎪GGaG⎪GG2πG⎪ai3=+()j⎪ba31=×()a2⎩2⎩ΩGGG13Ω=⋅×=aaa123()a4GGGijkaaaa00GGaaG2222GGaa23×=0=i+j+k22aaaa00−aa2222022aaa222GGG=−ij++k444GG2πG2πaaaa2222⎛⎞GGGG2πGGba1=×()23a=−3⎜⎟ijki++=()−+j+k同理Ωa2444⎝⎠a4GG2πGGGG2πGGbi23=−()j+=+k,bi()j−kaa⎧GG2πGG⎪bi1=−()+j+ka⎪⎪GG2πGG⎨bi2=−()j+k⎪a⎪GG2πGG⎪bi3=+()j−k⎩a由此可得出面心立方格子的倒格子为一体心立方格子；所以体心立方格子和面心立方格子互为正倒格子。2.2在六角晶系中，晶面常用四个指数（hkil）来表示，如图0所示，前三个指数表示晶面族中最靠近原点的晶面在互成120的JGJJGJJGaaa123共面轴aaa,,上的截距为,,，第四个指数表示该晶面123hkic在六重轴c上的截距为。证明：lih=−()+k并将下列用（hkl）表示的晶面改用（hkil）表示：2 第一章晶体的结构()001,133,110,323,100,010,213.()()()()()()证明：林鸿生1.1.4王矜奉1.2.3如图所示，某一晶面MN与六角形平面基矢JGJJGJJGJJGaaa,,轴上的截距123a3aaaOA==nOB,,−=nOCn,hkioDD且∠=AOB∠=∠=COB60,AOC120AJJG有++AOB()C()面积+=OB面积+AOC(面积)Ca2JGB即a1111OAOB•∠+•∠=•∠sinAOBOCOBsinCOBOAOCsinAOC222aaaDD代入OA==nOB,,−=nOCn,和∠=AOB∠=∠=COB60,AOC120，有hki111aa00aaaa0iinnn(−+−=)sin60ii()sin60ii()sin120222hkikhi111得−−=，两边同乘（hki）并移项得hkikhiih=−+()k得证（2）由上可知，h，k，i不是独立的，()001,133,110,323,100,010,213.()()()()()()中各i等于ih=−()(+k=−+00)=0,i=2，i=0，i=1，i=1i=1，i=3即得111234567()()001→→→→0001,133()(1323,110)()(1100,323)()(3213)()100→→→()1010,010()(0110,213)()(2133.)1.3如将等体积的硬球堆成下列结构，求证能占据的最大体积与总体积之比为：π3π2π（1）简单立方；（2）体心立方；（3）面心立方6862π3π（4）六角密积；（5）金刚石616解：设N为一个晶胞中的刚性原子数，R表示刚性原子的球半径，V表示晶胞体积，立方晶格的边长为a，则致密度为：3 第一章晶体的结构43NR⋅π3α=V（1）在简立方的结晶学原胞中，设原子半径为R，则原胞的晶体学常数a=2R，则简立方的致密度（即球可能占据的最大体积与总体积之比）为：43431⋅πR1⋅πR33πα===33a2(R)6（2）在体心立方的结晶学原胞中，设原子半径为R，则原胞的晶体学常数a=4R/3，则体心立方的致密度为：43432⋅πR2⋅πR333πα===33a4(R/)38（3）在面心立方的结晶学原胞中，设原子半径为R，则原胞的晶体学常数a=22R，则面心立方的致密度为：43434⋅πR2⋅πR332πα===33a2(2R)6（4）在六角密积的结晶学原胞中，设原子半径为R，则原胞的晶体学常数a=2R，c=2(6)3/a=4(6)3/R，则六角密积的致密度为：43436⋅πR6⋅πR332πα===223a2(3R)66⋅c6⋅4(6)3/R44（5）在金刚石的结晶学原胞中，设原子半径为R，则原胞的晶体学常数a=/8()3R，则金刚石的致密度为：43438⋅πR8⋅πR333πα===33316a/8()3RJGJJGJJG1.4设某一晶面族的面间距为d，三个基矢aaa,,的末端1234 第一章晶体的结构分别落在离原点距离为hdhdhd,,,的晶面上，试用反证法证明：hhh,,是互质的。123123解：参考王矜奉1.2.4设该晶面的单位法向矢量为n，由已知条件可得GGGanhdanhda⋅=,,⋅⋅=nhd,112233假定hhh,,不是互质的数，则有公约数p，且p>1；设kkk,,为互质的三个数，满足123123hhh123===pkkk123则有GGGankpdan⋅=,,⋅kpdankpd⋅=,112233今取离原点最近的晶面上的一个格点，该格点的位置矢量为GJGJJGJJGrlalala=++112233由于lll,,必定为整数而且123GGJGGJJGGJJGGrndlanlanlan⋅==⋅+⋅+⋅112233得dlkpdlkpdlkpd=++1122331即lklk++=lk112233p因为上式左边是整数，而右边是分数，显然是不成立的。要式成立，必须满足p=1。而此时hhh,,是互123质的。1.5证明：在立方晶系中，面指数为()hkl和(hkl)的两个晶面之间的夹角满足111223hh++kkll121212cosθ=1212222222()hkl111++i(hkl22++2)解：三个晶轴相互垂直且等于晶格常数a，则晶胞基矢为JGGJJGGJJGGaa===iaa,,jaak,123其倒格子基矢为JG22πGJJGGππJGG2bi===,,bibi123aaa倒格子矢量为JJGGGG2πGGGKhh′=++=bk123blb()hi++kjlka5 第一章晶体的结构代表晶面族(hkl)的法线方向。JJGG2πGG晶面族()hkl111的法线方向对应倒格矢Kh1=+()111ikj+lkaJJGG2πGG晶面族()hkl的法线方向对应倒格矢Kh2=+()ikj+lk223222a设两法线之间的夹角满足JJGJJGKK12ii=KKcosγ12JJGJJG22πGGGπGGG()hikjlk++i()hikjlk++KK12iaa111222cosγ==KK12i2222ππππGGGGGGGGGGGG()hikjlk++iii()hikjlk++()hikjlk++()hikjlk++111111222222aaaahh++kkll121212cosγ=1212222222()hkl111++i()hkl222++1.6有一晶格，每一晶格上有一个原子，基矢（以nm为单位）分别为a=3i，a=3j，a=(5.1i+j+k)。123试求：（1）此晶体属于什么晶系，属于哪种类型的布喇菲格子？（2）原胞的体积和晶胞的体积各等于多少？（3）该晶体的倒格子基矢；（4）密勒指数为（121）晶面族的面间距；JJGa（5）原子最密集的晶面族的密勒指数是多少？2JJGa（6）[111]与[111]晶列之间的夹角余弦为多少？3解：参考徐至中1-5，中南大学1.17JGaJGJJGJJG1（1）按基矢aa,,a在空间作重复平移，就可得到它的布喇菲格子，因为此晶体是简单格子，因此123晶体中原子位置可以认为与格点重合。由右图可见，它是体心立方布喇菲格子，属于立方晶系。JGJJGJJGGGGGG（2）原胞体积Ω=a•()aaij×=•3⎡⎤3×1.5(ijk++)=13.510×−27m3123⎣⎦GGGGGG−273晶胞体积Vaa=•×(aijk)()=•×=×3332710mV因为Ω=，知该晶体属于立方晶系；2参考王矜奉1.2.6我们可以构造新的矢量JGGG3GGGaca=−=−++()ijk126 第一章晶体的结构JJGGG3GGGacbijk=−=()−+22JJGGGG3GGGaabcijk=+−=+−()32JGJJGJJGJGJJGJJGaaa,,对应体心立方结构.aaa,,满足选作基矢的充分条件.可见基矢为,a=3i，1231231a=3j，a=(5.1i+j+k),的晶体为体心立方结构.23（3）由倒格子基矢的定义可知：⎧2π[a2×a3]2π⋅(5.4i−k)2πb===(i−k)⎪1a⋅[a×a]135.3⎪123⎪2π[a3×a1]2π⋅(5.4j−k)2π⎨b2===(j−k)a⋅[a×a]135.3⎪123⎪2π[a1×a2]2π⋅9k2πb===k⎪3a⋅[a×a]135.5.1⎩123（4）根据倒格矢的性质，可求得密勒指数为（121）晶面族的面间距为2π2πd==121K1⋅b+2b−b1211232π330===2π3010(i+2j−5k3以上是参考中南大学的，有些不妥，因为密勒指数是对晶胞基矢定义的，虽然《固体物理学》式（1-18）也适合计算相应面间距，但此时的倒格子基矢也应是对应的。从体心立方晶格的特点，结合图，易知JJGG⎧∗2πGG⎪ai=⎧ai=3⎪JJG3⎪⎪GG⎪∗2πG⎨bj=3，倒格基矢⎨bj=⎪G⎪3⎪⎩ck=3⎪JJG∗2πG⎪ck=⎩322ππ2π6d==JJGJJGJJG==121121∗∗∗242πππGGG2K121⋅+−⋅abcijk+−333（5）由于面密度β=ρd，其中d是面间距，ρ是体密度。对布喇菲格子，ρ等于常数。因此，我们可设原子最密集的晶面族的密勒指数为(hhh)，则该晶面族的面间距d应为最大值，所以有123h1h2h37 第一章晶体的结构2π2πd==h1h2h3Khb+hb+hbh1h2h31122332π3===max2πhi+hj+2(h−h−h)k12312[hi+hj+2(h−h−h)k]123123由此可知，对面指数为（100）、（010）、（101）、（011）和（111）有最大面间距/32，因而这些面即为原子排列最紧密的晶面族。（6）[111]与[111]晶列之间的夹角余弦为R⋅R(a+a+a)⋅(a+a−a)111111123123α=arccos=R⋅Ra1+a2+a3⋅a1+a2−a31111115.4(i+5.4j+5.1k)⋅5.1(i+5.1j−5.1k)D=arccos=48.535.4i+5.4j+5.1k⋅5.1i+5.1j−5.1k1.71.8六角晶胞的基矢为a3a=i+aj122a3a=−i+aj222a=ck3求倒格子基矢。解：参考王矜奉1.2.8，中南大学1.2.13aa3332Ω=⋅aaa[]×=(i+aaj)⋅−[(i+jk)×(c)]=ac12322222根据倒格子基矢的定义可知：a33acac()−+iacj×(k)i+jaa23×22222π2b=2π=2π=2π＝(i+j)1ΩΩ32a3ac28 第一章晶体的结构a33acac()(caki×−+j)−i+jaa31×22222π2b=2π=2π=2π＝(−i+j)2ΩΩ32a3ac2aa3332()i+×aaj(−i+j)akaa12×222222πb=2π=2π=2π=k3Ωaaa123⋅×[]32cac21.9矢量a，，构成正交系。证明晶面族bc(hkl)的面间距为1d=hklh2k2l2()+()+()abc解：由题意可知该简单正交系的物理学原胞的基矢为：⎧a1=ai⎪⎨a2=bj⎪a=ck⎩3由此可求得其倒格子基矢为：⎧2π[a2×a3]2π2πb==(bci)=i⎪1a⋅[a×a]abca⎪123⎪2π[a3×a1]2π2π⎨b2==(acj)=ja⋅[a×a]abcb⎪123⎪2π[a1×a2]2π2πb==(abk)=k⎪3a⋅[a×a]abcc⎩123根据倒格子矢量的性质有：2π2πd==hklKhb+kb+lbhkl1232π1==2πhi+2πkj+2πlkh2k2l2()+()+()abcabc1.10证明：晶面()hhh、()hhh′′′和(hhh′′′′′′)属于同一晶带的条件是123123123hhh123hhh′′′=0123hhh′′′′′′1239 第一章晶体的结构证明：参考王矜奉1.2.12，徐至中1-7相交于同一直线的二个或多个晶面就构成一个晶带，JJGJGJJGJG晶面(hhh)相应倒格矢可以写为Kh=++bhbhb123h112233假定三晶面属于同一晶带[uvw]（交线为晶带轴，此即为晶带轴的方向指数），带轴的方向矢量为JGJGJJGJJGRuavawa=++122因为倒格矢与晶面垂直，因而也必须与带轴垂直，即满足JJGJGJGJJGJGJGJJGJJGKRhbhbhbuh•=()11+22+33•(av1++aw2a2)=0JGJGJJGJJGJJGJGJGJJG因为ababab•=•=•=2,πab•=≠0(ij)112233ij得huhvhw++=0123同理有huhvhw′′′++=0123huhvhw′′++=′′′′0123[uvw]有解的条件即为hhh123hhh′′′=0123hhh′′′′′′123即证。1.11证明：一个晶体不可能有5重旋转对称轴。参考王矜奉1.2.16，教材1.7.3五边形沿竖直轴每旋转π/5（72º）恢复原状，但它不能重复排列充满一个平面而不出现空隙。因此晶体的旋转对称轴中不存在五次轴。证法2：如图所示，AB是同一晶列上O格点的两个最近邻格点．如果绕通过O点并垂直于纸面的转轴顺时针旋转θ角．则A格点转列入A′点．若此时晶格自身重合，A′点处原来必定有一格点．如果再绕通过O点的转轴逆时针旋转θ角，则晶格又恢复到末转动时的状态．但逆时针旋转θ角，B格点转到B′处，说明B′处原来必有一格点．可以把格点看成分布在一族相互平行的晶列上，由图可知，A′′B晶列与AB晶列平行．平行的晶列具有相同的周期，若设该周期为a则有A′′Ba==2cosθma其中m为整数，由余弦的取值范围可得cosθ=≤m/2110 第一章晶体的结构于是可得π3πm==0,θ,;22π245πππm==1,θ,,,;3333m==2,θππ,2;因为逆时针旋转3/2,4/3,5/3πππ分别等于顺时针旋转π/2,2/3,/3ππ，所以晶格对称转动所允许的独立转角为2112,,,,,πππππ323上面的转角可以统一写成2π,n=1,2,3,4,6n称n为转轴的度数，由此可知，晶格的周期性不允许有5度旋转对称轴。1.12试求面心立方和体心立方晶格中粒子密度最大的晶面。解：参考王矜奉1.2.10.11设布赖菲格子的体密度（单位格点数）为ρ，在某一晶面族中，取面间距为d的两相邻晶面为底面，（底面积取为1单位面积）做一个圆柱体，则该圆柱体内的格点数等于ρ••=()dd1ρ这些格点分布在上下底面上，但属于该圆柱体的只有一个底面，故晶面的面密度D=ρd。因为ρ是常数，所以的越大，面密度D也越大。21.面心立方133设面心立方的晶格常数为a，则其晶胞的体积为a，晶胞中含有四个格点，4因此面心立方结构体密度为ρ=3a选取面心晶体结构的固体物理学原胞，其基矢为→2π→→→→a→→b=(−i+j+k)a=(j+k)11a2→a→→→2π→→→a=(k+i)其倒格子基矢为b=(i−j+k)222a→a→→a=(i+j)→2π→→→3b=(i+j−k)23a根据《固体物理学》式（1-14）和（1-18）JJGGGG与晶面族()hhh正交的倒格子矢量为Kh=++(bh12bhb3)123h123则晶面族(hhh)的面间距为1232πad==JJGhhh132222Kh()−++hhh123+−+()hhh123++−(hhh123)显然，上式中分母越小，d越大，故面指数最简单的晶面族(111)面间距最大，面密度最大。11 第一章晶体的结构2.体心立方3设体心立方的晶格常数为a，则其晶胞的体积为a，晶胞中含有二个格点，因此面心立方结构体密度为2ρ=3a选取体心晶体结构的固体物理学原胞，其基矢为⎧GGaGG⎧G2πGG⎪ai1=−+−()jk⎪b1=()j+k2a⎪⎪⎪GGaGG⎪G2πGG⎨ai2=−()j+k其倒格子基矢为⎨bi2=()+k⎪2⎪a⎪GGaGG⎪G2πGG⎪ai3=+()j−k⎪bi3=()+j⎩2⎩aJJGGGG与晶面族()hhh正交的倒格子矢量为Kh=++(bh12bhb3)123h123则晶面族(hhh)的面间距为1232πad==JJGhhh132222Kh()hh23+++++()hh13(hh12)显然，上式中分母越小，d越大，故面指数最简单的晶面族()001,010,100,011,101,110()()()()()其面间距最大，面密度最大JGJGJGJG1.13电位移矢量D与外电场E的关系为D=εE，式中，ε为介电常数张量。试用根据晶体的对称性证明，⎛⎞ε//00⎜⎟对于简单六角晶体，有00ε，⎜⎟⊥⎜⎟00ε⎝⎠⊥解：参考王矜奉1.2.17晶体宏观对称性是用对称操作来描述的，即通过旋转。反演等，晶体自身重合，这个几何变换都是正交变换（保持两点距离不变的变换），所对应的变换矩阵为⎛⎞A11AA1213⎜⎟−1−1A=AAA，且有aa=，是转置矩阵，α是逆矩阵。⎜⎟212223⎜⎟AAA⎝⎠313233⎛⎞ε11εε1213⎜⎟晶体介电常数是二阶张量，表示为ε=εεε。⎜⎟212223⎜⎟εεε⎝⎠313233在坐标变换下，二阶张量的变换规律为ε′=aaε对称操作后，晶体还原，有ε′=ε。12 第一章晶体的结构以六角晶系主轴为c轴，a，a轴如图：12有一个过a轴和c轴的镜面，所以1⎛⎞εεε111213⎛100⎞⎛⎞εεε111213⎛100⎞⎜⎟⎜⎟⎜⎟⎜⎟εεε=−010εεε010−⎜⎟212223⎜⎟⎜⎟212223⎜⎟⎜⎟εεε⎜001⎟⎜⎟εεε⎜001⎟⎝⎠313233⎝⎠⎝⎠313233⎝⎠⎛⎞εεε−111213⎜⎟=−εεε−⎜⎟212223⎝⎠⎜⎟εεε−313233JGaJG1JJG得到ε12===0,εε130,210,a1a2⎛⎞ε11εε1213⎛ε110ε13⎞⎜⎟⎜⎟所以εεε=00ε⎜⎟212223⎜22⎟⎜⎟εεε⎜ε0ε⎟⎝⎠313233⎝3133⎠六角晶系有一个6度轴，所以⎛ππ⎞⎛ππ⎞⎜cos−sin0⎟⎜cossin0⎟⎛ε110ε13⎞⎜66⎟⎛ε110ε13⎞⎜66⎟⎜0ε0⎟⎟=⎜sinπcosπ0⎟⎜0ε0⎟⎜−sinπcosπ0⎟⎜22⎜22⎟⎜⎟⎜66⎟⎜66⎟⎝ε310ε33⎠⎜001⎟⎜⎝ε310ε33⎟⎠⎜001⎟⎜⎟⎜⎟⎝⎠⎝⎠⎛⎜131⎞⎟⎛ππ⎞ε11−ε22ε13⎜cossin0⎟⎜222⎟⎜66⎟⎜313⎟⎜ππ⎟=⎜ε11ε22ε13⎟−sincos0222⎜66⎟⎜⎟ε0ε⎜001⎟⎜3133⎟⎜⎟⎜⎟⎝⎠⎝⎠⎛13331⎞⎜ε+εε−εε⎟1122112213⎜44442⎟⎜33313⎟=⎜ε11−ε22ε11+ε22ε13⎟44442⎜⎟⎜13⎟εε1⎜231231⎟⎝⎠⎛⎞εε110013⎛⎞ε110⎛ε⊥00⎞⎜⎟⎜⎟⎜⎟所以00εεε==0000⎜⎟22⎜⎟11⎜⊥⎟⎜⎟ε00εε⎜⎟00⎜0ε⎟⎝⎠3133⎝⎠33⎝//⎠1.14证明：三角布赖菲格子的倒格子仍为三角布赖菲格子，并且倒格矢基矢间的夹角和基矢长度b分别满足13 第一章晶体的结构∗cosθcosθ=−1cos−θ1b=1a()12coscos+θθ∗2式中，a和θ分别为正格矢的长度和基矢间的夹角。Z证明：参考王矜奉1.2.18，陈金富8.16对于三角晶系，其三个基矢量大小相等，而且它们相互间的夹角也相等，即JGJJGJJGJJGaaaa===，α===βγθ123a3根据正倒格矢的性质θYJGJJGJJGaθ1G2π()aa×2X232sπθainθJJGbb1==≡aΩΩ2JJGJGG2π()aa×2sπθa2in31bb2==≡ΩΩJGJJGG2π()aa×2sπθa2in12bb3==≡ΩΩqJGJJGqJJGJGqJGJG设()bb12,=θ12，()bb23,=θ23，()bb31,=θ31，则有JGJJGJGJJG4sπθ24ain22bbii==bbcosθbcosθθ=cos12121212212ΩJJGJJGJJGJGJGJJGJ22ππ()aa23××()aa314π2JGJJGJJGJGbb12ii==2()aaaa2×3i()31×ΩΩΩ44ππ22JJGJJGJJGJGJJGJJGJGJJGJGJJG=×⎡⎤⎡()aaaa×ii=()aaaa()i−()aaai2⎤ΩΩ22⎣⎦⎣2331231312⎦244πa2=−()cosθθcos2Ω比较两式得2()cosθθ−coscos(1cos)θ−θθcoscosθ==−=−1222sinθ1cos−+θθ(1cos类似可以证明cosθcosθcosθ=−，cosθ=−2331(1cos+θ(1cos+θ∗得θ===θθθ12233114 第一章晶体的结构又因为JGJJGJGbbbb===123所以三角晶系的倒格子也属于三角晶系。且∗cosθcosθ=−(1cos+θ222sπθaain2sπθin2πb===Ωaa3sinθ12coscos++θθ∗12coscosθθ∗式中Ω通过如下计算出，如图，JJGJGJJGJJGJGJJGJJGJJGJGJJG2aaaaaaaa312ii()+=+=3132i2cosθ=aaa312i(+)cos/2()πϕ−JGJJG而aaa+=21cos()+θ，因此122cosθcos()πϕϕ/2−=sin=21cos()+θ224cosθ∗cosϕ=−1sinϕθ=−1=+12coscosθ21cos()+θJJGJGJJG33∗Ω=aaaa312i()×=sincosθϕθθ=asin12coscos+θ如图所示JGGai=a1JJGGGai=+acosθjasinθ2JJGGGGai=+acosαjacosβ+kacosγ3JGJJGGGGGaa•ia•++(iacosαβγjacoskacos)13cosθ===cosα22aaJJGJJGGGGGGaa•()iacosθθαβγ+•++jasin(iacosjacoskacos)23cosθ===coscosθαθβ+sincos22aacos(1cos)θ−θ得cosβ=sinθ22222cosθ(1cos)−θcosγα=−1cos−cosβθ=−1cos−2sinθ因为JG2πJJGJJGba=×()a123Ω15 第一章晶体的结构JJGJ2πJGJGba=×()a231ΩJG2πJGJJGba=×()a312ΩGGG所以bbb123,,分别垂直于正点阵初始晶胞的平面，且有相同的长度，bbbb===，根据对称性，123GGG∗bb12,,b3彼此间应有相同的夹角，设夹角为θ，22πJGJJGπ2ba=×aa=sinθ12ΩΩJGJJGJJGGGGGGG3Ω=•aaai(×)=•ai⎡⎤()acosθ+jasinθαβγθ×iacos+jacos+kacos=asincosγ123⎣⎦222cosθ(1cos)−θcosγθ=−1cos−2sinθ222πJGJJGππ21ba=×aa=sinθ==12ΩΩacosγJGJJG2JJGJJGJJGJG∗bb12•12⎛⎞πcosθ==⎜⎟(aaaa×)(•×)，22331bbb•Ω⎝⎠12JGJGJGJGJGJGJGJGJGJGJGJGJGJGJGJGJGJG因为ABCBCACAB•×=•×=•×()()(),ABCCABABC×(×=•−•)()()JGJJGbb•1JJGJJGJJGJGJGJJGcos2θ−cosθθcos∗122得cosθ==(aaaaaaa•)(••)(−•=)=−4223311232bba•+sinθsinθθ1cos12JGJG2JJGJJGJGJJG∗bb13•12⎛⎞πcosθ==⎜⎟(aaaa×)(•×)22312bbb•Ω⎝⎠131JGJJGJGJJGJGJJGcos2θ−cosθθcos2=•()aaaaaaa•()•−()•==−4213121322asinθsinθθ1cos+222222cosθ(1cos)−−θθcos(1cos)θcosγθ=−1cos−=−1cosθ−22sinθθ1cos−22cosθθθθ(1cos)cos++−(1cos)=−11cos+θ212cosθ∗=−1(=+1cosθθcos)21cos+θ222πJGJJGπππ2121ba=×aa=sinθ==121ΩΩaacosγ∗(1coscos+θθ)2JGJJGJJGJJGJJGJJG解法（二）设aa=a，aa=a，aa=a；11022033016 第一章晶体的结构JGJJGa•aJJGJJGJJGJJGJJGJJG12有cosθ==aaa•=•a=aa•102020103010aa12θθθθYAAD==OAsinasin,OD==OAcosacos,2222πθZCD==2cADosa3sinO62DX22θ222θC222aacos+−3asinOD+−OCCD22cosθcosα=∠=cosCOD==2OD•OC2ca2osθcosθ22B21cos2cos+−θθsinα=1cos+θJGGθGθJJGGθGθJJGGGai=+acosjasin，ai=acos−jasin，ai=+acosαkasinα1232222JG22ππJJGJJGGGGa2θθθba=×()(a=−isinsincα−jossinsαα+kincos)123ΩΩ222JJGJ22ππJGJGa2GθθθGGba=×()a=−(isinsincα+jossinsαα+kincos)231ΩΩ222JG22ππJGJJGGaa22θθπGba=(×a)=−sincosk=−sinθk312ΩΩ22Ω24242222⎡⎤θθθ2222πaaπ⎡2⎛222θ⎞⎤bb==sinsinα+cossinαα+sincos=sinα+⎜⎟cosα−coscosα12⎢⎥22⎢⎥⎣⎦222ΩΩ⎣⎝2⎠⎦2⎡⎤⎛⎞πθ24aa⎢⎥⎜⎟cosθπ2422=−×⎢⎥1cos⎜⎟=sinθ22θΩΩ⎢⎥2⎜⎟cos⎢⎥⎣⎦⎝⎠22422πab=sinθ32Ωbbb==12317 第一章晶体的结构⎡⎤ππaa22GGGG⎡2θθθ⎤JGJJG⎢⎥−•sinθkijk⎢(−++sinsinααcossinsincos)α⎥∗bb32•⎣⎦ΩΩ⎣222⎦cosθ==124bb32πa2sinθ2Ωθθsinsinθαθcossinsin22cosθθcos=−=−×=2θθθθθsin1cos+2sinsinθcoscos222⎡⎤ππaa22GGGG⎡2θθθ⎤JGJG⎢⎥−•sinθkijk⎢(−−+sinsinααcossinsincos)α⎥∗bb31•⎣⎦ΩΩ⎣222⎦cosθ==224bb31πa2sinθ2Ωθθsinsinθαθcossinsin22cosθθcos=−=−×=2θθθθθsin1cos+2sinsinθcoscos222JGJJG∗bb12•cosθ=2bb1222πθaa2GGGθθπθ2GGGθθ(−−+•ijksinsinαcossinααsincos)(−++ijksinsinααcossinsincos)αΩΩ222222=24πa2sinθ2Ω⎡⎤−++sin22θθθsinαααcos22sinsin22coscos(1cosθα−+22)sinθcos2α⎢⎥⎣⎦2222==22sinθθsin213coscos−θθcosθ+×22θcos2=2sinθ2212cosθθ2cos∗2sinα=−1cosαθ=−1=−1=+(12coscosθ)2θ1cos+θcos2242ππaa2sinθb==sinθ3Ω2⎡⎤⎛⎞GGGGθθθθ⎛⎞GG⎢⎥⎜⎟iacos+×−•+jasin⎜⎟iacosjasin()iacosαkasinα⎣⎦⎝⎠2222⎝⎠2−πθasin2π12π1===θθα13aasin∗2saincossinα(12coscos+θθ)22218 第一章晶体的结构JG22ππJJGJJGJa2JGJJGJJGJ22ππJGJGa2JJGJJGba=×()(a=a×a),ba=×()(a=a×a),12320302313010ΩΩΩΩJG22ππJGJJGJa2JGJJGba=×()(a=a×a)3121020ΩΩ⎡⎤22ππaa22JJGJJG⎡⎤JJGJJGJGJJG⎢⎥()()aaו⎢⎥aa×JJGJJGJJGJJG10203010∗bb3•×2⎣⎦ΩΩ⎣⎦()aa1020•(aa30×10)cosθ===bb22ππaa22JJGJJGJJGJJGsin2θ32()()aa××aa10203010ΩΩJJGJJGJJGJJG()aaaaו×()10203010=2sinθ1.15用波长为0.15405nm的X射线投射到钽的粉末上，得到前面几条衍射谱线的布喇格角θ如下序号12345θ（°）19.611°28.136°35.156°41.156°47.769°已知钽为体心立方结构，试求：（1）各谱线对应的衍射晶面族的面指数；（2）上述各晶面族的面间距；（3）利用上两项结果计算晶格常数a。解：参考王矜奉1.2.20，徐至中1-18，韦丹3.25（1）在用X射线衍射方法确定晶体结构时，采用晶胞而不是固体物理学原胞。因此面指数用密勒指数表示（h，k，l）,对于体心立方结构2πadhkl==JJG222Khhkl++根据布喇格公式2sdninθ=λhklnλλ222222sinθ==nh++nknl22dahklsinθ:sinθθθθ:sin:sin:sin=1:1.405:1.716:1.961:2.20612345222222222222222hklhklhklhklhkl++::::++++++++111222333444555=1:1.405:1.716:1.961:2.206对于体心立方晶系，衍射面指数的和nhkl(++)为偶数出现衍射极大。因此，对衍射角由小到大的晶面族是(110),(200),(121),(220),(310)，而19 第一章晶体的结构222222222222222110:200:121:220:310++++++++++=1:1.414:1.732:2:2.236在误差允许范围内很好符合。因而，对应的晶面族是(110),(200),(121),(220),(310)nnλλ0.15405m（2）dn====0.22949mhklD2sinθθ2sin2sin19.611×λ0.15405nmdn===0.22949m110D2sinθ2sin19.611×λ0.15405nmdn===0.16334m200D2sinθ2sin28.136×λ0.15405nmdn===0.13377m121D2sinθ2sin35.156×λ0.15405nmdn===0.11704m220D2sinθ2sin41.156×λ0.15405nmdn===0.10403m310D2sinθ2sin47.769×22222（3）adhkl=++=×0.229491+1+0=0.322nmhkl1.16铁在不同的温度下可能是体心立方结构（α-Fe）或面心结构（γ-Fe）。用x射线束照射铁晶体，当温度为20℃时，得到最初的三个衍射角为8°12′，11°38′，14°18′；当温度为1000℃时，衍射角为7°55′，9°9′，12°59′。试求：（1）在20℃和1000℃时，铁各属于什么结构？-3（2）若在20℃时，铁的密度为7.86g·cm,求其晶格常数和X射线的波长。解参考林鸿生1.1.21，王矜奉1.2.21（1）在X射线衍射方法决定晶体结构时，常采用晶胞而不是固体物理学原胞。因此决定散射波强度在空间分布时，先是根据晶体所属的晶体，按照晶系的布喇格格子，由布喇格反射条件决定衍射加强方向；其次在这些衍射加强方向上的散射波强度则由几何结构因子及原子散射因子决定，所以在晶体X射线衍射实验中，要在衍射角θ方向上观察到衍射斑点，首先必须满足布喇格反射定律2sdninθ=λhkl铁金属属立方结构，如图所示，这是简立方格子晶胞，正格矢基GGGGGG矢为aa===ibajca,,k,其倒格子基矢为JJGJGJGGGJJG∗∗∗22πππ2ai===,,biciaaa倒格子矢量为JJGJJGJJGJJGGGG∗∗∗2πKhhkl=++=akblc()hi++kjlka代表晶面族(hhh)的法线方向，其晶面族的间距为12320 第一章晶体的结构2πadhkl==JJG222Khklhkl++置换布喇格公式中d，得到hhh123nλλ222222222222sinθ==nh+nk+∝++nlnhnknl22dahkl表明衍射角正弦与衍射面指数的方均值成正比。上面的推导可以看出，对应三个最小衍射角要求三个最小最简单的晶面指数(hkl)；但晶格面指数(hkl)的选择还要考虑到，尽管这个选择满足X射线衍射理论的布喇格反射公式，在衍射角θ方向上衍射光是加强的，但由于晶胞内不同坐标上原子的散射波之间干涉也会相互抵消，在这些方向上的衍射强度仍可能为零，而看不到衍射斑点，这就说必须满足晶体的几何结构因子，立方晶系有体心和面心结构。==inh2π(ukjjj++vlw)⎡⎤+inπ()hnknl++Ffhkl∑je1f⎣⎦ej222*⎡⎤tt⎡⎤I∝=⋅=FhklhFklFhkl⎢⎥∑∑ficos2πnhu()jjj+++kvlw⎢fisin2πnhu(jjj++kvlw)⎥⎣⎦jj==11⎣⎦首先计算体心结构的结构因子，这时每个晶胞中有两个原子，其坐标(uvw,,)为jjj⎛⎞111()0,0,0和⎜⎟,,⎝⎠222==inh2π(ukjjj++vlw)⎡⎤+inhnknlπ()++则Ffhkl∑je1f⎣⎦ej2*2222I∝=⋅=+FhklFFhklhklf⎡⎤⎣⎦1cosππnhkl()+++fsin()hkl++因此当衍射面指数之和nhkl()++为奇数时，反射消失。只有当nhkl(++)为偶数时，才会见到衍射斑点。取n=1，则对应最小三个衍射角的最简单的面指数依次为(110)，(200)，()211，这三个衍射角的衍射面指数的方均根之比为2222222221++10:2++00:2++=111:1.41421:1.73205现在把这一数据与铁在20℃和1000℃时实验测得的最小三个衍射角的正弦值之比相比较，来确定铁在20℃和1000℃下是否属于体心立方结构。实验测得当温度为20℃时，得到最初的三个衍射角正弦值之比DDDsin812:sin1138:sin1418′′′==0.142628:0.201591:0.2469991:1.41340:1.73177实验测得当温度为1000℃时，得到最初的三个衍射角正弦值之比DDDsin755:sin99:sin1259′′′==0.137733:0.159020:0.2246681:1.15455:1.6311821 第一章晶体的结构比较看出，体心立方结构情况下三个衍射面指数的方均根之比与铁在实验测得当温度为20℃时，得到最初的三个衍射角正弦值之比非常接近，所以铁在20℃下是否属于体心立方结构。其次，在面心结构中，这时每个晶胞中有四个原子，其坐标(uvw,,)为jjj⎛⎞11⎛⎞11⎛⎞11()0,0,0，⎜⎟,,0，⎜⎟,0,和⎜⎟0,,⎝⎠22⎝⎠22⎝⎠22==inh2π(ukjjj++vlw)⎡⎤+inhnkπ()++einπ()knl++inhnlπ()+则Ffhkl∑je1f⎢⎥⎣⎦eej2*22I∝FFhkl=hkl⋅Ffhkl=⎡⎣1cos2++πn()hk++cos2πn(hl)+cos2πn()k+l⎤⎦2222++fh⎡⎤⎣⎦sin()()()kh+sin+lk+sin+l显然，当nhnknl,,奇偶相异时，I=0，衍射消失，但当nhnknl,,全为奇数或全为偶数时，衍射极大，取n=1，则对应最小三个衍射角的最简单的面指数依次为(111)，(200)，(220)，这三个衍射角的衍射面指数的方均根之比为2222222221++11:2++00:2++=201:1.15470:1.63299比较看出，面心立方结构情况下三个衍射面指数的方均根之比与铁在实验测得当温度为1000℃时，得到最初的三个衍射角正弦值之比非常接近，所以铁在1000℃下是否属于面心立方结构。（2）设铁原子质量为m，晶格常数为a，铁在20℃时为体心立方结构，一个晶胞有2个铁原子，则铁的质量密度2mρ=，3a于是铁的结构常数a等于1⎛⎞2m3−3a=⎜⎟，1mol铁质量为55.84710×kg,一个铁原子的质量⎝⎠ρ−355.847×10mk=g，236.0210×111⎛⎞2mM3⎛⎞23⎛⎞255.84710××−33an===⎜⎟⎜⎟⎜⎟=0.2868m23⎝⎠ρρ⎝⎠N⎝⎠78606.0210××A1.17证明：在晶体的X射线衍射中：（1）如果X射线的波长改变了Δλ，反射线束将偏转一个角度ΔλΔ=θtanθλ式中θ为布喇格角；（2）当晶体发生体膨胀时，反射线束将偏转一个角度3βΔ=−θtanθ，Δ=−θtanθβ322 第一章晶体的结构式中，β是晶体的体胀系数。证明：（1）布喇格反射定律2sdninθ=λhkl两边求导得2cddosθθλ=ndhklddλndλλ2sdinθdΔλhkldθ===tanθ，即Δ=θtanθ2cddosθθ2cosλλhklhkl（2）布喇格反射定律2sdninθ=λhklnλλ222222sinθ==nh++nhnh12322dahkl两边求导λ222222cosθθdn=−h+nk+nlda22aλ2222221dadnθ=−h+nk+nl2caaosθdVda设线膨胀系数为α，有β===33α，Va1daβdθ=−sinθ=−tanθcosθa3β即Δ=−θtanθ。3证法（二）对2sdninθ=λ两边求导hhh1232sinθδdd+=2cosθδθnδλ=0hhh123hhh1232sinθδδdd1δβVhhh123hhh123得δθθ=−=−tan=−tanθ=−tanθ2cddVosθ33hhh123hhh12323 第一章晶体的结构温度升高时,由于热膨胀,面间距逐渐变大.由布拉格反射公式可知,对应同一级衍射,当X光波长不变时,面间距逐渐变大,衍射角逐渐变小.所以温度升高,衍射角变小.当温度不变,X光波长变大时,对于同一晶面族,衍射角随之变大.1.18设由原子A和B组成的一维双原子晶体中，原子A和B的散射因子分别为fA和fB,A和B之间的距离为a/2，X射线垂直原子线入射，试证明：（1）干涉条件是naλ=cosθ式中，θ是衍射光速与原子线间的夹角；22（2）当n为奇数时，衍射强度I∝−ff；当n为偶数时，衍射强度I∝+ff。ABAB证明：参考林鸿生1.1.19，王矜奉1.2.26QBBAAθBBBBAAAAa/2a/2a/2a/2LPO（1）如图所示，复式格子对X射线的衍射，可以归结为晶体内各原胞散射波之间的相互干涉，因为晶体是由各原胞在空间周期性排列而成，而它的排列情况完全可由布喇格格子来表示，因此各原胞之间相互加强条件即是布喇格格子中被格点散射加强条件。因此本题可看做是一个相距为a一维布喇格晶体光栅，如图所示，其中每一个格点代表了原子A和B，各格点（原胞）散射波之间相互加强条件由期中任两束散射波的光程差来决定，当光程差等于入射X射线波长整数倍时，散射相互加强，即JJJGLQ===LPcosθθacosnλ(n=0,1,2•••)这与布喇格公式2sdninθ=λ不同，原因是这里不存在晶面族中各晶面之间干涉。hkl（2）几何结构因子inh2π(ujjj++kvlw)Ffhkl=∑jej1取原子A坐标为坐标原点r=0，则原子B的位置为ra=，方向沿X方向。AB224 第一章晶体的结构1inh2π()uk++vlwin×in2π×inFf==eejjjf2π0+ffe2=+feπhkl∑jABABj22*inπIFFFff∝=⋅=+ehklhklhklAB式中n为衍射级数，+-*（3）如果A，B为同一种原子，f=f，若A、B是不同原子（或离子），但有相同的散射因子，例如K,ClAB两离子组成的双原子链，由于两离子的最外层都是满壳层，2inπ当n为级奇数时，Iff∝+e0=AB2inπ2当n为级偶数时，I∝+ffe4=fAB1.19若波长为λ的X射线沿简立方晶胞的-z方向入射，求证：衍射束落在y-z平面的条件是λ2l=22alk+式中，l，k为整数，a为晶格常数。求衍射线束的方向余弦cosβ和cosγ。解：（参考林鸿生1.1.16，科学出版社，徐至中1-15）Oxyz直角坐标系Ox，Oy，Oz分别代表简立方晶胞zJJJJGK的三个晶轴，三个晶轴相互垂直且等于晶格常数a，则晶胞基矢为hklGGGGGJJGJJG0−kaa===ibajcak,,,0JG其倒格子基矢为γk′JJGJ222πGGJGJππJGJJGβy∗∗∗0ai===,,bjckaaaγ倒格子矢量为0JJGGJJGJJGJJGJGJG∗∗∗2π0xKhhkl=++=ablkc()hi++kjlk()1−−191aJJGJJG2π0kk0=−()1192−λ散射光线加强时，JGJJGJJGGJJGJGJG22π00πkkK′=+=0hkl−k+()hik++jlk()1−−193λaJJGJG因为kk=′021122⎛⎞l1得=+()hk+⎜⎟−22λaa⎝⎠λ2l1222=+()hkl+λaλ2l当=时，显然h=0，22alk+也即散射光衍射光束落在y-z平面内JJGJJG入射光线k和k满足布拉格散射公式025 第一章晶体的结构γ02sdnin=λ，令n=1hkl2γ0λλλ2212sin===+(kl)22daa2hkl212222()hkl++222γ0lk−cosγπ=cos()−γ00=−cosγ=−−(12sin)=222lk+⎛⎞π22klcosβγ=−cos⎜⎟==sinγγ1cos−=22⎝⎠2kl+JG而当衍射光束落在y-z平面时，设k′跟z轴的夹角为γ，从图知JGGJJG2π0kj′=−()sinγγ+cosk()1−193−λ比较两式有，h=−011()9−5λsinγ=−k()1196−aλcosγ=−−−l1()1197aλ2l得=22alk+JJGJG因为kk=′0221⎛⎞⎛kl1⎞即=+−⎜⎟⎜⎟2λ⎝⎠⎝aaλ⎠λ2l得=22alk+GG解：（方俊鑫）入射线S和衍射S之间夹角为2θ0Gs(衍射线)2dsinθ=nλ令n=1（1）β2简立方面间距为：ad=（2）2θhkl1(h2+k2+l2)2Gs0因衍射线和入射线必在一个平面内，（已知条件之一）26 第一章晶体的结构222l+kcosβ=cos(π−2θ)=−cos2θ=−1(−s2inθ)=222λ+k122⎡l⎤得sinθ=⎢22⎥（3）⎣l+k⎦由（1）、（2）、（3）得2lλ=（4）a22122221(l+k)(l+k+h)2但衍射线的a和λ还必须满足第二条件N2l=22akl上式与)4(式对比,可知必须h=,0而h=0的(h,k,l)面必须平行ox轴,即(okl)面→→法线与ox轴垂直,令N射线S0//OZ轴,所以衍射线S必在YZ面上Q,E,D。1.20氢原子的基态波函数为−1−r232a0ε0h−10Ψ=()rae()π0，式中am0==×20.52910为玻尔半径。试求氢原子的散射因子。πme解：（吴代鸣2.9）2r−1−氢原子基态电子密度为nr()=()πa3ea0，0其散射因子为2rJJGG2∞−f==dnreτ()−•iKrea0()eiKr−eiKrG∫iKa3∫00利用积分公式∞nx−αn!xedx=∫0an+1很容易算出21⎡⎤116f=−⎢⎥=G3222iKa⎢⎥()22−+iKa()iKa()4+Ka220⎣⎦00027 第一章晶体的结构2.10对一个三主轴方向周期分别为a，b和c的正交简28'