拉氏变换习题解答.pdf 26页

'拉氏变换习题解答习题一1．求下列函数的拉氏变换,并用查表的方法来验证结果.t−2t2(1)ft()=sin；(2)f()t=e；(3)f(t)=t；(4)f()t=sintcost；222(5)f()t=sinhkt；(6)f()tk=cosht；(7)f(t)=cost;(10)f()tt=cos.iitt−22−st+∞te−st+∞()−ee解(1)&⎡⎤⎣⎦f()t==∫∫sinedtdt0022iii⎡−−()st+∞+−(s+)t∞⎤iiee221+∞−−()st−(s+)t1⎢||⎥=−∫()ee22dt=−⎢00⎥2i02iii⎢−+ss−−⎥⎣22⎦⎡⎤iiss+−+11⎢⎥1122=−⎢⎥=2iii2i⎛⎞ii⎛⎞⎢⎥ss−+⎜⎟ss−+⎜⎟⎣⎦22⎝⎠22⎝⎠122==()Res>014122s+s+4+∞−+(2st)+∞+∞e|1−−2(tst−s+2)t0(2)&⎡⎤⎣⎦f()te==∫∫edtedt==>()Res−200−+(2ss)+2−st+∞22−−ste+∞1+∞st22−−st+∞+∞st(3)&⎡⎤⎣⎦f()tt==∫∫00edt−t|0+2tedt=−2te|0+2∫0edtssss22+∞−st=−es|=()Re>0ss32t=0+∞−−st1+∞st1+∞−−(2sti)−+(s2i)t(4)&⎡⎤⎣⎦f()t==∫∫00sintcostedtsin2tedt=∫0⎡⎤⎣⎦ee−dt24i+∞+∞⎡−(s−2i)t−(s+2i)t⎤1⎢e|0e|0⎥1⎛11⎞1=−=⎜−⎟=()Res>04i⎢−()s−2i−()s+2i⎥4is−2is+2is2+4⎝⎠⎢⎣⎥⎦kt−kt+∞−−st+∞ee−st1+∞−−()skt+∞−(s+k)t(5)&⎡⎤⎣⎦f()tk==∫∫00sinhtedtedt=(∫∫00edt−edt)22+∞+∞⎛⎞−−()skt−+(sk)t=−1⎜⎟ee||0011⎛⎞1k=−⎜⎟=()Resk>max{,−k}⎜⎟−−−+222(sk)(sk)2⎝⎠sk−+sks−k⎝⎠-1- 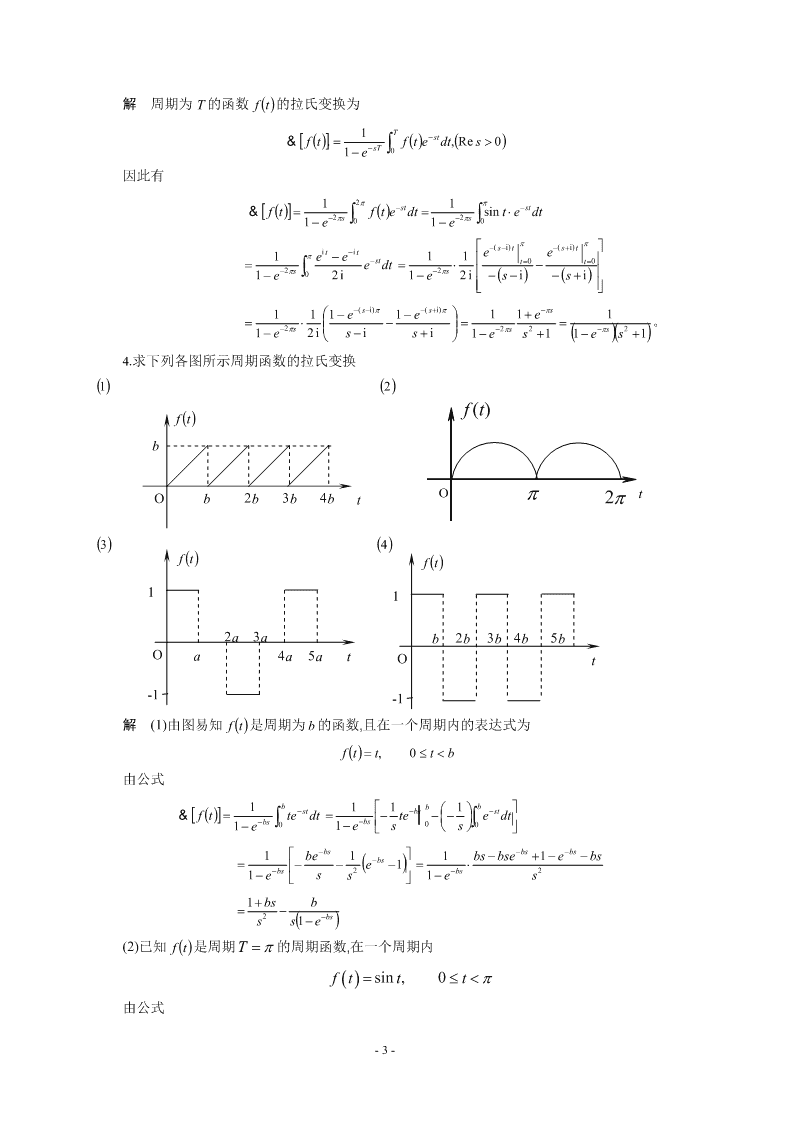kt−kt+∞−−st+∞ee+st1+∞−−()skt+∞−+(sk)t(6)&⎡⎤⎣⎦f()tk==∫∫00coshtedtedt=(∫∫00edt+edt)22+∞+∞⎛⎞−−()skt−+(sk)t=+1⎜⎟ee||0011⎛⎞1s=+⎜⎟=()Res>max{k,−k}⎜⎟−−−+222(sk)(sk)2⎝⎠sk−+sks−k⎝⎠+∞1+∞2−−stst(7)&⎡⎤⎣⎦f()t=⋅∫∫costedt=()1+cos2tedt00221⎛+∞−st+∞−st⎞1⎛1s⎞s+2=⎜∫0edt+∫0cos2t⋅edt⎟=⎜+2⎟=2()Res>02⎝⎠2⎝ss+4⎠s(s+4)+∞1+∞2−−stst(8)&⎡⎤⎣⎦f()tt=⋅∫∫sinedt=()1−cos2tedt0021+∞−−st+∞st11⎛⎞s2=−(∫∫00edtcos2t⋅edt)=⎜⎟−=22()Res>0224⎝⎠ss++s(s4)2．求下列函数的拉氏变换.⎧3,0≤t<2t<π⎪⎧3,2(1)f()t=⎨−1,2≤t<4;(2)f()t=⎨⎪⎩cost,t>π.⎩0,t≥4.22t(3)f()t=e+5δ(t).;(4)f(t)=δ(t)cost−u(t)sint.24−st−st+∞−st2−st4−st3e|3e|1−2s−4s02解（1）&[]f()t=∫∫f()tedt=3edt−∫edt=+=(3−4e+e)002−sssπ+∞+∞（2）&[]f()t=f()te−stdt=23e−stdt+cost⋅e−stdt∫0∫0∫π2πit−itπs3−st+∞e+e−st33−21+∞−(s−i)t−(s+i)t=e|2+∫πedt=−e+∫π(e+e)dt−st=02ss222+∞+∞⎡e−(s−i)te−(s+i)t⎤⎛ππ⎞πs⎢|π|π⎥πs−(s−i)2−(s+i)233−1t=2t=233−1⎜ee⎟=−e2+⎢+⎥=−e2+−⎜⎟ss2⎢−(s−i)−(s+i)⎥ss2⎜s−is+i⎟⎢⎣⎥⎦⎝⎠πsπs33−1−=−e2−e22sss+1+∞+∞+∞2t−st2t−st−st（3）&[]f()t=∫[]e+5δ(t)edt=∫eedt+5∫δ()tedt0001+∞−st1−st5s−9=+5∫δ()tedt=+5e|=s−2−∞s−2t=0s−2+∞+∞11s2−−stst−st（4）&⎡⎤f()t=⋅δ()tcost⋅edt−sintedt=cost⋅e|−=1−=⎣⎦∫∫−∞0t=0s2+1s2+1s2+13．设f(t)是以2π为周期的函数,且在一个周期内的表达式为⎧sint,00)1−e−sT∫0因此有12π−st1π−st&[]f()t=f()tedt=sint⋅edt1−e−2πs∫01−e−2πs∫0ππ⎡−(s−i)t−(s+i)t⎤1πeit−e−it11e|e|=e−stdt=⋅⎢t=0−t=0⎥1−e−2πs∫02i1−e−2πs2i⎢−()s−i−()s+i⎥⎢⎣⎥⎦⎛−(s−i)π−(s+i)π⎞−πs111−e1−e11+e1=⋅⎜−⎟==。1−e−2πs2i⎜s−is+i⎟−2πs2()−πs(2)⎝⎠1−es+11−es+14.求下列各图所示周期函数的拉氏变换(1)(2)ft()f(t)bOb2b3b4btOπ2πt(3)(4)f()tf(t)112a3ab2b3b4b5bOa4a5atOt-1-1解(1)由图易知f(t)是周期为b的函数,且在一个周期内的表达式为f(t)=t,0≤t−1，α+1s3⎡⎤&[()]&⎡⎤tt2++32=&⎡t2⎤+32ft=⎣⎦⎣⎦&⎢t⎥+2&[1]⎣⎦232=++32sss"tt1dt1⎛1⎞11（2）&[f()t]=&[]1−te=&[]1−&[te]=+&[]e=−⎜⎟−=−2sdss⎝s−1⎠s()s−122t2tdtdtt（3）&[f()t]=&⎡⎤(1t−=)e&⎡(2tt−+1)e⎤=&[e]＋2&[e]＋&[]e⎣⎦⎣⎦2dsds2ss−+45=3(1s−)⎡t⎤11d1⎛⎞as（4）&[f()t]=&sinat=&[tsinat]=−&[sinat]=−⎜⎟"=⎢⎥22222⎣2a⎦2a2ads2(as⎝⎠++asa)22d⎛⎞ss−a（5）&[f()t]=&[tacost]=－&[cosat]=−⎜⎟"=22222ds⎝⎠sa++()sa103s10−3s（6）&[f()t]=&[5sin2t−3cos2t]=5&[sin2t]−3&[cos2t]=−=222s+4s+4s+4−2t6（7）&[f()t]=&⎡⎤etsin6=⎣⎦2(2s+)+36这里有6&[]sin6t=2s+36再利用位移性质得到.s（8）同（7）利用&[]cos4t=及位移性质2s+16−4ts+4&[f()t]=&⎡⎤etcos4=⎣⎦2()s+41+6nn!（9）利用&[]t=及位移性质得n+1snatn!&[f(t)]=&[te]=()n+1s−a-5- ⎧5⎪1,t>（10）解法1由u()3t−5=⎨30,5⎪t<⎩3+∞−st&[f()t]=&[]u()3t−5=∫u()3t−5edt0+∞−st5e|5−s+∞t=e3−st3=∫5edt==−ss3解法2由相似性质111&[]u()3t=⋅=3ss3由位移性质5−s53⎡⎛5⎞⎤−se&[]u(3t−5)=&{u3t−⎥}=e3&⎡⎤ut()3=⎢⎜⎟⎣⎦⎣⎝3⎠⎦s−t−t⎧1,1−e>0,t>0（11）因为u()1−e=⎨−t⎩0,1−e<0,t<0所以+∞+∞1−st−st&[]f()t=∫f()tedt=∫edt=00s⎛1⎞1Γ⎜⎟⎡−2⎤⎝2⎠π（12）利用&⎢t⎥=1=1及位移性质⎢⎣⎥⎦s2s23t⎡e⎤π&[f(t)]=&⎢⎥=⎣t⎦s−31s2．若&[(ft)]=F(s)，a为正实数，证明（相似性质）&[(fat)]=F()。aas+∞−st11+∞−aats证&[f(at)]==∫∫f()atedtf()ated()at=F()00aaa()nn3．若&[(ft)]=F(s)，证明Fs()=&[(−tf)(t)]，Re(s)>c。特别&[(tft)]=−F"(s)，或1−1f()t=−&["Fs()]，并利用此结论，计算下列各式：tt−3t−3t（1）f()tt=esin2t，求Fs()；（2）f()tt=∫esin2tdt，求Fs()；0s+1t−3t（3）Fs()=ln，求f(t)；（4）f()tt=∫esin2tdt，求Fs()。s−10nnn()nddd+∞−−st+∞st+∞n−st解Fs()=&[(ft)]==f()tedt[ft()e]dt=(−t)ft()edtdsndsnn∫∫00ds∫0-6- n＝&[(−tf)(t)]，Re(s)>c。（1）利用公式&[]tf(t)=−F"(s)−3td−3t⎛⎞24(s+3)&[f()t]=&⎡⎤tesin2t=−&[setin2]=−⎜⎟′=⎣⎦222ds⎝⎠(3s++)2⎡⎤(3s++)42⎣⎦（2）由积分性质⎡t−3τ⎤1−3t12&esin2τdτ=&[esin2t]=⋅⎢⎣∫0⎥⎦ss()s+32+4再由像函数的微分公式2⎡t−3τ⎤d⎧2⎫2(3s+12s+13)&[f()t]=&⎢⎣t∫esin2τdτ⎥⎦=−⎨2⎬=2220ds⎩s[()s+3+4]⎭s[]()s+3+4⎛⎞s+1122（3）Fs"()==⎜⎟ln"−2=&[sttinh]，知f()tt=sinh2⎝⎠ss−−11tt⎡⎤t−3t1−3t4(s+3)（4）&[f()t]=&tesin2tdt=&[tesin2t]=⎢⎥⎣⎦∫0s[]()22ss+3+4⎡⎤ft()∞－1⎡∞⎤4．若&[(ft)]=F(s)，证明&⎢⎥=∫Fs()ds，或f()tt=&⎢⎣∫Fs()ds⎥⎦。并利用此⎣⎦tss结论，计算下列各式：−3tsinktetsin2（1）ft()=，求Fs()；（2）ft()=，求Fs()；tt−3tstetsin2（3）Fs()=，求f(t)；（4）f()td=t，求Fs()。(1s2−)2∫0t∞∞+∞−−st+∞∞st+∞ft()−st⎡⎤f()t解∫∫ssF()sds===∫00f(t)edtds∫∫sf(t)edsdt∫0edt=&⎢⎥t⎣⎦t⎡⎤sinkt∞∞ku∞（1）F()s=&=&[sinkt]du==duarctan|⎢⎥⎣⎦t∫s∫suk22+ksπss=−arctan=arccot2kk−3t⎡esin2t⎤∞−3t∞2u+3∞（2）F()s=&⎢⎥=∫&[]esin2tdu=2du=arctan|⎣t⎦s∫s()u+3+42sπs+3s+3=−arctan=arccot222⎡⎤∞−1⎢⎥∞u=−1⎡−11⎤−1⎡1111⎤1t−t（3）f()t=t&dut&⎢⋅⎥=t&⋅−⋅=t()e−e∫s22⎢⎥⎢⎥()u2−1⎢⎣2u−1s⎥⎦⎣4s−14s+1⎦4⎣⎦t=sht2-7- −3τ−3τ⎡tesin2τ⎤1⎡esin2t⎤1∞−3t1∞2（4）F()s=&⎢∫0dτ⎥=&⎢⎥=⋅∫s&[esin2t]du==⋅∫s2du⎣τ⎦s⎣t⎦ss(u+3)+41u+3∞1s+3=arctan|=arccots2u=ss25．计算下列积分：−t−2t−at−mt+∞e−e+∞1−cost−t+∞ecosbt−ecosnt(1)∫dt.(2)∫edt(3)∫dt0t0t0t+∞+∞+∞−3t−2t−3t(4)∫ecos2tdt.(5)∫tedt.(6)∫tesin2tdt.000−2t−t2+∞esht⋅sint+∞esint+∞3−t(7)∫dt.(8)∫dt.(9)∫tesintdt.0t0t0+∞sin2t+∞+∞−t(10)dt.(11)eterfdt.(12)J(td)t.∫0t2∫0∫00+∞k2k2t−u2(1−)⎛⎞t其中erft=∫edu称为误差函数，J(0t)=∑2⎜⎟称为零阶贝塞尔(Bessel)函π0k=0(!k)⎝⎠2数。+∞f(t)∞解(1)由公式∫∫dt=&[f()t]ds得00t−t−2t+∞e−e∞−t−2t∞⎛11⎞s+1∞∫∫dt=&[]e−eds=∫⎜−⎟ds=ln|=ln200t0⎝s+1s+2⎠s+20+∞1−cos−t∞−t∞⎡1s+1⎤s+1∞1(2)∫∫e=&[]e()1−costds=⎢−2⎥ds=ln|=ln200t∫0⎣s+1()s+1+1⎦()s+12+102−at−mt+∞ecosbt−ecosnt∞−at−mt∞⎡s+as+m⎤(3)∫∫00dt=&[ecosbt−ecosnt]ds=∫0⎢22−22⎥dst⎣()s+a+b()s+m+n⎦22221()s+a+b∞1m+n=ln2|=ln222()s+m+n2s=02a+b+∞−sts+∞−3ts3(4)已知&[]cos2t=cos2t⋅edt=，因此ecos2tdt==∫0s2+4∫0s2+4s=313+∞−2t11(5)tedt=&[]t==∫0s=224ss=22⎛2⎞4s(6)已知&[]sin2t=再由微分性质&[]tsin2t=−⎜⎟′=s2+4s2+422⎝⎠()s+4+∞−3t4s12得tesin2tdt==∫0()22s=3169s+4−2tt−t+∞esht⋅sint∞⎡−2te−e⎤1∞−(2−1)t−(2+1)t()7∫dt=∫&⎢esint⎥ds=∫&[esint−esint]ds0t0⎣2⎦201∞⎡11⎤1⎡∞∞⎤=∫⎢2−2⎥ds=⎢⎣arctan(s+2−1)|0−arctan()s+2+1|0⎥⎦20⎢()s+2−1+1()s+2+1+1⎥2⎣⎦-8- 1[]()()1π=arctan2+1−arctan2−1=arctan1=228−t2+∞esint+∞−t21∞−t(8)∫∫dt=&[]esintds=∫&[e(1−cos2t)]ds00t201∞⎡1s+1⎤1s+1∞1=∫⎢−2⎥ds=ln|=ln520⎣s+1()s+1+4⎦2()s+12+404313⎛1⎞24s−24s(9)已知&[]sint=,利用微分性质&[]tsint=−⎜⎟″′=s2+1s2+124⎝⎠()s+43+∞3−t324s−24stesintdt=&[]tsint==0∫0s=1()24s+4s=122+∞sint+∞2⎛1⎞sint∞+∞sin2t+∞sin2t(10)∫∫002dt=−sint⎜⎟′dt=−|0+∫∫00dt=dtt⎝t⎠ttt∞∞2s∞π=∫&[]sin2tds=∫ds=arctan|=00s+4202+∞12−t⎡⎤==(11)∫eterfdt=&⎣⎦erf(t)0s=1ss+12s=1+∞1(12)J(td)t=&[]J(t)==1∫000s=02s+1s=06．求下列函数的拉氏逆变换.111（1）F()s=.（2）F()s=.（3）F()s=.244s+4s()s+112s+3s+3（4）F()s=.（5）F()s=.（6）F()s=.2()()s+3s+9s+1s−3s+12s+5（7）F()s=.（8）F()s=.22s+s−6s+4s+13−11−1⎡2⎤1解（1）f()t=&[]F()s=&=sin2t⎢2⎥2⎣s+4⎦2−1⎡1⎤1−1⎡3!⎤13（2）f()t=&=&=t⎢4⎥⎢3+1⎥⎣s⎦3!⎣s⎦6−1⎡1⎤13−1at（3）由&=t及位移性质&[F(s−a)]=ef(t)得⎢4⎥⎣s⎦6()−1−1⎡1⎤13−tft=&[F(s)]=&⎢⎥=te4⎣()s+1⎦6−1−1⎡1⎤−3t（4）f()t=&[F(s)]=&⎢⎥=e⎣s+3⎦−1−1⎡s⎤−1⎡3⎤（5）f()t=&[]F(s)=2&+&=2cos3t+sin3t⎢2⎥⎢2⎥⎣s+9⎦⎣s+9⎦-9- −1−1⎡s+3⎤−1⎡1⎛31⎞⎤3−1⎡1⎤1−1⎡1⎤（6）f()t=&[F()s]=&⎢⎥=&⎢⎜−⎟⎥=&⎢⎥−&⎢⎥⎣()s+1(s−3)⎦⎣2⎝s−3s+1⎠⎦2⎣s-3⎦2⎣s+1⎦33t1−t=e−e22−1−1⎡s+1⎤−1⎡1⎛32⎞⎤（7）f()t=&[F()s]=&⎢2⎥=&⎢⎜+⎟⎥⎣s+s−6⎦⎣5⎝s−2s+3⎠⎦3−1⎡1⎤2−1⎡1⎤32t2−3t=&⎢⎥+&⎢⎥=e+e5⎣s−2⎦5⎣s+3⎦55−1−1⎡2s+5⎤−1⎡2(s+2)+1⎤（8）f()t=&[F()s]=&⎢2⎥=&⎢22⎥⎣s+4s+13⎦⎣()s+2+3⎦−1⎡()s+2⎤1−1⎡3⎤=2&⎢⎥+&⎢⎥()2222⎣s+2+3⎦3⎣()s+2+3⎦−−22tt11−2t=+2cetos3esin3t=e()6cos3t+sin3t337．求下列各图所示函数f(t)的拉氏变换.ft()ft()Aoτ2τ3τ4τ6t42−Aoτ3τ5τt(1)(2)ft()ft()48364221o2oτ2τ3τtt(3)(4)(1)由图易知,f(t)是周期为2τ的周期函数,在一个周期内-10- ⎧At,0≤<τft()=⎨⎩−At,2τ≤<τ由公式A2τ−stAττ−−st2st&⎡⎤f()tf=()tedt=+edt−1edt⎣⎦1−e−2τs∫01−e−2τs(∫∫0τ())ττ2A⎡⎤ee−−st||st−−τs2ττss−Ae1−+e−e=−⎢⎥tt==0τ=⋅−2τs−2τs1−−es⎢⎥−s1−es⎣⎦2−τsAA()1−eτs=⋅=tanh−2τsse12−s∞(2)由图易知f()t=2[ut(−τ)+−ut(3ττ)+−ut(5)+?]=2∑ut(−(2k+1)τ)，k=0∞−sτ22−+(2ks1)τe1当Re(s)>0时，&⎡⎤⎣⎦ft()==∑e⋅−2sτ=ssk=01s−esinhsτ(3)由图易知f()t=8ut()−2ut(−2)，当Re(s)>0时，∞−2s18−−ksτ2e22s&⎡⎤⎣⎦f()te==∑−=(4−e)k=0ssss∞(4)由图易知f(tu)=+[(t)(ut−τ)(+ut−2τ)+?]=∑u(t−kτ)，当Re(s)>0时k=0∞11−ksτ11sτ&⎡⎤⎣⎦ft()==∑e⋅−sτ=(1+coth)k=0ss12−es2习题三1．设f()t，f()t均满足拉氏变换存在定理的条件（若它们的增长指数均为c），且12&[(ft)]=F(s)，&[(ftF)]=(s)，则乘积f()tf⋅(t)的拉氏变换一定存在，且1122121β+∞j&[]f()tf⋅=()tF(q)F(s−q)dq12∫122jπβ−∞j其中β>c，Re(sc)>β+。证由于f()t,f(t)均满足拉氏变换存在定理的条件以及增长指数均为c，知乘积f()tf(t)也一12012定满足拉氏变换存在的定理的条件且增长指数为2c.根据拉氏存在定理的证明当β>c时，00+∞−st&⎡⎤f()tf⋅=()tf()tf()tedt在Res≥β+c上存在且一致收敛.由于⎣⎦12∫01201β+∞iqtf11()tF=∫()qedq2iπβ−∞i+∞−st+∞⎛⎞1β+i∞qt−st而&⎡⎤⎣⎦f12()tf⋅=()t∫0f1()tf2()tedt=∫∫0i⎜⎟β−∞Fq12()edqf(t)edt⎝⎠2iπ-11- 1β+∞i+∞−−()sq1β+∞i=∫∫β−∞i0Fq12()f(t)edtdq=−∫β−∞iFq12()F(sq)dq2iπ2iπ2．求下列函数的拉氏逆变换（像原函数），并用另一种方法加以验证.1s（1）F()s=.（2）F()s=.22()()s+as−as−b22s+cs+2a（3）F()s=（4）F()s=()s+a(s+b)2()222s+a11（5）F()s=.（6）F()s=223()()(s+a)sss+as+b21s+2s−1（7）F()s=.（8）F()s=442s−as()s−11s（9）F()s=.（10）F()s=2(2)()2(2)ss−1s+1s+4−1−1⎡1a⎤1−1⎡a⎤sinat（1）解法1f()t=&[F()s]=&⋅=&=⎢22⎥⎢22⎥⎣as+a⎦a⎣s+a⎦a⎡st⎤⎡st⎤iat−iateeeesinat解法2f()t=Res⎢22,ai⎥+Res⎢22,−ai⎥=−=⎣s+a⎦⎣s+a⎦2ai2aia−1⎡1⎤−1⎡1⎛11⎞⎤解法3f()t=&⎢22⎥=&⎢⎜−⎟⎥⎣s+a⎦⎣2ai⎝s−ais+ai⎠⎦1−1⎡1⎤−1⎡1⎤1iat−iatsinat=（&−&）=()e−e=⎢⎥⎢⎥2ai⎣s−ai⎦⎣s+ai⎦2aiastst−1−1⎡s⎤⎡se⎤⎡se⎤（2）解法1f(t)=&[F()s]=&⎢⎥=Res⎢()(),a⎥+Res⎢()(),b⎥⎣()s−a(s−b)⎦⎣s−as−b⎦⎣s−as−b⎦atbtaebe1()atbt=+=ae−bea−bb−aa−b−1−1⎡s⎤−1⎡1⎛ab⎞⎤解法2f(t)=&[F()s]=&⎢()()⎥=&⎢⎜−⎟⎥⎣s−as−b⎦⎣a−b⎝s−as−b⎠⎦1−1⎡1⎤−1⎡1⎤1atbt=（a&⎢⎥−b&⎢⎥=()ae−bea−b⎣s−a⎦⎣s−b⎦a−b⎡st⎤⎡st⎤−1(s+c)e(s+c)e（3）解法1f(t)=&[]F()s=Res⎢,−a⎥+Res⎢,−b⎥()()2()()2⎢⎣s+as+b⎥⎦⎢⎣s+as+b⎥⎦−at()c−aed⎛s+cst⎞c−a−atc−b−bta−c−bt=+⎜e⎟=e+te+e222()b−ads⎝s+a⎠s=−b()a−ba−b()a−b−1−1⎡s+c⎤−1⎡c−a1a−c1c−b1⎤解法2f()t=&[F(s)]=&⎢2⎥=&⎢2⋅+2⋅+⋅2⎥⎣()s+a(s+b)⎦⎣()a−bs+a()a−bs+ba−b()s+b⎦c−a−1⎡1⎤a−c−1⎡1⎤c−a−1⎡1⎤=2&⎢⎥+2&⎢⎥+&⎢2⎥()a−b⎣s+a⎦()a−b⎣s+b⎦a−b⎢⎣()s+b⎥⎦-12- c−a−ata−c−btc−b−bt=e+e+te22()a−b()a−ba−b⎡22⎤⎡"⎤−1−1s+2a−13a1⎛s⎞（4）解法1f()t=&[F()s]=&⎢⎥=&⎢⋅+⎜⎟⎥()2222as2+a22⎝s2+a2⎠⎢⎣s+a⎥⎦⎢⎣⎥⎦"3−1⎡a⎤11⎡⎛s⎞⎤31=&+&⎢⎜⎟⎥=sinat−tcosat⎢22⎥222a⎣s+a⎦2⎢⎣⎝s+a⎠⎥⎦2a2⎡s2+2a2⎤⎡s2+2a2⎤−1stst解法2f()t=&[]F()s=Res⎢e,ai⎥+Res⎢e,−ai⎥⎢()222⎥⎢()222⎣s+a⎦⎣s+a⎥⎦2222=ds+2aest+ds+2aest3i1i3−i1−iatatatatds()2ds()2=e−te−e−tes+ais=ais−ais=−ai4ai44ai431=sinat−tcosat2a2−1⎡1⎤1−1⎡11⎤1−1⎡1⎤−1⎡1⎤（5）解法1f(t)=&⎢()223⎥=2&⎢3−()22⎥=2(&⎢3⎥−&⎢()22⎥)⎣s+as⎦a⎣sss+a⎦a⎣s⎦⎣ss+a⎦113t−1⎡1⎤11⎛⎞31t=(t−&dt)=−⎜⎟tasintdta22∫0⎢⎣s2+a2⎥⎦22aa2∫0⎝⎠113=−ta()1c−ost242aa−1⎡1⎤解法2f()t=&⎢()223⎥⎣s+as⎦ststst⎡e⎤⎡e⎤⎡e⎤=Res⎢()223,0⎥+Res⎢()223,ai⎥+Res⎢()223,ai⎥⎣s+as⎦⎣s+as⎦⎣s+as⎦2stait−ait1d⎛e⎞ee=⎜⎟+−ds2⎜s2+a2⎟()3()32⎝⎠2aiai2ai−ais=0121()=t−1−cosat242aa−1⎡1⎤−1⎡111111⎤（6）解法1f()t=&⎢⎥=&⎢⋅+⋅−⋅⎥⎣s()s+a(s−b)⎦⎣absa()a−bs+ab()a−bs+b⎦1−1⎡1⎤1−1⎡1⎤1−1⎡1⎤=&⎢⎥+&⎢⎥−&⎢⎥ab⎣s⎦a()a−b⎣s+a⎦b()a−b⎣s+b⎦11−at1−bt=+e−eaba()a−bb(a−b)−1⎡1⎤解法2f()t=&⎢⎥⎣s()s+a(s+b)⎦⎡st⎤⎡st⎤⎡st⎤eee=Res⎢()(),0⎥+Res⎢()(),−a⎥+Res⎢()(),−b⎥⎣ss+as+b⎦⎣ss+as+b⎦⎣ss+as+b⎦-13- 11−at1−bt=+e−eaba()a−bb(a−b)−1⎡1⎤−1⎡1⎛11⎞1a⎤（7）解法1f()t=&⎢44⎥=&⎢3⎜−⎟−322⎥⎣s−a⎦⎣4a⎝s−as+a⎠2as+a⎦1()at−at11=e−e−sinat=()shat−sinat3334a2a2a−1⎡1⎤解法2f()t=&⎢44⎥⎣s−a⎦⎡st⎤⎡st⎤⎡st⎤⎡st⎤eeee=Res⎢44,a⎥+Res⎢44,−a⎥+Res⎢44,ai⎥+Res⎢44,−ai⎥⎣s−a⎦⎣s−a⎦⎣s−a⎦⎣s−a⎦st−atait−aiteeee1=−++=()shat−sinat333334a4a4()ai4()−ai2a⎡2⎤⎡⎤−1s+2s−1−1122（8）解法1f()t=&⎢2⎥=&⎢−++2⎥⎣s()s−1⎦⎣ss−1(s−1)⎦−1⎡1⎤−1⎡2⎤−1⎡2⎤tt=&⎢−⎥+&⎢⎥+&⎢2⎥=−1+2e+2te⎣s⎦⎣s−1⎦⎣()s−1⎦⎡2⎤⎡2⎤⎡2⎤−1s+2s−1s+2s−1sts+2s−1st解法2f()t=&⎢2⎥=Res⎢2e,0⎥+Res⎢2e,1⎥⎣s()s−1⎦⎣s()s−1⎦⎣s()s−1⎦2d⎛s+2s−1st⎞=−1+2et+2tet=−1+⎜e⎟ds⎜s⎟⎝⎠s=1−1−1⎡1⎤−1⎡1⎛11⎞1⎤1t−t（9）解法1f()t=&[F()s]=&⎢2(2)⎥=&⎢⎜−⎟−2⎥=()e−e−t⎣ss−1⎦⎣2⎝s−1s+1⎠s⎦2=sht−t⎡st⎤⎡st⎤⎡st⎤eee解法2f()t=Res⎢2()2,0⎥+Res⎢2()2,1⎥+Res⎢2()2,−1⎥⎣ss−1⎦⎣ss−1⎦⎣ss−1⎦stt−td⎛e⎞ee=⎜⎟+−=sht−tds⎜s2−1⎟22⎝⎠s=0−1⎡s⎤−1⎡1⎛ss⎞⎤（10）解法1f(t)=&⎢22⎥=&⎢⎜2−2⎟⎥⎣()s+1(s+4)⎦⎣3⎝s+1s+4⎠⎦1−1⎡s⎤−1⎡s⎤1=(&−&)=()cost−cos2t⎢2⎥⎢2⎥3⎣s+1⎦⎣s+4⎦3−1⎡s⎤解法2f(t)=&⎢()2(2)⎥⎣s+1s+4⎦⎡st⎤⎡st⎤⎡st⎤⎡st⎤sesesese=Res⎢()2(2),i⎥+Res⎢()2(2),−i⎥+Res⎢()2(2),2i⎥+Res⎢()2(2),−2i⎥⎣s+1s+4⎦⎣s+1s+4⎦⎣s+1s+4⎦⎣s+1s+4⎦it−it2it−2itit−it2it−2itie−ie2ie−2ieeeee1=+++=+++=()cost−cos2t()2()2()2()2()2ii+4−2ii+44i+14i4i+1−4i66663-14- 3.求下列函数的拉氏逆变换.1s（1）F()s=（2）F()s=(2)2s+2s+42s+11（3）F()s=（4）F()s=()()42ss+1s+2s+5s+42s+1s−1（5）F()s=（6）F()s=ln229s+6s+5ss+21（7）F()s=.（8）F()s=.(2)2()22s+4s+5s+2s+222s+4s+42s+s+5（9）F()s=（10）F()s=.(2)2s3+6s2+11s+6s+4s+132s+32s+3s+3（11）F()s=（12）F()s=323s+3s+6s+4()s+1(s+3)−2s1+e（13）F()s=2s−1⎡1⎤−1⎡121⎛s⎞⎤1−1⎡2⎤1−1⎡⎛s⎞⎤解（1）&⎢22⎥=&⎢2+⎜2⎟′⎥=&⎢2⎥+&⎢⎜2⎟′⎥⎢⎣(s+4)⎥⎦⎣16s+48⎝s+4⎠⎦16⎣s+4⎦8⎣⎝s+4⎠⎦11=sin2t−tcos2t168−1⎡s⎤−1⎡2⎤−1−1⎡2⎤−2t（2）f()t=&⎢⎥=&⎢1−⎥=&[1]−&⎢⎥=δ()t−2e⎣s+2⎦⎣s+2⎦⎣s+2⎦⎡st⎤⎡st⎤⎡st⎤−1⎡2s+1⎤()2s+1e(2s+1)e()2s+1e（3）f()t=&⎢⎥=Res⎢()(),0⎥+Res⎢()(),−1⎥+Res⎢()(),−2⎥⎣s()s+1(s+2)⎦⎣ss+1s+2⎦⎣ss+1s+2⎦⎣ss+1s+2⎦ststst()2s+1e()2s+1e(2s+1)e1−t3−2t=lim+lim+lim=+e−es→0()s+1(s+2)s→−1s()s+2s→−2s()s+122−1⎡1⎤−1⎡1⎤−1⎡1112⎤（4）f()t=&⎢42⎥=&⎢()2(2)⎥=&⎢⋅−22⎥⎣s+5s+4⎦⎣s+1s+4⎦⎣31ss+6+4⎦1−1⎡1⎤1−1⎡2⎤11=&−&=sint−sin2t⎢2⎥⎢2⎥3⎣s+1⎦6⎣s+4⎦36⎡⎤⎡⎤12⎢⎥⎢s+⎥（5）f()t=&−1⎡s+1⎤=&−1⎢s+1⎥=1&−1⎢3+3⎥⎢⎣9s2+6s+5⎥⎦⎢12⎥9⎢12221222⎥⎛⎞⎛⎞⎛⎞⎛⎞⎛⎞⎢9⎜s+⎟+4⎥⎢⎜s+⎟+⎜⎟⎜s+⎟+⎜⎟⎥⎢⎣⎝3⎠⎥⎦⎢⎣⎝3⎠⎝3⎠⎝3⎠⎝3⎠⎥⎦1111⎛2−t2−t⎞1⎛22⎞−t=⎜cost⋅e3+sint⋅e3⎟=⎜sint+cost⎟e39⎜⎝33⎟⎠9⎝33⎠⎡s2−1⎤1⎡⎛s2−1⎞⎤1⎡2s2⎤1⎡112⎤−1−1−1−1（6）f()t=&⎢ln2⎥=−&⎢⎜⎜ln2⎟⎟′⎥=−&⎢2−⎥=−&⎢+−⎥⎣s⎦t⎢⎣⎝s⎠⎥⎦t⎣s−1s⎦t⎣s−1s+1s⎦-15- 1()t−t2()=−e+e−2=1−chttt−1⎡s+2⎤−1⎡s+2⎤−1⎡1⎛1⎞⎤1−1⎡⎛1⎞⎤（7）f()t=&⎢22⎥=&⎢22⎥=&⎢−⎜⎜2⎟⎟′⎥=−&⎢⎜⎜2⎟⎟′⎥⎢⎣()s+4s+5⎥⎦⎢⎣[]()s+2+1⎥⎦⎢⎣2⎝()s+2+1⎠⎥⎦2⎢⎣⎝()s+2+1⎠⎥⎦1−1⎡1⎤t−2t1−2t=−⋅(−t)&⎢⎥=sint⋅e=tesint22⎣()s+2+1⎦22−1⎡1⎤−1⎡1⎤1−1⎧⎪1⎡s+1⎤⎫⎪（8）f()t=&⎢22⎥=&⎢22⎥=&⎨2+⎢2⎥′⎬⎢⎣()s+2s+2⎥⎦⎢⎣[]()s+1+1⎥⎦2⎪⎩()s+1+1⎣()s+1+1⎦⎪⎭1−1⎡1⎤−1⎡⎛⎜s+1⎞⎟⎤1−t−1⎡s+1⎤=(&⎢2⎥+&⎢⎜2⎟′⎥=(esint−t&⎢2⎥）2⎣()s+1+1⎦⎢⎣⎝()s+1+1⎠⎥⎦2⎣()s+1+1⎦1()−t−t1−t=esint−tecost=e()sint−tcost22⎡s2+4s+4⎤⎡()s+22⎤⎡19⎤−1−1−1（9）f()t=&⎢⎥=&⎢⎥=&⎢−⎥()22⎢22⎢()+22+9[]()22⎥⎢⎣s+4s+13⎥⎦⎣[]()s+2+9⎥⎦⎣ss+2+9⎦−1⎡131⎛⎜s+2⎞⎟⎤1−2t1−1⎡s+2⎤=&⎢6⋅22−2⎜22⎟′⎥=6esin3t+2t&⎢22⎥⎢⎣()s+2+3⎝()s+2+3⎠⎥⎦⎣()s+2+3⎦1−2t1−2t1−2t=esin3t+tecos3t=e()sin3t+3tcos3t6262⎡2⎤−1⎡2s+s+5⎤−12s+s+5（10）f()t=&⎢32⎥=&⎢⎥⎣s+6s+11s+6⎦⎣()s+1(s+2)(s+3)⎦⎡()2st⎤⎡(2)st⎤⎡(2)st⎤2s+s+5e2s+s+5e2s+s+5e=Res⎢,−1⎥+Res⎢,−2⎥+Res⎢,−3⎥⎣()s+1()s+2(s+3)⎦⎣()s+1()s+2(s+3)⎦⎣()s+1()s+2(s+3)⎦2222s+s+5st2s+s+52s+s+5st−t−2t−3t=lime+lim+lime=3e−11e+10es→−1()s+2(s+3)s→−2()s+1(s+3)s→−3()s+1(s+2)−1⎡s+3⎤−1⎡s+3⎤−1⎡12⎤（11）f()t=&⎢32⎥=&⎢3⎥=&⎢2+2⎥⎣s+3s+6s+4⎦⎣()s+1+3(s+1)⎦⎣()s+1+3[()s+1+3](s+1)⎦−1⎡1212s+1⎤=&⎢2+⋅−2⎥⎣()s+1+33s+13()s+1+3⎦1−1⎡3⎤2−1⎡1⎤2−1⎡s+1⎤=&⎢⎥+&−&⎢⎥3⎢22⎥3⎢⎣s+1⎥⎦⎢22⎥⎣()s+1+()3⎦3⎣()s+1+()3⎦1−t2−t2−t1−t=esin3t+e−ecos3t=e(2−2cos3t+3sin3t)3333⎡2⎤⎡⎤−12s+3s+3−11111311(12)f()t=&⎢3⎥=&⎢⋅−+2−6⋅3⎥⎣()s+1(s+3)⎦⎣4s+14s+32()s+3()s+3⎦1−1⎡1⎤1−1⎡1⎤3−1⎡1⎤−1⎡1⎤=&⎢⎥−&⎢⎥+&⎢2⎥−6&⎢3⎥4⎣s+1⎦4⎣s+3⎦2⎣()s+3⎦⎣()s+3⎦-16- 1−t1−3t3−3t32−3t=e−e+te−te4422−2s−2st,0≤t<2−1⎡1+e⎤−1⎡1⎤−1⎡e⎤()()⎧(13)f()t=&⎢2⎥=&⎢2⎥+&⎢2⎥=t+t−2ut−2=⎨()⎣s⎦⎣s⎦⎣s⎦⎩2t−1,t≥2习题四1．求下列卷积。（1）1∗1.（2）t∗tmn)t（3）t*t(m,n为正整数.（4）t∗e（5）sint∗cost.（6）sinkt*sinkt.（7）t*sinht.（8）sinhat*sinhat.（9）u()t−a*f(t).（10）δ(t−a)*f(t).解卷积定义:tf()t*f()t=∫f(τ)f(t−τ)dτ12120t（1）1*1=∫1⋅1dτ=t0ttt2131313（2）t*t=∫∫τ()t−τdτ=tτdτ−∫τdτ=t−t=t000236nιt⎛⎞mnmnmkkn−kk（3）t*t=τ()t−τdτ=τ⎜(−1)Ctτ⎟dτ∫∫00⎜∑n⎟⎝k=0⎠nn∑()kkn−k∫tm+k∑()kk1m+n+1=−1Ctτdτ=−1Ctnnk==00k0m+k+1n()kmn!!m+n+1−1kn!m+n+1mn++1=tC=t=t∑n()()()k=0m+k+1m+1m+2...m+1+n()mn++1!tttttt−τt−τt⎡−τ−τ⎤t（4）t*e=∫∫τedτ=eτedτ=e⎢⎣−τe|+∫edτ⎥⎦=e−t−10000tt11t（5）sint∗cost=∫∫sinτcos()t−τdτ=sintdτ+∫sin()2τ−tdτ0022011t1=tsint−cos()2τ−t|=tsint24τ=02t1tt1（6）sinkt*sinkt=∫sinkτ⋅sink()t−τdτ=∫∫cos()2kτ−ktdτ−cosktdτ0200211=sinkt−tcoskt2k2ttt−τ−−(tτ)t−tee−ett−τeτ（7）tt*sinh=−∫∫τsinh()tττd=τdτ=∫∫τedτ−τedτ0022002tte⎡−τt⎤e⎡τt⎤=−e()τ+1|−e()τ−1|=sinhtt−2⎢⎣0⎥⎦2⎢⎣0⎥⎦tteaτ−e−aτea(t−τ)(−e−at−τ)（8）sinhat∗=sinhat∫sinhaτsinha()t−ττd=∫⋅dτ0022-17- 1tttt⎡at−at2aτat−2aτ−at⎤=⎢⎣e∫0dτ−e∫0edτ−e∫0edτ+e∫0dτ⎥⎦411=tacosht−sinhat22at（9）u()t−a*f(t)=∫u(τ−a)f(t−τ)dτ0当t