反应堆物理分析 第一版 (谢仲生 著) 原子能出版社 课后答案 89页

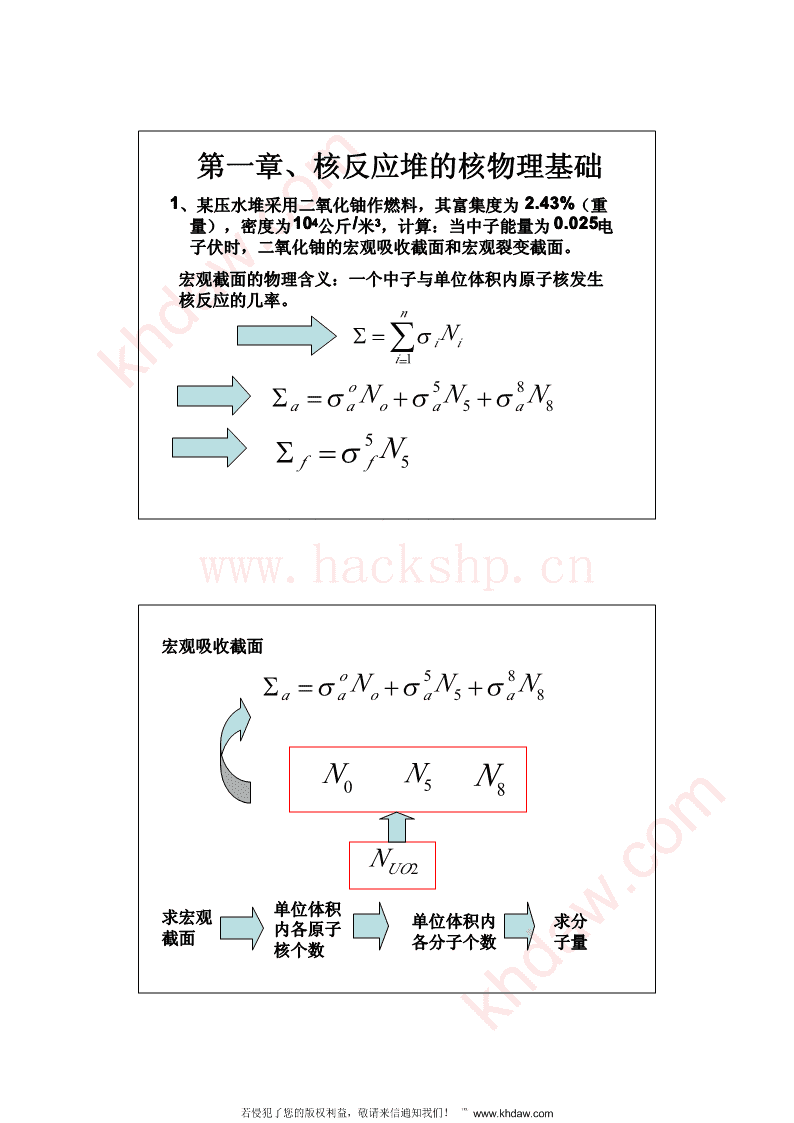
'课后答案网您最真诚的朋友www.hackshp.cn网团队竭诚为学生服务，免费提供各门课后答案，不用积分，甚至不用注册，旨在为广大学生提供自主学习的平台！课后答案网：www.hackshp.cn视频教程网：www.efanjy.comPPT课件网：www.ppthouse.com课后答案网www.hackshp.cn 第一章、核反应堆的核物理基础1、某压水堆采用二氧化铀作燃料，其富集度为2.43%2.42.43%3%（重量），密度为10104公斤/米3，计算：当中子能量为0.0250.00.02525电子伏时，二氧化铀的宏观吸收截面和宏观裂变截面。宏观截面的物理含义：一个中子与单位体积内原子核发生核反应的几率。nΣ=∑σiNikhdaw.comi=1o58Σ=σN+σN+σNaaoa5a85Σ=σN课后答案网ff5www.hackshp.cn宏观吸收截面o58Σ=σN+σN+σNaaoa5a8N0N5N8NUO2单位体积求宏观单位体积内求分内各原子截面各分子个数子量核个数khdaw.com若侵犯了您的版权利益，敬请来信通知我们！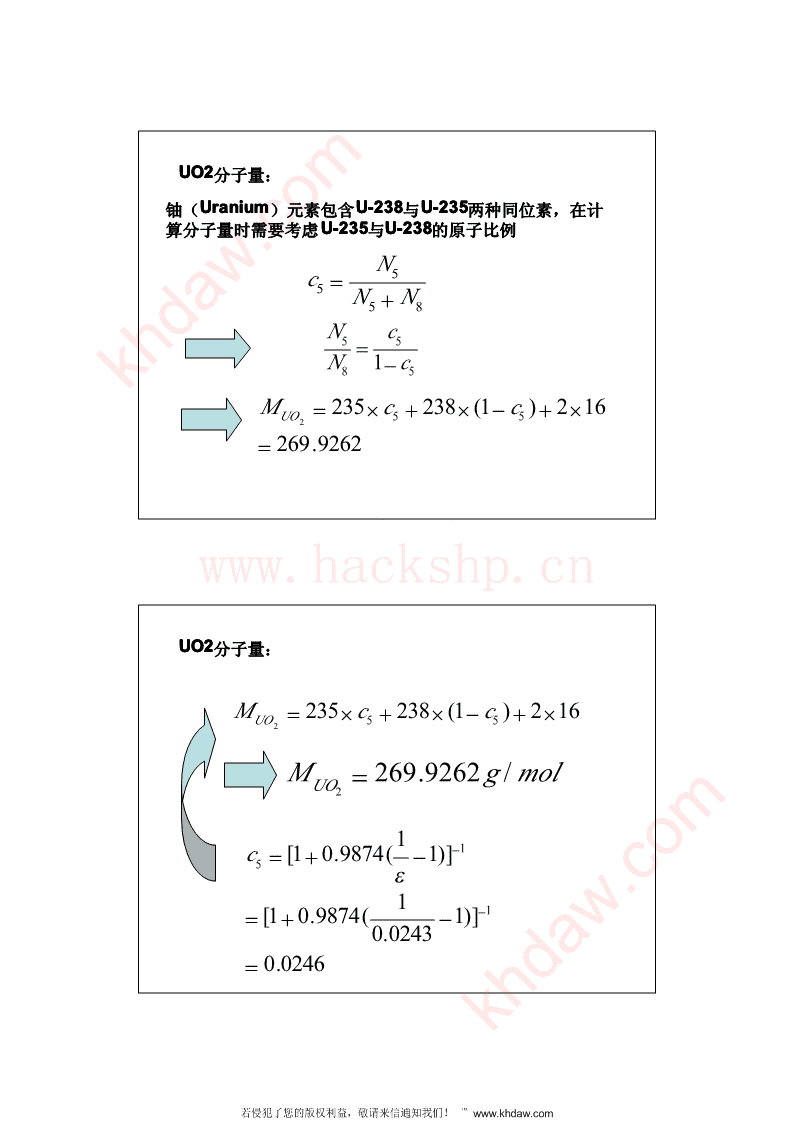℡www.khdaw.com UO2分子量：铀（UraniumUraUraniumnium）元素包含U-238U-2U-23838与U-235U-2U-23535两种同位素，在计算分子量时需要考虑U-235U-2U-23535与U-238U-2U-23838的原子比例N5c=5N+N58Nc5=5N1−ckhdaw.com85M=235×c+238×1(−c)+2×16UO552=269.9262课后答案网www.hackshp.cnUO2分子量：M=235×c+238×1(−c)+2×16UO552M=269.9262g/molUO21−1c=1[+.09874(−1)]5ε1−1=1[+.09874(−1)].00243=.00246khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 单位体积内UO2UUO2O2分子数目ρ41000UO21000×1023N=N=×.602×10UO2AM269.9262UO228=.223024×10khdaw.comUO2宏观吸收截面Σ=cNσ+1(−c)Nσ+2Nσa5UO25a5UO28aUO2Oa−1=43.23m课后答案网www.hackshp.cn与求宏观吸收截面类似的，有UO2宏观裂变截面Σ=cNσf5UO2f28−28=.00246×.223024×10×5835.×10−1=32.01m对于0.025eV0.00.025eV25eV的中子，UO2UUO2O2的宏观裂变截面只与U-235U-2U-23535核有关，而U-238U-2U-23838核属于阈裂变核素，在中子能量达到1.1MeV1.11.1MeVMeV以上时才有可能发生裂变。如果本题中的中子能量在1.1MeV1.11.1MeVMeV以上，求宏观裂变截面就必须考虑U-238U-2U-23838了。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com U-238裂变截面khdaw.com课后答案网www.hackshp.cn2、某反应堆堆芯由铀-235-23-2355、水和铝组成，各元素所占的体积比分别为0.0020.00.00202，0.6000.60.60000和0.3980.30.39898，计算堆芯的总吸收截面Σa（0.0250.00.02525电子伏）与前一题类似地，Σ=Σ+Σ+Σaa5aH2OaAl=σN+σN+σNa55aHOHOaAlAl226.0600×106ρ.0002×10ρ5H2O=N[σ+σAa5aH2O23518.0166.0398×10ρ+σAl]aAl26.98−1=5.8mkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 3、求热中子（0.0250.00.02525电子伏）在轻水、重水、和镉中运动时，被吸收前平均遭受的散射碰撞次数。热中子在介质中的运动散射吸收khdaw.com从产生点到吸收点穿过的平均路程吸收前的碰撞次数=每两次散射穿过的平均路程课后答案网www.hackshp.cnλΣNσσasssn====λΣNσσsaaa103n==156H2O.066136.n==13600D2O.00017−3n==.286×10Cd2450khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 4、试比较：将2.0MeV2.02.0MeVMeV电子伏的中子束减弱到1/101/11/100所需的铝、钠和铅的厚度。IIkhdaw.com0−Σtd窄束衰减规律：I=Ie0课后答案网www.hackshp.cn−Σd窄束衰减规律：I=Ie0I1=I100ln10d=Σt在10MeV10M10MeVeV以内，铝、钠、铅的吸收截面都满足1/V11/V/V定律.00253Σ=Σ.0(0253)aaEkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 与吸收截面不同的是，在10MeV10M10MeVeV以内，散射截面基本不变Σ≈Σ.0(0253)ss.00253Σ=Σ.0(0253)aaEΣtΣ≈Σ.0(0253)khdaw.comssln10d=Σ课后答案网twww.hackshp.cn分别求得：d=.0274mAld=.0226mNad=.00634mPbkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 如果不考虑散射导致的束流损失，只考虑吸收损失ln10d=Σa4d=.136×10mAl4d=.1575×10mkhdaw.comNa4d=.3412×10mPb这样的结果显然是低估了散射使得束流偏移而导致的束流损失，同时也说明窄射束衰减中散射效应对束流损失的较大贡献课后答案网www.hackshp.cn8、某反应堆在额定功率500550000兆瓦下运行了3131天后停堆，设每次裂变产生的裂变产物的放射性活度为1.081.01.088×1010-16--1616t-1.2-1.-1.22居里。此处t为裂变后的时间，单位为天，试估算停堆2424小时堆内裂变产物的居里数。首先，裂变率：6E=500×10×24×3600JdayEdayn=day6−19200×10×6.1×106500×10×24×3600=6−19200×10×6.1×1024=.135×10khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com t时间时间khdaw.comt0t0+dtt0+tt0～t0+dtt0+t0+dtdt的裂变对t时间后的放射性贡献为：24−16−1.2dA=.135×10×.108×10tdt课后答案网www.hackshp.cn第0天第3131天第3232天3224−16−2.1A=∫.135×10×.108×10tdt18=.362×10Cikhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 12、设核燃料中铀-235-23-2355的浓缩度为3.2%3.23.2%%（重量），试求铀-235-23-2355与铀-238-23-2388的核子数之比。1−1c=1[+.09874(−1)]5ε1−1=1[+.09874(−1)].0032khdaw.com=.00324nc.003245=5==.00335n1−c1−.0032485课后答案网www.hackshp.cn13、为了使铀的η=1.=1.77，试求铀中铀-235-23-2355的富集度为多少（设中子能量为0.0253eV0.00.0253eV253eV）。Σnσf55f5η=5.2=5.2Σ+Σnσ+nσa5a85a58a8nησ7.1×7.25a8===.001524n5.2σ−ησ5.2×5835.−7.1×6809.8f5a5n5n5n81−1c===1[+0.9874(−1)]5n5+n8n5+1εn8代入（n5/n/n8=0.01524)=0.=0.01524)01524)得ε≈5.1%khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 16、某压水堆的电功率为990MW990990MWMW，设电站的效率为32%332%2%，运行了三个月后停堆。试计算停堆后1分钟、1小时、1010小时、1天、1010天、1月后的衰变热。同样计算运行一年后停堆的情况。热功率：6Pe990×109P==≈1.3×10Wthkhdaw.comη.032衰变热功率：11−2.0−2.0P=4.1×10P[τ−(τ+T)](MeV/s)dth−2−2.0−2.0≈6.6×10Pτ[−(τ+T)](W)th8−2.0−2.0课后答案网≈2.1×10[τ−(τ+T)](W)www.hackshp.cn分别代入：1)T1)T11)T)T=3months=7.78=3m=3months=7.78onths=7.78×10106sss1τ=1minutes=60s=1m=1minutes=60sinutes=60s；12)T2)T22)T)T=3months=7.78=3m=3months=7.78onths=7.78×10106s2τ=1hour=3600s=1h=1hour=3600sour=3600s；23)T3)T33)T)T=3months=7.78=3m=3months=7.78onths=7.78×10106s3τ=10hours=36000s=10=10hours=36000shours=36000s34)T4)T4)T=3months=7.78=3m=3months=7.78onths=7.78×10106s4τ=1day=8.64=1d=1day=8.64ay=8.64×10104s4khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 5)T=3months=7.78=3m=3months=7.78onths=7.78×10106s5τ=10days=8.64=10=10days=8.64days=8.64×10105s56)T6)T6)T=3months=7.78=3m=3months=7.78onths=7.78×10106s6τ=1months=2.6=1m=1months=2.6onths=2.6×10106s6得：P=4.7=4.=4.77×10107W=47MWW=4W=47MW7MWd1d1P=3.2=3.=3.22×10107W=32MWW=3W=32MW2MWd2d2P=1.7=1.=1.77×10107W=17MWW=1W=17MW7MWkhdaw.comd3d3P=1.3=1.=1.33×10107W=13MWW=1W=13MW3MWd4d4P=0.5=0.=0.55×10107W=5MWW=5W=5MWMWd5d5P=0.03=0.=0.0303×10107W=0.3MWW=0W=0.3MW.3MWd6d6课后答案网www.hackshp.cn衰变热功率随时间的关系khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 核反应堆物理分析第二章习题11、有两束方向相反的平行热中子束射到、有两束方向相反的平行热中子束射到、有两束方向相反的平行热中子束射到U-235U-235U-235的薄片上，设其上某点自左的薄片上，设其上某点自左面入射的中子强度为面入射的中子强度为10101616中子中子///米米2秒。自右面入射的中子束强度为秒。自右面入射的中子束强度为222×××10101616中子中子///米米2秒。计算：秒。计算：（（（aaa）该点的中子通量密度；（）该点的中子通量密度；（）该点的中子通量密度；（bbb）该点的中子流密度。）该点的中子流密度。（（ccc）设）设）设ΣΣa=19.2=19.2×××10102米-1-1，求该点的吸收率。解：（a）中子通量密度为各方向中子束流强度值的总和∴Φ=10==101016+2++2+2×101016=3==3=3×101016中子/米2秒（b）中子流强度为各方向中子束流强度的代数和（即中khdaw.com子净流量），取向右为正方向∴J=10J=1J=10016-2--2-2×101016=-=-1=-1010016中子/米2秒（c）吸收反应率Ra=Φ×Φ×ΣΣ=3=3×××10101616××19.219.219.2×××10102=5.76=5.76×××10101919中子中子///米米3秒a课后答案网www.hackshp.cn55、在某球形裸堆（、在某球形裸堆（、在某球形裸堆（R=0.5R=0R=0.5R=0.5米）内中子通量密度分布为.5米）内中子通量密度分布为175×10πr2φ(r)=sin()中子/米⋅秒rR试求试求：（：（：（aaa）））φφφ（（（000）；（）；（）；（bbb）））JJJ（（（rrr）的表达式，设）的表达式，设D=0.8D=0D=0.8D=0.8×.8××10-210-10-210-2米；（2米；（米；（ccc）每秒从堆表面泄漏的总中子）每秒从堆表面泄漏的总中子数（假设外推距离很小可略去不计）。解：（（aaa）由中子通量密度的物理意义可知，）由中子通量密度的物理意义可知，）由中子通量密度的物理意义可知，φφφ必须满足有必须满足有限、连续的条件175×10πr∴φ(0)=limφ(r)=limsin()r→0r→0rR175×10πr=lim⋅r→0rR17π=5×10⋅R182=.314×10中子/米⋅秒khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com (b)中子流密度J(r)=−Dgradφ∂φ(r)→→=−Dee为径向单位矢量∂r⎡−5×1017πr5×1017πrπ⎤→∴−2J(r)=−0.8×10×⎢2sin()+cos()⎥e⎣rRrRR⎦12π→15⎡⎤=4×10sin(2πr)−cos(2πr)ekhdaw.com⎢r2r⎥⎣⎦课后答案网www.hackshp.cn（c）泄漏中子量=径向中子净流量径向中子净流量×××球体表面积球体表面积→→∴L=∫J⋅ds∵φ∵φ（（r）仅于r有关，是各向同性的2∴L=J(R)×4πR15π2=4×10××4π×0.520.517=1.58×10中子/秒khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 7、圆柱体裸堆内中子通量密度分布为16⎛πz⎞⎛.2405r⎞2φ(r,z)=10cos⎜⎟J0⎜⎟中子/米秒⎝H⎠⎝R⎠其中，H，R为反应堆的高度和半径（假设外推距离可略去不计）。试求：（a）径向和轴向的平均中子通量密度和最大中子通量密度之比；（b）每秒从堆侧表面和两个断面泄漏的中子数；（c）设H=7HH=7=7米，R=3RR=3=3米，反应堆功率为1010兆瓦，兆瓦，σσ5=410=41=4100靶，求反应堆内U-235U-2U-23535的装载量。khdaw.comf课后答案网www.hackshp.cn解：（a）1.1.径向中子通量密度平均值与径向中子通量密度最大值之比：R1∫φ(r,z)drφ(r)R0="（1）φ(r)φ(r)max∂φ(r,z)由：=0（2）∂r求出rr’’rr’’为为φφφ（（r）的极大值点khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 0阶第一类BesselBesBesselsel函数：2∞(−x)k4J0(x)=∑k=0k!Γ(k+)1⎛.2405r⎞由于题中x=⎜⎟⎝R⎠取r的最大值R，并且足够大，这里取x=2xx=2=2代入BesselBesBesselsel函数中，得到khdaw.com0阶BesselBesBesselsel函数的前4项的图像课后答案网www.hackshp.cnBessel函数前4项图像在图中可以看出当k=3kk=3=3时，函数值已经非常的小了，并且后面的项很快收敛到0，因此我们取前4项即可（误差计算此处并不给出）khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 因此246−xxx141664J(x)=++−0Γ)1(Γ)2(2Γ)3(6Γ)4(查表或者自行计算得到查表或者自行计算得到ΓΓΓ（（1，2，3，4）的值为（1，1，2，6）代入上式，并且令x=x=（2.405r/R2.42.405r/R05r/R）得到：2465.78r33.45r193.5rJ(r)=1−+−0246khdaw.com4R64R2304R将J代入代入φφφ（（r,zrr,z,z）并利用（2）求出极大值点rr’’035∂φ(r,z)⎡.578r33.45r1935.r⎤=C⎢−2+4−6⎥=0∂r⎣2R16R384R⎦16⎛πz⎞C=10cos⎜⎟课后答案网⎝H⎠www.hackshp.cn解以上方程得到r"=,0{±R−.109393,±R.524276}舍去无意义根和大于R的根（的根（∵∵0≤r≤R），得："r=0时，时，φφφ取极大值取极大值R1∴（1）∫φ(r,z)drφ(r)R=0"φ(r)φ(r)maxR2461.578r33.45r1935.rC1−+−dr∫246R4R64R2304R0=246.578r33.45r1935.rC[1−+−]2464R64R2304Rkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 代入rr‘‘并计算出积分值得到：φ(r)0.611==0.611φ(r)1max（a）2.2.∂φ(r,z)π⎛πz⎞=−C"sin⎜⎟（3）∂zH⎝H⎠16⎛.2405r⎞C"=10J0⎜⎟⎝R⎠令（3）=0=0，得：khdaw.comZ=Z=nHnHnH，n为整数∵∵从从从φφφ的形式可以看出，原点是建在柱体的中心的的形式可以看出，原点是建在柱体的中心的∴Z只能取0，φφ（（r，z）有极大值课后答案网www.hackshp.cn同理，可得：H2/1⎛πz⎞C"∫cos⎜⎟dzφ(z)H−H2/⎝H⎠=φ(z)C"max2==.0637πkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 该堆芯中子通量密度的分布图：khdaw.com课后答案网www.hackshp.cn轴向中子通量密度分布：khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 径向中子通量密度分布：khdaw.com课后答案网www.hackshp.cn（b）侧面中子流密度：∂φ(r,z)J=−D侧∂r35⎡.578r33.45r1935.r⎤=−DC⎢−2+4−6⎥⎣2R16R384R⎦16⎛πz⎞⎡−5.7833.45193.5⎤=−10Dcos⎜⎟⎢+−⎥⎝H⎠⎣2R16R384R⎦∴∴单位时间从侧面泄漏的中子数为：单位时间从侧面泄漏的中子数为：HL=J2πRdz侧∫侧016=5.2HD×10中子/秒khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 上下面中子流密度：∂φ(r,z)J=z∂z⎛π⎞⎛πz⎞=DC"⎜⎟sin⎜⎟⎝H⎠⎝H⎠分别代入z=-H/2,z=H/2z=-Hz=-H/2,z=H/2/2,z=H/2得：16⎛π⎞⎛2.405r⎞πJz=−H2/=10DJ0⎜⎟⎜⎟sin(−)khdaw.com⎝H⎠⎝R⎠216⎛π⎞⎛2.405r⎞负号表示中=−10DJ0⎜⎟⎜⎟子流密度指⎝H⎠⎝R⎠向z-方向课后答案网www.hackshp.cn16⎛π⎞⎛.2405r⎞Jz=H2/=10DJ0⎜⎟⎜⎟⎝H⎠⎝R⎠∴Lz=L−H2/+LH2/R2π16⎛π⎞⎛2.405r⎞=2∫∫10DJ0⎜⎟⎜⎟rdrdθ00⎝H⎠⎝R⎠D216=8.5R×10中子/秒Hkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com （c）堆内的裂变反应率为5.32π3R=φ(r,z)Nσrdrdθdzf∫∫∫f−5.3003.52π324616⎛πz⎞⎛.578r33.45r1935.r⎞=∫∫∫10cos⎜⎟⎜⎜1−2+4−6⎟⎟Nσfrdrdθdz−3.500⎝7⎠⎝4×364×32304×3⎠5.32π3⎛246⎞16⎛πz⎞5.78r33.45r193.5rm=∫∫∫10cos⎜⎟⎜⎜1−2+4−6⎟⎟NAσfrdrdθdzkhdaw.com−5.300⎝7⎠⎝4×364×32304×3⎠235裂变功率为：6−19Pf=200×10×6.1×10Rf7=10由以上两式可以算出课后答案网U-235U-2U-23535的装载量www.hackshp.cn9.设某石墨介质内，热中子的微观吸收和散射截面分别为σa=4.5=4.=4.55×1010-2-2靶和靶和σσs=4.8=4.=4.88靶。试计算石墨的热中子扩散长度L和吸收自由程和吸收自由程λλa，比较两者数值大小，并说明其差异的原因。解：单位体积内石墨的核数目为：σn=×NaM66.1×1023=×.602×1012283=8×10个/米Σ=nσaa28−2−28=8×10×4.5×10×10=0.36/米khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com Σ=nσ28−28ss=8×10×4.8×10=38.4/米1L=3ΣΣ(1−µ)as01=3×.036×384.×.09444=.016米khdaw.com11λa==Σa0.36解释：堆内热中子的平均行为是先扩散最后被=8.2米吸收，因此扩散长度<吸收自由程L<λ课后答案网awww.hackshp.cn12.如图2-152-12-155所示，在无限介质内有两个源强为S中子/秒的点源，试求p和p点的中子通量密度和中子流强度。12khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 解：无限介质点源中子通量密度为：−r/LSeφ()r=4πDr−2a/LSe1、中子通量密度φ()p=2142πDa−2a/LSe=22πDa−a/Lkhdaw.comSeφ(p)=224πDa−a/LSe=2πDa课后答案网www.hackshp.cn2、中子流强度∂φ(r)J(r)=−D∂r�J(p)=2cos(45)J(p)1s1⎡−r/L⎤∂⎛Se⎞=2⎢−D⎜⎜⎟⎟⎥(r=2a)⎣∂r⎝4πDr⎠⎦−2a/LSe⎛11⎞=⎜+⎟方向为p1->p-->p>p2的方向4πa⎝L2a⎠由于p2p2点处中子流强度大小相等方向相反，因此：J(p)=02khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 核反应堆物理分析第三章1、证明：当中子被自由质子散射时，散射中子和反冲质子的实验室系速度之间的夹角总是9090度khdaw.com课后答案网www.hackshp.cn解：能量守恒：121212mv=mv"+mv"（1）ppppnn222X方向动量守恒mv=mv"cosβ+mv"cosα（2）ppppnny方向动量守恒mv"sinβ=mv"sinα（3）ppnn令m=m=m=1=1pnkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com （2）两边平方，得：22222v=v"cosβ+v"cosα+2v"v"cosαcosβ（4）ppnpn把（1）代入（4），消去v，得：p222222v"+v"=v"cosβ+v"cosα+2v"v"cosαcosβ（5）pnpnpnkhdaw.com将（3）代入（5）消去vv’’n,并整理得：cosαcosβ−sinαsinβ=0即：cos(α+β)=0�由于0<0<（α课后答案网+β）<πα+β=90www.hackshp.cn2、设f(v->vf(vf(v->vf(v->v’->v’’)dv)dv))dv’dv’表示L系中速度v的中子弹性散射后速度在vv’’附近dvdv’’内的几率。假定在C系中散射是各向同性的，求f(v-f(vf(v-->v>v’’’))的表达式，并求一次碰撞后的平均速度。12解：由：E"=mv"2得：dE"=mv"dv"dE"代入：f(E→E)"dE"=−,αE≤E"≤E1(−α)2v"dv"得：f(v→v")dv"=−,αv≤v"≤v21(−α)vαvv=∫v"f(v→v)"dv"v2v2/3=(1−α)1(3−α)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 3、氢和氧在100010010000电子伏到1电子伏能量范围内的散射截面近似为常数，分别为2020靶和3.833.8.8靶。计算水的ξ以及在水中中子从100010010000电子伏慢化到1电子伏所需要的平均碰撞次数。2解：(A−1)⎛A−1⎞ξ=1+ln⎜⎟2A⎝A+1⎠2⎡(A−1)⎛A−1⎞⎤ξH=lim⎢1+ln⎜⎟⎥A→1⎣2A⎝A+1⎠⎦khdaw.com对中括号里面第二项用LL‘‘‘HospitalHosHospitalpital法则处理，得：ξ=1H2ξ==0.12O2A+3课后答案网www.hackshp.cn在水中散射的平均对数能降为：2σξ+σξHHOHξ=HO22σ+σHO2×20×1+3.8×0.12=2×20+3.8=.092平均碰撞次数：EEln0−ln0E"ElnE−lnE"n==ξξH2OH2Oln(1000)−ln(1)=0.92≈7.5次khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 4、（a）证明：一个中子依靠弹性散射从初始能量E慢化0到能量E所需的平均时间t（弹性慢化时间），可表示为E0λt=∫sdE3/2ξ2EE（b）设ξΣ与中子速度无关，试分别计算在轻水中s和石墨中裂变中子（取E0=2=2×10106电子伏）慢化到1电khdaw.com子伏所需要的慢化时间。课后答案网www.hackshp.cn解：（a）能量为E的中子在dtdt系统内发生的平均散射次数为：vdtdtn==2Eλ(E)λ(E)ss在dtdt时间内的对数能降增量为：dtdu=nξ=ξ2Eλ(E)s由：E0u=lnE得：−1du=dEEkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 若散射自由程与能量无关，则：Eλst=−∫dE3/2ξ2EE0E0λs=∫2/3dEξ2Ekhdaw.comE课后答案网www.hackshp.cn（b）利用上题的结论：E0λst=∫2/3dEEξ2E2λ⎛11⎞=s⎜−⎟ξ⎜EE⎟⎝0⎠2⎛11⎞=⎜−⎟ξΣs⎜EE⎟⎝0⎠分别代入轻水和石墨的Σ和ξ，得：s−7t=9.4×10ssHO2−5t=3.2×10ssCkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 6、在讨论中子热化时，认为热中子源项Q(E)Q(EQ(E))是从某给定分界能Ec以上能区的中子，经过弹性散射慢化而来的。设慢化能谱服从φ(E)=(E)(E)==φ0/E/E分布，试求在氢介质内每秒每立方米内有E以上能区，（a）散射到能量E(E∞x−xe+e化简方说明：下表c，r分cth=ex−e−x程别代表芯部和反射层；cthccthth为双曲余切无限厚反射层函数临界方程1−B⋅ctg(BR)=ccLrkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 1求出R−B⋅ctg(BR)=无限厚反射层ccL临界方程r临界时，芯部几何曲率2k∞−1求出B2B=cc2Lc1L=r对于纯U5U5组成的堆芯：3ΣΣkhdaw.com8a8trυσ1f=k∞=3NσΣσ8a8trf211L==c3ΣΣ3NσΣ课后答案网atratrwww.hackshp.cn在以上的过程中，已经求出了堆芯尺寸R43堆芯临界体积：V=πRc3堆芯临界质量：m=ρVc5ckhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 数学知识补习数学知识补习11、、、空间立体角课后答案网空间立体角khdaw.com22、、、TaylorTaylorTaylor级数级数www.hackshp.cn33、、、梯度、散度、旋度梯度、散度、旋度44、、、波动方程（亥姆霍兹方程）波动方程（亥姆霍兹方程）55、、、BesselBesselBessel函数函数khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 11、、、TaylorTayTaylorTaylor级数引入lor级数引入逼近（approximationappapproximationroximation）在某点x0附近用简单函数近似地代替一般函数f（x）课后答案网一阶逼近：利用微分的性质，在khdaw.comx=a,x=ax=a,,用切线代替f（x）www.hackshp.cn当△x=x-ax=xx=x-a-a很小时，f(xf(x))在x=axx=a=a处的一阶TaylorTayTaylorlor展开式f(x)≈f(a)+f"(a)(x−a)（1.111.1.1）khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网khdaw.comwww.hackshp.cny=5x2和y在x=1xx=1=1处一阶逼近函数y=10y=1y=100（x-1xx-1-1）的图像khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 二阶逼近用P（x）=C=C0+C+C1x+Cxx+C+C2X2逼近f（x）初值相等P2（0）=f（0）C0=f（0）课后答案网khdaw.com斜率相同P2’（0）=f’（0）C1=f’（0）www.hackshp.cn凹凸相同P2’’（0）=f’’（0）C2=（1/2）f’’（0）二阶TaylorTayTaylorlor级数展开式2f(x)≈f)0(+f)0("x+f)0(""xkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网khdaw.comwww.hackshp.cny=y=cosxcoscosxx，与它的二阶TaylorTayTaylorlor展开式y=1-(1/2)xy=1y=1-(1/2)x-(1/2)x2的图像khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com n阶多项式逼近：多项式函数：Pn（x）=C=C0+C+C1x+Cxx+C+C2x2+C+C3x3++………+++CCnxn满足：课后答案网khdaw.comPn（0）=f（0）n阶麦克劳林www.hackshp.cnPn’（0）=f’（0）展开式Pn（n）=f（n）（0）(n)f′)0(f′′)0(2f)0(nP(x)=f)0(+x+x+⋯+xn1!2!n!khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网khdaw.comwww.hackshp.cn在0附近两个函数的差别已经很小ex与它的5阶TaylorTayTaylorlor展开式图像khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 22、梯度、散度、旋度引入、梯度、散度、旋度引入2.1梯度课后答案网khdaw.comwww.hackshp.cnkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 偏导数表示(22)z=−x+y沿坐标轴的变化不沿坐标轴方向的变化如何表示？？？课后答案网khdaw.comwww.hackshp.cnkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 多元函数上某点的偏导数构成了沿坐标轴的变化，能否将沿某一给定方向的变化率看成是沿各坐标轴变化率的迭加呢？课后答案网khdaw.comwww.hackshp.cn从图上看是可以的！沿某一方向的方向导数可以这样计算：偏导数确定的导数向量×单位方向向量khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com (22)z=−x+y方向导数的等高线图由等高线图可课后答案网以看出：khdaw.com1、梯度方向是变化率最大梯度方向www.hackshp.cn方向2、任意方向的方向导数可以表示为偏导数的矢量和khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 对于二元函数，方向导数可以如此计算：→∂f⎛∂f∂f⎞l=⎜i,j⎟⋅⎜⎟∂l⎝∂x∂y⎠|l|课后答案网→khdaw.coml⎛∂f∂f⎞当与⎜i,j⎟方向相同时，⎜⎟www.hackshp.cn|l|⎝∂x∂y⎠方向导数有最大值。方向导数去最大值的方向称为：梯度方向∂f∂fgrad⋅f(x,y)=i+j∂x∂ykhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 对于三维变量函数：grad⋅f(x,y,z)=∇f课后答案网khdaw.com梯度是针对标量场而言的，梯度的正方向：高->->低www.hackshp.cnkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 2.2散度散度描述的是从无限小体积元表面流出的净流量。Gauss定理的引出：物理上如何解课后答案网释？？？khdaw.com→→→∫∫J⋅ds=∫∫∫divJdVwww.hackshp.cnkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 交界面上JdsJJdsds大小相等方向相反，抵消！课后答案网khdaw.comwww.hackshp.cnGauss定理！将封闭空间分成无数个小体积元，从面S流出的流量=各个小体积元流出量之和→→→→→→∫∫J⋅ds=∑∫∫J⋅ds=∑divJdV=∫∫∫divJdVsdVkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 2.3旋度Why？？？意Stokes公式的引入：课后答案网义何在？khdaw.com→→→∫J⋅dl=∫∫rotJdswww.hackshp.cnskhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 旋度作为无限小面积内的环流。计算在流速场J（x，y）中，环路中的流量交界处环流相互抵消课后答案网khdaw.comwww.hackshp.cn把以环路为边界的面分成无数个面元Why？？？通过环路的流量=微小面元环流之和→→→→→格林公式（斯托∫J⋅dl=∑∫J⋅dl=∫∫rotJds克斯的二维形式dsskhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 3.波动方程的引入：弦的振动（古典问题）设有一根均匀柔软的细弦，平衡时沿直线拉紧，而且除受不随时间而变的张力作用及弦本身的重力外，不受外力影响。下面研究弦作微小横向振动的规律。课后答案网（*所谓“微小”是指振动的幅度及弦在任意位置处切线的倾角都很小，以致它们的高于一阶次方都可以忽略不计。khdaw.com）www.hackshp.cn如何用数学描述弦振动？？？设弦上具有横坐标为x的点在t时刻的位置为M，位移NM记作u。显然，在振动过程中位移u是变量x与t的函数u（x，t）。首先，选取弦上长度为dsds的质量元，研究该质量元的运动情况，如果每小段质量元运动情况研究清楚了，那么，显然整个弦的运动也就清楚了。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 一维弦振动课后答案网khdaw.comwww.hackshp.cnkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 在弦上任取一段弧MMMM’’，长度为dsds，设ρ是弦的密度，弧MMMM’’两端的张力分别为T，TT’’。考虑无刚性（张力沿切线方向），现考虑MMMM’’的受力情况。课后答案网X轴方向受力：khdaw.comT"cosα"=Tcosα∵水平方向弦www.hackshp.cn（3.133.1.1）并没有发生移将cosccososα和cosccososα’进行TaylorTayTaylorlor展开：动24得：ααcosα=1−+⋅⋅⋅−2!4!24α"α"cosα"=1−+⋅⋅⋅−2!4!khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 得：∵考虑微小振动cosα≈1cosα"≈1α和α‘值很小，∴可以忽略代入（3.133.1.1），得：高阶项。课后答案网T=T"khdaw.com在u方向受力（取y+y+方向为参考方向）：www.hackshp.cn−Tsinα+T"sinα"−ρgds*因为αα‘很小，所以sinssininα==tantanttananα；sinssininα’’===tantanttananα’−Ttanα+T"tanα"−ρgdstanα和tanttananα’∂u(x,t)∂u(x+dx,t)分别是x和−T+T"−ρgds∂x∂xx+dxx+dx+dxx处弦曲线的导数∂u(x,t)∂u(x+dx,t)−T+T−ρgds∂x∂xT=T"khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com u方向，由牛顿第二定律，得：2∂u(x,t)∂u(x+dx,t)∂u(x,t)−T+T−ρgds=ρds∂x∂x∂t2由于2dsds≈dxdx，⎡∂u(x+dx,t)课后答案网∂u(x,t)⎤∂u(x,t)T−−ρgdx=ρdx替换整理khdaw.com⎢⎣∂xwww.hackshp.cn∂x⎥⎦∂t2上式中括号内可以看成是，u的一阶导数的微分，可以用u的二阶导数来表示：22∂u(x,t)∂u(xt),Tdx−ρgdx=ρdx22∂x∂t合并整理⎡2⎤2∂u(x,t)∂u(xt),T⎢2−ρg⎥dx=ρdx2⎣∂x⎦∂tkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com ⎡2⎤2∂u(x,t)∂u(xt),T⎢2−ρg⎥dx=ρdx2进一步简化方⎣∂x⎦∂t程，考虑具有理想刚性的弦，弦22∂u(x,t)∂u(x,t)上的力变化远远Tdx=ρdx22∂x课后答案网∂t大于重力影响khdaw.com2T22令a=2∂u(x,t)∂u(x,t)ρawww.hackshp.cn=（1.2）22∂x∂t一维无限长弦波动方程如何求解波动方程（1.211.2.2）？？？khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 3.1一维波动方程的求解思想：观察一维弦振动，各点的振动不光和位置有关，并且对于某一个位置上的点随时间的运动的遵循简谐振动的。因此，考虑时课后答案网-空分离。khdaw.com令：u(x,t)=X(x)Tt)(代入波动方程www.hackshp.cn222∂X(x)∂Tt)(aTt)(=X(x)22∂x∂t222adX(x)1dTt)(变量分离=22X(x)dxTt)(dt*一般地，要使上式成立，等式左右必须均等于一个常数，设为λ。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 分离出时间方程和空间方程22adX(x)2=λ（3.333.3.3）X(x)dx21dT课后答案网t)(（3.433.4.4）=λkhdaw.comTt)(dt22λ令k=2www.hackshp.cna首先求解波动方程的空间部分（3.333.3.3）2dX(x)2−kX(x)=0（3.433.4.4）2dx亥姆霍兹方程*通常（3.433.4.4）成为亥姆霍兹方程，但是又因为它是波动方程的空间部分，所以也称作波动方程。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 工作小结：物理模型变量分离古典弦振动偏微分方程常微分方程课后答案网（波动方程）khdaw.com如何求解（3.333.3.3）www.hackshp.cn和（3.433.4.4）这两个方程剩下的工作：khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 2Why???dX(x)22−kX(x)=0（3.433.4.4）dx就目前的知识而言，可以猜想到（3.433.4.4）的解具有指数或者正弦余弦函数的性质。两个特解：课后答案网由于三角函数可以通过欧拉公式khdaw.com−kxX=e1与指数函数联www.hackshp.cnkx系，因此，只考X=e2虑解具有指数函数形式是合适X1，X2X2称为（3.433.4.4）的！的基础解系，由线性叠加可知，普遍解−kxkxX1X1，X2X2的线性组X(x)=Ae+Be（3.533.5.5）合应当也满足方程（3.433.4.4）khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 考察普遍解−kxkx（3.533.5.5）的X(x)=Ae+Be（3.533.5.5）最基本约束，振动应−kxX(x)=Ae（3.633.6.6）该在无限远课后答案网处有限khdaw.com非增殖介质中子扩散方程：www.hackshp.cn2φ∇φ−=0（3.733.7.7）2L显然，（3.733.7.7）和（3.433.4.4）具有同样的形式因此非增殖介质中子扩散方程是一个典型的亥姆霍兹方程（波动方程）khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 考虑最简单情况（一维平板面源）课后答案网khdaw.comwww.hackshp.cn2()()dφxφx扩散方程：−=,0x≠0（3.833.8.8）22dxLkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 扩散方程与亥姆霍兹方程（波动方程）形式相同，故它们具有相同的解课后答案网（3.933.9.9）khdaw.comwww.hackshp.cn由一维的亥姆霍兹方程的通解（3.533.5.5）和约束条件得到的具有物理意义的解（3.633.6.6）也是同样满足反应堆中子扩散理论的！！！所以，从物理的意义和数学的解上都可以得知，无限平板源扩散的中子通量密度应该遵循指数衰减规律。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 回顾：前面我们只求解了一维波动方程的空间部分（亥姆霍兹方程），但是我们说解完了空间部分X（x）就足够了，因为在反应堆物理分析中，我们所求的稳态中子扩散方程是跟时间无关的。课后答案网反应堆在给定功率条件下，运khdaw.com行足够长的时间，若没有扰为什么认为中子www.hackshp.cn动，那么各点的中子通量密度通量密度跟时间应该是确定的，即平衡的。对无关？？？于反射层这样的非增殖介质，用稳态非增殖扩散方程描述是合适的。如果要用稳态非增殖扩散方程描述净堆启动过程，显然是不合适的，对于未达平衡的状态除了空间函数外还要加上时间函数T（t）来描述反应堆的动力学特性。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 另外一种情况：无限大非增殖介质内点源的情况课后答案网khdaw.comwww.hackshp.cn球坐标下，扩散方程（1.711.7.7）演变为：2()()()dφr2dφrφr2+−2=(,0r>)0（3.103.13.100）drrdrLkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 2()()()dφr2dφrφr2+−2=(,0r>)0（3.103.13.100）drrdrLu=rφ2duu课后答案网2−2（3.113.13.111）波动方程drLkhdaw.comwww.hackshp.cn（3.113.13.111）式是前面所讲的波动方程，不再详述khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 4.Bessel函数的引入热传导过程冷热不均的物体，热量要从温度高的地方向温度低的地方转移，形象的用热的流动来描述。将整个物理的温度看成温度场u（r课后答案网，t）（标量场）khdaw.com由高等数学的初等场论可知，标量场的梯度函数对应于矢量。结合热传导过程，温度场的梯度函数应该对www.hackshp.cn应于热流矢量。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com *而在反应堆中，中子密度为一个标量场，中子密度n标量的梯度函数应该对应于中子流密度J，但是对于单速中子而言，我们是可以用中子通量密度标量φ==nvnvnv来代替中子密度n标量的。课后答案网khdaw.comwww.hackshp.cn当然，用φ来替代n是考虑到物理的意义和计算的方便，你也完全可以不进行替代khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 回到热传导问题，单位时间某体积内的温度变化：∂u(r,t)（4.1）∂t是否应该等于从该体积内向外流出的净热量呢？？？课后答案网khdaw.comwww.hackshp.cndefinitelytrue!!!并且从场论初步我们知道从封闭曲面流出的净热流=热流场散度×封闭曲面所围的体积（GaussGauGaussss定理）khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com ∫Jds（4.244.2.2）∫Jds=∫divJdV=divJ（4.344.3.3）课后答案网dVA为表征热而，热流矢量khdaw.comJ=A⋅gradu（4.444.4.4）传导性质www.hackshp.cn的参数单位时间穿出无限2A⋅div⋅gradu=A⋅∇u小面s的净热流为：khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 由温度随时间的变化与单位时间穿出面s的净热流相等的关系，我们建立热传导方程∂u(x,t)2=A∇u(x,t)（4.544.5.5）2∂t令A=a课后答案网∂u(x,t)22三维热传khdaw.com=a∇u(x,t)（4.644.6.6）导方程www.hackshp.cn∂t*联想在一维弦振动求解时的变量分离：u(x,t)=T(t)X(r)（4.744.7.7）dT(t)22（2.622.6.6）X(r)=aTt)(∇X(r)dt变量21dTt)(a2分离=∇X(r)（4.844.8.8）T(t)dtX(r)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 一般地，要使（2.822.8.8）两边相等，这两边必须都等于一个不含变量的常数λ1dTt)(=λ课后答案网T(t)dt（4.944.9.9）khdaw.com2a2∇X(r)=λ（4.104.14.100）www.hackshp.cnX(r)*中子扩散理论研究是稳态后的中子通量密度分布，鉴于这样的考虑，我们还是只关心方程的空间部分（4.104.14.100）khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 现在考虑无限薄圆片的热传导方程：在圆柱体反应堆的径向中子通量密度分布中，出现了BesselBesBesselsel函数。WhyWWhy课后答案网hy？？？khdaw.comwww.hackshp.cn先对方程（4.104.14.100）λ进行化简k=2a2∇X(r)−kX(r)=0（4.114.14.111）又是我们熟悉的亥姆霍兹方程khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com *为了能在圆中更简单的求解方程，进行坐标变换22∂X(ρ,θ)1∂X(ρ,θ)1∂X(ρ,θ)++−kX(ρ,θ)=0（4.124.14.122）222ρ∂ρ∂ρ课后答案网ρ∂θkhdaw.comwww.hackshp.cn要对（2.122.12.122）求解，必须再次进行变量分离这又是一个偏ItIt’’’ssoboring!!!ssssoboring!!!oboring!!!微分方程！！！khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 22∂X(ρ,θ)1∂X(ρ,θ)1∂X(ρ,θ)++−kX(ρ,θ)=0（4.124.14.122）222ρ∂ρ∂ρρ∂θ变量分离又是一个课后答案网亥姆霍兹khdaw.com方程2dΘ(θ)+µΘ(θ)=0（4.134.14.133）www.hackshp.cn2dθ22dP(ρ)dP(ρ)2ρ+ρ+(kρ−µ)P(ρ)=0（4.144.14.144）2dρdρ前面已经求−µθΘ(θ)=Ce（4.154.14.155）出亥姆霍兹方程的解：khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com −µθΘ(θ)=Ce（4.154.14.155）由圆的对称−µθ−µ(θ+2nπ)性，温度分布课后答案网e=ekhdaw.com应该具有周期−µθ−2nπµ性！！！=ewww.hackshp.cn比较等µ=1,022,23,2...n2...（4.164.14.166）式两端代入（4.144.14.144）2ρ2dP(ρ)+ρdP(ρ)+(kρ2−n2)P(ρ)=0（4.174.14.177）2dρdρn阶BesselBesBesselsel方程khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 思考：对于圆柱体反应堆，求解中子通量密度分布时采用柱坐标亥姆霍兹课后答案网方程21∇φ−φ=0khdaw.com变量L2分离www.hackshp.cnφ(ρ,θ,z)=P(ρ)Θ(θ)H(z)*与前面引入的热传导方程的空间部分相比，中子通量密度函数的径向-角度分布应该是和热传导方程具有同样的形式！！！P(ρ)Θ(θ)是满足热传导方程的空间方程（4.124.14.122）的khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 而径向函数部分P（ρ）又满足BesselBesBesselsel方程（4.174.14.177）在圆柱形堆内，中子通量密度一定含有课后答案网BesselBesBesselsel函数khdaw.com的乘积项参看课本www.hackshp.cnp90-7p90p90-7-7中子通量密度的表达式khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com *热传导方程与扩散方程的类比时空空间变量变量分离分离温度的径向分无限薄圆片温度的空布满足热传导方程间分布BesselBesBesselsel方程空间课后答案网空间khdaw.com变量变量圆柱堆稳分离φ的径向分离φ的径向分布态单速中www.hackshp.cn-角分布满足BesselBesBesselsel子扩散方满足热传方程程满足波导方程空动方程间部分Bessel函数数理方程形式的类似起源于热传导出现在圆柱体反应堆的φ中方程的求解khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com n阶BesselBesBesselsel方程：如何求解？？？2ρ2dP(ρ)+ρdP(ρ)+(kρ2−n2)P(ρ)=0（4.174.14.177）2dρ课后答案网dρkhdaw.com这也是解微分方程的www.hackshp.cn一种通常考虑*思想：当微分方程很复杂时，我们不可能通过观察或者猜想求得其特解。但是，一个连续函数可以展开为级数形式，并且选定了级数的形式后，展开式一定！！！khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 以上热传导方程的解法与一般BesselBesBesselsel方程一样考虑一般BesselBesBessel课后答案网sel方程2khdaw.com2dydy22x+x+(x−n)y=02www.hackshp.cndsdx解方程的详细过程此处不再赘述，有兴趣的请参看《数学物理方程与特殊函数》p-103p-1p-10303页，5.255.2.2节。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com Bessel方程的解称为BesselBesBesselsel函数第一类BesselBesBesselsel函数Jn(x(x))Bessel函数课后答案网第二类BesselBesBesselsel函数（NeumanNeuNeumanman函数）Yn(x(x))khdaw.comwww.hackshp.cn*具体的函数形式请参看《数理方程与特殊函数》附录，或者数学手册，BesselBesBesselsel函数具体表达式中牵涉到的Γ函数同样。常用数学软件：Mathematica，MATLAB，Maple…参看的书：《大学数学手册》、《剑桥物理公式手册》、《数理方程与特殊函数》…khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com MayYouHaveaWonderfulExperienceinNuclear-reactorPhysicalAnalysisNucNuclear-reactorPhysicalAnalysisNuclear-reactorPhysicalAnalysisStudy!lear-reactorPhysicalAnalysisStStudy!udy!课后答案网khdaw.comTHANKSAGAIN!www.hackshp.cnkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com'