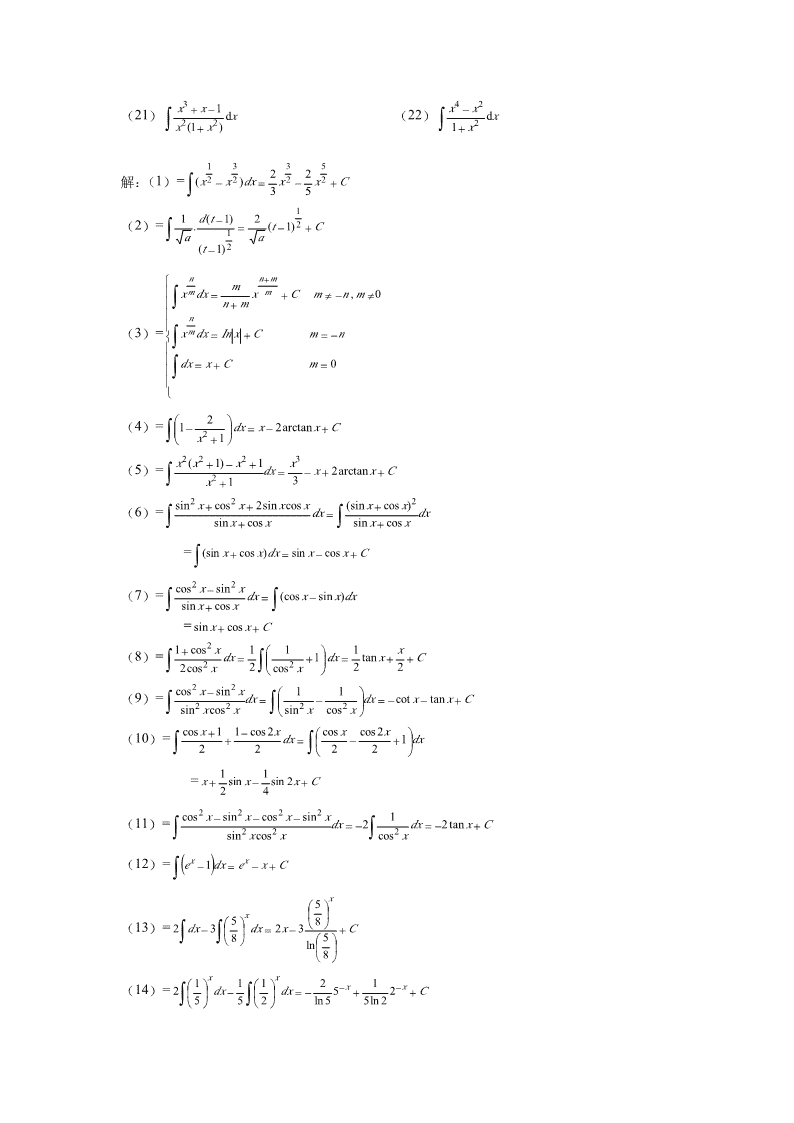《微积分》课后习题答案五.pdf 19页

'习题五（A）1．求函数f(x)，使f′(x)=(x−2)(3−x)，且f(1)=0.解：f′(x)=−x2+5x+61352⇒f(x)=−x+x+6x+C321523f(1)=0⇒−++6+C=0⇒C=326135223f(x)=−x+x+6x+3261x2．一曲线y=f(x)过点（0，2），且其上任意点的斜率为x+3e，求f(x).21x解：f(x)=x+3e212x⇒f(x)=x+3e+C4f(0)=2⇒3+C=2⇒C=−112x⇒f(x)=x+3e−1423．已知f(x)的一个原函数为ex，求∫f′(x)dx.22解：f(x)=(ex)′=2xexx2∫f′(x)dx=f(x)+C=2xe+Cdx24．一质点作直线运动，如果已知其速度为=3t−sint，初始位移为s0=2，求s和t的函dt数关系.解：S(t)=3t2−sint⇒S(t)=t3+cost+CS(0)=2⇒1+C=2⇒C=1⇒S(t)=t3+cost+1 ′15．设[lnf(x)]=，求f(x).21+x′1解：[lnf(x)]=2⇒lnf(x)=arctanx+C11+x⇒f(x)=earctanx+C1=Cearctanx(C>0)112x6．求函数f(x)，使f′(x)=+−e+5且f(0)=0.1+x1−x211x+512x解：f(x)=+−e⇒f(x)=lnx+1+arcsinx−e+5x+C1+x1−x2211f(0)=0+0−+0+C=0⇒C=2212x1⇒f(x)=lnx+1+arcsinx−e+5x+227．求下列函数的不定积分x−x2dt（1）∫dx（2）∫xa(t−1)x2−1mn（3）xdx（4）dx∫∫x2+1x4+11+sin2x（5）dx（6）dx∫x2+1∫sinx+cosxcos2x1+cos2x（7）∫dx（8）∫dxsinx+cosx1+cos2xcos2x⎛2x2⎞（9）dx（10）⎜cos+sinx⎟dx∫sin2xcos2x∫⎝2⎠cos2x−1e2x−1（11）dx（12）dx∫sin2xcos2x∫ex+12×8x−3×5x2x+1−5x−1（13）dx（14）dx∫8x∫10xex(x−e-x)（15）∫dx（16）∫(ex+2x)(1+3x)dxx⎛1+x1−x⎞(x2−1)1−x2−5x（17）∫⎜+⎟dx（18）dx⎜1−x1+x⎟∫2⎝⎠x1−x21−cos2x1+x（19）dx（20）dx∫4∫1+cos2x−sin2x1−x x3+x−1x4−x2（21）dx（22）dx∫x2(1+x2)∫1+x2133522解：（1）=∫(x2−x2)dx=x2−x2+C3511d(t−1)2（2）=.=(t−1)2+C∫a1a(t−1)2⎧nn+mm⎪∫xmdx=xm+Cm≠−n,m≠0⎪n+m⎪n⎪（3）=⎨∫xmdx=Inx+Cm=−n⎪⎪dx=x+Cm=0⎪∫⎪⎩⎛2⎞（4）=∫⎜⎜1−2⎟⎟dx=x−2arctanx+C⎝x+1⎠x2(x2+1)−x2+1x3（5）=dx=−x+2arctanx+C∫x2+13sin2x+cos2x+2sinxcosx(sinx+cosx)2（6）=∫dx=∫dxsinx+cosxsinx+cosx=∫(sinx+cosx)dx=sinx−cosx+Ccos2x−sin2x（7）=∫dx=∫(cosx−sinx)dxsinx+cosx=sinx+cosx+C1+cos2x111x⎛⎞（8）=∫2dx=∫⎜⎜2+1⎟⎟dx=tanx++C2cosx2⎝cosx⎠22cos2x−sin2x11⎛⎞（9）=∫22dx=∫⎜⎜2−2⎟⎟dx=−cotx−tanx+Csinxcosx⎝sinxcosx⎠cosx+11−cos2x⎛cosxcos2x⎞（10）=∫+dx=∫⎜−+1⎟dx22⎝22⎠11=x+sinx−sin2x+C24cos2x−sin2x−cos2x−sin2x1（11）=dx=−2dx=−2tanx+C∫sin2xcos2x∫cos2x（12）=∫(ex−1)dx=ex−x+Cx⎛5⎞x⎜⎟⎛5⎞⎝8⎠（13）=2∫dx−3∫⎜⎟dx=2x−3+C⎝8⎠⎛5⎞ln⎜⎟⎝8⎠xx⎛1⎞1⎛1⎞2−x1−x（14）=2∫⎜⎟dx−∫⎜⎟dx=−5+2+C⎝5⎠5⎝2⎠ln55ln2 ⎛x1⎞x（15）=∫⎜e−⎟dx=e−lnx+C⎝x⎠2x(3e)x6x（16）=∫[ex+6x+2x+(3e)x]dx=ex++++Cln2l+ln3ln61+x+1−x1（17）=∫dx=2∫dx=2arcsinx+C1−x21−x2⎛x2−15⎞1（18）=∫⎜−⎟dx=x2−lnx−5arcsinx+C⎜x2⎟2⎝1−x⎠1（19）=∫dx=arcsinx+C1−x21−cos2x111x⎛⎞（20）=∫2dx=∫⎜⎜2−1⎟⎟dx=tanx−+C2cosx2⎝cosx⎠22x(x2+1)−11111⎛⎞（21）=∫22dx=∫⎜⎜−2+2⎟⎟dx=lnx+x+arctanx+Cx(1+x)⎝xx1+x⎠x4−1−(x2+1)+22x3⎛2⎞（22）=∫2dx=∫⎜⎜x−2+2⎟⎟dx=−2x+2arctanx+C1+x⎝1+x⎠38．用换元积分法计算下列各题.x−48（1）∫dx（2）∫(3x−2)dxx+2e2xdx（3）dx（4）∫3+e4x∫2⎛π⎞cos⎜2x+⎟⎝3⎠x2dx（5）dx（6）∫3∫x2−2x+54−xdxdx（7）（8）∫ex+e−x∫ex−e−xdxdx（9）（10）∫cos2xtanx−1∫x(1-lnx)xdxe2（11）∫（12）∫dxx1−ln2x9−exsinxcosxx（13）dx（14）dx∫2+sin2x∫21−2xx+arctanxdx（15）dx（16）∫1+x2∫1+ex1arctan2（17）xdx（18）(x−1)ex−2x+4dx∫1+x2∫x5lnx（19）∫dx（20）∫dx31+x3x2+lnx sinxsinx−cosx（21）∫dx（22）∫dx1+sin2x1+sin2xdxlntanx（23）（24）dx∫(sinx+2cosx)2∫sinxcosxdxds（25）（26）∫sin2x+3cos2x∫2x+1+2x−1dxxdx（27）（28）∫1+x+(1+x)3∫x4+2x2+5xx（29）∫x(1+lnx)dx（30）∫dxx+x2−1dxarcsinx（31）（32）dx∫xlnx(ln2x+1)∫x(1−x)dxarctanx（33）∫（34）∫dxxsinxcosxx(1+x)cosx3（35）dx（36）sin2xcosxdx∫1+cos2x∫（37）∫(cosx−sinx)cos2xdx（38）sinxcosxdx∫1+sin4x13（39）dx（40）tanxdx∫sin4x∫31x+2−6⎛6⎞2解：（1）=dx=⎜x+2−⎟d(x+2)=(x+2)2−12(x+2)2+C∫x+2∫⎜x+2⎟3⎝⎠1819（2）=∫(3x−2)d(3x−2)=(3x−2)+C3271d(e2x)1e2x（3）==arctan+C2∫(2x)22333+e⎛π⎞d⎜2x+⎟1⎝3⎠1⎛π⎞（4）=∫=tan⎜2x+⎟+C22⎛π⎞2⎝3⎠cos⎜2x+⎟⎝3⎠1d(x3)1d(4−x3)2（5）=∫=−∫=−4−x3+C34−x334−x33d(x−1)1x−1（6）==arctan+C∫(x−1)2+422d(ex)（7）==arctanex+C∫e2x+1d(ex)1ex−1（8）==ln+C∫e2x−12ex+1 1d(tanx−1)（9）=∫=2(tanx−1)2+Ctanx−1d(1−lnx)（10）=−∫=−ln1−lnx+C1−lnxd(lnx)（11）=∫=arcsinlnx+C1−ln2x⎛x⎞⎜2⎟dex⎜⎟⎜⎝⎟⎠e2（12）=2∫=2arcsin+C23⎛x⎞⎜2⎟9−e⎜⎟⎜⎟⎝⎠sinxd(sinx)1d(2+sin2x)1（13）===ln2+sin2x+C∫2+sin2x2∫2+sin2x21d(1−2x2)1（14）=−∫=−1−2x2+C41−2x2231d(x2+1)12（15）=+arctanxd(arctanx)=ln(1+x2)+(arctanx)2+C2∫x2+1∫23exd(ex)d(ex)d(1+ex)⎛ex⎞（16）=dx==−=ln⎜⎟+C∫ex(1+ex)∫ex(1+ex)∫ex∫1+ex⎜1+ex⎟⎝⎠1⎛1⎞arctand⎜⎟2x⎝x⎠1⎛1⎞1⎛1⎞（17）=−∫=−∫arctand⎜arctan⎟=−⎜arctan⎟+C1+1x⎝x⎠2⎝2⎠x21x2−2x+421x2−2x+4（18）=∫ed(x−2x+4)=e+C221x31t（19）=d(x3)令x3=td(t)3∫333∫31+t1+x⎛21⎞1t+1−11⎜3−3⎟=d(t)=(t+1)d(t)−(t+1)d(t)3∫31+t3⎜⎜∫∫⎟⎟⎝⎠5252=1(t+1)3−1(t+1)3+C=1(x3+1)3−1(x3+1)3+C5252lnxd(lnx)td(t)（20）=∫令ln=t∫2+lnx2+t12+t−2d(t)d(2+t)=∫=∫(2+t)2d(2+t)−2∫2+t2+t313122=(2+t)2−4(2+t)2+C=(2+lnx)2−4(2+lnx)2+C33 d(cosx)cosx（21）=−∫=−arcsin+C2−cos2x2d(sinx+cosx)−1（22）=−=(sinx+cosx)+C∫(sinx+cosx)2d(tanx+2)−1（23）==−(tanx+2)+C∫(tanx+2)2lntanx12（24）=∫d(tanx)=∫lntanxd(lntanx)=(lntanx)+Ctanx2d(tanx)1d(3tanx)1（25）===tan(3tanx)+C∫1+3tan2x3∫1+(3tanx)23⎡33⎤2x+1−2x−1122（26）=∫dx=⎢(2x+1)2−(2x−1)2⎥+C24⎢33⎥⎣⎦⎡33⎤1=⎢(2x+1)2−(2x−1)2⎥+C6⎢⎥⎣⎦d(x+1)2t（27）=令x+1=tdt∫x+1+(x+1)3∫t+t31=2dt=2arctant+C=2arctan1+x+C∫1+t21d(x2+1)1x2+1（28）==arctan+C2∫(x2+1)2+442（29）=∫exlnx(1+lnx)dx=∫ld(exlnx)=exlnx+C=xx+C3（30）=x(x−x2+1)dx=x2dx−1x2+1d(x2+1)=1x3−1(x2+1)2+C∫∫2∫33d(lnx)d(t)（31）=lnx=t∫lnx(ln2+1)∫t(t2+1)1⎛d(t2)d(t2+1)⎞1t2=⎜−⎟=ln+C2∫⎜t2t2+1⎟2t2+1⎝⎠1ln2x1=ln+C=lnlnx−ln(ln2x+1)+C2ln2x+12（32）=arcsinx=t，则dt=2sintcostdt33t442sintcostdt=2tdt=t2+C=(arcsinx)2+C∫sin2tcos2t∫33d(x)d(tanx)（33）=2∫=∫=2lntanx+Csinxcosxtanxarctanx2（34）=2dx=2arctanxdarctanx=(arctanx)+C∫1+(x)2∫d(sinx)12+sinx（35）==ln+C∫2−sin2x222−sinx 3425（36）=∫2sinxcosxcosxdx=−2∫cosxdcosx=−cosx+C5（37）=∫(cosx−sinx)2(cosx+sinx)dx=−∫(cosx−sinx)2d(cosx−sinx)13=−(cosx−sinx)+C31d(sin2x)1（38）==arctansin2x+C2∫1+sin4x21sin2xd(cotx)213（39）=dx=−=−(cotx+1)d(cotx)=−cotx−cotx+C∫sin2x∫sin2x∫3212（40）=∫(secx−1)tanxdx=∫tanxdtanx−∫tanxdx=(tanx)−lncosx+C29．求下列函数的不定积分dx2（1）（2）x1−xdx∫x(1+x7)∫1dx（3）∫dx（4）∫1−2x+3(1+x)1-xdxx+1（5）（6）dx∫x+3x∫xx−26xx（7）dx（8）∫1+edx∫321+1+xx3x+2（9）dx（10）dx∫2∫(1−x2)3x−2x+4x61dx71解：（1）=dx==lnx−ln1+x7+C∫x7(1+x7)7∫x7(1+x7)7（2）令1−x=t，则x=1−t6,dx=−2tdt2642172513=∫(1−t)t(−2t)dt=−2∫(t−2t+t)dt=−2(t+t+t)+C7531−t2（3）令1−2x=t，则x=,dx=−tdt213=∫(−t)dt−∫(1−)dt=−t+3lnt+3+C=−1−2+3ln1−2x+3+Ct+3t+3（4）令1−x=t，则x=1−t2,dx=−2tdt−2tdt12+t12+1−x=dt=2=−2.ln+C=−2.ln+C∫(2−t2).t∫t2−2222−t222−1−x（5）令6x=t，则x=t6,dx=6t5dt 6t5t31=dt=6dt=6(t2−t+1)−dt∫t3+t2∫t+1∫t+11312=6(t−t+t−lnt+1)+C32=2t3−3t2+6t−6lnt+1+C（6）令x−2=t，则x=2+t2,dx=2tdtt2+31t=.2tdt=2(1+)dt=2t+2arctan+C∫t2+2∫t2+22x−2=2x−2+2arctan+C21（7）令(1+x2)3=t，则2xds=3t2dtt2t2−1+11=9∫dt=9∫dt=9(t2−t+lnt+1)+C1+t1+t2211=9(1+x2)3−(1+x2)3+ln(1+x2)3+1+C2x22tdt（8）令1+e=t，则x=ln(t−1),dx=t2−1t211−t11−1+ex=2dt=2(t+ln)+C=2(1+ex+ln)+C∫t2−121+t2x1+1+e（9）令x−1=t，则x=t+1,dx=dt1t+3t3222=∫dt=∫dt+∫dt=(t+3)+3lnt+t+3+Ct3+3t2+3t2+31=(x2−2x+4)2+3lnx−1+x2−2x+4+C（10）令x2=t，则x=t1t1t−1+11⎡11⎤=dt=−dt=−⎢+⎥dt2∫(1−t)32∫(1−t)32∫⎢(t−1)2(t−1)3⎥⎣⎦1⎡111⎤111=−⎢−−⎥+C=++C2⎢t−12(t−1)2⎥2(t−1)4(t−1)2⎣⎦1112x2−1=++C=+C2(x2−1)4(x2−1)24(x2−1)2sinxcosx10．设F(x)=∫dx,G(x)=∫dx求aF(x)+bG(x)；aG(x)−bF(x)；F(x)；asinx+bcosxasinx+bcosxG(x). asinx+bcosx解：aF(x)+bG(x)=∫dx=x+Casinx+bcosxacosx−bsinxd(asinx+bcosx)aG(x)−bF(x)=∫dx=∫dx=lnasinx+bcosx+Casinx+bsinxasinx+bcosx1⇒G(x)=(alnasinx+bcosx+bx)+Ca2−b21F(x)=(−blnasinx+bcosx+ax)+Ca2−b211．用三角代换求下列不定积分.dxdx（1）（2）∫∫2223x1−x(1-x)x2x2−a2（3）∫dx（4）∫dx1−x2xdxx98（5）（6）dx∫223∫101x(1−x)22(1−x)π解：（1）令x=sint，则dx=costdt(t<)2costdt1−x2=dt==−cott+C=−cot(arcsinx)+C=−+C∫sin2tcost∫sin2txπ（2）令x=sint，则dx=costdt(t<)2costdtx=∫dt=∫=tant+C=tan(arcsinx)+C=+Ccos3tcos2t1−x2π（3）令x=sint，则dx=costdt(t<)2sin2tcost1−cos2t11=∫dt=∫sin2tdt=∫dt=t−sin2t+Ccost22411112=arcsinx−sin2(arcsinx)+C=arcsinx−x1−x+C2424π（4）令x=asect，则dx=asectant，(0