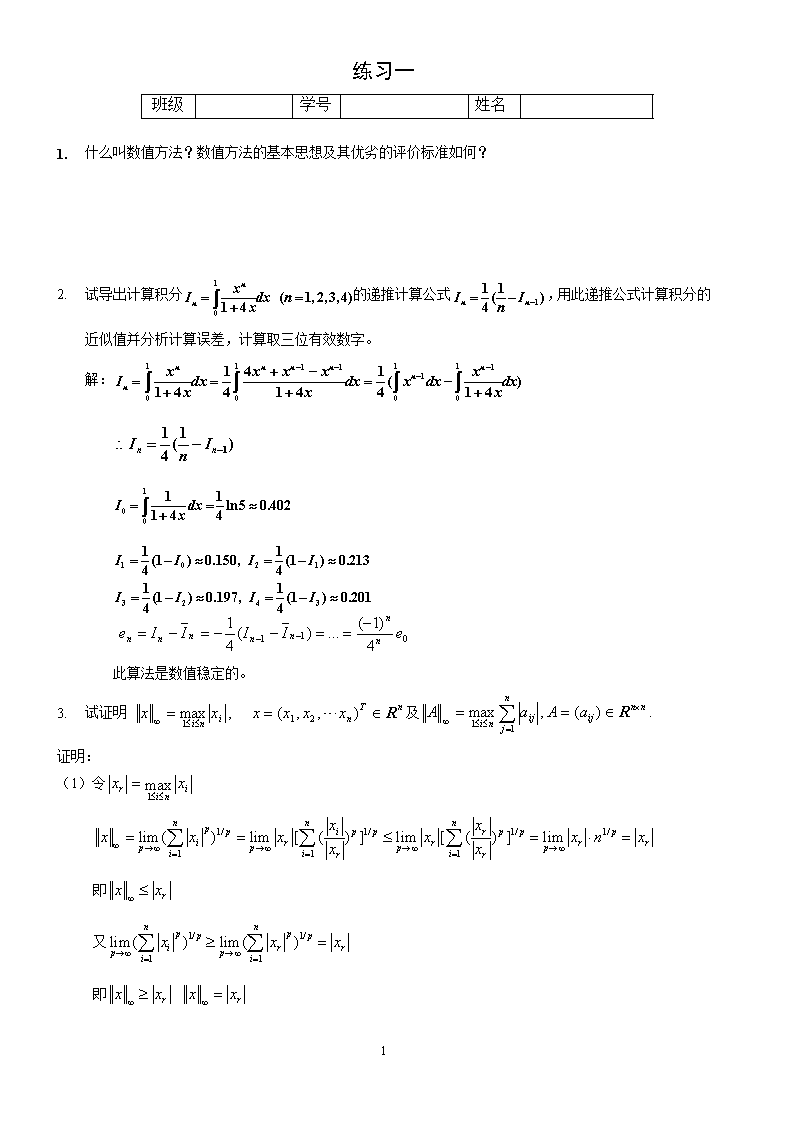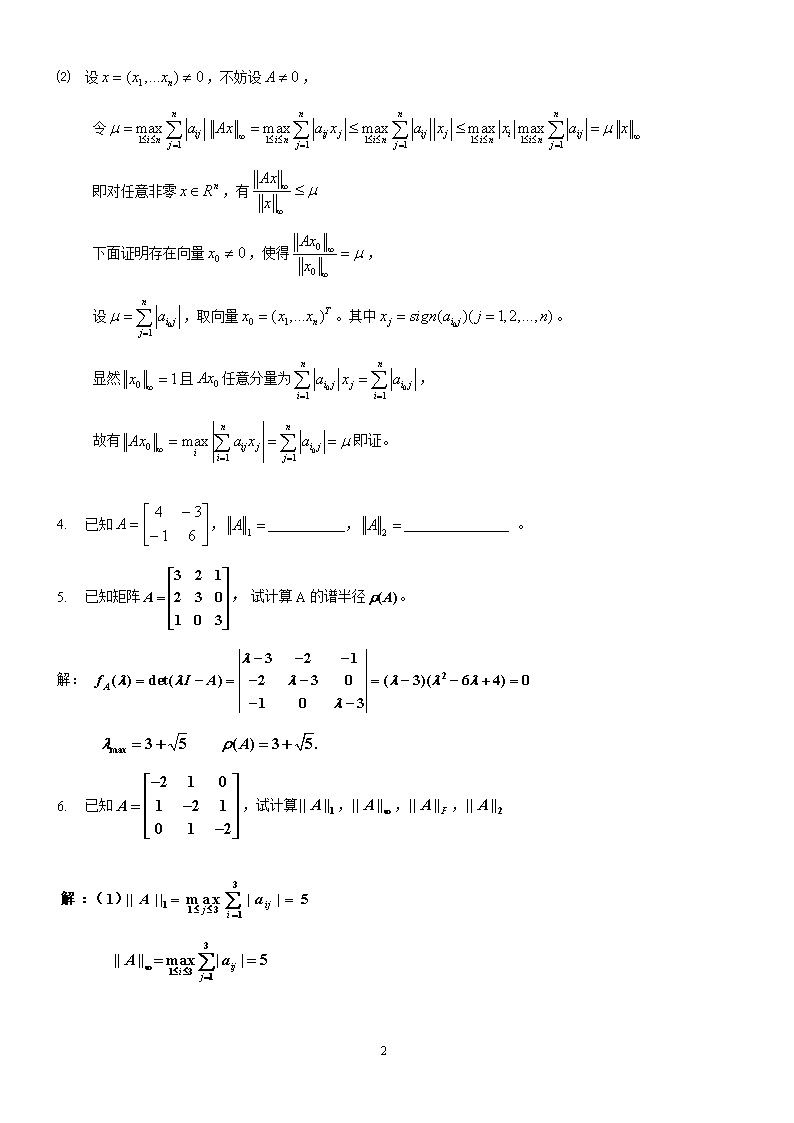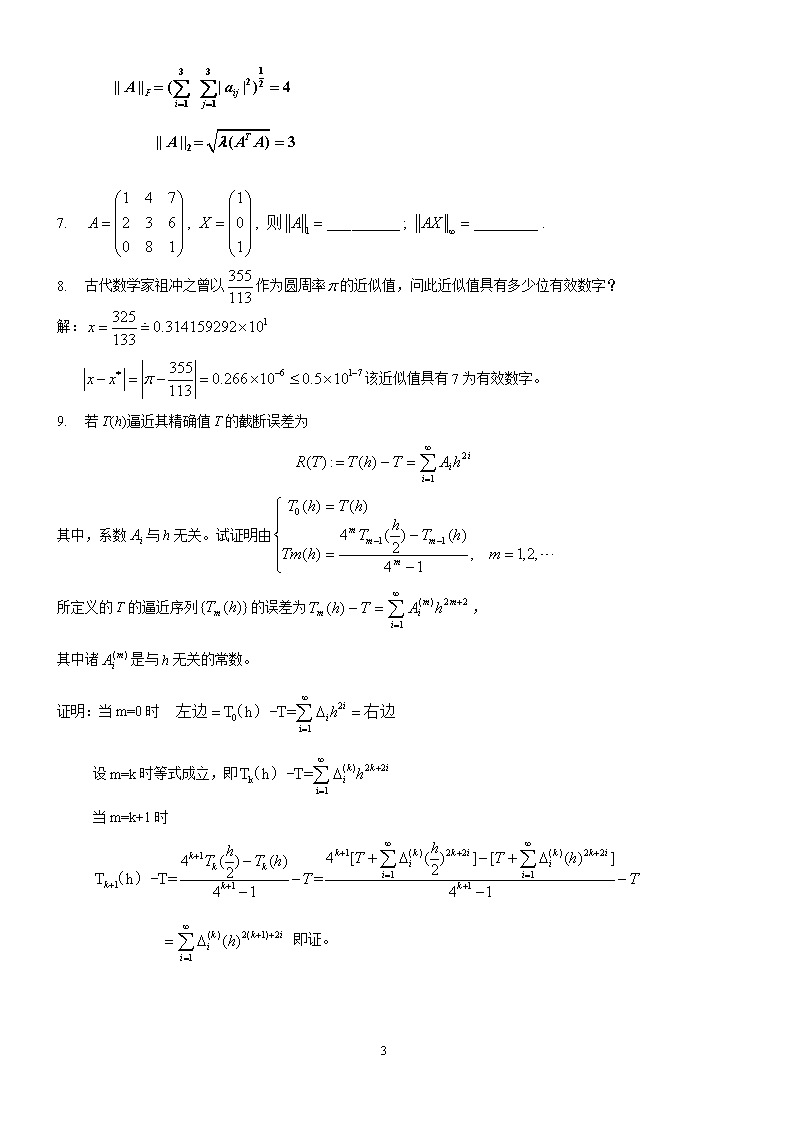计算方法习题集及答案.doc 33页

'练习一班级学号姓名1.什么叫数值方法？数值方法的基本思想及其优劣的评价标准如何？2.试导出计算积分的递推计算公式，用此递推公式计算积分的近似值并分析计算误差，计算取三位有效数字。解：此算法是数值稳定的。3.试证明及证明：（1）令即又即33 ⑵设，不妨设，令即对任意非零，有下面证明存在向量，使得，设，取向量。其中。显然且任意分量为，故有即证。1.已知，___________，_______________。2.已知矩阵，试计算A的谱半径。解：3.已知，试计算，，，33 1.2.古代数学家祖冲之曾以作为圆周率的近似值，问此近似值具有多少位有效数字？解：该近似值具有7为有效数字。3.若T(h)逼近其精确值T的截断误差为其中，系数与h无关。试证明由所定义的T的逼近序列的误差为，其中诸是与h无关的常数。证明：当m=0时设m=k时等式成立，即当m=k+1时即证。33 练习二班级学号姓名1.试构造迭代收敛的公式求解下列方程：（1）;(2)。解：（1）迭代公式，公式收敛k012300.250.250980.25098（2），，局部收敛k0123456789101.51.3221.4211.3671.3971.3801.3901.3841.3871.3861.3862.方程在附近有根，把方程写成三种不同的等价形式：（1）,对应迭代公式;（2），对应迭代公式;（3）,对应迭代公式。判断以上三种迭代公式在的收敛性，选一种收敛公式求出附近的根到4位有效数字。解：（1）局部收敛（2）局部收敛（3）不是局部收敛迭代公式（1）：01234567833 1.51.444441.479291.4569761.471081.462091.467791.44161.466479101112131415161.46501.465931.46531.465721.465481.465631.4655341.465595迭代公式（2）：k01234561.51.4811.4731.4691.4671.4661.4661.已知在[a,b]内有一根，在[a,b]上一阶可微，且，试构造一个局部收敛于的迭代公式。解：方程等价于构造迭代公式令由于在[a,b]上也一阶可微故上述迭代公式是有局部收敛性.2.设在方程根的邻近有连续的一阶导数，且，证明迭代公式具有局部收敛性。证明：在邻近有连续一阶导数，则在附近连续，令则取则时有从而故令，由定理2.1知，迭代公式是有局部收敛性。3.，要使迭代法局部收敛到，则的取值范围是______________。4.用牛顿法求方程在[3,4]中的根的近似值（精确到小数点后两位）。33 解：y次迭代公式k01233.53.643.633.631.试证用牛顿法求方程在[1,3]内的根是线性收敛的。解：令y次迭代公式故从而，时，故，故牛顿迭代公式是线性收敛的2.应用牛顿法于方程,导出求立方根的迭代公式，并讨论其收敛性。解：相应的牛顿迭代公式为迭代函数，，则，33 练习三班级学号姓名1.设有方程组(1)考察用Jacobi法，Gauss-Seidal法解此方程组的收敛性；(2)用Jacobi法及Gauss-Seidal法解方程组，要求当时迭代终止。解：（1）A是强对角占优阵。故用雅克比法及高斯-塞德尔法解此方程均收敛。（2）雅克比法：，，，取初始向量，迭代18次有（i=1,2,3），，高斯-塞德尔法：，，取初始向量，迭代8次有（i=1,2,3），，2.设有方程组,,迭代公式：,.33 求证由上述迭代公式产生的向量序列收敛的充要条件是.证明：迭代公式中的矩阵，，由迭代收敛的充要条件知即证。1.给定方程组，确定的取值范围，使方程组对应的Jacobi迭代收敛。2.用SOR方法解下列方程组（取松驰因子）,要求..解：SOR方法故，迭代初值k00.0000000.00000033 10.6000000-1.32000021.2720000-0.85440030.858240-1.07164841.071341-0.96426850.964293-1.01785961.017857-0.99107170.991071-0.99776881.004464-0.99776890.997768-1.001116101.001116-0.999442110.999442-1.000279121.000279-0.999861130.999861-1.000070141.000070-0.999965150.999965-1.000017161.000017-0.9999911.给定线性方程组AX=b，其中，1）求出使Jacobi迭代法和G-S迭代法均收敛的的取值范围。2）当时，给出这两种迭代法的收敛速度之比。2.用Gauss消去法解方程组33 1.用选列主元高斯消去法求解方程组解：解得2.用追赶法解三角方程组解：高斯迶元33 回代得解为1.用三角分解法求解方程组解：系数矩阵三角分解为：原方程可表为：解得33 解得1.用选主元法去法计算下列行列式的值.解：2.设计算.解：3.设方程组Ax=，其中A=，=33 ①计算，判断方程组是否病态。②用全主元消元法求解，结果如何？③用105除第一个方程所得方程组是否病态？解：①105+1又==（1+105）=〉〉1该方程组是病态②用全主元消元法求解。==〉〉1出现大数吃小数的现象，结果失真。③用105除第一个方程得：A1=，=方程组是良态的。33 练习四班级学号姓名1.给出概率积分的数据表：试用二次插值计算.X0.460.470.480.49f(x)0.48465550.49375420.50274980.5116683解：取插值节点：2.已知y=sinx的函数表X1.51.61.7sinx0.997490.999570.99166试构造出差商表，利用二次Newton插值公式计算sin(1.609)(保留5位小数)，并估计其误差.解：由题意得如下差商表故又33 故：1.设为互异节点(),求证(1)(2)证明：令又所以故原等式左边用二项式展开得：由结论得即证2.若，则，。3.若,求和.解：33 1.设为互异节点，为对应的5次Lagrange插值基函数，则___________________。2.证明两点三次Hermite插值余项是证明：且即为的二阶零点设令易知又由微分中值定理（Rolle定理），使得33 进而有三个零点，有两个零点，有一个零点，即使得得1.设是Lagrange基函数，则。2.求一个次数不超过4次的多项式，使它满足，并写出其余项表达式。3.求一个四次插值多项式，使时，；而时，，并写出插值余项的表达式。4.构造适合下列数据表的三次样条插值函数S(x)X-1013Y-11331428解：已知33 边界条件即从而解得当即时故同理，在及上均有33 1.已知实验数据X01235Y1.11.93.13.94.9试用最小二乘法求经验直线。2.利用最小二乘法求一个形如的经验公式，使它与下列数据拟合：x–2–1012y–0.10.10.40.91.63.用最小二乘法求一个形如的经验公式，使与下列数据相拟合X1925313844Y19.032.349.073.397.8解：依题意故33 正则方程为解得故拟合曲线为33 练习五班级学号姓名1．试确定下面求积公式使其具三次代数精度.解：要公式有3次代数精度，需有解得：故求积公式为2．设f(x)∈C[a,b]，则计算的复化梯形公式是_______阶收敛的，其代数精度为_______________。3．在区间上导出含五个节点的Newton-Cotes公式，并指出其余项及代数精度.解：当时，又故当时，有求积公式（＊）其中由Lagrange差值定理有：33 故余项对（＊）至少有四次代数精度时式（＊）左边=右边=时故（＊）式具有5次代数精度1．分别用复合梯形公式及复合Simpson公式计算,(取步长h=1/6).解：（1）用复合梯形公式故（2）用复合Simpson公式：33 1．用变步长梯形求积公式计算,(精确到).解：由得：33 1．用Romberg算法计算积分,(精确到).解：由公式得：33 又即已经达到预定精度取1．试构造两点Gauss公式,并由此计算积分(精确到).解：二次Lagendre多项式：Gauss点为由公式得令即使得33 1．利用正交多项式构造三点Gauss型求积公式并问：（1）所得求积公式的代数精度是多少？（2）用所得求积公式计算时截断误差是多少？33 练习六班级学号姓名1．试用三种方法导出线性二步方法解：（1）Taylor展开法线性k步公式为得即得且（2）数值积分法用矩形求积公式令（中矩形公式）即得：（3）由隐式欧拉法得①由显示欧拉法得②①代入②得33 1．用Taylor展开法求三步四阶方法类，并确定三步四阶显式方法.解：线性k步公式为，在（6.17）中令即取。即满足上述条件的多步方法即为一类三步四阶显示方法，令可得方法即为2．形如的k阶方法称为Gear方法，试确定一个三步Gear方法，并给出其截断误差主项。解：线性k步公式为由Gear法的定义知，三步Gear法满足33 方法为阶，故有得：取得得三步Gear方法：其中1．试用显式Euler法及改进的Euler法计算初值问题（取步长h=0.2）并比较两者的误差。解：步长,真解显式法：改进法：显然改进的法误差小于法。33 1．给出线性多步法为零稳定的条件，并证明该方法为零稳定时是二阶收敛的.证明：线性多步法的相应多项式多项式的两根为：，。由判断零稳定的充要条件根条件知：此方法的零稳定的条件为由于，，，，得：当方法为零稳定时，从而，故方法是二阶收敛的。2．给出题(6.5)题中时的公式的绝对稳定域.解：6.5中当时，即为方法其相应的差分方程的多项式为令，即方法的绝对稳定域为33 1．指出Heun方法00001/31/3002/302/301/403/4的相容阶，并给出由该方法以步长h计算初值问题(6.45)的步骤.解：法中对方法有类似例将方法应用到得其中上述步骤可按如下步骤完成：将原问题初值代入得出当前步的，然后代入，得出，，再以，作为第2个计算步的初值重复上述步骤可求出，，依次类推即可求出原问题的相继数值序列.经验证方法满足33 由方法阶相容的充要条件知方法具有三阶相容阶。1．试述刚性问题的基本特征，并给出s级Runge-Kutta方法为A-稳定的条件.解：刚性问题的基本特征即对于线性系统有设A的特征值为，满足级单步方法用于实验方程.令由得写成向量形式记则有即由得33 即由稳定性知方法稳定的充要条件是：稳定函数在上解析且，进一步由只可能在边界上去的极值的最大模原理，的边界即为虚轴，得法稳定的充要条件是：稳定函数在上解析，且满足，.1．设有，试构造形如的二阶方法，并推导其局部截断误差首项。2．设有常微分方程初值问题的单步法，证明该方法是无条件稳定的。33'